|
|
||||||||
|
|
||||||||
Volume 9, Number 2, July 2003
Copyright © 2003 Society for Music Theory
Alfred Cramer*The Harmonic Function of the Altered Octave in Early Atonal Music of Schoenberg and Webern: Demonstrations Using Auditory Streaming |
KEYWORDS: Schoenberg, Webern, Saussure, Strindberg, auditory scene analysis, auditory streaming, atonality, expressionism, altered octave, major seventh, minor ninth, masking, fusion
ABSTRACT: I present synthesized sound examples of several atonal expressionist excerpts to illustrate the effect of the altered octave as a sonority. Psychology, linguistics, and literature about 1900 suggest that early atonal expressionist music of Schoenberg and Webern may consist of a polyphony audible as coalescing and dividing sonorities. I argue that ideas about sound perception gathered together by A. S. Bregman under the rubric of auditory scene analysis provide a way to conceptualize such polyphony, and I propose that the altered octave is a harmonic element crucial in producing the coalescences and divisions.
Submission received June 2002
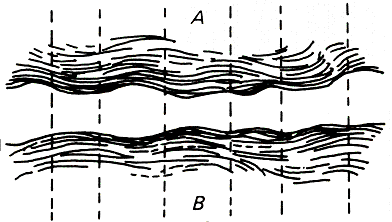
[1] Scientists, philosophers, writers, and artists at the beginning of the twentieth century were preoccupied by the empiricist realization that the stimuli reaching the senses were not orderly in themselves but were a messy mass of lines and noises, as were the thoughts in the mind which responded to those stimuli.(1) These empiricists believed that the orderly appearance of the environment was simply an interpretation formed by grouping those messy stimuli in conventional ways. As Figure 1 shows, the linguist Ferdinand de Saussure, for example, pictured both the "plane of sound" entering the ear (A) and the "plane of thought" of the hearer (B) as composed of many small, simple noises or ideas, representing both as streams of short, overlapping contours.(2) (Saussure's dashed lines represented divisions into words--in effect they were rationalizations allowing the relation of thought to sound. The contours of thought interacted with the contours of sound to produce a kind of interference pattern represented by the dashed lines, through which linguistic representation emerged.) William James, likewise, viewed the "stream of consciousness" as the sum of innumerable neural activations; each of these had a simple rising and falling contour, but when added together in a particular way their sum amounted to complex thoughts.(3)
Figure 1. Saussure's "plane of vague, amorphous thought" (A) and "the equally featureless plane of sound" (B)
[2] Many artists at the beginning of the twentieth century aspired to
be conscious of the processes by which the mind organized perceptions.
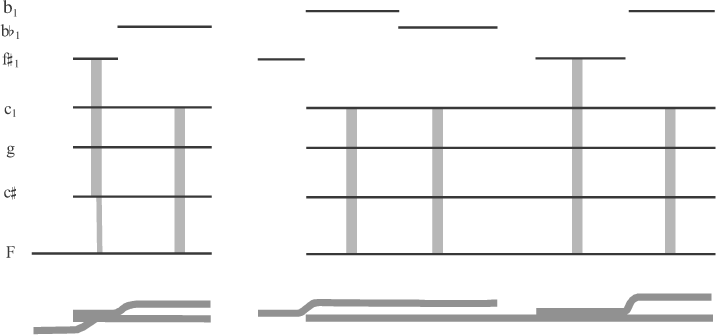
The dream plays of August Strindberg had plots intended, as Strindberg
put it,
to imitate the incoherent but ostensibly logical form of our dreams...Working with some insignificant real events as a background, the imagination spins out its threads of thoughts and weaves them into new patterns...The characters split, double, multiply, dissolve, condense, float apart, coalesce. But one mind stands over and above them all, the mind of the dreamer; and for him there are no secrets, no inconsistencies, no scruples, no laws.(4)
During the years when their atonal style was taking shape, Schoenberg and his circle were enthralled by Strindberg's dream plays,(5) and if the closing words of Schoenberg's Harmonielehre are to be believed, Schoenberg aspired to a dreamlike effect in his own music. There Schoenberg speculates about Klangfarbenmelodie, a spiritual music that "will bring us closer to the illusory stuff of our dreams."(6)
[3] If Schoenbergian atonal expressionism is indeed meant to access the dream state, one should be able to interpret it in terms of turn-of-the-twentieth-century conceptions of the mind. Saussure, James, and Strindberg were alike in conceiving of thought as a spinning-out and weaving-together of threads of ideas, a stream in which discrete ideas flow together and then eddy apart. Is it possible to interpret atonal expressionist music as a stream of sound resembling such a stream of thought? Following James and Saussure, one might seek ways in which the individual voices stream together; following Strindberg, one might look for ways in which harmonic sonorities divide into separate melodic lines which then coalesce again in new combinations.(7)
[4] Such division and coalescence would provide a point of comparison between atonal expressionism and the tonal common practice that Schoenberg and his students discarded. Much tonal music involves an equilibrium between the perception of tones individually and as fused members of chordal sonorities or melodic lines. The nineteenth-century theory of the Klang--which viewed the distinct tones of musical chords as reifications of the normally inaudible partials of a single complex tone--captured the sense that a triad could be perceived as a whole or as a collection of individual tones. Atonal expressionist harmony rarely features the triads of tonality, and its voices should not be expected to combine with the clarity found in common-practice tonality. But in atonal music, several seemingly distinct voices may concertedly produce a striking color, or a blended group of tones may decompose into interesting melodies. In a recent article I argued that Schoenberg meant his word Klangfarbenmelodie to refer to a modern analog to the Klang in which expressionistic harmony could be understood in terms of the variety of tone colors that could emerge when individual tones fused together into sonorities.(8) I suggested that the altered octave (the major seventh or the minor ninth) is crucial in giving many atonal chords this psychoacoustic property. In the present article I demonstrate this function of the altered octave using aural examples.
[5] My discussion focuses on the formation of cohesive sonorities that emerge as subdivisions of a musical texture. I pursue it in terms of recent research into auditory scene analysis (ASA). Over the past three decades, a number of psychologists and musicians have investigated a problem most extensively articulated by Albert S. Bregman: How does the auditory system parse complex stimuli into simple sound objects (auditory streams) that correlate with the objects producing the sounds (the objects forming the "scene" around the listener)?(9) This question is closely related to the basic puzzle of early twentieth century empiricists: how do the innumerable messy noises of the world somehow come to make sense, and to resemble reality, as they pass through the mind? The recent studies of ASA offer a relatively successful account of how people hear sounds in terms that would have been recognizable in the early twentieth century.
[6] Thus, in this article I interpret the altered octave in the context of ASA in order to suggest that early atonal expressionist compositions are constructed to promote the coloristic blend of separate voices. I approach musical surfaces in terms of perceived psychoacoustic groupings of various tones, using synthesized audio examples and graphic illustrations to illustrate the kinds of groupings that arise. The latter are modeled on the "schematic spectrographs" used by Bregman to illustrate the way the mechanisms of ASA tend to group complexes of sound into integrated perceptual objects.
[7] ASA is "the process whereby all the auditory evidence that comes, over time, from a single environmental source is put together as a perceptual unit."(10) Using the processes of ASA, the mind is able to hear, for example, the sounds uttered in a statement by a single person as belonging together, and it is able to distinguish that utterance from the many other sounds heard at the same time. Sounds grouped together through ASA have a quality of perceptual coherence. Experimental studies designed to pinpoint exactly what ASA does include tests of auditory stream segregation, the phenomenon in which a series of consecutive tones appears to be split into two separate streams. For example, in Figure 2a, listeners perceive the tones to be linked in a single stream, with the result that they hear a galloping rhythm. But if tone B is moved to a pitch further away from A and C as in Figure 2b, ASA produces two distinct perceptual streams. This is indicated experimentally by the fact that the tones' rhythmic placement with respect to each other is perceived entirely differently: listeners can tell that one stream contains a faster rhythm than the other, but they cannot hear the galloping rhythm. The words "over time" are in Bregman's definition of ASA are key. Consecutive tones in a series are more likely to split into separate streams if they move in a faster tempo. Thus, if Sound 2a is slowed down, it is possible for the listener to hear continuity between tones A, B, and C, as in Figure 2c.(11)
[8] When a single environmental source emits sound waves at various frequencies simultaneously, the psychoacoustic grouping together of the various component tones (as well as the separating of sounds that do not belong to the same source) is most strongly influenced by factors with a temporal dimension: If several tones rise or fall simultaneously in pitch or volume, they are likely to be grouped together; and if they have simultaneous onset they are also likely to be grouped together. If a series of tones is repeated over time, groupings are strengthened and ambiguity diminished. One major non-temporal factor promotes grouping: Groups of complex tones fuse insofar as their "combined spectral content conforms to a single hypothetical harmonic series." In pairs of complex tones, it happens that this occurs when their frequencies "are related by simple integer ratios."(12) Perfect unisons (1:1), octaves (2:1), fifths (3:2), and fourths (4:3) fuse strongly; thirds (5:4 and 6:5) fuse, but somewhat less strongly. About 1890, the psychologist Carl Stumpf claimed that such fusion, determined by simple frequency ratios, was the same phenomenon as consonance, and his understanding has held its grip ever since.(13) This factor functions in the dimension of pitch, not time. But temporal cues can undo this: if a harmonic partial begins earlier, or if its frequency is the same as that of an immediately preceding tone so that it seems to belong to an ongoing stream, it may be heard as separate from the other constituents of the harmonic partial-tone series. I summarize the factors promoting fusion and segregation in Table 1.(14)
Table 1. Factors in auditory stream integration and segregation | ||
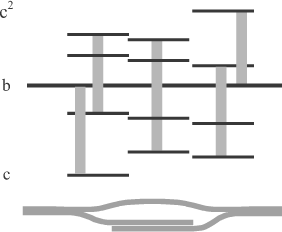
| Simultaneous tones | ||
| factors favoring fusion |
factors opposing fusion (favoring stream segregation) | |
|
| |
|
| ||
| factors favoring stream integration |
factors favoring stream segregation | |
|
| |
[9] ASA's perceptual grouping or segregation is rarely absolute. Individual tones may appear weakly grouped, individually discernible but with a sense of linkage, or so strongly grouped that there is no conscious awareness of the actual sounds of the individual tones, merely a sensation of their timbral effects on the global sound. Competition between different possible perceptual groupings can produce uncertainty. In the sound represented in Figure 3a, the simultaneous onset of tones B and C makes them likely to fuse almost into a single perceived sonority characterized by its own timbre. In Figure 3b, however, the pitch proximity of tone A to tone B makes it easier to hear continuity between A and B, while the tendency to hear B and C fused is correspondingly weakened. In Figures 3c and 3d, a fourth tone D is added to produce a stream between C and D. Since hearing a stream between tones C and D is inconsistent with hearing tones B and C in the same stream, it becomes harder to hear fusion between B and C, although in Figure 3c it is still possible to experience B as a timbral coloring of C. In Figure 3d, B is easily captured into the stream of A, and it is much more difficult to hear fusion of B with C.
[10] Auditory scene analysis is applicable to common-practice music in that a melody occurs when successive tones are integrated into a single auditory stream,(15) and in that tonal harmony is organized so that those simultaneities that are strongly integrated are consonances. Common-practice composers, in this view, treat dissonances (that is, simultaneities involving complex frequency ratios or sensory roughness) in such a way as to separate the dissonant tones into separate streams, so that they will be integrated only weakly or not at all. Common-practice voice-leading, rhythmic features, and other choices reinforce the tendency of simple harmonic ratios (or rather, the tendency of the overtone series) to cause fusion.(16)
[11] But this serendipitous conformity of sensory consonance to features such as voice-leading is not at work in atonality. Nor need it be. Sensory consonance is not synonymous with fusion, even though it stems from the simple frequency ratios that are also implicated in the fusion of the overtone series. Sensory consonance is merely one factor promoting integration, and sensory dissonance is not in itself a factor opposing integration as has often been supposed. Bregman emphasizes this distinction between consonance and fusion. He notes that sensorily dissonant tones may fuse, and when they do so, the resulting dissonance must be understood as a timbral feature.(17) On its face, Schoenberg's argument in his Harmonielehre that the higher overtones must be treated as consonances suggests that he viewed consonance as synonymous with fusion: the overtone series, his reasoning went, generates both consonance and fusion. But in the end, Schoenberg's purpose was to argue that any combination of tones--traditional consonances as well as traditional dissonances--could fuse. Schoenberg rejected the claim (common in his day) that the first six partials of the harmonic series dictate the primary chords, arguing instead in favor of a music in which any combination of tones might be treated as a harmonic unit.(18)
[12] My claim is that in their early atonal music Schoenberg and his students learned to treat the altered octave as such a harmonic unit. I argue that its psychoacoustic nature lets it function as a unified sonority. In this respect it is analogous to the common-practice major triad, which fuses when its various overtones conform to one harmonic series. I suggest, however, that rather than than organizing the music functionally the way triads do, the altered octave suggests an organizing resemblance between expressionist music and the conception of thought described at the start of this essay. Along with temporal ASA factors and, to some extent, traditionally fusing intervals such as the major and minor third, the altered octave is one atonal tool in the creation of constantly changing subgroupings within the musical texture.(19)
[13] The tones of an altered octave may be said to fuse, but in a different manner from the fusion of traditional consonances. Integration occurs in this class of "sensory dissonances" (in Schoenberg's terminology, "remote consonances") because of the masking produced when two frequencies are within a critical bandwidth of one another. According to the understanding that began to take shape in the 1960s, in the inner ear, the frequencies of tones are transduced as excitations at particular positions along the length of the basilar membrane, which then sends signals of these excitations to the brain. When two tones activate positions on the basilar membrane close to one another, one masks the other. This masking is substantial when the activated positions are within about 1 mm of each other (at the bottom of the bass-clef staff, this means the frequencies are within about a fifth of each other; at the top of the treble, about a half step). The distance in pitch at which such masking takes place is known as the critical bandwidth. When two frequencies are within a critical bandwidth, the hearing has difficulty resolving them.(20)
[14] Whether because of neural properties inherent in the masking or because the critical band coincides with intervals at which beats are maximally "rough," the critical band is associated with a dissonant "color." The greatest roughness occurs when one partial is near the edge of the other's critical band. When partials are well within each other's critical band (i.e. very close in pitch), there is little roughness; it is almost as if they coincided exactly. Figure 4 gives an approximate representation of the masking involved in various intervals, with a lower tone in middle treble register such as g1. For traditional consonances such as the M3 and P5, several partials of each tone are not masked, and many of those that are masked are so close in frequency that they do not produce sensory dissonance. The augmented 4th presents little more masking than these consonances, but a greater degree of roughness. In the minor 2nd, masking and dissonance are both high. It is difficult to hear the two complex tones separately from each other.
Figure 4. Critical band interactions of intervals. Long dark lines represent partials of a pitch in mid-treble register, such as g1. Short dark lines represent the partials of tones at the specified interval above mid-treble pitch. Shaded bands represent critical bands.
|
|
|
|
|
|
|
|
|
P5 |
M3 |
A4/d5 |
m7 |
M7 |
m9 |
m2 |
|
<less< critical
band masking >more> |
||||||
[15] Intervals such as the minor 2, minor 9, and major 7 are highly non-fusing; but I contend that, in early twentieth-century expressionism, the difficulty of perceptually resolving individual tones in these highly masked intervals is a substitute for fusion. Like fusion, such masking can unite several tones into a single perceptual object. (Much other music from the twentieth century also uses traditional dissonances for this purpose.) Schoenberg and Webern, searching for coloristic variety in the progression from one sonority to another, used the characteristic beating and roughness of the altered octave as a color structurally equal to the colors of the traditional consonant intervals. Used in this fashion, the color of an altered octave would no longer merely connote tension requiring resolution.
[16] The following informal demonstrations illustrate the interplay of
streaming and altered-octave masking. There are two possible ways to hear the
sequence F-sharp - B-flat - F-sharp (Sound 5).
It can be heard as an integrated stream as in
Figure 5a, or segregated into two streams as in Figure 5b. To me, it is easier to hear the single
stream shown in Figure 5a than to hear the two streams of Figure 5b, although
the latter is also possible. But when a continuous G is added an altered
octave below the F-sharp (Sound 6), my hearing
changes. It is still possible to hear F-sharp and B-flat in a single stream as
in Figure 5a, but it becomes easier to hear the F-sharp in a separate stream
from the B-flat, by hearing the F-sharp and G as a single sonority separate from
the B-flat (Figure 6).
[17] This integration of F-sharp with G may be partly due to the fact that
the two tones begin simultaneously. Yet the effect remains if the order of the
F-sharp and the B-flat is reversed. I find
Figure 7a to be a more persuasive representation of my hearing of
Sound
7 than Figure 7b; yet when G is added (Sound
8), I perceive the F-sharp as a coloration of the G, and above this sonority
I hear a stream of pulsing B-flats (Figure 8).
[18] In this case, it may be suggested that the G captures the F-sharp more than it
captures the B-flat because G is closer to F-sharp than to B-flat. But
while this may be a factor, the parsing remains the same when the G is
placed above the other two tones. This is heard in Sound
9, seen in Figure 9, and in
Sound 10, seen in Figure 10. (For comparison, hear
Figure
9 without g1; Figure 10
without g1.) I can only conclude that the
altered octave is responsible for the sense of integration.
| Figure 9 | Figure 10 |
|
| Sound 9 |
without g1 | |
| Sound 10 |
without g1 | |
[19] Clearly these demonstrations of this sort can be heard in various ways,
and certainly any conclusions drawn from them must remain tentative at least
until more formal experimental study. The masking effect of the altered octave
is less ambiguous, though, in chords with more tones--for example, in the series
of sonorities found in Example 1 ([GIF] [Scorch]), the end of Webern's
quartet movement, op. 5, no. 5, from which the previous demonstrations are
abstracted. In this passage the first violin leaves and rejoins the underlying
sonority. As with the previous demonstration, the changes in sonority can be
investigated by means of fast repetition, in which changing degrees of masking
and fusion are manifested as auditory stream segregation. The exaggerated
comparisons resulting from high-speed repetitions reveal aspects of the sonority
that present themselves as subtle but palpable shifts at the music's actual
tempo. In measure 24, the first violin's F-sharp has a different sense of
belonging to the underlying sonority than the B-flat. The F-sharp has an
altered-octave relationship with the viola's G, but the B-flat does not have an
altered-octave relationship with any element of the sonority. In addition, the
F-sharp is probably significantly masked by the 2nd violin's C. When the F# is
quickly alternated with the B-flat as in Figures
11 and 12, the B-flat stands out from the sonority, but the F-sharp blends in.
[20] In Sound 12 at this speed, I hear the F-sharp as part of the sonority that
includes the three lower tones, and it is difficult for me to "hear" that in
fact the F-sharp begins later than the three other tones. Beneath the B-flat I
hear a single sonority; the passage sounds more like Figure 13a
than like Figure 13b. No doubt because the F-sharp
is masked partly by the C and C-sharp in addition to the F-sharp (none
of which masks the B-flat as strongly), this effect is much stronger than
the corresponding effect in the earlier demonstration (Sound
7). It may be suggested that the F-sharp appears to belong to the
underlying tones not because of critical-band masking but because the example is
played too quickly for a stream to be heard incorporating B-flat and F-sharp (as
in Figure 7a). As a result, one might argue, an interpretation such as the one
illustrated in Figure 13b is heard but mistakenly represented as in Figure 13a.
The point, though, is not that at a certain speed B-flat and F-sharp are
segregated into separate streams with the result that it is difficult to
recognize their temporal relationship. Rather, what is interesting is that when
such segregation takes place, the B-flat stands out while the F-sharp is folded
into the tones below it. That is, accompanying the b-flat, one hears a sonority made up
of the four tones of Figure 13c, instead of hearing a sonority that sounds like Figure 13d.
[21] As might be expected, the integration of the F-sharp but not the
B-flat is even stronger when the cello's F is added to the sonority;
Sound
14a and
Sound 14b confirm this.
[22] This means, of course, that five tones are heard together as a sonority
as in Figure 14c.
[23] Altered-octave masking accounts for the integration of the F-sharp, but
other phenomena such as registral distance play roles as well. B-flat stands out
partly because it is in a much higher register than all of the other tones, and
if it is replaced in the sonority by B-natural as in Figure 15, the B-natural stands out at least as much. The increased interval--F-sharp
- B-flat to F-sharp - B-natural--increases the tendency for stream segregation,
making the B-natural stand out, despite that the B-natural forms an altered
octave with the C-natural.
[24] The informal experiments just discussed suggest that it should be
possible to perform the passage in such a way as to bring out the connections
shown in Figure 16. Below
the analysis I have given a drawing showing each sound-object as a line
or stream. Separate streams are represented by separate lines, and integrated
sounds are represented by single or touching lines. As the figure shows,
when the three upper instruments enter, the cello's F may at first be heard
separately, but as the chord is held the F-sharp blends in, changing the
timbre emerging from the chord. The violin moves to B-flat, again splitting
the mixture into two sonorities. The next gesture begins with the F-sharp
alone in the violin (mirroring the cello's earlier isolated low F). When
the other instruments join, the violin stays in its own stream. In the
final gesture, the violin again begins as part of the underlying sonority,
moving later to B. At actual tempo, these streams are not clear-cut, but
they represent a subtle partitioning in the harmonic stream. A particularly
nuanced performance might even succeed in using the F-sharp to establish
the first violin in a blend that is maintained even when the violin changes
pitch, so that the violin's motion to B-flat and B produces a change in
color of the continuous sonority, not a splitting of the sonority.
| Figure 16 |
|
| Sound 16 | |
|
[25] Stream- and color-creation cannot simply be inferred from the score. The fusing of sonorities depends greatly on balance between voices and on other factors in performance. The divided cellos' accompaniment near the beginning of Example 2 ([GIF] [Scorch]), Schoenberg's orchestral song "Seraphita," op. 22, no. 1 (1913), is a case in point.(21) The opening diminished fourth in the inner voices expands to a perfect fourth and finally a tritone (Sound 17c). If these intervals can be heard as single sound objects, the passage may be heard as an evolving succession of colors. Their simultaneity indeed promotes perceptual integration, but the fact that they move only in similar motion, not parallel motion, does not. Whether the effect of evolving color is achieved depends on the playing of the altered octaves in the outer voices.
[26] If the outer voices are played loudly enough, they mask the inner voices
of chord 3, as in Figure 17a (where vertical lines with arrows indicate
that the inner voices seem to "belong" to the outer voices). Because each
inner voice is masked by a different outer voice, the inner voices' own
integration is minimized. (Sound 17a(i);
the effect is strengthened further in Sound 17a(ii).)
Chord 3 will then consist of two sonorities. (The decreasing integration is
indicated by the thicker vertical line in chord 1, the thinner line in chord 2,
and the line's disappearance in chord 3.) On the other hand, if the outer voices
are quieter, they are masked by the inner voices, as in Figure 17b. The altered-octave shimmer steadily accruing to the inner
voices adds to the evolving color of the inner voices' own integration.
Thus, the inner voices of chord 1 are heard as simply a major third (with
the outer voices forming their own, separate, sonority). As the inner voices
move to chord 2, a new color emerges not only because the inner voices
now form a perfect fourth but also because this pair of tones is now colored
by the altered octave of the lowest voice. Finally, the color of the augmented
fourth of chord 3 is enhanced as a second altered octave is contributed
by the highest voice. (Hear this effect in Sound
17b(i), and more strongly in Sound
17b(ii).)
|
Figure 17. Schoenberg, "Seraphita," op. 22, no. 1, mm. 2-3, cellos after Cramer, "Klang and Klangfarbenmelodie," p. 29
|
|||||
| Realizations of Example 2 / Figure 17: |
|||||
|
<<< more like Figure 17a |
more like Figure 17b >>> |
|
|||
|
|
|
||||
[27] Parallel motion between tones increases their fusion. Composers seem to
find this principle useful for increasing the perceptual coherence of sonorities
with a moderate but not overwhelming tendency to fuse. Thus, in both
common-practice and early atonal music, major and minor thirds frequently appear
in parallel motion; and altered octaves often appear in parallel motion in early
atonal music. In Webern's orchestral piece op. 6, no. 1, mm. 2-4 (Example 3 [GIF]
[Scorch]), parallel motion fuses the top three
tones of the first two tetrachords; in the second chord an altered octave
captures the bottom tone as well; and parallel motion fuses the bottom three
tones of the third chord. As is shown in Figure
18a, this leaves
a low C and a high C free, and in Sound
18a these tones stand out. But the Cs are not entirely free; they
form altered octaves with the B of the French horn, as shown in Figure
18b (hear
Sound 18b(i) or
Sound
18b(ii) with simultaneous onset of horn and cellos). In the demonstrations,
the Cs are less prominent when the horn's B is sounding than when it is
not--another way of saying that the Cs start and end as colorations of
the B, flowing from the B into the stream of chords and back. During these
three chords, altered octaves are the key to associative relationships
in which the melodic lines "split, double, multiply, dissolve, condense,
float apart, coalesce" like characters in a Strindberg dream play.
| Figure 18 | |
|
18a. |
18b. |
 |
 |
[28] Although this example shows a clean and simple use of the combination of parallel motion and altered octaves, most instances are not as neat. Altered octaves are often small details in complex, ornate progressions; and there are cases in which the use of the altered octave appears to be a governing principle even though its effect is difficult to precisely hear or predict. Example 4 from later in Op. 6, No. 1 illustrates such a case. Here the d - a - c-sharp - b-flat - b line played by the flute and oboe may function as a compound melody, an instrumental line divided into two perceptual objects through the auditory streaming created by relatively wide melodic intervals. Each "voice" of the compound melody joins another voice of the texture through altered octaves; in a sense, the separate components of the compound melody are harmonically dependent on (that is, coloristically related to) different voices elsewhere in the polyphony.
[29] For the first four notes, the high notes are introduced in altered-octave relationships to the triplet melody of the clarinet, bassoon, and pizzicato cellos; the lower tones are related to the B-flat and A of the solo cello. The fifth note, B, fulfils the convergent implications of the compound melody while providing an altered-octave anchor for the newly-entered horns (whose opening pitches, incidentally, alternate in altered-octave relationships with the flute-oboe and the solo cello lines). If it were this simple, the oboe-flute line would be fully explainable in terms of its colorations of, alternately, the cello solo and the clarinet-bassoon-cello lines. But the altered-octave harmonies are brief, lasting only until one voice or the other moves to a new pitch, and many other factors are at work. In Sound 19a, the altered octaves are hard to hear as such. They become a bit easier to hear in Sound 19b, in which rubato lengthens the durations of altered octaves. Several possible interpretations may be competing: hearing the flute-oboe line as one melody or two; hearing it as a perceptually salient melody or as a series of colorations applied to other voices; hearing the altered octave for its acoustic impact or for other properties of ic1.
[30] Auditory scene analysis has been promoted for its ability to explain
traditional musical elements such as melody and counterpoint. In this article
I have drawn on it for a different reason: its ability to move the discussion
of harmony beyond the categories implied by such traditional terms. Moving
beyond the traditional categories was a chief purpose of Schoenberg and
Webern, evident in Webern's claim that their music ushered in a new era
of polyphony (which he called "a new interpenetration of music's material
in the horizontal and the vertical"),(22) evident in Schoenberg's claim
that in modern music the vertical and horizontal were unified,(23) and
evident in Schoenberg's claim that the new sonorities might be explained
not in terms of the traditional dimensions of Klang-based harmony
and melody but in terms of a fusion called Klangfarbenmelodie. My
analyses speak to all of these, positing that in the Viennese School's
polyphony, sonorities of varying color merge and separate, so that at any
given moment the total sound is articulated into perceived groupings, much
the way a melody over time is articulated into perceived groupings.
Copyright © 2002 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
prepared by
Brent Yorgason, Managing Editor
Updated
18 August 2003