MTO

Volume 13, Number 3, September 2007
Copyright � 2007 Society for Music Theory


Scott Murphy*

Considering Network Recursion and Bartók’s “Fourths”
   

 

KEYWORDS: Klumpenhouwer network, recursion, self-similarity, Bartók, analysis, inversion, mirror, axis, register

 ABSTRACT: Notions of network recursion, as they have been designated in music analyses, may be organized into five categories that range from exact self-similarity to self-dissimilarity. This perspective reveals that Michael Buchler’s critique of network recursion does not necessarily fully apply to analyses in all categories of network recursion. An analysis of Bartók’s “Fourths” serves as an example of how network recursion analysis can achieve significant results and avoid most of, if not all of, Buchler’s critique.

REFERENCE: Michael Buchler, “Reconsidering Klumpenhouwer Networks,” Music Theory Online 13.2

Received September 2007

[1] In his article “Reconsidering Klumpenhouwer Networks,” Michael Buchler advocates for a stronger perceptual salience of the types of observations that Klumpenhouwer networks afford. In the course of his critique, he presents two criteria that perceptually salient K-net analyses should meet: they should take place in registral space (henceforth, p-space) to an appreciable degree,(1) and they should not endure the perceptual strain of negative isography, i.e. dual- or hyper-inversions (<In>).(2) The price for the former is an increase in analytical exclusivity, since such relationships do not occur as often in the literature. The price for the latter seems steeper, as Buchler explains: “One could avoid the particular phenomenological problem of dual inversion by resolving to employ only positively isographic K-nets, but doing so effectively forfeits one’s ability to produce recursive network structures, and these are perhaps the greatest incentive for using K-nets in the first place.”(3) Part II of this article presents a K-net analysis of Bartók’s “Fourths” from Mikrokosmos that meets both of these criteria. In using this analysis as part of my pedagogy of K-nets, I am initially willing to pay the price of analytical exclusivity: the student will likely, and correctly, surmise that such a custom-fit analytical method has little significant applicability beyond “Fourths”. (Two other passages from Bartók, for which the method delivers more modest results, will be mentioned toward the end of this article.) However, sometimes I use this payment as an upfront pedagogical investment in the student’s understanding of K-nets, and, if there are any dividends, I use them to fund my promotion of the apperception of pc-space K-nets: “if you can value that in p-space, how about this in pc-space?”(4)

[2] However, as for dropping the problematic hyper-inversions at the price of losing recursion, I believe Buchler may have overcharged K-net theory, a matter I wish to cover in Part I. (Readers interested in only the analysis may proceed directly to Part II, although the two parts will correspond at certain junctures.) The crux of my audit is the definition of K-net “recursion.” Early in his article, Buchler adopts a “broad” definition of the term, in that he recognizes the ability of K-net technology to “facilitate hierarchical structures in which individual chords are shown to be comparable to networks of chords, networks of networks, and so forth. To many proponents, this potential for ‘recursive’ relations serves as the K-nets’ raison d’être.”(5) Later in his article, Buchler adopts a “narrow” definition of the term: “‘Recursion,’ in the K-net sense, refers to networks of networks, or a grouping of K-nets arranged such that the transformations between selected K-nets mimics the transformations within a single constituent network.”(6) The inclusion of the word “constituent,” along with the absence of the word “chord,” distinguishes the narrow definition from that of the broad. Throughout the K-net literature, there are many broad recursive analyses that are not narrow recursive analyses: in each case, the analysis compares a network with a hyper-network where the former is not a member of the latter. Furthermore, any implicit consensus there is for the definition of “recursion” among K-net authors comes much closer to broad instead of narrow, as will be shown below. Yet, as Buchler builds his case against recursion—citing not only the phenomenological problem of <In> but also other points of concern—those familiar with this literature will likely infer that his target is narrow (more or less) instead of broad. Therefore, if and when one accepts Buchler’s critique, the payment exacted should not be the dismissal of all recursive analyses as they have been dubbed in the literature, but only of those analyses to which his critique directly applies. The first part of this article details the difference.

I. Organizing in Fifths: Recursive Analyses and Buchler’s Critique

[3] For starters, I suggest that some kind of terminological standardization is in order, one that teases apart the different kinds and degrees of match between a network and a hyper-network, and that sidesteps the equivocation of the term “recursion.” I recommend the related but more focused term self-similar for the situation in which a hyper-network matches, to some degree, one of its constituent networks, and the term self-dissimilar for matches that are not self-similar. The list below organizes some (but by no means all) published network analyses that could be understood as recursive into five categories, in which the first four additionally tease apart degrees of self-similarity, and the fifth category is solely devoted to self-dissimilarity. (I will limit each survey to those self-similar matches that are “strongly isographic,”(7) where every <OPn> in the hyper-network corresponds to a OPn in the same place in the corresponding network. I use the notation OP because, in some cases, the analysis involves another transformation group besides the T/I group, which is placed afterwards in brackets.) An asterisk (*) following the citation means that the author explicitly refers to the analysis as “recursive”; the scattered distribution of the asterisks among the five categories supports my earlier argument that the relevant literature has collectively construed the term more broadly.

  1. Exact self-similarity: The hyper-network is “strongly isographic” to one of its constituent networks.
    1. Lewin 1990, 94 (Figure 12)
    2. Klumpenhouwer 1991b, 7:23 (Examples 7.22, 7.23, and 7.25) [permutation]
    3. Lambert 2002, 167 (Example 5)*
    4. Lambert 2002, 185 (Example 26)
       
  2. Retrograde self-similarity: The hyper-network, which includes a network that interprets set X, is “strongly isographic” to a network that reinterprets set X as a K-net in “retrograde.”(8)
    1. Lewin 1994, 90 (Example 13)*(9)
       
  3. Modal self-similarity: The hyper-network, which includes a network that interprets set X, is “strongly isographic” to a network that reinterprets set X as a K-net in a different “mode.”(10)
    1. Lewin 2002, 208 (Example 4.6)
       
  4. T-net self-similarity: The hyper-network, which includes a network that interprets set X, is “strongly isographic” to a network that reinterprets set X as a T-net. (NB: The hyper-network is composed of K-nets.)
    1. Klumpenhouwer 1994, 231-233 (Examples 16 and 20)*
    2. Klumpenhouwer 1994, 236 (Example 24)
       
  5. Self-dissimilarity: The match between the network and hyper-network does not fall into any of the four self-similar categories.
    1. Lewin 1990, 93 (Figure 11)
    2. Lewin 1990, 98 (Figure 15)
    3. Klumpenhouwer 1991a, 343-344 (Examples 39 and 40)
    4. Klumpenhouwer 1991a, 352-353 (Examples 55 and 57)
    5. Klumpenhouwer 1991b, 7:23-7:24 (Examples 7.26 and 7.27)* [permutation]
    6. Klumpenhouwer 1994, 242-243 (Examples 29-31)
    7. Gollin 1998, 51 (Figure 10)* [Q/X]
    8. Stoecker 2002, 244 (Example 12)* [axial isography]

[4] I count five arguments against network recursion that Buchler puts forth in his critique:

  1. “Recursive analysis requires us to locate positive and negative surface-level isographies in the same quantity as shown in any one local K-net. This often entails skewing surface readings into representations that simply provide the right type of graph to fit the situation.”(11)
     
  2. As reviewed earlier, it requires the presence of hyper-inversions, which are phenomenologically suspect.
     
  3. “K-nets of size q must be grouped into q-sized hyper-networks for recursion to be drawn...There are not many musical situations where q-note chords cluster into q-chord progressions (and q progressions of progressions, and so on). Therefore, musicians who choose to frame their analyses around hyper-networks are often left with the choice of selectively omitting some chords or reusing some chords in other structures.” (12)
     
  4. “We also force ourselves to designate a single K-net [from among the K-nets in the matched hyper-network] as the sort of mother network, and that priority does not need to be grounded in musical salience.”(13)
     
  5. “At every level other than the ‘foreground,’ K-nets interpret increasingly abstract relationships of relationships, not relationships of notes or pitch classes.”(14) 

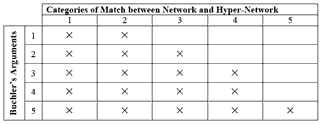
[5] My primary objective for disassembling Buchler’s critique of recursion is not to find faults in his arguments, but to understand exactly which kinds of matches between a network and a hyper-network have been targeted by his arguments. Table 1 indicates with a “×” those categories of match between a network and a hyper-network that are necessarily affected by each of Buchler’s five arguments as outlined and numbered above. For example, the first three categories of match are subject to Buchler’s hyper-inversion argument (argument #2): that is, in these three categories, the hyper-networks must include hyper-inversions to achieve self-similarity, or, at the least, avoid triviality.(15) The fourth and fifth categories do not require hyper-inversions and thus may avoid any phenomenological problems they might raise.

             

Table 1.


(click to enlarge)

Table 1 demonstrates how unevenly Buchler’s critique of recursion applies to these five categories of recursion. Only Buchler’s fifth argument applies to all five categories, suggesting that, if it is toward broad recursive analyses that Buchler aims his critique, then much of it has been for naught. But if Buchler’s critique is aimed at a narrower slice, then what defines the parameters of “narrow”? Only the first two categories—exact self-similarity and retrograde self-similarity—suffer the full force of Buchler’s critique. The third and fourth categories, considered together, experience more of a glancing blow, in that the �s literally taper off in Table 1, and the fifth category, which boasts the longest of the lists of representative examples offered earlier, escapes nearly scot-free. This unevenness recommends that the price of dismissing recursive analyses that is paid by adopting Buchler’s multi-faceted critique should at least be prorated among the various categories of recursive analysis.

[6] It is worth noting that a recursive analysis may still deserve one or more of Buchler’s criticisms, even though the analysis belongs to a category that does not necessarily warrant that criticism. For example, a self-dissimilar match may still incorporate hyper-inversions, although it does not have to. However, within this category, Buchler’s concerns regarding hyper-inversion seem to have been partially allayed pre hoc: the five representative self-dissimilar recursive analyses cited above that use standard Klumpenhouwer networks of Tns and Ins—two in Lewin 1990, two in Klumpenhouwer 1991a, and one in Klumpenhouwer 1994—do not use hyper-inversions.

[7] To summarize (and to gloss over the diagonal slope of the ×s in Table 1), if one wishes to avoid, as best one can, the pitfalls of recursive analysis that Buchler has uncovered, then one should stick with self-dissimilar matches. This is, however, a considerable trade-off, as self-similarity is attractive given its company: consider natural examples such as fern leaves or coastlines, mathematical examples such as the Mandelbrot set or the Koch curve, or musical examples such as the diatonic scale.(16) Furthermore, the notion that a chord is “prolonged” by a progression of which it is a part provokes a “powerful” analytical narrative, to use Lewin’s characterization.(17) Lastly, restricting oneself to self-similar matches automatically (but perhaps surreptitiously) curbs analytical promiscuity to some degree, in that one cannot simply pair up a hyper-network with just any network. The analytical significance of a network that matches a proposed hyper-network is already vouched for—perhaps not as a mother, but at least as an equal sibling—if the analyst has selected the network to be part of the hyper-network.

[8] Yet even this last inequity between self-similar and self-dissimilar matches has already been compensated for in the K-net literature. Often the author attaches a formal-rhetorical significance to the network involved in the match. Typically the network earns this significance by beginning or ending a formal unit of which the sets interpreted in the matching hyper-network are a part, or through other persuasive means.(18) This facilitates analytical narratives such as “cause and effect,”(19) “elaboration,”(20) “structuring influence,”(21) or dialectical “synthesis”(22) that can also be quite powerful. (Therefore, to those desiring a comparison between Schenkerian and K-net Schichtenlehren, I recommend embracing an analogy with “motivic parallelisms”—which, as Charles Burkhart notes, may be nested or not—in addition to entertaining strict “prolongational” analogies.(23)) In the analysis that follows, I endeavor, among other things, to construct the foundations for such a narrative.

II. Organization in “Fourths”: P-Space Network Recursion without Negative Isography in Some Music of Bartók

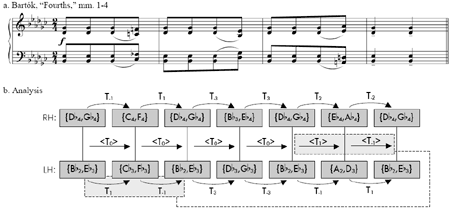
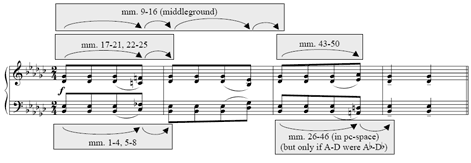
[9] Figure 1a provides the first four measures of Bartók’s “Fourths,” no. 131 from Mikrokosmos. In rapid-fire eighth notes, the opening presents and embellishes an E-flat minor-minor-seventh harmony—what Richard Parks labels as the piece’s “referential sonority”(24)—that Bartók partitions into two perfect fourths for the two hands. Each hand then retains this titular interval for the remainder of the piece. The embellishments are quick, slight melodic deflections on the last eighth note of each of the first three measures, deflections that are mirrored between the two hands in p-space. Bartók maintains this p-space mirroring throughout the first four measures within the exception of the chord at m. 3.4(25), when one of the fourths is deflected one semitone “too high” relative to a strict preservation of the established axis. (I prefer to hear the left hand’s fourth as the aberrant one, as this honors the melody’s allegiance to a diatonic collection.)

         

Figure 1.


(click to enlarge)

Brian Alegant hears this lopsided moment as serving the harmonic texture’s maintenance of four different pitch classes: were Bartók to both continue the p-space mirror and symmetrically move apart the two hands by half or whole step, a doubling of a pitch class would occur for the first time in the piece.(26) I would like to offer a complementary reading of the lopsided moment that suggests a correspondence between two different kinds of trajectories, both of which take place entirely within p-space: the left hand during the first five eighth notes presents a reiteration of a sonority followed by a upwards semitonal deflection from, and then a return to, that sonority; analogically, both hands during the first four measures present a reiteration of chords using a particular inversional axis followed by a upwards semitonal deflection from, and then a return to, chords using that axis.

[10] This analogical relationship may be demonstrated using K-net technology. Rather than use K-nets and group automorphisms, Figure 1b uses Buchler’s visual makeover of the traditional network design, although either approach would suffice. However, Figure 1b has been modified to operate in p-space. First, the T-sets, in solid grey boxes, contain registral pitches instead of pitch classes; they are horizontally aligned into right- and left-hand parts, and roughly positioned below their corresponding notes in Figure 1a. Second, the transpositions operate on registral pitches(27); therefore, any simultaneity of a p-space transposition and its inverse conveys an exact registral mirroring at that point, and any immediate succession of a p-space transposition and its inverse conveys a registral undulation. Third, each hyper-transposition (<Tn>) also operates in p-space, and is calculated using Buchler’s method of summing the concurrent dual transpositions.(28) Hence, the recurrence of <T0> in the opening of the four-measure phrase signifies the constancy of the p-space mirror, despite the variability of the dual transpositions.(29) As highlighted with dashed boxes and lines in Figure 1b, a match between a sub-network of transpositions in the left hand to begin the phrase (T1-then-T-1) and a sub-hyper-network of hyper-transpositions between the hands to end the phrase (<T1>-then-<T-1>) formalizes the aforementioned analogy, or at least the “deflection” part.

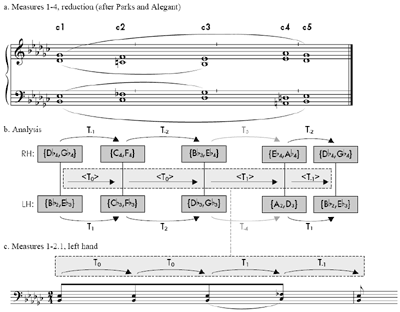
[11] I find the “reiteration” part of the analogy best captured by slightly reducing these four measures to the five chords, labeled c1-c5, shown in Figure 2a. These five chords, which are the same five chords that Alegant chooses in his reduction,(30) are the five novel registral-durational events of the phrase; in other words, these are the chords that remain after omitting all eighth-note repetitions of the opening registral harmony.

As highlighted with dashed boxes and lines in Figure 2b, the progression of these five chords create a <T0> <T0> <T1> <T-1> hyper-network that matches the T0 T0 T1 T-1 progression of the left hand’s first measure as given in Figure 2c, thus accommodating the distinctive eighth-note repetitions. Furthermore, the isochrony of the first four eighth notes in Figure 1c roughly matches the near-isochrony of the corresponding chords c1-c4 of Figure 1a (note the tick-mark barlines). Parks’s hierarchical analysis of these measures, summarized with the slurs in Figure 2a, supports the “middleground” dual transpositions of Figure 2b to some extent: in particular, the T-1 T-2 progression in the right hand and its mirror in the left correspond with stepwise Terzzugen that prolong the referential sonority.(31) The T5 and, by association, the T-4 however, are more removed from Parks’s hierarchy, in that they cut across it, spanning the gulf between two stepwise voice-leading strata (the passing motion of chords c1-c3 and the neighbor motion of c1, c4 and c5). Therefore, although the T5 and T-4 contribute to the middleground hyper-transposition progression, I have written them in gray, to signify that they cannot be as readily perceived as middleground transpositions as the T-2 and T2 transpositions can be. (This seemingly inconsequential detail will strengthen a match asserted later.)

              

Figure 2.


(click to enlarge)

[12] The matches of network and hyper-network in Figures 1 and 2 are self-dissimilar, in that the network is not a member of the matched hyper-network, or is not a reinterpretation of a member network’s set. Although the music of Figure 2c is embedded within the phrase of which Figure 2a is a slight reduction, it is still self-dissimilar because the network whose transformations are T0, T0, T1, and T-1 is not a node (or reinterpreted as a node) in the hyper-network whose hyper-transformations are <T0>, <T0>, <T1>, and <T-1>. However, since both matches are self-dissimilar, they can, and do, circumvent Buchler’s first four arguments (as numbered above). For example, they involve no hyper-inversions, and also do not have to fret about the right balance of positive and negative isographies. In addition, each of the networks in each hyper-network has four nodes (i.e. they are interpretations of tetrachords), but the matching hyper-network of Figure 1b has three nodes (i.e. the three tetrachords participating in the <T1>-then-<T-1> hyper-network), and the matching hyper-network of Figure 2b has five nodes (i.e. the five tetrachords c1-c5). Whereas anxieties about a “mother network” arbitrarily chosen from within the matching hyper-network are moot, it is nonetheless important to point out that the neatness of each match is balanced by a neatness of the interpreted sets’ formal position. In Figure 1, the network interprets a component at the beginning of the phrase and the matching hyper-network interprets its end (“cause and effect”?). In Figure 2, the network interprets a component at the beginning of the phrase and the matching hyper-network interprets the entire phrase (“elaboration”?). Within the scope of the entire piece, the matches are also formally marked, because the deflection and correction by the interval of a registral semitone is both the first melodic transformation and the first inversional-axis transformation in the piece.

[13] I should demur with regard to this last interpretation: the semitonal deflection and correction specifically involves the left hand in mm. 1–2. Yet, by virtue of a top voice’s natural prominence, the left hand’s semitonal rise-then-fall is perhaps less obvious to the listener than the right hand’s semitonal fall-then-rise. I could account for this by generalizing the observation to that of a “one-notch difference” in both registral-pitch and registral-axis domains, rather than focusing on the direction of the difference, and end the analysis there. But there is also reason to press on. In the paragraphs that follow, I will propose that most of the remaining melodic intervals in the first phrase match registral hyper-transpositions throughout “Fourths”; furthermore, the matches for the most part preserve chronological ordering. These correspondences undergird an analytical narrative in which the melodic motions in the first three measures are linearized and enlarged (both chronologically and conceptually) to forge a path of registral-axis change that spans the entire piece.(32)

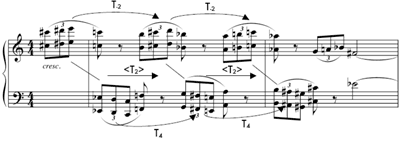
[14] Measures 5–8 project the same pitch materials as the first four measures of the piece. The next eight measures are given in Figure 3a. These measures relieve the previous homophony with melodic motions often staggered between the two hands, but the contrary motion encourages a continued hearing of registral mirroring. When there are chronological displacements from the mirroring, they are slight, as shown with the diagonal lines in between the staves. Thus, each of the right-hand fourths (minus immediate repetitions) bijectively pairs up with one of the left-hand fourths with which it sounds simultaneously, thus creating tetrachords. (Alegant’s first-species reduction of this passage comports with mine.) For greater visual clarity, the hyper-transpositions in Figure 3a that map one tetrachord to the next are calculated in the absence of accompanying dual transpositions, but they can be confirmed easily enough.

For example, in mm. 9–10, the left hand moves up then down by one semitone each (T1-then-T-1), but the right hand simultaneously descends and ascends by two semitones each (T-2-then-T2). This slight imbalance translates, by component-wise addition, to a hyper-transposition progression of <T-1>-then-<T1>. (The arrows for the “foreground” hyper-transpositions below the music begin and end exactly when the tetrachords whose networks they hyper-transpose are sounding.) This hyper-transposition progression matches the opening registral undulation of the right hand, as shown in Figure 3b. However, the two progressions diverge from there: another <T-1> in m. 10 minimally distorts the mirror again, and the distortion persists through mm. 11–12. Nonetheless, the match reveals a broader symmetry: while one the two last fourths at m. 3.4 is “too high”, one of the two last fourths at mm. 9.3–9.4 is “too low.” Elliot Antokoletz observed this “larger symmetrical balance”(33) in his analysis of “Fourths”; my contribution to this observation posits that this larger (hyper-transpositional) symmetry between measures 3 and 9 is an exact match of the smaller (transpositional) symmetry between the two hands particularly in the first measure, in that both involve semitonal deflections.

      


Figure 3.

(click to enlarge)

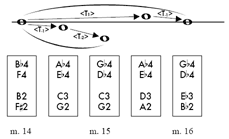
[15] The rest of Figure 3 displays how melodic motions involving mm. 2–3 correspond with hyper-transpositions in mm. 13–16. Measures 13–14 repeat measures 9–10, with the exception of a pragmatic left-hand octave shift that sets up a properly mirrored return at m. 16.1 to the first measure’s referential sonority in its original registration. (This octave shift would technically change the subscripts for the transpositions and hyper-transpositions as shown, since they operate in p-space. For example, the <T(1)> spanning mm. 13 and 14 should be <T-11>, since the right hand ascends by two semitones and the left hand descends by thirteen. However, I propose that T-sets that differ by one or two semitones in pc-space may still be interpreted as part of a registral mirror, just as Schenker allows registral diatonic pitches adjacent in pc-space but non-adjacent in p-space to be in the same linear progression. A subscript in parentheses indicates this cosmetic pitch-class wrinkling of p-space.) There is a strong expectation for a left-hand A-D fourth to be paired up with the right-hand D-G fourth at the start of m. 15, for this is exactly what happened during the corresponding moment in m. 11. A realization of this expectation would continue the registral mirroring in its slightly <T-1>-distorted form. Yet the left hand stubbornly restates the G-C fourth soon after the right hand drops a major second, thus distorting the mirror even more, as represented by the <T-2>. The progression of <T-1>-then-<T-2> matches Parks’s T-1-then-T-2 middleground Terzzug reduction of the right hand in mm. 1–2.4 as shown in Figure 3c. Consequently, the concatenation of the foreground <T-1>-then-<T-2> to a middleground <T-3> matches the foreground minor-third drop in the right hand of m. 2. Indeed, as shown above Figure 3a in a middleground hyper-transposition analysis and its match with the Figure 3d, the progression of four hyper-transpositions on a middleground hypermetric level in mm. 9–16 matches the progression of the first four melodic transpositions in mm. 1–3.1.

[16] To return to the match between Figures 3a and 3c, the last tetrachord in m. 2 and the first tetrachord in m. 15 each achieve, in their respective spaces of middleground registral-pitch relations and foreground inversional-axis relations, the heretofore farthest reach from the starting point, and this apogee is achieved through two cumulative “stepwise” motions. This match is fortified as the music continues from these two moments, in that these two trajectories in their respective spaces do not reverse course but simply dead-end. As aforementioned, the T5 that follows the Terzzug in Figure 2b will likely be perceived as

connecting two voice-leading strata instead of a middleground transposition per se, and was grayed out as a consequence. Likewise, the <T4> in m. 15 that follows the <T-1>-then-<T-2> progression has also been grayed out in Figure 3a for an analogous reason: the move from the first tetrachord to the second in m. 15 is much more easily perceived as a straight T2 transposition that nullifies the currently prevailing “mirror,” rather than a <T4> hyper-transposition that further distorts this “mirror.”(34) Instead, the T2 transposition transports the music back to the cadential gesture from mm. 3.4–4, and back to its mirror characterized by a fourth “too high.” Figure 4 borrows Schenkerian slur notation to represent this visually: the noteheads represent the registral tetrachords in mm. 14–16 (the pitches of each tetrachord are detailed below each corresponding notehead) and slurs connect tetrachords if their component T-sets are related by contrary or oblique motion. In other words, a slur connects moments that can be heard, allowing for minor distortion, as realizing a single “mirror.”(35) The resemblance between Figure 4 and the analysis of the right hand of Figure 2a is intended to portray the aforementioned analogy.

           

Figure 4. Visualization of two different “mirrors” in mm. 14–16

(click to enlarge)

[17] So far, I have demonstrated that the two p-space intervals of a semitone and a minor third, which distinguish mm. 1–3.1, match the two p-space “hyper-intervals” (one and three “notches away,” respectively, from a referential axis) that distinguish mm. 3.4–16. It remains to be demonstrated that the remaining dissimilar melodic interval in the first phrase—the major second—matches the remaining dissimilar “hyper-interval” in the piece. The following imitative section (mm. 17–30) returns to a predominance of <T0> hyper-transpositions in the foreground, relieved by two <T-1>-then-<T1> progressions in mm. 17–21 and mm. 21–25 (not shown) that revisit the same tetrachords from mm. 9–12 and thus perpetuate a match with the right-hand’s T-1-then-T1 sequence from mm. 1–2.1. As shown in the first part of Figure 5a, this section concludes in mm. 24–30.2 with a conspicuous prolongation of the referential sonority and a strict adherence to a registral axis. After an eighth-rest gasp, the music in mm. 30.4–34 returns to the tetrachordal homophony of the opening, compressing the minor-second and minor-third undulations of mm. 1–3.1 into a single measure repeated four times. As shown in Figure 5a, the harmony that initiates the section from mm. 30.4–34 can be considered either as a T-7 of the comparable referential sonority that occurs throughout mm. 25–29, or as a T5 of the very first chord of the piece.

        

Figure 5.

(click to enlarge)

[18] Whereas the T5 p-space transposition is perhaps most easily conceived as a “composing-out” of the titular interval, it also registers a <T10> hyper-transposition in pc-space (T5 + T5), which is then answered by a <T2> in pc-space when the music regains the original pitch-class axis in mm. 42.4–46.2. These hyper-transpositions are placed below Figure 5a. Therefore, in pitch-class terms, the major-second melodic intervals of mm. 3–4 match these hyper-intervals. However, a p-space hyper-transposition at this moment is much more difficult to justify, since there is no obvious mirrored motion between the two components bridged by the hyper-transposition. This suggests that a narrative told with pitch classes instead of registral pitches, and therefore without such a significant phenomenological subplot, might yield a better story. But it bears mentioning that, while mm. 1–4 do contain a melodic major second, a pitch-class T10-then-T2 melodic undulation that would match the <T10>-then-<T2> axis progression does not exist in this opening phrase; in fact, it is this exact melodic undulation that was denied the left hand in mm. 3–4 (Figure 5b) to avoid pitch-class duplication. Therefore, I prefer a registral-pitch narrative that 1) acknowledges transpositional progression (particularly deflection and return) above the more generic idea of “interval” or “x notches apart,”and 2) matches—in the manner of a negative image, as depicted by the oval “negation” icons in Figure 5—the phenomenological denial of <T-2> as deflection from a referential inversional axis to the textural denial of T-2 as deflection from the referential sonority in the left hand at m. 3.4.

[19] I also prefer such a narrative, because the T2 deflection in the right hand of m. 3 does achieve a match with a hyper-transpositional deflection at the very end of the piece. Measures 35–42.1 feature no p-space mirrors, at least none that incorporate ordered pitch sequences. As shown in the opening of Figure 6a, mm. 42.4–46.2 transpose the mirrored music of mm. 30.4–34 back to start on the referential sonority, resetting the inversional axis to an octave below

that of the opening. The final measures of the piece (46.4–50) also create a registral mirror, although with reflections slightly displaced chronologically from their subjects as in earlier passages. In pitch-class terms, the referential “sum-4” axis in mm. 42.4–46.2 changes to a “sum-6” axis for the conclusion; therefore, a pitch-class <T2> hyper-transposition links these two passages. But I believe that this pitch-class <T2> hyper-transposition can be more easily heard as a p-space <T2> hyper-transposition than the same in m. 30. The difference comes from using Bartók’s ossia passage, provided in Figure 6b. This alternate ending affixes the Aussensatz notes of the referential sonority (G-flat in the right hand, B-flat in the left hand) to the registral extremes of the fourth-stacks. This addition strengthens the ties between these last two sections: before the final measure’s E-flat, the essential melody in these two final sections remains G-flat, but the essential bass shifts from B-flat up to the pc-proximal C, as shown with the T(0) and T(2) transpositions in Figure 6b (again, the parentheses signify the allowance of octave transfers in the case of pitch-class stepwise motion). This permits the hearing of the bass as two semitones “too high”—or, more generally, <T2>—from where it should be if the axis were to remain in place.

           

Figure 6.

(click to enlarge)

[20] This divergence is even more apparent when comparing the ossia ending to the recomposition in Figure 6c. On the one hand, my staid recomposition maintains not only the same axis, but also the Aussensatz of the previous section (mm. 42.4–46.2); furthermore, the notes of the referential sonority dominate the texture. On the other hand, Bartók’s <T2> merges the left-hand’s D-flat with the right-hand’s E-flat, creating tonal concord and closure on the root of the referential sonority. Hence, whereas the T2 of m. 3 threatened pitch-class duplication, the <T2> of the end embraces pitch-class duplication, and axis centricity gives way to pitch-class centricity.

[21] Figure 7 summarizes the proposed matches. Each progression of arrows creates a network of transpositions specified by the directed pitch intervals of the corresponding hand. Each network then matches a hyper-network of hyper-transpositions that governs the change of axes over the accompanying span of measures (or each of the spans, if there are multiple spans). All of the pitch-axis divergences match melodic divergences in this first phrase with the exception

of mm. 26–46. In this case, both network and hyper-network are anomalous: the network avoids a realization of the expected whole-tone left-hand descent that would maintain p-space symmetry, and the hyper-network avoids a realization of the change of axis in p-space. Figure 7 could support a number of analytical narratives where a structure of the whole is synecdochally encapsulated by one of its parts. Such narratives could just as well be recounted using pitch classes instead of registral pitches, and Figure 7 would serve as a fine storyboard either way. But, p-space relationships deliver potentially intricate narratives in plain talk, a balance that may help make the story worth retelling.(36)

           

Figure 7. Summary of matches between hyper-networks in “Fourths” and networks in mm. 1–4


(click to enlarge)

***

[22] As Richard Cohn points out, registral inversional mirroring is not common in Bartók’s music, suggesting the analytical method used above does not have wide applicability to the composer’s music.(37) Furthermore, in some instances of Bartók’s mirroring, entire works or long excerpts thereof adhere to a single axis. In such passages, the mirror becomes the ground for other interesting figures, instead of the figure itself. But, Bartók also occasionally made room for distortions and displacements of p-space inversional symmetry as musical tokens in their own right, and some of these distortions, interpreted as hyper-transpositions, match significant transpositions. I can report two such examples from Book 6 of Mikrokosmos. In “March” (no. 147), the two most important three-note motivic successions can be represented by the pitch interval series +2, +2 and +1, +2, along with their inverses and, in the case of the latter, their retrogrades. The most conspicuous registral mirroring in “March” akin to that seen in “Fourths” is in mm. 39.4–41.1, shown in Figure 8.

While the triplets present forms of the +1, +2 motive on the surface, the right hand transposes the four-note motive down twice by major second, composing-out the inverse of the +2 +2 pattern. Moreover, the left hand’s motives ascend by major third, creating a series of <+2> <+2> hyper-transpositions if one considers the relation between the hands. In “Minor Seconds, Major Sevenths” (no. 144), the opening thematic statement, provided in Figure 9, occupies the first eight measures. In contrast to “March,” “Minor Seconds” is preoccupied with inversional axes from the outset: the right hand’s music in the first three and a half measures is perfectly reflected in the left hand’s music around a G4/A4 axis. Minor-third leaps, represented in Figure 9 with T3’s and their mirrored T-3’s, articulate the downbeats of measures 2 and 4. When the succeeding music briefly departs from the G4/A4 axis but still employs synchronous contrary motion between the two hands, the resulting <T-3>s articulate the downbeats of measures 6 and 8.

[23] One final loose end needs tying up. I have yet to respond to Buchler’s fifth argument: since “the objects of a ‘foreground’ K-net are (generally) pitch classes and the transformations that map those pitch classes to each other,” and “the objects of a ‘middleground’ K-net are transformations and the transformations that map those transformations to each other,”(38) then there is a “musical incommensurability of upper- and lower-level structures.”(39) Even self-dissimilar analyses must face this argument. One rebuttal is to draw on the concept of analogy, as I have done periodically throughout. Although registral pitches and registral axes are not alike, the conceptual schema of “x notches up/down” or “x notches apart” in some ordered space allows us to match pitch comparisons (transpositions) with axes comparisons (hyper-transpositions).

[24] But I would like to end by entertaining a different perspective of such matches: one that compares apples with apples, at least as far as the transformations themselves are concerned. Consider Figures 10a and 10b, which compares the ending of the “Fourths” recomposition from Figure 6c with that of Bartók’s original ossia ending. Instead of speaking in hyper-transpositions, one can simply state that the T2 transposition maps what is expected in the left hand—given a preservation of the axis—to what actually occurs in the left hand. This T2 transposition is the same kind of transposition that maps successive or simultaneous pitches to one another. However, rather than mediating across a chronological span between two successive pitch sets, this T2 transposition mediates the span between a pitch set that is at hand and a pitch set that could have served in its stead. Linguists refer to these two types of relations as syntagmatic (the this-AND-that axis of combination) and paradigmatic (the this-OR-that axis of selection), respectively. A work that establishes and reinforces a clear and reliable inversional scheme makes it possible for one to predict what pitch events will follow when the mirrored events are chronologically staggered. Predicted pitch events can then be compared along the paradigmatic axis to what actually occurs in the place of the expected pitch event. In “Fourths,” these paradigmatic relations, formulated as pitch transpositions, are rendered in the first three measures along the syntagmatic axis, in that they are realized through successive combinations of pitches. (Note that those hyper-transpositional networks that involve staggered reflections match only right-hand networks in mm. 1–3.)

         

Figure 8. Bartók, “March,” mm. 39.4–41.1


(click to enlarge)
 

Figure 9. Bartók, “Minor Seconds, Major Sevenths,” mm. 1–8


(click to enlarge)
 

Figure 10. Projecting the paradigmatic to the syntagmatic

(click to enlarge)

 

[25] In answering the question “What makes a verbal message a work of art?”, the linguist Roman Jakobson offered this oft-quoted solution: “The poetic function projects the principle of equivalence from the axis of selection into the axis of combination.”(40) By “principle of equivalence,” Jakobson meant that a word could be replaced by something identical to it in some way (phonological, semantic, etc.); the poetic function then turns such paradigmatic equivalences into syntagmatic iterations. Nicolas Ruwet grasped onto this particular paradigmatic relation of “equivalence” when he applied Jakobson’s axis projection to a semiotic analysis of music, the art form whose lifeblood is repetition.(41) But Jakobson notes other paradigmatic relations: “The selection is produced on the base of equivalence, similarity and dissimilarity, synonymity and antonymity...”(42) My focus particularly on deflections in “Fourths” has particularly concerned the paradigmatic relation of dissimilarity, in that I have highlighted those moments when, assuming the maintenance of a registral axis, “what could (should) be” and “what is” are different. And yet, when such paradigmatic differences, which constitute an inversional grammar private to this work, are concentrated and reified to form the syntagmatic substance of its first phrase, I cannot help but speculate that this too is poetic.


Scott Murphy
University of Kansas
Department of Music and Dance
1530 Naismith Dr Rm 220
Lawrence, KS 66045-3102
smurphy@ku.edu 

Bibliography

Alegant, Brian. 1999. “When Even Becomes Odd: A Partitional Approach to Inversion.” Journal of Music Theory 43.2: 193–230.

Antokoletz, Elliott. 1984. The Music of Béla Bartók: A Study of Tonality and Progression in Twentieth-Century Music. Berkeley: University of California Press.

Buchler, Michael. 2007. “Reconsidering Klumpenhouwer Networks.” Music Theory Online 13.2.

Burkhart, Charles. “Schenker’s ‘Motivic Parallelisms’.” Journal of Music Theory 22.2: 145–175.

Carey, Norman and David Clampitt. 1996. “Self-Similar Pitch Structures, Their Duals, and Rhythmic Analogues.” Perspectives of New Music 34.2: 62–87.

Cohn, Richard. 1988. “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 12: 19–42.

Cohn, Richard, and Douglas Dempster. 1992. "Hierarchical Unity, Plural Unities: Toward a Reconciliation." In Katherine Bergeron and Philip Bohlman, eds., Disciplining Music: Musicology and Its Canons (Chicago: University of Chicago Press), 156–181.

Gollin, Edward. 1998. “Some Unusual Transformations in Bartók’s ‘Minor Seconds, Major Seconds’.” Intégral 12: 25–51.

Jakobson, Roman. 1958. “Concluding Statement: Linguistics and Poetics.” Style in Language, 350–377. Ed. Thomas A. Sebeok. Cambridge: MIT Press.

Klumpenhouwer, Henry. 1991a. “Aspects of Row Structure and Harmony in Martino’s Impromptu Number 6.” Perspectives of New Music 29: 318–54.

__________. 1991b. “A Generalized Model of Voice-Leading for Atonal Music.” Ph.D. dissertation, Harvard University.

__________. 1994. “An Instance of Parapraxis in the Gavotte of Schoenberg’s Opus 25.” Journal of Music Theory 38: 217–48.

__________. 1998. “Network Analysis and Webern’s Opus 27/III.” Tijdschrift voor Muziektheorie 3.1: 24–37.

Lambert, Philip. 2002. “Isographies and Some Klumpenhouwer Networks They Involve.” Music Theory Spectrum 24.2: 165–195.

Lewin, David.1990. “Klumpenhouwer Networks and Some Isographies That Involve Them.” Music Theory Spectrum 12: 83–120.

__________. 1994. “A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg’s Opus 11, No. 2.” Journal of Music Theory 38: 79–101.

__________. 2002. “Thoughts on Klumpenhouwer Networks and Perle-Lansky Cycles.” Music Theory Spectrum 24.2: 196–230.

Parks, Richard. 1981. “Harmonic Resources in Bartók’s ‘Fourths’.” Journal of Music Theory 25.2: 245–274.

Rahn. John. 1980. Basic Atonal Theory. New York and London: Longman.

Ruwet, Nicolas. 1987. “Methods of Analysis in Musicology.” Trans. by Mark Everist. Music Analysis 6.1–6.2: 3–36.

Stoecker, Philip. “Klumpenhouwer Networks, Trichords, and Axial Isography.” Music Theory Spectrum 24.2: 231–245.

Vishio, Anton. 1991. “An Investigation of Structure and Experience in Martino Space.” Perspectives of New Music 29.2: 440–476.

References

1.  At multiple moments, Buchler (2007) shows a preference for p-space relationships, although he does not explicitly mandate them at the exclusion of pc-space relationships. First, he finds K-net analyses “compelling” when “the T-sets that form K-nets are presented in similar registers, timbres, dynamic ranges, etc.” (53). He applauds Catherine Nolan’s “well-grounded” analysis of Webern’s Das Augenlicht, op. 26 for, among other things, the fact that “the intervals of transposition were literally projected in p-space, and her graphical display maintained registral integrity.” (53) He also chides David Lewin’s analysis of the “chorale” from Schoenberg’s op. 11/2 for rejecting “p-space consistency.” (61)
Return to text

2. Buchler 2007, 56.
Return to text

3. Ibid, 59.
Return to text

4. This pedagogical strategy of using p-space relationships as a stepping stone toward the apperception of pc-space relationships occurs in the K-net literature. For example, both David Lewin (1990, 85, Example 1) and Philip Lambert (2002, 167–168, Example 6) provide very similar approaches to hearing the <T0> relationship between {A4, F5, B5} and {C4, F4, B4} in the opening of Schoenberg’s op. 19/6: both tease apart the pc relationship into multiple stages, of which the first operates in p-space. My recommendation is to use my analysis of “Fourths” to do the same thing, but as the initial stage in understanding K-nets in general, rather than a specific work’s chordal relationship in particular.
Return to text

5. Buchler 2007, 2. I am assuming that, in his broad definition, “hierarchical” refers only to different levels of structure, and not necessarily a tree structure that organizes these levels.
Return to text

6. Ibid, 59.
Return to text

7. The use of quotation marks around “strong isography” follows in part from Lewin 1990, 95–96, who makes a distinction between “isographies” (with quotes) between two different levels, and isographies (without quotes) within a single level.
Return to text

8. Network Z is a retrograde of network Y if every transposition in network Y is replaced by the inverse of this transposition in network Z, and every inversion in network Y is replaced by an inversion in network Z such that network Z is well-formed. “Transposition,” speaking generally of any dihedral group whose members constitute the networks, refers to a member of the largest cyclic subgroup of the dihedral group, whereas “inversion” refers to any member that is not a transposition.
Return to text

9. It is possible to arrange the chords g1, g2, g3, and g4 in the “chorale” of Schoenberg’s op. 11/2 (Lewin’s 1994, 87) into isographic networks and then into a hyper-network that would achieve exact self-similarity with one of its constituents: it requires interpreting each chord as a combination of an ic1 and an ic2. The ensuing hyper-network is exactly self-similar to g1. The fact that g1 is the “prolonged” chord in both Lewin’s hyper-network and mine seems rather remarkable.
Return to text

10. Two networks are in different modes if they are not strongly isographic nor retrogrades of one another.
Return to text

11. Buchler 2007, 64.
Return to text

12. Ibid, 65.
Return to text

13. Ibid, 68.
Return to text

14. Ibid, 66. In this critique, Buchler shows a preference for the consistency of object across hierarchical levels. He argues that the hierarchy of Schenkerian analysis, to which K-net hierarchies are sometimes compared, has this consistency: “In Schenkerian analysis, notes are present at every level and pitch structures are never replaced by relational structures.” Richard Cohn and Douglas Dempster (1992) have criticized this “representational” view of Schenkerian hierarchy as arbitrary and non-intuitive of certain voice-leading patterns; rather, they show a slight preference for an “inclusional” view of Schenkerian hierarchy, in which events removed from the foreground “represent abstract classes of events” (163). This description comes considerably closer to Buchler’s description of K-net hierarchy.
Return to text

15. As an informal proof of this, imagine a hyper-network with only hyper-transpositions. A self-similar correspondence would then require that one of the hyper-network’s constituent networks be structured the same: it would have a Tn in every place that the hyper-network has a <Tn>. Since hyper-transpositions map transpositions to themselves, every network in the hyper-network would be strongly isographic to every other network, including the network engaged in the self-similarity. This would seem to augment the self-similarity: not only a part, but every part, of the whole would have the same structure as the whole. However, any set of hyper-transpositions could create an equally well-formed hyper-network, thus trivializing the self-similarity.
Return to text

16. For more on self-similar scales, see Carey and Clampitt 1996.
Return to text

17. “More colloquially, a certain structure of interrelations among interpretations of the first three chords, Figure 12a, ‘prolongs’ at a hierarchical level the interpretation of the first chord [of the three], Figure 12b. The notion of ‘prolongation’ is powerful here.” (Lewin 1990, 94)
Return to text

18. In Lewin 1990, 93 (Figure 11), the matching network interprets the first chord of the progression. In Lewin 1990, 98 (Figure 15), the matching network interprets the last chord of the progression. In Klumpenhower 1991a, 343–344 (Examples 39 and 40), the set that the matching four-node network interprets comprises two overlapping trichordal members of the set-class that pervades the excerpt. In Klumpenhouwer 1991a, 352–353 (Examples 55 and 57), multiple matches involve networks that interpret the melodic notes of germane progressions. In Klumpenhouwer 1991b, 7:23–7:24 (Examples 7.26 and 7.27), the network for the first three instances of triple counterpoint matches the hyper-network that comprises three subsequent networks-of-instances. In Klumpenhouwer 1994, 242–243 (Examples 29–31), the matching network interprets the first chord of the progression. In Gollin 1998, 51 (Figure 10), the two equivalent matching networks are both cadential sonorities that conclude the phrases containing the sets involved in the hyper-network. Stoecker 2002, 244 (Example 12) creates dual matches for a six-chord progression that symmetrically engage both extremities: the network interpreting the first chord matches the hyper-network interpreting the last three chords, and the network interpreting the last chord matches the hyper-network interpreting the first three chords.
Return to text

19. Klumpenhouwer 1991b, 7:24.
Return to text

20. Lewin 1990, 98.
Return to text

21. Ibid, 99.
Return to text

22. Gollin 1998, 51.
Return to text

23. Toward the conclusion of Burkhart’s article, he writes: “A brief résumé of the foregoing examples will show that they exhibit a diversity of structural characteristics. In some, the motivic statements nest one within the other; in others, they are temporally separate.” (Burkhart 1978, 167)
Return to text

24. Parks 1981, 264.
Return to text

25. For the purposes of indicating precise metrical moments in the analysis, the notation “x.y” indicates the temporal position of the yth eighth note in the xth 2/4 measure.
Return to text

26. Alegant 1999, 201.
Return to text

27. These pitch transpositions are those of Rahn 1980, 40 ff., although the superscript “p” has been omitted for the purposes of this article, as all of the transpositions herein operate in p-space unless stated otherwise.
Return to text

28. Anton Vishio’s “divergences” (1991, 458 ff.) are comparable to p-space hyper-transpositions, since they are formulated within p-space as well as pc-space. One could also re-engage group theory and conceive of p-space hyper-transpositions as well-defined group automorphisms that operate on pitch transpositions and pitch inversions.
Return to text

29. Buchler’s concerns about packing “too much information” (2007, 30) into the subscript number of a hyper-transposition are hopefully mollified in the particular case of <T0> in p-space, in that the loss of information is balanced by the snug fit between the label and the general perception of exact registral mirroring.
Return to text

30. Alegant 1999, 201 (Figure 5b).
Return to text

31. Parks 1981, 266.
Return to text

32. In his critique of analysts who exclusively employ the inversional-symmetry (IS) model, Richard Cohn states that they “have been committed to the idea that IS-pieces derive their coherence from tracing monophonic paths between these various axes. The commitment to such paths is often incompatible with the analytical demands of complex musical structures.” (1988, 27) The hierarchies proposed in this analysis of Bartók’s “Fourths” suggest one way of weaving such paths into more “complex musical structures,” provided that such structures are an analytical priority.
Return to text

33. Antokoletz 1984, 198.
Return to text

34. Buchler (2007, 54) shows a preference for fuzzy transpositions in p-space over hyper-transpositions. I would imagine that hyper-transpositions would fare even less well when compared to crisp transpositions in p-space.
Return to text

35. For interpretations such as this, I embrace Buchler’s recommendation that the hyper-transpositions be differentiated by their constituent dual transpositions; for example, <T-1> ((-2)+(+1)). As a general rule, I propose that p-space hyper-transpositions may perpetuate a mirror if the signs (+, -, or 0) of the dual transpositions are unlike (contrary or oblique motion), and they may not if the signs are the same (parallel or similar motion). As with Schenker’s linear progressions, octave transfers may be accommodated.
Return to text

36. It needs to be mentioned that this is nothing new to K-net analysts, who occasionally demonstrate how certain relationships afforded by their network analysis unfold in p-space. For one example, see Klumpenhouwer 1998, 28 (Example 9).
Return to text

37. “Although textures such as those in Example 1 [which gives three brief excerpts that project symmetry about a central pitch axis] easily draw one’s attention, they actually comprise only a small fraction of Bartók’s total compositional output. That is, it is unlikely that the surface of a randomly chosen Bartók fragment would suggest an inversional design as clearly as these passages.” (Cohn 1988, 20)
Return to text

38. Buchler 2007, 66.
Return to text

39. Ibid, 68.
Return to text

40. Jakobson 1958, 358.
Return to text

41. Ruwet 1987.
Return to text

42. Jakobson 1958, 358.
Return to text


Copyright Statement

Copyright � 2007 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Brent Yorgason, Managing Editor
Updated 15 May 2008

Number of visits since September 2007:

free web tracker