An Algorithm for the Direct Generation of Set Class Representatives in Any Pitch Class Space ^*

[1] Introduction

[1.1] A program for generating equivalence classes (set classes) of pitch class sets is an essential tool to support music theory mathematical research, with concomitant repercussions in compositional exploration. For example, a researcher might wish to investigate possible chord types with respect to transposition and inversion in a 24 pitch class space with a view to some mathematically interesting property; an analyst might be working on classifying harmonic content in Ives’ Three Quartertone Pieces for Two Pianos (1903–23); a composer might wish to explore some novel pitch combinations with respect to that space. Unfortunately, as the number of pitch classes increases, a combinatorial explosion occurs in the number of classes which must be catalogued. The naive approach to finding set classes is an exhaustive search, whereby one generates all possible pitch class sets, adding a set to the list of representatives only where it is not equivalent to a set earlier on the list. Each passed candidate can then be placed in a ‘prime form’ as a suitable representative. This naïve approach becomes too slow for practical purposes for spaces not much larger than the aforementioned quartertone space. This article provides an algorithm that should give more efficient access to equivalence classes, making the construction of complete lists of set classes computationally tractable for much larger spaces.

[1.2] The terminology of music theory mathematics herein shall follow Fripertinger’s excellent foundation (1999) but with some service to the standard pitch class analytic terms of Forte 1973 for those less versed in combinatorics. As terms are introduced, I will try to illustrate them with a Fortean example. To Fripertinger the n-scale \(Z_n\) provides the pitch material, which to the music theorist raised on Forte just means the set of integer pitch classes \(\{0, 1, \ldots , n-1\}\). Therefore, the standard music theoretic world of 12 pitch classes uses pitch material from the 12-scale \(Z_{12}\) or \(\{0, 1, \ldots , 11\}\). Pitch class sets are constructed in the usual manner, as some collection of pitch classes without duplication, and the pc set [1, 2, 5, 7] is taken as an example for this paragraph (pc set is Forte’s shorthand for pitch class set). Fripertinger’s k-chords are pitch class sets of cardinality k, so our example pc set is of course a 4-chord. What are conventionally referred to as set classes are collections of pitch class sets which can all be interrelated by some musically relevant operations, conventionally transposition and inversion. The set class is tagged by a representative pc set from which all other members of the class can be generated by the operations in question. Our tame pc set is in the set class (with respect to transposition and inversion) which has representative [0, 1, 4, 6], named 4-Z15 in the Forte list (1973, 179), and our pc set may be recovered from this representative after transposition up by a semitone. In more mathematical language, set classes are equivalence classes (orbits) under the action of some group operations which define equivalence.

[1.3] The equivalence classes of k-chords under some group action are the set classes whose representatives have cardinality k. If a set class has a representative pc set of cardinality k (a k-chord), it shall be referred to as a k-set.⁽¹⁾ As a set class, 4Z-15 is a 4-set. Pitch class spaces of pitch class sets on n pitch classes are termed n-spaces, or \(Z_n\) for convenience. It is trusted that this informal notation for the space, which overlaps with the pitch materials definition, will not be confusing and that context will make such usages clear.⁽²⁾

[1.4] It is left to formally describe the equivalence relation with respect to which set classes are constructed. The exposition here is somewhat mathematical; the casual reader is referred to Morris 1987 for a lighter introduction. The permutation operators of transposition T and inversion I are generators for a permutation group which acts on \(Z_n\).⁽³⁾ The standard group generated by transposition and inversion \(<T, I>\), being the dihedral group \(D_n\), is the usual case for pitch class analysis. Forte’s list of set classes is with respect to transposition and inversion; the acting group is \(D_{12}\). Permutation under the action of a group defines the equivalence relation from which the classes must be generated. In mathematical parlance, the action of the permutation group generates orbits; an orbit is simply an equivalence class. The algorithms discussed below should cope with any valid equivalence relation, so have utility to help construct any desired set of set class representatives in pitch class mathematics.

[1.5] An exhaustive search approach was already mentioned as the straight forward but impractically slow method to generate set class representatives. Fripertinger treats the problem of generating representatives by utilizing Read’s Orderly Algorithm (1978), an approach from the mainstream of combinatorial mathematics. He also notes that the step of testing a candidate pc set for canonicity (whether it is a representative) can have shortcuts based on the permutation subgroup in question. When that subgroup is \(<T, I>\), as in standard music theoretic work, there are only 2n possibilities for the representative anyway, allowing a simple method of creating the class and checking against its prime form. Fripertinger acknowledges the difficulties of set class generation for larger n; for large spaces, he recommends probabilistic sampling of representatives.

[1.6] Read’s Orderly Algorithm (1978) is a general method for exhaustively generating equivalence classes without any backtracking through that same list, when certain conditions are met.⁽⁴⁾ The construction can be adapted to the combinatorial objects of pitch class analysis in a similar way to Read’s treatment of digraphs, using the schema of ‘a general problem’ on page 112. Let S be the set of dimension n vectors with elements 0 or 1; members of S can be imagined as characteristic function vectors across \(Z_n\). The characteristic vector form is further discussed in the next section. To temporarily relate the notation of Read’s paper to that within this, Read’s \(S_q\) will be those vectors where the sum of elements is q, i.e. q-chords. The equivalence classes are Read’s lists \(\mathcal{L}_q\) of q-sets. In Read’s method, the representatives of a certain cardinality are generated from those of cardinality of size one less, so an iterative process produces the equivalence classes of a space, that is, \(\mathcal{L}_{q+1}\) is generated from \(\mathcal{L}_q\). The production of (q+1)-sets requires the q-sets to be created first. This places restrictions on getting directly at objects of interest, particularly where the combinatorial explosion in the number of objects means that many intermediate objects must be generated prior to those sought. Because pitch classes yield to a simple binary number coding, and some leveraging of that representation allows improvements on Read’s methods for the particular case of interest to music theorists, an alternative algorithm can be created which can more directly produce the q-sets in any given n-space.

[1.7] The remaining sections of this paper work to outline this algorithm. In section 2 a natural binary coding in common use in computational work with pitch class sets is described. In section 3 pseudocode and rationale for the algorithm is provided.

[2] Coding of Pitch Class Sets

[2.1] Computational work with pitch class sets has a very natural encoding available; sets are identified with integers by a binary or base two code. Given any pitch class set \(S \subseteq Z_n\), characteristic functions \(\chi_S\) return 1 or 0 for an input \(i \in Z_n\) depending on whether \(i \in S\) or \(i \notin S\) respectively. Again, using Forte 4Z-15 in \(Z_{12}\), and the representative pc set S = [0, 1, 4, 6] as an example: $$ \chi_{[0, 1, 4, 6]}(0) = 1 \\ \chi_{[0, 1, 4, 6]}(1) = 1 \\ \chi_{[0, 1, 4, 6]}(2) = 0 $$ etc. Necessarily, the characteristic function of this 4-chord will output a 1 for four values and a 0 for eight in \(Z_{12}\).

[2.2] A vector form for the pc set can be defined using the characteristic function. Each pc set \(S\) in n-space is represented by an n component vector which contains the output of the characteristic function across the domain of pitch classes of the space: $$ {\chi_S(i) : i \in Z_n} $$ So for S = {0, 1, 4, 6}, an equivalent vector form of characteristic function is [1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0]. By thinking of this vector form as a binary number, a single number can be produced for any pc set.

[2.3] Now to the coding. A decimal number can be associated with any binary number vector such that $$ {\chi_S(i) : i \in Z_n} \equiv \sum_{i=0}^{n-1} \chi_S (i) 2^{n-1-i} $$ As an example, for S = {0, 1, 4, 6}, the single unique number associated is $$ 1 \times 2^{11} + 1 \times 2^{10} + 0 \times 2^9 + 0 \times 2^8 + 1 \times 2^7 + 0 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + 0 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 0 \times 2^0 =\\ 2048 + 1024 + 128 + 32 =\\ 3232 $$

[2.4] The equation above is just an explicit way of saying that \((110010100000)_2 = (3232)_{10}\). The characteristic function gets us into base 2; we may then convert to base 10. Read calls the vector v and the coding code(v) (1978, 112).

[2.5] Especially for any reader familiar with programming, this binary representation should seem a very natural one. Each n-bit decimal number has an associated pc set in \(Z_n\), for the characteristic function demonstrates that an n-digit binary number can represent any pitch class set in n-space. In terms of computer storage, a 4 byte integer can cope with pitch class sets below n = 32 (each byte has 8 bits, so 4 × 8 = 32 bits). An 8-byte integer,⁽⁵⁾ would deal with cases below n = 64, which is also a likely practical limit for exhaustive manipulation (recall the ancient story of the gift of salt on a chessboard . . . ). Advantage can be taken of computer architecture in that all operations on pc sets work with the codes that represent them.

[2.6] The essential advantageous property of this coding is to define a set class representative as the pitch class set in that class with maximal code. Given any pitch class set, an immediate test for canonicity is: generate the set class, testing for any equivalent pitch class set with a higher code. Since the music theory operations of transposition, inversion or optional multiplication are simple to apply, and the permutation subgroup is not that large (2n for dihedral \(<T, I>\)), generation of the set class is easily achieved. Computationally, comparison of two pc sets in a class is simply a matter of comparing their codes, so that, code(a) < code(b) implies b is a better representative for the set class than a. There will never be a case of equality since each code is a unique pc set.

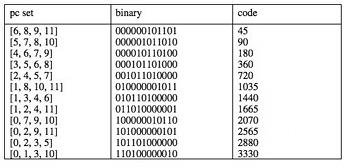
[2.7] For a particular example, consider the possible representatives for the (transposition and inversion) set class containing pc set [0, 2, 3, 5]. Table 1 describes each distinct member of the set class, giving the Fortean array, binary, and decimal code representations. There are 12, not 24, because this pc set is self inverse after a transposition of 7 semitones. The maximal code is 3330, so that the equivalence class representative is [0, 1, 3, 10] with this coding. Forte’s prime form algorithm gives a representative of [0, 2, 3, 5] for the 4-10 class (because of his compactness of set elements condition), but note that for the binary coding used here, code([0, 2, 3, 5]) = 2880 < 3330. In general, Forte’s set class representative list (1973, 179–81) would differ in some cases from that produced by the natural coding, and Forte’s prime form algorithm is thus unnecessarily complicated as a computational entity compared to the coding described here.

[2.8] The maximal code pc set as representative idea leads directly to a first draft algorithm—exhaustively produce all possible pitch class sets, testing each for canonicity (maximal number code within its class). Add representatives to the output list. The coding thus avoids isomorphism search through the list of representatives garnered so far, which is one step up from the naive algorithm introduced at the beginning of this paper.

[2.9] We can do better. An exploitation of the maximal code property of representatives is a sufficient basis to go directly to finding all representatives of cardinality k, with an adapted use of Read’s orderly generation based on augmentation. The naive approach of generating all pitch class sets in that space can be reduced to a more manageable generation of all k-chords. A refinement to achieve this will now be described which uses a stack data construction.

[3] An Algorithm for Generating k-sets

[3.1] The problem of the direct generation of all k-sets in \(Z_n\) has been reduced to the question: is there an efficient way to generate all k-chords? Given an exhaustive list of k-chords, representatives are found using the maximal code test described in the previous section. In fact, finding all k-chords is the same as producing all binary numbers which have k 1s in their bits. The algorithm to be described in this section tackles this problem. Considering the problem domain, some inspiration was gleaned from computer science, in particular from Sedgewick’s descriptions of tree traversal, recursion and stack methods (1992). A stack is an efficient data structure for these goals, used to traverse a tree of possible binary numbers, the traversal being intimately related to a recursive procedure. The reader might intuitively appreciate that finding all k-chords can be an iterative construction that may leverage the (k – 1)-chords and thus act recursively. There is a similar iterative constructive process in the standard Orderly Algorithm, but tricks particular to set classes and the stack data container can be applied to reduce the workload, both in terms of the number of pc sets (binary numbers) to be tested, and in the working memory required.

[3.2] A few immediate shortcuts are noted. Degenerate cases for \(k = 0, 1, n-1\) and \(n\) are readily dispensed with. Complementation means that only k less than or equal to \(\lfloor\frac{n}{2}\rfloor\) need be calculated.⁽⁶⁾ Critically, since all solutions have at least one 1, and the maximal code is the representative, the leading (leftmost in the base two number) bit is always a 1. Hence, the problem reduces to finding all ways of placing \(k-1\) 1s into \(n-1\) slots.

[3.3] Using a stack data structure avoids holding too much data in memory at any one time; as exploited in the algorithm here, it naturally provides the next pitch class set to consider at each step. The representation used for descriptive convenience is the array form of a binary number (Read’s vector) as introduced above.⁽⁷⁾ With each array in the stack, an associated recursion level is recorded, identifying the number of 1s in that set, and the position of the last 1 is also stored for convenience.

[3.4] An essential lemma used to keep the stack small and the number of tree branches low is Read’s theorem on canonical elements and the augmentation operation (1978, 112–14). This is also used in the original Orderly Algorithm to justify the augmentation step. In short, the lemma means that only representatives need be kept in the stack as generating elements for further possible representatives. Intermediate stack pitch class sets will be representative M-sets for \(M < k\).

[3.5] Pseudocode for the equivalence class generation algorithm is presented in Figure 1. Please be aware that this describes generating the \(k-1\) 1s into \(n-1\) slots as noted as a shortcut above. Whilst the canonicity test algorithm has already been described, the generation of candidates must be explained; it is basically Read’s augmentation operation with a further shortcut. Pseudocode for this subroutine is presented in Figure 2. Given any pitch class set in array form, trailing zeroes at the right are successively converted from left to right into 1s. So, the array [1, 0, 0, 0] would be augmented to the set [1, 1, 0, 0], [1, 0, 1, 0] and [1, 0, 0, 1]. If the current recursion level is l, less than k, there must be space for \(k-1\) further 1s, and any arrays without adequate space on the right can be discarded at this point. This gives a further performance enhancement over the Orderly Algorithm.

[3.6] By studying the pseudocode (particularly Figure 2) and example below the reader may be able to convince themselves that the stack size can never exceed \((n - k + 1)(k-1)\), and in practice, through the requirement that any pc set in the stack be canonical, is always smaller.

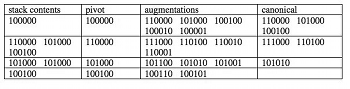
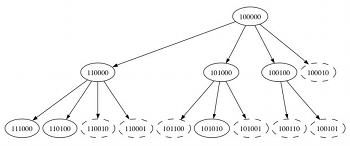
[3.7] As an example of the algorithm’s approach, the discovery of the 3-sets in \(Z_6\) is made explicit in Table 2. Each successive line of the table gives the current contents of the stack, the next pivot element read off the stack (current generator) and the augmentations and successful canonical elements discovered. Note that the augmentations ignore any element where there would not be room for the target three 1s (see pseudocode in Figure 2). Furthermore, only canonical elements make it through onto the stack, because of Read’s lemma mentioned above. 3-sets themselves do not have to go onto the stack, they are simply output to the file when they appear. To show the relation to a tree traversal, Figure 3 shows the same algorithm at work, in terms of the creation of a tree of binary numbers. Each row is one recursion level of the algorithm, so that the 1-sets are the first row, the relevant 2-sets the second and the candidate 3-sets the third. Non-canonical elements discarded along the way are denoted by the dashed rather than solid ellipses.

[3.8] In performance, the stack version uses only memory storage rather than intermediate files to hold representatives, and the tricks built into the optimization detailed here mean that less testing of canonicity is carried out. For finding the 4752 \(<T, I>\) 10-sets in \(Z_{20}\) the original Orderly Algorithm must create eight intermediate output files (for the 2-sets through 9-sets) and call a canonicity test 41834 times. The stack algorithm which tries to go more directly to the 10-sets does so with 29397 tests, with a stack that never holds more than 11 numbers! Note that a naïve approach would require 184756 tests if it could generate just the 10-chords (using a stack algorithm without any refinements), or 220 = 1048576 tests to work on every binary number.

[3.9] There is no guarantee that representatives will be generated in order of code, but a single sort of the output file solves that if it is an issue.

[4] Implementations of the Algorithm

[4.1] The algorithm was prototyped in the SuperCollider 3 audio programming language (2002), and a library of extensions for the manipulation and generation of pitch class sets and set classes created to support the work. This PCSet Library has been released under the GNU GPL and is available from http://www.sicklincoln.org/code.htm. Whilst this code is adequate for the exploration of pitch class universes for \(n \leq 20\) it is too slow for creating the representative lists for large n. An efficient C++ implementation has been created (in the Mac OS X XCode compiler) for large n, specifically for the standard \(<T, I>\) group, though other groups could easily be programmed. A binary number coding is exploited, alongside binary masking versions of transposition and inversion, using the unsigned long long type, which can cope with up to 64 bit integers; thus, \(n \leq 64\) is the scope of the implementation. Given the combinatorial explosion involved, it is unlikely that anyone would attempt to go higher, except for finding k-sets within n-space for \(n \gg k\). The performance gain is worthwhile; generating the 12-sets in \(Z_{24}\) takes 3.21 seconds on a 400MHz G4 powerbook. As a test of its facility, this code was used to show that there are 34,324,174 17-sets (representing 2.3 billion or so pitch class sets) in \(Z_{34}\), generating a 385MB ASCII output file in 39 minutes. The source code C++ file is released with this paper for the use of researchers and composers, under the GNU General Public License.

[5] Conclusions

An algorithm has been described which allows the generation of all k-set representatives in a pitch class spaces on n pitch classes. Whilst the Orderly Algorithm is still useful for generating all set class representatives of a space across all cardinalities, the refined algorithm herein goes directly to the k-sets and requires very minimal memory requirements to run.

Nick Collins
Centre for Music and Science
Faculty of Music, University of Cambridge
11 West Road, Cambridge, CB3 9DP, UK
http://www.cus.cam.ac.uk/nc272
nc272@hermes.cam.ac.uk

Works Cited

Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.

Fripertinger, Harald. 1999. “Enumeration and Construction in Music Theory.” In Proceedings of the Diderot Forum on Mathematics and Music, 170–203. Vienna.

Lewin, David. 1987. Generalized Musical Intervals and Transformations. Yale University Press.

McCartney, James. 2002. “Rethinking the computer music language: SuperCollider.” Computer Music Journal 26(4).

Morris, Robert D. 1987. Composition with Pitch Classes. Yale University Press.

Read, Ronald C. 1978. “Every One a Winner or How to Avoid Isomorphism Search When Cataloguing Combinatorial Configurations.” Annals of Discrete Mathematics 2:107–20.

Sedgewick, Robert. 1992. Algorithms in C++. Addison-Wesley.

Footnotes

* Many thanks to MTO editor Timothy Koozin and the two anonymous reviewers for helpful suggestions and encouragement in the preparation of the final article.
Return to text

1. David Lewin introduced these objects as M-sets (1987), referring to the set of set classes whose representatives have cardinality M, where M is conventionally a positive integer; k is used in the sequel, since the integer variable label is obviously arbitrary.
Return to text

2. As Fripertinger notes the Abelian group is implied but not the same as this construct. This paper will use the looser style to avoid an overburdening of notation.
Return to text

3. These are not the only possible generators. Consider Fripertinger’s quart-circle symmetry Q (multiplier coprime to n), also called M in the literature (Morris 1987).
Return to text

4. Recall that in the naïve approach, one tests the next candidate against all existing representatives in the list, which can be very time consuming.
Return to text

5. Provided as an unsigned long long type in C on some systems.
Return to text

6. Complements are generated by switching 0s and 1s and substituting new maximal representatives as needed—the list of set classes is already complete.
Return to text

7. The decimal integers themselves are the entities stored in the output file, where storage space is at a premium. Indeed, a binary file format would allow us to store the bit forms of the representatives very efficiently. The stack, however, is never excessively large, even for large n, and thus array forms may be stored therein. The array form makes it conceptually simpler to do operations like augmentation, though it would be equally possible to achieve this with bit operations on binary numbers.
Return to text

Copyright Statement

Copyright © 2004 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.