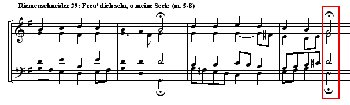Models for Chord Doubling (and Spacing): Which Ones Don’t We Need?
Roger Wibberley
REFERENCE: http://www.mtosmt.org/issues/mto.04.10.2/mto.04.10.2.aarden_hippel.php
KEYWORDS: Bach, chorale, spacing, voice-leading
ABSTRACT: This Commentary will discuss some aspects of the model recently presented by Bret Aarden and Paul T. von Hippel in MTO 10.2 in their article “Rules for Chord Doubling (and Spacing): Which Ones Do We Need?”. Their model will hereinafter be called the OSU Model. Any language—written or spoken—is a code. Through this code the ideas of the originator can be understood by the recipient, and any language thus learnt becomes a suitable and effective medium for scientific or artistic intellectual communication. In this respect the language of tonal music is no different from any other language. As a medium it has its own syntax and structure. But as with any other language its effectiveness as a means of discourse rests upon the assumption that the syntax used by the originator (here the composer) is the same as that to be understood by the recipient (here the listener or the performer). In an age such as ours—far removed from the musical syntax used by those living and working in the age of Bach, Mozart and Haydn—we can only approach the ideas communicated by those of the distant past by revealing exactly what is encoded in the notes they wrote: these are all we have. To understand them is not obvious, self-evident or in any way instinctive to us who live in the 21st Century, and neither could it be. In order to decode such music we must ourselves relearn the code employed. We may then be able to understand not only how they used the syntax, but (arguably more urgently) why and when they employed it in the ways they did.
Copyright © 2004 Society for Music Theory
[1] It is my belief that a meaningful understanding of any composer’s model rests upon the forensic identification of three clear attributes: Motive, Means and Opportunity. Of these, we can simply view each surviving written musical note (in whatever context) as an instance of Opportunity: whatever may have been the reason (or Motive) for writing it, and whatever may have been the factors that bear upon using it in that way (these constituting the Means), its consequent use stemming from these two attributes marked the Opportunity evidenced by its committal to paper. Within this unbreakable chain of creative activity—which begins with a Motive—Opportunity can be seen only as the final link.
[2] The difficulty with any model, including the OSU Model, is that statistical information alone can only record countless numbers of individual opportunities. In this instance the OSU Model has sampled 2643 four-part triads from Bach’s chorale harmonizations, together with 960 four-part triads from the string quartets of Haydn and Mozart. Through an analysis of the note-doubling and chord-spacing tendencies that have been recorded and processed by this model, clear principles for “correct” spacing and doubling can—it is believed—be codified. Yet these principles or “rules” can only provide an abstract insight into the composer’s Means (i.e. his specific technical articulations) that identify each individual Opportunity (i.e. each specific recorded instance of triad notation). No such model can explore a composer’s actual reason or Motive for realizing an opportunity in the way he did.
[3] What I am suggesting is that a composer’s choice of note doubling or chord spacing (or anything else for that matter) was never made simply in order to follow established rules and procedures. Rather each choice was made only because it was a composer’s “preferred solution” that was deemed at that moment to be aesthetically and artistically the best available. As soon as musical practice is described in terms of “rules” we immediately step away from the language of the musician and become engaged with that of the theorist. What therefore begins life as an artistic musical expression then simply ends up trapped in the world of “theorist-speak.”(1) I should therefore like to examine the workings of the OSU Model, and to consider exactly what its pronouncements reveal. This examination will, I think, have more to say about the Model than about the music it tries to analyze.
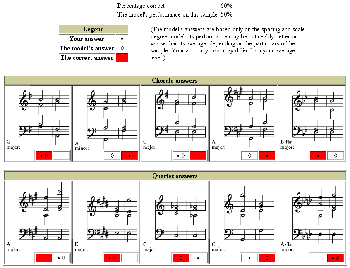
[4] The first procedure, therefore, must be to test the OSU Model in order to probe its brain. For this purpose I clicked on the sidebar headed “Can you beat the computer?” and then selected one of each pair of radio buttons. The result that was returned can be viewed as Figure 1.
[5] As readers will notice, I decided—irrespective of whatever chords had been presented—automatically to select alternately the first then the second of each alternate pair (i.e. for the first pair I selected chord 1, for the second pair chord 2, for the third pair chord 1 and so on). My score of “60%” (being above average) in no way therefore resulted from musical decision-making. Indeed had I decided at the outset to select chords in the opposite order (i.e. starting with chord 2, then chord 1 etc.) my score would have been only “40%.” What is of greater interest, however, is to note that the OSU Model’s own score was only “50%” verifiable when each of its own decisions is compared with what is stated as being “The correct answer.” By “The correct answer” (which must therefore be not only predetermined by the OSU Model, but also then rendered independent from its own adjudication, even though the raw data that define it are contained within the same Model) we have to assume that the “correctness” of each example rests solely upon its authority as having been specifically selected as a real composed chord. The alternative choice in each case is by analogy “incorrect” not because it does not also exist in the repertory as a composed chord, but rather because it did not happen to be the actual composed chord chosen for the test (being instead a randomly reconstituted version of that chord). One, however, is stated as being “correct” while the other must therefore be inferred as “incorrect.”(2)
[6] This particular example of “theorist-speak” has therefore introduced two new technical terms that need urgent qualification: “correct” and (by inference) “incorrect.” Unless they are so qualified and clarified a confusion in the minds of students will immediately exist. They will perhaps take the words at face value (not understanding that these words are themselves merely code) and then mistakenly believe that certain chord spacings and doublings are empirically correct merely because they (the students) have misunderstood what is here meant by the coded word “correct.” Perhaps the greater hazard is presented by the inference that certain triadic configurations are (by default) incorrect. Again taken at face value, the use of the coded (but here only deductively inferred) term “incorrect” may lead students to assume that such configurations are to be avoided. This, again, is because the student will have failed to understand that the inferred term “incorrect” means absolutely not that the particular chord was not freely used by the composers, but only (and merely) that the particular test did not select it as the raw material from which a restructured version was created. It is therefore obvious, surely, that the OSU Model is being neither prescriptive nor proscriptive. Nobody can possibly know which particular chords actually were the pre-selected “correct,” “composed” chords as opposed to being those that were computer-generated alternative versions of the same. Indeed the OSU Model—even though it obviously begins its operation by knowing which are which—is even itself denied such knowledge at the point of its own adjudication. The danger is, surely, that we might be led to believe that the OSU Model’s own judgment is likely to be significantly (or at all) better than our own. But is it, and if so where is the evidence?
[7] As Figure 1 demonstrates, the Model scored only 50% as against my own 60%. Yet it must be remembered that my score resulted from no musical decision-making whatsoever. Had I seen fit to indulge in this, I might well have managed a higher score—who knows? What is particularly alarming, however, is that the Model was apparently unable to avoid getting 50% of its own answers “wrong.” As the Model states, a score of 50% is the target score when chords are chosen only randomly; but here the Model was supposed to be making informed judgments. I am no more impressed by the authors’ claim that a Model score of 70% is acceptable, especially since this is only 10% better than a score I have achieved on the basis of zero musical judgment and insight.(3) Such a score also presupposes that the Model’s failure to avoid getting as many as 30% of its own answers wrong is “acceptable.” Is this credible?
[8] The starting point must be an examination of some of the numerous instances where those chords deemed (inferentially) to be “incorrect” are to be found in the actual surviving music. Unlike the OSU Model, we may then be in a position to perceive through the “opportunities” presented some tangible “motives” that explain the “means.” It will also elevate (of necessity) the status of those chords from “incorrect” to that of “correct” (since the examples now to be given will also be actual “composed” examples). These have currently been denied to the OSU Model even though they freely exist in the repertory alongside the others.
[9] For this examination I have decided to restrict myself to the Bach chorale harmonizations, but have little doubt that a similarly fruitful exercise could be undertaken also with reference to the quartet repertory. In what follows, therefore, only the first five examples (i.e. the first row of chords) from Figure 1 will be re-appraised.
[10] The Model recognizes that key is important (and therefore the
tests all state the keys within which given triads are deemed to
exist). A particular triad can therefore be properly assessed only in
relation to the prevailing key within which it is used. The triad
f-c'-f'-a'' is, for example, likely to exist because of particular
voice-leading and harmonic requirements when it functions within the
key of
[11] I should submit, however, that key is not intrinsically so
important that the harmonic, chord-spacing and voice-leading syntax
used for a chorale in (say)
[12] In Figure 1, three simultaneous choices are unanimously selected for the first pair of chords (but all for totally different reasons): first, the Model indicates by the red shading that the first chord of the pair was the “correct” chord (i.e. the one actually taken as a “composed” chord, its knowledge of this fact being then independent from its own subsequent adjudication); second, the OSU Model selected it as being the more likely of the two to have been “composed” (being at that point unaware that it had previously been entered in any case as “correct”); third, I chose it purely because for that one I selected the first (in a system of pragmatic alternate selections). We all agreed (for very different reasons) that the first chord was “correct.” But what about the second?
[13] The three independent reasons why the second chord was “incorrect” are: first, the Model indicates that the first was indeed “correct” (knowing initially that it was the given chord from which it then recomposed the notes to arrive at for the second); second, the Model (being, after that, rendered innocent to the previous facts) adjudicated that the layout of the first was “better” than the second; and third, I selected the first because (and only because) it was the first chord. (For the next one I shall have pragmatically selected the second.) The conclusion is therefore undoubtedly that the second chord is “incorrect.” But as can now be seen below in Example 1, it occurs quite unashamedly and routinely as a “composed” chord deliberately chosen by Bach (in preference to all others) as being the most suitable for the purpose.
[14] Why, therefore, did Bach place the alto on a', thereby creating
the large gap between the two inner voices (which obviously offended
the OSU Model)? Only by understanding his motive (rather than merely
perceiving his means) can this question be answered. But the OSU
Model is not equipped to adjudicate upon the motive, being capable
only of noting the means and thereby recording yet another
opportunity (in this case perhaps a rare one). An answer can be
arrived at by understanding that here the
[15] Returning to Figure 1, the second pair of chords shows the model to have made an “incorrect” choice. This is because it did not know (as I also did not) that in fact it was the second of the pair that had been provided as the composed data. (The Model did, of course, originally “know” this, but only before it was then instructed to forget it in order to make an impartial adjudication.) But as Example 2 below shows, the configuration chosen (“incorrectly”) by the Model also freely occurs. Within the context provided here, the layout and spacing is the only obvious one. While this chorale could be said to be in A minor, it really belongs to the kind described within the article as “modal” rather than “tonal.” It might be argued, therefore, that when this chord arrives the passing tonality is really F major rather than A minor. Nonetheless its function is part of an overall modulation from A minor to D minor. The apparent tonality of C major (at the beginning of the phrase) results only from the modal character which, within a tonal context of A minor, makes C major harmony freely available.
[16] The third pair of chords in Figure 1 provides two configurations that, without question, are both completely routine and as likely to be found. While the second is “correct” (being the actual given one) both I and the Model have selected the first (being therefore “incorrect”). The Model has performed more poorly than I have however, because while my selection was deliberately made without exercising any musical judgment at all, its was supposed to be a musically-preferred selection. But as can be seen below in Example 3, both chords are freely used. The “correct” chord appears on the third beat of measure 1, while the “incorrect” one becomes the ultimate goal of the whole phrase (i.e. the final chord). Who could possibly deny that this “incorrect” chord is the only one that clearly fulfils all the voice-leading, melodic and harmonic requirements of the phrase? What actual choice (as such) is therefore offered by the Model? Like completing a lottery ticket, the hope can only be (for whatever amusement purpose) that the final guess will miraculously concur with the programmer’s unknown (and unknowable) random selection.
Example 4. Riemenschneider 239: Den Vater dort oben (mm. 5–6)—transposed
(click to enlarge)
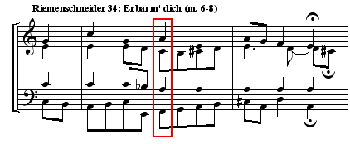
Example 5. Riemenschneider 4: Es ist das Heil uns kommen her (mm. 6–8)—transposed
(click to enlarge)
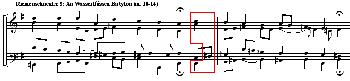
[17] The fourth pair of chords shown in Figure 1 again offers little means for making an informed choice, since either chord can (and does) freely occur in the repertory. Particular usage arises only from the voice-leading requirements at any particular moment, and there is no basis for believing that the second chord (here deemed the “correct” one) is any more likely than the first. Indeed the OSU Model has adjudicated that the first is the more likely, thereby being both implicitly “incorrect” (since the second chord is deemed “correct”) and factually incorrect (in that it is, in reality, no more likely to be found than the second). As Example 4 below shows, the “incorrect” first chord is the one deliberately chosen by Bach himself.(4)
[18] In the fifth pair of chords offered by Figure 1, the first looks decidedly unpromising despite being shown as “correct.” The chorale source is not identified, but there are clearly various possibilities for using this configuration in a manner that yields natural voice leading. As the Model indicates (“incorrectly”) by its preference, the second chord is a more likely distribution of the notes since here it is the root that is doubled rather than the third, and (unlike the first chord) the space between alto and tenor is only a fourth as opposed to an eleventh. Unsurprisingly, therefore, one does not have to look far to find its free use by Bach, as shown below in Example 5.(5)
[19] So how did the Model perform overall in these five chorale extracts, and what does this say about its value as a tool?
[20] To be honest, its performance was in my view of only limited value: it only “correctly” identified the first “correct” chord, while it failed for the other four (giving a staggering 80% failure rate). But we must not be too harsh for these failings, any more than I deserve to be congratulated for having conversely managed for the same extracts a success rate of 80% (having managed by pure accident to identify four of the “correct” chords). While the informed (or uninformed) judgment of a person can be correlated with that person’s state of knowledge and experience (or in my case, in this instance, sheer luck), a computer’s performance is limited only by the nature and scope of the data given to it in the first place. We know that these data consisted of 2643 four-voice triads, but we do not know (and neither can the OSU Model know) upon what basis this selection was made. Was it representative, and if so how?
[21] To provide some idea of scale, let us suppose (for the sake of argument only) that on average each chorale consists of (say) four phrases, and that each phrase has a minimum of (say) eight chords. (This might at least serve as a notional benchmark only.) This should mean that within the 371 four-voice chorales found in Riemenschneider (alone) there will be (on this basis only) at least 11872 chords. It would, in my view, therefore be necessary for the data input to contain an absolute minimum of all these 11872 chords, together with whatever program instructions are necessary to process the information in a meaningful and useful way. The Model’s judgment that one chord configuration is “better” than another would then at least be the result of a rational statistical evaluation. The results currently being generated (as in Figure 1) seem only tangentially connected with the broad range of data available, and more to stem from certain kinds of evaluative parameters implanted within the Model. It is not clear to me exactly how the 2643 sampled chords (only) feed into the evaluative process itself.
[22] Within the language of tonal music, the music is of course not the end product of chord spacing. The exact opposite is the case: chord spacing is the end product of musical judgment. The difficulty with the OSU Model (or indeed any similar model) is that “musical judgment” inhabits a totally different universe from that inhabited by “computer science.” It stands to reason therefore that this Model can be of only limited assistance to those who strive to unlock what is encoded in the notes left to us by composers such as Bach, Haydn and Mozart (indeed any composer living at any time). It might (and does) provide evidence of some of the opportunities, and gives insight into some of the means. But only when, at a purely human level, actual musical judgment is perceptible (and recoverable) can the works of these old masters (including their motives) be meaningfully understood.(6)
Roger Wibberley
Goldsmiths University of London
Department of Music
New Cross, London SE14 6NW
r.wibberley@gold.ac.uk
Footnotes
1. I do not use the term “theorist-speak” in a pejorative sense,
but rather in order to draw a clear distinction between the prospective minds of
composers (on the one hand) and the retrospective constructions of theorists (on
the other). In the sometimes strange twilight world of the latter, it is
tempting to assume (by default) that actual composers were somehow
rule-bound (in a manner that we might perhaps wish our students to be). As
Aarden and von Hippel so eloquently put it in [10], “The difference between
composed and random triads was that random triads were innocent of rules for
doubling or spacing.” The implication here is that composers were guilty of
restricting their activity so as to comply with predetermined regulations, and
that such phenomena as chord spacing were simply the result of applying such
rules. In reality the opposite was the case: chord spacing (and every other
structural aspect of a composition) was the outcome only of a purely
musical judgment that sprang from an artistic motive. Rules as such were only
ever a way of subsequently explaining the procedures that earlier composers
seemed (for artistic purposes) to have adopted. They have always provided
students through the ages with a simple and useful way of approaching and
understanding musical practices no longer current or familiar, but they have
seldom permitted access to the minds and artistic motivations of composers of
the past.
Return to text
2. This calls to mind a lottery game in which numbers are to be
chosen in the hope that an unforeseeable match with randomly-selected balls will
bring untold riches.
Return to text
3. The authors state in [15] that “
Return to text
4. In order to fulfill the requirements of the Model, this
chorale has been transposed down from C major to A major. We need not worry that
in doing so the bass now has to reach low
Return to text
5. In order once more to bring the example into alignment with
the Model, this extract has also been transposed into the predicated key of
Return to text
6. This might then improve the
performance of students who (as reported by Aarden and von Hippel in [1]) are
“struggling to remember and apply the rules, taking perhaps half an hour to
harmonize a 3- or 4-bar diatonic melody.” If they were taught that composers did
not compose in order to apply rules, but rather in order to communicate coherent
musical ideas, they might find that through an understanding and re-creation of
those ideas the rules might more or less take care of themselves.
Return to text
Copyright Statement
Copyright © 2004 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Rebecca Flore and Tahirih Motazedian, Editorial Assistants