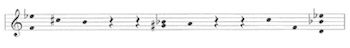Bruno Maderna’s Serial Arrays *
Christoph Neidhöfer
KEYWORDS: integral serialism, array, matrix, twelve-tone, compositional process, filter technique, magic square, Latin square, Maderna, Nono, Improvvisazione N. 1, Musica su due dimensioni, Serenata N. 2, Darmstadt
ABSTRACT: A central figure at the Darmstadt Summer Courses for New Music in the 1950s, Bruno Maderna (1920–73) pioneered a type of serialism that was as deeply rooted in the contrapuntal tradition of the past, as it was committed to the exploration of new avenues in musical expression. This article investigates the serial arrays that lie at the core of his works written between 1951 and 1956. The constructive principles behind Maderna’s tone rows are explained, as are the ways in which he subjected them to order permutations that he represented graphically in matrices, tabulating order positions and pitch-class space. The article further examines how Maderna’s matrices served as the source for his rhythmic language. With evidence from the sketch materials and other sources, the analyses show how Maderna designed his serial arrays in response to what he considered to have been the shortcomings of the twelve-tone technique.
Copyright © 2007 Society for Music Theory
[1] A central figure of the post-war generation of young Italian serial composers, Bruno Maderna (1920–73) championed a musical aesthetic that was as deeply rooted in the past as it was committed to the exploration of new compositional techniques and new avenues in musical expression. Closely affiliated with the Darmstadt Summer Courses for New Music since 1949, Maderna held the modernist view that music follows a continuous historical development and hence there could be no return to older musical styles. “Music is a continuous movement like human life,” he explained in a lecture he wrote in 1953–54, rejecting neo-classicism, neo-romanticism, and other “neo” aesthetics as being too limited in their narrow, naïve views of earlier music, and as lacking involvement with the present.(1) “But these images [of earlier musical periods],” he continued, “are precisely only images and not a general reconsideration of music as human expression.”(2) Instead, Maderna called for the exploration of new compositional techniques and expressive means in a progressive musical language that assimilated elements of the old in the new.
[2] Maderna strongly believed that musical expression should be grounded in structural frameworks that in some way reflected life in its continuous development and mutation.(3)He found serial techniques to serve him best in this regard: a chosen material—a pitch-class series, a series of durations, etc.—could be transformed by way of serial permutations, usually to the extent that the original version of the material was no longer recognizable. To this end Maderna developed a rich palette of compositional strategies, quickly moving beyond the basic twelve-tone operations employed by the composers of the Second Viennese School and their followers. In addition, he gradually extended serial principles to a number of musical dimensions (such as rhythm, pitch register, and orchestration), and developed his own version of integral serialism.
[3] This article examines Maderna’s serial techniques from the period 1951–56, during which time his compositional language reached its first maturity. Focusing on excerpts from three central works from the period—Improvvisazione N. 1 (1951–52), Musica su due dimensioni (1952), and Serenata N. 2 (1953–54, rev. 56)—the article investigates the serial arrays that lie at the core of Maderna’s compositional procedures. The arrays will be studied in the context of the compositional process, as documented in his sketch materials.(4) Maderna’s sketches provide us with a clear picture of his compositional strategies, although not every stage of the creative process is documented.(5)
Example 1. Serial features in Improvvisazione N. 1, Musica su due dimensioni, and Serenata N. 2
(click to enlarge)
[4] Example 1 itemizes in the top row the serial features commonly found in Maderna’s music from the period. The entries below each heading identify serial devices employed in each of the three works discussed in this article. The shaded fields highlight materials that will be analyzed in the examples to follow. As we shall see, Maderna generally constructed his serial materials in the order listed from left to right, without using every serial device in every work. At the bottom of the example I have marked the distinct stages of the compositional process, which generally unfolded as follows:
Stage 1) Maderna first designed one or several pitch series, twelve-tone or otherwise.(6) Some series were constructed from the two sizes of a (non-perfect) diatonic interval (e.g., series built from a succession of major and minor seconds).
Stage 2) The order of the pitch classes in the series was then permuted, represented graphically in a succession of matrices, as discussed shortly. The permutations were guided by numeric values taken from a number table, often a magic or Latin square.
Stage 3) Rhythmic values were assigned to the pitch-class materials following serial principles. Those principles may or may not have been related to the serial permutations in the pitch-class domain.
Stage 4) Starting in 1953–54, Maderna often fed the pitch-class and rhythmic materials through filters, canceling some of these materials.
Stages 5) and 6) During the final scoring process Maderna frequently determined pitch register and orchestration via serial principles as well.
Definition and Notation of Maderna’s Serial Arrays
[5] Following Morris 1987, we shall define an array as “a two-dimensional arrangement of rows and columns which intersect in positions.”(7) The positions may contain numerical values or other designated symbols. Numerical values may be defined as musical objects or may be used for the serial transformations of such objects. Although mathematicians make no strict distinction between “array” and “matrix,” we shall presently reserve the latter term for a specific notation that tabulates pitch-class successions in a time-point grid, in distinction to other kinds of arrays.(8) Example 2 provides an overview of the types of serial arrays found in the works discussed in this article.
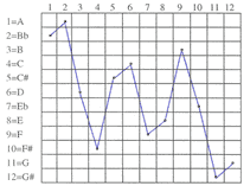
[6] Example 2a illustrates the notation of Maderna’s common pitch-class array. We shall call this type of array
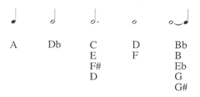
matrix.(9) Each of the twelve rows of the matrix represents one pitch class, with 1 = A, 2 = B![]() ,
,![]() . The twelve columns project a succession of time points, read chronologically from left to right. Maderna represents a twelve-tone series or any other type of (ordered or partially ordered) set by placing dots in the corresponding positions of the matrix. The succession of dots connected with straight lines in the example, read from left to right, defines the twelve-tone series used in
Improvvisazione N. 1 (B
. The twelve columns project a succession of time points, read chronologically from left to right. Maderna represents a twelve-tone series or any other type of (ordered or partially ordered) set by placing dots in the corresponding positions of the matrix. The succession of dots connected with straight lines in the example, read from left to right, defines the twelve-tone series used in
Improvvisazione N. 1 (B![]() –A–D–F
–A–D–F![]() –C
–C![]() –C–F–E–B–E
–C–F–E–B–E![]() –A
–A![]() –G), to be discussed below. Maderna’s matrices are not always squares; they could use fewer than twelve pitch classes, and a larger or smaller number of time points. In addition, each row and column could contain more than one dot or none at all (if, for example, the succession omits or duplicates any pitch classes).
–G), to be discussed below. Maderna’s matrices are not always squares; they could use fewer than twelve pitch classes, and a larger or smaller number of time points. In addition, each row and column could contain more than one dot or none at all (if, for example, the succession omits or duplicates any pitch classes).
[7] The content of Example 2a could also be represented in a one-dimensional array, as shown in Example 2b. Each position contains one pitch class; the array defines the exact order of the pitch classes in the twelve-tone series. The representation, as such never used by Maderna, simply translates ordinary staff notation into letter notation (compare with Example 3 below). The distinction between Examples 2a and b—both of which tabulate the same twelve-tone series—is conceptually significant, however. Example 2a assigns the individual members of the series to twelve different lynes, whereas Example 2b represents the series in one single lyne.(10) As we shall see, Maderna may realize different lynes with different instruments.
[8] The entries in an array can also tabulate pitches, rather than pitch classes, as shown in the one-dimensional array of Example 2c (compare with Example 8 below). Example 2d shows another one-dimensional array that contains empty positions as well as positions filled with single pitch classes or unordered pitch-class sets. As we shall see, this array is derived from the matrix of Example 2a by way of an elaborate permutation procedure (to be discussed in Examples 4–6 below).
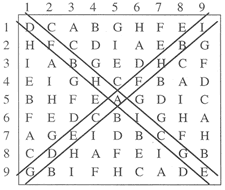
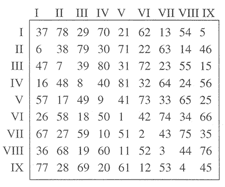
[9] Example 2e illustrates another type of array. The individual letters in the 12×12 grid can be assigned specific pitch classes, or they could be substituted by numbers to be interpreted as rhythmic values or to be used for serial permutations. Often, as here, such arrays form Latin squares: all rows and columns (and in the present case also both main diagonals) contain each of n letters (or numbers) exactly once. Maderna also uses magic squares, defined as grids of size n×n, whose cells hold values 1 to n2 such that the rows, columns, and main diagonals add up to the same sum. In addition, he may also use rectangular arrays or other types of squares that are not magic or Latin squares. We shall now examine the construction of Maderna’s serial arrays and their compositional realizations for each of the three works in turn.
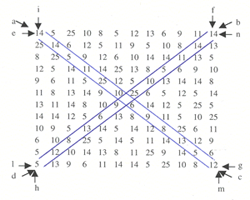
Improvvisazione N. 1 (1951–52)
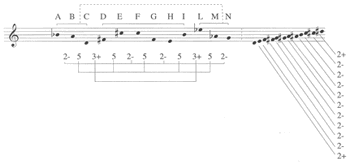
[10] Example 3 transcribes Maderna’s sketch for the twelve-tone series used in this work for orchestra.(11) The twelve pitches of the series are labeled A through N, with the first trichord, central hexachord, and last trichord bracketed.(12) Below the series Maderna analyzes the succession of intervals, identified by their diatonic labels (“2-” = minor second, “5” = perfect fifth, “3+” = major third). The purpose of Maderna’s labels is to show that the intervals form a palindrome, illustrated by the brackets below. Since the intervals that appear in symmetrical order positions in the pitch series (i.e. the first and last interval, the second and penultimate interval, etc.) have the same size and direction, the series is retrograde-inversionally symmetrical. While the retrograde-inversional symmetry pertains to the series as a pitch-class series, that symmetry is also clearly visible (and audible) in the actual pitch representation of Maderna’s sketch. As we shall see again later, Maderna always thinks of a series initially as a succession of pitches, rather than as a sequence of abstract pitch classes. This is also evident from Maderna’s listing of all the pitches in ascending order on the right of Example 3. Since the series in its pitch representation is retrograde-inversionally symmetrical, the registral distribution of the pitches is inversionally symmetrical. This is shown by Maderna’s interval labels on the right margin: the pitch collection projects a major second (“2+”) at the bottom and top, and minor seconds in between. As demonstrated below, Maderna will later map the series onto other symmetrical registers as well, exploiting their properties in his orchestration.
[11] At the next stage of the compositional process Maderna subjects the twelve-tone series to a process of order permutation, using a technique he developed in 1949.(13) As can be seen in the transcribed sketch of Example 4, Maderna represents the twelve-tone series and its permutations in a series of matrices. The first of these is the one from Example 2a above, with an additional three dots that are not connected by straight lines (to which we shall return later). All dots represent pitch classes, rather than pitches. Since the series is its own retrograde-inversion under RIDD# and since D/D![]() also lie midway in the vertical arrangement of the pitch classes in the matrix (6 = D, 7 = D
also lie midway in the vertical arrangement of the pitch classes in the matrix (6 = D, 7 = D![]() ), the retrograde-inversional symmetry of the series produces an RI-symmetrical picture.(14) The lower case letters to the very left of the first matrix indicate the order of entry of the twelve pitch classes: “a” next to 2 means that 2 (B
), the retrograde-inversional symmetry of the series produces an RI-symmetrical picture.(14) The lower case letters to the very left of the first matrix indicate the order of entry of the twelve pitch classes: “a” next to 2 means that 2 (B![]() ) is the first pitch class of the series, “b” next to 1 means that 1 (A) is the second pitch class, etc.
) is the first pitch class of the series, “b” next to 1 means that 1 (A) is the second pitch class, etc.
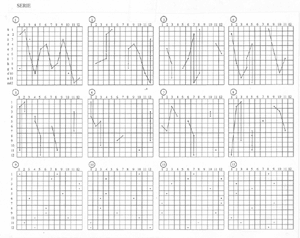
[12] Following their first appearance in the series, the dots are shifted horizontally to the right into the following matrices. Each dot is moved an individual number of positions, with the result that the overall order of the pitch classes is permuted. As Maderna’s connecting lines between dots in the second and following matrices illustrate, completely new graphic shapes, and hence completely new pitch-class successions arise. These successions no longer relate to the original series via any of the canonic twelve-tone operations.(15) Whereas the original series in the first matrix has a dot in every column, in the following matrices some columns remain empty while others contain more than one dot. In Maderna’s transformational procedure each dot of the original series in the first matrix is moved twelve times, each time skipping a certain number of order positions (columns).
[13] The number values for the skips are taken from another array, the number square transcribed in Example 5. Each row, column, and diagonal contains values 5 and 14 twice each and 6, 8, 9, 10, 11, 12, 13, and 25 once.(16) Maderna marks with arrows the twelve paths chosen for the serial transformations in Example 4. For instance, arrow “a” in Example 5 selects the diagonal that runs from the top left to the bottom right, with values 14, 14, 5, 11, etc. These values determine the shifts for the dots in the second row (marked “a”) of the matrices in Example 4. The first dot in this row, in the first column of matrix 1, is initially shifted to the right by skipping over 14 columns, ending up in column 4 of matrix 2. It is then shifted by skipping over another 14 columns, ending up in column 7 of matrix 3, and so forth. Arrow “b” in Example 5 selects the diagonal that runs from the top right to the bottom left. Its succession of numbers determines the shifts for the dots in the top row (“b”) of the matrices in Example 4. And so forth for the remaining ten rows of the matrices.
[14] While each dot of the original series is shifted the same number of times (twelve times), the identity of the original series is completely obliterated after its first appearance. The original series will eventually resurface in its original form, however: since the numbers in each row, column, and diagonal of the number square in Example 5 add up to the same sum (132), the thirteenth dot in each row of the matrices will occur exactly 144 positions after its first appearance in the series of the first matrix (132 positions skipped plus the 12 positions occupied by the dots). Thus the thirteenth dots in all rows taken together will reproduce the original series. This takes place twelve full matrices after the first statement of the series (after 144 positions = 12 matrices), that is, in the thirteenth matrix, which Maderna elides with the first. The original series in the first matrix is thus doubly accounted for, starting and closing the permutation cycle.(17)
Example 6. Improvvisazione N. 1, matrix 11 in staff notation (sketch)
(click to enlarge)
Example 7. Improvvisazione N. 1, measures 36–39, final version
(click to enlarge)
Example 8. Improvvisazione N. 1, register plan for measures 36–39 (sketch)
(click to enlarge)
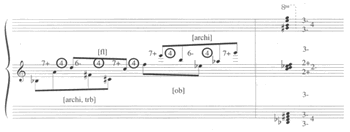
[15] Next in the compositional process Maderna transcribes the content of all matrices into staff notation. Example 6 excerpts his transcription of the eleventh matrix.(18) The twelve successive events correspond to the twelve columns of the matrix. Each pitch class is shown by a stemless note-head. Each empty column from the matrix is represented by a quarter rest. This material is realized in measures 36–39 of the final version, the beginning of the waltz section shown in Example 7.
[16] Maderna translates each order position of Example 6 into an eighth note in Example 7 for a total of four measures of 3/8. The points of attack are thus determined directly by the serial permutations in the matrix. The durations of the individual pitches are also read directly off the matrix: every pitch class is assigned the duration of an eighth note unless it recurs again later in the matrix, in which case it will be sustained until its second appearance. This is the case for E![]() 5/F5 (oboes) and B
5/F5 (oboes) and B![]() 3 (trombone).(19) Of these, E
3 (trombone).(19) Of these, E![]() 5 is the only pitch that is reattacked, and the only one to enter after the onset of the time point, on the last sixteenth of measure 39. The four measures of the excerpt now form a single phrase with three pitches sustained and the strings and flute adding short two-note gestures.
5 is the only pitch that is reattacked, and the only one to enter after the onset of the time point, on the last sixteenth of measure 39. The four measures of the excerpt now form a single phrase with three pitches sustained and the strings and flute adding short two-note gestures.
[17] How, then, does Maderna assign pitch register and orchestration? The sketch transcribed in Example 8 illustrates. On the left, Maderna takes the original twelve-tone series from Example 3 and inverts its contour. The succession of pitch classes is preserved, but the directed pitch intervals of the original series are replaced in Example 8 by their complements within the octave, moving in the opposite direction. The first descending minor second in Example 3 becomes an ascending major seventh in Example 8, and so forth. Since not only the pitch-class succession but also the contour of the original pitch series (Example 3) is RI-symmetrical, the derived version in Example 8 also projects an RI-symmetrical contour. This new version defines a new pitch collection that is itself again inversionally symmetrical, as illustrated by Maderna’s intervallic analysis on the right (“3-” = minor third, “4” = perfect fourth, etc.). This new pitch collection now serves as a template for the waltz phrase in Example 7; the pitch-class material obtained from matrix 11 (Example 6) is assigned to the registers of Example 8. Not all twelve pitches of Example 8 are sounded in Example 7 because matrix 11 does not contain all twelve pitch classes.
[18] Maderna’s beams in Example 8 partition the series into four distinct registral segments. The highest and lowest four pitches are each grouped together; the four pitches in the middle range are divided into two adjacent dyads, D5–C5 and F5–E![]() 5. As a result, the partitioning of the series is symmetrical. As indicated by the added instrument labels (in square brackets), Maderna assigns the highest and lowest four pitches to the strings, with the addition of trombone in the lowest group, and the two dyads in the central register to the woodwinds (flute and oboe respectively).(20)
The orchestration reflects the serial symmetry of the pitch collection.(21)
5. As a result, the partitioning of the series is symmetrical. As indicated by the added instrument labels (in square brackets), Maderna assigns the highest and lowest four pitches to the strings, with the addition of trombone in the lowest group, and the two dyads in the central register to the woodwinds (flute and oboe respectively).(20)
The orchestration reflects the serial symmetry of the pitch collection.(21)
[19] As this brief analysis of the compositional process for an excerpt from Improvvisazione N. 1 shows, Maderna abandons the traditional twelve-tone operations—which preserve the intervals of a series under transposition, inversion, retrogradation, or any combination thereof—in favor of a new technique of serial permutation that completely obliterates the identity of the original series. Maderna’s musical language thus shares with the twelve-tone music of his predecessors the unifying element of a series while creating a musical surface that avoids repetition at all costs. In addition, Maderna’s serial array leads to a new concept of counterpoint and harmony. Harmony no longer results from a superposition of different contrapuntal layers (such as when several series unfold simultaneously) or from a verticalization of segments from a series. Rather, harmony arises directly from the serial permutations themselves: in Example 4, the permutation (horizontal shifting) of the dots (pitch classes) assigns them to specific columns in specific matrices. The permutation is an operation on the order positions occupied by each pitch class, with each being shifted following a unique pattern of displacement (no two pitch classes are shifted the same number of positions in the same order). A simultaneity arises when different pitch classes occur in the same column. The number of pitch classes per column fluctuates greatly. The matrices do not suggest a specific number of contrapuntal voices. Rather, the counterpoint we hear in Improvvisazione N. 1 is an interpretation of the matrices; by associating certain pitch classes with each other through register and orchestration—themselves based on serial permutation (contour inversion of the original pitch series)—Maderna creates a texture with clearly articulated, distinct instrumental voices.
[20] Improvvisazione N. 1 is one of the earliest works to use the permutation technique illustrated thus far. In the compositions to follow Maderna expands the technique in conjunction with a number of other features, including
- multiple series: a work may use more than one series. Often, the different series are developed from a small pool of intervals, as discussed below in an early draft for Musica su due dimensioni.
- other kinds of number tables: in addition to Latin squares of size 12×12, Maderna uses number tables of various other types and dimensions (such as a magic square of size 9×9 in Serenata N. 2 and a number table of size 12×16 in Musica su due dimensioni, discussed below).
- more elaborate rhythmic schemes: instead of assigning the same basic note value to every column (time point) of a matrix, Maderna may choose more complex rhythmic materials, themselves often subjected to serial permutations.
- filter technique: filters serve to adjust the pitch-class and rhythmic structure by shortening or eliminating individual pitch classes or by breaking longer note values into shorter ones (such as in Serenata N. 2).
[21] These features present Maderna with a wide variety of choices, allowing him to control the outcome of his serial machinery with a great deal of flexibility, as we shall see in the following excerpts from Musica su due dimensioni and Serenata N. 2.
Musica su due dimensioni (1952)
[22] Musica su due dimensioni (1952) for flute, cymbal, and tape is Maderna’s first electro-acoustic work and one of the first works ever to pair acoustic instruments with a prerecorded tape part.(22) A second, completely different work for flute and tape with the same title dates from 1958.(23) As is evident from the sketch materials and Maderna’s correspondence, Musica su due dimensioni (1952) had originally been planned as a large-scale work that included a number of other instruments as well, but its forces were reduced for reasons of time and practicality.(24) As a result, only some of the preparatory materials documented in the sketches found their way into the final version of the work. Unlike Improvvisazione N. 1, Musica su due dimensioni uses several twelve-tone series, each generated from a predetermined pool of intervals.
Example 9. Musica su due dimensioni, construction of four twelve-tone series A-D (sketch)
(click to enlarge)
Example 10. Musica su due dimensioni, the six permutations of three interlocking interval successions (sketch)
(click to enlarge)
Example 11. Musica su due dimensioni, series [a] and three derivations [b]-[d] (sketch)
(click to enlarge)
[23] The sketch transcribed in Example 9 shows how Maderna creates a set of four series, labeled in the lower part A through D, each of which uses only two kinds of melodic intervals, ascending or descending. Series A, for instance, is generated from ascending and descending major and minor sixths exclusively. Each of the four series A-D is thus derived from a pool of four directed intervals. Each pool of intervals is in turn selected from the nine-tone row listed at the top. This row establishes a melodic pattern that uses each of the two sizes of the non-perfect diatonic intervals smaller than an octave exactly once, that is, a major and minor sixth, second, third, and seventh once each. The ordered trichords formed by successive intervals of the same diatonic type—that is, the three pitches projecting successive sixths, the three pitches forming successive seconds, etc.—are then integrated in the four series A through D below. For instance, the first three pitches of the nine-note row at the top provide the fourth through sixth pitches of series A. And so forth—with octave transpositions—for series B, C, and D.(25)
[24] Evidently, series A through D are intended to be twelve-tone. But as it turns out, series A does not fulfill this requirement as it contains both G![]() and A
and A![]() , omitting E
, omitting E![]() . To the right, on the second staff, Maderna fixes the problem by constructing another series, changing the distribution of major and minor sixths. This series is now twelve-tone, marked “Buono.” The sketch also bears witness to the evocative character of Maderna’s serial construction. At the top of the sketch, he reflects upon the generative process: “NASCE LA SERIE – strani, flebili, dolce funerei richiami – nella notte” (the series is born—strange, faint, soft, mournful calls—at night).(26)
In addition to series A-D Maderna derives a further twelve twelve-tone series from the same pool of intervals, at times including one tritone and a fourth and/or fifth. The corresponding sketches (not shown here) are titled “LA SERIE SI SVILUPPA” and “SERIE SVILUPP. al rovescio” (the series develops / series developing in reverse). The original nine-note row at the top of Example 9 thus serves as the generator for sixteen twelve-tone series. Unlike what we have seen in
Improvvisazione N. 1, these series are not subjected to further permutation, however.(27) Instead, Maderna develops another series, derived from a different pool of intervals, that is then subjected to his permutation procedure.
. To the right, on the second staff, Maderna fixes the problem by constructing another series, changing the distribution of major and minor sixths. This series is now twelve-tone, marked “Buono.” The sketch also bears witness to the evocative character of Maderna’s serial construction. At the top of the sketch, he reflects upon the generative process: “NASCE LA SERIE – strani, flebili, dolce funerei richiami – nella notte” (the series is born—strange, faint, soft, mournful calls—at night).(26)
In addition to series A-D Maderna derives a further twelve twelve-tone series from the same pool of intervals, at times including one tritone and a fourth and/or fifth. The corresponding sketches (not shown here) are titled “LA SERIE SI SVILUPPA” and “SERIE SVILUPP. al rovescio” (the series develops / series developing in reverse). The original nine-note row at the top of Example 9 thus serves as the generator for sixteen twelve-tone series. Unlike what we have seen in
Improvvisazione N. 1, these series are not subjected to further permutation, however.(27) Instead, Maderna develops another series, derived from a different pool of intervals, that is then subjected to his permutation procedure.
[25] Example 10 transcribes the first sketch for this new series, in which Maderna works out the six permutations of three interlocking interval successions.(28) The three successions are {2+, 2+, 2+, 2+}, {5, 4, 3-, 2+}, and {4, 3-, 2+, 5}, resulting at [1] in the overall interval pattern {2+, 5, 4, 2+, 4, 3-, 2+, 3-, 2+, 2+, 2+, 5 }. Maderna realizes this pattern as shown at [a] in Example 11, using the intervals—ascending or descending—to build a twelve-tone series. The twelfth interval is used as the “wrap-around.” Maderna is blessed with considerable luck here: not all of the six interval patterns [1]–[6] in Example 10 can be realized as twelve-tone series.(29) In addition, the directed pitch-class intervals at [a] in Example 11 add up to 0 mod12, hence allowing for the wrap-around. Series [b] rotates I4 of series [a] at order position 9, [c] rotates P4 of [a] at order position 6, and [d] rotates I3 of [a] at order position 3.(30) Maderna will only use [a] and [b] further in the compositional process, subjecting each to the kind of order permutation we saw earlier in Improvvisazione N. 1. We shall examine the process for series [a] here.
[26] Example 12 transcribes the matrices that tabulate the permutations of this series. The series itself appears in the first matrix, represented by the dots connected by straight lines. No sketch survives that documents how Maderna determined the permutations in the following matrices, but the principle is easily reconstructed, as shown in Example 13. Each column of the table lists the values used for the shifts of the pitch class shown at the top. For instance, the first dot in the first matrix of Example 12 (pitch class C), is first moved to the right by skipping over 11 empty positions, then 15, then 9, etc., following the values in the first column of Example 13 (read from top to bottom). And so forth for the remaining pitch classes.
Example 12. Musica su due dimensioni, matrices for series [a] (sketch) (click to enlarge) | Example 13. Musica su due dimensioni, number table (reconstruction) (click to enlarge) |
Example 14. Musica su due dimensioni, orchestration of matrices 15 and 16 (sketch)
(click to enlarge)
Example 15. Musica su due dimensioni, opening (ultimately all performed on the melochord)
(click to enlarge)
Example 16. Musica su due dimensioni, assignment of rhythmic values in measures 1–17
(click to enlarge)
[27] The array of Example 13 is not a magic or Latin square. Each row contains a different set of numbers (adding up to various sums). Each column, on the other hand, contains a different arrangement of the same set of 16 values: values 9 and 11 occur four times, value 10 three times, value 12 twice, and values 13, 14, and 15 once each. The sum of all values, for each column, is 176. This means that in Example 12 the permutational procedure will ultimately map the original series in the first matrix onto itself via a wrap-around: each dot of the original series in the first matrix is moved a total of 192 positions to the right (176 positions skipped plus the 16 positions occupied by the dots = 192), that is, a total of 16 matrices (192 = 16*12). The first matrix serves simultaneously as the seventeenth matrix, closing the permutation cycle.(31)
[28] Following the transcription of the sixteen matrices in Example 12 into staff notation (not shown here), Maderna separates the pitch-class materials into three discrete instrumental layers. The beginning of the corresponding sketch is transcribed in Example 14. On the top staff, Maderna copies out the content of matrices 16 (retrograde) and 15 (recto). Underneath, he distributes the pitch-class material among three instruments, two acoustic (flute and piano) and one electronic (“El.”). The electronic instrument used is the melochord, a keyboard instrument that offers a variety of timbres to be recorded on tape.(32) The pitches are distributed over a wide range. The temporal order follows the one given in the matrices; no rhythms are assigned as of yet.
[29] Example 15 transcribes the opening of the unpublished full score in which rhythms, dynamics, and tempo are fully worked out. No sketches survive that document Maderna’s rhythmic and dynamic choices. The dynamics appear to have been freely chosen. The rhythmic values, on the other hand, follow a pattern in which each pitch class (with the exception of D) always occurs with the same note value. A total of five different values are used, each of which is a multiple of a quarter note, as shown in Example 16.(33) The pitch material, as orchestrated in Example 14, is realized in Example 15 such that the flute always holds a pitch preceding a general pause until it is reached (the “general pauses” are the quarter rests in Example 14, resulting from empty columns in the matrices). The same holds for the melochord (“El.”) before the first two general pauses.(34) The onset of these pitches, and hence of those that precede them, is thus calculated backwards from the general pauses. Overall, Maderna takes the opportunity to turn what could be realized mostly as a single line (see first staff of Example 14) into a texture that projects single pitches as well as simultaneities in Example 15 (via the orchestration of Example 14). Following the second general pause in measure 5 of Example 15, the third “phrase” in measures 6 (with pickup) to 9 is realized as a single line of Klangfarbenmelodie, moving from one instrument to another.(35) In the final version of the work, contrary to the instrumentation indicated, the score of Example 15 is performed entirely on the melochord and recorded on tape.(36)
[30] Maderna’s work in the studio, first at Werner Meyer-Eppler’s institute in Bonn in 1952 and later at the Studio di fonologia musicale in Milan (which officially opened in 1955), had a profound impact on his compositional strategies. In 1954 Maderna started to subject his serial arrays to a device often used in the studio: the filter. This tool allowed him to control the outcome of his serial processes more flexibly by readjusting the materials of his arrays. Maderna did this either on an ad hoc basis—freely shortening or removing materials—or more formally with the help of further serial procedures, as in the second part of Serenata N. 2, to which we shall now turn.
Serenata N. 2 (1953–54/56)
[31] Serenata N. 2, scored for eleven instruments, was premiered in 1954 and revised two years later for its publication by Edizioni Suvini Zerboni.(37) The first part of the work, which we will not discuss here, builds a serial array from an eleven-tone series, omitting pitch class B![]() throughout.(38) The second part is divided into four sections (24, 25, 23, and 39 measures in length), each of which uses a different collection of nine pitch classes.(39) The permutations of the pitch-class and rhythmic materials in each section are determined via different readings of the same two squares, shown in Examples 17 and 18.
throughout.(38) The second part is divided into four sections (24, 25, 23, and 39 measures in length), each of which uses a different collection of nine pitch classes.(39) The permutations of the pitch-class and rhythmic materials in each section are determined via different readings of the same two squares, shown in Examples 17 and 18.
Example 17. Serenata N. 2, Latin square (sketch) (click to enlarge) | Example 18. Serenata N. 2, magic square (sketch) (click to enlarge) |
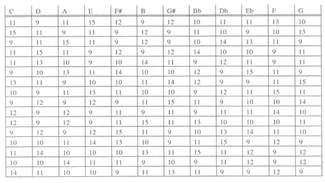
[32] Both are of size 9×9. Each row, column, and diagonal of the Latin square in Example 17 contains the first nine letters of the alphabet exactly once, each time in a different permutation. The magic square in Example 18 contains the values 1 through 81 once each, with the values in each row, column, and diagonal adding up to the same sum 369.(40) Maderna uses Example 17 to determine the pitch-class permutations and Example 18 to generate the rhythmic structure of each of the four sections. We shall examine here the compositional process for the second section (measures 183–207).
[33] Example 19 identifies the pitch-class and rhythmic content of the array used in this section.(41) Maderna assigns the nine pitch classes (shown in ascending order at the top) to the letters A through I, and enters them into the Latin square of Example 17, rotated 90 degrees counterclockwise.(42) Each row, column, and diagonal of the array in Example 19 contains each of the nine pitch classes exactly once. Each position is then assigned a durational value with the help of the magic square in Example 18. Example 20 transcribes the beginning of the corresponding sketch.
Example 20. Serenata N. 2, beginning of array for measures 183–207 realized (sketch) (click to enlarge) | Example 21. Serenata N. 2, paths chosen in the magic square of Example 18 (click to enlarge) |
[34] The nine lynes of the array in Example 19 are notated in Example 20 in score format in
[35] Unlike the pitch-class arrays (matrices) in Improvvisazione N. 1 and Musica su due dimensioni (Examples 4 and 12), the array of Example 19 has an entry in every field, leaving no room for rests. Hence, the nine lynes in Example 20 are filled with sound at all times. In order to lighten the (still abstract) structure, Maderna sends it through a filter that shortens every sound by the length whose value is indicated above the staff. For instance, the first pitch (-class) in lyne 1, E, is to be shortened at the end by 5 sixteenths, as marked above the staff in the fourth measure. Whereas each notated pitch (-class) in the example (and the rest of the sketch) has a unique duration, between 1 and 81 sixteenths, Maderna uses only nine different values for the filters, as summarized in Example 22.(47)
[36] The values form a succession of decreasing numbers, skipping over one value at the beginning (12, 10, 9, 8,
Example 23. Serenata N. 2, array with rests entered (sketch)
(click to enlarge)
Example 24. Serenata N. 2, final version, measures 183–88
(click to enlarge)
[37] Example 23 transcribes Maderna’s sketch in which the individual note values have now been adjusted according to the filter values from Example 20. A filter value may be greater than the duration assigned to an individual pitch class, in which case the pitch class is filtered out entirely. This is the case, for instance, at the sixteenth note E![]() in measure 4 of the sixth lyne (Example 20), whose assigned filter value is a dotted eighth. The filter eliminates the pitch altogether (see measure 4 of the sixth lyne in Example 23).(48) The adjusted array of Example 23 now forms the basis for the final version.
in measure 4 of the sixth lyne (Example 20), whose assigned filter value is a dotted eighth. The filter eliminates the pitch altogether (see measure 4 of the sixth lyne in Example 23).(48) The adjusted array of Example 23 now forms the basis for the final version.
[38] Maderna orchestrates the individual entries of Example 23 by circling each pitch class with one of three colors, indicated in my transcription with solid horizontal brackets (pitch classes circled in black pencil in the original), dotted brackets (pitch classes circled in red pencil), and with unbracketed pitch classes (circled in blue pencil in the original). The pitch classes circled in black pencil (solid brackets) are assigned to the wind instruments, those circled in red and blue pencil to the strings, harp, and piano.(49) Example 24 reproduces the final score of the beginning of this section (measures 183–88).
[39] The excerpt fixes each of the nine pitch classes in register.(50) In the first measure (measure 183), the nine lynes from the array of Example 23 are distributed among the five wind instruments. The flute and clarinets realize several lynes each (Example 24), filtering them further by moving back and forth between them in a kind of compound melody. The resulting arpeggiations give the passage a rhythmic profile not guided by serial principles: the arpeggiations occur within the total time spans assigned (serially) to the pitches, but reattack them freely. In general, the superimposed arpeggiations subdivide the quarter or half beat differently. Since in addition the onset of a new event can fall on any sixteenth within the beat, one no longer hears a clearly articulated meter.
Conclusion
[40] The foregoing analyses highlight the central role Maderna’s serial arrays played in the creative process. But, as is clear from annotations in the sketches (such as in Example 9) and from his comments on his compositional technique in the lecture mentioned at the beginning of this article, his arrays also have meaning beyond mere practical concerns. In Maderna’s view, the continuous permutation of pitch-class and rhythmic materials is a reflection of life itself:
“A return [of previous material] has to happen under different conditions. The voyage of Ulysses is a famous example. It teaches us that there can be no return, and that life, in its eternal becoming, changes continually. Hence, why should one not have a technique that resembles the technique of life in its becoming?”(51)
[41] Maderna’s arrays are a response to, and critique of, the dodecaphony of the Second Viennese School and Luigi Dallapiccola (and hence of his own earlier twelve-tone music):
“What I did not like about twelve-tone theory is the principle by which, once a series is given, it has to reappear in its entirety, continuously, vertically and horizontally, for the sake of consistency in the musical discourse.
. . . Slowly but surely I proceeded to the study of serial [per]mutation, until I succeeded in developing more and more complex and rigorous systems of mutation.”(52)
[42] Maderna considers such systems—his serial arrays—to be objective. Far from being restrictive, the systems provide him with the structural framework from which individual expression can arise:
“It is evident that a composer achieves more, as a creator, through a synthesis of technique and its application as an expression of his/her own time. What I personally find very important in Schoenberg is above all precisely this understanding of the importance of objective technique in contrast to the individuality of expression.”(53)
[43] For Maderna, it is the objective materials and procedures—matrices, magic and Latin squares, number tables, etc.—that give rise to musical expression.(54) But the objective materials have no expressive quality per se. Expression arises only once the materials are compositionally realized. The compositional process entails a dialectic between the “objectivity” of the material and the “subjectivity” of its realization. The material is objective in the sense that the principles behind the pitch-class permutations, rhythmic transformations, register plans, etc. are independently verifiable. Their elaboration is subjective, in that beyond the serial processes the composer’s choices are not bound by specific rules.
[44] Theodor W. Adorno voiced concern over the extension of serial principles to an increasing number of musical dimensions, because he believed that the objective side would take over the subjective one.(55) Adorno’s assessment stands in stark contrast to what Maderna (and other Darmstadt composers) believed and experienced. As Maderna put it in 1965,
“I have my own grammatical system. It arises from the principle of serialism and is sufficiently flexible. Above all it is sufficiently abstract to allow me complete freedom in realizing my musical imagination—which is not at all abstract—in a thousand ways.”(56)
[45] As the above analyses of the generative process have shown, the dialectic between compositional objectivity and subjectivity not only pertains to the commitment to serial mechanisms, on one hand, and the freedom of choice during their compositional realization, on the other, but also enters the construction of the serial machinery itself. The serial mechanisms are objective—because they are independently verifiable—but the choice of the particular mechanisms and of the basic materials they elaborate (such as the pitch-class series, rhythmic values, etc.) is subjective, because they are freely selected. All in all, subjective choices lead to, and interact with, objective procedures throughout the creative process.
Christoph Neidhöfer
McGill University
Schulich School of Music, Department of Theory
555 Sherbrooke Street West
Montreal, Quebec H3A 1E3 CANADA
christoph.neidhofer@mcgill.ca
Works Cited
Adorno, Theodor W. 1964/1966. “Difficulties.” In Essays on Music. Selected, with Introduction, Commentary, and Notes by Richard Leppert, new translations by Susan H. Gillespie. Berkeley and Los Angeles: University of California Press, 2002, 644–79.
Baroni, Mario, and Rossana Dalmonte, editors. 1985. Bruno Maderna documenti. Milan: Edizioni Suvini Zerboni.
Berio, Luciano. 1989. Studi su Bruno Maderna. Milan: Edizioni Suvini Zerboni.
—————. 1985. Two Interviews with Rossana Dalmonte and B´lint András Varga. Translated and edited by David Osmond-Smith. New York and London: Marion Boyars.
Borio, Gianmario. 2004. “Tempo e ritmo nelle composizioni seriali. 1952–1956.” In Le musiche degli anni cinquanta (Archivio Luigi Nono, Studi II, 2003). Edited by Gianmario Borio, Giovanni Morelli, and Veniero Rizzardi. Florence: Leo S. Olschki, 61–115.
—————. 1999. “Sull’interazione fra lo studio degli schizzi e l’analisi dell’opera.” In La nuova ricerca sull’opera di Luigi Nono (Archivio Luigi Nono, Studi I). Edited by Gianmario Borio, Giovanni Morelli, and Veniero Rizzardi. Florence: Leo S. Olschki, 1–21.
—————. 1997. “Kontinuität der Moderne? Zur Präsenz der frühen Neuen Musik in Darmstadt.” In Im Zenit der Moderne. Die Internationalen Ferienkurse für Neue Musik Darmstadt 1946–1966. Edited by Gianmario Borio and Hermann Danuser. Vol. 1. Freiburg: Rombach, 141–283.
Brindle, Reginald Smith. 1959. “Italy.” The Musical Quarterly 45: 388–92.
Fearn, Raymond. 1990. Bruno Maderna. Chur: Harwood Academic Publishers.
Fein, Markus. 2001. Die musikalische Poetik Bruno Madernas: Zum “seriellen” Komponieren zwischen 1951 und 1955. Frankfurt am Main: Peter Lang.
—————. 2000. “Im Dialog mit dem Material. Anmerkungen zur ‘Filtertechnik’ in Bruno Madernas Serenata N. 2 (1953–54/56).” Mitteilungen der Paul Sacher Stiftung 13: 33–37.
Ghersi, Italo. 1988. Matematica dilettevole e curiosa. 5th edition. Milan: Hoepli.
Guerrero, Jeannie Ma. 2006. “Serial Intervention in Nono’s Il canto sospeso.” Music Theory Online 12.1.
Karlen, René, and Maurizio Romito. 1990. Bruno Maderna Musikmanuskripte (Inventare der Paul Sacher Stiftung 6). Winterthur: Amadeus.
Kassler, Michael. 1967. “Toward a Theory That Is the Twelve-Note-Class System.” Perspectives of New Music 5/2: 1–80.
Maderna, Bruno. 2001. Musica su due dimensioni per flauto e nastro magnetico (1952). Edited by Nicola Scaldaferri. Milan: Edizioni Suvini Zerboni.
—————. 1965. “La révolution dans la continuité.”Preuves 15/177: 28–29.
—————. 1959. “Introduzione al concerto del 4. 9. 1959.” In Baroni and Dalmonte 1985, 85–86.
—————. 1957. Serenata N. 2. Milan: Edizioni Suvini Zerboni.
—————. 1953–54. [Lecture without title]. Reprinted in Italian with French translation in Verzina 2003, 38–58.
—————. 1952. Improvvisazione N. 1. Milan: Edizioni Suvini Zerboni.
Manzoni, Giacomo. 1958. “Bruno Maderna.” Die Reihe 4: 113–18.
Mead, Andrew. 1994. An Introduction to the Music of Milton Babbitt. Princeton: Princeton University Press.
Mila, Massimo. 1976. Maderna Musicista Europeo. Turin: Giulio Einaudi.
Montecchi, Giordano. 1989. “Il lavoro di precomposizione in Serenata N. 2.” In Baroni and Dalmonte 1989, 109–37.
Morris, Robert D. 1987. Composition with Pitch-Classes: A Theory of Compositional Design. New Haven and London: Yale University Press.
Nielinger, Carola. 2006. “‘The Song Unsung’: Luigi Nono’s Il canto sospeso.” Journal of the Royal Musical Association 131/1: 83–150.
Noller, Joachim. 1992. “Musica su due dimensioni e l’unidimensionalità della musica nuova: sul concetto di dimensione e sulla concezione di due dimensioni.” Quaderni della civica scuola di musica 10/21–22: 65–69.
Rizzardi, Veniero. 2004. “La ‘nuova scuola veneziana’. 1948–1951.” In Le musiche degli anni cinquanta (Archivio Luigi Nono, Studi II, 2003). Edited by Gianmario Borio, Giovanni Morelli, and Veniero Rizzardi. Florence: Leo S. Olschki, 1–59.
Scaldaferri, Nicola. 2001. “Introduction.” In Maderna 2001, vii–xix.
—————. 1997. Musica nel laboratorio elettroacustico. Lucca: LIM.
Ungeheuer, Elena. 1992.
Wie die elektronische Musik “erfunden” wurde
Verzina, Nicola. 2003. Bruno Maderna. Étude historique et critique. Paris: L’Harmattan.
Weber, Horst. 1978. “Form und Satztechnik in Bruno Madernas Streichquartett.” In Die Stellung der italienischen Avantgarde in der Entwicklung der neuen Musik (Symposion des Instituts für Wertungsforschung, Graz 1975), Miscellanea del Cinquantenario. Milan: Edizioni Suvini Zerboni, 206–15.
Footnotes
* Earlier versions of this paper were presented at the 2004 Annual Meeting of the Music Theory Society of New York State in Rochester NY and the 2004 Annual Meeting of the Society for Music Theory in Seattle.
Return to text
1. “La musica è un movimento continuo come l’uomo.” Maderna 1953–5, 38. This lecture, preserved in a typescript without title in the Bruno Maderna Collection of the Paul Sacher Foundation in Basel, Switzerland, was probably never read in public (Verzina 2003, 36). Translations from Italian and French sources are mine.
Return to text
2. “Ma queste immagini sono appunto solo immagini e non una rassegna generale della musica come espressione dell’uomo.”
Ibid.
Return to text
3. Ibid., 46.
Return to text
4. Maderna’s sketches are housed in the Bruno Maderna
Collection of the Paul Sacher Foundation and (mostly in photocopies) in the
Archivio Bruno Maderna at the University of Bologna, Italy. I wish to thank the
Paul Sacher Foundation for a research grant that enabled me to study Maderna’s
sketches from the period. My thanks go to Johanna Blask, Carlos Chanfón,
Isabelle Equilino, Sabine Hänggi-Stampfli, Henrike Hoffmann, Petra Kupfer, Felix
Meyer, Ulrich Mosch, Robert Piencikowski, Tina Kilvio Tüscher, and to the
Foundation’s research coordinator, Prof. Hermann Danuser. I also wish to thank
the two anonymous reviewers for MTO for their generous comments and suggestions,
and Sebastiano Bisciglia for his help with the musical examples. My
transcriptions of Maderna’s sketches are reproduced by kind permission from the
Paul Sacher Foundation.
Return to text
5. As will be demonstrated, missing links in the sketch
materials can be reconstructed based on a general knowledge of Maderna’s
working methods.
Return to text
6. The two pitch series used in Serenata N. 2 are eleven- and nine-tone. Maderna also used series derived from tonal melodies, as for example in
Quattro Lettere (1953), where the series for each movement was taken from one of the four phrases of the partisan song “Fischia il vento.”
The diatonic series contain pitch repetitions.
Return to text
7. Morris 1987, 339.
Return to text
8. For this reason, my use of the term “matrix” deviates
from Morris 1987 (339), who reserves the term “for special two-dimensional
tables of numbers.” For Morris, “matrices are not usually compositional objects”
(Ibid.).
Return to text
9. Maderna’s student Renzo dall’Oglio (1925–2003), in an interview with Gianmario Borio and Veniero Rizzardi in 1994, credits Maderna with the invention of this type of array (non-commercial video recording kept at the Archivio Luigi Nono in Venice). Maderna and his friends summarily called the matrix, the other types of tables discussed below, and the permutation procedures performed in these arrays “quadrato/quadrati” (Rizzardi 2004, 33). My choice of the term “matrix” follows Borio 2004, 109. Fein 2001 and Rizzardi 2004 use “square” (“Punktquadrat” and “quadrato” respectively). In her recent study of similar notations and procedures in Luigi Nono’s
Il canto sospeso (1955–56), Jeannie Guerrero refers to the configuration as “Position-Grid” (Guerrero 2006, paragraph 24).
Return to text
10. Lynes are the rows of an array (matrix). The term
lyne was first introduced in Kassler 1967, 14. See also Mead 1994, 20 and 31–34.
Return to text
11. Improvvisazione N. 1 was premiered on February 18, 1952 in Hamburg by the Sinfonieorchester des Nordwestdeutschen Rundfunks (NWDR),
conducted by the composer.
Return to text
12. Note that the Italian alphabet omits J and K. Improvvisazione N. 1
is dedicated to Maderna’s second wife Beata Christina Köpenik. Another notation of the series, not shown here, indicates that Maderna derived the first two pitches from Beata’s name (“Be” = B![]() , “A,” “T” = rest, “A,” with the rest and second A eventually eliminated). See also Fein 2001, 15.
, “A,” “T” = rest, “A,” with the rest and second A eventually eliminated). See also Fein 2001, 15.
Return to text
13. Rizzardi 2004, 32. This technique was first analyzed in the works of Maderna and Nono in the early 1990s by Gianmario Borio and Veniero Rizzardi, who termed it “tecnica degli spostamenti” (Borio 1999, 2004, Rizzardi 2004). Selected serial charts for
Improvvisazione N. 1 (including my Examples 2a, 2e, 5, and the first four matrices of Example 4) have been discussed before by Fein (2001, 15–27) and Rizzardi (2004, 31–46).
Improvvisazione N. 1 was likely the second work in which Maderna used the kinds of serial matrices to be discussed. He probably employed them for the first time in
Studi per il “Llanto” di G. Lorca, an unfinished composition for tenor, flute, and guitar, that cannot be dated with certainty. Fearn 1990, 345, and Karlen and Romito 1990, 22, date
Studi “1950–1952?”
Return to text
14. The graphic representation of the series maps onto
itself if the matrix is rotated by 180 degrees.
Return to text
15. Under transposition, the graphic shape of a given
pitch-class series would remain the same, moved up or down in the matrix (and
“wrapped around” its edges). A pitch-class series is retrograded by mirroring it
around a vertical axis of the matrix and inverted by flipping it around a
horizontal axis.
Return to text
16. Maderna’s sketch also shows how he assigned
number values to letters, which in turn allows for the reconstruction of the
original Latin square in Example 2e, itself not preserved in the sketches (A=14,
B=14, C=5, D=11, E=25, F=10, G=6, H=9, I=8, L=13, M=5, N=12).
Return to text
17. The elision accounts for the first two unconnected
dots in the first matrix. They are the penultimate dots in their respective rows
before “catching up” with the original series. The third unconnected dot (in the
tenth column of the first matrix) results from the first shift of that pitch
class F![]() .
.
Return to text
18. The array is the one shown earlier in Example 2d.
Return to text
19. The technique of sustaining a pitch beyond its
assigned duration and until its next occurrence in the matrix is featured
prominently later in the string parts of the fourth movement from Luigi Nono’s
Il canto sospeso (1955–56). See Guerrero 2006, paragraph 27, and Nielinger 2006, 102.
Return to text
20. Maderna’s sketch transcribed in Example 8 lists a different instrumentation for a different section of the work. I have adjusted that information in the square brackets.
Return to text
21. Maderna’s orchestration assigns each lyne of the eleventh matrix (Example 4) that contains dots to a specific instrument. The flute and first violin play two lynes
(pitch classes) each.
Return to text
22. See Maderna 1959, Baroni and Dalmonte 1985, 205, and Scaldaferri 2001, viii. The work was premiered on July 21, 1952 by Severino Gazzelloni (flute) and Romolo Grano (percussion) at the Ferienkurse für Neue Musik in Darmstadt. Maderna produced the tape part with the assistance of Werner Meyer-Eppler at the
Institut für Phonetik of the University of Bonn.
Return to text
23. For the history of the work from 1952 see Baroni and Dalmonte 1985, 205, Baroni and Dalmonte 1989, 62–63, Noller 1992, 65–66, Scaldaferri 1997, 59–61, and Scaldaferri 2001, vii–x.
Return to text
24. Fearn 1990, 69–70 and 78–83, Noller 1992, 65–66, and Scaldaferri 2001, viii. None of these authors analyzes the sketches.
Return to text
25. The open note-heads in Example 9 appear in red pencil
(filled-in) in the original.
Return to text
26. Series A (revised) through D use hexachords whose
interval vectors are saturated with the interval classes that correspond to the
intervals chosen for each series. Series A (revised) and C use hexachord 6-20,
the hexachordal set class with the largest content of interval classes 3 and 4
(realized as major and minor sixths in series A and major and minor thirds in
series C). The hexachords of series B and D belong to set class 6-1, the
hexachordal set class with the largest content of interval classes 1 and 2
(realized as major and minor seconds in series B and major and minor sevenths in
series D). Maderna’s choice is interesting in light of the fact that other hexachord set classes could have been used as well for the generation of series built from the same kinds of intervals. Maderna’s choice of 6-20 (Ode to Napoleon hexachord) and 6-1 (chromatic hexachord) was probably motivated by his study of the music of the Second Viennese School. Nono used the series from Schoenberg’s
Ode to Napoleon Buonaparte in 1949–50 in Variazioni canoniche sulla serie dell’op. 41 di Arnold Schönberg.
Return to text
27. Following a continuity draft (probably intended for
the tape part) that superimposes four series at a time, Maderna abandons this
material altogether.
Return to text
28. As before, added information that does not appear in
the original sketch is shown in square brackets.
Return to text
29. It is impossible to produce twelve-tone series
with patterns [2], [3], [4], and [6]. For instance, pattern [2] only
produces non-duplicating series of at most eight pitch classes, as
illustrated in the following diagram. All pitch-class successions shown
below the double line (to be read from left to right) end with a pitch-class
duplication, shown in italics. Thus, if we ignore the last entry in each
row, we obtain all possible non-duplicating pitch-class successions that can
be generated with the sequence of intervals from pattern [2] shown above the
double line. “Ascending” and “descending” intervals are indicated by
![]() and
and
![]() respectively.
The table is exhaustive.
respectively.
The table is exhaustive.
30. The twelve order positions are counted 0 through 11.
Return to text
31. The dot in the second column of the first matrix not
connected by lines spills over from the end of the example.
Return to text
32. The melochord was invented by Harald Bode in 1949. The instrument used for
Musica su due dimensioni was built for Werner Meyer-Eppler’s Institut für Phonetik at the University of Bonn where Maderna produced the tape part. The melochord spans five octaves, and can also be used to produce impulses and to filter sounds from an external source. See Scaldaferri 2001, xi, and Ungeheuer 1992, 133–35.
Return to text
33. Maderna uses another partitioning of the aggregate for
the assignment of durations in the following section of measures 17–26 (not shown). A
and F are assigned the note value of a dotted half, D![]() five eighths, C/D/E/F
five eighths, C/D/E/F![]() /A
/A![]() a half note, and B
a half note, and B![]() /B/E
/B/E![]() /G/G
/G/G![]() /F
/F![]() a quarter.
a quarter.
Return to text
34. Maderna moves the second pitch of the piano part in
Example 14 (B2) into the melochord part in Example 15 (measures 3–4).
Return to text
35. In Maderna’s manuscript of Example 15 the quarter rests marked with an arrow in measures 2, 5, 10, and 13 (the “general pauses”) appear in red pencil. The notes in the melochord (“El.”) marked “suono” are written in blue pencil in the original. They designate the moment when the melochord timbre has reached the pitch indicated (“suono”).
Return to text
36. Scaldaferri 2001, xi. The tape part contains part of the first 63 measures of the manuscript full score—the beginning of which is shown in Example 15—moving through the pitch-class materials of the 16 matrices in Example 12, omitting measures 45–60 (Scaldaferri 2001, xi). This is followed by a section for flute solo that moves through the first eight matrices (not shown here) that permute series [b] from Example 11. On the recording of the Darmstadt premiere (as described in Scaldaferri 2001, xi) this section is followed by what appears to be a flute improvisation on Maderna’s scoring of matrices 9–13 of series [b] (not shown here). The work concludes with a section for tape solo.
Return to text
37. The world premiere took place on April 10, 1954 at a
concert of Domaine Musical in Paris, Hermann Scherchen conducting. The German premiere took place at the Darmstädter Landestheater in April 1956, Hans Zanotelli conducting, at which time Maderna revised the work for publication. See Baroni and Dalmonte 1985, 216–17, and Fein 2001, 28–32.
Serenata N. 2 has been discussed on several occasions in the literature (Manzoni 1958, Brindle 1959, Mila 1976, 26–31, Montecchi 1989, Fein 2000 and 2001, 29–99). Since the sketch materials became accessible only in the late 1980s, the only studies to examine them are Montecchi 1989 and Fein 2000 and 2001. Both authors discuss the Latin and magic squares of Examples 17 and 18 (without making the terminological distinction). My analysis supplements theirs based on my own study of the sketch materials, and with a focus on Maderna’s
construction of his serial arrays. The sketches of Examples 20 and 23 are
reproduced here for the first time.
Return to text
38. For a detailed examination of the first part, see Fein 2001, 29–61.
Return to text
39. The four sections are measures 159–182, 183–207, 208–230,
and 231–269.
Return to text
40. See also Fein 2001, 63. The magic square in Example 18
is constructed using a method derived from that of De la Loubère. The succession 1-n2 follows the NW-SE diagonals, starting with 1 in the central column (column V, row VI). The succession wraps around the edges; once all positions of a (wrapped-around) diagonal are filled, the succession continues two diagonals below. As Veniero Rizzardi has pointed out, Maderna likely owned the book
Matematica dilettevole e curiosa by Italo Ghersi that contains a chapter and appendix on magic squares. The method of De la Loubère is discussed on pages 294–5 of the fifth edition still available today (Ghersi 1988). See Rizzardi 2004, 33.
Return to text
41. There is no sketch of Maderna’s that shows this;
the content of Example 19 is derived from the sketch whose beginning is
transcribed in Example 20 below.
Return to text
42. The collection of nine pitch classes is taken from a
sketch in which Maderna removes various trichords from the complete aggregate,
creating various nine-pitch-class subsets, each listed in ascending order as at
the top of Example 19.
Return to text
43. Maderna’s staff notation shows pitches, not
pitch classes, obviously, but as is evident from what follows, Maderna clearly
thinks in terms of pitch classes here.
Return to text
44. See also Fein 2001, 66.
Return to text
45. For the sake of clarity, I have underlined the first
and last value on each path.
Return to text
46. This property is also discussed in Fein 2001, 66.
Return to text
47. Maderna’s technique of shortening pitch durations or eliminating pitches altogether has been widely noted in the String Quartet of 1955 (Manzoni 1958, 115, Weber 1978, 207–14, Berio 1985, 68, Fearn 1990, 97, Fein 2001, 183–204), and has variously been termed “suspension of the material” (“Materialsuspension,” Fein), “technique of omission” (“Auslassungstechnik,” Fein), “filter” (Berio, Fein), and “spacing-out” (Fearn). Montecchi 1989, 137, first mentions the use of filters (“filtraggio”) in the second part of
Serenata N. 2, without further analysis. With the help of the sketches,
Fein 2000 provides the first detailed analysis of the technique for the final
section (measures 231–69, using multiple filters). In addition, Fein 2001, 66–77,
discusses the use of the technique in the two preceding sections, measures 183–207
and 208–30, presenting a full analysis for measures 208–30 (multiple filters).
Return to text
48. Also eliminated for the same reason (filter values
equal to or longer than the pitch durations) are the D![]() in measure 6, lyne 4, the D in measures 3–4, lyne 6, and the E in measure 6, lyne 8.
in measure 6, lyne 4, the D in measures 3–4, lyne 6, and the E in measure 6, lyne 8.
Return to text
49. Nowhere in the sketches does Maderna specify the color
code, but it can be inferred from two sketches (not shown here) that follow
Example 23. They establish the orchestration of the final version. It is not
clear what kind of distinction between red and blue Maderna had in mind, as both
colors are assigned to the same instrumental forces.
Return to text
50. The fixed pitch collection is B2, C![]() 3, G
3, G![]() 3, B
3, B![]() 4, E
4, E![]() 5, E5, F5, D6, G6.
It lasts until measure 195.
5, E5, F5, D6, G6.
It lasts until measure 195.
Return to text
51. “Un ritorno deve potersi compiere in condizioni diverse. È celebre il viaggio d’Ulisse. Esso insegna che non vi può essere un ritorno, che la vita nel suo eterno divenire muta continuamente. Ora perché non si doveva possedere una tecnica che alla tecnica della vita nel suo divenire assomigliasse?” Maderna 1953–5, 46. As is evident from our analyses, however, the analogy is limited in light of the cyclicity of Maderna’s
permutation procedures: they ultimately do bring us back to the original series.
Return to text
52. “Quello che non mi piaceva della teoria dodecafonica
era il principio che una volta data una serie questa dovesse, per necessité di
conseguenza nel discorso musicale, riapparire nella sua integrité continuamente
sia verticalmente che orizzontalmente.
Return to text
53. “È evidente che un compositore vale più come creatore
di una sintesi tra mezzo e applicazione, in quanto espressione della sua epoca
contemporanea. Ciò che io personalmente in Schoenberg trovo soprattutto valido è
appunto questa esatta comprensione dell’importanza del mezzo obiettivo in
contrasto con l’individualité dell’espressione.” Ibid., 38–39.
Return to text
54. “
Return to text
55. “Compositional subject and compositional objectivity face each other
across an abyss.
Return to text
56. “J’ai mon
propre système grammatical, qui relève du principe sériel, et qui est
suffisamment souple, surtout suffisamment abstrait pour me laisser toute liberté
d’y incarner de mille manières mon imagination musicale, qui n’est nullement
abstraite.” Maderna 1965, 28. Italics in the original.
Return to text
Copyright Statement
Copyright © 2007 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Tahirih Motazedian, Editorial Assistant