Embracing Relational Abundance
Shaugn O’Donnell
REFERENCE: http://www.mtosmt.org/issues/mto.07.13.2/mto.07.13.2.buchler.html
ABSTRACT: This brief essay addresses some concerns raised by Michael Buchler in “Reconsidering Klumpenhouwer Networks” (MTO 13.2) regarding the alleged promiscuity of K-nets and their use in music analyses.
Copyright © 2007 Society for Music Theory
[1] In his provocative article “Reconsidering Klumpenhouwer Networks” (MTO 13.2), Michael Buchler offers readers a useful analogy comparing “network structures” to “modeling clay” [par. 46]. In Buchler’s hands this is cast as a dangerous similarity, but in contrast I’m excited to take a seat at the potter’s wheel and throw some clay in this brief response to his essay. As with many of Buchler’s observations, his analogy is equally applicable to all we do as music analysts, rather than a critique specific to “K-nets and their analytical deployment” [par. 1]. Acknowledging at the outset that K-nets “are elegant structures,” Buchler goes on to state that they open “Pandora’s Box of relational permissiveness” and that “clearly, the more ways that it is possible to draw equivalent relations, the less significant those relations become” [par. 2]. The alleged clarity eludes me, so I’ll take a more extreme position and suggest no relations are inherently significant, that is, I propose that all relations—common or rare—are comparably context dependent. I would reformulate Buchler’s criticism to state that the relational abundance generated by K-nets further emphasizes that musicality, whatever that means in a given context, is in the hands and ears of the analyst rather than the theoretical apparatus itself.(1) Of course, this is nothing new; it’s true for all of our interpretive work and all of our analytical models.
[2] Shifting analogies, performing music analysis is like storytelling. For example, despite his graceful precision, I don’t read David Lewin’s work for his mathematical proofs of abstract relations. Instead, I read Lewin’s essays because he was a gifted raconteur, a writer who spun compelling tales about specific musical passages, with the ability to alter my understanding of the selected music in a meaningful and permanent way.(2) A convincing analysis forges a narrative pathway through a musical passage, and individual relations or transformations only gain meaning in the context of the story. I might even suggest that relations, as well as our desire to create them, are merely a byproduct of the temporal nature of music. From this perspective, Buchler’s repeated emphasis on “relatedness” as a central problem in K-net analyses, particularly the greater abstraction of potential relatedness, is off target. I will directly address some of his criticisms of K-net mechanics in the next section, but first I must note that when these abstract relations have no intrinsic meaning, the only remaining analytical benchmark is how persuasive we find any individual narrative. Again, musical relevance as the measure for our analyses is not K-net specific; it applies to all our endeavors. We are writing analytical fictions about musical gestures as they unfold in time and/or space.
[3] Although Buchler’s primary concern with K-nets is their potential promiscuity, he only compares them to the canonical operators transposition and inversion. Furthermore, he does so in terms of the abstract equivalence classes generated by those very operations, thus stacking the deck against K-nets. A good example is his defamatory characterization of [026]: “once [026] comes to the party, every other trichord enjoys at least one mutual relation” [par 36]. While the metaphor is entertaining, [026] can never come to the analytical party, only a member of [026] can occur in a musical work. In the literature under examination, transformations occur among pcsets, generally not set classes. In that practical context, K-net promiscuity is not nearly the serious problem suggested by Buchler. In the puritanical world of canonical transforms, {0,2,6} can only have relations with twenty-three of the remaining possible 4,094 pcsets; that’s less than 1% of the population.(3) This inability to communicate with other pcsets creates glaring problems of fragmentation and gaps in many post-tonal analyses.(4) In the more social circle of K-nets, {0,2,6} can have relations with approximately 3.5% of the population, or up to 10.5% if one is willing to explore the multiple configurations afforded by double emploi.(5) In other words, a K-net {0,2,6} is still rather discerning in rejecting 90–96% of its potential suitors, and only against Buchler’s backdrop of canonical set classes does a K-net {0,2,6} seem promiscuous. It’s not freely partying with i>all the other 4,094 pcsets!
[4] Buchler is also careless in distinguishing “split” and “dual” transformations throughout his essay(6) While most readers will understand that he’s using the terms as synonyms, with the word split referring to the act of parsing pcsets into two subsets, it’s important to be careful about this seemingly minor distinction. If we’re splitting pcsets to better describe the musical surface, one of Buchler’s frequent pleas, what prevents us from splitting them into as many subsets as necessary to match the literal lines (registral, etc.) in the musical score? The answer is nothing, but that would be a virtual Bacchanalia, with all pcsets potentially having relations with all the others.(7) Buchler provides an informal proof that any K-net partitions into exactly two T-sets [par. 17], and he then consistently limits himself to two subsets and dual transpositions in his analyses. As he demonstrates in his own proof, it is specifically the structure of K-nets that motivates and models this otherwise arbitrary constraint.(8) The discriminating power of K-nets and dual transformations—allowing many times more relations than the canonical operators, yet filtering out most relations (90–96%)—is located at a comfortable place on the exclusivity–promiscuity continuum for many of us, thus yielding the large body of analytic literature in question.
[5] I agree with Buchler that ’dual transpositions or inversions’ present ’a simpler musical scenario’ than K-nets [par. 19], and that many K-net analyses and abstractions would benefit by their inclusion.(9) However, I disagree that “network-internal In values are unnecessary” [pars. 12 and 15]. Buchler’s reasons for this statement are accurate; internal In arrows aren’t necessary to recognize isography [par. 12] or calculate hyper transformations [par. 15], but they’re still necessary for the unity of the musical sonorities participating in these transformations. Even when we hear the independent paths of two subsets in a dual transformation, we very often hear the supersets as single, unified musical “objects,” particularly in homorhythmic contexts. A good example would be Catherine Nolan’s analysis of Webern’s Das Augenlicht that Buchler champions as a successful use of K-nets [pars. 53’55].(10) Is there anyone among us that doesn’t hear the chorale sonorities in Buchler’s Figure 24 (Nolan’s Example 1a) as unified chords? If we only trace the paths of the independent T-sets, we emphasize the horizontal dimension at the expense of the vertical; it’s an old, familiar problem. Furthermore, if we do eliminate the In arrows, then how and why are we relating the two internal T-sets? Do we only hear the separate, completely independent linear streams in such cases? If so, then what exactly do Buchler’s vertical lines mean in his Figures 5, 6, 11, and so on? He declines to tell us.(11)
Figure 1. (Buchler’s Figure 14). Lutoslawski, Symphony No. 4, Rehearsal 92, vc. (tutti)
(click to enlarge and listen)
Figure 2. An initial aural impression
(click to enlarge)
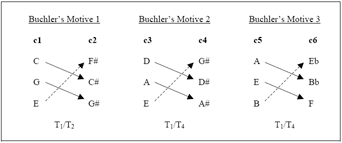
[6] Let’s “reconsider” one of Buchler’s examples—the celli passage from the end of Lutoslawski’s Symphony No. 4—to imagine an alternative reading. Depending on one’s perspective, the narrative I present below will support Buchler’s arguments, my own, or ideally, both. Figure 1 reproduces his example [Figure 14]. Listening to this passage, I immediately notice its saturation with ic5s, as well as the contour pattern (<013245>) that Buchler emphasizes. However, these sounds don’t lead me to hear his three motivic hexachords, but rather the six component trichords defined by that contour. I also notice that almost all six are quartal harmonies, or members of sc [027], but I don’t necessarily hear them as transpositions of one another. Instead, the contour pattern highlights the semitones between the paired trichords. I summarize this initial aural impression in Figure 2.
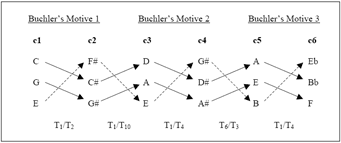
[7] While Buchler “intuitively” prefers “simple transformations” whenever possible [par. 29], I don’t particularly hear the progressions c3–c4 and c5–c6 as T6 (or I0 and I2 respectively), despite the ability to interpret them in that manner. I hear them as T1ish as shown by the arrows in my figure. If I want a model that emphasizes the T1s in these motions, then the remaining tones—first and last, lowest and highest—must leapfrog around the T1 dyad pairs, yielding the dual transpositions shown in Figure 3, which best captures what I hear happening within Buchler’s three motives. If we continue the narrative to link the motives by undoing the registral permutations shown in Figure 3, we arrive at Figure 4.(12) Imagining his motives 2 and 3 as a dual T7/T7 particularly disturbs Buchler, but the mappings in the smaller stages of my Figure 4, T1/T4 followed by T6/T3 in the paired trichords, illustrate why one might interpret it this way. Furthermore, it shows what’s similar about T2/T0 and T7/T7 in this particular musical circumstance.
|
Figure 3. Dual transpositions modeling Buchler’s three motives (click to enlarge) |
Figure 4. Motivic dual mappings through all six trichords (click to enlarge) |
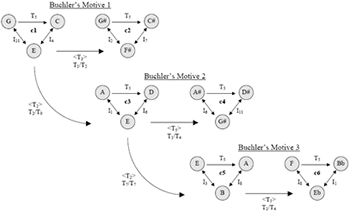
Figure 5. K-nets modeling all six trichords
(click to enlarge)
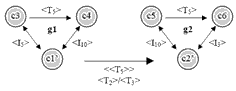
Figure 6. An irresistible supernetwork
(click to enlarge)
[8] Figure 5 illustrates these motions in K-net form. Each row in the figure is one of Buchler’s motives, and the hyper-transforms within each row are the dual transpositions between my trichords. As a music theorist, I can’t help but notice the correspondence between the T5s that saturate this entire passage and the <T5>s that define Buchler’s motives 2 and 3 (c3–c4 and c5–c6) in this model. Are they the same thing? Well, yes and no. They’re both transpositions of five semitones, but the objects being transposed are different; one is a literal pitch and the other is an inversional wedge. One might think of it as a transposition of an expectation. For example, we may expect the singleton in c4 to be
[9] Playing the role of Buchler’s fatally flawed K-net analyst, I blindly fall victim to the elegant seduction of <T5>. I’m powerless to prevent myself from producing Figure 6. The upper nodes in this supernetwork, the <T-sets>, keep the two final two motives intact and emphasize the isography between the primary interval of the passage, T5, and the dual transposition, T1/T4 or <T5>, that generates these two motives. Networks c1 and c2 must be inverted to create the negative isography shown in the figure, but this still keeps the first motive intact, as it doesn’t affect the T1 surface mapping that generates the motive.(14) Finally, though my reinterpretation of this passage may seem to convincingly support Buchler’s complaints regarding K-net promiscuity and malleability, the middleground network in Figure 6 is actually quite an exclusive structure. If we’ve traveled through the celli passage until the final trichord, c6, there are only twelve pcsets that can complete this <<T5>> network, and that’s already a more exclusive group than many of our canonical set classes, but if we wish to retain the T1-ness that defines our motive and still complete this isographic supernetwork, c6 is the sole pcset capable of that accomplishment.(15) However, this interpretation may be too far down the road of abstraction for some readers.
[10] I thoroughly enjoyed Buchler’s essay and firmly believe all of our ideas should receive this kind of intense public scrutiny. His clear explanation of K-nets and dual transformations are an excellent primer on these concepts, and I plan to make it required reading in several courses. I find myself agreeing with many of his proposed refinements in K-net practice, such as including dual transformation labels, and further distinguishing among types of isography (“consistent, grand,” etc.) [par. 30]. He also successfully highlights many problem areas in K-net practice, such as repeating and omitting tones [pars. 52 and 65], and perceptual difficulties, such as hearing <In> [par. 56]. On the other hand, I don’t always agree with Buchler’s subsequent conclusions. I’m not ready to dump internal In arrows, <In>, or even recursion yet, though I’m always willing to revisit the question. As I hope my brief analysis illustrates, supernetworks can fall out of an analysis; they’re not always the result of the difficult and manipulative search portrayed in Buchler’s essay [pars. 64–65]. Rather than fearing the proliferation of possibilities afforded by K-nets and their alleged promiscuity, we should embrace this relational abundance and use it as justification for further exploration.
Shaugn O’Donnell
The City College and Graduate Center, CUNY
Music Department, S72
160 Convent Ave.
New York, NY 10031
sodonnell@ccny.cuny.edu
Works Cited
—————. 1998a. “The Inner and Outer Automorphisms of Pitch-Class Inversion and Transposition: Some Implications for Analysis with Klumpenhouwer Networks.” Intégral 12: 81–93.
—————. 2002. “Isographies and Some Klumpenhouwer Networks They Involve.” Music Theory Spectrum 24.2: 165–195.
Lewin, David. 1982–83. “Transformational Techniques in Atonal and Other Music Theories.” Perspectives of New Music 21: 312–71.
—————. 2002. “Thoughts on Klumpenhouwer Networks and Perle-Lansky Cycles.” Music Theory Spectrum 24.2: 196–230.
Nolan, Catherine. 2005. “More Than Meets The Eye: Text, Texture, and Transformation in Webern’s Das Augenlicht, Op. 26.” Paper presented at the Dublin International Conference on Music Analysis, Dublin, Ireland, June 2005.
O’Donnell, Shaugn. 1996. “Transformational Voice Leading in Two Songs by Charles Ives.” Paper presented at the Society for Music Theory Annual Conference, Baton Rouge, LA.
—————. 1997. “Transformational Voice Leading in Atonal Music.” Ph.D. dissertation, City University of New York.
—————. 1998. “Klumpenhouwer Networks, Isography, and the Molecular Metaphor.” Intégral 12: 53–80.
—————. 2005. “If-Only Networks and Analytical Desire.” Paper presented at the Dublin International Conference on Music Analysis, Dublin, Ireland.
Roeder, John. 1994. “Voice Leading as Transformation.” In Musical Transformation & Musical Intuition: Essays in Honor of David Lewin. Edited by Raphael Atlas and Michael Cherlin. Roxbury, Massachusetts: Ovenbird Press, 41–58.
Footnotes
1. Buchler repeatedly emphasizes analytical musicality throughout his essay, perhaps best summarized in this statement: “analysts ought to exercise particular diligence and discretion in making a strong case for the uniqueness and musicality of their readings” [par. 37].
Return to text
2. I could cite numerous examples, but I’ll simply offer his reading of Webern’s Op. 5, No. 2, in “Transformational Techniques” as an ideal instance (Lewin 1982–83).
Return to text
3. A bit of clarification is in order. I randomly selected {0,2,6} to represent sc [026] for the purposes of this discussion. I omit abstinence (the null set) as a non-relation and, empathizing with the canonical puritans for the moment, I also omit the self-indulgent T0. That yields my 23/4,094 or just over half of one percent (approximately .56%).
Return to text
4. “The exclusivity of traditional set classes not only leads towards a fragmented analytical approach that traces independent paths for each prominent set class within a given musical work, but often also leaves large temporal gaps between two ‘adjacent’ members of the same set class” (O’Donnell 1998, 61). O’Donnell 1997 includes more detailed discussion of the exclusivity–promiscuity continuum.
Return to text
5. These numbers are derived from Lambert’s K-families (Lambert 2002) with 144/4,095 yielding the first number (approximately 3.5%), and
double emploi (O’Donnell 1997 and 1998) allowing relations with to up to two other K-families, or 432/4,095 (approximately 10.5%).
Return to text
6. The casual interchange of split and dual occurs throughout the essay, most notably in pars 18–20, 25, and 28–31.
Return to text
7. The literal voice-leading model in Roeder 1994 comes close to this extreme.
Return to text
8. The fact that K-nets partition into exactly two T-sets was first illustrated in O’donnell 1996, and then developed more explicitly in 1997 and 1998. Later, Lewin referred to this property as “Whincop’s Observation” in “Thoughts on Klumpenhouwer Networks and Perle-Lansky Cycles” (2002, 216). Buchler’s proof is significant in providing more formal support for these earlier discussions.
Return to text
9. I wouldn’t go as far as Buchler’s statement that “it would be difficult to imagine a situation in which dual transformation did not provide a more straightforward phenomenological account than K-nets” [par 58], but the merger of K-nets and dual transformations is the core point of O’Donnell 1998.
Return to text
10. Nolan 2005, but I’ll leave further comments to the author.
Return to text
11. I can only venture two plausible options: (1) they represent all the In arrows in a notational compression, making Buchler’s networks nothing more than K-net abbreviations; or (2) they have no specific meaning, they’re just lines, in which case we’re at a conceptual impasse. I understand Buchler’s phenomenological resistance to internal In arrows, but I’m surprised by his failure to at least embrace them metaphorically, particularly given his understanding of the metaphorical nature of the easier-to-hear Tn bonds with his “glue” imagery [par. 16].
Return to text
12. Linking the motives by undoing the previous registral permutations is not an arbitrary choice; it has phenomenological roots. Like Buchler, I hear the opening low E map onto its repetition three measures later. The mappings shown between c2 and c3 in Figure 4 accomplish that, as well as continue the climbing semitones of the dyads. The mappings from c4 to c5 are slightly different in that they continue the now motivic registral permutations, but not the semitone motion. An alternative interpretation might just slide all of c4 up a semitone to c5, but that would destroy the integrity of the leap-frogging motion and its consistent mapping, a feature most audible in the metric emphasis on the initiating notes of Buchler’s motives.
Return to text
13. See Klumpenhouwer 1998 for further discussion of these issues.
Return to text
14. The inversion of networks c1 and c2 only alters the surface-level mapping between c2 and c3, making it I10/I10 rather than T1/T10, but this is not particularly problematic for me when a cadence and fermata intervene between those sonorities anyway.
Return to text
15. O’Donnell 2005 explores this form of exclusivity in greater detail.
Return to text
Copyright Statement
Copyright © 2007 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo, Editorial Assistant
Number of visits: