Without a Safety (k)-Net
Philip Stoecker
REFERENCE: http://www.mtosmt.org/issues/mto.07.13.2/mto.07.13.2.buchler.html
Copyright © 2007 Society for Music Theory
[1] When analyzing a passage of music with K-nets, the transformational operation from one K-net to the next is just as important as the construction of each individual K-net. To ensure that different K-nets are related, various authors have proposed that either an interval (Lewin 1990 and Klumpenhouwer 1991) or an inversional relationship (Stoecker 2002) from one K-net to the next must remain invariant. And with all the isographic tools that are available—strong, positive, negative, and axial isography—virtually every trichordal K-net can be isographically related to any other trichordal K-net. This high degree of isographic relatedness is a concern for Michael Buchler. In his critique of K-nets and K-net analyses, Buchler points out that
“[s]ince the most promiscuous trichord classes include many of the most common and familiar melodic and harmonic structures found in a wide range of repertoire, trichordal isography generally comes easily to those who seek it. When the standard for pcset relatedness is this low, analysts ought to exercise particular diligence and discretion in making a strong case for the uniqueness and musicality of their readings.”(1)
[2] Though Buchler warns us about the promiscuous nature of trichordal isography, there are times when adjacent, trichordal collections do not share an interval or an inversional relationship. As a result, the K-nets that model these sonorities cannot be isographically related, creating a gap in our transformational pathway. These isographic holes are the focus of my article. Trichordal K-nets that cannot be conventionally and axially isographic are extremely rare in the literature. It is unusual to find two collections that do not share an interval class or an inversional relationship.(2) To better understand how these analytical gaps occur, I will focus on the voice leading between K-nets that cannot be isographically related.
[3] In his first published study of K-nets, David Lewin analyzes a few brief passages from “Eine blasse Wäscherin,” the fourth song from Arnold Schoenberg’s Pierrot Lunaire, op. 21.(3) The Pierrot passages that Lewin analyzes are good ones for illustrating the strengths of a K-net analysis. Lewin effectively demonstrates how to construct coherent, transformational pathways and introduces K-net recursion. But if we analyze the entire song with a K-net lens, we will find that the isographic tools that Lewin introduced cannot relate a few K-nets.
Example 1. Schoenberg, “Eine blasse Wäscherin,” Pierrot Lunaire, op. 21, mm. 1–4
(click to enlarge)
Example 2. Schoenberg, “Angst und Hoffen,” Das Buch der hängenden Gärten, op. 15, mm. 1–2
(click to enlarge)
Example 3. Voice-leading scenarios from Schoenberg’s “Angst” trichord
(click to enlarge)
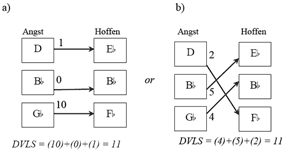
Figure 1. Cohn’s Directed Voice-Leading Sum (DVLS) applied to “Angst” and “Hoffen”
(click to enlarge)
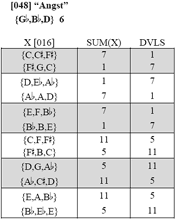
Figure 2. The [016] presets that cannot be isographically related—strong, positive, negative, and axial—to {G,B,D}, the “Angst” sonority
(click to enlarge)
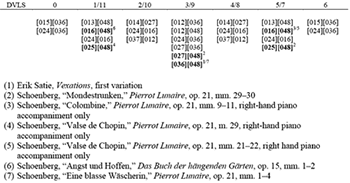
Figure 3. Set-class pairs that are not isographic organized into DLVS categories
(click to enlarge)
[4] Example 1 includes the score for the opening instrumental phrase of “Eine blasse Wäscherin.” Most of the trichords in this passage contain a dyad of interval-class 3, and the K-nets that model these collections could be configured in such a way that T3 and T9 arrows are drawn. From an isographic perspective, virtually every trichordal K-net in this passage is strong, positively, or negatively isographic to its adjacent K-net. In m. 3, however, the K-net that interprets the [036] diminished trichord cannot be isographically related to the K-net that interprets the [048] augmented trichord. Since these two collections do not share an interval class, the K-nets cannot be related by strong, positive, or negative isography. And since these particular diminished and augmented trichords do not share an inversional relationship, they cannot be related by axial isography. As a result, the K-nets that interpret these two collections cannot, in any way, be isographically related.
[5] An even more remarkable passage to explore non-isographic K-nets occurs in Schoenberg’s song “Angst und Hoffen” from his Buch der hängenden Gärten, op. 15, no. 7, given in Example 2.(4) The first three collections of the piano accompaniment are members of three different set classes: [048], [016], and [03] respectively. The augmented triad accompanies the word “Angst” while set-class [016] accompanies the word “Hoffen.” The A4/C5 dyad on the downbeat of the second measure accompanies the word “wechselnd.” Throughout the song, the “Angst” [048] and “Hoffen” [016] sonorities alternate with one another, reflecting the anxious longing for love by the narrator. What makes the opening accompanimental passage so remarkable from a K-net perspective is that these three adjacent collections do not share an interval or an inversional relationship, two requirements to ensure K-net relatedness.(5)
[6] Example 3 presents models that review voice-leading properties for three different types of isographies—the example does not include negative isography—and the last progression is Schoenberg’s “Angst” trichord to the “Hoffen” trichord. When trichords are strongly isographic (Ex. 3a) the registral, voice-leading lines feature three moves, all by the same interval class. When trichords are positively (Ex. 3b) or axially isographic (Ex. 3c) the registral, voice-leading lines will always feature two different interval-class moves. When trichordal K-nets cannot be isographically related, the registral lines will always feature three different voice-leading moves.(6) In Example 3d, the progression from the “Angst” trichord to the “Hoffen” trichord features three different registral voice-leading moves.
[7] An effective way to measure the voice leading of non-isographic K-nets is to use Joseph Straus’s “total displacement,” which is the sum in absolute value of the three voice-leading moves from one trichord to the next.(7) In Example 3d, the registral voice leading from the “Angst” to the “Hoffen” trichord features three different interval classes (2, 0, and 1), and these three voice-leading intervals sum to a total displacement of 3. A total displacement of three is significant since this is the smoothest possible voice leading for trichordal K-nets that cannot be conventionally and axially isographic. Since non-isographic K-nets will always feature three different voice-leading moves, a total displacement of 0 (0+0+0), 1 (0+0+1), and 2 ((0+1+1) or (0+0+2)) is not possible.(8)
[8] Another way to measure all the possible voice-leading lines between non-isographic K-nets is to use Richard Cohn’s
directed voice-leading sum
[9] If the original “Hoffen” trichord is transposed, different DVLS numbers emerge. Figure 2 shows that the “Angst” trichord cannot be conventionally or axially isographic with twelve of the twenty-four members from the [016] “Hoffen” family.(12) The figure also illustrates that four different DVLS numbers are possible when the “Angst” trichord is followed by one of the non-isographic, [016] pitch-class sets: 7 and its complement 5, 1 and its complement 11.(13)
[10] One of the advantages of using Cohn’s DVLS is that it helps catalog the different types of voice leadings for non-isographic K-nets, which I have included in Figure 3.(14) Each DVLS number is paired with its complement and listed along the top. Beneath each DVLS category I have included all set-class pairs that cannot be conventionally or axially isographic. For example, DVLS 0 contains only two set-class pairs that cannot be isographic: [015][036] and [024][036]. What the figure does not tell us is which [015] is not isographic with which particular [036]. Note that each non-isographic progression listed in the figure has at least one symmetrical trichord; these sonorities contain a limited number of different interval classes, which increases the chances that it will not be isographic with its adjacent sonorities. In addition to the symmetrical set classes, another manifestation of symmetry occurs in Figure 3: the trichordal progressions that are listed in DVLS 0 also appear in DVLS 6; the set-class pairs listed in 1/11 also appear in 5/7, and so on.(15)
[11] The set-class pairs highlighted in bold (Fig. 3) represent examples I found in the literature. Of the twenty-four possible pairs of non-isographic K-nets listed in the figure, only six are represented here. And in every case, an augmented triad plays a role in establishing the non-isographic relationship. In fact, the chance that an augmented triad plays the spoiler is quite high. Recall that in Figure 2, the [048] “Angst” trichord cannot be isographic with twelve different pitch-class sets from the [016] family.(16) In addition to its intervallic redundancy, all four members of the [048] family feature only even In labels. This is a significant property since all the other trichordal set classes feature two odd In labels and only a single even In label.(17) So when it comes to network isography, [048] functions as an isographic renegade.
[12] Though the augmented triad is responsible for most of the transformational gaps, trichordal K-nets that are not conventionally or axially isographic are quite rare. If we were to analyze the rest of the trichords in Schoenberg’s “Eine blasse Wäscherin,” network isography will be easily achieved. It should come as no surprise that in all the analyses that use trichordal K-nets, the analyst has presented coherent, transformational pathways since K-net relatedness is so common. Still, there is a definite limit to the abundant isographic relations among trichordal K-nets. But what do these isographic holes tell us about the music it models? As Figure 3 illustrates, all non-isographic progressions include at least one trichord that is symmetrically organized. In addition, non-isographic K-nets will always feature three different voice-leading moves, creating a maximally diverse pitch-class counterpoint. Recall that in Schoenberg’s “Angst und Hoffen,” the opening [048] to [016] progression features a variety of different voice-leading lines, and it is not difficult to imagine Schoenberg choosing two trichords that do not share any similarities; for me, Schoenberg’s diverse voice-leading lines appropriately accompany the words fear and hope of the text. So when it finally happens that K-nets cannot be isographically connected, the transformational paths are momentarily thwarted and the voice leading from one trichord to the next is maximally diverse. Rather than search for cues elsewhere to bridge these transformational gaps, I wish to highlight and celebrate those extraordinarily unique moments when our transformational safety (k)-net has been taken away.
Philip Stoecker
Oberlin College Conservatory
philip.stoecker@oberlin.edu
Works Cited
Buchler, Michael. 2007. “Reconsidering Klumpenhouwer Networks.” Music Theory Online 13.2: 1–69.
Cohn, Richard. 1998. “Square Dances with Cubes.” Journal of Music Theory 42.2: 283–296.
—————. 1991. “A Generalized Model of Voice-Leading for Atonal Music.” Ph.D. dissertation, Harvard University.
Lambert, Philip. 2002. “Isographies and Some Klumpenhouwer Networks They Involve.” Music Theory Spectrum 24.2: 165–195.
Lewin, David. 1981. “A Way Into Schoenberg’s Opus 15, Number 7.” In Theory Only 6.1: 3–24.
—————. 1990. “Klumpenhouwer Networks and Some Isographies That Involve Them.” Music Theory Spectrum 12: 83–120.
Stoecker, Philip. 2002. “Klumpenhouwer Networks, Trichords, and Axial Isography.” Music Theory Spectrum 24.2: 231–245.
Straus, Joseph N. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25.2: 305–352.
Footnotes
1. Michael Buchler (2007, [37]).
Return to text
2. Though some K-nets can only be related by axial isography, the invariant inversional relationship often exists in pitch-class space. For me, axial isography is a much stronger relationship when it unfolds in pitch space.
Return to text
3. Lewin (1990, 91–95 and 98–99).
Return to text
4. David Lewin (1981, 3–24), Philip Lambert (2002, 165–195), and Philip Stoecker (2002, 231–245) have analyzed passages of this song that resonate with my current analysis in meaningful ways.
Return to text
5. The K-net that models the A4/C5 dyad could be configured in such a way that it shares an I0 arrow with the first trichordal K-net.
Return to text
6. The reverse, however, is not true. Two trichords that feature three different voice-leading moves can, at times, be isographically related.
Return to text
8. On the other end of the spectrum, 15 will be the highest total displacement for K-nets that cannot be isographic. A trichordal progression that features a total displacement of 16 (5+5+6 or 6+6+4), 17 (6+6+5), and 18 (6+6+6) will have two (or three) voice-leading moves by the same interval class. Thus, the K-nets that model these trichordal progressions can be isographic.
Return to text
10. Unlike Cohn’s DVLS, if we choose different voice-leading lines Straus’s total-displacement number changes.
Return to text
11. As Cohn points out, the DVLS number can also be measured by calculating the difference between the SUM of the pitch-class integers for set (X) with the SUM of the pitch-class integers for set (Y). That is, if C = 0, then SUM(Y) – SUM(X) = DVLS.
Return to text
12. Tritone transpositions for each [016] set class are listed next to each other since a T6 operation on any set class preserves all the In labels.
Return to text
13. Unlike Straus’s total-displacement numbers, DVLS numbers for non-isographic K-nets do not have a minimum value of 3.
Return to text
14. [026] is the only trichordal set class not included in this figure since it can be isographic with all trichordal K-nets.
Return to text
15. The symmetrical organization of Figure 3 can be explained as follows: If pcset X is not isographic with pcset Y, then pcset T6X will also be non-isographic with pcset Y—a tritone transposition of a pcset preserves both the interval content
and the In labels. From a voice-leading perspective, the DVLS numbers for X to Y and T6X to Y will differ by six, e.g., DVLS 1/11 (X to Y) and DVLS 7/5 (T6X to Y). Thus the non-isographic progressions in the figure appear in two different DVLS categories related by a tritone. DVLS 3/9 is a self-mapping category, i.e., DVLS 3/9 and its tritone partner DVLS 9/3 are the same category.
Return to text
16. To offer a different scenario, {C,C![]() ,E}, a member of set class [014], cannot be isographic with only two pcsets from the [027] family: {C,D,G} and
,E}, a member of set class [014], cannot be isographic with only two pcsets from the [027] family: {C,D,G} and ![]() ,G
,G![]() ,C
,C![]() }.
}.
Return to text
17. In addition to [048], all members of the [024] and [026] families feature only even In labels.
Return to text
Copyright Statement
Copyright © 2007 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo, Editorial Assistant
Number of visits: