Recasting K-nets *
Dmitri Tymoczko
REFERENCE: http://www.mtosmt.org/issues/mto.07.13.2/mto.07.13.2.buchler.html
ABSTRACT: In this article I propose a new notation for hyper-transpositions and hyper-inversions, in which the usual subscripts are divided by 2. This new notation allows us to recast the hyper operations as ordinary transpositions and inversions operating on equivalence classes in 24-tone equal temperament. This suggests a response to Buchler and Losada, who both criticize the conceptual foundations of standard K-net analysis.
Copyright © 2007 Society for Music Theory
I. The Problem
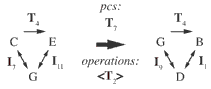
[1] In a recent article, Michael Buchler observes that K-nets such as those in Figure 1, which I will notate as
[2] This question is worth taking seriously. Although hyper-transposition is different from ordinary transposition, being a function over functions rather than a function over pitch classes, comparisons between these two types of “transposition” are intrinsic to the practice of K-net analysis. And although the primary analytical use of K-nets is to relate sets belonging to different set classes, the technology applies equally well to chords such as C major and G major. Buchler has uncovered an example that seems to demonstrate that there is only a tenuous analogy between the two sorts of transposition. It will not do simply to reiterate that they are different. For Buchler’s challenge is, given that they disagree so dramatically about such a simple case, what’s the musical value of comparing them?
[3] It is possible, however, that a simple change in notation might help meet his objection. For suppose we used the label <T7> to refer to the hyper-transposition linking {C, E} + {G} to {G, B} + {D}. In that case, the force of Buchler’s worry would be significantly ameliorated, since there is obviously something T7-like about the relationship. We might therefore ask whether it is possible to label the members of the hyper-TI group <TI>, such that, if Tx or Iy transforms the pitch classes in one K-net K into those of another K′, with arrows being updated accordingly, <Tx> or <Iy> transforms the arrow-labels in K into the arrow-labels in K′? (See Figure 2.) In other words, can we label the elements of the hyper-TI group in a way that is consistent with the TI group?
II. The Solution
[4] Yes. Simply divide the current hyper-T and hyper-I labels by 2. The only complication is that division is not uniquely defined in circular pitch-class space.
[5] As shown in Figure 1, {C, E} + {G} relates to {G, B} + {D} by <T2> in ordinary K-net notation. I propose instead that we label this hyper-transposition <T1 or T7>. This is because 1 + 1 = 7 + 7 = 2 (mod 12). In other words, “2 divided by 2” can be either 1 or 7 in pitch-class space. Note that the label <T1 or T7> does not refer to a “dual transposition”: it does not mean that one part of the K-net moves by 1 semitone while the other moves by 7 semitones. Instead, it says that the two parts of the K-net move by a total distance that is equal to both 1 + 1 and 7 + 7 (mod 12). Intuitively, the parts move by an average distance of 1 or 7 (mod 12): thus they might move by 1 and 1, 7 and 7, 0 and 2, 6 and 8, and so on.
[6] Now what’s T1 or T7-ish about the relation between C major and G major? The T7 relationship is obvious. What about T1? Well, {C, E} + {G} is strongly isographic (<T0>) to {
[7] Q: In the new system, what hyper-transposition relates {C, E} + {G} and {C, E} + {![]() , E
, E![]() } + {G
} + {G![]() } (C and E quarter-tone flat, G quarter-tone sharp) are strongly isographic, and hence related by <T0>. Transposing the second chord up by half a semitone yields {C, E} + {
} (C and E quarter-tone flat, G quarter-tone sharp) are strongly isographic, and hence related by <T0>. Transposing the second chord up by half a semitone yields {C, E} + {
[8] The new notation suggests a response to those, like Buchler, who worry that hyper-T and hyper-I are too abstract. Every K-net defines an equivalence class of strongly isographic chords in 24-tone equal-temperament, as shown in Figure 4. The statement that two (12-tone equal-tempered) K-nets are related by <Tx> or <Iy> is logically equivalent to the statement that these equivalence classes relate by Tx or Iy (Figure 4). Thus we need not think of “hyper-transposition” and “hyper-inversion” as being extremely abstruse “functions over functions”: instead, we can understand them as ordinary transpositions and inversions of equivalence classes.(4) In principle, there is nothing problematic about using transposition and inversion to relate equivalence classes; we do this every time we talk about transpositionally related pitch-class sets. The only question is whether equivalence classes of strongly isographic chords are analytically or perceptually meaningful—an issue we will return to shortly.
[9] I know that many music theorists dislike quarter tones. So here’s an argument for my new notation that relies on 12-tone equal temperament exclusively: in twelve-tone equal-temperament, no chord that is strongly isographic to {C, E} + {G} is transpositionally related to {C, E} + {
[10] Since there are several ways to notate ordinary inversions, there are several ways to notate hyper-inversions.
Alternative 1. If you label inversions with index numbers, you should divide the current hyper-I labels by 2. In this new system, <Tx>Iy = I2x+y and <Ix>Iy = I2x–y. Some hyper-inversions will be labeled with half-integers, just like hyper-transpositions.
Alternative 2. If you use Lewin-type labels, such as
I , then<Tx>I will transpose a and b by an average of x semitones. Thus<T1/2>I since here we transpose= I
,
E♭ by 1 and E by 0, for an average transposition of (1 + 0)/2 = 1/2. In this system, some hyper-inversions will be labeled with quarter tones.Alternative 3. Perhaps the best solution is to divide ordinary inversion labels by 2, labeling inversions by their fixed points, or
. In this system,
I is represented by I3.5. (Informally, this is an inversion that maps pitch class 3.5, or E, to itself.) This allows us to keep the traditional rule <Tx>Iy = Ix+y. However, in this system, some hyper-inversions will have quarter-integer labels, such as <I1/4>.
[11] Table 1 compares these alternatives. Note the consistency, in Alternative 3, between the way the TI operations operate on pitches, collections, and operations: in each case, T adds x to something (a pitch or an inversion subscript), while I subtracts something from 2x (a pitch or an inversion subscript). In standard notation, there is an inconsistency between the way TI operate on collections and operations, while in Alternative 1, there is an inconsistency between the way TI operate on pitches and on collections and operations. My goal here is to ensure consistency between collections and operations.(6)
III. Problems for recursivity
[12] What happens to existing K-net analyses if we adopt my proposal? Well, ordinary T labels stay the same while hyper-T labels are divided by two. This means that in the new notation, existing “recursive” K-net analyses—purporting to demonstrate isographies between K-nets and “hyper K-nets”(7)—will no longer seem to be recursive. It follows that their apparent “recursivity” depends on a particular (and possibly ad hoc) way of labelling hyper-operations. I therefore agree with Buchler that we should be concerned about the significance of these analyses.
[13] One can save these analyses by asserting that they require only a group isomorphism between the hyper-TI group and the ordinary TI group. My rejoinder is threefold:
- Group isomorphism is actually a weak relationship.(8)
- The use of labels like <T1> and T1 misleads people by making the isomorphism look stronger than it actually is: if all we care about is group isomorphism, then we can associate <T1> with either T1, T5, T7, or T11. From the standpoint of group theory, there’s no principled reason for choosing among these.
- In the new notation, we can have recursive K-net analyses that are underwritten by something stronger than mere group-theoretical isomorphism. My <Tx> really can be described as transpositions: they transpose equivalence classes of strongly isographic chords by x semitones. (Similar points apply to <Ix>, which invert these equivalence classes.) Consequently, there is a canonical way to associate each ordinary transposition Tx to a particular hyper-transposition <Tx>—something that group theory alone does not provide. Furthermore, in the new system, there is a clear analogy between the techniques of K-net analysis and those of standard set theory—the main difference being that K-net analysis manipulates equivalence classes of strongly isographic chords, rather than equivalence classes of transpositionally or inversionally related chords.
All of this, in my view, argues strongly in favor of the proposal.
IV. Going up the hierarchy
[14] Q. Can we do this again at the next level? That is, can we label hyper-hyper-transpositions <<Tx>> consistently with our labeling of the transpositions and hyper-transpositions?
[15] A. Yes, as Figure 5 demonstrates. There are no new difficulties here—and no need for anything other than half-integer labels. (In particular, there is no cascade to ever-smaller fractions, as the hyper-operations get more hyper.) I’ll leave the details up to the reader. The resulting system has the nice feature that if you take a big hyper-hyper-hyper -...-hyper-network of pitch classes, transpose all the pitch classes by x semitones, update all your arrow-labels accordingly, doing the same for your hyper-arrows, your hyper-hyper-arrows, etc., your two networks are related by Tx, <Tx>, <<Tx>>, and so on. (Similar points apply to inversion and hyper-hyper-...-hyper-inversional labels.) In other words, the ordinary transpositional and inversion labels propagate up the system. This is not the case in standard notation, a fact that can lead to philosophical puzzles.(9)
V. Hyper-transposition and dual transpositions
[16] Buchler perceptively remarks that K-net analyses try to pack too much information into a single number. He suggests that we use O’Donnell’s “dual transpositions” and “dual inversions” rather than hyper-transposition and hyper-inversion, identifying the particular TI operations that apply to each of the K-net’s two parts.(10) This is illustrated in Figure 6. I think this is a reasonable suggestion. However, it should be noted that there are two independent questions here. First, should we describe the relation between K-nets using one number or two? And second, should we use “dual transpositions” or hyper-transpositions?
[17] Buchler labels the relation between K-nets {C, E} + {G} and {C, E} + {
[18] What do these numbers mean? Figure 7 presents a two-dimensional graph listing all the K-nets, in 24-tone equal-temperament, that are positively isographic to {C, E} + {G}, and that belong to set classes found in 12-tone equal temperament. Strongly isographic chords lie on the same vertical line. Transpositionally related chords lie on the same horizontal line. The graph should be interpreted as a 2-torus, with its right edge glued to its left, and the top edge glued to the bottom. (As in early video-games such as Pac-Man or Asteroids, one can move off of an edge to reappear on the opposite side of the figure.(11)) What I am calling the <Xx> transform moves the K-net 2x vertical steps on this figure, while hyper-transposition <Ty> moves 2y steps horizontally. The first transformation represents motion within the equivalence class of strongly isographic chords, and describes how the structure of the set class is altered: under <Xx> each part of the K-net moves by x semitones in contrary motion, possibly changing the set class in the process.(12) The second transformation represents motion from one equivalence class to another, moving all the pitch-classes in the K-net upward by y semitones. As can be seen from the figure, dual transpositions represent an alternative way of describing relationships on this two-dimensional surface: the dual transposition Ta/Tb moves a chord a positions diagonally southeast, and b positions diagonally northeast. The two notational systems are fundamentally equivalent, and are related by what physicists would call a “coordinate transformation.”(13)
[19] Let's now return to the issue of K-nets’ abstractness. Buchler is right to observe that standard K-net analyses use one number where it is possible to use two. In fact, we can restate his observation more precisely: K-net analyses use only the x-coordinate to refer to relationships between objects situated on a two-dimensional surface. One possible response is to adopt “dual transposition” labels. A slightly more conservative alternative, from the standpoint of traditional K-net theory, is to use the <Xx/Ty> labels described here. These simply extend the techniques of K-net analysis by adding the missing coordinate, representing motion within equivalence classes of strongly isographic chords.
[20] To my mind, the deepest question raised by Buchler’s article is this: what coordinate system should we use when navigating Figure 7? I share his feeling that “dual transformations” are somewhat more general than hyper-transpositions and inversions. (In particular, I think we should be reluctant to use standard K-net technology in cases where the musical surface does not clearly project exact contrary motion.) Furthermore, I am sympathetic with Buchler’s complaint that K-net analysis throws away too much information. I see no reason why we should have developed an analytical tradition that pays attention to only one of the two dimensions of Figure 7. Buchler’s worry, which I share, is that our analytical practices may derive not from deep conceptual reflection, or from underlying musical necessity, but simply from the force of institutional habit: we disregard the second coordinate because we have always done so, perhaps without even noticing that it could be incorporated into our K-net analyses.
VI. Philosophical issues
[21] The proposal in this paper is at bottom notational, a suggestion that we use new words to describe familiar relationships. It might therefore seem that I do not go to the musical heart of the matter. My response is that notation is not at all trivial, but is rather something that shapes thought. The importance of good notation is well understood by physicists and mathematicians, and is an issue that deserves more music-theoretical scrutiny—especially since some of our basic notational conventions are conceptually quite confusing.
[22] Among these is the practice of referring to inversions by index number. Ultimately, the notational question I have been pursuing is this: what should we call the function
F(Ix) = T1(Ix)T-1 = Ix+2? My suggestion is that we should call it <T1>, or “hyper-T1,” because it shifts the axis of inversional symmetry up by semitone: C is mapped to C under I0, and
[23] Familiar K-net terminology inherits this problem, using the label <T2> to refer to the operation F(Ix) = T1(Ix)T-1 = Ix+2. This may be a case of bad notation leading to confused thought. For though it can feel like we are transposing by two when we increase the index numbers by two, and though thinking in this way may help us calculate, this is not at all what is happening musically: transposition by x changes index numbers by 2x, as both Figure 2 and Table 1 demonstrate. I worry that David Lewin may have been mislead by this simple but pernicious feature of our ordinary notation when he invented the now-standard labels for hyper-transpositions and hyper-inversions.
[24] However, it may be that Lewin was motivated not by conceptual confusion, but by the desire to identify T1, a generator of the T group, with <T1>, a generator of the hyper-T group. Presumably, this desire was in turn motivated by Lewin’s goal of exploiting the group isomorphism between the <TI> hyper-operations and the TI operations. But is it so clear that this particular group isomorphism is, musically speaking, the most important one? My notation emphasizes a different isomorphism: that between the quotient group TI/T6 (the TI group for tritone-symmetrical objects, such as equivalence classes of strongly isographic chords) and a particular subgroup of <TI>—those that relate K-net arrows in networks whose pitch classes are related by ordinary transposition and inversion. (In Lewin’s notation, these are the hyper-operations with even-numbered subscripts; in my notation, they have integer subscripts.) This relationship is more than a mere group isomorphism: any action of TI/T6 on K-net nodes induces a corresponding action of the <TI> subgroup on arrows; conversely, any action of the <TI> subgroup on arrows can be realized by networks whose PCs are related by a corresponding action of TI/T6 on nodes. In many circumstances, the two perspectives provide alternate descriptions of the same musical process.
[25] The interesting point is that Lewin chose to emphasize a relatively weak relationship (group isomorphism) at the expense of this stronger relationship—and that almost all subsequent users of K-nets have followed him. In doing so, they have asked us to overlook the fact that <T1> (in my notation) actually transposes something by one semitone and focus instead on the very abstract fact that my <T1> generates only half of the <T> operations. But it should be understood that this approach is rooted in a discrete, group-theoretical perspective. I would argue that it’s not necessary—and perhaps not even productive—to think about K-nets in this way. In fact, there’s a very beautiful (and in my view much more natural) geometrical interpretation of K-nets and their significance.(14)
[26] What rests on the choice between standard notation and my own? First, convenience and conceptual clarity: the system I advocate is (I claim) simpler and more logical, once you get used to it. Second, generalizability: K-nets define “wedge” voice leadings in which the two parts of the K-net move in exact contrary motion;
the system I propose can be extended to “generalized K-nets” whose parts move along arbitrary voice leadings—and not simply those involving exact contrary motion. These arbitrary voice leadings define generalized analogues to “strong isography” and give rise to equivalence classes related by generalized analogues to the
[27] How should we understand Buchler’s criticisms in light of my proposed notational reforms? As I have indicated, I believe that some of his complaints can be ameliorated by a simple change of notation. There is indeed a close relationship between hyper-transposition and ordinary transposition, though it is obscured by standard K-net terminology. At the same time, even in my new notational system, it is clear that some of Buchler’s criticisms remain intact. K-nets are woven with a very coarse mesh, allowing a lot of useful musical information to wriggle free. (Indeed, relative to Figure 7, K-nets are not nets at all, but rather threads—using one dimension where two are needed!) I applaud Michael for having the courage to point this out, and for challenging us to think about how the practice of K-net analysis might be improved.
Dmitri Tymoczko
Princeton University
dmitri@princeton.edu
Works Cited
Buchler, Michael. 2007. “Reconsidering Klumpenhouwer Networks.” Music Theory Online 13.2: 1–69.
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2007. “Generalized Voice Leading Spaces.” Unpublished draft.
Klumpenhouwer, Henry. 2007. “Aspects of Depth in K-net Analysis with special reference to Webern’s opus 16, 4.” Forthcoming in the Journal of Music Theory.
Lewin, David. 1990. “Klumpenhouwer Networks and Some Isographies That Involve Them.” Music Theory Spectrum 12: 83–120.
Losada, Catherine. 2007. “K-nets and Hierarchical Structural Recurrence: Further Considerations.” Music Theory Online 13.3.
O’Donnell, Shaugn J. 1997. “Transformational Voice Leading in Atonal Music.” Ph.D. dissertation, City University of New York.
Tymoczko, Dmitri. 2007. “Lewin, Intervals, and Transformations: A Response to Hook.” Forthcoming in Music Theory Spectrum.
Footnotes
* Thanks to Michael Buchler, Norman Carey, Henry Klumpenhouwer, and Steven Rings for helpful conversations and suggestions.
Return to text
1. As Buchler points out, a K-net partitions a chord into two parts. I will therefore use the notation {x1} + {x2} to refer to K-nets. Pairs of notes within a single set are connected by T-arrows, while pairs of notes from different sets are connected by I-arrows.
Return to text
2. Buchler actually uses different sets, but the essential point is the same. See Figures
14 and
15 in Buchler 2007. All subsequent references to Buchler’s work refer to this paper.
Return to text
3. This is mere notational shorthand: <Tx> should always be taken to abbreviate <Tx
or Tx+6 (mod 12)>.
Return to text
4. Of course, the <TI> operations can still be understood as “functions
over functions.” The point is that any statement about these functions over functions can be translated into an equivalent statement about ordinary transposition and inversion of equivalence classes.
Return to text
5. Or 13/2. In some sense, what’s happening here resembles what happened when your teacher started talking about negative and zero exponents in junior high-school algebra. We extend our system by introducing new notation, at first a little paradoxical, but in a way that is consistent, and that increases the formal system’s power.
Return to text
6. In her response to Buchler, Catherine Losada shows that when we
relabel pitch-class space by adding c to every pitch-class label, we
add 2c to every inversion label and 4c to to every hyper-inversion
label. (See Examples
8 and
9 in Losada 2007, where c = 8.) It
follows that associations between ordinary inversions and hyper-inversions
will depend on which pitch class we arbitrarily choose to label 0.
Under the alternative notation described here, this problem does not
arise: inversion and hyper-inversion labels transform in the same way
under relabelings of pitch class 0.
Return to text
7. The nodes of a “hyper-K-net” are themselves K-nets, connected by arrows indicating hyper-transpositional and hyper-inversional relationships. See
Figure 5.
Return to text
8. See my “Lewin, intervals, and transformations,” forthcoming in
Music Theory Spectrum.
Return to text
9. In a forthcoming article in the Journal of Music Theory, Henry Klumpenhouwer sorts through these puzzles, engaging in a careful investigation of the ontological difference between transposition, hyper-transposition, hyper-hyper-transposition, and so on. By contrast, I propose an alternative notation in which the inconsistencies between these levels simply evaporate, along with the appearance of a philosophical puzzle.
Return to text
10. See O’Donnell 1997.
Return to text
11. Here, however, the left edge needs to be glued to the right with in a “diagonal” fashion as shown by the
lines A and B. Note that, for reasons of space, chords on the top edge also appear on the bottom edge, but chords on the left do not also appear on the right.
Return to text
12. Given a K-net {a1} + {a2}, the <Xx> transformation transposes {a1} up by
x semitones and {a2} down by
x semitones. Thus the notation requires us to identify which of the K-net’s two parts is the first and which is the second.
Return to text
13. Indeed, physicists have a specific name for the coordinate transformation involved: they would say that my labels use the
center-of-mass reference frame to relate K-nets. In elementary physics, one often represents the motion of a group of particles as having an “internal component” defined relative to a coordinate system in which there is zero total momentum, and an “external component” representing the motion of this coordinate system relative to some other reference frame. If we imagine the two parts of the K-net to have equal mass, then motion between strongly isographic chords occurs in the center-of-mass reference frame.
Return to text
14. Clifton Callender, Ian Quinn, and I describe this interpretation in a collaborative paper which we hope to finish (and publish) soon. A preliminary draft can be found at
http://music.princeton.edu/~dmitri/geometry.pdf.
Return to text
15. See the paper cited in the previous footnote. Interested readers can probably work out the details themselves: the idea is to consider all the equal-tempered set classes produced by an arbitrary voice leading—even if the sets themselves do not lie in 12-tone equal-temperament. These sets can be understood as equivalence classes, can be related by transposition and inversion, and can be used to construct two-dimensional spaces exactly analogous to
Figure 7.
Return to text
Copyright Statement
Copyright © 2007 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo, Editorial Assistant
Number of visits: