Exploring Complementation in Bartók’s Third Quartet

[1] Bartók scholarship relevant to the six quartets enjoys a long, illustrious history in Hungary, the Unites States and United Kingdom.⁽¹⁾ Its span extends from writings published soon after Bartók’s death (see Abraham 1945 and Seiber 1945), through to those which point up the composer’s continuing status in the twenty-first century, especially the fine volume edited by Antokoletz, Fischer, and Suchoff (2000), supplemented by that of Amanda Bayley (2001).⁽²⁾ Nonetheless, as noted in the comprehensive article by Malcolm Gillies (2001, 808): “The history of Bartók analysis has been one of slow changes in trend: from early postwar concerns with style analysis, mainly in the pitch domain, through to the more structural concerns of the 1950s to 70s . . . During the 1980s and 90s, despite an apparently ever-growing divergence of methods, the tendency has again been to concentrate on more ‘micro’ levels of compositions.”

[2] Equally, in furthering approaches to post-tonal music, whilst still questing after an elusive system of the stature and universality of Schenkerian voice-leading within tonal music, analysts have increasingly recognized complementation as a useful concept. Properly embraced, complementation can facilitate a breakaway from restrictive notions of large-scale unity and a corresponding move toward a dynamic, coherent diversity, by elucidating contrasts and discontinuities rather than overstating weak similarities.⁽³⁾ However, despite on the one hand an ongoing healthy interest in Bartók studies and on the other a growing awareness of complementation, I argue that the concept’s full potential and applicability has not been realized in reading Bartók’s Third Quartet of 1927, especially its Prima parte. Although I might be accused of furthering research at “more ‘micro’ levels,” it is precisely through this attention to detail that Bartók’s special qualities are revealed, in particular the operation of complementary complexes within and beyond the domain of pitch.

I. Charting complementation and Bartók Studies

[3] Complementation involves a process whereby the whole is composed of distinct, yet in some sense matching, parts which co-exist within a dynamic balance.⁽⁴⁾ The term is derived from the Latin complere, to fill up, thus to achieve a state of completeness. Each element implies the existence of, and indeed completes the other.⁽⁵⁾ Ultimately, there is a contradiction because the elements may be, at the same time, both opposites and yet intricately connected.⁽⁶⁾ Since an element may in fact be articulated as powerfully by its absence as by its presence, we may also connect complementation with the post-structuralist thought of Derrida, fulfilling specifically one of the two conditions of his concept of “différance.”⁽⁷⁾ “Différance” encapsulates a pun since, in its French inflection, the word suggests both difference and deferral, and it is the notion of constant, ultimately infinite, deferral which is germane here. This might further suggest an affinity with the psychoanalytical critical concept of deriving meaning through omission or suppression. In this fulfilling of expectation, there is a parallel, unconnected, evolution in the notion of “implication-realization” propounded by Leonard B. Meyer (1978, 1989). And in just the same way, implied complementations may themselves be fully or only partially realized, resulting in incompletion, instability, and scope for further extension.

[4] The history of complementation in music theory commenced, effectively, with its deployment by Allen Forte (1973, 73–74), specifically in a pc-set-oriented context. In the 1980s, complementation was discussed more widely in a useful volume by Jonathan Dunsby and Arnold Whittall (1988), together with coverage by James Baker (1986), Richard Parks (1989) and Marianne Kielian-Gilbert (1982–83, 1991), focusing mainly on music by Stravinsky, Scriabin and Debussy.⁽⁸⁾ Moving out from strict pc-set complementation, the concept evolved within the pitch domain to embrace octatonic complementation, that between harmonic units, and motivic and structural complementations. Joseph Straus (1982) in particular advocated “complementary axes.” An undervaluing of complementation was evidenced, however, by its limited inclusion in Bent and Drabkin (1987, 62, 105, 106) with references confined to set theory; similarly, in the otherwise admirable text by Lester (1989), the concept was also undersold.⁽⁹⁾ More positively, in the later 1990s, David Lefkowitz (1997) considered the crucial role of hexachordal complementation, while more recent research on pc-set complementation, founded on the work of Robert D. Morris, includes that of Michael Buchler (2001) and Paul Nauert (2003), which considers through a process of modeling the effect of complementation on pc-sets within a progression.

[5] Outside of pitch relations, instrumental complementation may result from solo versus group, with textural oppositions of polyphony and “heterophony”; distinctions between textural polyphony and “heterophony” were explored quite early on by Dunsby (1989). Similarly, stylistic complementation may arise from the confrontation of old and new, which, in the language of Whittall (1987, 1989) may “converge precariously” to form a certain “symbiosis.”⁽¹⁰⁾

[6] In Bartók studies, the cultural and stylistic synthesis of East and West had long been a concern of scholars such as Ernö Lendvai (1971).⁽¹¹⁾ But more analytically-focused research on inversional pitch symmetry, as a distinct complementary subset of mirrored, rather than opposed elements, has also proved very fruitful. The notion was initiated in the early post-war period by George Perle (1955, 1977), then followed up by Wallace Berry (1980) in his extensive article on the Third Quartet itself.⁽¹²⁾ The substantial contribution of Antokoletz (1984) with his “Intervallic cells,” emerged from work on the Fourth Quartet (1977),⁽¹³⁾ and was supplemented by more specific research on symmetry, combined with other phenomena, by Jonathan Bernard (1986), Richard Cohn (1988), and Christopher Mark (1992). Detailed contributions by Gillies (1989, 1993) to understanding Bartók’s tonal structuring should also be properly credited. Research on these and broader issues was then provided in the crucial, enduring book on analyzing Bartók’s music, including the Third Quartet, by Paul Wilson (1992). Around the same time, our pitch understanding of the Third Quartet was enhanced by further research of Antokoletz (1993).

[7] Beyond the strict considerations of a music-theory-led history of complementation and particular applications to Bartók, a survey of this type would not enjoy any measure of completeness without acknowledging the profound influence of Olivier Messiaen on this area of musical thought. Messiaen’s example is relevant both in a general sense—as a theorizing of musical practice, and, specifically, in terms of his enthusiasm for palindromic manipulations.

[8] In addition to drawing together the types already discussed, we may add those of “modal” and “bimodal complementation.” “Modal complementation” may be defined as that which involves a division, or partitioning, within a given collection,⁽¹⁴⁾ and “bimodal complementation” as that which may exist between similar collections at different transpositions, e.g. between pentatonic collections on C♯ and C, or between dissimilar collections, e.g. between pentatonic and chromatic segments.⁽¹⁵⁾ Indeed Bartók (1976, 365ff.) discussed the term “bimodality” in his own Harvard Lectures, explaining how: “Just as the two types of the minor scale can be used simultaneously, two different modes can be used at the same time too.” An extension of this idea leads to our acknowledging Forte (1988) in his quest for a theoretical means to bridge and compare tonal and post-tonal musics through use of pc-set genera as distinct harmonic types which might then be related. The consideration and tabulation by Forte (1988, 220–24) of a quantitative measure of difference between two competing genera in the form of a “Difference Quotient (Difquo)” offers particular scope and strength.

[9] We need too to consider the relationships involved in strongly contrasting timbre and register, and the potential for formal and rhythmic complementation, where a clear sense of “opposition” or, alternatively, symmetry may be perceived. In fact, in discussing “Symmetrical Interval Sets,” Berry (1980, 325) mentions “opposition and textural-rhythmic separation of two combinatorially associated pentachords,” although he does not really develop the idea. Specifically on rhythm, in his own volume on Hungarian Folk Music published just four years after the Third Quartet, Bartók (1931, 29, 30) noted occurrences of reversed patterns, perceiving two schemata as among the most common for openings of folk melodies: (form no. 7) “short–long, long–short” and its converse (form no. 8) “long-short, short-long.” Thus the notion of applying this to his music is hardly inappropriate, and similar reversed patterns do occur in the Quartet.

[10] Presented simultaneously or successively, these bare ingredients can produce a whole variety of effects and cross-relationships, whether it be a simple juxtaposition, or collage (devoid of tension), a precarious polarity (imbued with tension), or more rarely a “symbiosis,” even synthesis. These states are to some extent comparable to “stages” outlined by Kielian-Gilbert (1991, 451–52), although she is more concerned with establishing a neoclassical aesthetic to relate old and new. Complementation across several parameters may operate as a multi-faceted complex, and at different levels of significance—an idea apparently not discussed elsewhere. Thus the effect of a complementation may be heightened, or, conversely in different circumstances, contradicted, confused or diffused. Across a section, movement or work, particular complementations may cause and maintain instability, although they may also represent a powerful means of achieving a new “unity” or completeness.

[11] From this point on, the reader is referred to the miniature score of the Third Quartet published by Universal Edition in 1929.

II. Founding principles: the Prima parte (measures 1–6)

[12] Complementation has a role to play throughout the Quartet, so that discussion may usefully commence with the opening measures, as shown in Example 1. Although their pitch structure has been well documented, especially in Berry (1980), Wilson (1992, 89) and Antokoletz (1993, 260), they still merit further consideration and offer a strikingly lucid illustration of complementation.

[13] In fact measures 1–6, concluded by Bartók’s articulative modulus, neatly encapsulate the activity of the whole Quartet. Cello, viola and violin II present and sustain a semitonal germinal cell: C♯, D, D♯, E (pc-set 4-1), which we may label as segment A. Against this, across measures 2–6, violin I presents both the pitch complement and pc-set complement: pitches E♯ through to B♯ inclusive (set 8-1): segment A'. Violin I supplies six pitches across the first two sub-phrases: A♯, B♯, A, G, G♯, B (set 6-1), followed by E♯, measures 4–5 and finally the F♯, measure 5. (Repetition of previously stated pitches along the way serves to “soften” the complementary effect.) This aggregate C♯–E, E♯–B♯, subscribes clearly to Forte’s Genus 5 (chroma). Opposition specifically between C♯ and B♯/C is an important driving force behind the work as a whole, a matter covered in some detail by Whittall (1995, 33–42). For an illustration of these fundamental features, see Example 2.

[14] In addition to these discrete unordered pitch segments, there is, in the motivic patterning, a bimodal complementation of two distinct collections which operate across the Quartet,⁽¹⁶⁾ that is, total chromaticism and pentatonicism, generally indicative of Forte’s pc-set Genus 5 (chroma) and Genus 11 (dia). The point is illustrated by looking again at ordered presentations within the opening measures. Segment A is entirely chromatic, albeit with octave displacements and semitonal pairings (Genus 5, Supragenus II). Meanwhile the violin I melody that comprises segment A' (violin I) tends to avoid adjacent semitones, outlining rather the major second/minor third intervals characteristic of pentatonic syntax (a more tentative Genus 11, certainly Supragenus IV). Particularly striking are the violin pitches marked with a tenuto stress: A♯, G, E♯ (set 3-7), which commence each subphrase and are then brought together in the upper registral climax across measures 4–5 with a small-scale mirror image (as a specific complementary type): E♯, F, A♯ and back again. Thus this perspective on the opening demonstrates both bimodal complementation (opposition) and symmetrical motivic patterning (along the lines of Kielian-Gilbert’s “apposition”). For detail, see Example 3.

[15] This bimodality to some extent articulates a stylistic complementation between Western European modernism, probably inspired by Berg’s Lyric Suite which Bartók had heard in July 1927, and Bartók’s Eastern European heritage of folksong. Bartók (1976, 323) acknowledges this differentiation in his lecture on “The Relation of Folk Song to the Development of the Art Music of our Time,” commenting that “genuine folk music of Eastern Europe is almost completely diatonic and in some parts, such as Hungary, even pentatonic.” And yet there is “Curiously enough, at the same time, an apparently opposite tendency . . . towards the emancipation of the twelve sounds comprised within our octave.”

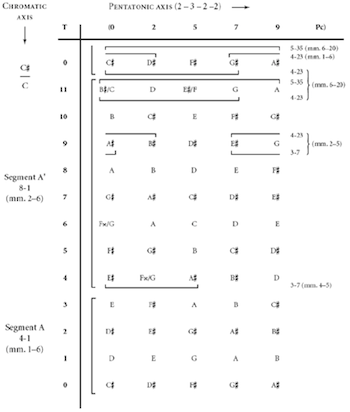
[16] Having launched the analysis, I want to step back briefly to introduce some more theoretical “models”: Figures 1–4. These models aim to show how aspects of Bartók’s practice, particularly the fundamental bimodal complementation of chromaticism and pentatonicism, may be underpinned by theory. (They will also point up how the apparently opposed worlds of chromaticism and pentatonicism enjoy a certain mediation, crucial to the notion of complementation itself.) The applicability of Figure 1 to measures 1–6 is considered here, while the extent of instantiation within Bartók’s score of the remainder of Figure 1 and Figures 2–4 is clarified below, especially in section III. An initial “Chromatic/pentatonic matrix” (Figure 1) offers a possible representation of the “chromatic-non-chromatic dialectic” identified by Berry (1980, 359).⁽¹⁷⁾

[17] We can map the opening segments A (set 4-1) and A' (set 8-1) onto the left-hand vertical, chromatic axis, where C♯ = 0 (acting, to some extent, as a referential pitch centre). The horizontal axis denotes pentatonic activity, with various formations mapped out, including the 3-7 set of measures 4–5 and a 4-23 set (measures 1–6), explained in paragraph [21] below. Sometimes the chromatic and pentatonic constructions involve particularly prominent common pitches as an “interactive” element (initially C♯ and also E♯, plus B♯/C from measure 6 onwards), which produces aspects of bimodal synthesis. It should be noted that the pentatonic collection is ordered as C♯, D♯, F♯, G♯, A♯ in Figure 1 simply because this is the configuration of the collection that Bartók initially invokes. The “normal” Hungarian ordering from C♯ would be C♯, E, F♯, G♯, B.

[18] The potential “interaction,” or intersection, between chromatic and pentatonic collections is illustrated in a slightly different way in Figure 2, still bearing in mind the initial chromatic collection (4-1/8-1). Pentatonic constructs on C♯ and C, taken compositely, will yield a collection which is almost totally chromatic, with the exception of two missing pitches, E and B (a theoretical scenario with applicability below).

[19] Figure 3 maps the tritonal relations which can feature as a result of interaction between pentatonic constructs (on C♯ and C) and a totally chromatic collection. The chromatic collection is mapped from left to right; diagonal brackets denote pentatonic collections, while the horizontal brackets denote resulting tritones. Within this context, such tritonal relations do prove an important trait of the Third Quartet (especially those founded on C♯–G and D♯–A, but also as noted in regard of measures 4–5 those on B–E♯ and B♯–F♯).

[20] A final model (Figure 4) shows a theoretical octatonic perspective where the collection C♯, D♯, E, F♯, G, A, A♯, C (0, 2, 3, 5, 6, 8, 9, 11), with prominent tritones denoted by horizontal brackets, results from the encounter of semitonally opposed pentatonic constructs on C♯ and C—that is, segments derived from pentatonic sets. This may provide a useful way of defining, as a single entity, a synthesis which results from bimodal complementation, and one which proves relevant in practice across measures 6–20.

[21] Of course the opening of the Quartet thrives not solely because of various polarized elements. As in the theoretical models, there are also subtle aspects of modal synthesis in the presentation of the complementary pc-sets, associating the apparently quite different domains of chromaticism and pentatonicism. On the one hand, the most sustained pitches of the violin I phrase (refer again to Example 1), i.e. the initial re-sounded pitch (A♯), the dotted quarter notes (A, B) and final quarter note (G♯), yield another 4-1 chromatic set: A♯, A, B, G♯, mutually exclusive in pitch content from the C♯, D, E, D♯ of violin II, viola and cello: Genus 5. On the other hand, the opening and closing pitches (also representing the registral extremities) of segment A: C♯ (cello), D♯ (violin II), plus the opening and closing pitches of segment A': A♯ (measure 2), G♯ (measure 6) produce the pentatonic construct C♯, D♯, G♯, A♯: set 4-23. And, by Forte’s “Rule of Singleton Extension” (1988, 234), the presence of 4-23 indicates Genus 11. Appropriately 4-23 also forms the final sonority of the whole work. Constructs from the two genera are firmly interlocked, as shown in Example 4.

[22] Where the interaction of Genus 5 and Genus 11 is concerned, it is worth pointing out that these genera, as the main sources of reference across the work, have a notably high Difference Quotient (Difquo) among the 66 possible pairs of genera: 0.79227. Thus the intuitive perception of these as broadly “complementary,” or at least close to being maximally dissimilar, is borne out by Forte’s calculations. Even so, the genera combination is not quite as differentiated as it might be, this distinction being reserved for Genus 4 and Genus 11 with the highest Difquo of 0.87058. Again, we have to accept a measure of relativity: this cannot be a true, absolute complementation.

[23] This opening phrase is already demonstrably complementary in three ways: firstly, pitches and sets; secondly, modality; and thirdly, symmetrical motivic patterning. But there are also further extensions of complementation in other parameters. Cello, viola and violin II present segment A as an uninflected four-part sonority: essentially devoid of rhythmic identity, the four pitches simply articulate the quarter note pulse. In marked contrast, segment A' is presented by the first violin as a lyricized solo line, with a distinct rhythmic identity, articulated by a leaning into the first note of each clearly marked, anacrusic phrase. Timbre too is used in complementary (or at least oppositional) fashion: the lower strings are designated con sord, while violin I is to be unmuted. Additionally, segment A is presented with a timbral heterogeneity, each pitch separately articulated by a new instrumental timbre (C♯: cello, D: cello harmonic, E: viola, D♯: violin II), while segment A' maintains a more homogeneous timbre. Thus these looser complementary instances of texture, rhythm and timbre are added to the strict instances of pitch content, set identity, modality and symmetrical patterning, producing a composite complementation, or complex, which serves to heighten the polarity between segments A and A'.

III. Scope elsewhere in the Prima parte

[24] Having given some idea of localized complementation, I wish now to show its scope and extent by summarizing other instances from the Prima parte, concentrating primarily on complementary types, complexes and effects not examined above. The imitative section across measures 6–20 uses complementary pitch processes that are increasingly concerned with, in the terminology of Whittall (1995, 34), “black-note/white-note” collections of pc-set 5-35: C♯, D♯, F♯, G♯, A♯ against C, D, F, G, A.⁽¹⁸⁾ This activity can clearly be seen to operate within the upper portion of the Chromatic/pentatonic matrix (Figure 1 again), and in this way the large-scale C♯ versus C polarity is maintained. These collections on C♯ and C provide an apt illustration of what Wallace Berry (1980, 299) would have termed “combinatorial pairs.” Again there is potential interaction with total chromaticism (refer back to Figure 2, which superimposes the 5-35 sets on 4-1/8-1), and indeed with octatonicism. With reference back to Figures 3–4, from measure 7 onwards we see the emergence of prominent tritones (violin I: D♯–A, measure 7; cello: E–A♯, measure 8, and C♯–G, measures 11–12), which play an increasingly important role as the work unfolds (e.g. Rehearsal Mark 8 onwards of the Prima parte; the return of D♯–A at the start of the Ricapitulazione, see paragraph [37]). And although the embedding of these pentatonic collections in the overall texture often promotes modal synthesis within each instrumental line (see Figure 4 with its resultant single octatonic collection), there are moments of direct contradiction.

[25] Across measures 9–12 (just before Rehearsal Mark 1), we may contrast the F, G, D, C pitches of violin I with those of violin II and cello: F♯, G♯, D♯, C♯: set 4-23. This contradiction is highlighted by dynamic swells and imitative phrasing, and should undoubtedly be “argued out” in performance, especially between the two violins. (Fleeting, even teasing, appearances of E and B just soften these distinctions slightly and provide one of several possible examples of Bartók resisting his music becoming over-systematized. Nonetheless, connection with Figure 2 is apparent.) The opposition between “sharpened” and “naturalized” pitches, including C♯ and C, produces further resultant pentatonic/chromatic interaction (shown schematically in Figure 1), indicative of Genus 11 and Genus 5.

[26] A new instance of set and pitch complementation occurs at the Quasi a tempo tranquillo (Rehearsal Mark 2, measure 21). Here Violin I presents a chromatic segment: 5-1 (C♯, B, D, C, D♯), against which the cello, with its tritonal articulation: E–B♭, and inner strings provide the remaining pitches: set 7-1 (E, F, F♯, G, G♯, A, B♭). These sets are of course embraced within the single Genus 5. Across the following measures 23–25, we encounter chromatic/pentatonic polarity simply in the violin I line: a repeat of 5-1 contrasts with a pentatonic fragment 3-7 presented in a symmetrical configuration as in the opening measures: B, D, E, D, B. These sets articulate the opposition between Genus 5 and a diatonic genus—most likely a continuation of Genus 11. Further “black/white” pentatonic polarities ensue across measures 27–33, heightened by the consistency of distinct sharpened and naturalized instrumental lines (viola: C♯, F♯, D♯, set 3-7; against cello: G, D, A, set 3-9), and followed by the extraordinary purity of the “white”-note collection, G, A, C, D, E, at the Sostenuto (measure 33), which precedes the general pause.

[27] Pentatonic complementations return at the Più andante (Rehearsal Mark 4; measures 35–42): viola on C♯, F♯, D♯, and cello also projecting 3-7, with pitch exclusivity: G, C, A. Although these opposed 3-7 constructs may be seen as self-standing complement relations, at another level these partial pentatonic presentations may “imply” a completion that is on this occasion denied, or left “unrealized”. Such a notion is to some extent supported by Antokoletz (1993, 264) in his observation, with regard to the Seconda parte, that “The chromatic D♯ implies the presence of the complete E Lydian mode.” Alternatively, as perhaps implicit in Antokoletz’s remark, we might argue that, given our pentatonic familiarity by this point in the piece, these constructs now act as metonymic utterances whereby a part may stand convincingly for the whole, effectively as a musical shorthand. Superimposed from measure 36 onwards are the chromatic 4-1 sets of violins I and II, creating a bimodal conflict of genera between lower and upper strings (G11; G5). Additionally, a loose scalic partitioning operates between lower strings which favor the lower pitch segment: C, C♯, D♯, F♯, G [A], and upper strings which favor the other pitch segment: G, G♯, A, A♯, B. At Gillies’ “micro” level, there is a process of chromatic contradiction between the violin lines, with overlapping fragments of 4-1 in measure 37 derived from the opening: I: A♯–B, A–G♯ (upper); II: A♭–G, A–B♭ (lower). Theoretically at least, these fragments embody a mirror-image about a central axis on D♯/E♭, as shown in Example 5, and thus we can appreciate the potential common ground between pitch-symmetry and complementation.

[28] In terms of a complementary complex, the aspects just described which differentiate lower and upper strings are supported by a third parameter—a looser timbral contrast (con sord versus senza sord, the latter exaggerated in its harshness by means of sul ponticello). A fourth parameter is that of broadly opposed rhythmic identities. Viola and cello supply a regular background of eighth notes, against which are counter-pointed the violins’ intricate patterns of quintuplet, triplet sixteenth notes and dotted groupings. A further, fifth, dimension appears across measures 37–38 and 40–41, with the simultaneous statement and reversion (i.e. mirror-imaging) of two sets of rhythmic patterns between the violins, interspersed each time by rests; see Example 6. Pattern 1—a repeated thirty-second note plus double-dotted eighth note—is particularly apt in view of Bartók’s observations about this “short–long, long–short” schema in his Hungarian Folk Music. In an act of calculated overloading is added a disruptive sixth parameter: that of dynamic scaling. In measure 40 (Rehearsal Mark 5), the mf marking of the repeated, rather straightforward lower-string figures, threatens to undermine the more intricate upper lines, marked merely mp, thus offering a useful illustration of emphasis through suppression. The effect is to cue change.

[29] Bold textural complementation is focused upon in the ensuing Tempo I, in modo ordinario (measures 43–46); it operates across a horizontal plane, with upper strings imitated by lower strings within a biting, entirely chromatic pitch context. There is a sense of progression from the Più andante since all instruments share the same figurations and syntax, presented at f dynamic, without mutes or sul ponticello effects. Overlapping 4-1 units are presented in a block-type (partial) complementary complex: each unit involving symmetry through contrary motion, and so confirming the potential inter-relationship suggested above. All twelve pitches are embraced across the first four units (measures 43–44) in a reworking of the opening, as represented in Figure 5. The pitches are given in a uniformly ascending format in order to clarify the collective pitch saturation.

[30] Textural complementation is followed through in the poco a poco allargando portion (see Rehearsal Marks 7–8). Functioning now primarily on a vertical plane, linear/legato fragments, at piano through to forte dynamic, are contrasted by chordal/detached fragments, with reiterated down-bows, at ff dynamic, their opposition articulated by eighth-note rests. This procedure combines with the typical pitch opposition of “white”-note modality in violins, contrasted by “black”-note in lower strings (occasionally a chord reverses the natural-over-flat layering with flats presented on top, e.g. measure 55), which maintains the earlier horizontal plane. Quartal and quintal constructs are evident within a pentatonic syntax, as is the continuing larger-scale preoccupation with semitonal polarity, as occurs with G versus G♭ in measures 54–55. So composite complementation of texture and modality causes a pulling in two directions: in terms of the score, both vertically and horizontally; or in aural terms successively (textural parameter) and simultaneously (bimodal parameter).

[31] This negating of one dimension by the other actually serves to diffuse the complementation and achieve an increased modal fusion through measures 57–59, necessary so as to shift the focus onto a so far less explored complementation—that of pitch symmetry, especially in violins: initially A, G, F, E, F, G, A. Two further examples of symmetrical pitch-patterning, achieved through melodic (and chordal) reversion, are worthy of mention in the latter portion of the Prima parte. Measures 79–80 yield a brief pattern: F, G, A♭, G, F, which contrasts with the previous example in its shape (now ascent-descent), inflection (now contracted from A to the minor third, A♭), and instrumental involvement (four lines as opposed to two). Finally, at measures 81–82, there appears an embellished and extended version of the previous gesture, moving up through the flattened seventh: F, G, A♭, B♭, D♭, B♭, A♭, G, F. Although there are only three functional lines since the cello pitches are doubled by viola, the presentation is enriched through pitch reiteration and double-stopping in violins. (This gesture is combined with a natural versus flat bimodal complementation between lower and upper strings.) Such instances, occurring both in the Prima and Seconda parte, confirm complementation through symmetry, which exists on a parallel status with the rhythmic reversion explored earlier.

IV. The Quartet’s large-scale design

[32] Having discussed particular examples of localized complementation pertaining to pitch (i.e. chromatic and modal collections), rhythm and timbre, operating both singly and compositely, it now makes sense to consider possible, admittedly more speculative, large-scale formal complementation. The overall formal design of the Quartet has been discussed often enough in the analytical literature, but as far as I am aware no one has yet suggested that the concept of complementation might have something useful to offer here. Interestingly, though, there may be a precedent in the work of Colin Mason (1957, 189), who argued of the Fourth Quartet that “the general tonal scheme [of the middle movement in D, with prominent G♯] seems in effect to be complementary to the fourth movement [Lydian in A♭, with prominent D].”

[33] I would suggest that two complementary levels operate across the work: the first concerns the parallel relationships between the Prima parte (section A) and its shortened Ricapitulazione (A'), and between the substantial Seconda parte (B) and its corresponding recapitulation (B') embraced within the brief Coda. The second, more fundamental, level involves the possible relationship between sections A and A' (viewed collectively as alpha), and sections B and B' (viewed collectively as alpha'). It is this idea of a hierarchical complex, owing much to complementation, which I believe may offer a useful means of viewing the form of the Third Quartet.

[34] In terms of the first formal level, we need to be convinced that the two recapitulations are sufficiently different from their respective expositions to render them somehow “opposite.” The recapitulations of the First and Second Parts are in no sense literal; rather they balance their expositions in somewhat condensed format across far shorter temporal spans. The recapitulation of theSeconda parte has in any case to fulfill a dual function, re-invoking ideas from the central Allegro and, in its role as Coda, concluding the whole work.

[35] It is as though the essential material for each part of the Quartet existed in some paradigmatic or Grundgestalt state, conceivably as a pre-compositional notion.⁽¹⁹⁾ Bartók seems to be offering the listener and performer alternative views of this material. In terms of the relationship between the First and Second Parts and their respective recapitulations, as Whittall (1995, 34) acknowledged, the third and fourth sections do offer a “remarkably free rethinking of the issues.”

[36] If the explanation of complementation is to be deemed plausible, there needs also to be an element of correspondence and inevitability in terms of exposition and subsequent recapitulation. Both expository parts are left initially incomplete, and there is a consequent sense of implication, or expectation, which is at least partially realized in their recapitulations. Although the recapitulations are quite strikingly different in their presentation from the expositions, there is of course a common core between the instances which we have considered in the Prima parte and their alternative readings in the Ricapitulazione della prima parte.

[37] We may broadly compare measures 1–8 of the Ricapitulazione with the opening of the Quartet through to Rehearsal Mark 1. As Wilson (1992, 109) observes, the “goal tones” here, i.e. C♯, D♯, F♯, were also crucial bass pitches in measures 1–21 of the Prima parte. The same partial complementation occurs between sharpened (cello: C♯, D♯, F♯, G♯ [A♯]) and naturalized (viola: G, A, C, D) pentatonic constructs of 3-7 and 4-23 as was remarked upon early in the First Part, producing another illustration of pentatonic/chromatic interaction (Genus 11 and Genus 5), now articulated at the tritone D♯–A.

[38] Measures 17–18 of the recapitulation reintroduce pitch-exclusive sets of 4-1 reminiscent of Part One (both its opening and measures 43–44), here inversionally related in their pitch ordering and producing a composite 8-1 (viola/cello: A, A♯, B, B♯ [descent]; violin II/I: C♯, D, D♯, E [ascent]). They also partake of the rhythmic complementation through reversion, first noted apropos Rehearsal Mark 5 of the Prima parte. The return constitutes an embellishment with several “short [notes]–long” sustained note in violin I, presented simultaneously with its reversal “long–short” note cluster in cello. Strangely, despite his otherwise extensive treatment of the work, Berry (1980) largely ignores the relationships between the Ricapitulazione and the Prima parte. Similar parallels exist between the Seconda parte and Coda, most obviously the symmetrical pitch-patterning and the initial focus on E♭.

[39] The possibility of the larger-scale complementary relationship between the First and Second Parts is of course more speculative, but may still make a useful contribution to understanding this work. Even at the most basic level, the contrasts between the two parts are extreme enough to render them opposites. As Whittall (1995, 34) emphasized: “Part One is slow, Part Two is fast; Part One is lyrical and builds to a melodic statement of gravely simple beauty; Part Two is hectic, dramatic (and distinctly more folk-like).” Walsh (1982, 40) developed the point further, referring to a “drastic contrast between two autonomous kinds of music,” and “a more serious duality of the kind associated previously above all with late Beethoven.”

[40] Yet beyond the extreme contrasts and oppositions, in order to satisfy a complementary perspective, the two parts must be intricately related. This crucial criterion is fulfilled by indisputable motivic correspondence, all the more so since, despite this, in the words of Walsh (1982, 44), the character of the motives in the Second Part is “altered beyond recognition.” The point is illustrated by examining the opening measures of the Allegro, apparently unrelated to the First Part, but which yet exhibit a similar polarity between chromatic (Genus 5) and diatonic (Genus 12, Supragenus IV) syntax: pc-set 5-1 played quasi glissando on viola (B, C, C♯, D, E♭) pitted against the arpeggiated folk-like melody given on pizzicato cello (sets 3-11, 5-23 and 5-24). This Allegro opening also focuses on competing semitonal pitch centers: E♭ and D, as opposed to the initial C♯ and C—thus creating a large-scale chromatic set 4-1.

[41] The Seconda parte reveals a further correspondence with the Prima parte in that those germinal opening pitches of the First (C♯, D, D♯, E) also function as large-scale centers in the Second, particularly in the central portion across measures 182–240. These pitches recur too in small-scale motivic references, as found in measures 374–78 (i.e. two measures before Rehearsal Mark 46). This small portion of the Second Part shares the preoccupation of the First with chromatic fragments on C♯ (indicative of Genus 5): pc-set 4-1 then extended to 5-1: C♯, D, D♯, E, F. The C♯/C opposition of the Prima parte also features in the Seconda parte especially beyond Rehearsal Mark 43 of the score, including the stark iteration at measures 374–75 which operates both simultaneously and successively.

[42] The occurrence of the Seconda parte, rather as a sonata form “second subject,” before the Ricapitulazione della prima parte undoubtedly influences the presentation of the latter material, notably more spacious, yet succinct, as a reaction against the large-scale frenetic activity of the Seconda parte. Equally, elements of the Seconda parte have been subsumed in the Ricapitulazione della prima parte: most strikingly the focal E♭ is mutated into the initial D♯ sustained by the cello.

[43] It should also be acknowledged that once the listener has experienced the completion of the Prima parte, by virtue of the occurrence of its Ricapitulazione, there is an increased sense of inevitability or complementary pull operative where the recapitulation (Coda) of the Seconda parte is concerned. It is as though the work is presented as a jigsaw, with certain key pieces missing at first, but, gradually, we can perceive the outline shape of what is missing and are therefore expecting its subsequent appearance.

[44] Finally, it is significant that the Coda (B') is so called: although at one level it functions as the recapitulation of the Seconda parte, it also relates to the Prima parte (and its Ricapitulazione), re-establishing the pitch centre on C♯ (measure 83) and providing the last inflections of the various thematic transformations. (Violin I has that opening 4-1 cell: C♯, D, D♯, E, across measures 84–93.) This powerful complementary process with its dynamic balance eventually creates some sort of stability, albeit fragile. And although we might argue that, hypothetically at least, there are an infinite number of realizations of the material of the First and Second Parts, within the actuality of Bartók’s score each type of material has only two alternative presentations. My advocating of a complementary formal framework is not to claim that all aspects of the internal arguments have been resolved, or that they have reached some tidy point of closure. Rather it is to stress a unique and audacious approach to formal structure in this landmark work of 1927.

V. Conclusion

[45] It might be argued that I am in danger of seeing complementation at every turn, and so I emphasize that it involves a special relationship, achieved only by fulfilling specific criteria of opposition, inter-relation and wholeness; that it operates at very different structural levels, and across a continuum from looseness to rigor, from ambiguity to clarity of application. Bartók’s Third Quartet provides an exceptional example of such complementation functioning as a structural determinant on both small and large scales, where the rich and diverse embeddings may result in juxtaposition, polarity or synthesis. Although in his pitch study of this piece, Berry (1980, 379) was convinced that “the pentatonic, diatonic, or chromatic content of these sets—and of their ‘combinatorial’ or overlapping associations—is a vital style-defining factor in Bartók’s work,” the Quartet is atypical in the extent and sheer intensity of its complementary obsession.

[46] Finally, while I am not suggesting that the concept of complementation alone offers some neat answer to the many questions raised by the work, I conclude that an understanding of the musical processes of the Third Quartet is significantly enhanced through its use.

Deborah Mawer
Lancaster University
Lancaster Institute for the Contemporary Arts
Bailrigg
Lancaster, LA1 4YW, UK
D.Mawer@lancaster.ac.uk

Works Cited

Abraham, Gerald. 1945. “The Bartók of the Quartets.” Music & Letters 26: 185–94.

Antokoletz, Elliott. 1977. “Principles of Pitch Organization in Bartók’s Fourth String Quartet.” In Theory Only 3/6: 3–22.

—————. 1984. The Music of Béla Bartók: A Study of Tonality and Progresson in Twentieth-century Music. Los Angeles: University of California Press.

—————. 1993. “Middle Period Quartets.” In The Bartók Companion. Edited by Malcolm Gillies. London: Faber and Faber: 257–77.

—————. 2005. “Los cuartetos de cuerda de Bartók del periodo medio. [Bartók’s middle-period string quartets.]” Quodlibet: Revista de especializacion musical 31: 86–103.

Antokoletz, Elliott, Victoria Fischer, and Benjamin Suchoff (eds). 2000. Bartók Perspectives: Man, Composer and Ethnomusicologist. New York: Oxford University Press.

Babbitt, Milton. 1949. “The String Quartets of Bartók.” Musical Quarterly 35: 377–85.

Baker, James. 1986. The Music of Alexander Scriabin. New Haven: Yale University Press.

Bartók, Béla. 1931. Hungarian Folk Music. Translated by M-D Calvocoressi. London: Oxford University Press.

Bartók, Béla. 1976. Essays. Edited by Benjamin Suchoff. New York: St. Martin’s Press.

Bayley, Amanda. 2000. “Bartok’s String Quartet No. 4/III: A New Interpretative Approach.” Music Analysis 19/3: 353–82.

Bayley, Amanda (ed.). 2001. The Cambridge Companion to Bartók. Cambridge: Cambridge University Press.

Bent, Ian and William Drabkin. 1987. Analysis: The New Grove Handbooks in Music. London: Macmillan.

Berger, Arthur. 1963. “Problems of Pitch Organization in Stravinsky.” Perspectives of New Music 2: 11–42.

Bernard, Jonathan. 1986. “Space and Symmetry in Bartók.” Journal of Music Theory 30/2: 185–201.

Berry, Wallace. 1980. “Symmetrical Interval Sets and Derivative Pitch Materials in Bartók’s String Quartet No.3.” Perspectives of New Music 18: 287–379.

Buchler, Michael. 2001. “Relative Saturation of Interval and Set Classes: A New Model for Understanding Pc-Set Complementation and Resemblance.” Journal of Music Theory 45/2: 263–343.

Cohn, Richard. 1988. “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 10: 19–42.

—————. 1991. “Bartók’s Octatonic Strategies: A Motivic Approach.” Journal of the American Musicological Society 44/2: 279–97.

Delcambre-Monpoel, Marie. 2004. “Le quatrième quatuor de Béla Bartók ou la transmutation d’une tradition.” Musurgia 11/4: 31–53.

Dunsby, Jonathan, and Whittall, Arnold. 1988. Music Analysis in Theory and Practice. London: Faber.

Dunsby, Jonathan. 1989. “Considerations of Texture.” Music & Letters 70/1: 46–57.

Eagleton, Terry. 1983. Literary Theory: an Introduction. Minneapolis: University of Minnesota Press.

Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press.

—————. (1988). “Pitch-class Set Genera and The Origin of Modern Harmonic Species.” Journal of Music Theory 32/2: 187–270.

Gillies, Malcolm. 1989. Notation and Tonal Structure in Bartók’s Later Works. New York: Garland.

—————. 2001. “Béla Bartók.” In The New Grove Dictionary of Music and Musicians. Edited by Stanley Sadie. London: Macmillan. 2: 787–819.

Gillies, Malcolm (ed.). 1993. The Bartók Companion. London: Faber and Faber.

Kárpáti, János. 1975. Bartók’s String Quartets. Translated by Fred MacNicol. Budapest: Corvina Press.

Kielian-Gilbert, Marianne. 1982–83. “Relationships of Symmetrical Pitch-Class Sets and Stravinsky’s Metaphor of Polarity.” Perspectives of New Music 21: 209–40.

—————. 1991. “Stravinsky’s Contrasts: Contradiction and Discontinuity in His Neoclassic Music.” Journal of Musicology 9/4: 448–80.

Lefkowitz, David S. 1997. “Listening Strategies and Hexachordal Combinatorial ‘Functions’ in Schoenberg’s, Op. 23, No. 4.” Music Analysis 16/3: 309–48.

Lendvai, Ernö. 1971. Béla Bartók: An Analysis of His Music. London: Kahn & Averill.

Lester, Joel. 1989. Analytic Approaches to Twentieth-Century Music. New York: W. W. Norton.

Mark, Christopher. 1992. “Symmetry and Dynamism in Bartók.” Tempo 183: 2–5.

Mason, Colin. 1957. “An Essay in Analysis, Tonality, Symmetry and Latent Serialism in Bartók’s Fourth Quartet.” The Music Review 18: 189–94.

Mawer, Deborah. 1997. Darius Milhaud: Modality and Structure in Music of the 1920s. Aldershot: Ashgate.

Meyer, Leonard B. 1978. Explaining Music: Essays and Explorations. Chicago: University of Chicago Press.

—————. 1989. Style and Music: Theory, History and Ideology. Chicago: University of Chicago Press.

Morrison, Charles D. 1991. “Prolongation in the Final Movement of Bartók’s String Quartet No. 4.” Music Theory Spectrum 13/2: 179–96.

Nauert, Paul. 2003. “The Progression Vector: Modeling Aspects of Post-Tonal Harmony.” Journal of Music Theory 47/1: 103–23.

Norris, Christopher. 1987. Derrida. Cambridge: Cambridge University Press.

Novak, John. 2001. “Review of The Cambridge Companion to Bartók. Edited by Amanda Bayley.” Music Theory Online 7/5: http://www.mtosmt.org/issues/mto.01.7.5/mto.01.7.5.novak.html (Accessed April 15 2007).

Parks, Richard. 1989. The Music of Claude Debussy. New Haven: Yale University Press.

Perle, George. 1955. “Symmetrical Formations in the String Quartets of Béla Bartók.” The Music Review 16: 300–12. Reprinted in Twenty-three Selected Essays by George Perle on Twentieth-Century Music. 1995. Stuyvesant: Pendragon, 189–205.

—————. 1977. “The String Quartets of Béla Bartók.” In A Musical Offering: Essays in Honour of Martin Bernstein. Eds E.H. Clinkscale and C. Brook. New York: Pendragon Press, 193–210.

Seiber, Matyás. 1945. The String Quartets of Béla Bartók. London: Boosey & Hawkes.

Somfai, László. 1989. “Bartók and the Paper-Studies: The Case of String Quartet No.4.” Hungarian Music Quarterly 1/1: 6–13.

Straus, Joseph. 1982. “Stravinsky’s Tonal Axis.” Journal of Music Theory 26: 261–90.

van den Toorn, Pieter. 1983. The Music of Igor Stravinsky. New Haven: Yale University Press.

Walsh, Stephen. 1982. Bartók Chamber Music. London: BBC Music Guides.

Whittall, Arnold. 1987. “The Theorist’s Sense of History: Concepts of Contemporaneity in Composition and Analysis.” Journal of the Royal Musical Association 111/2: 1–20.

—————. 1989. “Review Survey: Some Recent Writings on Stravinsky.” Music Analysis 8/1–2: 169–70.

—————. 1995. Music since the First World War. Oxford: Oxford University Press.

Wilson, Paul. 1992. The Music of Béla Bartók. New Haven: Yale University Press.

Footnotes

1. In the course of developing this article, I have benefited from feedback offered by various scholars; in particular, I should like to thank the anonymous MTO readers and Tim Koozin. I am also very grateful to Ronald Woodley for his accomplished setting of the music examples and figures.
Return to text

2. Especially relevant in Antokoletz et al. 2000 is the contribution of Malcolm Gillies, “Analyzing Bartók’s Works of 1918–1922: Motives, Tone Patches and Tonal Mosaics,” 43–60. For a review of Bayley 2001, including comparison with Antokoletz et al. 2000, see Novak 2001, in this journal. For other pertinent literature, see Antokoletz 2005 and Bayley 2000.
Return to text

3. See, for instance, influential ideas expressed by Whittall 1987.
Return to text

4. A definition offered by Kielian-Gilbert 1982–83, 210, seems today unnecessarily restrictive: “Complementation refers to the process of pairing entities on either side of a center of symmetry.”
Return to text

5. As rightly acknowledged early on by Berger 1963, 25, the term “polarity ... cannot accurately be applied to one thing without its opposite.” I maintain that the same is true of complementation.
Return to text

6. Indeed a notion of “apposition” was proposed by Kielian-Gilbert 1991, 451.
Return to text

7. For further detail, see the classic introductory texts of Norris 1987, or Eagleton 1983.
Return to text

8. See too Whittall 1989.
Return to text

9. See Lester 1989: “complement,” 69, 76; “set-inversion,” 83–84.
Return to text

10. See too Kielian-Gilbert 1991, 448.
Return to text

11. Other significant Hungarian contributions to the quartets include those of Kárpáti 1975 and Somfai 1989.
Return to text

12. On the role of contrast in the Third Quartet, we should also recognize fully the important study by Whittall 1995, 33–42, first published in 1977.
Return to text

13. For more recent approaches to the Fourth Quartet, see Somfai 1989, Morrison 1991, Bayley 2000 and Delcambre-Monpoel 2004.
Return to text

14. Partitioning of collections is a useful notion, as employed by van den Toorn 1983, 48ff., and most probably originated by Milton Babbitt. Note too the early interest of Babbitt 1949 in Bartók’s quartets.
Return to text

15. Beyond Bartók, such ideas proved pertinent in analysis of Milhaud’s music by Mawer 1997.
Return to text

16. A further sense in which the opening embodies characteristics of the Quartet as a whole lies in the clear articulation of a tritone B–E across the mid-point of the violin I phrase (measure 4), together with another (complementary) tritonal reference: B–F across the mid-point of measure 5. These semitonally-opposed tritonal constructs are an integral part of the syntax of the Third Quartet.
Return to text

17. This idea adapts a Chromatic Matrix developed by Mawer 1997, 49. The concept combines notions of axes (after Straus), with modal partitioning (after van den Toorn).
Return to text

18. “Black/white-key” pentatonic, octatonic and whole-tone collections are also discussed by Antokoletz 1993, 261–64, who considers black/white “polarization” as part of a broader concern with “transformational processes” (259). Antokoletz explores Bartók’s “extension in range,” as the diatonic expansion of chromatic material and its converse, “chromatic compression,” referring to interval-cycles (1/11 and 5/7) rather than set theory.
Return to text

19. It is possible that an examination of the sketches might prove valuable here, though this lies beyond the remit of the present study.
Return to text

A further sense in which the opening embodies characteristics of the Quartet as a whole lies in the clear articulation of a tritone B–E across the mid-point of the violin I phrase (measure 4), together with another (complementary) tritonal reference: B–F across the mid-point of measure 5. These semitonally-opposed tritonal constructs are an integral part of the syntax of the Third Quartet.

Copyright Statement

Copyright © 2007 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo and Tahirih Motazedian, Editorial Assistants
Number of visits: