A Tetrahelix Animates Bach: Revisualization of David Lewin’s Analysis of the Opening of the F Minor Fugue from
WTC I
Minor Fugue from
WTC I
Jacob Rosenthal Reed and Matthew Neil Bain
KEYWORDS: 3-D geometry, animation, J.S. Bach, David Lewin, inversion, voice-leading, Cohn flips
ABSTRACT: Music theory has long benefited from the use of visualizations to demonstrate analyses. This article presents one example of how music theorists might implement contemporary methods in graphic design and computer modeling. We apply three-dimensional geometric modeling and animation to a concise analysis on the opening of Bach’s F![]() Minor Fugue from WTCI by David Lewin. The application models the voice-leading of Cohn flips on Forte-set 3-2 with a triple helix whose structuring tetrahedrons combine chromatic, trichord, tetrachord and octatonic elements. The animations of the music through this model depict the pattern and relationships of the (013) forms described in Lewin’s article but demonstrate how a 3-D figure and animation elucidate and amplify his analysis and reveal an unusual aspect of these six measures.
Minor Fugue from WTCI by David Lewin. The application models the voice-leading of Cohn flips on Forte-set 3-2 with a triple helix whose structuring tetrahedrons combine chromatic, trichord, tetrachord and octatonic elements. The animations of the music through this model depict the pattern and relationships of the (013) forms described in Lewin’s article but demonstrate how a 3-D figure and animation elucidate and amplify his analysis and reveal an unusual aspect of these six measures.
Copyright © 2007 Society for Music Theory
[1] Lewin’s 2-D Visualizations
[1.1] In his article “Notes on the Opening of the
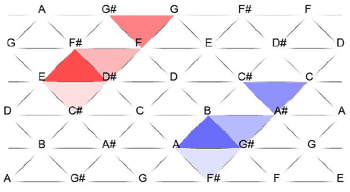
Forms of (013) that are displayed as adjacent vertically include the same minor-second dyad. Forms that are adjacent upper-left-and-lower right include the same major-second dyad. Forms that are adjacent lower-left-and-upper-right include the same minor-third dyad.(3)
Figure 1. David Lewin’s isolation of (013) forms appearing in the first six measures of Bach’s
(click to enlarge)
Example 1. David Lewin’s reduction of the first six measures
(click to enlarge)
The graph is divided into lower-and-uppercase lettering, where lowercase trichords distinguish forms of pcset (013) that appear in the opening of the fugue. Lewin extracts these and presents them in a separate figure with annotated numbers that “key in to the numbers on the musical example.” Lewin’s figure and musical example accompany this article as Figure 1 and Example 1.
[1.2] While these visualizations suffice to assist Lewin’s analysis, many of their structural characteristics and Lewin’s own statements suggest the use of more explicitly geometric models. To begin with, the graph duplicates common tones of the (013) forms appearing in Bach’s first six measures. For example, notice that the (
[1.3] As Lewin alludes, his graph can be easily reconstructed as a Tonnetz. The equilateral triangles in Figure 2 represent (013) forms. Moves along the horizontal axes are moves of interval class 1. Moves on the diagonal axes are either ic2 or ic3. This (013) Tonnetz succeeds in restructuring the trichords as individual pitch classes grouped in a triangular form so that neighboring sets can literally share common tones. The triangulation of trichords provides a more accurate representation of common tone retention between Cohn-flip-related sets. Furthermore, each triangle is adjacent to three and only three other triangles, each of which is one of the three possible Cohn flips respectively. Take, for example, the triangle
[1.4] Structurally, the (013) Tonnetz resolves the issues of repetition and order. In addition, under this revisualization the three possible Cohn flips on any given set are no longer forced into an arbitrary hierarchy. Each triangle is bordered by its three Cohn-flip-related sets on its three edges respectively. Despite this the (013) Tonnetz cannot resolve the fundamental issue of register. Neither Lewin’s graph, and descriptions of it, nor the (013) Tonnetz delineate a registration or pitch-specific structure. This slows the transfer from the aural perception of Bach’s music to the visual representation of Lewin’s analysis. In other words, while the progression through the graph is roughly analogous to the music itself, there is no rigorous system of correlation between musical and visual direction.
[1.5] A theoretical issue underlying this problem of register is the distinction between pitch space and pitch-class space. When he introduces his graph of Cohn flips on the pcset (013) in the article “Cohn Functions,” Lewin is working in the pitch-class universe, despite occasional use of letter names.(6) When he introduces the graph at the beginning of his article “Notes on the Opening of the
[1.6] Thus we searched for geometry that could visualize the interrelation of (013) forms by Cohn flip, demonstrate the general and specific spatial functions described in Lewin’s analysis, and solve problems of register, pitch-specific structure and order. The integration of the first two goals with the third proved the most challenging but also the most fruitful.
[2] Development of 3-D Geometric Models
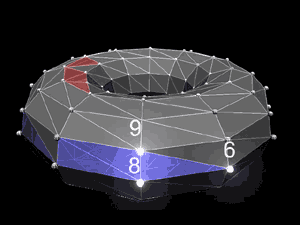
[2.1] Acknowledging the preclusion of register, this section introduces a modularization of our (013) Tonnetz. The subsequent comparison of this model to some similar examples of geometric modeling will provide context to the reader and further define our method. Theoretically, just as a triadic Tonnetz in equal temperament becomes a torus so may the (013) Tonnetz. However what the resulting torus looks like depends greatly on the limits of the (013) Tonnetz and our method of elevating it out of two dimensions. When we introduced the Tonnetz of Figure 2 we did not specify if and when it terminated. If the (013) Tonnetz were constructed in just intonation or even in equal tempered pitch space it would theoretically continue indefinitely. If the (013) Tonnetz is modularized into mod12 pitch-class space, then its spatial map in two or three dimensions would consist of only twelve sites. The
[2.2] Contemporary music theory contains many examples of the use of geometric modeling and computer animation. Neo-Riemannian related work in particular is well suited to such visualization. In his dissertation, “Tonal Intuitions in Tristan und Isolde,” Brian Hyer maps Riemann’s dominant, leittonwechsel, relative and parallel transformations around a hypertorus—a torus with four dimensions. The torus appears again in his article “Reimag(in)ing Riemann.” Unlike Figure 5 Hyer’s torus locates triads on the vertices or sites. Jack Douthett and Peter Steinbach use 3-D geometry to visualize voice-leading transformations between and within set classes. Their article, “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations and Modes of Limited Transposition,” maps voice-leading and transpositions with several models including two tori, a “cube dance,” and “power towers.” As with Hyer, Douthett and Steinbach use vertices to represent triads or seventh chords not individual pitches. This leaves the visualization of common tones to the reader but enables moves along edges or between sites on Hyer’s torus to define transformations.
[2.3] In his articles “Neo-Riemannnian Operations, Parsimonious Trichords, and Their “Tonnetz” Representations” and “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions,” Richard Cohn depicts trichords with triangles, using vertices to represent pitch classes. Furthermore, his in-depth work investigates the mathematical properties underlying generalized Tonnetz presentations as well as the problems of 2-D and toroidal tonnetze. Edward Gollin also conceives of a hypertorus in his article “Some Aspects of Three-Dimensional ‘Tonnetze.’” However, Gollin works with tetrachords situated in a 3-D space lattice. Vertices represent pitch classes and “units in a positive direction” along each of three axes represent 4, 7, and 10 semitones respectively. Gollin cleverly constructs a pitch-class space lattice containing tetrahedrons whose edges fall nicely onto three axes. This exemplifies a successful re-designation of points in 3-D. While the edges on the surface of the torus in Figure 5 are not as easily described with respect to axes they do represent constant interval cycles. Gollin investigates “the relation of a Tonnetz’s geometry to the group structure of the transforms relating its elements” coming to some conclusions that will prove useful in a discussion of the pedagogical worth of our work.(10)
[2.4] As stated earlier, the pitch class modularization of the (013) Tonnetz ignores the very musical concept of registration and thus prevents a rigorous directional correlation to the music itself. An attempt to trace the tenor voice up to the downbeat of measure four and begin the fugue’s answer on any (013) Tonnetz with duplications will demonstrate that allowing these duplications does not fix the problem. None of our preliminary models or Lewin’s 2-D model assigns a global direction to register.
[2.5] From a geometric perspective, the problem with our preliminary models is that their elevation into a 3-D realm is partially flawed. The (013) torus fails to define the Z-axis that adds the third dimension. Bending the right and left ends of 2-D Tonnetz around to meet each other bends the X-axis around a newly added Z-axis. Bending the ends of the resulting rod around to meet each other bends the Y-axis around the Z-axis as well. Yet this change leaves the Z-axis undefined and does not actually re-designate the three Cohn flips to three different dimensions. It simply wraps them around so that their constrained range or repetition is pictured cyclically. The solution to both problems becomes obvious—their integration. The successful model will bend a map of Cohn flips around a Z-axis defined by register thereby creating a 3-D geometry with rigorously defined axes that can incorporate a fundamental aspect of Bach’s fugue.
[3] A Tetrahelix
[3.1] To introduce our figure we will emulate a graphic presented by Carol L. Krumhansl in “The Geometry of Musical Structure: A Brief Introduction and History” and proposed by R. N. Shepard. Krumhansl presents a single helix on which “neighboring tones
[3.2] Similar to models of tetrachords constructed by Edward Gollin and Richard Cohn, the volume, not just the surface, of our three dimensional figure is decisively relevant. Richard Cohn’s work, “A Tetrahedral Graph of Tetrachordal Voice-Leading Space,” begins on a similar premise as ours. Cohn takes a 2-D graph of voice-leading relations and extends it in three dimensions constructing a large tetrahedron with vertices and additional sites representing 29 T/I-type tetrachord classes. Cohn extensively defines the figure, discusses several results of generalization and investigates some of the inherent peculiarities. Cohn focuses on the theoretical implications of his geometric model—how the location of tetrachord classes within the symmetry of the graph correlate to their inherent voice-leading relations and what certain parallels and discrepancies suggest. As our dismissal of the pitch class tori makes clear, our focus is on developing a model that can be readily applicable to Lewin’s analysis of Bach’s music.
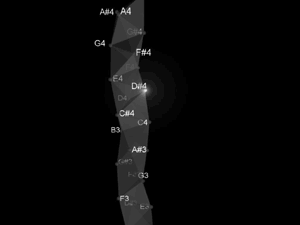
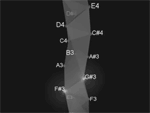
[3.3] Figure 6 presents our tetrahelix in more detail. It is composed of tetrahedrons adjoined at faces on alternating sides so that it could potentially spiral endlessly in two directions. Note that most triangles can be said to be on the surface of the model but that some of the triangles, those that adjoin tetrahedrons, are inside the model. In Figure 7 these adjoining faces are highlighted and a closer view is provided. Because our goal is to model Bach’s realization of the voice-leading between (013) forms in pitch space, Figure 6 maps pitches represented by letter names onto the vertices of the tetrahedrons. Since we are mapping pitches and not pitch classes our mapping could continue endlessly with the geometry of the model. However, in this case, our model spans about two octaves as the registral subscripts illustrate.
[3.4] In similar work, Elaine Chew and Alexandre R. J. Francois extend
Krumhansl's helix into a spiral array. The outer spiral represents pitch classes. Major and minor triads create triangles connecting pitch classes on this spiral. Spatial points within each triangle create a second inner spiral of chords. In a similar manner “the union of pitch classes in three adjacent major triads
[3.5] Returning to our tetrahelix, notice that all outside faces present forms of pcset (013) and consequently the edges connecting the vertices of any given surface triangle represent the appropriate interval content: one minor second, one major second, and one minor third. All inside faces present chromatic trichords and, as will be shown, define a Z-axis with register.
[3.6] In “Polyhedra: a visual approach” Anthony Pugh describes a tetrahelix as follows:
A helix is a curve which runs around an imaginary cone or cylinder, a common example being a spring. Tetrahedra can be joined together face to face to create a form which can be likened to a twisted column with triangular faces. The edges of that arrangement of tetrahedra follow helical lines, so the figure is often referred to as a tetrahelix. The figure can be long or short, depending on the number of tetrahedra incorporated in it.(15)
What separates our tetrahelix from any other is the way in which it maps pitches. The construction of our tetrahelix, described as follows, integrates the chromatic scale with a voice-leading map of (013) forms. A tetrahedron is constructed and assigned pitches (0123), one to each vertex. Picture triangle (012) as the base lying flat on a table with point (3) above. Next, a second tetrahedron, (1234), is created using triangle (123) as its base. Then another tetrahedron, (2345), is created using triangle (234) as its base. Thus, the structure of the tetrahelix is determined by subsequent additions of tetrahedrons such that each new tetrahedron shares the last three added points, and thus pitches, with the previously added tetrahedron. After at least one octave three ribs, or strands, of a triple helix will be easily visible. Taken individually, they each create the repeating tetrachords mentioned earlier, (0369), (147T) and (258E) respectively. Spiraling together in a triple helix, they produce the chromatic scale. The method of constructing the tetrahelix, as determined by the strict rule for the exact placement of each additional tetrahedron, besides the first, creates the very regular pattern of adjoined faces. These inside triangles, previously mentioned as the only triangles containing chromatic trichords, connect the three strands of the helix. These triangles, and the slow spiral they create between the three tetrachord strands, help create a model that accurately maps all the possible Cohn flips of (013) forms and simultaneously allows Bach’s lines to be correctly visualized with regards to register. This aspect of the fundamental structure of the tetrahelix creates as a skeleton for the geometric modeling of Cohn flips, a chromatic scale capable of depicting registration.
Animation 2 presents the first six measures of Bach’s
Animation 2
(click to view animation)
Animation 3
(click to view animation)
Animation 4
(click to view animation)
Animation 5
(click to view animation)
Animation 6
(click to view animation)
Animation 7
(click to view animation)
[3.7] On the tetrahelix, like the 2D tonnetz or the torus, any move from one surface face to another surface face is a Cohn flip and adjacent triangles maintain the same relationships. Again the entire surface of the tetrahelix can be traversed, like the 2-D Tonnetz, with literal Cohn flips. In
Animation 3, forms of pcset (013) that are created by Bach’s subject are colored blue and forms of pcset (013) created by the subsequent answer are colored red. When the notes of the subject or answer complete a triangle and thus a form of (013), that triangle is colored red or blue respectively. Here, each vertex that creates a (013) remains lit, despite the notated duration, until the triangle is created, and is only released at the approximate time that the last note of that form is released. To preserve the shape of Bach’s gestures the triangles created remain colored. Notice also that the first triangle colored blue turns a lighter color blue when the subject cadences in measure three and repeats form (
[3.8] In Animation 4 only the (013) forms of the answer and countersubject are highlighted. Animation 5 adds the crosstalk forms created between the answer and counter subject in purple. In Animation 6 the (013) forms of the subject are reinserted so that all forms appearing in measures one through six are represented. Lastly Animation 7 again shows all (013) forms appearing in the first six measures. We remove the tetrahelix base and vertex labels in this animation to emphasize the constellation-like aesthetic created by Bach’s music. Each animation focuses on a different area of the six measures and visualizes a different aspect of Lewin’s analysis. Without demonstrating the entire analysis in these new visualizations we will highlight a few areas where the transfer may not be immediate.
[3.9] At the beginning of his analysis Lewin points out that a pattern of “two-ranks-up-and-one column-right” is established during the statement of the subject by the first three (013) motives.(17) This pattern, in a sense, skips two forms on his figure, our Figure 1, those labeled with the numbers 5, 9 and 7. Similarly, on the tetrahelix, the first three forms (
[3.10] Next, Lewin introduces the concept of vertical cross-talk explained as the creation of (013) forms between the lines of two voices. The (013) forms created by cross-talk are labeled 10, 11, and 17 and complete his list of seventeen appearances. Form 10 is a restatement of the trichord (
[3.11] Animation 5 highlights the forms created by the answer, countersubject and the vertical cross-talk between the two. The forms created by cross-talk, (
[4] Amplifying the Analysis
[4.1] On a basic level the media of computer modeling and animation provide us with new tools with which to demonstrate the analysis. On a deeper level the structure of our geometric model facilitates and augments comprehension of the analysis.
[4.2] Lewin’s analysis shows the reader how the opening measures of the
[4.3] Another aspect of Lewin’s analysis amplified by computer modeling and animation is the way his forms 4, 7, and 11 fill the gaps created by the subject and answer on the graph or model. Here the difference between the way Lewin’s graph and the tetrahelix animations represent this phenomenon is simple yet drastic. The use of color to distinguish the subject, answer, countersubject and crosstalk creates a realization of the gap-filling that is instantly clearer. On Lewin’s graph the reader tracing the temporal pattern of the subject or answer in his/her mind sees how forms 4 and 11 are first skipped over and then later filled in. However, the pattern, its gaps, and the filling in of those gaps are really only understood after several steps in a logical process. First, the reader must study the graph, then the score and the musical example. Next, the reader must see how the figure is an isolation of the shape made as music of the example surfs the graph. Finally, the reader may see how the forms fill in skipped areas of the figure. On the tetrahelix the music is correlated with the illumination of vertices representing pitches. This allows the viewer to understand immediately movement on the model as visualization of the music. Furthermore, the triangles representing forms become highlighted with color as the form is heard in the music. This illustrates the pattern of the subject and answer as pathways traced in time. Thus, forms skipped by the subject and answer appear immediately as gaps recognizable as uncolored or grey triangles. Subsequently, when a musical gap is filled, a grey triangle is colored visualizing the aural and analytical concept instantly. Consider the gap of the subject filled in by form (
[4.4] In discussing the function of the three cross-talk forms, 10, 11, and 17, our (
Form 11 also connects to the “Answer-region” the form labeled “1,5,10”
. . . In sum, we see how the two cross-talk forms 10 and 11 have special spatial functions on the figure suturing together and connecting the spatial realms of Subject and Answer.(22)
The exact meaning of the metaphor aside, it is clear that these two cross-talk forms in some way unite the subject and answer areas of Lewin’s figure. However, notice that on the figure the idea of form 10 suturing the answer area to the subject area again requires a bit of imagination on the reader’s part. The fact that the form is a restatement of the initial trichord (
[4.5] As previously mentioned, in Animations 5 and 6 these cross-talk forms, (
[4.6] Lewin writes the following about the last form of cross-talk, form 17:
Form 14, the final form of the countersubject, has a like function: it connects the “high point” of the subject on the map, form 3, recalled as form 13, to the (local tonic) “low point” of the Answer, form 6. The cross-talk of the Countersubject and Answer, at form 17, cements the connection.(23)
Pitch (
[4.7] The most intriguing part of this new visualization of the cross-talk forms relates to Lewin’s endnotes 5 and 6. These two endnotes partly detail the success with which the 3-D animations realize Lewin’s analysis and suggest that he might have approved of their use. Lewin’s Endnote 5 reads
The “spatial” functions of forms 10 and 11 on the figure are nicely projected, allegorically, by the maximum vertical distance between the voices during the time these forms sound in the music. As one notes on the example, that maximum vertical distance is the seventh
Lewin, in describing how significant musical phenomena emerge in the visual field of his graph, is pointing out aspects of the analysis that, only implied by his visualizations, stand out under 3-D modeling.
[4.8] Seeing the vertical distance between the voices as forms 10 and 11 with Lewin’s visualizations requires cross-referencing the score with his figure. Under 3-D modeling the score remains helpful but is not required. Because the model’s skeleton is a chromatic scale the vertical distance between the lines is clearly articulated as the appropriate vertices light at distant ends of the tetrahelix.
[4.9] Similarly, it is much easier to see this largest interval of a seventh (
[4.10] In his Endnote 6, Lewin remarks on the spatial allegory of cross-talk form 17 that unites the subject and answer areas of the figure in a clausula gesture at the cadence. The tetrahelix analog of this spatial allegory is clear. The two voices of the fugue lighting the tetrahelix vertices converge onto the final note (
[4.11] Returning to the ‘surfing’ nature of Bach’s Gesture, the geometry of the tetrahelix strengthens another aspect of the analysis. Investigating the details of this surfing motion, Lewin shows how chronologic forms 7 and 9, or forms (
[5] A New Perspective
[5.1] 3-D animation of the opening of the
[5.2] Begin by noticing that, on the tetrahelix, each helix constructs a cycle of IC3s in pitch space not pitch-class space. Straus’ circles present interval cycles in a closed mod12 pitch-class space with octave equivalence. The tetrahelix takes his circles of C3 and pulls them out into the third dimension spiraling them in a pitch space. Of course, the tetrahelix used in all the visualizations provided here only presents about two octaves, but could be extended further. Nevertheless, beyond register, this conversion enables us to see the combination of all three cycles, represented in 3-D, into a modular geometric structure. This geometric integration allows a fluid visualization of the musical movement between the cycles about to be discussed.
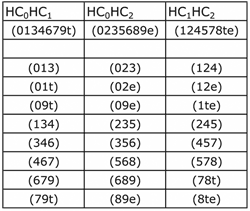
Table 1. Three octatonic collections and the list of (013) forms they each contain
(click to enlarge)
[5.3] If the octatonic collection can be derived from a combination of any two C3-cycles, then analogously, the three permutations of Forte-set 8-28 (0134679T), can be derived from the combination of any two helices on the tetrahelix. Walking the alternating half and whole steps of an octatonic collection on the model traces a lattice between two of the three helices and traverses one of the three twisting sides of the tetrahelix. Each side will be referred to as a combination of helices. Thus, the octatonic collection (0134679T) will be called HC30HC31, the collection (124579TE) HC31HC32, and the collection (0235689E) HC30HC32. Again, these lattice pathways are also visible on the 2-D Tonnetz, though, not as explicitly. These three octatonic pitch collections each contain eight of the twenty-four permutations of Forte-set 3-2 (013). These relations are apparent in the structure of the tetrahelix where each triangle is composed of two points from one helix and one from a second helix. Put another way, each triangle lies within one of the three octatonic pathways on the tetrahelix. Table 1 presents the three octatonic collections and lists the (013) forms that they each contain.
[5.4] Returning to Bach, the progression of (013) forms appearing in the subject delineates a distinct pattern with regard to the divisions in Table 1. The five appearances, (
[5.5] Certainly, it is easy to see octatonic relationships wherever Forte set 3-2 (013) is present, often without any musical impetus or relevance. Admittedly, these octatonic patterns have minor significance in any satisfactory analysis of Bach’s fugue. Note also, that the 2-D Tonnetz could easily be extended to permit the continuation of octatonic lattices and a chromatic scale can be traced through them. However, with regard to this specific concept and visualization, we are more interested in demonstrating the potential of the geometric model than in enhancing the analysis. To that extent, the helical model better depicts the cyclical nature of the tetrachordal and octatonic elements, their internal relationships and their realization within the music. If the tetrahelix can reveal this noticeable pattern in these six measures of Bach’s music then it may prove useful in the investigation of the music of more modern composers. Nevertheless, without implying that Bach was composing with trichord sets, tetrachord cycles or octatonic collections in mind, these patterns add another perspective on the nature and effect of the chromaticism present in the opening of the
[6] Conclusions and Some Prospects for Further Research
[6.1] Three-dimensional animation and the tetrahedral triple helix elucidate Lewin’s analysis of the opening of Bach’s
[6.2] This article is not intended as pedagogical theory. Nor is it intended to advance a specific lesson, model or method for practical classroom use. However, the general nature of our media and design of our model correspond to established theories and techniques in the fields of music education and education in general. Wide-ranging evidence has shown that “the listening condition that include[s] both visual and kinesthetic elements in addition to the aural component [is] most effective in enhancing children’s aural perception of musical form.”(26) Entire methodologies of music education such as Kodaly or Dalcroze are founded on such concepts. In an article discussing reference maps and their effects on prose learning, educational psychologists Abel and Kulhavy state that “maps consistently have been found to improve memory for related prose” and that “maps add a dimension to pictorial adjuncts by depicting logical relations among individual features.”(27) However, referring to past experiments they reiterate that “the mere presence of extratextual information fails to account for increased learning when maps and prose are combined” but that “what matters is how the map information is provided.”(28) In previous work, Kulhavy and Schwartz explained that “figural characteristics work to maintain relational context, at least in the case in which a recall task demands performance that is spatially isomorphic with the original stimuli.”(29) Concluding their study, Abel and Kulhavy write:
Our results are consistent with Levie and Lent’s (1982) conclusion that ‘learner generated imaginal constructs are generally less helpful than provided illustrations’ (p. 226), and lend credence to the idea that attending to provided images requires fewer cognitive resources than generating and attending to idiosyncratic images.
. . . Data from the cued recalls demonstrate that spatiality and feature mimeticism led to the most learning.. . . By adding a perceptual component to abstract (verbal) information, map features seem to function transformationally by supplying learners with an easily accessible analog of text context.
[6.3] This concept is readily seen in common tools of music educators worldwide: listening maps, form charts and call charts. Music educator Samuel Miller writes: “A ‘listening map’ is a graphic representation that symbolizes the essential features of a musical selection in a visual format. It is a valuable teaching aid
[6.4] As demonstrated in section 4, our revisualization operates in two ways to make the analysis more accessible. It reduces the number of things the reader must keep in his/her head to visualize the theory by synthesizing the components of Lewin’s analysis. With one figure we can see the complete (013) graph, the musical line with register, and a graph of the forms in the subject, answer, counter-subject and cross-talk. Secondly, the animation weds the music and the analysis, portraying a second synthesis between the abstract concepts and the actual notes. Admittedly all the theory cannot be grasped at the speed at which even this slow fugue passes by and much of the analysis must be read prior to understanding the model. Nevertheless, both of these operations facilitate connections that, however easy for Lewin, may be more difficult for others. Lewin writes:
To be sure, the inversional relation between the opening of the subject and the opening of the countersubject is manifestly audible in the pitch intervals and contours of the music itself; we do not need the fancy spatial map of the figure to hear the relation as such. What the map does bring out is the way in which the particular inversional relationship of the forms employed fills in a connected spatial region on the figure.(32)
[6.5] This relation serves as an excellent example of a place where the real-time animation helps readers hear things Lewin hears easily. Our model, as an extension of Lewin’s visualizations, adds meaning to the analysis in exactly the same way. The overall meaning Lewin imparts to the analysis is that Bach’s realizations of (013) forms creates an intricate pattern on a map of Forte Set 3-2 as related by Cohn flips. This pattern is both aesthetically pleasing and rife with voice-leading and inversional relationships. Thus, as the example shows, and as detailed in section 4, our even fancier spatial map brings out these relationships and the way they fill the region of the tetrahelix. As Gollin writes at the end of his work on 3-D Tonnetze:
We may view the Tonnetz as an independent framework that allows one to make distinctions among the (otherwise indifferent) transforms that underlie its elements. It allows one to posit analytical meaning or value to certain families of transforms
. . . based on the distance between elements mapped by those transforms, whose geometry in turn is determined contextually by the intervallic structure.(33)
[6.6] The design and realization of the 3-D geometric animations presented here required us to make many decisions with regard to language, labeling, audio/visual relationships, timing, duration, camera angle, color, and most obviously geometric structure. Although we are confident that our choices were informed and find our results satisfactory, we fully acknowledge that many other ways to visualize Lewin’s analysis exist. Beyond this, more work remains available within the
[6.7] Outside of the
Jacob Rosenthal Reed
Ohio State University
School of Music
1866 College Road
Columbus OH, 43210
ejacobreed@yahoo.com
Matthew Neil Bain
Ohio State University
Department of Industrial, Interior, and Visual Communication Design
128 N. Oval Mall
Columbus OH, 43210
bain.28@osu.edu
Works Cited
Abel, R. Robert, and Raymond W. Kulhavy. 1986. “Maps, Mode of Text Presentation, and Children’s Prose Learning.” American Educational Research Journal 23, no. 2: 263–274.
Bletstein, Beverly. 1987. “Call Charts: Tools from the past for Today’s Classroom.” Music Educators Journal 74, no. 1: 53–56.
Chew, Elaine. 2006. “Slicing It All Ways: Mathematical Models for Tonal Induction, Approximation, and Segmentation Using the Spiral Array.” INFORMS Journal on Computing 18, no. 3: 305–320.
Chew, Elaine, and Alexandre R. J. Francois. 2005. “Interactive Multi-scale Visualization of Tonal Evolution in MuSA.RT Opus 2.” ACM Computers in Entertainments 3, no. 4: 1–16.
Cohn, Richard. 1996. “Maximally Smooth cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15, no. 1: 9–40.
—————. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41, no. 1: 1–66.
—————. 2003. “A Tetrahedral Graph of Tetrachordal Voice-Leading Space.” Music Theory Online 9, no. 4: 1–19.
Douthett, Jack and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2, Neo-Riemannian Theory: 241–263.
Gollin, Edward. 1998. “Some Aspects of Three-Dimensional ‘Tonnetze’.” Journal of Music Theory 42, no. 2, Neo-Riemannian Theory: 195–206.
Gromko, Joyce Eastlund, and Christine Russell. 2002. “Relationships among Young Children’s Aural Perception, Listening Condition, and Accurate Reading of Graphic Listening Maps.” Journal of Research in Music Education 50, no. 4: 333–342.
Hyer, Brian. 1989. “Tonal Intuitions in Tristan Und Isolde.” PhD diss., Yale University.
—————. 1995. “Reimag(in)ing Riemann.” Journal of Music Theory 39, no. 1: 101–138.
Krumhansl, Carol L. 2005. “The Geometry of Musical Structure: A Brief Introduction and History.” ACM Computers in Entertainments 3, no. 4: 1–14.
Kulhavy, Raymound W., and Neil H. Schwartz. 1980. “Mimeticism and the Spatial Context of a Map.” Bulletin of the Psychonomic Society 15, no. 1: 416–418.
Lewin, David. 1996. “Cohn Functions.” Journal of Music Theory 40, no. 2: 181–216.
—————. 1998. “Notes on the Opening of the F![]() Minor Fugue From WTCI.” Journal of Music Theory 42, no. 2, Neo-Riemannian Theory: 235–229.
Minor Fugue From WTCI.” Journal of Music Theory 42, no. 2, Neo-Riemannian Theory: 235–229.
Miller, Samuel D. 1986. “Listening Maps for Musical Tours.” Music Educators Journal 73, no. 2: 28–31.
Pugh, Anthony. 1976. Polyhedra: a Visual Approach. Berkeley and Los Angeles, CA: University of California Press.
Rogers, Nancy and Michael Buchler. 2003. “Square Dance Moves and Twelve-Tone Operators: Isomorphisms and New Transformational Models.” Music Theory Online 9.4: 1–12.
Straus, Joseph. 2005. Introduction to Post-Tonal Theory, 3rd ed. Upper Saddle River, NJ: Pearson Prentice Hall.
Footnotes
1. Lewin, “Notes on the Opening of the F![]() Minor Fugue from WTCI,” 235.
Minor Fugue from WTCI,” 235.
Return to text
2. Ibid., 236.
Return to text
3. Ibid., 235.
Return to text
4. Ibid., (emphasis mine).
Return to text
5. Cohn, “Neo-Riemannnian Operations, Parsimonious Trichords, and Their “Tonnetz” Representations,” 14.
Return to text
6. Lewin, “Cohn Functions,” 189.
Return to text
7. Lewin, “Notes on the Opening of the F![]() Minor Fugue from WTCI,” 235.
Minor Fugue from WTCI,” 235.
Return to text
8. Ibid., 238 (emphasis mine).
Return to text
9. Ibid.
Return to text
10. Gollin, 195.
Return to text
11. Krumhansl, 9.
Return to text
12. Chew, “Slicing It All Ways: Mathematical Models for Tonal Induction, Approximation and Segmentation Using the Spiral Array,” 7.
Return to text
13. Chew and Francois, “Interactive Multi-scale Visualizations of Tonal Evolution in MuSA.RT Opus 2,” 1.
Return to text
14. Ibid., 3.
Return to text
15. Pugh, 53.
Return to text
16. In “Square Dance Moves and Twelve-Tone Operators: Isomorphisms and New Transformational Models” Nancy Rogers and Michael Buchler show a correlation between “musical and square dance transformations.” No 3-D geometry is used, unless, of course, the reader performs the dances, but simple animations demonstrate the square dance moves and their twelve-tone analogs.
Return to text
17. Lewin, “Notes on the Opening of the F![]() Minor Fugue from WTCI,” 236.
Minor Fugue from WTCI,” 236.
Return to text
18. Ibid., 237.
Return to text
19. Ibid.
Return to text
20. Ibid. , 238 (emphasis mine).
Return to text
21. Ibid.
Return to text
22. Ibid.
Return to text
23. Ibid.
Return to text
24. Ibid., Notes, 239.
Return to text
25. Straus, Introduction to Post-Tonal Theory,
154–155.
Return to text
26. Gromko and Russel, “Relationships among Young Children's Aural Perception, Listening Condition, and Reading of Graphic Listening Maps,” 334-335.
Return to text
27. Abel and Kulhavy, “Maps, Mode of Text Presentation, and Children’s Prose Learning,” 263.
Return to text
28. Ibid., 265.
Return to text
29. Kulhavy and Schwartz, “Mimeticism and the spatial context of a map,” 418.
Return to text
30. Miller, “Listening Maps for Musical Tours,” 28.
Return to text
31. Bletstein, “Call Charts: Tools from the past for Today's Classroom,” 54.
Return to text
32. Lewin, Notes, 237–238.
Return to text
33. Gollin, 204
Return to text
Copyright Statement
Copyright © 2007 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo and Tahirih Motazedian, Editorial Assitants
Number of visits: