A Transformational Space Structuring the Counterpoint in Adès’s “Auf dem Wasser zu singen”

[1.1] Like many contemporary composers, Thomas Adès draws upon a wide range of historical and contemporary musical styles. His eclecticism manifests itself not only in the diversity of genres in which he writes (his catalog includes symphonies, operas, string quartets, choral works, songs, concerti, and solo piano pieces as well as less traditional ventures, such as hybrid video-musical works and transcriptions of popular music), but also in the musical materials and processes he employs, and in the many allusions they make to the Western art-music repertoire. He often exploits extremes of timbre and register in polyphonic and polymetrical textures that, while partaking of the highest musical modernism, are shaped into coherent, accessible phrase structures with discernible short- and long-range goals. In any given passage of his music one may find intermingled hexatonic, octatonic, and diatonic collections, interpenetrated with triad-like structures connected in stepwise voice leading. His music is an intriguing but analytically challenging post-tonal counterpoint.⁽¹⁾

[1.2] A concise example of his techniques and the challenges they pose is the beginning of the third movement, “Auf dem Wasser zu singen”, of his string quartet, Arcadiana, Op. 12 (1994). Its title alludes to the eponymous Schubert song, which sets an elegiac text to an obsessively repeating, descending figure. (The connotations of death and transcendence contribute to the overall program of the quartet, which treats “ideas of the idyll, vanishing, vanished or imaginary” (Adès 1995, title page). Example 1 presents measures 1–9, in wide format, as an analytical transcription that clarifies their content. The movement begins strikingly by transmuting Schubert’s monophonic, regular accompanimental motive into a temporally and texturally varying polyphony of overlapping, pizzicato-glissando gestures. In the transcription they appear on the lower two staves. Each gesture presents an accelerating descent through a series of regularly expanding pitch intervals, usually realized as <-1, -2, -3, -4, -5, -6, -7>. The first few descents begin on G4, but later statements begin on other pitches as well; also the gestures sometimes omit intervals or otherwise vary the series, as is evident in measures 4–5. Two other streams soon join the texture. One, shown on the top staff, is a sustained, bowed, monophonic melodic line that descends gradually by semitone, with some elaboration, then quickly arpeggiates upwards, only to glide slowly down again from C6. The other stream, notated on the second staff, consists of overlapping, sustained, bowed, ic5 double-stops, most of which are highlighted with boxes and alphabetical labels.

[1.3] To some degree, the diverse materials and differently paced continuities of these streams convey a postmodern sense of multiple temporalities (Kramer 1996; Roeder 2006). Yet, one would hope that an analysis could say more than that about how this passage works. After all, Adès has notated timing and content quite precisely, and so one might want to describe and explain the counterpoint. Specifically, do the contents of the different streams cohere? Are they coordinated from moment to moment in order to shape this segment into a phrase and, if so, how does their combination produce a sense of direction and closure?

[1.4] At first glance, transformational theory would not appear to be a promising medium for such an account. It has usually been employed as a sophisticated means of motivic analysis, not as a description of counterpoint. Such analyses identify small families of equal-sized objects (sets, series) defined by a coherent system of relationships, but the surface features of the streams in Example 1, as described above, appear quite diverse in size and nature. Recent efforts to adapt transformational theory to analyze objects of different types are still too constraining to deal with the many different sizes and types of structures that seem to be salient here (Hook 2007). This brief paper demonstrates, nevertheless, that a transformational approach can address productively many of the questions about how this passage works. It does by adopting a “transformational attitude” that explains each stream not as a sequence of motives, but as actions in a space of very elementary objects (Lewin 1987, 159). The space thus provides a context in which the diverse events can be heard to be coordinated.

[2.1] Annotations on Example 1 show some crucial observations about this passage that point the way towards such a unifying space. Each expanding-interval series (necessarily) belongs to a single octatonic collection, and features a dominant-seventh-sounding 0258 subset. The double-stop ic5s partition registrally into two series of three, respectively labeled and color-coded <A, B, C> and <X, Y, Z>, such that the unions of order-corresponding dyads, A+X, B+Y, and C+Z, all belong to the same tetrachord-class 0257. A rest divides the melody into two segments belonging to different octatonic collections. On Example 1, color identifies the octatonic collections to which these various segments belong. There are also hints of hexatonic collections (one is the succession of X to Y in measures 5–6, and the other is marked by a triangle in measure 7), which become prominent later in the movement and elsewhere in the quartet.

[2.2] Acknowledging the emphasis on perfect fifths and on common fifth-containing sets, it seems appropriate to consider the twelve dyads belonging to interval class 5 as the basic family of objects, and the set of transpositions as the operations on them. Two of these transpositions seem especially characteristic. T₃ organizes fifths into 0358s and into octatonic collections, for example, {C,G} combined with T₃ ({C,G}) is the 0358 chord {C, E, G, B}, and {C, E, G, B} combined with T₃T₃ ({C, E, G, B}) is the octatonic collection including C and D. Another transposition, T₄, connects double-stop dyads in the same register, for example X and Y. In some segments, inversion might be heard abstractly to govern some pitch-class relationships; for instance in the first pizzicato gesture I₁₀ might be understood to generate E from F, and A from C. However, inversions are not plainly manifested between obvious larger structures in the passage. For instance, the pizzicato motives are transposed, never inverted, and the double-stop dyads do not manifest any consistent inversion relationships. So inversions are not “characteristic” in the same sense as the transpositions I have identified.

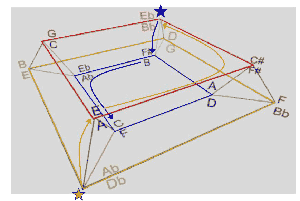
[2.3] Accordingly, Example 2 presents a network with twelve nodes, each representing a distinct member of ic 5. The nodes are connected by edges, each symbolizing a pair of oppositely directed arrows labeled respectively by inversely related transpositions. The dyads are arranged in three squares, each side representing transposition by 3 (or 9, in the other direction), such that the four dyads at the corners of each square constitute one of the three octatonic collections. Different primary colors distinguish the squares. Edges connecting the corresponding corners of the squares represent transposition by 4 (or 8, in the other direction), and they make a triangle comprising one of the four hexatonic collections. This network thus constitutes a space—a complete, minimal configuration of all objects, each oriented to the others by the characteristic transformations T₃ and T₄.⁽²⁾

[3.1] Adopting Lewin’s “transformational attitude,” let us imagine that our perception of each event in the passage positions us at one of the nodes “inside” this space, and that each succeeding pitch changes our location along the edges of the graph, that is, through T₃, T₄, their inverses, or some series of them.⁽³⁾ Such a conception of the music is compelling for the progression of ic5 arco dyads, represented by the arrows on Example 1. The first dyad-event, A, positions us at the EB node, highlighted on the example by a dark blue star. Dyad-event B changes our position to node BF, that is, along one of the T₄/T₈ edges, as shown by the curved blue arrow. The last lower-register ic5 event, C, similarly changes our position, but since there is no direct connection from BF to FC in the space, we understand it as a composite of two T₉ actions, symbolized on the figure by an arrow traversing two edges of the lower square. The orange arrows show similarly how we would conceive of the succession of the upper-register arco ic5 dyads, <X, Y, Z>, in this context.

[3.2] With the orientation provided by the space, we can understand how upper- and lower-register dyad-successions cooperate contrapuntally to give the passage direction and closure. The very first dyads, A and X, stake out the entire space, in the precise sense that they occupy diametrically opposed locations. Each move in one register is paralleled by an exactly corresponding move in the other register—first a change by T₄ to another square, then a change by a 180-degree gesture to the opposite corner of that square—so the same distance is always maintained between corresponding dyads. (This signifies a constant transpositional relation, T₂ = T₈T₃T₃, maintained between the two registers.) The combined motions provide completion to the passage in two senses: together they touch upon all three octatonic squares, and the upper register path terminates at exactly the same place that the lower-register path began. The identity of Z and A is more telling when we understand them not as isolated events but as termini of a series of actions.

[3.3] To suggest an actual temporal experience of these actions, Animation 1 displays the paths of these two ic5 streams in real-time synchronization with a recording.⁽⁴⁾ (The animation begins with the appearance of dyad A in measure 3, skipping the preceding music.) Each stream is represented by a persistently glowing star, evoking the sustaining continuity of the bowed pitches, which traces a particular path touching on three vertices of the space. The color of each star results from the combination of the primary colors of the two squares that it visits. With a “transformational attitude” we may conceive of each star as a performer that plays the particular ic5 determined by its location, and who “dances” around the space in a particular pattern that constitutes a “characteristic gesture,” combining a series of node-to-node transformations. The two stars mirror each other’s gestures, and closure is made apparent by the arrival of the orange star at the node where the purple star began.

[3.4] This animation also clarifies some metrical aspects of the passage. It takes about 2 seconds for X (which first appears at 0:06) to change to Y (at 0:08), and the following imitative change from A, to B (at 0:10) follows after the same duration. Then both streams change nearly simultaneously (at 0:14) after a duration, 4 seconds, that can be anticipated metrically, since it is the sum of the duration of the earlier changes.⁽⁵⁾ These last changes appear to involve motion across a greater distance in the space (around two sides of a square instead of just along a single T₄ triangle leg), so the corresponding actions seem more significant than the earlier ones, evoking the sense of an anacrusis to a cadential downbeat.⁽⁶⁾ (The prominent first-violin melody, whose accelerating rhythm supports this hearing, will be analyzed below.)

[4.1] The other layers of texture in this piece do not involve ic5s as explicitly as the sustained arco dyads do, yet many aspects of the textural counterpoint become clear when we imagine their pcs to be structured by this same toroidal space. To do so, let us imagine separating the pcs of each ic5 node and connecting them by edges representing transposition by 5 in one direction and 7 in the other. The resulting network has two instances of each pc, so it is a minimal space only in the sense that we imagine it to be derived from the ic5 space; nevertheless, I will represent it simply by the same diagram as those above, leaving implicit the transpositional connection between pcs within each ic5. To determine which of the two possible locations will represent the pc of any given event in the piece, one can take into account the textural context of that event, and choose the location that seems best to express its relation to the temporally proximate events in the same stream.

[4.2] This representation enables us to attribute a clear transformational-spatial unity to the diverse gestures in the pizzicato stream. For example, referring back to the color-coding on Example 1, we see that each distinct descending series of pcs belongs entirely to one of the octatonic scales. Since, in the space we are considering, each square constitutes such a collection, it seems natural to locate all the pcs of each descent on one square. (Indeed, the colors indicating octatonic membership on Example 1 correspond to those in the space, except that brown substitutes for yellow, for greater legibility.) Accordingly, Animation 2 portrays each series of pizzicato descents as a bouncing ball. As with the transformational account of the stars, each ball represents an agent who plucks (and then glissandos down from) the pitch corresponding to one of the letter names on each node that the ball touches. The shapes of the objects and the motion are intended to evoke the aural affect of the pizzicato, and, in order to evoke the glissandi, the bounces appear slightly sticky, and they are spread across each pitch’s entire duration. Since each ball restricts its motion to the nodes of a single octatonic square, it is given the corresponding color.

[4.3] Like Animation 1, but for a different textural stream, this visualization clarifies the contrapuntal shaping and closural processes across the passage. The following narration, keyed to the times displayed on Animation 2, makes these explicit:

• 0:00—0:06. Starting from the note G on the CG node, a red ball performs a complex but distinctive maneuver, which I will describe here as a series of motions from node to node on a square: <diagonal, clockwise, counter-clockwise, clockwise, bounce-in-place, diagonal>.⁽⁷⁾ (Hold down the left or right arrow key while viewing the animation to replay the motion backwards or forwards, respectively.) This gesture can be understood as structurally complete when it has visited all four nodes of the red octatonic square, and, indeed, this is when it ceases, on the node BE.

• 0:06—0:08. A second red ball begins from the same node to perform the same complete maneuver, representing the exact repetition within the red (01) octatonic collection.

• 0:08—0:10. Before this ball gets very far, however, the texture thickens as a third red ball enters and performs the same maneuver. Strikingly, the second clockwise motion (C to A) of the second ball synchronizes with the first clockwise motion (F to E) of the third ball: they arrive nearly simultaneously (at 0:09) on the CF node, then move in parallel to arrive nearly simultaneously on the AE node. Although this synchrony glosses over some details of melodic transformation, it does call attention to the contrapuntal coordination of these two voices as they together sound one ic 5, {C,F}, then another, {A,E}.⁽⁸⁾

• 0:11—0:12. The second ball’s completion of the entire gesture cues the appearance of a fourth red ball, again beginning to repeat the same gesture starting on the same CG node. The third red ball, however, stops on C, without completing the last three moves of the gesture, just as the fourth ball leaps to F on the same node. Thus, the fourth ball appears to take over the third ball’s gesture.

• 0:12—0:18. Cooperation increases among the separate voices as the materials diversify. Another ball enters, but this time it starts on another octatonic square, so it is colored yellow. The node on which it enters, DA, is diametrically opposed to the node EB on which the complete red-ball gestures have concluded, thus staking out the space as the stars do. It executes the first four motions, <diagonal, clockwise, counter-clockwise, clockwise>, and as it reaches the BF node, a second yellow ball strikes the same node (substituting for the expected bounce-in-place) then continues with a truncated version of the gesture.

• 0:17—0:18. As the second yellow ball bounces in place on the DA node, a red ball suddenly restarts at the diametrically opposed node, EB, at which none of the previous balls began; again, this stakes out the space with respect to the yellow ball’s position.

• 0:18—0:19. The second yellow ball (the cello’s pizzicato) completes its gesture on GD node. This node holds the pc G in common with the CG node on which the first red-ball gestures began, and, indeed, a red ball immediately appears there to begin another gesture. This pivoting between octatonic collections is simultaneously apparent elsewhere in the texture, as we shall see.

• 0:20—0:23. Just after this new red ball touches the BF node, another switch between octatonic collections occurs in the established manner: with the space-spanning entrance of a yellow ball at the diametrically opposed node AE.

• 0:24—end. After a suspenseful two seconds during which no balls are active, a new ball enters and executes the first part of the characteristic gesture. As shown by its blue color, its notes belong to the third octatonic collection that has not yet sounded in the pizzicato stream, so its appearance here creates a sense of completion and closure, paralleling the concurrent and similar completion in the ic5 stream.

[4.4] The moving ring on Animation 3 makes apparent the gestural qualities of the third textural stream, the arco melody, in the context of this space. The melody begins with an alternation between two pcs on the same ic5 node, DA, then executes a move to the node GD diagonally opposite on the same yellow octatonic square. As in the pizzicato stream in the same measure, the G acts as a pivot to another octatonic collection, represented on the red square, and the rest of the arco melody remains in that collection. Towards the end (starting at 0:09), its moves string together into a sequence <diagonal, bounce-in-place, clockwise, counter-clockwise, clockwise> that retrograde-inverts all but the first move of the balls’ characteristic gesture. Thus, all three streams share a common repertoire of transformations that the animations represent as similar moves.

[5.1] Beyond this unity of gesture, however, the counterpoint of these streams subsists in the close coordination of location and action in this space that are visually apparent when the animations of all three streams are combined, as in Animation 4. Consider the following brief catalog of some of the more significant ways in which the streams interact, coordinate, and cue each other to shape the passage into a complete phrase:

• 0:11. The node at which the pizzicato gestures conclude, EB, is where the first lower-register ic5, A, begins. Accordingly, at this point in the animation a red ball appears to morph into the purple star.

• 0:12. I mentioned above how a fresh octatonic collection (symbolized by a yellow ball) appears at the node DA, which is diametrically opposed to the concluding node of the earlier pizzicato gestures. This is also where the arco melody begins.

• 0:16. As the melody departs this same node (symbolized by the ring making its diagonal move) it seems to leave its trace behind in the first upper-register ic5, X, whose orange star ignites at exactly this moment. As reinforcement, a pizzicato gesture (yellow ball) immediately comes to the node and dwells there with a bounce-in-place.

• 0:17. As the pizzicato gesture departs DA, so does the upper-register ic5, which arrives at ic5 Y, {A,E}, in the original (red) octatonic collection just as a pizzicato gesture arrives at the same node (0:19).

• 0:25. Although the arco melody and the upper-register ic5 begin on the same node DA at 0:16, they stay entirely apart until their very last move, when they arrive simultaneously at the diametrically opposed node EB, reinforcing the closure in the ic5 stream, mentioned above.

• Across the passage the textural complexity gradually increases, from one element (0:00—0:07, a single ball) to multiple elements of the same type (0:07—0:11, two balls), then single elements of different types (ring, ball, star), then multiple elements of multiple types. The density decreases only towards the end, when a single element is in motion, perhaps suggesting a cadential relaxation.

[5.2] To the extent that we understand all the pitches in this passage to be structured by this transformational space, we can recognize one further, impressive way in which closure is achieved by completion. Animation 5 combines the objects and gestures of the three streams, as did Animation 4, but rather than the entire space being displayed in its entirety throughout the beginning of the passage, each pc appears at the moment when it (as a member of an ic5) is first played. This representation shows that the music gradually builds the space that structures it. Observe, for instance, how the opening pizzicato stakes out one complete red octatonic collection, setting the stage for the first ic5 to arrive (0:00—0:12). The second (yellow) octatonic collection is not completely manifest until 0:21, when a yellow ball arrives at B. This is the same moment when the lower-register ic5, {E,B}, moves to the other node containing B, BF, which is the first foray into the third (blue) octatonic collection. That collection is completed very concisely by the last few moves of the passage, so that at the end every node in the space has been touched by some gesture in a stream.

[6.1] When transformational theory is construed narrowly to describe relationships among a family of motives, it may seem inappropriate for polyphonic passages with varying motives, such as Example 1. But the analysis above shows that a transformational network of very elementary objects can flexibly accommodate such variability, inasmuch as we understand it as a space that structures object-changes as multipartite gestures. For instance, the space proposed here reveals the essential gestural identity of the pizzicato gestures and the arco melody, even though they involve different interval series starting on different pcs, and it functions as a site where all the concurrent actions of the various textural streams are coordinated. The comprehensive view it provides of Adès’s post-tonal counterpoint suggests that other pieces might also benefit from such an approach.

John Roeder
University of British Columbia School of Music
6361 Memorial Road
Vancouver, B.C.
V6T 1Z2 Canada
j.roeder@ubc.ca

Works Cited

Adès, Thomas. 1995. Arcadiana for string quartet. London: Faber Music.

Cohn, Richard. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41/1: 1–66.

Fox, Christopher. 2004. “Tempestuous Times: The Recent Music of Thomas Adès.” The Musical Times 145: 41–56.

Hasty, Christopher. 1981. “Rhythm in Post-Tonal Music: Preliminary Questions of Duration and Motion.” Journal of Music Theory 25: 183–216.

—————. 1997. Meter as Rhythm. New York: Oxford.

Hook, Julian. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29/1: 1–39.

Hyer, Brian. 1995. “Reimag(in)Ing Riemann.” Journal of Music Theory 39/1: 101–38.

Kramer, Jonathan. 1996. “Postmodern Concepts of Musical Time.” Indiana Theory Review 17/2: 21–61.

Lewin, David. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University.

Mazzola, Guerino. 2002. The Topos of Music. Basel: Birkhäuser.

Roeder, John. 2006. “Co-operating Continuities in the Music of Thomas Adès,” Music Analysis 25/1–2: 121–54.

Travers, Aaron. 2005. “Interval Cycles, Their Permutations and Generative Properties in Thomas Adès’ Asyla.” Ph.D. thesis, University of Rochester.

Footnotes

1. An overview of Adès’s techniques, a consideration of their temporal processes, and some detailed analysis of his music, may be found in Roeder 2006. Travers 2005 demonstrates how chord progressions constructed from concurrently unfolding interval cycles permeate various levels of structure in Adès’s 1997 symphony Asyla. Further analytical observations of his later pieces can be found in Fox 2004.
Return to text

2. T₃/T₄ toruses—of pcs, rather than the ic5s of this space—appear in many other guises in the theoretical literature, notably: Hyer 1995, Cohn 1997 and Mazzola 2002.
Return to text

3. This attitude seems especially appropriate for a piece whose title juxtaposes place (auf dem Wasser) and music (singen). Adès has conceived of other pieces through spatial metaphors, too. About the second movement of Asyla he said, “I wanted the sense that you were a human inside this huge space which I built through details on the score” (Gerald Fox, director. Thomas Adès: Music for the 21st Century. 1999. DVD. 21:03—21:14).
Return to text

4.   This animation, as well as the others in this article, were realized according to my specifications by a research assistant, Ali AbdulHussein, using 3D Studio Max.
Return to text

5. My description of metrical sensation here derives from Hasty 1997.
Return to text

6. In Animation 1, the “motion” from one dyad to the other is depicted as occurring towards the end of the first dyad’s duration. This seems intuitively appropriate to me for such slow changes, but my interpretation of it is worded to apply also to a visual representation that spreads the motion out across the entire duration. For a theoretical discussion of how “motion” is perceived between discontinuous musical entities, see Hasty 1981.
Return to text

7. These motions do not visibly represent all the transpositions involved in each change of pitch. For instance, the first “diagonal” bounce is the composite of two T₃s from G to C, then T₅ to F. See also note 8 below.
Return to text

8. The second red ball’s C-to-A change is actually the composite of T₃ from C to E, the transformation indicated by clockwise motion, and T₅ from E to A, which is not represented in the diagram; similarly the third red ball’s F-to-E is actually the composite of T₃ from F to A, the transformation indicated by clockwise motion, and the T₇ from A to E, which is not shown. However, even in a more complete representation of the space, showing the T₅/ T₇ edges, the coordinated motion of the balls through the T₃ edge would still be striking. The combination of the two ic5s, {F,A,C,E}, is a type of tetrachord characteristic of both octatonic and diatonic music.
Return to text

Copyright Statement

Copyright © 2009 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Sean Atkinson, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: