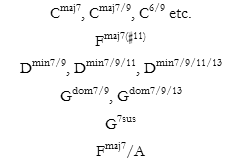Modeling Diatonic, Acoustic, Hexatonic, and Octatonic Harmonies and Progressions in Two- and Three-Dimensional Pitch Spaces; or Jazz Harmony after 1960 (1)
Keith J. Waters and J. Kent Williams
KEYWORDS: Neo-Riemannian, Tonnetz, Hexatonic, Jazz Harmony, Scale, Octatonic, Acoustic, Diatonic, Wayne Shorter, Miles Davis, Ninth Chords, Harmonic Progression, Chord/Scale Theory
ABSTRACT: The paper provides methods for modeling harmonies and harmonic progressions based on diatonic, acoustic, hexatonic, and octatonic collections. It examines these four spaces in relation to jazz harmony, particularly post-1960s jazz compositions in which harmonic function is suppressed or absent. It discusses the opening progression to Wayne Shorter’s composition “Vonetta” (from the 1967 Miles Davis Quintet recording Sorcerer), and ultimately provides a three-dimensional Tonnetz that permits moves among ninth chords, showing them as trapezoidal moves in all four spaces. The article makes use of interactive graphics to illustrate its procedures.
Copyright © 2010 Society for Music Theory
[1.1] Theories of harmony rest on two fundamental questions: 1) What are the objects (i.e., the harmonies) and; 2) What are the relationships among the objects (i.e., harmonic progressions/successions)? The success of recent work in neo-Riemannian theory addresses situations for which the answer to the first question involves standard or syntactic harmonies, but the answer to the second question involves non-standard or non-syntactic progressions (Childs 1998, Cohn 1998a and 1998b, Douthett and Steinbach 1998, Gollin 1998, Hyer 1995). A roughly analogous situation arises for addressing jazz harmonic progressions, particularly for compositions after 1960. Compositions of this period often use standard jazz harmonies, but in progressions that suppress or ignore harmonic function. Yet the analogy is rough because, in general, jazz harmonies employ chordal extensions of sevenths, ninths, elevenths, and/or thirteenths. Further, harmonies in a number of jazz compositions after 1960 also make use of non-syntactic (or non-standard) chords, many of which are derived from the hexatonic collection and use pcset [0148] as a subset.(2)
[1.2] In this paper I continue to examine these issues. I first delimit the harmonies in this repertory as subsets of one of four collections: diatonic, acoustic, octatonic, and hexatonic. I use recent work in neo-Riemannian theory as a springboard to suggest methods to model harmonic succession, and ultimately supply a three-dimensional Tonnetz in order to consider ways in which ninth-chord harmonies from these four underlying collections interact. I use the opening progression of Wayne Shorter’s composition “Vonetta” (recorded in 1967 by the Miles Davis Quintet on the album Sorcerer) as a test case in order to examine progressions of chords derived from different collections. Throughout, the essay uses interactive graphics for modeling these two- and three-dimensional pitch spaces.
Chord Quality
Example 1. Jazz harmonies from Diatonic, Acoustic, Octatonic, and Hexatonic Collections
(click to enlarge and see the rest)
[2.1] Jazz compositions of the 1960s draw primarily from harmonies that are subsets of four fundamental collections: the diatonic, the acoustic (also considered a mode of the ascending melodic minor scale), the octatonic, and the hexatonic.(3) Example 1 indicates some representative jazz harmonies from these four underlying collections. Example 1a shows harmonies derived from the C Diatonic Collection. I refer here to diatonic collections by the letter D and a number that corresponds to the pitch class of the major form of the collection: the label D0 refers to the C major collection, D1 the C![]() /D
/D![]() major collection, etc. The diatonic harmonies include major seventh harmonies (and their extensions), minor seventh harmonies (and their extensions), dominant seventh harmonies (and their diatonic extensions), and others. Example 1b reveals harmonies derived from the F acoustic collection. I refer to acoustic collections by the letter A and a number that corresponds to the pitch class of the final of the acoustic collection: A5 is the F acoustic collection, A6 is the F
major collection, etc. The diatonic harmonies include major seventh harmonies (and their extensions), minor seventh harmonies (and their extensions), dominant seventh harmonies (and their diatonic extensions), and others. Example 1b reveals harmonies derived from the F acoustic collection. I refer to acoustic collections by the letter A and a number that corresponds to the pitch class of the final of the acoustic collection: A5 is the F acoustic collection, A6 is the F![]() acoustic collection, etc. (The F acoustic collection may also be regarded as a mode of the C ascending melodic minor scale.) Common jazz harmonies from this A5 collection include F13(
acoustic collection, etc. (The F acoustic collection may also be regarded as a mode of the C ascending melodic minor scale.) Common jazz harmonies from this A5 collection include F13(![]() 11), CminM7 with extensions, Amin7/9(
11), CminM7 with extensions, Amin7/9(![]() 5), B7(altered), and E
5), B7(altered), and E![]() maj7(
maj7(![]() 5). Many of these acoustic harmonies include pc-set class [0148]: with the A5 collection [0148] consists of the pitch classes of either C, E
5). Many of these acoustic harmonies include pc-set class [0148]: with the A5 collection [0148] consists of the pitch classes of either C, E![]() , G, B, or E
, G, B, or E![]() , G, B, D.
, G, B, D.
[2.2] Example 1c contains chords from the D/E![]() octatonic collection (Oct 2,3), indicating ic3-related dominant and diminished chords. Example 1d contains ic4-related hexatonic chords, primarily minM7 and maj7(
octatonic collection (Oct 2,3), indicating ic3-related dominant and diminished chords. Example 1d contains ic4-related hexatonic chords, primarily minM7 and maj7(![]() 5), which form set-class [0148]. Note that [0148] harmonies also appear as subsets of acoustic collection harmonies. In jazz compositional contexts, however, hexatonic harmonies appear as supersets of [0148], typically [01458]. Many of these hexatonic harmonies are overlooked in jazz pedagogy texts, but are ones I have encountered transcribing or performing this music. Example 1e contains specific examples of [01458] hexatonic harmonies used in specific compositions from the 1960s and early 70s: A
5), which form set-class [0148]. Note that [0148] harmonies also appear as subsets of acoustic collection harmonies. In jazz compositional contexts, however, hexatonic harmonies appear as supersets of [0148], typically [01458]. Many of these hexatonic harmonies are overlooked in jazz pedagogy texts, but are ones I have encountered transcribing or performing this music. Example 1e contains specific examples of [01458] hexatonic harmonies used in specific compositions from the 1960s and early 70s: A![]() maj7(
maj7(![]() 5/
5/![]() 9) (Shorter, “Vonetta”), A
9) (Shorter, “Vonetta”), A![]() maj7(
maj7(![]() 5)/E and EMinMaj 7th/A
5)/E and EMinMaj 7th/A![]() (Corea, “Song of the Wind”), and A
(Corea, “Song of the Wind”), and A![]() maj7(natural 5,
maj7(natural 5, ![]() 5) (Shorter, “Iris”). Such hexatonic harmonies emerged in jazz composition only in the 1960s, and represented new harmonic resources for jazz composers such as Shorter, Corea, Hancock, and others. In sum, the jazz harmonies in works of the 1960s (by composers such as Shorter, Corea, and Hancock) are primarily subsets (or complete statements) of four collections: diatonic, acoustic, octatonic, and hexatonic.
5) (Shorter, “Iris”). Such hexatonic harmonies emerged in jazz composition only in the 1960s, and represented new harmonic resources for jazz composers such as Shorter, Corea, Hancock, and others. In sum, the jazz harmonies in works of the 1960s (by composers such as Shorter, Corea, and Hancock) are primarily subsets (or complete statements) of four collections: diatonic, acoustic, octatonic, and hexatonic.
Chord Progression: Mapping Diatonic and Acoustic Spaces
[3.1] Example 1 relates chord type to underlying collections, and thus provides some explanatory power for understanding chords in isolation. In fact, what I have done is slightly recast the primary focus of jazz pedagogy and theory since at least 1959: the mapping of underlying collections to individual chords in order to suggest methods for improvisation and/or composition.(4) Such discussions do not always say much about principles of chord succession, however, particularly for music of the 1960s whose progressions may avoid or suppress functional harmonic patterns. Further, if collections of 6-8 pitches—particularly the four indicated above—do provide the source sets for post-1960s harmonies, their relationship may be abstract: in practice all members of the underlying collection need not be stated by the harmonic accompanying instruments (or by improvisers). Thus two questions remain: how do we address post-1960s harmonic progressions, and how do we do it in a way that more clearly models harmonic practice? These two questions can lead us past the chord/scale taxonomy of jazz pedagogy to consider harmonies instead as subsets of these collections and examine the ways in which the harmonies connect.
Mapping Hexatonic Harmonies and [0148]
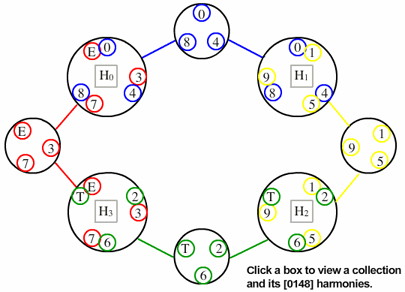
Example 2. [0148] through the Hyper-Hexatonic System (Cohn, 1996)
(click to view animation)
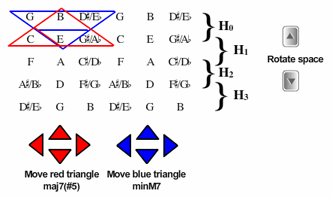
Example 3. [0148] on the [7, 4, 3, E] Tonnetz
(click to view animation)
[4.1] Example 2 starts to address those questions. It indicates the Hyper-Hexatonic System (Cohn 1996). The system labeled H0 has two constituent augmented triads, shown by the blue- and red-circled pc numbers adjacent to H0. The example also shows how any two adjacent H systems share an augmented triad (H0 and H1 share 0, 4, and 8, for example). This example also locates all instances of [0148] within each system. By clicking on the “H0” label, the example displays the three minMaj 7th chords (whose roots are C, E, and ![]()
![]() 5) chords with the same roots. It is worth observing some common-tone relationships that
are obtained between these H0 [0148] harmonies. In comparison with one another, each minMaj 7th harmony preserves three elements and alters one element. Likewise, in comparison with one another, each Maj7(
5) chords with the same roots. It is worth observing some common-tone relationships that
are obtained between these H0 [0148] harmonies. In comparison with one another, each minMaj 7th harmony preserves three elements and alters one element. Likewise, in comparison with one another, each Maj7(![]() 5) harmony preserves three elements and alters one element. In comparing any minMaj 7th with any Maj7(
5) harmony preserves three elements and alters one element. In comparing any minMaj 7th with any Maj7(![]() 5),
two elements are preserved and two are altered. (The interactive example also displays constituent Maj7(
5),
two elements are preserved and two are altered. (The interactive example also displays constituent Maj7(![]() 5) and minMaj 7th harmonies for each of the remaining H systems when accessed.)
5) and minMaj 7th harmonies for each of the remaining H systems when accessed.)
[4.2] Example 3 now models some of those common tone relationships more concretely. It includes a Tonnetz whose upward verticals progress by seven semitones, and whose horizontals progress by four semitones. The Tonnetz descriptor is [7, 4, 3, E] (Morris 1998). All Tonnetze that I use will consist of pitch class letters (rather than numbers), and assume equal temperament and enharmonic equivalence. To the right of the Tonnetz, the overlapping brackets (and designations H0, 1, 2, 3) show that any two adjacent horizontals represent one of the four hexatonic systems. On the left of the Tonnetz are two overlapping triangles. The red triangle indicates the pitch classes of C Maj7(![]() 5), the blue triangle the pitch classes of E minMaj 7th.(5) (Each triangle also contains an additional internal line, setting off the chordal root from its upper structure). The common-tone relationships are made particularly apparent with the example, indicating that the two harmonies share the pitch classes of E and B. The brackets on the right show that both these harmonies are derived from H0, as would any harmony formed by those two adjacent horizontals. By clicking the bottommost arrow directly above the instructions “move blue triangle (minMaj 7th),” the example translates the triangle down, yielding a move to A minMaj 7th. This move shows the preservation of three pitch classes (C, E, and G
5), the blue triangle the pitch classes of E minMaj 7th.(5) (Each triangle also contains an additional internal line, setting off the chordal root from its upper structure). The common-tone relationships are made particularly apparent with the example, indicating that the two harmonies share the pitch classes of E and B. The brackets on the right show that both these harmonies are derived from H0, as would any harmony formed by those two adjacent horizontals. By clicking the bottommost arrow directly above the instructions “move blue triangle (minMaj 7th),” the example translates the triangle down, yielding a move to A minMaj 7th. This move shows the preservation of three pitch classes (C, E, and G![]() ) between the original red triangle (C Maj7(
) between the original red triangle (C Maj7(![]() 5)) and the new blue one; the fourth pitch class inverts around this augmented triad (B inverts to A). The overlapping brackets on the right indicate that these two harmonies come from two different hexatonic systems, the two that share pcs C, E, and G
5)) and the new blue one; the fourth pitch class inverts around this augmented triad (B inverts to A). The overlapping brackets on the right indicate that these two harmonies come from two different hexatonic systems, the two that share pcs C, E, and G![]() . The interactive example allows the blue and red triangles to move vertically and horizontally; “rotate space” moves the Tonnetz through vertical space.
. The interactive example allows the blue and red triangles to move vertically and horizontally; “rotate space” moves the Tonnetz through vertical space.
Mapping Hexatonic and Diatonic Harmonies
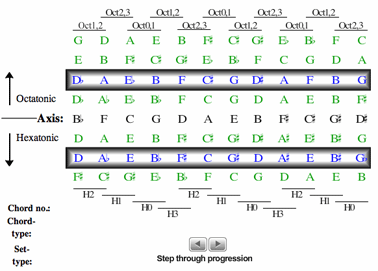
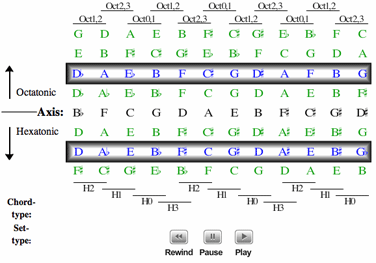
[5.1] So far, we have modeled particular hexatonic harmonies on the Tonnetz. This particular Tonnetz is useful because it also shows relationships between hexatonic and diatonic harmonies. This is the purpose of Example 4, which includes the opening progression
of Wayne Shorter’s composition “Vonetta” (from the Miles Davis Quintet 1967 recording The Sorcerer). Clicking on the right-button arrow traces the progression of the first six chords, from C-9 (diatonic harmony) to A![]() maj7
maj7![]() 5/
5/![]() 9 (hexatonic harmony), then to Amaj9 (diatonic), D
9 (hexatonic harmony), then to Amaj9 (diatonic), D![]() /E
/E![]() -9(
-9(![]() 5) (acoustic), Dmaj9 (diatonic), and D
5) (acoustic), Dmaj9 (diatonic), and D![]() min9 (diatonic). This presentation idealizes all harmonies as ninth chords in order to show harmonic progression more clearly. In practice, of course, chords are often multiply realized, and the chordal instrument often adds or subtracts harmonic extensions. The harmonies indicated here were determined both by Shorter’s copyright deposit (contained at the Library of Congress) as well as a personal transcription of the recording.(6)
min9 (diatonic). This presentation idealizes all harmonies as ninth chords in order to show harmonic progression more clearly. In practice, of course, chords are often multiply realized, and the chordal instrument often adds or subtracts harmonic extensions. The harmonies indicated here were determined both by Shorter’s copyright deposit (contained at the Library of Congress) as well as a personal transcription of the recording.(6)
[5.2] The progression of the six chords seems to resist standard tonal interpretation. The motions through the Tonnetz do show something of the harmonic logic of the progression, however. The first three harmonies show the progression as a series of rotations that preserve at least two pitch classes: Chords 1 to 2 preserve C/G; Chords 2-3 preserve E/B. The Tonnetz graphically depicts the inversional relation between these two diatonic harmonies of Chords 1 and 3 (the relation between Chord 1 [T0237] and Chord 3 [489E1] is TEI). Chord 2, though, is a different set type, and mediates between the two harmonies of C-9 and Amaj9. The disposition of
Chord 2 on this particular Tonnetz tells us several things. Chord 2 relates to
Chords 1 and 3 via two common tones. In addition, Chord 2, or any chord made up of two adjacent horizontals on this particular Tonnetz, is a subset of one of the hexatonic systems. Further, the clockwise rotation of the trapezoid by 90 degrees from
Chord 1 to Chord 2 suggests that the two harmonies are organized according to similar cyclic principles. We can understand Chord 1 (the “Nevada-shaped” chord) as a diatonic-based harmony that contains
two strands of ic5 (C/G/D and E![]() /B
/B![]() ). Two dyads, one from each strand, are in an ic4 relation (G to E
). Two dyads, one from each strand, are in an ic4 relation (G to E![]() = ic4; D to B
= ic4; D to B![]() = ic4). Chord 2 (the “Tennessee-shaped” chord) is a hexatonic-based harmony that contains 2 strands of ic4 (A
= ic4). Chord 2 (the “Tennessee-shaped” chord) is a hexatonic-based harmony that contains 2 strands of ic4 (A![]() /C/E and G/B). Two dyads, one from each strand, are in an ic5 relation (C to G = ic5, E to B = ic5)]. Chord 3 is a diatonic-based harmony (upside-down Nevada). We may consider the preservation of the trapezoid (and of two common tones) in the move between
Chords 1-3 as a contextual operation that relates one set type to a different one, and that moves from diatonic space (Chord 1) to hexatonic space (Chord 2) and back to diatonic space (Chord 3).(7) Thus the Tonnetz models the progression of the first three harmonies, and indicates the communication between diatonic (Nevada-shaped) chords and hexatonic (Tennessee-shaped) chords.
/C/E and G/B). Two dyads, one from each strand, are in an ic5 relation (C to G = ic5, E to B = ic5)]. Chord 3 is a diatonic-based harmony (upside-down Nevada). We may consider the preservation of the trapezoid (and of two common tones) in the move between
Chords 1-3 as a contextual operation that relates one set type to a different one, and that moves from diatonic space (Chord 1) to hexatonic space (Chord 2) and back to diatonic space (Chord 3).(7) Thus the Tonnetz models the progression of the first three harmonies, and indicates the communication between diatonic (Nevada-shaped) chords and hexatonic (Tennessee-shaped) chords.
[5.3] The Tonnetz also models the progression from Chords 5 to 6, which comes about by rotation. The move from
Chords 5 to 6 preserves the pitch classes C![]() /D
/D![]() and E/F
and E/F![]() , and the reflection is inversionally symmetrical around those two pitch classes (mapping
Chord 5 to 6 at T5I). Both Chords 5 and 6 are diatonically-based. (We may also note that the composite of these two individually diatonic harmonies creates the diatonic octad, or begins to access what one writer refers to as “Dasian” space. Martins 2003 and 2006.)
, and the reflection is inversionally symmetrical around those two pitch classes (mapping
Chord 5 to 6 at T5I). Both Chords 5 and 6 are diatonically-based. (We may also note that the composite of these two individually diatonic harmonies creates the diatonic octad, or begins to access what one writer refers to as “Dasian” space. Martins 2003 and 2006.)
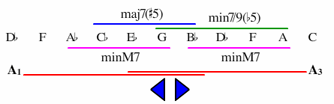
[5.4] However, Chord 4, represented by the dotted line, does not reflect the same construction on this Tonnetz as
Chords 1, 2, 3, 5, and 6. Chord 4 contains pcset [0148] (G![]() , B
, B![]()
![]() , D
, D![]() , F), but its root (E
, F), but its root (E![]() /D
/D![]() ) means that this harmony is not hexatonic, but based on the acoustic collection. This 7/4 Tonnetz models diatonic and hexatonic-based ninth chords analogously as trapezoids, but not acoustic collection-based ninth chords such as Chord 4. We will return to
Chord 4 eventually, after considering the acoustic collection and its harmonies more generally.
) means that this harmony is not hexatonic, but based on the acoustic collection. This 7/4 Tonnetz models diatonic and hexatonic-based ninth chords analogously as trapezoids, but not acoustic collection-based ninth chords such as Chord 4. We will return to
Chord 4 eventually, after considering the acoustic collection and its harmonies more generally.
The Hyper-Acoustic System
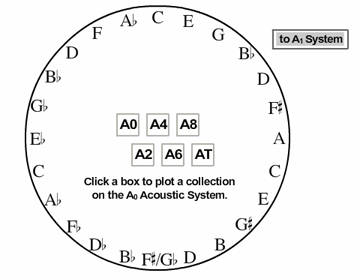
Example 5a. A0 and A1 Acoustic Systems
(click to view animation)
Example 6. Maj7(![]() 5), minMaj 7th, and Chord 4 of “Vonetta” on A1
5), minMaj 7th, and Chord 4 of “Vonetta” on A1
(click to view animation)
Example 7. Hyper-Acoustic System and Chord 4 of “Vonetta”
(click to view animation)
[6.1] Among any two representatives of the acoustic collection, there can only be a maximum of five common tones, and this relation occurs only with acoustic collections that are two semitones apart. That particular property allows us to represent all the acoustic collections in two separate networks. Example 5a displays initially what I call the A0 acoustic system, consisting of all the even-numbered acoustic collections and contained within a circular strand of thirds. A click on the interior boxes, labeled as A0, A2, A4, etc., enables the display of the pitch classes of each acoustic collection.(8) Accessing the “to A1 system” yields the cyclic third configuration of the odd-numbered acoustic collections.
|
Example 5b. A0 Acoustic System (= A0, 2, 4, 6, 8, T) (click to view animation) |
Example 5c. A1 Acoustic System (= A1, 3, 5, 7, 9, E) (click to view animation) |
[6.2] Examples 5b and 5c show the same A0 and A1 systems but they are now organized in a linear fashion; the red and blue arrow buttons will advance (or retard) each set of acoustic collections. Such a representation helps us see the harmonic possibilities of the acoustic collection as adjacent members along either of the cyclic strands. Any individual seven-note acoustic collection (A0, A2, for example) arranged in thirds forms the common jazz harmony of a dominant-thirteenth chord with a raised eleventh. We can also locate other acoustic harmonies consisting of seven-note strands (thirteenth chords) or subsets (forming seventh, ninth, and eleventh chords). Example 6 contains the A1 system, and it indicates constituent minMaj 7th chords with
the lilac-colored line, and Maj7(![]() 5) with the blue line. The green line shows a half-diminished ninth chord, min7/9(
5) with the blue line. The green line shows a half-diminished ninth chord, min7/9(![]() 5), and using the blue arrow to advance to the A9 and A11 segment will yield Chord 4 of “Vonetta”: D
5), and using the blue arrow to advance to the A9 and A11 segment will yield Chord 4 of “Vonetta”: D![]() , F
, F![]() , A, C
, A, C![]() , and F. All the individual harmonies placed in Example 6 might suggest that we can move these lines like a slide rule and obtain constituent A1 system harmonies. However, there seems to be no communication between A0 and A1. These two systems are configured as mutually exclusive.
, and F. All the individual harmonies placed in Example 6 might suggest that we can move these lines like a slide rule and obtain constituent A1 system harmonies. However, there seems to be no communication between A0 and A1. These two systems are configured as mutually exclusive.
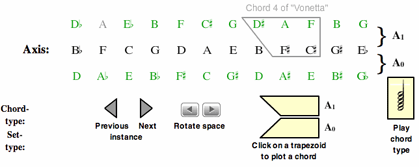
[6.3] Can we understand any degree of communication between A0 and A1? Example 7 addresses this by a representation that I’ve indicated as the “Hyper-Acoustic” system. Note that this Example 7 takes into account both A0 and A1 systems, indicated by brackets on the right. These brackets show that the A1 system is formed by the upper two rows, while the A0 system is formed by the lower two rows. The central axis contains ic5 cycles, moving left to right as interval 7 (shown in bold). The upper row moves in alternation of intervals 8 and 6.(9) To locate the third-based harmonies of A1, you may begin on the uppermost line, move southeast to the center, then vertically back to the upper row. The central axis and the lower horizontal row establish A0. Again, the central axis consists of interval 7 cycles, and the lower row alternates interval 6 and 8 cycles. To locate the third-based harmonies of A0, one may move northeast from the lower row to the center, then vertically back to the lower line.
[6.4] Clicking on a trapezoid button of Example 7 displays these acoustic collection harmonies as ninth chord trapezoids, and suggests moves among and between both A0 and A1 systems by
reflecting (“Click on a trapezoid”) and translating (“Previous/Next Instance”)
the trapezoids. A representative of each chord type may be heard by clicking “Play Chord Type,” while the “Rotate Space” buttons advance the pitch collections horizontally.
Example 7 also indicates Chord 4 of “Vonetta” (D![]() /E
/E![]() min9(
min9(![]() 5)).
5)).
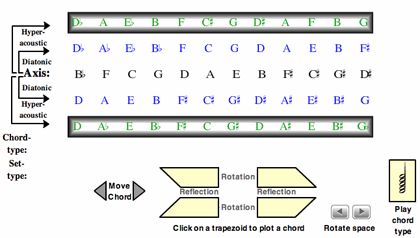
[6.5] This Hyper-Acoustic System only allows us to consider acoustic collection harmonies in isolation, of course, and I am unaware of any jazz compositions that use acoustic collection harmonies exclusively. Thus the question remains of how to place these acoustic collections in a broader context. Can these acoustic-based harmonies (or at least their ninth-chord trapezoids) interact with harmonies from other collections? I show that they can in several stages. The first stage concatenates diatonic and acoustic space in a three-dimensional Tonnetz, the following stage then expands this space into one that also allows octatonic and hexatonic harmonies.
Mapping Diatonic and Acoustic Harmonies: A Three-Dimensional Tonnetz
Example 8. Three-dimensional tonal map (Diatonic and Acoustic Systems): Diatonic Harmonies
(click to view animation)
[7.1] Example 8 shows the first stage, which adds an additional element to the Hyper-Acoustic system. The central axis remains, consisting of interval 7 cycles. The rows directly above and below the axis are likewise formed of interval 7 cycles. The axis row and a row either directly above or below will allow the representation of trapezoidal diatonic harmonies. The axis row and the outer horizontal rows form the hyper-acoustic system.
[7.2] At the instructions “Click on a trapezoid to plot a chord” are four trapezoid buttons. A click on the upper-right trapezoid supplies on the tonal map a minor-ninth chord trapezoid. A click on the lower right trapezoid supplies on the tonal map a major ninth trapezoid. These ninth chord trapezoids access diatonic harmonies that alternate ic3 and ic4. By configuring diatonic space in this fashion, it is then possible to consider contextual moves as rotations, reflections, or translations of a trapezoid on this map. Thus the min7/9 and maj7/9 harmonies just described indicate the Riemannian Parallel (P) operation with ninth chords, shown here as a reflection across the axis.(10) Here the two reflected harmonies preserve three elements. Further, the root of the min7/9 and maj7/9 chords remains invariant.
[7.3] A click on the upper leftside trapezoid button likewise provides a maj7/9 harmony. It arises as a rotation of the upper rightside trapezoid. A click on the lower leftside trapezoid reflects that maj7/9 harmony across the axis, supplying a min7/9 harmony. Note that the reflection that arises with these two leftside trapezoids preserves two of the five elements. Further, the root of the two reflected harmonies changes. In comparison with the Parallel (P) operation with the rightside trapezoids, we may indicate this relationship as P’ (Morris 1998). The arrows labeled “move chord” translate the trapezoids. Further, the pitch space can be advanced horizontally (“rotate space”), and instances of each harmony can be heard (“play chord type”).
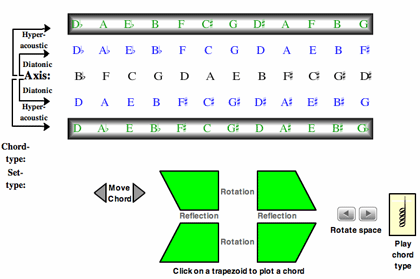
Example 9. Three-dimensional tonal map (Diatonic and Acoustic Systems): Acoustic Harmonies
(click to view animation)
[7.4] Example 8 uses the central axis and an adjacent row to configure diatonic harmonies. It also contains outer rows that, together with the central axis, form the Hyper-Acoustic system. This confects a potential three-dimensional Tonnetz. With this, the central axis forms diatonic trapezoids with the adjacent rows, and acoustic trapezoids that bypass the adjacent rows and connect with the outer rows. Example 9 shows more clearly its three-dimensional configuration. Thus, even while the axis and the two outer rows are not contiguous in two-dimensional space, they may be considered contiguous in three-dimensional space.
[7.5] At Example 9’s instructions “Click on a trapezoid to plot a chord” are four trapezoid buttons. A click on the upper right trapezoid plots on the tonal map a minM7/9 harmony, derived from A1. A click on the lower right trapezoid elicits a dom7/9 chord, derived from A0. By configuring acoustic space in this fashion, it is then possible to consider contextual moves as rotations, reflections, or translations of a trapezoid on this map. Thus the minM7/9 and dom7/9 harmonies just described indicate the Riemannian Parallel (P) operation with ninth chords, shown here as a reflection across the axis. Here the two reflected harmonies preserve three elements. Further, the root of the min7/9 and maj7/9 chords remains invariant.
[7.6] A click on the upper leftside trapezoid button plots a maj7/9(![]() 5) harmony. It arises as a rotation of the upper rightside trapezoid. A click on the lower leftside trapezoid reflects the maj7/9(
5) harmony. It arises as a rotation of the upper rightside trapezoid. A click on the lower leftside trapezoid reflects the maj7/9(![]() 5) harmony across the axis, supplying a min7/9(
5) harmony across the axis, supplying a min7/9(![]() 5) harmony. The reflection that arises with these two leftside trapezoids preserves two of the five elements. Further, the root of the two reflected harmonies is not consistent. In comparison with the Parallel (P) operation with the rightside trapezoids, we may indicate this relationship as P’ (Morris 1998). As in Example 8, the arrows labeled “move chord” translate the trapezoids; the pitch space can be advanced horizontally (“rotate space”); and instances of each chord type can be heard (“play chord type”).
5) harmony. The reflection that arises with these two leftside trapezoids preserves two of the five elements. Further, the root of the two reflected harmonies is not consistent. In comparison with the Parallel (P) operation with the rightside trapezoids, we may indicate this relationship as P’ (Morris 1998). As in Example 8, the arrows labeled “move chord” translate the trapezoids; the pitch space can be advanced horizontally (“rotate space”); and instances of each chord type can be heard (“play chord type”).
Mapping Diatonic, Acoustic, Hexatonic, and Octatonic Harmonies in a Three-Dimensional Tonal Map
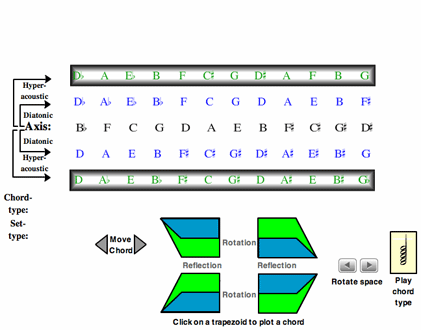
Example 10. Three-dimensional tonal map: Diatonic and Acoustic Harmonies
(click to view animation)
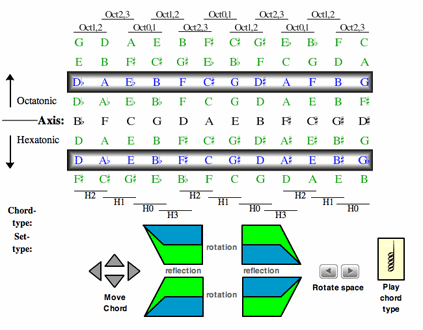
Example 11a. Three-dimensional tonal map (Diatonic/Acoustic/Hexatonic/Octatonic Systems)
(click to view animation)
[8.1] Example 10 allows a dialogue between diatonic and acoustic harmonies. At the instructions “Click on a trapezoid to plot a chord” are four variegated trapezoids. A click on the right uppermost blue trapezoid forms a diatonic minor ninth (min7/9) harmony. A click on the right uppermost green trapezoid forms an acoustic-based minor ninth harmony (minM7/9). This creates a hinge motion that swings from diatonic (blue and two-dimensional) into acoustic (green and three-dimensional) space. This three-dimensional space suggests ways that acoustic and diatonic harmonies might relate. The interactive nature of the example allows translations, rotations, and reflections of the ninth chord trapezoids to further form dom7/9, min7/9(![]() 5), maj7/9, and maj7/9(
5), maj7/9, and maj7/9(![]() 5) harmonies. The instructions “advance space,” “move chord,” and “play chord type” operate in analogous fashion to the previous examples. The example indicates the dialogue between diatonic and acoustic spaces, still requiring the participation of octatonic and hexatonic ones.
5) harmonies. The instructions “advance space,” “move chord,” and “play chord type” operate in analogous fashion to the previous examples. The example indicates the dialogue between diatonic and acoustic spaces, still requiring the participation of octatonic and hexatonic ones.
[8.2] This is the goal of Example 11a, which vertically expands the previous examples. It continues the motion of interval cycles both upward and downward, indicated by the green pitch-class letters. From the central axis, the columns progress upwards in ic3 cycles in two-dimensional space. From the central axis, the columns progress downward in ic4 cycles in two-dimensional space. Thus below the axis, harmonies constructed of two contiguous columns represent one of the four hexatonic collections. Above the axis, harmonies constructed of two contiguous columns represent one of the three octatonic collections. This map thus suggests moves between the four collectional spaces identified at the outset: diatonic, acoustic, hexatonic, and octatonic. We can imagine, then, motion between harmonies as shifting between and within these four spaces. For ninth-chord representations, this will consist of trapezoidal moves.
[8.3] As Example 11b indicates, that is precisely how the opening progression to “Vonetta” operates. Again, we can locate the opening three harmonies (numbered 1-3) as trapezoidal moves from diatonic to hexatonic space, then back to diatonic, through operations of rotation then reflection. We were unable to account for Chord 4 earlier (E![]() min9(
min9(![]() 5)), a subset of the acoustic collection, but now Chord 4 appears in three-dimensional space. Moreover, the connection of Chord 4 to Chord 5 is now explicit: the progression to the following Dmaj9 consists of a hinge motion, moving from acoustic space to diatonic space. The move from Chords 5 to 6 rotates the trapezoid. The mapping of these harmonies shows the six chords progressing in triples: Chords 1-3 involve contiguous moves, as do Chords 4-6. Example 11c plays and proceeds directly through the six chords.
5)), a subset of the acoustic collection, but now Chord 4 appears in three-dimensional space. Moreover, the connection of Chord 4 to Chord 5 is now explicit: the progression to the following Dmaj9 consists of a hinge motion, moving from acoustic space to diatonic space. The move from Chords 5 to 6 rotates the trapezoid. The mapping of these harmonies shows the six chords progressing in triples: Chords 1-3 involve contiguous moves, as do Chords 4-6. Example 11c plays and proceeds directly through the six chords.
Conclusion
[9.1] This three-dimensional map is a modified Tonnetz that allows connections between constituent harmonies of all four collections, and suggests that a series of operations can map all ninth chords onto one another by processes of rotation, translation, and reflection, as well as hinge motions that move the trapezoids in and out of three-dimensional space. My purpose here is not to show specific contextual operations or groups of operations, but rather to provide a space in which ninth chords of these four collections may map into one another. Note that within this tonal map, the space is circular in the horizontal dimension: it wraps around from right-to-left, as do equal-tempered Tonnetze. However, the vertical space is not circular: unlike traditional toroidal (equal-tempered) Tonnetze, it does not wrap from top to bottom.
[9.2] It is possible to continue the vertical motion outward. For example, the upper leftmost vertical pitches consist of E and G. This allows the possibility of E’s row to form a new axis, creating diatonic space between that row and the one directly above formed by G’s row. This then could allow an acoustic collection “stripe” directly above G’s horizontal. Such a move duplicates the tonal space found in the given axis of Example 11b, begun from the E six steps to the right of the B![]() that forms the leftmost member of the axis. Thus the structure of the map has a symmetry that produces invariance on such actions.
that forms the leftmost member of the axis. Thus the structure of the map has a symmetry that produces invariance on such actions.
[9.3] Further examination might suggest that not all 1960s repertories consist of similar moves on this three-dimensional Tonnetz, but may reveal consistencies within compositions or among different works of the same composer. The discussion here also does not engage the problem of octatonic harmonies, which are structurally inconsistent with diatonic, acoustic, and hexatonic harmonies. In jazz, octatonic harmonies typically operate as dominant-functioning chords, and therefore would be less likely to be modeled as trapezoidal ninth chords in the same fashion as are diatonic, acoustic, and hexatonic harmonies. General issues of voice-leading parsimony are not relevant to ninth chord representations in the same way that they are to P, L, and R triadic transformations on a neo-Riemannian Tonnetz. Further, this three-dimensional Tonnetz shares some of the same limitations of the more standard Tonnetz, which does not comfortably model moves between chords of different cardinality, and idealizes harmonies consistently as stacks of thirds.
[9.4] Such a three-dimensional Tonnetz begins to account not only for the more standard harmonies already in practice by 1960, those derived from diatonic, acoustic, and octatonic collections, but also addresses the newer hexatonic harmonic resources that emerged during the decade. It provides the playing field on which we may observe the progressions of these harmonies in jazz composition. While standard jazz pedagogy likewise regards these four collections, its focus remains on relating harmonies to entire collections on a chord-by-chord basis (Levine 1995, Miller 1996). In contrast, this model addresses ninth chord subsets of these collections, and models more directly the ways in which these harmonies progress. The above discussion is intended to show a degree of underlying coherence to these chord progressions, and to move beyond local chord/scale taxonomy. If the objects—the chords—are largely standard and syntactic, their connections—the harmonic progressions—are what makes much post-1960s jazz composition tantalizingly resistant to analysis.
Keith Waters
University of Colorado at Boulder
Campus Box 301
Boulder, CO 80302
Keith.Waters@colorado.edu
J. Kent Williams
University of North Carolina at Greensboro
School of Music
P.O. Box 26170
Greensboro, NC 27402-6170
jkwillia@uncg.edu
Works Cited
Aebersold, Jamey. 1975. A New Approach to Jazz Improvisation. New Albany, Indiana: Aebersold.
Baker, David. 1969. Jazz Improvisation. Chicago: Maher Publications.
—————. 1974. Advanced Improvisation. Chicago: Maher Publications.
Brown, Stephen C. 2003. “Dual Interval Space in Twentieth-Century Music.” Music Theory Spectrum 25/1: 35-58.
Childs, Adrian. 1998. “Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42/2: 181-194.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Stystems, and Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15/1: 9-40.
—————. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations.” Journal of Music Theory 41/1: 1-66.
—————. 1998a. “Introduction to Neo-Riemannian Theory: A Survey and Historical Perspective.” Journal of Music Theory 42/2: 167-180.
—————. 1998b. “Square Dances With Cubes.” Journal of Music Theory 42/2: 283-296.
Coker, Jerry. 1964. Improvising Jazz. Englewood Cliffs, New Jersey: Prentice-Hall.
Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42/2: 241-264.
Gollin, Edward. 1998. “Some Aspects of Three-Dimensional Tonnetze.” Journal of Music Theory 42/2: 195-206.
—————. 2007. “Multi-Aggregate Cycles and Multi-Aggregate Serial Techniques in the Music of Béla Bartók.” Music Theory Spectrum 29/2: 143-176.
Haerle, Dan. 1975. Scales for Jazz Improvisation. Lebanon, Indiana: Studio P/R.
Hyer, Brian. 1995. “Reimag(in)ing Riemann.” Journal of Music Theory 39/1: 101-138.
Julien, Patricia A. 2003. “The Structural Function of Harmonic Relations in Wayne Shorter’s Early Compositions: 1953-1963.” Ph.D. Diss., University of Maryland.
Keller, Gary. 2002. The Jazz Chord/Scale Handbook. Rottenburg, Germany: Advance Music.
Lawn, Richard, and Jeffrey Helmer. 1993. Jazz Theory and Practice. Belmont, California: Wadsworth.
Levine, Mark. 1995. The Jazz Theory Book. Petaluma, California: Sher Music.
Lewin, David. 2002. “Thoughts on Klumpenhouwer Networks and Perle-Lansky Cycles.” Music Theory Spectrum 24/2: 196-230.
—————. 2005. “Some Thoughts About Aspects of Harmony in Mahler’s Symphonies,” essay in Music and the Aesthetics of Modernism, ed. Karol Berger and Anthony Newcomb. Cambridge: Harvard University Press.
Martins, José António. 2003. “Bartók’s Polymodal Chromaticism and the Dasian System.” Paper given at SMT-Madison Wisconsin.
—————. 2006. “Dasian, Guidonian, and Affinity Spaces in Twentieth-Century Music.” Ph.D. Diss., University of Chicago.
Miller, Ron. 1996. Modal Jazz: Composition and Harmony. Rottenburg, Germany: Advance Music.
Morris, Robert. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20/2: 175-208.
Pressing, Jeff. 1978. “Towards an Understanding of Scales in Jazz.” Jazz Research 9: 25-35.
Russell, George. 1959. The Lydian Chromatic Concept of Tonal Organization, 2nd ed. New York: Concept Publishing.
Strunk, Steven. 2000. “Analytical Approaches to Chick Corea’s Compositions of the 1960s.” Paper given at European Music Analysis Conference, Oxford, England.
—————. 2003. “Wayne Shorter’s Yes and No: An Analysis.” Tijdschrift voor Muziektheorie 8/1: 40-56.
—————. 2005. “Notes on Harmony in Wayne Shorter’s Composition, 1964-67.” Journal of Music Theory 49/2: 301-332.
Tymoczko, Dmitri. 1997. “The Consecutive Semitone Restraint: A Link Between Impressionism and Jazz.” Intégral 11: 135-179.
—————. 2004. “Scale Networks and Debussy.” Journal of Music Theory 48/2: 219-294.
Waters, Keith. 2005. “Modes, Scales, Functional Harmony and Non-Functional Harmony in the Compositions of Herbie Hancock.” Journal of Music Theory 49/2: 333-357.
Waters, Keith, and David Diamond. 2000-2001. “Out Front: The Art of Booker Little.” Annual Review of Jazz Studies 11: 1-38.
Footnotes
1. This paper was originally presented at the SMT national conference in Seattle 2004. I would like to acknowledge input and suggestions from several theorists, including Dave Headlam, Steve Larson, Justin Lundberg, and Steven Strunk. The article’s text was authored by Keith Waters and the interactive examples were created by Kent Williams
Return to text
2. Recent analytical work examines harmony and harmonic progression in such 1960s compositions by composers including Wayne Shorter, Chick Corea, Herbie Hancock, Booker Little, and others (Julien 2003; Strunk 2000, 2003, and 2005; Waters 2005, Waters and Diamond 2000–2001).
Return to text
3. In comparison with the four collections listed here, Levine 1995 excludes hexatonic, but includes whole tone. By 1960, however, the use of the whole tone collection seemed to recede, although there are exceptions: Wayne Shorter’s 1964 “Juju,” for example, opens with a whole-tone based sonority (Strunk 2005, 319).
Return to text
4. Abersold 1975, Baker 1969 and 1974, Coker 1964, Haerle 1975, Keller 2002, Levine 1995, Miller 1996, Russell 1959. For music theoretical considerations of scalar organization in jazz, see Pressing 1978, Tymoczko 1997 and 2004, Waters 2005.)
Return to text
5. Strunk 2000 and 2003 represent 7th and 9th chords on Tonnetze and define operations of rotation, reflection, and translation.
Return to text
6. Library of Congress Copyright Deposit Eu 42291 (March 13, 1968). Shorter’s copyright deposit lead sheet of “Vonetta” consists of a 14-bar composition in 4/4, with measure 12 a 5/4 bar. Although Shorter’s lead sheet indicates the opening chord as Emaj7(![]() 5), the group more consistently plays that measure as Cminor9. Pianist Herbie Hancock does state a version of that E harmony (usually played as Emaj7
5), the group more consistently plays that measure as Cminor9. Pianist Herbie Hancock does state a version of that E harmony (usually played as Emaj7![]() 5) in m. 1 (mid-measure) three times: during the opening head, during Davis’s second improvised chorus, and during his own first improvised chorus.
5) in m. 1 (mid-measure) three times: during the opening head, during Davis’s second improvised chorus, and during his own first improvised chorus.
Return to text
7. Brown generalizes this process as “interval exchange” in Brown 2003.
Return to text
8. The two larger systems that subsume all even or odd numbered acoustic collections are represented by “A” and a subscript zero or one (A0, A1). Individual seven-note acoustic collections are represented by “A” and a non-subscript pitch class number (A0, A2, A4, etc.)
Return to text
9. Lewin 2005 and Gollin 2007 consider such double interval cycles in other contexts
Return to text
10. Although not shown here, it is also possible to show the R and L relations with 9th chords on this map. Strunk 2003 examines these standard Riemannian moves with 9th chords on a Tonnetz.
Return to text
Copyright Statement
Copyright © 2010 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sean Atkinson, Editorial Assistant
Number of visits: