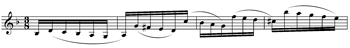Stream Segregation and Perceived Syncopation: Analyzing the Rhythmic Effects of Implied Polyphony in Bach’s Unaccompanied String Works
Stacey Davis
KEYWORDS: Bach, implied polyphony, rhythm, perception
ABSTRACT: Many movements from Bach’s unaccompanied string works contain implied polyphony. Although earlier approaches describe this technique as a way of using arpeggiation to embellish a melodic line, disguise an otherwise unacceptable melodic progression, delay the resolution of dissonance, or create underlying voice-leading patterns, these descriptions cannot account for the variety and complexity of the implied polyphony in these pieces. This paper presents an additional analytical approach that uses research on auditory stream segregation and phenomenal accents to determine transitions between implied voices. Based on this type of analysis, it is proposed that Bach did not treat implied polyphony as solely a melodic feature. He instead used implied polyphony to apply irregular accent patterns to the isochronous surface of the music, thereby creating perceived rhythmic variety at the fastest levels of the metric hierarchy.
Copyright © 2011 Society for Music Theory
[1] In contemplating Bach’s works for solo cello, Pablo Casals remarked, “It is fantastic to think that with one note after the other there can be melody, the central voices and the bass all together. A wonderful polyphony—and this is an invention of Bach. We have to give the proper expression to each voice” (Blum 1977, 143–144). And in reference to Bach’s works for solo violin, Jaap Schroeder observed, “We should also realize that Bach often writes a single melodic line that has polyphonic implications which should be brought out in performance . . . Bach and Telemann knew that a single melodic line, as well as two juxtaposed melodic lines, could suggest polyphony and would be perceived as such by the listener if the player were skillful” (Schroeder 1977, 10–12).(1) The compositional technique to which they refer is typically called implied polyphony, compound melody, polyphonic melody, or pseudopolyphony. It is the perception of multiple voices or melodic lines within a strictly monophonic texture.
[2] Most existing analytical approaches focus on identifying the underlying voice-leading patterns that are created by implied polyphony, both within and between implied voices. Fewer studies combine this analysis with an investigation of the degree to which these implied voices are perceived by listeners and emphasized by performers. After a brief survey of previous approaches, this paper presents an additional way to analyze implied polyphony and hear these pieces. Rather than focusing solely on harmony or voice-leading, this analysis is based on perceptual principles of auditory stream segregation and generates alternate interpretations of the number of implied voices and the content of each voice. This approach draws attention to the rhythmic effects of implied polyphony by highlighting how transitions from one implied voice to another create phenomenal accents that might otherwise not be present. In many instances, these implied voice changes generate a sense of syncopation by creating groupings of attacks at the fastest level of the metric hierarchy that are contrary to the accent patterns of the notated meter. This preserves a fundamental characteristic of Bach’s metric structure that could be lost if the music is perceived as unrelentingly monophonic and isochronous.
Earlier Approaches to Implied Polyphony
[3] In the seventeenth and eighteenth centuries, implied polyphony was most often described as a way to transform a multi-voiced harmonic progression into a single melodic line through the use of arpeggiation. Among the many possible roots of this practice was the Baroque style brisé (“broken style”), a technique that lute players often used to adapt the improvisatory style of thoroughbass accompaniment to their own solo instrumental repertoire. Since a lute is not capable of performing sustained tones, arpeggiation provided a way to play chordal passages that still had a sense of voice-leading. Performers of other instruments soon adopted this stylized form of arpeggiation, with the well-known Prelude in C Major from Book I of Bach’s Das wohltemperierte Clavier providing a clear example of how a Baroque composer would write out the arpeggiations of a simple harmonic progression for performance on a keyboard instrument.
[4] Various eighteenth-century theoretical treatises reflect a similar approach to explaining implied polyphony. Johann Mattheson (1739) called this technique the “theory of broken chords” and devoted an entire chapter of Der volkommene Capellmeister to illustrating the different ways that arpeggiation can be used to represent various polyphonic textures. To Mattheson, “breaking” meant that “the pitches are not perceived together all at once but one after another” (Harris 1981, 670). This technique was therefore a way of reducing the total number of voices while still retaining the full harmonic content. Johann Philipp Kirnberger (1774) discussed “Embellished or Florid Simple Counterpoint” in the eleventh chapter of Die Kunst des reinen Satzes in der Musik and demonstrated how arpeggiation could be used to transform various multi-part pieces into monophonic melodies.
[5] Kirnberger also referred to implied polyphony in his discussion of how to treat augmented and diminished intervals and thereby avoid “unacceptable” melodic progressions. As one method of disguising these intervals, Kirnberger stated that “when a single-line melody is composed in such a way that its harmony is implied and sounds like a two- or three-part piece, the forbidden progressions no longer sound bad” (Beach and Thym 1982, 156). Johann David Heinichen (1728) shared a similar perspective and “acknowledges implied voices as a way of explaining unconventional leaps to dissonances as well as delayed resolution of dissonances” (Rothfarb 1988, 103). For instance, it is typical to follow a suspended note with its immediate resolution. Heinichen considered delayed resolutions of suspensions to be acceptable if the intervening pitches provide variations that postpone the moment of resolution. Since these variations sometimes contain large interval separations, they often create a texture where the notes of suspension and resolution belong to one implied voice and the intervening pitches belong to another. Ornamenting a dissonance prior to its resolution could therefore create a sense of implied polyphony.
[6] Two twentieth century theorists, Heinrich Schenker and Ernst Kurth, also wrote extensively about implied polyphony. Although there are fundamental differences in their approaches, both Schenker and Kurth were essentially searching for linear progressions that are not explicitly stated at the foreground of the music. But these progressions did not necessarily represent the same thing, nor did they always possess the same characteristics. According to Schenker’s theory, implied polyphony is associated with the basic principles of arpeggiation, diminution, and voice-leading. As Forte and Gilbert described, “Whereas the arpeggiation is the projection of a single voice through the notes of a consonant triad, compound melody involves arpeggiation and partial arpeggiation in the more elaborate sense . . . as conveyors of two or more voices over a longer span of music” (1982, 67–68). Kurth, on the other hand, suggested that these underlying linear progressions are implied or apparent voices (“Scheinstimme”) that are created by “manifest characteristics of linear contour and their psycho-auditive ramifications” (Rothfarb 1988, 37).(2) This reflects Kurth’s interest in psychology and his insistence that polyphonic melody is a linear (or melodic) feature, rather than a solely harmonic one. As he stated, “The line did not emerge from primary, latent harmonic formation, but rather, conversely, embodies in its form the harmonic factors out of which grows harmonic meaning in developed musical consciousness” (Rothfarb 1988, 79). In his writings on this topic, Kurth used multiple examples from Bach’s solo string works to demonstrate how registral prominence, harmonic dissonance, melodic dissonance, and directional interruption are used to create a sense of polyphonic melody. Unlike Schenker’s voice-leading reductions, Kurth’s apparent voices occur in both ascending and descending patterns and sometimes contain intervals greater than a second. In addition, Kurth made no attempt to present any systematic method for determining the content of these Scheinstimme.
A Perceptual Approach to Analyzing Implied Polyphony
[7] Many instances of implied polyphony in Bach’s unaccompanied string pieces can be explained by these principles of arpeggiation, delayed dissonance resolution, and voice-leading. However, while arpeggiation may be a straightforward procedure when the number of voices remains fixed and when all voices sound continuously, most instances of Bach’s implied polyphony contain an ambiguous or changing number of voices. Implied voices seem to emerge and then vanish, a circumstance that is not easily derived from arpeggiation techniques alone. Likewise, a lack of voice continuity can present challenges for following the content of each implied voice over the course of an entire piece. It is therefore proposed that an analysis of arpeggiation and voice-leading be supplemented with an analysis of listening and perception. This perceptual approach was influenced by research on auditory stream segregation, which aims to identify the characteristics of sound that might cause a monophonic tone sequence to be perceived in multiple streams. Emphasis is therefore shifted back toward the original monophonic sequence and away from a reduction that reflects an imagined substrate of fully contrapuntal, previously composed material.
[8] The fundamental principles of auditory stream segregation can be viewed as modern formulations of the laws of Gestalt psychology (particularly the law of proximity). According to this body of research, the tendency for certain monophonic tone sequences to split into multiple perceptual streams is a function of the auditory system, with segregation being most powerfully affected by the frequency separation between tones in a sequence (interval size) and the rate of presentation of tones in that sequence (tempo). In general, a monophonic sequence is most likely to split into separate perceptual streams when it contains large intervals and is played at rapid tempos.(3)
[9] From a theoretical approach, the large intervals that are crucial to stream segregation give emphasis to specific pitches and create examples of what Lerdahl and Jackendoff (1983) call phenomenal accents. These phenomenal accents play a role in delineating both grouping and metric structure. For instance, Lerdahl and Jackendoff’s third grouping preference rule states that the transition between two notes will be heard as a grouping boundary if its interval is larger than those that both precede and follow it. Music cognition research has also contributed information about the perception of melodic accents. Boltz and Jones (1986) proposed that changes in interval size and contour create melodic accents, with the accent being placed on the pitch that follows the change. When these changes occur at regularly spaced intervals of time, melodies are perceived to be simpler and easier to remember. In contrast, unexpected or temporally irregular changes create melodic complexity and become “psychologically important because they mark deviations in a pattern’s context and thus capture a listener’s attention” (Boltz and Jones 1986, 407).
[10] Although Boltz and Jones made no specific mention of implied polyphony in their study, they still focused on the two structural features that play the most important role in its creation. If the combination of large intervals and changes of contour creates a sense of melodic accent, then implied polyphony also creates a sense of melodic accent (since stream segregation is caused by the same two structural features). The accents created by changes from one implied voice to another activate the isochronous, monophonic musical texture and create meaningful rhythmic activity at the fastest level of the metric hierarchy. The fact that Bach avoids placing these changes at regularly spaced intervals of time contributes to the increased complexity of these melodies, as well as to their potential to “capture a listener’s attention.”
[11] This approach to explaining the rhythmic effects of implied polyphony coincides with Carl Schachter’s (1976) definition of “tonal rhythms.” In an essay intended mostly as a defense against the claim that Schenkerian theory neglected the analysis of rhythm, Schachter described rhythm as having two main components—tonal rhythms and durational rhythms. Tonal rhythms are those that “flow from the succession and combination of tones, for the tonal system itself has rhythmic properties” (313). With this definition, Schachter is referring to the rhythmic patterns that can be created by tonal (or pitch-related) elements such as “the recurrence of a tone after one or more different ones, the octave relationship, chordal and linear associations, consonance and dissonance” (313). Durational rhythms, on the other hand, are those created by actual variations in duration and grouping, without any respect to the specific pitches that are used.
[12] Schachter subsequently stated that “tonal rhythm is most easily perceived where there is little or no durational patterning” (315). This would certainly apply to the monophonic and isochronous movements from Bach’s solo string music. Although the continuous repetition of a single duration eliminates the possibility of variety in the durational rhythms, tonal rhythms are created by accent patterns that emerge as the melody switches from one implied voice to another. Schachter summarized by saying that since the rhythmic character of any piece is a combination of both durational and tonal elements, “the same ‘rhythmic figure’ can embody different rhythms, depending upon what the tones do” (326). The presence or absence of implied polyphony can therefore affect what the “tones do” and allow the same isochronous rhythmic figures to “embody different rhythms.”(4)
[13] This research on stream segregation, melodic accent, and tonal rhythms informed the analysis of the specific points at which Bach’s monophonic lines would be perceived to separate into multiple implies voices. Using this approach, the likelihood of segregation between consecutive pitches is determined by the relationship between interval size (large intervals vs. conjunct motion) and melodic contour (Davis 2006). As van Noorden’s (1975) research indicates, streams played at rapid speeds tend to divide into multiple streams when the interval separation is greater than five semitones. The perfect fourth was therefore chosen as the smallest interval that might suggest a change from one implied voice to another.(5) Perceptual research has also shown that V-shaped contours are more likely to split into multiple streams than linear contours (Heise and Miller 1951).(6) An immediate change of contour on either side of a large interval therefore strengthens the likelihood of segregation. Conjunct motion surrounding a large interval is also considered, thus accounting for the fact that two stepwise melodic lines that are separated by a large interval will likely be perceived as two distinct implied voices. In the analyses that follow, circled notes mark the point of transition between different implied voices as determined by large interval size, change of contour, and significant change in interval size relative to the surrounding pitches.
[14] Although melodies that are influenced by these perceptual tendencies can be created using the previously mentioned compositional devices (arpeggiation, dissonance resolution, and voice-leading), this approach emphasizes the perceptual tendencies in order to investigate the degree to which they can offer an additional explanation for how these pieces can be heard. Also, this approach does not attempt to identify the total number of implied voices or to follow the path of each voice over the course of any passage of music. A general analysis of all movements from these pieces (both polyphonic and monophonic) shows that Bach frequently varied the number of simultaneous voices, thus making it difficult to identify a continuous melodic path for each voice. One therefore needs a fluid approach to the total number of implied voices and an acceptance of the lack of complete melodic continuity within implied voices over the course of an entire piece. Analyzing the music in this way identifies the salient points of transition between one implied voice and another, as well as the locations where such a change might add a phenomenal accent to the otherwise isochronous texture and thereby affect the rhythmic and metric (rather than just the melodic or contrapuntal) characteristics of the piece.
Example 1. J.S. Bach: Sarabande Double from Partita No. 1 in B Minor, measures 1–4
(a. Analysis of implied voice changes; b. Forte and Gilbert’s harmonic reduction)
(click to enlarge and listen)
[15] Example 1 contrasts two approaches to analyzing the implied polyphony in the opening measures of the Sarabande Double from Bach’s Partita No. 1 in B minor.(7) Forte and Gilbert’s Schenkerian analysis of this passage is based on fundamental principles of arpeggiation and diminution, with emphasis placed on how the diminutions in the Double create an elaboration of the basic voice-leading patterns in the original Sarabande. Example 1b shows their reduction of this passage, with the different voices in the Double verticalized to show the underlying voiceleading connections (Forte and Gilbert 1982, 79).
[16] Example 1a shows an alternate analysis of this passage. Instead of focusing on
underlying voice-leading patterns, this analysis simply identifies the points at which this
monophonic line will most likely split into different perceptual streams. This fission is caused
by the basic principles of auditory stream segregation (rapid tempos, large intervals surrounded
by conjunct motion, and changing contours). Based on these principles, the arpeggiation of a
single harmony (the B minor triad) and the subsequent small intervals will keep the first two
beats of this passage fused as a single voice (Bregman 1990). The first perceived voice change
would therefore occur at the leap to the A5 in the third beat of measure 1. Although Forte and
Gilbert acknowledge that the descending third motion that begins with this note (moving from
A5-G5-
[17] Both of these approaches produce valid analyses of implied polyphony. They also produce different, valid ways that a listener might hear the compound melody in a passage such as this. One could pay attention to arpeggiation and diminution patterns in order to hear an underlying voice-leading or harmonic structure. Or one could instead be attracted by phenomenal accents that are created by transitions from one implied auditory stream to another at the surface of the music. Cambouropoulos (2006) summarized the difference between these two interpretations by stating that auditory stream segregation “determines how successions of musical events are perceived as belonging to coherent sequences and, at the same time, segregated from other independent musical sequences,” while a more harmonic or contrapuntal approach suggests that “tones that correspond to the implied chords may be considered as implying a horizontal organization into a number of separate voices” (2).
Example 2. J.S. Bach: Corrente from Partita No. 1 in B Minor, measures 65–68. Content of three implied voices marked with +, *, and ^
(click to enlarge and listen)
[18] In some passages from Bach’s pieces, these two approaches produce similar analyses.
For instance, the excerpt in Example 2 contains a one-measure motive that is sequenced in a
descending, stepwise pattern. This sequential repetition creates a sense of voice-leading between
the notes on the downbeat of each measure. Due to the interaction between large intervals,
conjunct motion, and changes of contour, this motive could also be perceived as containing three
implied voices, with each voice inhabiting its own registral space and thus creating three distinct
descending melodic lines within the overall sequential repetition. Because the change from one
voice to the next always occurs on a weak beat of the measure, and because that pitch is always
the highest in the texture, the implied polyphony allows this sequence to also be perceived as
beginning on the second eighth note of each measure. This metric shift highlights the voiceleading
pattern in the top voice (C6-B5-A5-G5) and creates a middle voice that emphasizes the
last eighth note of each measure (D5-C5-B4-A4), rather the downbeats of each measure (
[19] Other passages from these pieces highlight the difference between analyzing implied polyphony from a compositional, voice-leading approach and a perceptual, stream segregation approach. In these passages, implied voice changes are created by the repetition of a single motive (or parts of a motive) in various ranges or by large interval separations between the legs of a sequence. The implied polyphony therefore cannot be explained as mere harmonic arpeggiations or voice-leading patterns. It instead helps to foster a sense of successive grouping structure as certain implied voices state the motive(s) and others are momentarily silent.
Example 3. J.S. Bach: Presto from Sonata No. 1 in G Minor, measures 32–35
(click to enlarge and listen)
[20] The excerpt in Example 3 is characterized by groups of descending sixteenth notes, each separated by large interval leaps that create a change of contour. If these large intervals were eliminated through the use of octave transfer, this passage would consist entirely of an extended descending scale. As a result, these leaps not only allowed Bach to compose a lengthy scalar passage while limited by the lower range restrictions of the violin, but also to create an interesting perceptual illusion by placing literal descending motion in a passage that ascends in overall pitch height. In addition, the large interval leaps place phenomenal accents on the highest note of each group of sixteenth notes and create the perception that a new implied voice has entered the texture at that moment. Although these voice changes do not create a sense of stepwise voice-leading, and although all of these implied voices overlap in range, the listener can still get the impression that a similar motive is being passed around multiple implied voices.
Example 4. J.S. Bach: Chaconne from Partita No. 2 in D Minor, measures 49–51
(click to enlarge and listen)
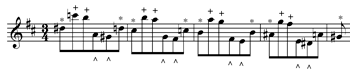
[21] Example 4 displays a passage from Bach’s D minor Chaconne that contains a descending, stepwise sequence of a one-measure motive. Large interval leaps and changes of contour highlight the transition from one implied voice to another, with each voice containing either a single pitch or exclusively conjunct motion. Based on repetition within each leg of the sequence, these implied voice changes create three distinct motives. The highest voice contains a single pitch and creates a descending, stepwise melodic line from one measure to the next (indicated with + on the score). The seven descending sixteenth notes that occupy the middle of each measure create a second motive, with the last note of each statement of the motive creating another stepwise descent that functions as a perceived bass line (indicated with * on the score). A third voice contains just three sixteenth notes (the last two of each measure and the downbeat of the next measure). This voice completely overlaps the pitch space of the bass voice, but placement of the last note on the downbeat emphasizes another stepwise descent and creates a perceived alto voice within the overall texture (indicated with ^ on the score). Although range is no longer identifying the content of three simultaneously streamed voices, Bach still combined large intervals, conjunct motion, changes of contour, and motivic repetition in a way that would create the perception of three different implied voices in a brief monophonic passage.
[22] To summarize, this approach suggests that there is sometimes a difference between implied voice-leading and the perception of multiple implied voices in a passage of monophonic music. Bach’s use of implied polyphony went beyond arpeggiating originally homophonic material or elaborating the resolution of dissonance. In addition, the voice-leading patterns that can be identified by other analytical approaches do not always coincide with the moments in a monophonic texture that might be perceived as the transition between two implied voices. Therefore, the focus of these analyses is to identify melodic features that are influenced by perceptual tendencies involved in stream segregation. Highlighting these features examines the degree to which basic auditory phenomena affect the perception of implied polyphony in complex music, generates an analysis that identifies moments of likely fission and phenomenal accent, and provides an additional perceptually relevant way to interpret these pieces that can stand beside other analytical approaches.
Implied Polyphony and Perceived Rhythm
[23] In a previous study, empirical research methods were used to examine the extent to which listeners are aware of and affected by the frequency and clarity of implied voice changes in Bach’s solo string music (Davis 2006). Results indicated that the presence or absence of implied polyphony affects the aesthetic evaluation of these pieces, with original passages containing implied polyphony being judged to be significantly more “engaging” than those that were recomposed (using octave transfer) to eliminate the implied polyphony as much as possible. This suggests that implied polyphony adds some degree of expression to the notes themselves, as opposed to the typical sources of performed expression (e.g., rubato, dynamics, articulation, and vibrato).(9) It is proposed that this structural expression is at least partially created by the way the implied polyphony interacts with and affects the perception of rhythmic and metric structure.(10)
[24] One possible distinction between Bach’s treatment of meter and that of later composers is the degree of attention given to the fastest levels of the metric hierarchy. Rather than emphasizing the measure level and treating the faster metric levels as mere subdivisions, Bach typically created significant and purposeful activity at all metric levels. He accomplished this by placing different simultaneous rhythmic patterns and accent structures in the various polyphonic voices or instrumental parts of a given composition.(11) Joel Lester provided evidence for this idea by comparing the “regularity of patternings and accentuations at the fastest levels” in the music of Mozart and Beethoven with the “greater complexity of accentuation patterns at the fastest levels” in the music of Bach. A distinction is therefore made between metric levels that are perceived as “subdivisions of larger groupings” and those that “become a possible focus of attention (1986, 127).(12)
[25] Bach could easily articulate each level of the metric hierarchy by placing different accent patterns in various instrumental groups or timbres. But these different instruments or voices do not exist in monophonic music. In his unaccompanied string works, Bach defined the slower levels of the metric hierarchy with regularities in harmonic rhythm and sequential (or motivic) repetition. He then used implied polyphony as one method of creating contrametric accents at the fastest level of the metric hierarchy, where isochronous rhythms would have left a rhythmic surface devoid of any differentiation. Transitions between implied voices were placed on weak beats at this fastest level, which highlighted otherwise unaccented foreground notes and created a sense of tension against the established and regular pulse. Surface rhythms that might have become a “mere stream of activity filling the space between downbeats” (Lester 1986, 153) were instead enlivened by a clever manipulation of musical texture and the foreground of these pieces acquired the potential to become a focus of the listener’s attention.
[26] Bach further emphasized these metric irregularities by avoiding any consistent use of implied polyphony throughout an entire piece. The musical texture instead moves freely between passages that are truly monophonic (meaning only that a single note is played at one time) and passages that contain different instantiations of implied polyphony. Attention is therefore only periodically drawn to the alternate surface rhythm patterns that are created by the various durations between implied voice changes. In this way, the structural features that create implied polyphony (rapid tempos, large intervals, and changing contours) compensate for the lack of foreground rhythmic differentiation in these pieces by generating what are often called “inherent” rhythms.
[27] Carterette and Kendall (1999) define inherent rhythms as:
. . . patterns that emerge from the overall melodic-rhythmic complex and are not produced directly by any musician. Prerequisites of these inherent auditory patterns are a very quick sequence of notes; many jerky intervals with an ensuing split into pitch layers; and a regular internal structure of an entire passage so that high, low, and middle pitch layers form distinct rhythmic melodies (760–761).
These inherent rhythms are the opposite of composite rhythms, which have been defined as the “durational pattern of all parts in a texture” that is “neither expressed nor approximated by any single part in the texture (Lester 1986, 6). A polyphonic passage containing various rhythmic patterns in each voice (or instrumental part) could therefore have a composite rhythm of continuous sixteenth notes. In contrast, many of the monophonic movements from Bach’s unaccompanied string pieces already contain these isochronous surface rhythms. Bach therefore needed a way to create the rhythmic variety that existed in the truly polyphonic compositions. Implied polyphony provided one source of foreground phenomenal accents that could produce these inherent rhythmic patterns.
[28] Bach generated these surface rhythms and had them interact with the underlying voiceleading in a variety of different ways. Some passages containing implied polyphony can be separated into multiple voices that each maintain their own pitch space. A clear sense of melodic continuity is created and it is possible for a listener to follow the path of each implied voice over the course of an entire passage (as in the excerpt shown in Example 2). The rhythm of each individual voice thus creates rhythmic patterns that are perceived but not explicitly performed.
Example 5. J.S. Bach: Minuet II from Cello Suite in G Major, measures 1–8
(a. Original score, circles indicate transitions from one implied voice to another; b. Orchestration of rhythmic pattern in each implied voice)
(click to enlarge and listen)
Example 6. Harmonic reduction indicating content of implied voices in the Minuet from Bach’s Cello Suite in G Major, measures 1–4
(click to enlarge)
[29] An illustration of this can be found in the opening eight measures of the Minuet II from Bach’s Cello Suite No. 1 in G major. Example 5a shows the score of this excerpt, with circles placed around notes that serve as the transition between three different implied voices. Each of these voices follows stepwise motion and large intervals separate the different voices. Example 5b shows the inherent rhythmic pattern of each voice. Metric placement of each pitch is maintained and non-consecutive pitches belonging to a single implied voice are lengthened, thereby highlighting the rhythmic interplay between the three voices. Agogic accents place emphasis on the second beat of each measure in the highest voice, the third beat of each measure in the middle voice, and the downbeat of every other measure in the bass voice. Each voice is therefore given its own rhythmic space in the overall musical texture and a pattern of inherent rhythms is created as the change from one implied voice to another receives a phenomenal accent. This analysis can be compared to Forte and Gilbert’s voice-leading reduction of the first four measures of the same passage (see Example 6).(13) In this analysis, “the voices are verticalized to show the voice-leading connections as though the three voices were literally present at every moment instead of being presented in the form of a compound melody” (Forte and Gilbert 1982, 70). This places emphasis on the underlying voice-leading and implied harmony, rather than on phenomenal accents created by stream segregation.
[30] Many other passages from Bach’s pieces lack the clear sense of melodic continuity exhibited by the implied voices in this Minuet. The implied polyphony in these passages instead creates something more similar to syncopation, where the accentuation of weak beats within a regular metric construct contradicts the prevailing meter or pulse. These accents are created when changes of voice (or entrances of new voices) are placed on weak beats at the fastest level of the metric hierarchy, thereby causing stronger beats to feel either anticipated or delayed and creating an “expressive surface.”(14) Identifying these implied voice changes allows for the perception of an additional set of inherent rhythms overlaid onto the original isochronous stream of pitches, with that part containing various syncopated rhythmic patterns that enliven the texture and contradict the listener’s expectations.
Example 7. J.S. Bach: Allemande from Partita No. 2 in D Minor, measures 4–7
(a. Original score, circles indicate transitions from one implied voice to another; b. Inherent rhythmic pattern created by implied voice changes; c. Revised version; d. Inherent rhythmic pattern in revised version)
(click to enlarge and listen)
[31] An example of this can be found in a passage from the Allemande of Bach’s Violin Partita No. 2 in D minor. Example 7a shows the original score of measures 4–7 and Example 7b notates the implied voice changes as a continuous rhythmic stream. The opening of this excerpt highlights the relationship between interval size and contour in creating implied voice changes. Based on interval size alone, measure 4 contains five possible changes of implied voice (since each of these intervals is ≥ P4). However, only three of these intervals are indicated as signaling a change to a new implied voice. The two ascending perfect fourths (C5-F5 and D5-G5) continue triadic arpeggiations and are not surrounded by changes in contour, thus making them unlikely to trigger stream segregation or receive phenomenal accents. This measure also contains motivic repetition, with the repetition being delineated by changes in implied voice. Bach consistently started motives and sequential repetitions on weak beats, therefore making it likely that the motive in measure 4 begins on the second sixteenth note of the measure and lasts two full beats. This motive is sequenced up a step after a change in implied voice on the second sixteenth note of the third beat. Within this motive, however, exists a stepwise, ascending, two-note pattern. This pattern always begins and ends with a change in contour as related to the rest of the two-beat motive. When combined with the large intervals, this contour change suggests a new implied voice and serves to isolate those two notes from the rest of the motive. Bach fragmented this two-note pattern from the rest of the motive at the beginning of measure 5, with large intervals and changes of contour again highlighting the entrance of a new implied voice at the beginning of each repetition.
[32] After identifying these implied voice changes, it would be natural to try to determine the total number of implied voices and the content of each voice over the course of the entire passage. However, most of these implied voice changes delineate motivic repetition, thereby creating successive (rather than simultaneous) grouping structure. The content of all implied voices overlaps in pitch space and it is impossible to use range as a way of identifying and following the path of each voice. Unlike the Corrente excerpt in Example 2 and the Minuet excerpt in Example 5, the implied voices in the Allemande are not being simultaneously streamed throughout the passage. Instead, the voice changes create the impression that different motives are being passed between multiple implied voices. Since these voice changes tend to occur on weak beats and over irregular intervals of time, the accents that occur at the beginning of each change of voice create the inherent rhythmic pattern shown in Example 7b. Listeners could therefore allow principles of auditory stream segregation to highlight this pattern of accents or allow principles of harmony and counterpoint to instead draw their attention to voiceleading connections between non-consecutive pitches.
[33] As a point of comparison, Example 7c contains a revised version of this same passage. This revision was created by applying octave transfer to the largest intervals in order to diminish the sense of implied polyphony as much as possible. Examining the inherent rhythmic pattern of this revised version reveals how the presence or absence of implied polyphony dramatically changes the rhythmic character of this passage (see Example 7d). For instance, the original version of measures 6–7 contains the largest intervals of this entire excerpt. These large intervals are surrounded by conjunct motion and changes in contour, thereby creating the clear perception of two implied voices. Accents are placed on weak beats at the fastest level of the metric hierarchy as the melody changes from one implied voice to the other. When octave transfer is applied to these measures, most of the large intervals and contour changes necessary for stream segregation disappear. The resulting reduction of implied polyphony eliminates many of the surface accents that created syncopated inherent rhythms in Bach’s original version of this passage.
Example 8. J.S. Bach: Fugue from Violin Sonata No. 1 in G Minor, measures 91–93
(a. Original score; b. Inherent rhythmic pattern created by implied voice changes; c. Revised version)
(click to enlarge and listen)
[34] A similar passage can be found in the closing measures of the Fugue from Violin Sonata No. 1 in G minor (see Example 8). In this two-measure sequence, the interaction between large intervals, changes of contour, conjunct motion, and fast tempo creates the obvious perception of two implied voices. Each of these voices occupies its own range of pitch space and creates a lengthy descending scale (the upper one diatonic and the lower one chromatic), with two-note fragments of each scale alternating between the two implied voices. Because phenomenal accents can be perceived at the entrance of each new voice (or the return to the previous voice), Bach’s use of implied polyphony emphasizes the second and fourth sixteenth notes in each beat and creates a sense of syncopation (see inherent rhythmic pattern shown in Example 8b).
[35] Example 8c shows a revised version of this same passage, where octave transfer was again used to diminish the sense of implied polyphony. Although the same sequence and underlying voice-leading patterns still exist, there is no longer a clear sense of two distinct voices trading off with each other. Without the phenomenal accents created by stream segregation, the sense of syncopated inherent rhythms is reduced. The entire sequence could now be perceived as a monophonic melody that follows a descending D major scale created by the notes that fall at the beginning of each beat, thus emphasizing the arrival on the dominant chord in measure 93. A listener might also hear this scale as being chromatic, elaborated by the pitches that fall on the last sixteenth note of each beat. If this is the case, a voice-leading pattern that matches the lower implied voice of the Bach’s original melody is created. But the upper voice that was once made obvious by differences in interval size and range is now hidden in the texture and less likely to be noticed.(15)
Example 9. J. S. Bach: Allemande Double from Violin Partita No. 1 in B Minor, measures 1–3
(a. Original score, circles indicate transitions from one implied voice to another; b. Kurth’s analysis of the “apparent voice”; c. Inherent rhythmic pattern created by implied voice changes)
(click to enlarge and listen)
[36] The relationship between implied polyphony, voice-leading, and syncopation can also be found in the excerpt shown in Example 9. Kurth (1917) analyzed this passage and identified an “apparent voice” that contains the first and fourth sixteenth notes of each measure (see Example 9b).(16) This suggests that he was emphasizing motivic parallelism, registral reversals, and rhythmic consistency in his analysis. He then left this regular rhythm behind in the middle of measure 2 in order to highlight the stepwise descent to the tonic pitch that occurs within the first beat of measure 3. This reflects Kurth’s desire to find stepwise linear progressions beneath the surface of the music and to identify “hidden” statements of the main motives at this more background level.
[37] An analysis based on principles of stream segregation suggests another possible
interpretation. Example 9c indicates the inherent rhythmic pattern that emerges as pitches acting
as transitions between different implied voice receive phenomenal accents. Instead of
highlighting motivic parallelism, rhythmic consistency, and voice leading, the metric placement
of these implied voice changes creates an irregular accent pattern that adds a syncopated inherent
rhythm to the original isochronous melody. This is particularly apparent in the first two voice
changes (the G5 in m. 1 and the
Example 10. J.S. Bach: Presto from Violin Sonata No. 1 in G Minor, measures 1–42
(a. Original score; b. Inherent rhythmic pattern created by implied voice changes)
(click to enlarge, see the rest, and listen)
[38] A final excerpt shows how implied polyphony can create a variety of different perceived rhythmic patterns over the course of a longer passage of music. Example 10a contains the first half of the Presto from Bach’s Violin Sonata No. 1 in G minor and Example 10b contains the inherent rhythmic pattern of the implied voice changes. Although an analysis based on harmony and voice-leading would identify multiple melodic components in the lengthy arpeggiation in measures 1–4, perceptual principles suggest that harmony fuses pitches together into a single voice (Bregman 1990). When this is combined with the lack of large intervals, it is unlikely that this arpeggiation would separate into multiple perceptual streams. But even without implied polyphony, the different accent patterns of this passage already place emphasis on multiple levels of the metric hierarchy and make it possible for the opening bars of this piece to be interpreted in either 3/8 or 6/16. One could hear the continuous repetition of the original three-note pattern outlining an overall arpeggiation of the tonic chord, with a new note of the chord being introduced every half measure. Or one could instead hear a two-note pattern whose first note outlines the same tonic chord at the measure level, thereby dividing each measure into three beats.(17) Like implied polyphony, this metric ambiguity draws attention to the fastest level of the metric hierarchy in an isochronous passage of music.
[39] As the piece continues, implied polyphony creates a variety of different effects. In measures 17–24, changes of voice are only suggested because large interval leaps occur between each leg of a sequence. When combined with overall stepwise sequential motion, these large intervals highlight the first note of each sequential leg and allow an underlying sense of voiceleading to be perceived. These voice changes occur on downbeats, thereby corresponding exactly with the underlying harmonic rhythm and the slower levels of the metric hierarchy. The implied polyphony in this passage therefore does not create any syncopated surface rhythms. By comparison, the smaller intervals, narrower range, and simple chord arpeggiations in measures 9–11 will likely generate the perception of a single voice even though a sense of voice-leading is still created by the sequential repetition.
[40] In contrast, other implied voice changes accent weak beats in the fastest level of the metric hierarchy and create syncopated, inherent rhythmic patterns. For instance, the voice changes in measures 12–16 place accents on the second and sixth notes of each measure, thereby creating syncopation and animating the otherwise isochronous rhythms. Similarly, measures 32–34 contain a descending, stepwise motive that is passed between multiple implied voices. Because these implied voice changes occur on the weakest sixteenth notes in each measure, this passage creates a sense of syncopation against the measure-level pulse (see discussion of Example 3).
[41] Bach also used implied voice changes to create metric ambiguities at the level just below the one-measure tactus, thus making it possible to interpret this piece as constantly shifting between duple and triple metric structures. For example, the large intervals that occur in the middle of measures 25–28 create two implied voices—a lower voice that contains a three-note ascending, stepwise pattern and an upper voice that contains a three-note neighbor tone figure that serves as a pedal point. Because the alternation between these two motives is consistent, and because it is reinforced by changes in articulation, the voice changes in these measures compel the listener to hear the piece in a duple meter of 6/16. The passage from measures 35–42 then forces the listener back into the perception of triple meter (3/8). In these measures, Bach composed a sequence that alternates between a five-note descending scalar pattern and three groups of two sixteenth notes. Each scalar group (see measures 35, 37, 39, and 41) belongs to a single implied voice because it contains entirely conjunct motion and is preceded by a large interval leap and a change of contour. In the alternating measures, the relatively smaller intervals and lack of conjunct motion might prevent stream segregation (see the first two beats of measures 36, 38, 40, and 42). But principles of voice-leading and motivic repetition would certainly identify two voices in each of these measures, one that contains the notes of the three strong beats (which create an ascending line) and another containing those on the weak beats (which create descending motion and lead to the downbeat of each subsequent measure). As a result, this passage provides another example of how stream segregation and voice-leading interact to create implied polyphony, sometimes identifying the same moments and other times highlighting different aspects of the musical structure.
[42] In general, all of these different accent patterns and metric possibilities combat the potential monotony of isochronous rhythmic patterns. Rather than becoming too comfortable with regularly occurring accent patterns that consistently coincide with the notated meter, listeners can be engaged by implied voice changes that create syncopated inherent rhythms. These inherent rhythms draw attention to the fastest level of the metric hierarchy, thereby maintaining the multi-leveled metric interest that Bach more explicitly outlined in his truly polyphonic compositions.
Conclusion
[43] This research contrasts different approaches to analyzing the implied polyphony in Bach’s solo string works and emphasizes the rhythmic effects of this compositional technique. Although Bach sometimes used implied polyphony as an arpeggiation technique that would transform a multi-voiced harmonic progression into a single melodic line, as a way to disguise or delay the resolution of dissonance, or as something that would create underlying voice-leading patterns, he also used implied polyphony to preserve a basic attribute of his metric structure. By placing implied voice changes on weak beats and with variable frequency, he created a sense of multiple voices that applied irregular accent patterns to the surface of these pieces. This creates purposeful, engaging, and attention-grabbing activity at the fastest level of the metric hierarchy and infuses the isochronous surface rhythms with an additional source of structural expression.
[44] Overall, this suggests that implied polyphony may not always be synonymous with implied contrapuntal voice-leading. There are many monophonic passages where Bach created the implication of multiple linear voices that could be followed over the course of an entire piece. Likewise, a sense of underlying voice-leading can exist in passages that contain no implied polyphony at all. Listeners can certainly choose to follow any of these voice-leading patterns. But they might also be engaged by phenomenal accents that are created as implied voices transition from one to another, thereby creating inherent rhythmic patterns that produce the perception of a richer, multi-voiced texture.
[45] This analytical approach could also provide an additional explanation for the lofty status of these pieces within the string repertoire. In combination with the underlying voice-leading, the complexities and variety of other structural features, and the immense technical difficulty, implied polyphony creates one more source of structural expression in these pieces by providing listeners with multiple perceptual possibilities. Albert Bregman commented on this while comparing Bach’s implied polyphony to the specially constructed auditory patterns that he used for studying stream segregation. He suggested that the musical examples were more ambiguous than the laboratory examples because their intervals are slightly smaller and tempos slightly slower (due only to human physical capabilities). He then proposed that “it is not certain that the composers who used this technique would have called for such an unambiguous separation of musical lines even if the players could have achieved it” and concluded with the following statement.
Transitions between high and low registers were used by composers of the Baroque period to create compound melodic lines—the impression that a single instrument, such as a violin or flute, was playing more than one line of melody at the same time. These alternations were not fast enough to cause compulsory segregation of the pitch ranges, so the experience was ambiguous between one and two streams. Perhaps this was why it was interesting (Bregman 1990, 675–676).
Stacey Davis
University of Texas at San Antonio
Department of Music, Institute for Music Research
One UTSA Circle
San Antonio, TX 78249
stacey.davis@utsa.edu
Works Cited
Beach, David and Jürgen Thym. 1982. The Art of Strict Musical Composition by Johann Philipp Kirnberger. New Haven, CT: Yale University Press.
Blum, David. 1977. Casals and the Art Of Interpretation. Berkeley, CA: University of California Press.
Boltz, Marilyn and Mari Riess Jones. 1986. “Does Rule Recursion Make Melodies Easier to Reproduce? If Not, What Does?” Cognitive Psychology 18: 389–431.
Bregman, Albert. 1990. Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press.
Bregman, Albert and Jeffrey Campbell. 1971. “Primary Auditory Stream Segregation and the Perception of Order in Rapid Sequences of Tones.” Journal of Experimental Psychology 89: 244–249.
Buelow, George. 1986. Thoroughbass Accompaniment According to Johann David Heinichen, Lincoln, NE: University of Nebraska Press.
Cambouropoulos, Emilios. 2006. “Voice Separation: Theoretical, Perceptual, and Computations Perspectives.” In Proceedings of the 9th International Conference on Music Perception and Cognition, edited by M. Baroni, A.R. Addessi, R. Caterina, and M. Costa. Bologna, Italy.
Carterette, Edward C. and Roger A. Kendall. 1999. “Comparative Music Perception and Cognition.” In The Psychology of Music, 2nd ed., ed. D. Deutsch. San Diego, CA: Academic Press.
Cone, Edward T. 1968. Musical Form and Musical Performance. New York: W. W. Norton.
Cooper, Grosvenor and Leonard B. Meyer. 1960. The Rhythmic Structure of Music. Chicago: University of Chicago Press.
Davis, Stacey. 2006. “Implied Polyphony in the Solo String Works of J.S. Bach: A Case for the Perceptual Relevance of Structural Expression.” Music Perception, 23, no. 5: 423–446.
—————. 2009. “Bring Out the Counterpoint: Exploring the Relationship Between Implied Polyphony and Rubato in Bach’s Solo Violin Music. Psychology of Music, 37, no. 3: 301–324.
Deutsch, Diana. 1999. “Grouping Mechanisms in Music.” In The Psychology of Music, 2nd ed., ed. D. Deutsch. San Diego, CA: Academic Press.
Dowling, W. Jay. 1973. “The Perception of Interleaved Melodies,” Cognitive Psychology 5: 322–337.
Forte, Allen and Gilbert, Steven E. 1982. Introduction to Schenkerian Analysis. New York: W.W. Norton.
Harris, Ernest C. 1981. Johann Mattheson’s “Der vollkommene Capellmeister”: A Revised Translation with Critical Commentary. Ann Arbor: UMI Research Press.
Hasty, Christopher F. 1997. Meter as Rhythm. New York: Oxford University Press.
Heinichen, Johann David. 1728. Der General-Bass in der Composition. Dresden.
Heise, George A. and George A. Miller. 1951. “An Experimental Study of Auditory Patterns.” American Journal of Psychology 64: 68–77.
Huron, David. 2001. “Tone and Voice: A Derivation of the Rules of Voice-Leading from Perceptual Principles,” Music Perception 19: 1–64.
Huron, David and Matthew Royal. 1996. “What is Melodic Accent? Converging Evidence from Musical Practice,” Music Perception, 13: 489–516.
Jones, Mari Riess and Peter Q. Pfordresher. 1997. “Tracking Melodic Events Using Joint Accent Structure,” Canadian Journal of Experimental Psychology 51: 271–291.
Kirnberger, Johann Philipp. 1774–79. Die Kunst des Reinen Satzes in der Musik. Berlin.
Kramer, Jonathan D. 1988. The Time of Music: New Meanings, New Temporalities, New Listening Strategies. New York: Schirmer Books.
Kurth, Ernst. 1917. Grundlagen des Linearen Kontrapunkts: Bachs Melodische Polyphonie. Berne: Drechsel.
Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge: MIT Press.
Lester, Joel. 1986. The Rhythms of Tonal Music. Carbondale, IL: Southern Illinois University Press.
—————. 1994. “Reading and Misreading: Schumann’s Accompaniments to Bach’s Sonatas and Partitas for Solo Violin.” Current Musicology 56: 24–53.
—————. 1999. Bach’s Works for Solo Violin: Style, Structure, and Performance. Oxford: Oxford University Press.
—————. 2005. “The Presto from Bach’s G-minor Sonata for Violin Solo: Style, Rhythm, and Form in a Baroque Moto Perpetuo. In Engaging music: Essays in music analysis, ed. D. Stein. New York: Oxford University Press.
Mattheson, Johann. 1739. Der Vollkommene Capellmeister. Hamburg: Christian Herold.
Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures. Chicago: University of Chicago Press.
Niedt, Friedrich Erhardt. 1700. Die Musicalische Handleitung. Hamburg.
van Noorden, L.P.A.S. 1975. Temporal Coherence in the Perception of Tone Sequences. Ph.D. Dissertation, Eindhoven University of Technology.
Poulin, Pamela L. and Taylor, Irmgard C. 1989. The Musical Guide. New York: Oxford University Press.
Rothfarb, Lee. 1988. Ernst Kurth as Theorist and Analyst. Philadelphia: University of Pennsylvania Press.
—————. 1991. Ernst Kurth: Selected Writings. Cambridge: Cambridge University Press.
Rothstein, William. 1991. Phrase Rhythm in Tonal Music. New York: Schirmer Books.
Schachter, Carl. 1976. “Rhythm and Linear Analysis. In The Music Forum, vol. IV, ed. F. Salzer and C. Schachter. New York: Columbia University Press.
—————. 1987. “The Gavotte en rondeaux from J.S. Bach’s Partita in E Major for Unaccompanied Violin.” Israel Studies in Musicology 4: 7–26.
—————. 1994. “The Prelude from Bach’s Suite No. 4 for Violoncello Solo: The Submerged Urlinie.” Current Musicology, 56: 54–71.
Schenker, Heinrich. 1925. “The Prelude of Bach’s Partita No. 3 for Solo Violin.” In Das Meisterwerk in der Musik, vol. 1, Munich: Drei Masken Verlag. Translated by John Rothgeb in The Masterwork in Music: A Yearbook, 1. New York: Cambridge University Press, 1994.
Schroeder, Jaap. 1977. “Jaap Schroeder Discusses Bach’s Works for Unaccompanied Violin.” Journal of the Violin Society of America 3: 10–12.
—————. 2007. Bach’s Solo Violin Works: A Performer’s Guide. New Haven, CT: Yale University Press.
Thomassen, Joseph M. 1982. “Melodic Accent: Experiments and a Tentative Model,” Journal of the Acoustical Society of America 71: 1596–1605.
Willner, Channan. 1991. “Stress and Counterstress: Accentual Conflict and Reconciliation in J.S. Bach’s Instrumental Works.” Music Theory Spectrum 20, no. 2: 280–304.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. New Haven, CT: Yale University Press.
Footnotes
1. Schroeder (2007) contains extensive comments about the analysis and performance of these pieces.
Return to text
2. For Kurth’s extensive writings on polyphonic melody, see Kurth 1917. English translations of Kurth’s treatise are found in Rothfarb 1991 and Rothfarb 1988.
Return to text
3. For information on auditory stream segregation, see Bregman 1990; Bregman and Campbell 1971; and Deutsch 1999, 299–348. David Huron (2001) used similar perceptual tendencies to explain the derivation of voiceleading (or part-writing) conventions in Western tonal music.
Return to text
4. Although he makes no reference to implied polyphony in particular, Hasty (1997, 154–167) uses passages from two Bach cello suites to demonstrate how identical rhythmic patterns can produce dramatically different metric interpretations depending on surrounding context, contour changes, melodic accents, and harmonic implications.
Return to text
5. Narmour (1990) also identified the perfect fourth as the dividing point between small and large intervals in his research on melodic structures.
Return to text
6. Empirical research on melodic accents has also identified contour changes as a type of accent that can contribute to the perception of grouping boundaries. See Huron and Royal 1996; Jones and Pfordresher 1997; and Thomassen 1982.
Return to text
7. Example adapted from Forte and Gilbert 1982, 79, Example 78c.
Return to text
8. Schenker published an analysis of a monophonic movement from Bach’s solo string pieces in the first volume of Das Meisterwerk in der Musik (1925). Although his middleground graph provides information about underlying contrapuntal lines, the content of these inner voices is not consistently determined by those features that are apt to cause stream segregation. Likewise, melodic patterns that clearly imply multiple voices do not necessarily contain the primary voice-leading patterns that Schenker sought to find. For this reason, Schenker’s analysis of this piece contributes more information about underlying voice-leading patterns than about the creation and perception of multiple voices within a monophonic texture. Schenker also analyzed two other movements from these pieces (the Sarabande from Cello Suite No. 3 in C major and the Largo from Violin Sonata No. 3 in C major). Because these movements contain many multiple stops, they are truly polyphonic and not relevant to a discussion of implied polyphony. Additional Schenkerian analyses of Bach’s pieces can be found in Schachter 1987 and Schachter 1994.
Return to text
9. An examination of the way performers use rubato to “bring out” implied polyphony can be found in Davis 2009.
Return to text
10. Different approaches to analyzing rhythmic and metric structure in tonal music can be found in Cooper and Meyer 1960; Hasty 1997; Kramer 1988; Lerdahl and Jackendoff 1983; Lester 1986; Rothstein 1991; and
Yeston 1976.
Return to text
11. Edward Cone (1968) used a passage from Bach’s Concerto for Clavier and Orchestra in D minor to demonstrate how each instrumental part emphasizes a different level of subdivision in the overall metric structure.
Return to text
12. Lester (1986, 1999, 2005) illustrated these different metric approaches by comparing the accompaniments that both Bach and Schumann wrote to the Preludio from Violin Partita No. 3 in E Major.
Return to text
13. Example adapted from Forte and Gilbert 1982, 70, Example 63b.
Return to text
14. Implied polyphony could therefore also be defined as a source of metric counterstress, which Channan Willner (1991, 280–281) describes as being “a rhythmic cross-accent that comes about through an unexpected gesture—a sudden leap, a textural intensification, a change in figuration—that falls on a weak beat within the measure, on the downbeat of a weak measure, or (if a clear-cut periodicity prevails) on the downbeat of a weak hypermeasure . . . Though it is a rhythmic detail of the surface, counterstress serves as a bridge between the foreground and the underlying tonal and durational middleground because its conflict with metric and hypermetric accents at various levels calls attention to larger issues.”
Return to text
15. Dowling’s (1973) research on “interleaved melodies” demonstrates this same perceptual phenomenon. In
these experiments, Dowling alternated the notes of two familiar melodies and asked participants to identify both melodies. When the range of the melodies overlapped, the overall sequence was heard as a random pattern of notes. But when the melodies were transposed to each occupy distinctly different ranges, with at least a semitone
difference between them, participants were able to accurately identify both melodies.
Return to text
16. Adapted from Rothfarb, Ernst Kurth as Theorist and Analyst, 87, Example 4-14.
Return to text
17. Analyses of this passage in comparison to an isochronous excerpt from Paganini’s Moto Perpetuo can be found in Lester 1999 and 2005.
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor
Number of visits: