A Tonal Revolution in Fifths and Semitones: Aaron Copland’s Quiet City

[1] A number of pieces written in the first half of the twentieth century sound tonal while also containing decidedly modern elements. The label “neo-tonal” or “centric” is often applied to such works, which include music by Britten, Prokofiev, Shostakovich, Stravinsky during his neoclassical period, and others. Zimmerman (2002) and Silberman (2006) point out that readings of neo-tonal music often combine techniques of both tonal and post-tonal analysis, an approach that opens the question of precisely which elements of the tonal idiom are applicable to the work under discussion.⁽¹⁾ Such readings also raise a related question of whether a single mode of analysis can apply to an entire composition, or whether we must jettison the assumption of stylistic unity and find the best possible method for each individual section.⁽²⁾ Aaron Copland’s Quiet City (1940) raises similar questions for analysts. The work has a consonant musical surface yet often strips away many markers of common-practice tonality. This paper offers a hearing of Quiet City that is oriented toward two of its most salient features: motives built from pentatonic subsets and semitonal shifts. An ic1/ic5 Tonnetz models the pitch-class collections that generate musical material in the work and motion between them. Completion of normative sets and salience conditions serve to define central pitches. In addition, motion within the Tonnetz shows a large-scale coherence within the work’s pitch organization, and provides an example of Copland’s expansion of tonal techniques.

[2] Critics faced with the task of describing the pitch structure of Aaron Copland’s compositions often resort to the explanation that it is tonally ambiguous. For example, Wilfrid Mellers (2000) states that many of Copland’s Twelve Poems of Emily Dickinson can be heard either as tonal or as in one of the diatonic modes. In his analysis of Copland’s Sextet, Daniel Mathers (1989, 56–57) identifies a “tonal axis”—that is, a dichotomy between two competing tonal centers—between the lower tonic and upper dominant. Howard Pollack (1999, 384) states that the violin part in the second movement of Copland’s Violin Sonata suggests different keys with each melodic turn, and suggests that Copland learned how to write such a melodic line in part by studying the music of Stravinsky. He also remarks that the ending of Copland’s concert work Quiet City can be heard in either C major or F major. Copland wrote Quiet City for trumpet, English horn, and strings in 1940, a year after he wrote incidental music for a play called The Quiet City by Irwin Shaw.⁽³⁾ The concert work recycles many themes from the incidental music, and Pollack (Pollack 1999) speculates that the close relationship allows a programmatic reading of the tonal ambiguity of the concert work’s ending:

Whether one considers the final pitch an unresolved dominant or a more restful tonic, the work ends on a hesitant note; like Shaw’s play, the music raises more questions than it answers. (332)

[3] The ending of Quiet City is reduced in Figure 1. A solo trumpet reprises the main theme of the work—Copland called it a portrait of David Mellnikoff, one of the characters from Shaw’s play—against a C pedal (Copland and Perlis 1984, 287). If we were to assume a preference for hearing a diatonic collection as indicating either a major or minor scale, we would hear the passage in F major and conclude that the work ends on the dominant harmony.⁽⁴⁾ The trumpet uses pitches from the F-major scale, save for one note. A B♮ occurs in the middle of the trumpet solo nine measures after rehearsal 16, as if the instrument were feinting toward the C-major scale, but in the following measure the trumpet reverts to using B♭. There is little other strong support for hearing the passage in F major; moreover, Copland’s use of diatonic modes in other compositions renders tenuous the assumption that the tonic can be determined simply from the scale used in a passage. Position assertion—that is, the use of music-rhetorical devices and formal placement to establish a tonic—favors hearing the passage in C (Harrison 1994, 75–90). The trumpet begins and ends on this note, the strings hold it throughout, and the note is the last one heard in the composition. Other than repeated C’s, the final two notes are G₄ and C₄, played by the English horn three measures after rehearsal 17. These two notes could suggest the root and fifth of a tonic sonority. Other indicators of C major are likewise spare: B♮, its leading tone, appears for only a fleeting moment, as does E, the tonic triad’s third. As Pollack suggested, interpreting the ending according to tonal norms yields conflicting conclusions.⁽⁵⁾ Such an interpretation also does little to reveal relationships among the work’s constituent parts, and does not address ways in which most of the work eschews pitch constructions reminiscent of common-practice tonality in favor of others.

[4] Building on the work of Stephen Brown (1999, 80–141) and others, my analysis uses an ic1/ic5 Tonnetz, shown in Figure 2, to model pitch-related events in Quiet City.⁽⁶⁾ Both individual motives and motion between referential collections are represented spatially within this network. The primary referential collection in the work is the pentatonic collection; this is expressed on the horizontal axis as a multiplication by five of a generating perfect fifth.⁽⁷⁾ A semitone generates the vertical axis; it represents marked semitone shifts that occur throughout the composition. Brown defines a number of operations within the Tonnetz; the most important for the present study is T(x,y), which moves an object x spaces to the right and y spaces up (Brown 1999, 14). This paper will informally express T operations as horizontal or vertical steps on the Tonnetz; for example, moving from C to G is equivalent to making one rightward step. The dotted paths in Figure 2 show that, in equal temperament, the network “twists” upon itself so that the E♭ at the top right corner links directly by one rightward step to the first B♭ in the second row, and the D at the right edge of the second row links directly by one rightward step to the A in the third row. These direct links could be represented in three-dimensional space by placing the pitches along a helix. In addition, the F♯ in the bottom row links directly to the D♭ in the top row, so that the two points in the path marked with the symbol “α” connect by one horizontal step.⁽⁸⁾ The vertical axis twists upon itself in a similar fashion, but this feature of the network does not play a major structural role in Quiet City, so it is not represented. The twist at the α symbol could be represented in three-dimensional space by connecting the ends of the helix to form a torus.

[5] Many stretches of Quiet City can be represented as filling up horizontal spans within the Tonnetz.⁽⁹⁾ The opening five measures of the piece, shown in Figure 3, provide an example. The passage fills the span {B♭ F C G D}, and the opening three measures repeat a motivic dyad C-F, which represents two horizontally adjacent notes in the Tonnetz. Brackets in the reduction show appearances of this C-F dyad: the violas state it melodically, the violins repeat it vertically in measure 2, and the violins repeat it again melodically two octaves higher over measures 2–3. It is the pentatonic collection itself and the C-F dyad that are highlighted in the opening; no specific pitch emerges as central. A perfect fourth or fifth might suggest the root and fifth of a tonic sonority, but after the statements of the C-F dyad, the centricity of either pitch is undercut by the ’celli, which descend from F₃ to B♭₂. The centricity of B♭ is then undermined when the ’celli descend to G₂ in measure 5 and form a perfect fourth with the English horn’s C₄. The opening measures are also notable for their avoidance of stating triads: the violas state an [025] trichord C-F-D in measures 1–3, and form a vertical instance of the same trichord with the violins when they reach their last note. The ’celli imitate the same trichord a fifth lower, with octave displacement, over measures 3–4.⁽¹⁰⁾

[6] Brown (1999, 6) suggests that an analyst take into account the proclivity for associating the x-axis with time and the y-axis with vertical sonorities when deciding on an orientation of a dual interval space, or DIS.⁽¹¹⁾ I have chosen instead to use the axes of the Tonnetz to highlight a qualitative difference between different types of intervals in Quiet City. Motion by ic5 in Quiet City is common and also generates harmonic collections. Motion by ic1, by contrast, is comparatively rare, and occurs exclusively between events separated in time.⁽¹²⁾ Thus, vertical motion suggests salience, markedness, or even effort. In order to keep in mind the qualitative difference between the types of intervals in Quiet City, it might be helpful to imagine the helical arrangement of pitch classes as if they were placed on the surface of a mountain, as depicted in Figure 4a. Horizontal motion consists of walking around its perimeter, while vertical motion requires the effort of pushing against gravity and stepping upward or downward. Figures 4b and 4c show two marked semitone motions that occur in the first section of Quiet City (from the beginning to rehearsal 3). Both involve salient parts within the texture that transform significant [025] trichords into [015] trichords. Figure 4b shows the inflection of the trichord C-F-D, which the violas introduce in the first three measures. Four measures after rehearsal 2, the strings and English horn play a brief interlude to the trumpet solo. Its uppermost line, played by the first violins, lowers the final note of the trichord by semitone to transform it to C-F-D♭. Figure 4c shows a chromatic inflection that takes place in the trumpet solo. The solo begins one measure after rehearsal 1 by alternating between C and B♭. Given the exclusive use of the pentatonic collection thus far in the composition, a continuation to G, the note enclosed in parentheses, is expected. Eight measures after rehearsal 8, the middle note is inflected to create C-B♮-G. In the score, a unique legato articulation mark on the B♮ in the trumpet part provides a phenomenal accent to highlight the fact that the note is unexpected.

[7] The Tonnetz admits to multiple possible pathways between pitches. For example, a “downward” step is equivalent to five “rightward” steps.⁽¹³⁾ My analysis follows the law of the shortest way—that is, a preference for motion involving the least number of steps—and prefers to find paths that minimize vertical motion.⁽¹⁴⁾ This is not to say that any Tonnetz analysis must provide only one possible path between any two of its members. Gollin (2000, 99–102) shows that a network defined by a closed mathematical group can still allow for multiple pathways between members, and there may be times when exploring alternate concepts of distance opened up by different pathways is analytically appropriate.

[8] Within normative collections, central pitches assert themselves through salience and through the process of pattern completion. This is a voice-leading technique that Joseph Straus (1982) found in Stravinsky’s music; it occurs when a missing pitch from a collection established as normative sounds prominently in order to create a sense of arrival and define formal boundaries.⁽¹⁵⁾ Pattern completion creates arrivals on the pitches F and C in the first appearance of the trumpet’s main theme (one measure after rehearsal 1). Figure 5 shows an animated Tonnetz analysis (Flash plugin required) of this passage. A dotted box around the horizontal span {B♭ F C G D} indicates the five-note collection undergoing completion. A solid box encloses notes that have prominently sounded. The animation shows that within the first phrase, the trumpet effects a vertical motion of a single pitch on the Tonnetz through chromatic inflection. The rest of the phrase sounds the remaining notes of the pentatonic collection except for F. At the end of the phrase, F sounds as a long-held pitch to complete the collection. The pitch C marks the end of the second phrase in a similar manner. (The second phrase also contains a rapid arpeggio. Because it gives the effect of a sweeping gesture, rather than a series of discrete pitches, I have not included it in my analysis.) These two arrival pitches—F and C—are a retrograde of the C-F dyad established as motivic at the work’s opening.

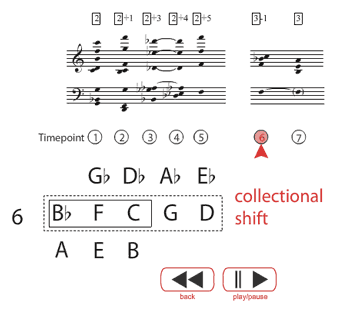
[9] After the trumpet solo, the strings and English horn provide a brief interlude before the trumpet restates the opening of its theme. The interlude, which begins at rehearsal 2, intensifies the trumpet melody’s vertical motion by shifting the entire pentatonic collection. In addition, it changes the central pitch from C back to F, reversing the order of the trumpet’s two arrival pitches. Figure 6 (Flash plugin required) provides a reduction and analysis of the passage. For ease of discussion, the reduction is divided into a number of “timepoints,” indicated by a circled number. As in Figure 5, the prevailing pentatonic collection is enclosed in a dotted box, and notes that are sounding are enclosed in a solid box. The interlude revisits gestures characteristic of the string introduction, but the instruments’ articulation is influenced by the nervous character of the trumpet solo. The upper strings play in a forceful homorhythmic texture, each chord marked with a fp, and the English horn plays the same repeated-note motive found in the opening of the trumpet’s melody. The chords in timepoints 1 and 2 combine the first two dyads played by the violins in the string introduction with the first two pitches of the trumpet melody transposed down by octave, and stay within the primary {B♭ F C G D} pentatonic collection. The chord at timepoint 3 (three measures after rehearsal 2) introduces several new pitch classes: {G♭ D♭ A♭ E♭ B♭}. This novel harmony coincides with the first violins’ D♭, which creates a chromatic inflection of the opening trichord (see Figure 4b). This chord is represented on the Tonnetz as a shift of the entire pentatonic collection by upward vertical step followed by rightward horizontal step. Two measures later, the strings arrive on a single pitch F; this provides an accompaniment for the trumpet’s re-entrance. The arrival on F is also achieved through pentatonic completion, which requires that the strings first effect a horizontal shift to a collection that contains F, the goal note. The ’celli accomplish this at timepoint 4 by changing from an arco G♭ to an A♭ and E♭ played pizzicato. If the B♭ from the previous chord is included, this cadential arrival indicates a completion of this new collection. Because the strings play a long-held C to accompany the first trumpet solo, their two different pedal notes repeat, at a large scale, the C-F motive presented at the opening. The second arrival also raises ambiguity over which note is the tonic, a fact that Howard Pollack pointed out in his discussion of this work. It is unclear whether the change from a C pedal to an F pedal represents a motion away from the tonic (to a subdominant, for example) or toward it. More music is needed to restore a sense of balance to the tonal organization and assert a single pitch center.

[10] At timepoint 7 (rehearsal 3), the trumpet makes another semitonal descent, this time to A; notably, the English horn’s melody that follows begins with notes that are also displaced by a descending semitone from the strings’ vertical trichord immediately preceding. The trumpet’s motion effects a shift to a new pentatonic collection that will gradually undergo completion in the following section. The trumpet’s note also completes the twelve-note chromatic collection, since A is the only pitch class that does not sound throughout the entire first section.

[11] Following Fred Lerdahl’s system of creating both chordal and regional spaces, we can create a space of pentatonic collections, rather than single pitch classes. I will adapt Lerdahl’s notation system and use a bold letter to represent all five notes of a pentatonic collection (2001, 64–67). A represents the pitch class collection {G D A E B}, B♭ represents {A♭ E♭ B♭ F C}, etc. The middle note within the chain of fifths acts as a collection’s representative pitch because this note asserts itself as central within the collection in its normative form in Quiet City. In other statements of pentatonic collections, a different member may temporarily assert itself as central, as in the arrival on F five measures after rehearsal 2. In this respect, the bold letters differ from Lerdahl’s regional space. A closer analogy might be found in Harold Powers’s (1981) concept of the tonal type in sixteenth-century polyphony; that is, a fixed collection of pitch classes that is distinct from the modal category, which determines the final pitch.

[12] Figure 7a shows that the network of pentatonic collections is isomorphic to the ic1/ic5 network of pitch classes defined in Figure 2. Moving a collection a given number of steps on the Tonnetz is accomplished by moving each one of its members by the same number of steps. Figure 7b shows an extension operation that transforms a pentatonic collection into a seven-note diatonic collection. Extension, for the purpose of this analysis, adds the next two pitch classes that appear on the right side of the horizontal axis. For example, the extension operation converts {G D A E B} into {G D A E B F♯ C♯}. Diatonic collections, like pentatonic collections, will be labeled by their representative pitch, followed by the subscript “dia,” such that in the previous example the extension transforms A into A_dia. The representative pitch is chosen because it asserts itself as central within a diatonic collection in its normative form. As a result, the work suggests the Mixolydian mode.⁽¹⁶⁾ Figure 7c shows the network of diatonic collections, which is also isomorphic to the ic1/ic5 Tonnetz. The truncation operation is the inverse of the extension operation. As shown in Figure 7b, it removes the rightmost two pitch classes on the horizontal axis of the Tonnetz, leaving a pentatonic collection. For example, the truncation operation converts {B♭ F C G D A E} into {B♭ F C G D}.

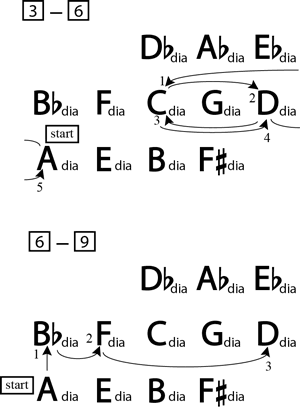
[13] These networks of pentatonic and diatonic collections reveal a similarity between Quiet City’s first section and the first part of the central section. Figure 8 (Flash plugin Required) shows a reduction of rehearsal 3 to rehearsal 9. A principal melodic line, which is always played by either the trumpet or English horn, runs throughout most of the section; its pitches are shown on the top staff. The lower staff shows a reduction of the string parts. Salience determines the relative hierarchy of each note in both parts: notes in the principal melodic line that are emphasized through repetition or longer duration are given stems. Long-held string chords are likewise stemmed. The reduction reveals a melodic focus on the pitch A and a large-scale harmonic motion from the A_dia to the D_dia collection. The principal melodic line begins and ends with the pitch A. In addition, its emphasized notes, with the exception of F, gradually complete the A pentatonic collection over the entire section, a truncated version of the A_dia with which the section began. An upper beam connects the notes that complete this collection. The F fills in the passing motion between E and G; it is marked with a “p” on the reduction. The final A that occurs at rehearsal 9 is the only salient occurrence of this pitch class in the principal melodic line. As such, it creates a large-scale pattern completion over the entire excerpt, and receives extra emphasis through its status as the “withheld” pitch that subsequently occurs at a significant formal juncture. The string parts reinforce the centricity of the pitch A over rehearsals 3 to 6 by placing this pitch in the lowest voice of all of their long-held chords, save for the first. Their most salient chords, notably, are nearly all instances of set-class [0257], continuing the avoidance of triads established in the first section. The first exception is the strings’ chord six measures after rehearsal 6, which is an instance of set-class [027], a subset of [0257]. The second is the C-minor triad in second inversion that occurs at rehearsal 7, which marks the beginning of an interlude passage that uses different melodic material.

[14] Figure 8 also shows the diatonic collections that supply the pitches for each timespan. Passages that use a single diatonic collection are enclosed; the enclosures overlap where pitches belong to more than one collection. The A_dia collection supplies the pitches for the first part of the section. One measure before rehearsal 5, the long-held G in the principal melodic line leads to a brief punctuation by strings, which use pitches from the C_dia collection. The strings’ first chord, which contains the pitches {G D A E}, is the intersection of the A_dia and C_dia collections and provides a pivot between the two. This chord is an instance of set-class [0257], which also characterizes the long-held chords used in the section. The final chord at rehearsal 5 is {C G D A}, another [0257] that allows for a pivot to the D_dia collection. After another brief detour to the C_dia collection, the principal melodic line pivots back to the A_dia collection in the second system of the reduction.

[15] Three measures after rehearsal 6, the principal melodic line makes a marked vertical shift from the A_dia to the B♭_dia collection. This shift is the only point where neighboring collections do not overlap, and it corresponds with the melodic line’s high point.⁽¹⁷⁾ The third system of the analysis shows a shift to the F_dia and finally the D_dia collections.

[16] Figure 9 translates the analysis of these collectional shifts from rehearsal 3 to rehearsal 9 as motions along a Tonnetz. Two of the most salient motions that the trumpet part made in the first section—namely, the horizontal step between C and F, and the vertical step from B♭ to A—are repeated in the central section as motions among collections. The central section also adds another characteristic motion by three horizontal steps. This motion is closely related to the [0257] chords that saturate the string parts, since it represents the widest possible horizontal distance between two diatonic collections that share this set-class. Rehearsal 3 begins at the A_dia collection, and then moves briefly to the C_dia collection by making three leftward steps. After moving between the C_dia and D_dia collections, the passage moves back to the A_dia collection. Disregarding the subsidiary motion to C_dia shows that the first half of the section makes collectional shifts between A_dia and D_dia, two collections related by horizontal step, echoing the horizontal steps between the pitches C and F seen in the work’s opening. Three measures after rehearsal 6 the work makes a marked upward step from A_dia to B♭_dia, a collectional shift that counterbalances the downward step made by the trumpet’s melodic line at rehearsal 3. The passage then moves between the B♭_dia and F_dia collections, a reversal of the left-to-right horizontal motion between A_dia and D_dia undertaken in the first half of the section. At the end of the section, F_dia proceeds to D_dia via three rightward horizontal steps, a reversal of the three leftward steps taken at the section’s opening.

[17] The instruments begin a gradual increase in dynamic intensity at rehearsal 11, signaling the start of a climactic zone. This section effects a dramatic reversal of the collectional shifts made previously in the work, and then makes a gradual horizontal motion to restore the original pitch collection. Figure 10 (Flash plugin required) shows a reduction and Tonnetz analysis of the climactic zone. As shown at timepoint 1, the beginning of the section uses pitches from the D_dia collection, the same collection that appeared at rehearsal 9, at the end of the previous section. At timepoint 2 (one measure after rehearsal 11), the first violins shift from C₅ to C♯₅. This vertical shift in a single pitch is equivalent to a collectional shift one step to the right from D_dia to A_dia. Since the shift in pitch occurs prominently within the uppermost voice, it creates a palpable increase in tension.⁽¹⁸⁾ At timepoint 3 (two measures after rehearsal 11), the ’celli and basses move to G to complete this diatonic collection. The outer voices then move in contrary motion until timepoint 4 (five measures after rehearsal 11), where the basses reach D₂ and hold it for four measures, all the while continuously growing in volume to reach a fortissimo dynamic level. Over this D₂, the upper strings play a thick chord that contains every note in the diatonic collection except C♯. The suppression of this pitch allows its enharmonic equivalent, D♭, to sound novel when it appears in the following chord.

[18] At timepoint 5 (rehearsal 12), the entire ensemble effects a collectional shift down by vertical step. Immediately following this shift, the strings make an impassioned restatement of the two melodic ideas from the beginning of the section in reverse order. Before this climactic section, there were a total of only 13 measures at the forte dynamic level, and rarely did all instruments play at once. In the context of the piece, the shift is an event of momentous rhetorical power. The two measures also nearly complete the chromatic aggregate; the only missing pitch classes are F and C, which occur three measures later as the diatonic collection is completed at timepoint 6. This collectional shift down by step inverts the preference for upward vertical collectional shifts shown in the first two sections. As such, the climax also represents a point of dramatic reversal.

[19] Figure 11a provides a more detailed analysis of the voice leading shown at timepoint 5 (rehearsal 12). The outer voices, trumpet, and English horn make a wholesale shift up by semitone, a counterpoint to the collectional shift down by one vertical step in the Tonnetz. Figure 11b shows that the wind instruments reverse the descending B♭–A that initiated the middle section at rehearsal 3.

[20] At timepoint 7 (rehearsal 13), the strings initiate a gradual motion back to the original collection. First, they move up by whole step, which effects a collectional shift by two rightward steps. An isolated B♭ that occurs mid-phrase at timepoint 8 (rehearsal 14) ends the climactic zone. The ’celli take up this pitch and restate another earlier theme, and, at timepoint 9 (rehearsal 16), the strings restate the introductory material, creating another rightward collectional shift by two steps and a truncation back to a pentatonic collection. As in the collectional shifts at rehearsal 2, a marked vertical collectional shift (from A_dia to A♭_dia), is succeeded by horizontal shifts that gradually return to the original pitch collection.

[21] Figure 12 shows that at rehearsal 16 the strings restate the introductory material and truncate it to create a final cadential arrival, through completion of the original pentatonic collection, on C. This pitch class acts again as axis of inversion of the pentatonic collection, in contrast with the arrival on F that occurred six measures after rehearsal 2. As such, the final point of arrival restores a sense of balance to the pitch organization, and restates the pentatonic collection in its normative form.⁽¹⁹⁾

[22] Figure 13a shows that C, the central pitch, is not only the axis of inversion of the opening pentatonic collection; it also provides the axis of inversion for D_dia and A♭_dia, the two most prominent diatonic collections in the central section at rehearsals 11 and 13. Figure 13b shows how this symmetry in pitch space produces a chronological symmetry: the departure from the original pentatonic collection to the collection at rehearsal 11 is the retrograde inversion, around the pitch C, of the motion from the pitch collection at rehearsal 13 back to the original pentatonic.

[23] Examination of salient notes in the melodic line yields another type of symmetry, as shown in Figure 14. The opening melody is centered on C, moves to B♭, and makes a marked semitonal shift to A at rehearsal 3 (shown in Figure 6). The middle section concludes at rehearsal 12 with a prominent shift from A back to B♭ (shown in Figure 11). When the principal melody enters a final time it is again centered on C. The most salient collections in which this melody is embedded are shown on the bottom half of Figure 14, and a path through Tonnetz space is shown underneath the score. This path, in contrast with the melody, displays no symmetry. The beginning of the middle section at rehearsal 3 creates three rightward horizontal steps along the network. The middle section shifts between the A_dia and D_dia collections, and then makes a marked shift from the A_dia down to the A♭_dia collection. Two rightward horizontal shifts, each totaling two steps, lead back to the original collection in the transition back to the opening section. The large-scale form exploits the cyclic nature of the network: the original pitch collection is both departed from and approached via rightward horizontal motion, producing a sense that we, as listeners, have traveled a far distance away from the original pitch collection, and have also somehow returned to it. The return of the trumpet theme at the end of the work sounds both familiar and novel. Commentators who wish to make a programmatic reading of Copland’s work may wish consider the implication of this journey through pitch space, and the marked vertical motions it makes along the way. Whether the ending represents an achievement of new insight through struggle, or whether it represents a self-defeating motion back to the starting point, may depend on the individual interpreter.

[24] Quiet City allows us to hear radically transformed relationships among basic building blocks of tonality—pentatonic and diatonic collections, the concept of privileged register, and the conceptual model of the cadence.⁽²⁰⁾ This hearing is consistent with Copland’s own compositional aim, which was to explore what he saw as undiscovered potentials of the tonal system. This is an enterprise he shared with several of his contemporaries, and one that he considered as modern and relevant as other trends in music composition of his time.

[25] Copland himself stated this aesthetic aim in his 1941 book Our New Music:

In writing about music composed of intervals of the quarter-tone Krenek says: “...it is questionable if the technique of such a multitonal system [quarter-tone music] is suitable for the presentation of musical ideas, at least today, when we have not come to the end of twelve-tone atonality—in fact when we have just begun to tap its sources.” It follows that we have just as little need for atonality if we believe that the freer interpretation of the ordinary tonal system now in use opens a far from exhausted field of possibilities. (Copland 1941, 55, footnote)⁽²¹⁾

Copland himself did not view his music as occupying a state of transition between tonality and atonality, but rather viewed it as a transformation of constituent elements of the tonal system. His work was, in his view, as modern and forward-looking as music by any of his contemporaries.⁽²²⁾ Analyses of other centric or neo-tonal works might do well to consider Copland’s words seriously.

David J. Heetderks
Oberlin Conservatory of Music
143 East College St., Apt. 418
Oberlin, OH 44074
david.heetderks@oberlin.edu

Works Cited

Agmon, Eytan. 1989. “A Mathematical Model of the Diatonic System.” Journal of Music Theory 33, no. 1: 1–25.

Antokoletz, Elliott. 1984. The Music of Béla Bartók: A Study of Tonality and Progression in Twentieth-Century Music. Berkeley: University of California Press.

Baker, James M. 1986. The Music of Alexander Scriabin. New Haven: Yale University Press.

Balzano, Gerald J. 1980. “The Group-Theoretic Description of 12-Fold and Microtonal Pitch Systems.” Computer Music Journal 4, no. 4: 66–84.

Bartók, Béla. 1976. “Harvard Lectures.” In Béla Bartók Essays, ed. Benjamin Suchoff, 354–92. London: Faber.

Berger, Arthur. 1945. “The Music of Aaron Copland.” The Musical Quarterly 31, no. 4: 420–47.

—————. 1963. “Problems of Pitch Organization in Stravinsky.” Perspectives of New Music 2, no. 1: 11–42.

Brown, Stephen C. 1999. “Dual Interval Space in Twentieth-Century Music.” PhD diss., Yale University.

—————. 2003. “Dual Interval Space in Twentieth-Century Music.” Music Theory Spectrum 25, no. 1: 35–57.

Carter, Chandler. 1997. “Stravinsky’s ‘Special Sense’: The Rhetorical Use of Tonality in “The Rake’s Progress.” Music Theory Spectrum 19, no. 1: 55–80.

Clough, John, and Jack Douthett. 1991. “Maximally Even Sets.” Journal of Music Theory 35, nos. 1–2: 93–173.

Cole, Hugo. 1970–71. “Popular Elements in Copland’s Music.” Tempo 95: 4–10.

Copland, Aaron. 1941. Our New Music: Leading Composers in Europe and America. New York: Whittlesey House.

—————. 1949. “The World of A-Tonality (Review of Rene Leibowitz, Schoenberg and His School).” The New York Times, 27 November.

Copland, Aaron, and Vivian Perlis. 1984. Copland 1900–1942. New York: St. Martin’s/Marek.

Day-O’Connell, Jeremy. 2007. Pentatonicism from the Eighteenth Century to Debussy. Eastman Studies in Music. Rochester: University of Rochester Press.

Forrest, David. 2010. “Prolongation in the Choral Music of Benjamin Britten.” Music Theory Spectrum 32, No. 1: 1–25.

Gollin, Edward. 2000. “Representations of Space and Conceptions of Distance in Transformational Music Theories.” PhD diss., Harvard University.

Harrison, Daniel. 1994. Harmonic Function in Chromatic Music. Chicago: University of Chicago Press.

—————. 2002. “Nonconformist Notions of Nineteenth-Century Enharmonicism.” Music Analysis 21, no. 2: 115–60.

Hindemith, Paul. 1942. The Craft of Music Composition, Vol. 1, Theory. Trans. Arthur Mendel. New York: Schott.

Hyde, Martha. 1996. “Neoclassic and Anachronistic Impulses in Twentieth-Century Music.” Music Theory Spectrum 18: 200–35.

Kleppinger, Stan. 2009. “The Tonal Drama of Quiet City and its Emergence from Copland’s Sketches.” Presentation (via proxy), 29 October, Society for Music Theory Annual Meeting, Montreal, Quebec.

Krenek, Ernst. 1939. Music Here and Now. New York: Norton.

Lerdahl, Fred. 2001. Tonal Pitch Space. New York: Oxford University Press.

Mathers, Daniel E. 1989. “Closure in the Sextet and Short Symphony by Aaron Copland: A Study Using Facsimiles and Printed Editions.” MA thesis, Florida State University.

Mellers, Wilfrid. 2000. “Copland, Dickinson, and the Noise in the Pool at Noon.” Tempo, New Series, 214, American Music Issue: 1–18.

Meyer, Leonard. 1956. Emotion and Meaning in Music. Chicago: University of Chicago Press.

Minturn, Neil. 1997. The Music of Sergei Prokofiev. New Haven: Yale University Press, 1997.

Morris, Robert D. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20, no. 2: 175–208.

Pollack, Howard. 1999. Aaron Copland: Life and Work of an Uncommon Man. New York: Henry Holt.

Powers, Harold. 1981. “Tonal Types and Modal Categories in Renaissance Polyphony.” Journal of the American Musicological Society 34: 428–70.

Silberman, Peter. 2006. “Neighbor Spaces: A Theory of Harmonic Embellishment for Twentieth-Century Neotonal Music.” PhD diss., Eastman University.

—————. 2008. “Analyzing Tonal Embellishment in Post-Tonal Music.” In Musical Currents from the Left Coast, ed. Jack Boss and Bruce Quaglia. Newcastle upon Tyne: Cambridge Scholars Publishing.

Slottow, Stephen P. 2000. “Fifths and Semitones: A Ruggles Compositional Model and Its Unfoldings.” Theory and Practice 25: 87–104.

—————. 2009. A Vast Simplicity: The Music of Carl Ruggles. Hillsdale: Pendragon Press.

Straus, Joseph N. 1982. “A Principle of Voice Leading in the Music of Stravinsky.” Music Theory Spectrum 4: 106–24.

—————. 1986. “Recompositions by Schoenberg, Stravinsky, and Webern.” The Musical Quarterly 72, no. 3: 301–28.

—————. 1990. Remaking the Past. Cambridge, MA: Harvard University Press.

Zimmerman, Daniel. 2002. “Families without Clusters in the Early Works of Sergei Prokofiev.” PhD diss., University of Chicago.

Zweifel, Paul. 1996. “Generalized Diatonic and Pentatonic Scales: A Group-Theoretical Approach.” Perspectives of New Music 34, no. 1: 140–61.

Footnotes

1. Berger was one of the first writers to bring up the issue of pitch centricity in twentieth-century music Berger 1963. Antokoletz 1984) analyzes the music of Béla Bartók and suggests that movements display a single pitch center that often acts as a significant axis of inversion. Several analytical approaches combine tonal and post-tonal analytical techniques. These include Straus, who shows how twentieth-century composers often arrange tonal pieces by extracting motives and subjecting them to serial operations such as verticalization, transposition, and inversion Straus 1986 and Straus 1990; and Carter, who combines Schenkerian reduction with set-class theory to describe Stravinsky’s pluralistic language in The Rake’s Progress (Carter 1997. Another combination of these two analytic disciplines can be found in Baker’s study of Scriabin (Baker 1986). Minturn 1997 uses Fortean set-class analysis to analyze so-called “wrong notes” in Prokofiev’s music (that is, notes that contradict tonal expectation). Recently Forrest 2010 has analyzed prolongation in music by Benjamin Britten through background completion of pitch-class sets that equally divide the octave. Other recent analytical approaches to neo-tonality include Zimmerman’s, which defines neo-tonality through pitch-class sets that do not contain chromatic clusters combined with dissonant prolongation (Zimmerman 2002), and Silberman’s, which defines a theory of embellishment for post-tonal sonorities (Silberman 2006 and Silberman 2008).
Return to text

2. For theories of conflict between old and new styles see Hyde’s discussion of neoclassicism (Hyde 1996).
Return to text

3. The relationship between Copland’s concert piece and the incidental music for Irwin Shaw’s play from which Copland drew will not receive extensive discussion in this paper, but Howard Pollack and, more recently, Stan Kleppinger have tackled this subject (Pollack 1999, Kleppinger 2009). Copland made significant alterations to his source material as he created his concert version, so it can be treated as a separate work.
Return to text

4. Daniel Harrison suggests that in chromatic tonality position finding—the use of the rare intervals in a diatonic collection to determine the tonic—remains a significant means of determining the key (Harrison 1994, 73–75).
Return to text

5. Other Copland compositions evince conflicting tonal cues that suggest two different fifth-related keys. The first movement of the Twelve Poems of Emily Dickinson and the second movement of the Violin Sonata mentioned previously are two examples. “Lento Molto” for String Quartet and the “Corral Nocturne” movement from Rodeo are two others: the former suggests the key of F♯ but ends on a C♯, while the latter suggests the key of C major but ends on a G major triad.
Return to text

6. For more on two-dimensional Tonnetze based on generating intervals other than ic5 and ic4, see Morris 1998, 188. Edward Gollin discusses how a set of transformations can generate a network whose geometric structure is determined by different “words,” or sequences of basic generative transformations (Gollin 2000). Brown discusses the properties of networks created by two generating intervals, which he calls Dual Interval Spaces (DIS), and his dissertation uses the ic1/ic5 DIS to analyze the music of Shostakovich (Brown 1999; Brown 2003). Brown’s space treats repeated pitch classes within his space as different locations, while my space, following Robert Morris, treats the two pitch classes as the same location. Brown has also defined several functions, including transposition, partial and full inversion, and interval exchange, some of which allow him to establish equivalence relations between pitch-class sets that are unrelated by standard T_nI operations. My analysis is solely concerned with the transposition and full inversion operations, and shows how gradually filling and shifting between collections can create larger form. An important precedent for the present study, in that it examines how sonorities built from two generating intervals can govern an entire texture, is Stephen Slottow’s analysis of the late music of Carl Ruggles (Slottow 2000; Slottow 2009, 118–32). Slottow notes that in his late pieces, Carl Ruggles sought to simplify his musical language, and he often did so by focusing on patterns created by cycles of fifths and semitones.
Return to text

7. This paper defines the diatonic collection by a generating interval, a strategy also used by Gerald J. Balzano and others (Balzano 1980). Other theorists characterize it in different ways. Clough and Douthett (1991) describe the diatonic and pentatonic as maximally even divisions of the 12-note chromatic space into seven and five notes respectively, and note the many properties that the two sets share with other maximally even sets such as the whole-tone and octatonic scales Clough and Douthett 1991. Zweifel 1996 suggests that coherence is a more intuitively plausible defining feature of diatonicism, and demonstrates that it is equivalent to maximal evenness.
Return to text

8. Daniel Harrison advocates considering the local non-equivalence of pitches that sound the same but are spelled differently (Harrison 2002). In his conceptualization, each of the twelve pitch classes is a potential point of enharmonic exchange and the tonal field becomes theoretically boundless, rather than cyclical. This paper will assume enharmonic equivalence for reasons that will soon become clear.
Return to text

9. Stephen Brown suggests that an interval space be constructed so that significant groups of notes are horizontally and/or vertically contiguous (Brown 1999, 39). His analyses of Shostakovich, Schoenberg, and Webern provide a precedent for this paper in that they represent pitch classes used in a section as a “region” of notes within a DIS (80–196).
Return to text

10. In an earlier sketch of the opening, the ’celli imitate the violas’ line exactly one perfect fifth lower, suggesting that the [025] trichord serves as a constructive motive in the opening measures. In a later sketch, Copland transposed the second two notes of the ’celli down an octave, obscuring the relationship. Copland’s sketches are at The Aaron Copland Collection, Library of Congress, Music Division, Box 68/Folders 43.4 and 43.2.
Return to text

11. A DIS, or dual interval space, is a two-dimensional musical space defined by an ordered pair of pitch-class intervals [x,y], which generate the horizontal and vertical axes. Each location in the space contains a pitch class, and movement within the space is expressed as an ordered pair (x,y), where x is the number of steps to the right and y is the number of steps up. Given generators [x,y], movement through (a,b) is equivalent to T_(ax+yb). If desired, a theorist can select a “tonic” (0,0) location for a space. Dual interval spaces are defined in Brown 1999 and Brown 2003. Footnote 6 describes the distinctions between Brown’s spaces and the Tonnetz used in this article.
Return to text

12. Although the semitones do not generate harmonic material in the final version of Quiet City, apparently Copland toyed with the idea in his sketches for the work. Box 68/Folder 43.3 of The Aaron Copland Collection, available at the Library of Congress, contains several drafts of the opening of his concert version. In an early sketch, the trumpet’s melody is accompanied at one point by a C/C♯ cluster.
Return to text

13. Stephen Brown also discusses equivalent moves within Dual Interval Spaces (Brown 1999, 12–13). Given two pitch-class interval generators p and q, and given two intervals defined by the ordered pair (a1, b1) and (a2, b2), where a indicates the number of horizontal steps and b indicates the number of vertical steps, two intervals are equivalent if a1p + b1q = a2p + b2q (mod 12). Brown discusses the significance of equivalences in ic1/ic5 space in several late pieces by Dmitri Shostakovich (103, 114–115).
Return to text

14. The only motion on the ic1/ic5 Tonnetz that cannot be reduced to a single shortest pathway is a tritone, which can be represented by an upward and leftward step or by a downward and rightward step. The point is moot with respect to Quiet City, since shifts by tritone do not occur in my analysis.
Return to text

15. Straus’s theory of pattern completion builds on Leonard Meyer’s observation that there is a close relationship between completion of a melodic, rhythmic, or harmonic pattern and closure (Meyer 1956, 148–133). Meyer states that the musical culture establishes the conditions for melodic completeness, but an individual work also “establishes norms which condition our feelings and opinions as to completeness and closure” (138).
Return to text

16. We might use the extension to explain the ascending arpeggiation D-F-G-B♭-C-E-G that occurs in the second phrase of the trumpet melody, shown in Figure 6. The arpeggiation represents an extension of the normative pentatonic into the C_dia collection {B♭ F C G D A E}. This broader collection supplies the pitches for the trumpet’s figure, but the trumpet suppresses A in order to reserve it for the initiation of the following section. After the arpeggiation, the referential collection is summarily truncated back to the C collection. This reading suggests that the opening trumpet theme adumbrates the change to diatonic collections in the middle of Quiet City.
Return to text

17. At the point of the collectional shift, the melodic line completes an [024] trichord, a pentatonic subset. This set that overlaps the juncture creates a smooth transition between the two diatonic sets.
Return to text

18. The interchangeability of vertical shift of a single note and horizontal collectional shift is due to a unique property of the diatonic and pentatonic collections in the 12-note chromatic universe: in both, a semitonal shift of a single element yields a transposition of the same collection, and a continued application of semitone shifts generates all possible transpositions. See Zweifel 1996. The gesture of shifting up by semitone also appears in Copland’s incidental music for The Quiet City.
Return to text

19. Copland’s sketches reveal that he initially wrote a different ending for the concert version of Quiet City. In the original ending, the string parts play a progression of chords that end with a fortissimo C-major triad. The chords encompass a wide range and are drawn from a permutation of the ascending F melodic minor scale. This ending clearly does not fit with the character of the rest of the work, nor does it conform to the avoidance of triads and arrival through pentatonic completion that the final version displays. This first version of the ending may have been influenced by the original incidental music, which concludes by blasting a loud, widely spaced B♭-major chord. Whatever its origin, Copland rejected it as unsuitable for the concert version of Quiet City, and crossed it out several times in favor of the version shown on the lower system, which fades out on the single pitch C.
Return to text

20. Readers might not deem the pentatonic collection a particularly common element in tonal music, but Jeremy Day-O’Connell notes that composers began to use the pentatonic scale in the nineteenth century, and its roots extend back to the eighteenth (Day-O’Connell 2007).
Return to text

21. Copland is quoting from Ernst Krenek’s Music Here & Now(Copland 1949, 164). See also Copland 1949. In this review, he states that Schoenberg’s music presents the question: “Has the tonal system really been exhausted and should it be abandoned or are there still hidden resources to be tapped?”
Return to text

22. Copland was not alone in believing that the full potential of the tonal system was yet untapped. Other composers took this view, and some hardened their opinion into an even more trenchant position: they stated that tonality was a fixed law of musical organization, and that every work, nolens volens, had a single tonic. In his Harvard Lectures from 1943, Béla Bartók stated his belief that every note is related to a fundamental (Bartók 1976, 365): “real or ‘perfect’ atonality does not exist, even in Schoenberg’s works, because of that unchangeable physical law concerning the interrelation of harmonics and, in turn, the relation of the harmonics to their fundamental tone. When we hear a following, different tone, we will...project it against the first tone...and interpret it according to its relation to the latter.” Hindemith gives an extended argument for the same viewpoint in The Craft of Musical Composition: he asserts that the pitches of any composition can be related to a single progenitor tone, which is equivalent to the tonic (Hindemith 1942). To prove his point, he subjects a twelve-tone work, Schoenberg’s Op. 33a, to the method of analysis the book describes, and shows how sequences of events are grouped around tonal centers (217–219). Copland himself appeared to be persuaded that tonality was a fundamental property of music, though in twelve-tone serialism that tonic was pushed far to the periphery of consciousness. In his discussion of Schoenberg (Copland 1941, 52–53 footnote), he states, “Several recent theorists have flatly denied the possibility of any progression of chords made up of two or more notes being without a tonal center.... Let us admit the correctness of their assumption. The fact still remains that we are dealing here with a music whose tonal center of gravity is so remotely discernable as to be nonexistent in comparison with more ‘normal’ music in which it is quite evident. Perhaps it would be truer, though more cumbersome, to speak of quasi-atonal music.”
Return to text

Copyright Statement

Copyright © 2011 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by John Reef, Editorial Assistant
Number of visits: