Music, Memory, and Memes in the Light of Calvinian Neuroscience

1. Introduction: Evolution, Memory, and Memes

[1] This article explores the interface between evolutionary thought, cognitive science, and music theory. It focuses on how patterns hypothesized to function as memes in music (Jan 2007) are encoded neurobiologically, using ideas developed by the American theoretical neurophysiologist William Calvin. Its premise is that while the speculative, sometimes fantasia-like, quality of “analytical grammars” is to be celebrated, a closer alignment between them and “compositional” and “listening” grammars represents an ideal to which music theory and cognitive science should strive.⁽¹⁾ I therefore take a tentative step in the direction of integrating these three syntaxes under the aegis of Darwinian thought, contending that memetics, cognitive science, and music theory can interact synergistically in order to refine memetic accounts of music, to advance understanding of music cognition, and to develop richer theoretical accounts of music.

[2] The philosopher and evolutionary theorist Daniel Dennett condenses evolution by natural selection to a three-stage algorithmic process, asserting that

evolution occurs whenever the following conditions exist: (1) variation: there is a continuing abundance of different elements [;] (2) heredity or replication: the elements have the capacity to create copies or replicas of themselves [;] (3) differential ‘fitness’: the number of copies of an element that are created in a given time varies, depending on interactions between the features of that element and features of the environment in which it persists (Dennett 1995, 343).

[3] Calvin refines this scheme, identifying “six essential aspects of the creative Darwinian process that bootstraps quality”:

(1) There must be a reasonably complex pattern involved. (2) The pattern must be copied; that which is copied may serve to define the pattern. (3) Variant patterns must sometimes be produced by chance. (4) The pattern and its variant must compete with one other for occupation of a limited work space. (5) The competition is biased by a multifaceted environment (natural selection). (6) There is a skewed survival to reproductive maturity (environmental selection) or a skewed distribution of those adults who successfully mate (sexual selection); new variants preferentially occur around the more successful of the current patterns (after Calvin 1996a, 21).⁽²⁾

[4] The advantages of these substrate-neutral formulations are that they allow one to see instantiations of the algorithm in realms other than the biological. Indeed, Dawkins goes so far as to posit a “Universal Darwinism,” hereafter “UD,” asserting that “we must begin by throwing out the gene as the sole basis of our ideas on evolution...Darwinism is too big a theory to be confined to the narrow context of the gene” (Dawkins 1989a, 191). For Plotkin, however, Dawkins’ intent in his classic formulation of UD (Dawkins 1983a) is primarily to hypothesize the origin and evolution of life on other worlds; yet Plotkin contends that

Darwinian evolution is also operating to produce the transformations in time that we see in certain other spheres, such as immune system function and even the way science itself operates. This is not a new position. It began with Darwin himself and with his friend T.H. Huxley. It has been developed by a number of eminent scholars in the last 140 years...in at least some respects, our brains are Darwin machines too, and the way in which we gain knowledge is another form of universal Darwinism (Plotkin 1995, xviii).

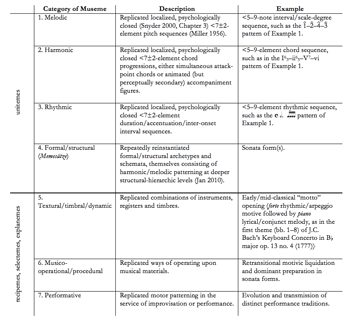
This is an oblique reference to one of Dawkins’ signal contributions, for in rejecting the “narrow context of the gene,” he is positing the extension of the evolutionary algorithm to the realm of human culture, to which Plotkin alludes in his reference to “the way science itself [as a cultural process] operates.” This extension is the basis of the field of memetics (Blackmore 1999), the study of self-replicating particles in the realm of human culture, including music.

[5] The central thesis of UD is that the evolutionary algorithm operates across a variety of systems and substrates—media within which heredity, variation, and differential fitness can be implemented, and in which quality and complexity can be bootstrapped. UD therefore encompasses physics (the theory of evolutionary physics and the selection of alternative universes (Dennett 1995, 177; David Deutsch 1997)), biology (both terrestrial and, in principle, extra-terrestrial; immunology), culture (both human and non-human (Laland and Galef 2009)), and cognition (evolutionary epistemology (Campbell 1974, 1990); the brain as a Darwin machine).

[6] In biological evolution the substrate is DNA, and a distinction can be drawn between a chemical configuration (an arrangement of nucleotides) and the information this configuration encodes. Similarly, in cultural evolution a distinction obtains between a biological configuration (a constellation of neurons) and the information it encodes. In Delius’s beautiful formulation,

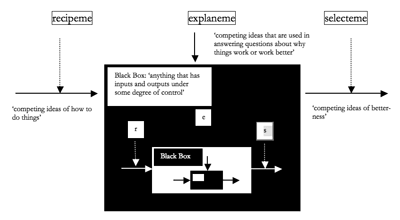
[a]ny cultural trait taken over by a given individual from another individual must accordingly be thought of as the transfer of a particular pattern of activated/inactivated synapses from the associative networks of one brain to another...Naturally the synaptic constellation that a trait has in one brain will not be geometrically arranged in exactly the same way as the pattern that the same trait has in another brain...Functionally however, the two patterns could still be equivalent when effectively identical traits were represented in memory. In any case, following Dawkins...synaptic patterns that code cultural traits will be called memes, by analogy with the molecular patterns that code biological traits and which are called genes (Delius 1991, 82–3).

[7] Synaptic constellations are the mechanism by which memory is implemented in living organisms. More broadly, all forms of complexity in the universe require some form of memory, a method of preserving the hard-won information content of the system against environmental depredations; there could be no development without some means of sustaining it long enough for it to be copied or transmitted. In view of this, memory is sometimes defined in too narrowly human terms: to recall the above equation, the configurations of DNA are a form of memory for the information held by genes.

[8] An understanding of the psychology and neurobiology of memory is central to the development of memetics as a metatheory of human culture, although it is worth noting that evolutionary biology made considerable advances while ignorant of the detailed mechanisms of heredity. One reason for the centrality of memory to memetics is that it constitutes an environmental invariable or constant for memes in the same way that the laws of physics and chemistry constitute an environmental invariable for genes. A meme can no more transcend the constraints of memory than a gene can escape the valencies of carbon chemistry—in our universe, at least. Such factors constitute some of the most important “compositional [and listening] constraints” identified by Lerdahl, and they powerfully select what can and cannot exist as a meme in music (Lerdahl 1992). They ought also to serve as “theoretical constraints,” because it surely behooves music theory to accord with known principles of perception, cognition, and memory, either generally or in terms of their specific interpretation by memetics.

[9] In view of this, I aim here to apply Calvin’s hexagonal cloning theory (hereafter “HCT”), one of the most compelling and powerful accounts of memory, to certain aspects of the model developed in The Memetics of Music (Jan 2007) in order to hypothesize aspects of the underlying mechanism for a memetic theory of music. From a Darwinian hypothesis for observed pattern replication in music, I progress, via a consideration of psychological constraints, to a discussion of the neurobiological mechanism. I shall: i) recapitulate the precepts and predictions of UD and meme theory as to what might constitute a meme in music (Section 2); ii) outline current understanding of the psychology of musical memory (Section 3.2) before summarizing Calvin’s general Darwinian-neurobiological perspective on information storage and recall (Section 3.3); and then iii) relate i) and ii) by hypothesizing how certain types of musical memes might be implemented by Calvinian mechanisms (Section 4). I conclude by considering neural network models of memory, one system developed by Gjerdingen aligning broadly with certain aspects of Calvinian theory (Section 5).

[10] This approach cannot necessarily determine the veracity of memetics. A psychological and/or neurobiological account might not be able to falsify memetics’ claims (in the Popperian sense (Papineau 1995)) on the grounds that the underlying psychology and/or neurobiology does not support them, for if the psychology and/or neurobiology is neutral in this respect, then only weight of evidence can serve to convince one of the truth of memetics, a situation not dissimilar to that obtaining with epistemological support for Darwinian evolutionary theory in general. Also, given the vast literature on perception, cognition, and memory, it is clearly beyond the scope of this article to offer a comprehensive treatment in which memetics is weighed and tested against every extant theory. Calvin’s model is chosen as the basic conceptual framework on account of a number of factors, including its parsimony, its concordance with empirical data on brain function, its ready applicability to a variety of musical data-representation problems, and its explicitly Darwinian orientation, which readily accords with a memetic perspective. Although Calvin regularly uses music to illustrate his model, his examples are generally metaphorical and often somewhat basic and so, while grounded on his ideas, my treatment goes beyond the musical content of his theoretical writings.

2. Precepts of Memetics and Categories of Musemes

[11] In addition to learning various motor skills essential for music’s re/production, we acquire by enculturation a lexicon of musical patterns. Transmitted “vertically” and “horizontally” between individuals by imitation (Shennan 2002, 48–51; Blackmore 1999, 47–51), these patterns constitute memes in music, or musemes.⁽³⁾ We learn them as discrete patterns because human memory, having evolved strategies to minimize overload and maximize efficiency, tends to partition information digitally in ways which are described by gestalt psychology and derived theories, rather than learning them as analogue information streams. As well as learning patterning, we also learn the ways in which those patterns may be arranged; that is, we learn a syntax which describes and prescribes legitimate combinations of patterns. This grammar is a description of patterns at more remote structural-hierarchic levels, these higher-level musemes resulting from the tendency of lower-level musemes repeatedly to form a multitude of structure-generating collections (Jan 2007, 227–30).

[12] Because musemes exist as discrete units, because they are transmitted between individuals, and because such transmission is often imperfect, the sphere of human cultural information supports the operation of the Darwinian algorithm: musemes evolve selfishly (Dawkins 1989a) as a result of the operation of principles parallel to those driving biological evolution. Fundamentally this evolution affects the brain-encoding of musemes (the memotype (Jan 2007, 28–31)), just as evolution by natural selection ultimately affects genes; but it is manifested in the cultural products of such code (the phemotype; the music, in all its manifestations).

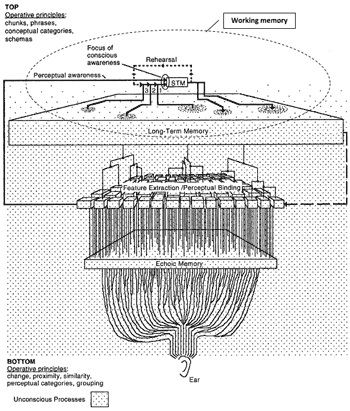
[13] As Table 1 indicates, it is possible to outline a number of parameter-specific museme forms ranging from the localized and specific—the most tangible and real examples of musemes—to the more distributed and generalized—the most intangible and virtual. These categories are not hypothetical but empirical: they accord with that which is heard and observed (analytically and musicologically) to be replicated. It would not be possible, for instance, to hypothesize a category of textural/timbral/dynamic museme were it not for observed recurrences of such patterning in numerous real musical contexts. Unsurprisingly, they do not conflict with what is currently understood of the psychology of pattern perception, cognition, and memory.

[14] Meyer distinguishes between “primary” and “secondary” parameters (Meyer 1989, 14–16). Musemes in the former category, the four above the bold line in Table 1, range from small-scale patterns in pitch and rhythm to more extended patterning at the level of the phrase, section, and global structure. Musemes in the parameter of pitch are not always easily untangled, however. In particular, there is no category of “contrapuntal museme” in between categories one (melodic museme) and three (harmonic museme) of Table 1. This is because a contrapuntal combination of melodies will generally devolve to both replicated horizontal pitch sequences and an implied harmonic progression. A chord sequence might therefore be generated as a shallow-middleground-level structure by a series of interlocking contrapuntal melodies; or it might be presented as a foreground-level progression of sustained chords; or it might arise from some intermediate combination of these extremes. Rather than constituting a distinct and separate type, musemes in category four are perhaps best regarded as occupying the far end of a continuum which, at its beginning, encompasses certain replicated shallow-middleground-level structures, such as those underpinning various melodic schemata (for example, Gjerdingen’s $\hat{1}$–$\hat{7}$...$\hat{4}$–$\hat{3}$ (“Meyer”) schema (Gjerdingen 1988; 2007, 112; see also 459)) and stereotypical phrase types (such as the antecedent-consequent formula).

[15] More cryptically, and apropos the three categories below the bold line, some musemes do not exist as (primary) patterning in pitch and rhythm but, in the case of textural, timbral, and dynamic musemes, are replicated in the secondary parameters as ways of nuancing the primary parameters (and therefore being logically dependent upon them). Musico-operational/procedural musemes are ways of manipulating primary- and secondary-parameter patterning, and include such operations as transposition, inversion, and other more individualized techniques, which may be motivated/mediated by the theoretical literature known to composers directly or indirectly, through their enculturation. Performative musemes are arguably the most complex of the seven categories, in that they integrate memory for primary-parameter patterns with the muscle-memory sequences which control their shading by secondary parameters (Leech-Wilkinson 2009).

[16] One way of understanding categories five to seven of Table 1 is to invoke Langrish’s notion of “recipemes, selectemes and explanemes” (Langrish 1999). Concerned that memetics has to date relied too heavily on the idea of unit replication operating predictably according to a limited set of laws (this paradigm influenced by what he regards as a physics-based (“P”) view of the world), he argues for the corrective invocation of a more fuzzy, nested view of replication operating unpredictably according to a broader set of laws (this paradigm influenced by a biology-based (“B”) perspective) (Langrish 1999, Section 1). While P and B are perhaps not as easy to distinguish as Langrish implies, representing what might be regarded as the extreme points of a continuum, museme categories one to four are more amenable to a P view, whereas categories five to seven accord more closely with a B view. Figure 1 represents and defines these three Langrishian meme-types (definitions are taken from Langrish 1999, Sections 4.2 and 4.3).

[17] A brief discussion of the application of these terms to music will help flesh out the definitions in Figure 1. While “[k]nowing how to do something often involves ‘finger tip’ knowledge which can only be obtained through doing” (Langrish 1999, Section 4.2), many musical recipemes are more abstract. A good example is the case of the sonata-form retransition (which may serve as a microcosm of the mechanics of composition more generally). In crafting this section of the form, the “something” that composers need to know includes how to effect motivic liquidation (Schoenberg 1970, 58) in the context of a dominant prolongation in ways which maintain interest and create expectation in the listener. The composer may arrive at a variety of solutions which are tested according to various criteria of satisfactoriness—against a range of selectemes (which themselves “compete with other selectemes” (Langrish 1999, Section 4.2))–in order to determine the optimum solution in the given context. At a deeper level, a composer will wish to understand, via an appropriate (and selecteme-filtered) explaneme, not just what solutions to the problem of the retransition work best, but why they are effective, both for reasons of intellectual curiosity and, more pragmatically, in order to facilitate repeatability.

[18] While somewhat sketchily formulated, Langrish’s notion of the black box refers to “anything that has inputs and outputs under some degree of control” (1999, Section 4.2). It appears to relate to any collection of processes (such as may occur both within and without the brain) in which inputs give rise to outputs under the influence of recipemes and selectemes. As will be argued later, it might be understood to be operationalized in Calvin’s (grey) cortex, the site of violent Darwinian copying and selection processes (Calvin 1996a, 99–101). Whereas recipemes determine what enters the black box, and selectemes evaluate what exits, explanemes are “ideas about what is happening inside the black box”—how its internal processes are operating (Langrish 1999). Note that the concept of the black box allows both chaining (the output of one black box serving as the input to another) and nesting (Langrish uses the metaphor of Russian dolls (1999, Section 2.2)), the latter concept represented by the three levels of hierarchic inclusion in Figure 1.

[19] Musemes in categories one to four are clearly substantially different from those in categories five to seven, and this ontological distinction has profound methodological implications for memetics. Given their orientation to the P end of the continuum, musemes in the former group, labeled unitemes in Table 1, are relatively simple, discrete, and objective. They exist as short sequences of pitch or rhythm or, in the case of formal/structural musemes, they can be represented relatively easily as, in effect, short structure-marking melodic and harmonic patterns spread out over time by intercalated material. They are thus fairly readily definable and categorizable, most easily according to their occurrence in musical scores. By contrast, musemes in the latter group are, given their orientation to the B end of the continuum, more complex, blended and subjective. The main traces of their activity left behind are the sequences of unitemes their operations motivate. Whereas studies of memetics in the humanities and social sciences have tended to focus on the latter (B) types of memes (particularly upon the interactions between and evolutionary success of ideas in culture), music tends to lend itself more readily to be studied in terms of the former (P) types, in terms of chunks of sound demarcated from their surrounding information. These leave a visible trace as graphical analogues to the parcellated sound waves which survive long after the instruments and voices have stilled (Jan 2007, 31). In view of this distinction, and owing to constraints of space, I shall consider only the former group here, and with particular reference to melodic and harmonic musemes.

3. Models of Memory

3.1. Overview

[20] Models of memory might be divided into two broad categories, the neurobiological and the psychological. Essentially they hinge on the apparent dichotomy between the brain and the mind; but unless we wish to fall back upon a hackneyed Cartesian dualism it is necessary to accept Warnock’s view that

mental events and events in the brain are in some sense identical events, not that one kind causes the other, nor that each happens coincidentally or in parallel with the other, but that they are the same happening. Such a view is widely held and is now generally known as Identity Theory (Warnock 1987, 3; see also Ryle 2000).

In this sense models in different categories are not strictly separable; moreover, in a pragmatic sense, a psychological model of memory which does not attempt to take into account the nature of the underlying neural substrate is almost as inadequate as a neurological model which does not relate to observable facts of mind. Nevertheless, the latter is arguably more deficient, for a psychological account of memory may be empirically verifiable even if its underlying neural substrate is unknown.

[21] Any attempt to understand memory, in connection with memetics and more broadly, must account for the diversity of mental phenomena subsumed under the term. In view of this,

[i]t is better to think [of memory] in terms of a continuum, at one end of which is the mysterious phenomenon of consciousness. Somewhere along the line animals must begin to know what they are doing in remembering. There is a distinction to be drawn at the edges of the continuum between habit memory and conscious memory. But neither is irrelevant to the other (Warnock 1987, 14).

This continuum is in part a consequence of the interconnectedness of the brain’s functions, which cannot be neatly parceled into discrete competences. Many capacities overlap owing to shared neural substrates, and so it is difficult to draw a clear distinction between such attributes as perception, cognition, memory, imagination, and motor action, and the complex role consciousness plays in these. Perceptions and actions may become encoded as memories, and then go on to serve as the basis of imaginative re-perceptions (in music, internalized replayings of remembered—and fresh—sounds (Halpern 2003)), of expectations, or of imagined or real actions. As Warnock notes, “memory and imagination overlap and cannot be wholly distinguished. Both consist in thinking of things in their absence” (1987, 12). In this connection, perception (both sensory and proprioreceptive) is of particular importance for, as the gatekeeper of memory, it dictates the nature of the information passing to higher brain centers and therefore indirectly shapes the content of culture.

[22] To consider all of these phenomena is beyond the scope of this article. I shall therefore focus here upon memory in a fairly restricted sense: on memory for the musemes encompassed by categories one to four of Table 1; and the frame of reference will be Euro-centric, concentrating on patterning in western music. I do not deal with the role of emotion and affect in memory (for an up-to-date account, see Juslin and Sloboda 2009), although these factors have an important role to play in determining what is retained and the strength and durability of these memories; or with how memory for abstract patterning is associated with that for verbally-expressible concepts. Even with this restricted remit, however, it is necessary to consider certain related subjects, such as expectation and probability. Given the guiding orientation around evolutionary theory, however, my principal focus is essentially upon memory insofar as it shapes musemes, and to the wider implications for memetics and music theory.

3.2.Psychological Models of Memory

[23] Psychological models attempt to take into account a number of observed attributes of and constraints on memory, such as volatility (the time span of information persistence), the extent to which stored information is accessible to consciousness, and the nature of that which is retained.⁽⁴⁾

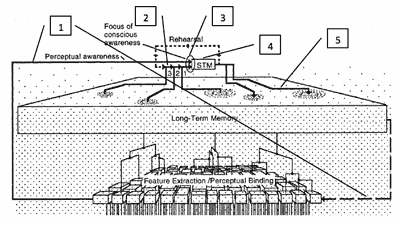
[24] Snyder’s is the most comprehensive recent psychological account of musical memory, being a condensation of a wide range of recent research (Snyder 2000, 2009; see also Važan 2000). A largely volatility-based model, it represents the structure of human memory in the diagram reproduced as Figure 2 (Snyder 2000, 6; reproduced with permission). In brief, incoming signals from the ear are sustained at the level of echoic memory (hereafter “EM”) before passing to the feature extraction/perceptual binding (hereafter “FE/PB”) stage (see Stainsby and Cross 2009 for a discussion of the anatomy, physiology, and psychoacoustics of these processes). Here, and before reaching higher brain centers, a preliminary categorization of incoming data is made, according to the primary musical parameters of pitch and duration and partly with reference to existing knowledge stored in long-term memory (LTM). Some of this data will go beyond perceptual awareness and enter the focus of conscious awareness, whereupon it can be sustained in short-term memory (STM), in which information may persist for 3–5 seconds, longer with rehearsal (Snyder 2000, 9), and which normally encompasses, in Miller’s classic formulation, “seven, plus or minus two” elements (Miller 1956). Some information in STM may pass into LTM (where it may be retained for decades) and, importantly, some existing LTM information (perceptual and conceptual categories) will influence the content of STM (Snyder 2000, 5–12; 2009, 109). Recent refinement of STM by means of the concept of working memory (WM) attempts to account more fully for this input of LTM into STM; Snyder suggests that WM “is an umbrella [term] for a number of distinct memory phenomena that all have limits in the time range of several seconds” (Snyder 2009, 109; see also Snyder 2000, 48–9).⁽⁵⁾

[25] In terms of the nature of that which is retained, Snyder’s model encompasses a number of distinctions. That drawn by Tulving between episodic and semantic memory distinguishes between diachronic (memory of a sequence of temporally connected events) and synchronic (memory of concepts, often highly networked) storage respectively (Snyder 2009, 108). A further distinction, between explicit and implicit memory, acknowledges that not all that we remember is overtly accessible to consciousness and readily amenable to verbal description. The implicit category (Warnock’s “habit memory”) relates to acquired skills in motor control such as those required for instrumental performance (Snyder 2009, 108). A third distinction, that between recognition, identification, and recollection, relates respectively to the capacities of understanding something to be familiar upon seeing or hearing it, of associating the familiar object with the memory of its name, and of retrieving this pairing (Snyder 2000, 10–11).

3.3. A Neurobiological Model of Memory: Calvin’s Spatiotemporal Hexagonal Cloning Theory

[26] Since the 1940s a significant body of research in the neurosciences, particularly that of Donald Hebb and later of Vernon Mountcastle, has suggested that cells in the cerebral cortex are not randomly or irregularly spaced (as might be implied by Delius’s term ‘constellation’ in the quotation in Section 1) but are grouped in columnar assemblies of synchronously firing neurons which are themselves organized in a broadly geometric fashion (Hebb 1949; Mountcastle 1957, 1978, 1997). Perception, learning, recognition, and memory has been accounted for by the relative strengths of interconnections, and their fluctuations over time, between such columns. More recent work has attempted to read and model, both theoretically and computationally, the operation of Darwinian processes in such interconnections (Leng et al. 1990; Leng and Shaw 1991).

[27] One of the most powerful columnar theories of brain function of recent years has appeared in the work of Calvin (Calvin 1996a, 1996b, 1998). His model overlaps in significant respects with other columnar theories, and so can be regarded as a particular interpretation placed upon a set of broadly accepted principles. Perhaps more so than other columnar theories, Calvin’s is a full-blown Darwinian model of certain of the brain’s functions, including information encoding, propagation, and recall, and based upon his concept of “mosaics of the mind.” This phrase, he argues,

is not just a literary metaphor. It is a description of mechanism at what appears to be an appropriate level of explanation for many mental phenomena—that of hexagonal mosaics of electrical activity, competing for territory in the association cortex of the brain...The pattern within each hexagon of this mosaic may be the representation of an item of our vocabulary: objects and actions such as the cat that sat on the mat, tunes such as Beethoven’s dit-dit-dit-dah, images such as the profile of your grandmother, a high-order concept such as a Turing Machine—even something for which you have no word, such as the face of someone whose name you haven’t learned. If I am right, the spatiotemporal firing pattern within that hexagon is your cerebral code for a word or mental image (Calvin 1996a, 2).

[28] To understand how this “mechanism” operates, it is necessary briefly to review some aspects of the brain’s anatomy, specifically that of the cerebral cortex, the 2 mm-thick outer layer of the cerebrum whose characteristic concave furrows (the sulci) and convex ridges (the gyri) allow a relatively large surface area to be accommodated within the skull. While some areas of cortex are devoted to sensory perception and others to motor control, a third type, the “association areas,” are believed to be responsible for abstract thought and decision making. The cortex may be subdivided into six layers, each of which has a distinct function, differences in the structure and function of these allowing Brodmann to map the cortex into fifty-two distinct areas (Brodmann 1909), since further subdivided (see Parsons 2003 for an overview related to music). In Calvin’s desk-tray metaphor, the intermediate layer 4 is an “in” tray, receiving messages from other parts of the brain; the deep layers 5 and 6 are the “out” tray, sending messages to other parts of the brain; and the superficial layers 1, 2 and 3, with which his theory is primarily concerned, are the “internal” tray, “specializing in the interoffice memos” (Calvin 1996a, 30).

[29] The cortex is populated by “pyramidal neurons” (tree-like nerve cells with the cell body at the base of the trunk), “basal dendrites” forming the roots (which send out “axon branches” to communicate, via a synapse or junction, with the dendrites of other neurons), and with the upper branches as the “dendritic tree” (forming an inverted pyramid). As mentioned, these neurons are organized vertically into clusters of interconnected cells with relatively less densely populated areas between them, forming a polka-dot pattern perpendicular to the surface of the cortex (Calvin 1996a, 26, 29). Calvin defines such “minicolumns” as “a cylindrical group of about 100 neurons extending through all the layers of neocortex and about 0.03 mm in diameter” (1996a, 205).⁽⁶⁾

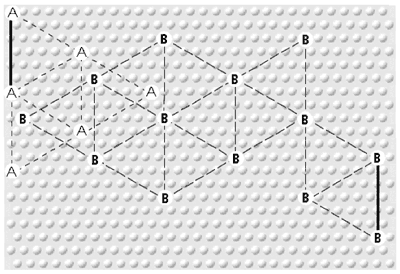
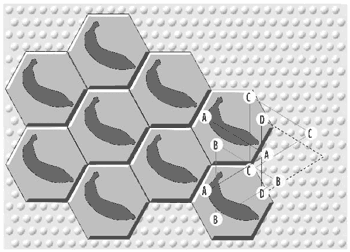
[30] Although widely interconnected, local inhibition—what Calvin calls, apropos Conan Doyle’s short story Silver Blaze (1892), “the dog that didn’t bark in the night” (Calvin 1996a, 31)—means that a minicolumn tends to communicate not with its immediate neighbors, but with more distant minicolumns, generally those c. 0.5 mm distant. Such inhibition constitutes a type of automatic gain control (AGC), “useful for avoiding a fog of the characteristic patterns” (1996a, 77). If two minicolumns are tuned to—if they are a “fan” of (1996a, 43)—the same stimulus (a feature of the environment, an object or a concept), interconnections between them result in their tending to resonate together, such entrainment creating a pair of synchronously firing minicolumns. Further recruitment of equidistant minicolumns tends to result in the formation of roughly triangular arrays, owing to the fact that minicolumnar interconnections are described by an annulus radiating from the starting point (1996a, 34). If an object were being attended to or remembered, its color might be encoded by one set of triangular arrays, its shape by another, and its smell by yet another.

[31] This network of “interdigitating” (Calvin 1996a, 118, 179) triangular arrays is represented in Figure 3, in which the raised dots represent the c. 0.03 mm diameter minicolumns and the distance between points with the same letter name (each triangular collection representing a feature or attribute) is c. 0.5 mm (Calvin 1996a, 44; reproduced with permission). “Reality” is normally represented by “four or more sets of triangular arrays” (1996a, 62). Interdigitation is therefore normally associated with coordination of attribute/parameter representation, but “triangular arrays might [also] interdigitate without interaction” (1996a, 118), interdigitate competitively, or even interdigitate mutationally (see 4.1.2, “Museme Mutation”).

[32] As the central “B” array of Figure 3 shows, the most parsimonious geometrical representation of a network of interconnected triangular arrays is the hexagon. As with the triangular arrays, the hexagons are not strictly geometrical, particularly in places where a gyrus folds over into a sulcus, but they are not dissimilar to this shape. Moreover, whereas the triangular arrays are real phenomena in brain tissue, the hexagons are a virtual artefact, a way of modeling the operation of triangular array proliferation. As Calvin argues,

[t]he hexagon is a committee comprised of one member from each of a number of different triangular arrays...If you also consider what cells must remain silent [the mute canine] to avoid fogging the characteristic pattern, the cerebral code for [object/concept] occupies the full hexagon...Because it takes two cells 0.5 mm apart to start generating a triangular array, the minimal Hebbian cell-assembly [Hebb’s 1945 precursor to Calvin’s triangularly interconnected minicolumns] is two adjacent hexagons worth of the characteristic spatiotemporal [firing] pattern (1996a, 45, 47).

[33] Delius’s “constellation” is thus made Euclidean in Calvin’s theory, and despite Delius’s claim that “the synaptic constellation that a trait has in one brain will not be geometrically arranged in exactly the same way as the pattern that the same trait has in another brain” (Delius 1991, 82–3), there may well be more inter-brain similarity between meme-representations than he suggests. If so, this might lead to what Dennett calls an “unlikely blessing”: the situation, “certainly not necessary” for the progress of memetics, “that we will someday discover a striking identity between brain structures storing the same information, allowing us to identify memes syntactically” (Dennett 1995, 354). In this sense, Calvin’s is a syntactic theory of meme structure.

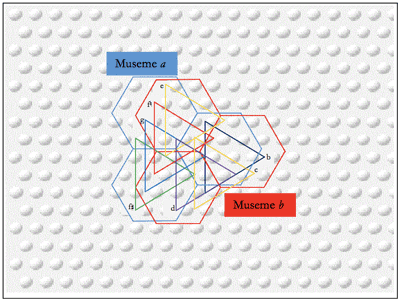
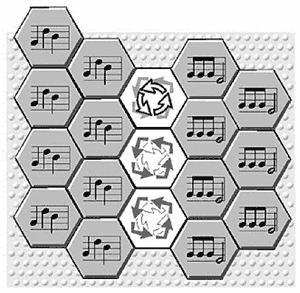
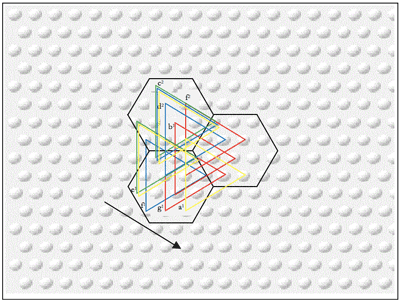
[34] Figure 4 (Calvin 1996a, 48; reproduced with permission) shows Calvin’s representation of an object, in this case a banana, as a mosaic made up of a number of hexagonal areas of cortex tiling the upper layers of cortex in the manner, to use his metaphor, of concrete pavers arranged on a mortar bed to make a patio (1996a, 55–7).⁽⁷⁾ As noted above, attributes of the object or concept (in this case the banana’s color, shape, and smell) are encoded by individual triangular arrays. While a static object such as a banana might be encoded by a purely spatial pattern of hexagons, a sequential pattern, such as a motor action or a melodic phrase, is encoded by hexagons whose triangular arrays fire in a specific order, Calvin’s “spatiotemporal pattern.” Our recognition of an object (our understanding, for instance, that an observed item is a banana, not an apple) is represented by the successful cloning of the “banana” hexagonal pattern over the surface of the cortex, out-competing the rival “apple” interpretation.

[35] The notion of cloning and competition between hexagonal patterns makes clear the explicitly Darwinian aspect of Calvin’s theory. In parallel with the struggle between species for the limited resources of the natural world, our mental life—the interpretations we place upon our sensory perceptions, the ideas which occur to us, the memories we cherish and the decisions we make—is dictated by the outcome of Darwinian competition between rival territories of hexagonal mosaics fighting for the limited territory of cortex. Beyond a certain critical expanse of hexagonal plating, an idea comes to mind, a memory is recalled, a decision is made and a conclusion is reached about a sight, sound, touch, taste, or smell; in all these cases, the success of the victorious pattern is marked by its entry into Snyder’s “focus of conscious awareness.”⁽⁸⁾ In this sense, the HCT is not just a theory of memory, but also one of perception, cognition and even (in the case of patterns regulating motor control) one of action.⁽⁹⁾

[36] Calvin balances the partly “soft-wired” (real-time) nature of hexagonal cloning competitions by certain “hard-wired” (persistent but acquired, not innate) factors, the latter accounting, among other things, for LTM. One outcome of a successful competition might be changes in the underlying neural connectivity which can bias the cortical environment in favor of another success for the pattern in a future cloning competition. While the causes for such bias are varied, one such is the increase in synaptic strength termed long-term potentiation (LTP), responsible for the creation of “Hebbian” synapses.⁽¹⁰⁾ Calvin explains this phenomenon partly in terms of ideas from chaos theory, specifically the notion of the attractor. He contends that

‘[c]apture’ is another aspect of resonance/attractors that will be useful here: a spatiotemporal pattern that comes close to an attractor’s pattern will be altered to conform with that of the attractor. When [driving a car] you feel captured by that washboarded road, it’s because you really are being shoehorned into an attractor. This convergence is another way of saying that attractors have a basin of attraction, a wide set of starting conditions that all eventually lead into the same attractor cycle (1996a, 68; emphasis in the original).

[37] To express this metaphorically, the vertices of the triangular arrays (the minicolumns to which the sides point) are situated in depressions in the gravel upon which the hexagons are overlaid. Rolling a marble along the unpaved surface is likely to result in the capture of the marble in the basin of attraction represented by the depression. Thus the embedded attractors determine the nature of that which may be cloned across them and account for the memory of previously cloned patterns. A given area of cortex can contain hundreds of such imprinted biases—LTMs, together with fading STMs—which, to change the metaphor, Calvin imagines as existing in the form of numerous layers, arranged like the thin, overlapping slices of fish in the Japanese delicacy sashimi (Calvin 1996a, 107). Older configurations of attractor bias are overlain by more recent ones, but all layers are in principle capable of exerting their influence “upwards” to influence the current pattern of connectivity (1996a, 106). This mechanism accords with Snyder’s view that “it is probably best to think of LTM and STM as two memory states—two processes taking place within one memory system—rather than as two completely independent memory systems. Short-term memory may be the part of long-term memory currently most highly activated” (Snyder 2000, 9; emphasis in the original).

[38] An important facet of columnar theories of neocortical function—and one not necessarily in contradiction to the Lockian position articulated in Section 2—is their contention that “humans start with some basic structure...in the brain around the time of birth, giving rise to a huge repertoire of inherent spatial-temporal firing patterns” (Leng and Shaw 1991, 252). This implies that the neonate brain has the neuronal foundation for all possible memes already provisionally laid out in its connectivity before any learning begins, and that exposure and enculturation reifies these inherent possibilities. With a normal complement of 10¹⁰ neurons linked by 10¹⁴ synapses this seems eminently feasible (Leng and Shaw 1991, 241, Fig. 7). In terms of Calvin’s metaphor, this “formatting” of the neural hard drive is akin to the foundations of a patio, with a near infinite number of possible paver arrangements tentatively marked out with billions of wooden pegs and millions of miles of string arranged on top of the vast expanse of the mortar bed.

[39] In this sense, the neonate cortex is, in Borges’ terms, a potential “Library of Babel,” or a multimemetic hypervolume encompassing all possible memes, which awaits the activation and attractor embedding induced by environmental stimulation (Jan 2007, 196–201). To paraphrase Borges, “the cortex is total and its gyri and sulci register all the possible chunk-sized combinations of the twelve pitch classes and rhythmic patterns (a number which, though extremely vast, is not infinite): in other words, all that it is given to express in all musics” (after Borges 1970, 81–2).

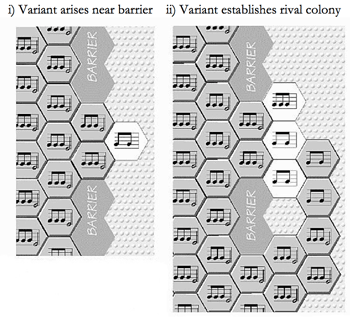
[40] In the light of these various neurobiological observations, we might reimagine Dawkins’ definition of the meme—“a unit of cultural transmission, or a unit of imitation” (Dawkins 1989a, 192; his emphasis)—in explicitly cortical terms by integrating the HCT with it. At its most fundamental level (i.e., the memotype, as opposed its phemotypic products), a meme is

an imitation-transmitted replicator existing as a sound/image/concept-encoding, quasi-stable, periodic SFP which is embedded as a series of attractors in the underlying minicolumnar connectivity of the cortex by recurrent excitation resulting from sensory or motor input and which is capable of colonizing large areas of cortex (and of other brains’ cortices) according to Universal-Darwinian principles of replication, variation, and selection.

4. Musemes and Memory

[41] I now attempt to map museme categories 1, 2, and 4 in Table 1 against the HCT outlined in Section 3.3. As with the order followed in Section 3, I discuss the observed psychological phenomena and constraints first and then apply Calvin’s theory as a hypothesized neurobiological mechanism for their implementation.

4.1. Melodic Musemes

4.1.1. Psychological Constraints on Melodic Musemes

[42] Melodic musemes arise from processes operative at both the “atomic” (or phonological) and the “molecular” (or lexical) levels. The former is the level of the musical event, a specific and discrete pitch sustained for a specific time interval; the latter is that of the event sequence, a higher-order grouping or collection of connected events which, if replicated, becomes a museme (Snyder 2000, 32).⁽¹¹⁾ Events are engendered by primitive (bottom-up) grouping and event sequences by a combination of both primitive and learned (top-down) grouping (Snyder 2000, 32–3).

[43] The two grouping processes are implemented by different parts of the system represented in Figure 2. Primitive grouping is principally implemented at the levels of EM/FE/PB, wherein a fuzzy and analogue data input is discretized into pitches and rhythms (events), which are then further grouped into discrete collections (event sequences). The formation of event sequences operates according to processes described under the rubric of gestalt psychology, being mediated by proximity, similarity, and continuity (common direction/fate) between events.⁽¹²⁾ Learned grouping is largely accomplished by mapping event sequences against patterning already stored in LTM (I term this coindexation-determined segmentation in Section 4.1.2). Primitive and learned grouping interact within STM (but see also point 1 after Figure 7), in that event sequences held in STM are provisionally gestalt pre-partitioned, but are subject to revision in the light of information stored in LTM, which either supports or contradicts those partitionings which are not unambiguous. While the notion of learned grouping might be taken strictly to apply to the recognition of incoming information already stored in LTM (grouping by identity), a sound stream might be segmented by learned grouping if incoming information maps onto broadly analogous stored material (grouping by similarity).

[44] Event sequences are shaped by the two principal constraints operating upon STM, namely time (3–5 seconds is the normal temporal window of STM) and length (the Millerian <7±2 elements is the normal event-limit of STM). Snyder argues that these two constraints operate independently, in that

the formation of [provisional] boundaries takes place in the early processing stage, before information persists as short-term memory. This means that although a single grouping cannot exceed the time limit of short-term memory, grouping is independent of the structure of STM: more than one melodic or rhythmic grouping [and more than one boundary between two or more groupings] may exist within the time limit of STM (Snyder 2000, 34–6; emphases in the original).

[45] The four-way interaction between the time and length constraints of STM and the interactions between primitive/gestalt forces and learned/schematic knowledge lead to musical data streams being “chunked” into discrete units (Snyder 2000, 53–6). Chunking acts to produce units which are sustainable by rehearsal in STM and which can, therefore, be preserved over more extended time spans in LTM. Chunking is a hierarchical process in that “[w]hole chunks at ‘lower’ levels in the hierarchy [such as <7±2-element pitch sequences] become the elements of chunks at ‘higher’ levels [such as <7±2-chunk phrases]” (Snyder 2000, 55). The limit to such “hierarchical rechunking” is estimated at five levels, even though this might violate the time (but not the Millerian) constraint of STM (Snyder 2000, 55). Two levels appear to be normal in musical processing.

[46] Chunking is the driving force behind the genesis of musemes. If the psychology of pattern perception, cognition, and memory limits the size and number of entities which can be sustained in STM, and if this constraint leads to the existence of relatively short, particulate segments of musical material, then these units may possess sufficient longevity, fecundity, and copying-fidelity (Dawkins 1989a, 18, 194) to motivate and survive a process of copying which initiates the Darwinian algorithm. On this reasoning, music based upon a continuous (analogue) pitch spectrum, such as much electroacoustic music, appears inherently less amenable to musemic propagation than that based on a categorized (digital) spectrum (see Adkins 2007, 2009). Indeed, from the perspective of production, composers have until relatively recently tended not to create music which is “cognitively opaque” to listeners (Lerdahl 1992, 115).

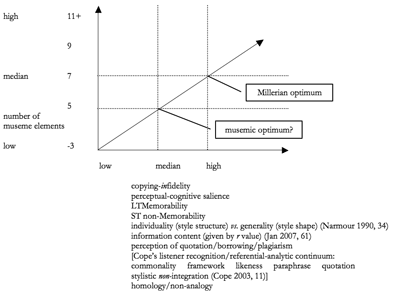
[47] Cope’s formulation of these issues is cast in terms of a “referential-analytic” continuum of “listener recognition” (Cope 2003, 11; Jan 2007, 37–8, Figure 2.2). He hypothesizes that those patterns with fewer than seven elements will tend to function as generic commonalities of a musical style, whereas those with more than seven will tend to acquire the singularity of a quotation. Figure 5 represents this diagrammatically, incorporating various other related concepts (after Jan 2007, 62, Figure 3.2).

[48] On Millerian grounds the optimum length for a museme would appear to be seven elements, although analytical study of music tends to suggest the value to be perhaps nearer five. While this hypothesis awaits confirmation, the further below this latter number of elements one descends, the more a museme appears to become a commonality of the style, as likely to arise spontaneously (analogously) as to be copied memetically (homologously). The further above this number of elements one ascends, the museme appears to gain too much singularity to withstand the dual pressure of copying-infidelity and (in the European tradition) the replication-impeding taint of perceived plagiarism.

4.1.2. Calvinian Implementation of Melodic Musemes

[49] While the relationship between memetics and the HCT is not explored in any depth in The Cerebral Code, it is clear that, beyond the fundamentally Darwinian orientation of his theory, Calvin adopts a memetic explanation for certain aspects of mental function, and he sees the hexagon (as noted in Section 3.3, strictly “two adjacent hexagons worth of the characteristic spatiotemporal [firing] pattern”) as the minimal neuronal implementation of a meme’s information content, its memotype. He argues that

[m]emes are those things that are copied from mind to mind...Cell division may copy genes, but minds mimic everything from words to dances. The cultural analog to the gene is the meme...; it’s the unit of copying...The spread of a rumor is cloning a pattern from one mind to another, the metastasis of a representation. Might, however, such cloning be seen inside one brain and not just between brains? Might seeing what was cloned lead us to the representation, the cerebral code? (Calvin 1996a, 18; emphasis in the original)

[50] Calvin’s exposition of the HCT is regularly illustrated with musical exemplars. These go beyond metaphor and offer suggestions as to how the theory might be adduced as a mechanism for musemic processes. For instance, the triangular arrays within a hexagon are variously described as being analogous to the individual instruments in a string quartet (Calvin 1996a, 40), to the separate voices in a choir, and to the individual keys of a harpsichord (1996a, 78). Apropos the second of these, he maintains that

...the choir coalesce[s] into sections [a hexagon], each of which sings the complete song. Unlike the placements favored by choirmasters, the sopranos are not grouped together; it’s more like each section has one soprano [or, to use the example from Section 3.3, the color of the banana], one alto [the banana’s shape], one bass [its smell], and so forth, each singing a different part [the triangular array coding each attribute]. Each section is surrounded by neighbors [adjacent, cloned hexagons], sections that are similarly diverse (Calvin 1996a, 39–40).

[51] Thus the hexagon can be understood as encoding a discrete, Millerian chunk of sequential information, encompassing one vertex from each of <7±2 separate triangular arrays with a particular firing sequence regulating the entrance of the voices. Note, however, that the “performance” of a melody is equivalent to a fugue made up of a one-note subject. The imposition of the Millerian chunking constraint at lower levels of the auditory nervous system (FE/PB) affects the number of triangle vertices encompassed by a hexagon and their firing quotient. Were this not so, then rather than containing a <7±2-part choir, a hexagon could encompass a multitude of parts, and melodic musemes could potentially be extensively serpentine.

[52] For this model to function as an account of pitch encoding, each minicolumn needs to be attuned to a specific pitch. While the neural substrate for pitch processing is incompletely understood, “[o]ne of the salient features of the auditory nervous system...is that a tonotopic organization exists from the earliest level of the periphery, at the basilar membrane [the locus of Snyder’s EM], to many fields within the auditory cortex. This topographic organization along the frequency axis points to the importance of pitch information in auditory processing generally” (Zatorre 2003, 233; see also Stainsby and Cross 2009, 48–9). Assuming the existence of repeating (triangle-distance) homotonal minicolumns, a given environmental pitch lights up a series of neurons from the cochlea to the surface of the cortex.

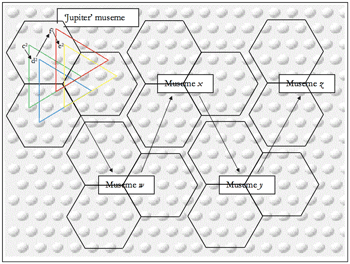
[53] Applying these principles to a concrete example, the pitch sequence shown in measures 1–4 of Example 1 above—Gjerdingen terms it the “Jupiter” schema (Gjerdingen 2007, 116–17)—may be represented by the spatiotemporal firing pattern (hereafter “SFP”) shown in Figure 6. Each of the four triangles codes for a specific pitch, and the firing sequence (indicated by the arrows) represents the diachronic ordering.⁽¹³⁾

[54] Exploring this process in its broader context, Figure 7 (after the upper part of Figure 2) indicates how Snyder’s model of music perception, cognition, and memory relates to and is implemented by the HCT. The five callouts appended to parts of Figure 7 are discussed below.

1. During audition of the passage in Example 1, incoming information from the peripheral auditory system eventually reaches auditory cortex. Having passed through the FE/PB stage it is already grouped into events and tentative event sequences, in this case a pattern of four notes, the “Jupiter” museme, followed by four other potential musemes, labeled w, x, y, and z in Example 1. Exciting minicolumns tuned to c², d², f² and e², the first of these musemes initiates triangular array formation and hexagonal cloning which, once a certain critical area is covered, begins to move the pattern into “perceptual awareness.” The dotted arrow feeding down from LTM to FE/PB indicates the potential influence of triangular arrays on more peripheral processing, possibly by what Calvin terms “faux-fax” links (discussed in Section 4.3.2), allowing a degree of subconscious input into grouping from previously learned patterning.
    
2. Some of these newly firing triangular arrays may align closely with existing basins of attraction embedded in the connectivity. Because these encode the same pattern as the incoming information, the latter will be (re)cognized as identical to the LTM version (scenario i). In this way, basins of attraction offer a potential mechanism for melodic similarity perception (Lartillot and Toiviainen 2007; Lartillot 2009). The LTM version will also, by coindexation, confirm the provisional segmentation posited by FE/PB. If, however, existing attractors encode a similar but not identical version of the incoming pattern, such as c²–d²–f²–c², then the incoming version may be mis-cognized as the more established LTM version, owing to hexagons encoding the incoming data being drawn by attraction towards alignment with the established version (scenario ii). Alternatively, “[t]acking on yet another attractor may not always be possible. One reason is that strong local attractors can likely capture the new pattern once lateral copying is discontinued, altering the pattern to the previously stored one, and so the new one[, while being perceived as new,] is never memorized” (Calvin 1996a, 70) (scenario iii). Another outcome is that the force of existing attractors distorts the incoming pattern so that its triangular arrays sit at some orientation between the configuration encoding the reality of the incoming information and that of the embedded attractors, such as c²–d²–f²–d² (scenario iv). In this situation—or the converse of it (the force of the incoming pattern distorting existing attractors)—any resultant pattern which itself becomes embedded in the connectivity constitutes a mutation of the incoming (or the existing) information (see “Museme Mutation” below).
    
3. A critical mass of cloned hexagons will push the “Jupiter” museme into the “focus of conscious awareness” by overwhelming the population of hexagons encoding the temporally antecedent pattern (in this case, perhaps the audience’s coughs preceding the start of the movement). This small region of the diagram is the only part of an overwhelmingly parallel (synchronic) system where a serial (diachronic) order is experienced (Dennett 1993, 210; Snyder 2000, 10).
    
4. While musemes w, x, y, and z are passing in sequence through the focus of conscious awareness, the “Jupiter” museme remains semi-activated in STM, as do subsequently w, x, y, and z. Even though not directly stimulated by input, the “Jupiter” museme’s population of hexagons are still firing owing to the gradualistic nature of decay, giving a fading memory of the museme which is capable of being reactivated by “rehearsal” and, if previously unmemorized, embedded in the connectivity (scenario v). This window of STM potentially encompasses a chunk of <7±2 units (here five, the “Jupiter” museme plus musemes w, x, y, and z), each of which is itself a Millerian chunk (in this case it is 4–8: “Jupiter”=4 units, w=4, x=5, y=8, z=8). Slightly exceeding Snyder’s 3–5 seconds as the average time frame of STM, the five-chunk segment of Example 1 occupies just under six seconds in performance, in the (typically measured) Karajan 1956 recording (Mozart et al. 1956/2008).
    
5. Apropos scenarios i, iv, and v, the colony of “Jupiter” hexagons may alter the underlying connectivity so as to reinforce or modify extant basins of attraction, or create new ones. As the implementation in LTM of these various patterns, “[m]emorizing a spatiotemporal pattern would seem to be a matter of creating a new connectivity, probably in a number of hexagons. Although the usual LTP-to-structural-enhancement model of learning...seems to suffice here, remember that we are superimposing some connectivity changes upon a pre-existing cortical connectivity [scenario iv], one that already has some attractors inherent in it” (Calvin 1996a, 70). This (over)writing is especially likely in the case of movements such as this, whose sonata form optimizes the repetition and mutation of certain musemes. The larger form (the Memesatz, Section 4.3) fosters the evolution of lower-level musemes and, as a consequence of this and of its implementation of the “evolution of evolvability” (Dawkins 1989b), itself.

Absolute and Relative Pitch Encoding

[55] While the discussion has so far been framed in terms of absolute pitch, memory for melody and harmony is normally encoded in relative pitch, for

[a] familiar melody can be presented at almost any tempo and at any pitch level and remain recognizable; hence memory encoding of familiar melodies is not an exact (episodic) copy of particular pitches and time intervals, but a higher-order abstraction (schema) of particular features of the melody. In addition to some surface-level aspects of the music, possible features encoded in memory include interval [relative], contour, and scale-step context (position in a scale) (Snyder 2009, 111; emphasis in the original).

[56] The HCT can readily account for all four formats (absolute, relative, contour, scale-degree), in that the SFP of a given museme may be connected to a more abstract representation (and thereby indexed) by faux-fax linkages (the implementation of such processes is considered in Section 4.3.2, on account of their involvement in formal/structural-level processes). This representation may encode the museme as both an interval pattern (by quantifying the frequency differentials between its arrays) and a scale-degree sequence (in conjunction with connections to brain regions encoding conceptual information about these higher-level pitch representations (Ockelford 2009, 70, 81–3, Figure 31)). Hypothetically, this higher-level representation may be connected to myriad other minicolumns, such that basins of attraction are set up which create “ghost images” of the museme at the other eleven transpositional levels. These can be activated/cued on the fly when a form of the museme occurs at other than the original transpositional level, such as the appearance of the sequence e²–f♯²–a²–g♯² (K. 551, IV, measures 166–9) which, perhaps after its third element, activates the abstract representation of the “Jupiter” museme. For a detailed treatment of pitch encoding, see (Brattico 2006).

Melodic Segmentation and Museme Coindexation

[57] Sound-stream segmentation by gestalt forces is closely linked with (indeed subserves) the notion of coindexation, the mapping of a posited museme against a hypothesized antecedent or consequent pattern. While Calvin’s second “essential aspect” from Section 1 contends that “that which is copied may serve to define the pattern” (Calvin 1996a, 21), it is sometimes the case that such top-down grouping (LTM-mediated coindexation-determined segmentation) is in conflict with bottom-up grouping (provisional gestalt-driven EM/FE/PB chunking). A passage may therefore have more than one possible segmentation, motivated by a combination of gestalt grouping forces and coindexation, and even though one of the resultant groupings may be “preferred,” a range of candidate groupings may nevertheless be “well formed” (Lerdahl and Jackendoff 1983). Consequently, a given musical sound-stream may give rise to discrete, overlapping (whereby a second partially intersects with the first) and nested (whereby a second is wholly encompassed by the first) musemes (Jan 2007, 74–7).

[58] This tension between bottom-up and top-down forces might be called, apropos Tovey, “top-knotism.” With characteristic tartness he observes that

[v]ery clever persons, who take in music by the eye, have pointed out the extraordinary resemblance between [the opening theme of the first movement of Haydn’s Symphony no. 88] and that of the finale of Beethoven’s Eighth Symphony. The resemblance is equivalent to the scriptural warrant of the minister who, wishing to inveigh against a prevalent frivolity in head-gear, preached upon the text, ‘Top-knot, come down!’—which he had found in Matt. xxiv.17 (‘Let him which is on the housetop not come down’). The Top-knot school of exegesis still flourishes in music (Tovey 1935, 141).

[59] The passages Tovey refers to are shown in Example 2, but (beyond the fact that those who take things in “by the eye” can see the orthographic difference between “Top-knot” and “Top-not”) they do not constitute an example of top-knotism, if the sense of Tovey’s maxim is strictly followed. The resemblance, while perhaps not “extraordinary,” is certainly close; but it inheres as much in contour as in more specific aspects of scale-degree sequence. As the overlays show, the pitch configuration marked Museme b is replicated (the similarity inhering in an abstraction/schematic relationship between the “sub-foreground-level” framework of the two segments (Jan 2007, 155)), but other than that, the scale-degree sequences described by the openings of the antecedents and consequents (demarcated by vertical lines) are different ($\hat{2}$–$\hat{3}$ in Haydn, $\hat{3}$–$\hat{4}$ in Beethoven; Beethoven’s consequent sequence is that of Haydn’s antecedent). As a result of this, the larger, shallow-middleground, structures, Musemes x and y respectively, are different.

[60] A genuine case of top-knotism would occur when a pitch sequence segmented in a particular way in one context (“housetop | not | come”) is mapped against one segmented in a different way in another (“house | top[k]not | come”) and held to be psychologically equivalent and/or evolutionarily significant. Such a situation obtains in Example 3 iii, which shows a passage within which two rival musemes, labeled a and b, might be defined variously on gestalt criteria and by reference to coindexes from earlier contexts, the latter shown in Example 3 i and ii. Museme a has a possible gestalt end-boundary at the c¹/c² of measure 54¹ (Haydn), owing to its strong metric position and the following reversal of melodic direction and non-conjunct motion to e♭¹/ e♭² (this and the others mentioned below are, however, not strictly Reversals in Narmour’s sense (Narmour 1990, 150–52)). The d²/d³ at measure 75 of the Beethoven passage has a similarly strong metric position but, lacking Haydn’s subsequent melodic reversal, relies on its two-beat duration as a further segmentational force. Museme b has a possible gestalt end-boundary at the b¹ of measure 4¹ (Haydn), again owing to the following reversal of melodic direction and non-conjunct motion to e². In Beethoven’s measure 76 the reversal is smaller, but its effect is augmented by the two-beat duration of the b♮¹/b♮², which parallels the d2/d3 at the end of Museme a. Additionally, on the principle of continuity, the b♮¹/ b♮² marks the end of a falling group and the beginning of a rising one.

[61] Calvin’s model allows such overlapping and also nested coindexations to be understood in terms of alternative SFPs across collections of embedded attractors, allowing two ostensibly different musemes to share common musical features. To understand this fully, it is necessary to consider two perspectives, that of the composer and that of the (contemporary) listener.

[62] From the composer’s perspective, and as represented in Figure 8, it is hypothesized that Beethoven, having heard Musemes a and b in either the proposed antecedent coindexes, or others, formed a mental representation of them as embedded attractors which linked the minicolumns coding for the set of pitches G–F♯–F♮–E–D–C–B♮ in two specific but partially overlapping hexagonal configurations, each with its own SFP. It is possible that the highly activated area of overlap (the intersection set G–F♮–E–D linking the subsets G–F♯–G–F♮–E–D and G–F♮–E–D–C–B♮) motivated the combination of the subsets which coded for the particular phemotypic forms of these musemes in Symphony no. 8.

[63] From the listener’s perspective, both musemes potentially exist in the brain of an individual familiar with the Beethoven passage. On hearing the passage in Example 3 ii or another (not necessarily historically antecedent) coindex, the pattern coding for Museme a is activated. That is, the SFP encompasses the subset G–F♯–G–F♮–E–D, and successful cortical cloning may bring the Beethoven passage into conscious focus and particularly strengthen the connectivity of Museme a, giving it a Darwinian advantage in future cloning competitions. Similarly, on hearing the passage in Example 3 i or another coindex, the pattern coding for Museme b is activated. The SFP encompasses the subset G–F♮–E–D–C–B♮, and successful cortical cloning may bring the Beethoven passage to the forefront of consciousness and particularly strengthen the connectivity of Museme b. In this way, the passage’s gestalt partitioning into (at least) two perceptual units is reinforced by means of coindexation-determined segmentation.

Museme Mutation

[64] One way of categorizing the variety of ways in which museme mutation occurs is to make a distinction between that arising from real-time listening/perception and that arising from reflection/introspection. The first category involves situations where incoming external sensory information from music audition is distorted and memorized in a form different to that of the original. This may occur as a result of capture by an embedded attractor, scenario iv in the list following Figure 7. The second category involves situations where internal imagination changes the information content of cortex, modifying information which is already encoded and resulting in the generation of new patterning (one might also hypothesize the operation of scenario iv in such situations).

[65] Calvin’s discussion of “variations on the cloned pattern” (Calvin 1996a, 58), the underlying mechanism of museme mutation, appears to relate most closely to the second of these categories and is understood by him in terms of two processes. The first is “caused by the failure of one or more of the triangular arrays to clone new nodes,” resulting in a hexagon arising with fewer triangular arrays than its parent. He equates this to a missing note on a musical instrument, “in the manner of a piano with a dead key” (Calvin 1996a, 59). This corresponds to musical situations where a recalled museme is mutated by the omission of one or more of its component pitches (Jan 2007, 116–17; 119, Example 4.1 ii).

[66] The second process involves the notion of pattern overlap and resultant hybridization. Here two (or more) colonies of hexagons confront each other across a cortical no-man’s land (an area not occupied by active hexagons) and the “undecided region may receive equal doses of both melodies” (Calvin 1996a, 59). The new pattern is therefore some interdigitating mixture of the attributes of its “parents,” arising in a manner analogous to the “crossing over” occurring during meiosis (Jan 2007, 34; see also 122, Figure 4.2). This process corresponds to musical situations where a new museme is imagined as a result of recalling two possibly similar musemes. It is represented in Figure 9, Calvin speaking of the hybridization of “3-note ‘Bach’ hexagons” and “4-note ‘Beethovens’” (Calvin 1996a, 59; see also 89).

[67] Both these processes rely upon the failure of “error correction” for their operation. In an open expanse of cortex, a variant pattern which arises by means of either “dead-key” silence or no-man’s land hybridization will normally be rapidly overwhelmed by the up to six surrounding hexagons and will be forced back into conformity with the configuration of the surrounding plating. For a variety of physiological reasons, certain areas of cortex may be resistant to overplating, serving as a barrier to further expansion of a spatiotemporal pattern. Some barriers may nevertheless have small gateways, which can permit any variants arising in their vicinity to slip through and escape the error-correcting pressure of adjacent hexagons. Figure 10 i (Calvin 1996a, 88; reproduced with permission) represents this phenomenon, whereby a pattern lodged in the aperture of a gateway (the “Beethoven” museme) has insufficient weight of numbers to overwrite the adjacent two-quaver “dead-key” variant which, having created a two-hexagon beachhead, Figure 10 ii, is able thereby to establish a rival colony resistant to the might of its three-quaver parent. This process may have occurred idiostructurally during the poiesis of the Fifth Symphony, and may account for the variant | pattern, which first appears at measure 177 of the first movement and which briefly competes with the prevailing  | .

[68] When a pattern such as the two-quaver variant arises in the manner described above, it has not been directly copied from an antecedent in the “dialect” (Meyer 1989, 13–24) (although it might be drawn towards attractors which have been embedded in this manner) and therefore is a mnemon, an unreplicated memory trace (Lynch 1998, Section 4; Jan 2007, 27–8; see also 30, Table 2.1). Only when a phemotypic product of the variant (in a musical score, for instance) engenders the copying of the pattern to a second brain does the variant pattern become a museme. In some cases, however, the variant is a very common pattern which is extensively distributed, as a style shape, in the dialect. Arising as a result of non-error-corrected variation at the level of “idiom,” it is therefore not a homologue (a direct transmissional-evolutionary descendant) but rather an analogue (a pattern bearing a coincidental similarity to another) of a dialect-level pattern. Such patterns are evolutionary “good tricks,” configurations in some way favored and sitting in conceptual space waiting to be discovered (Dennett 1995, 77–8). As argued in Section 4.1.1, the higher the number of elements in a museme the greater the likelihood that it is a homologue and not an analogue and so, conversely, some very simple (low-element) components of culture are probably not memetic in the “strong” sense of (only) being directly copied from brain to brain (Jan 2007, 115).

Melodic Expectation, Implication and Probability

[69] While not easily separable, expectation and implication differ in that the former is often held to be predominantly top-down, whereas the latter is generally held to be predominantly bottom-up (Huron 2006). Accordingly, it appears that implication, as a member of a series of evolved survival responses, is processed primarily at the FE/PB stage of Figure 2, whereas expectation is processed, by means of Calvinian mechanisms, via the intercession of LTM. This difference in perspective is reflected in Narmour’s development of Meyer’s work, where the substitution of the latter’s concept of “expectation” by the former’s “implication” reflects a change of focus from the primarily learned to the principally innate (Meyer 1956; Narmour 1990). Both phenomena relate to the more abstract notion of probability for, however motivated, certain antecedent stimuli are associated with a finite set of consequents, the appearance of any one of which is governed by probabilistic rules (Temperley 2007).

[70] In implication, the note-to-note progression of a pitch sequence is predicted according to the gestalt principles of similarity, proximity, and continuity. As sub-Calvinian processes, they tend not to feed into consciousness: one somehow expects a rising scale to continue rising or a gap to be filled (Meyer 1973), but this expectation often does not reach the level where it is amenable to introspection, especially during the rapid flux of musical listening (Narmour 1990, 138). In expectation, the note-to-note progression of a pitch sequence is predicted according to its conformity with similar sequences stored in LTM. In this sense the beginning of the melody serves as a cue or trigger for the continuation and the stored sequence serves as a schema, guiding the perception of the remaining features.

[71] The mechanism of expectation may be derived from the precepts of the HCT. Assuming the pattern is held in LTM, and ignoring contextual information such as accompaniment figuration, incoming information from FE/PB to the cortex, such as the first note of the “Jupiter” museme of Example 1, excites those minicolumns tuned to this pitch. These will be connected to myriad others as the uncontextualized first element in a vast number of potential SFPs and their associated (but as yet inactive) basins of attraction, set x. When the second note, d², is processed the number of possible correspondences is considerably narrowed, given that only a subset of set x, set y, will begin with a rising major second. With the processing of the third note, f², set y will be further narrowed, to set z, an even more limited number of possible musemes beginning with a rising major second followed by a rising minor third.

[72] By this stage, the pattern may have been captured by existing attractors and hexagonal cloning will reach a sufficient extent to allow a dual-track firing of the triangular arrays, namely that associated with the ticking-off of incoming pitches as they reach the cortex and the “running-ahead” firing responsible for imagination and expectation. The latter allows the prediction of the musical future, in this case the fourth pitch, e², whose arrival may decisively confirm (via recognition) the input pattern. Because discrete hexagons may be connected by faux-fax links, running-ahead prediction might also anticipate the arrival of subsequent patterns, such as musemes w, x, y, and z of Example 1, and this process, operating at several hierarchical levels, may therefore account for the memorization and prediction of musical form (Section 4.3.2).

Rhythm

[73] Calvin distinguishes between spatial-only (semantic) and spatiotemporal (episodic) patterns by asserting that

[t]here isn’t a one-to-one mapping between spatial-only and spatiotemporal patterns within the nervous system in the manner of a phonograph recording or sheet music. A given long-term connectivity surely supports many distinct spatiotemporal patterns. In the spinal cord, for example, a given connectivity supports a half-dozen gaits of locomotion, each a distinct spatiotemporal pattern involving many muscles and the relative times of their activation. It is presumably the initial conditions that determine which pattern is elicited from the connectivity. One aspect of initial conditions is that ghostly blackboard, the fading facilitation of synapses that was caused by earlier activity in the hexagon. Another aspect is the pitter-patter of inputs from thalamus and elsewhere; inputs that are not strong enough to initiate impulses can nonetheless bias the hexagon’s resonances (Calvin 1996a, 65–6).

[74] The HCT therefore implies that the primary parameter encoded by triangular arrays is pitch, and that rhythm is a secondary or emergent property resulting from the particular sequential activation (firing-order) of these pitch-encoding arrays. To this extent, melodic musemes are real, being wired into the connectivity of the cortex, whereas rhythmic musemes are virtual, being engendered by particular patterns of activation within that wiring. Whereas the sequential order of firing in perception/cognition is a response to incoming stimuli, in memory it is an artifact of the interaction between “initial conditions” and attractor embedding. To visualize this, the cortical surface might be imagined as multileveled, attractors sitting at different depths (owing to the sashimi principle noted in Section 3.3) below “sea level.” A particular stimulus cue—perhaps the previously heard or recalled museme—may activate the arrays for a given melodic museme to fire in a variety of patterns according to the progress of the activation down a range of possible paths from attractor to attractor to the stasis of the sea bed. These paths constitute the memories of specific durational, accentual, or inter-onset-interval configurations, the defining attributes of a range of rhythmic musemes.

4.2. Harmonic Musemes

4.2.1. Psychological Constraints on Harmonic Musemes

[75] As suggested in Section 2, it is sometimes difficult to distinguish between melodic and harmonic musemes. When two or more horizontal strata of music sound simultaneously, harmony is produced and a sequence or progression of chords is heard. However, if those strata have sufficient melodic individuality they are perceived as independent and a contrapuntal texture of interacting melodic musemes is engendered. The issue is complex, in that in a Bach chorale, for instance, the lower three parts serve to support the melody and thus arguably have a more harmonic than contrapuntal role, yet often they have a good deal of independence and therefore contrapuntal salience. A Bach fugue, by contrast, normally eschews such a melody-accompaniment polarity and generally accords the lines equal weight, but sometimes the lower parts revert to more stereotypical accompanimental figures and the upper voice, already privileged by the tendency to focus upon the highest sounding part, predominates.

[76] In listening, FE/PB abstracts both the vertical and the horizontal dimensions of the input, processing the progression of simultaneities and (in accordance with the gestalt principle of continuity) tracking the individual melodic strata (Bregman 1990). Which of these dimensions is perceived as more salient depends upon a variety of factors, including the information content of the component strata (Meyer 1956; Knopoff and Hutchinson 1981). This value is partly contingent upon the number of attack points and the incidence of directed, implicative melodic motion, such as is described by Narmour’s notion of Process (Narmour 1990, 99–100). A part which is moving relatively quickly and/or changing unpredictably will possess high information content and will be assigned a greater share of attentional resources owing to its being regarded as constituting part of the perceptual foreground; whereas a part which is moving relatively slowly and/or changing predictably (such as one based upon the Alberti bass accompaniment texture) will possess low information content and will—as a result of the phenomenon of “habituation” (Snyder 2000, 23–5)—be assigned a smaller share of attentional resources owing to its being regarded as constituting part of the perceptual background.

[77] For present purposes, I define a harmonic museme as one whose horizontal strata do not perceptually usurp the vertical, whose strata have broadly simultaneous, not staggered, terminal nodes, and which, as a result, forms a discrete chunk. (The principle of hierarchical rechunking means that a chord is a three- or four-element (note) chunk and the progression/harmonic museme is a higher-level chunk. Several such chunks can assemble to form a chunk at a still higher hierarchic level.) Where this is not the case, it is more appropriate to speak of a series of simultaneously (contrapuntally) presented melodic musemes, which may nevertheless imply harmony as a by-product of their interaction.

4.2.2. Calvinian Implementation of Harmonic Musemes

[78] A harmonic museme may be understood as implemented in the same manner as a melodic museme, except that the one-pitch-at-a-time firing of the melodic museme is replaced (or in some cases supplemented) by additional triangular arrays coding for other pitches and firing in synchrony. To adapt Calvin’s metaphor from Section 3.3, a melodic hexagon is a disciplined committee where each member waits for their turn to speak, whereas a harmonic hexagon is one where several members speak at once. Example 4 ii shows a simple three-voice, four-chord harmonic progression, a reduction of that of measures 1–4 of Example 1. Its Calvinian implementation, as a hexagon of eight arrays (not, owing to note repetition, twelve), is given in Figure 11, the arrow to the lower left of the hexagons representing (aside from the repeated pitches) the activation sequence (green-blue-red-yellow) and therefore the passage of time.

[79] This example is considerably simpler than most harmonic musemes. Even within the constraints of the definition attempted in Section 4.2.1, the pitches of harmonic musemes do not normally change simultaneously, as is illustrated by Example 4 i, which clarifies the two separate parts amalgamated in the lower stave (the second violin part) of Example 1 and which are reduced (as a simulation of habituation) in Example 4 ii. But Calvin’s model is capable of accounting for such situations, for any combination of pitches can in principle be accommodated by cortical hexagons. While music theory appears determined to make a firm distinction between “melody” and “accompaniment,” and between “harmony” and “counterpoint,” these phenomena devolve to sequences of triangular arrays firing in various patterns of synchrony—in much the same way as the moving images and patterns on a computer screen devolve to patterns of transistor switching in a processor chip. The percept of a passage of music, just like the images on the screen, are the florid products, the echoes in a “Cartesian auditorium” (after Dennett 1993, 107), of mechanistic neuronal processes.

[80] The perception of underlying harmonic progressions in complex contrapuntal textures noted in Section 4.2.1 may arise from alignment of array SFPs with the firing patterns articulating the regular underlying pulse or tactus of the music, which is thought to be processed separately from the patterns of duration, accentuation, and inter-onset intervals characterizing rhythm (Samson and Ehrlé 2003, 206). In this hypothesis, those notes directly coinciding with the tactus are perceived as more prominent owing to greater excitement (possibly via amplifying linkage), and perhaps more extensive cloning, of their triangular arrays, and vice versa. To illustrate the outcome of this process, Example 5 i shows an extract from a Bach fugue (the passage outlines a Romanesca, in Gjerdingen’s terms (Gjerdingen 2007, 39; see also 454)), the three linear strata of which are “cortically reduced”—as opposed to the verbal-conceptual-meme-mediated reduction characterizing formal music analysis (Jan 2012)—to the harmonic progression of Example 5 ii by amplification of those pitches aligned with the tactus, of which there are four per bar here. Note that this “filtering” does not always give the smoothest voice leading from a pure Fuxian-Schenkerian point of view (Fux 1965), because privileging a pitch aligned with the tactus may lead to inelegant melodic motion, compared with favoring one on a subdivision of the tactus (the removed upper-voice, weak-subdivision f♯² in measure 24² is a case in point).

[81] In addition to this relatively mechanistic, bottom-up process, top-down/schematic knowledge (implemented by means of attractor embedding) is also implicated in the perception of underlying harmonic structure, as indicated by the tendency to prefer the note of resolution in suspensions over the note of suspension, irrespective of their positions with respect to the tactus. This tendency is sometimes in contradiction with cortical reduction, as seen in the middle voice in measures 25–6 of Example 5 ii, regularized according to top-down criteria in the small stave above these bars. (It might nevertheless derive from a FE/PB-implemented preference for consonance over dissonance.) Lastly, and perhaps most fundamentally, the filtered pitches are presumably those connected, via faux-fax linkage, to higher order representations of such contrapuntal-harmonic passages, which encode the underlying harmonic progression as part of a multi-leveled structural hierarchy (see Section 4.3.2).

Pattern Memory versus Systemic Memory

[82] The memory discussed so far has been that for specific patterns, for discrete units which are memorized as “individuals” different from other patterns and competing with them for the cortical territory which gives them life. But there is another, more generalized, type of memory which might be termed systemic memory. Arguably the most important example of this category is memory for the melodic, harmonic, and modulatory regularities of tonal systems, such as the major-minor key system. Tillman et al. argue that

[w]estern tonal listeners become sensitive to the [synchronic] musical structures [of the tonal system] by mere exposure to [diachronic] musical pieces obeying this system of regularities...The implicit knowledge embodies the functions of tones and chords in a key, the relations between different keys, and the change in tonal functions depending on the context. The influence of this internalized representation has been reported for musical memory, musical expectancies, and with electrophysiological and brain imaging methods (Tillman et al. 2003, 112–13).

[83] Such abstraction of general systemic attributes from numerous particular instantiations may be the outcome of two related processes hypothesized in the HCT. The first of these, the mechanism for a number of different properties of musemes, relies upon the phenomenon of attractor embedding. Like the fields of Flanders, the constant battle for cortical territory waged by hexagonal plaques leaves the surface pock-marked with remnants of the conflict, the attractors embedded in the connectivity. These encode regularities in the system, such as the tendency of leading notes to rise and of sevenths to fall. None of these is “natural,” an innate property of perception and cognition, but arises through the force of convention, which is ultimately dictated by the victors in Darwinian selection. As attractors, they contribute to the future propagation (replication) of systemic regularities by biasing the perception, mutation, and memorization of musemes.

[84] The second process is the indexation of such crater-trapped regularities by means of faux-fax links, whereby a number of melodic and harmonic musemes—each of which expresses, in different ways, particular features of the system (rising leading notes, falling sevenths, etc.)—are connected, many-to-one, to a central representation which encodes their common features. Such sets of common-feature memes might be regarded as the cultural equivalent of gene alleles (Dawkins 1983b, 283) (see Section 4.3.1). This phenomenon, and processes based upon similar mechanisms discussed earlier, attests to the centrality of structural-hierarchic abstraction by faux-fax indexation to many aspects of music perception, cognition, and memory.

Calvin and Neo-Riemannian Transformational Theory

[85] It is interesting to relate the HCT to neo-Riemannian transformational theory (Cohn 1997; Hyer 1995). As has been widely theorized, certain harmonic progressions may be understood in terms of the perturbation of one of the three notes of a triad via the R(elative), P(arallel) or L(eittonwechsel) shifts, giving rise to a different triad and a concomitant motion on the two-dimensional Tonnetz used to plot triadic relationships. This is shown in Figure 12 i, where a C minor triad (C, E♭, G; 0/0, 3/x, 7/2x + 1 respectively on the Tonnetz) is flipped by Leittonwechsel (represented by the dotted arrow and the “l” on Figure 12 i) to an A♭ major triad (C, E♭, A♭; 0/0, 3/x, 8/2x + 2).

[86] The relationship between neo-Riemannian theory and Calvin’s model is more than metaphorical, because two musemes based upon different R-, P- or L-related triads may literally compete (in perception and/or memory) for cortical territory. As is represented in Figure 12 ii, a C-minor-triad-based museme (left-hand part of the figure), with triangular arrays for the pitches C, E♭ and G, and an A♭-major-triad-based museme (right-hand part of the figure), with arrays for C, E♭ and A♭, may be adjacent in cortex. Were the latter museme’s territory to overwhelm the former’s, then a literal topographical shift, a neuronal Leittonwechsel, would occur on the Tonnetz of the cortex, whereby the minicolumns for G would be silenced (becoming the dog that didn’t bark in the night) by those for A♭. While this may not be a geometric flip in the neo-Riemannian sense (each array codes for one pitch, not three), it is a change in the orientation of triangles on a tonotopic surface reflecting a changed harmonic environment.

4.3. Formal/Structural Musemes (Memesätze)

4.3.1. Psychological Constraints on Formal/Structural Musemes

[87] Sections 4.1 and 4.2 drew upon the notion of schemata, representations which encode procedural and structural commonalities in recurrent sequences of features (Gjerdingen 1988; 2007, 10–16; Leman 1995). Schemata and features are often aligned with a top-down versus bottom-up dichotomy, the former being learned multiparametric complexes, the latter being uniparametric simplexes driven by more innate forces (Narmour 1990, 55). Local-level schemata are a function of hierarchical rechunking (Section 4.1.1), which allows STM to sustain relatively large amounts of information within the Millerian constraint-frame. In addition to their involvement in the perception, cognition, and memory of small- and intermediate-scale musemes (up to such phenomena as antecedent-consequent and three-phrase binary-form phrase types), schemata also encode the global structure of a movement. Snyder argues that

[t]he process of chunking can lead to hierarchical organization in LTM, and most theories of the structure of long-term representations of music use the concept of hierarchy to varying degrees, applied both to episodic memories and abstract schemas. Hierarchical levels in music may range from local groupings up to entire pieces. When memory passes beyond the limits of STM, it is thought to persist in a more schematic form: to become a kind of reduction. Exactly what remains of actual musical details in musical LTM is an important question. Typically, theories of musical LTM reduction involve ideas of hierarchies of structural importance...in which certain events in music are structurally more important than others, and these constitute the gist of a listener’s memory representation... These salient structurally important events can be said to constitute the ‘deep’ level of structure in music, more rapidly changing details forming the musical surface or foreground (Snyder 2009, 113; emphasis in the original).

[88] There are two major issues related to the LTM representation of musical structure. The first is that the sophistication of representation varies significantly according to the competencies of individual listeners. These variations sit on a continuum which ranges from individuals who are musically uninterested and unenculturated, via Meyer’s “competent, experienced listener” (one who is not formally educated in music, but is nevertheless “familiar with and sensitive to [a] particular style”) (Meyer 1973, 110), Tovey’s “naïve listener” (one perhaps with Meyer’s level of “competence,” but with some additional knowledge of notation, albeit without “any more technical knowledge than is likely to be picked up in the ordinary course of concert-going by a listener who can read the musical quotations or recognize them when played”) (Tovey 1935, 2), to the musically educated and/or trained listener (one with a high level of academic musical knowledge and, often, instrumental or vocal proficiency). This continuum is of course blatantly Eurocentric, and a “flatter” model would appear to obtain beyond it. As Cross asserts, our “culture-specific ‘music’ is scarcely representative of the complex and embodied set of activities and interpretations that are evident in most nonwestern ‘musics’” (Cross 2003, 50).

[89] Even in the last category, there are some skilled performing musicians, and even musicologists, who know little of the major hierarchically reductive theories of musical structure, such as Schenker’s (1979) or Lerdahl’s and Jackendoff’s (1983). Those who are familiar with such theories have supplementary conceptual frameworks (regardless of their intrinsic veracity) with which to augment their innate hierarchical structure-representation capacities. But this benefit is probably not restricted to the present day and to the particular theoretical models mentioned above: it is perhaps historically true of all musicians who have taken an interest in theoretical perspectives on music, particularly in those models orientated to global-structural aspects of music. Naturally, such an interest might serve ends other than memory representation, being perhaps chiefly pursued in order to facilitate composition: Beethoven, for instance, copied out passages of concept-illustrating music from various theoretical texts for ultimately poietic, not esthesic, ends (Nattiez 1990).

[90] The pinnacle of the skill continuum is represented by the small handful of “great” composers, whose powers of internalization and representation appear to have vastly exceeded those of even their most musically literate (but otherwise “normal”) contemporaries. Even if romantic accounts of certain composers’ ability to grasp the essence of a composition in quasi-photographic form are fabrications, as indeed appears to be so in some cases (Solomon 1991; Stafford 1991, 151), such individuals as Bach, Mozart, and Beethoven appear to have had prodigious powers of memory. Of course, this is to ignore the availability and influence of manuscript copies and printed editions of their predecessors’ and contemporaries’ music, which to some extent would have circumvented the necessity for LTM structure representation based solely upon on-the-hoof salon- or concert-hall-based hearing. Nevertheless, Langrish argues that “[c]ymbals [and cembalos] can be better than symbols for the transmission of musical ideas” (Langrish 1999, Section 2.3).

[91] The second major issue related to the LTM representation of musical structure concerns the question of the mode of exposure, including the distinction between “‘real-time’ models of ongoing music perception [and] ‘post hoc’ accounts of the representations that might be formed after listening to a piece of music” (Deliège and Mélen 1997, 387). That is, the representation formed by a listener in real time during the first hearing of a hitherto unknown piece of music may be different from that (re)formed/revised during a subsequent hearing (or during later introspection). Furthermore, some highly trained musicians may even form a representation of a work from perusal of the score, either before (and therefore without sonic input, only aural imagination) or after their first hearing. Sometimes (but not necessarily) this representation is formed via the intercession of various theoretical models of hierarchical structure, and it may be refined during a subsequent reading-imagining and/or hearing. Of course, in these latter scenarios, we are moving from listening proper into the territory of theory and analysis (“‘post hoc’ accounts of the representations”). This summary also ignores the further complicating factor of representations formed by performers, which additionally involve motor-control schemata.

[92] One theory proposed to account for psychological mechanisms of structure encoding is the cue abstraction model of Deliège and Mélen (1997; Deliège 2000). It proposes that listeners “latch onto” salient points in a piece’s unfolding narrative—cues, arising from segmentation/chunking processes—and use them to build an episodic-memory map (Snyder’s “gist”) of the music. These maps may be categorized as either “schemata of order” (cumulative, often found in non-tonal music, normally formed by articulations many in number but of low salience, and often associated with “weak hierarchies”); or as “schemata of order-relation” (syntactic, often found in tonal music, normally formed by articulations few in number but of high salience, and often associated with “strong hierarchies”) (Deliège and Mélen 1997, 387–8). One virtue of this theory is that unlike pitch-centered models of musical structure it is not prescriptive as to which aspects of music may serve as cues. Deliège and Mélen argue that “from [the fifteenth century] until the end of the period of common tonal practice, cues may well be provided principally by [pitch-based] motivic elements. In more recent periods—and most likely, in other cultures—other types of musical elements (acoustic, instrumental, or temporal parameters) may operate to fulfill this role...” (1997, 391).

[93] Musemes which function as cues may belong to allele-classes, such that a variety of configurationally different but functionally analogous versions of a given sub-foreground-level museme (such as those articulating a perfect cadence or a dominant pedal) may be capable of performing broadly comparable structural roles at the same locus in a piece of music and may therefore be interchangeable between movements. The global structure described by a sequence of such cue-musemes may be replicated by the same allele-class succession but different cue-musemes in another movement, giving rise to a formal-structural museme or (to adapt Schenker’s term) a Memesatz (Jan 2010, 11). In the case of sonata form, a certain sequence of events is required in order for a movement to satisfy the typicality constraints necessary for exemplars of this form (Gjerdingen 1988, 94, 103–104). These events will tend to be perceived as cues owing to their innate prominence and to the highly segmented/chunked nature of the form, a consequence of the normally high salience of its structure-defining articulations. When another exemplar of sonata form replicates the same allele-class sequence of cue-musemes, it indirectly replicates the underlying Memesatz.

4.3.2. Calvinian Implementation of Formal/Structural Musemes

[94] The HCT affords a mechanism for hierarchical structure encoding by invoking longer-range neural connections that those implicated in hexagonal cloning. Developing an idea of the neuroscientist Antonio Damasio’s, Calvin argues that “there are specialized places in the cortex, called ‘convergence zones for associative memories,’ where [representations in] different modalities come together” (Calvin 1996a, 129–30). Memory codes for the multimodal attributes of an object are stored in different cortical locations and integrated, by hexagonal overlapping/interdigitation, in association cortex. The connections between modality-specific hexagonal codes (a sub-committee, to reuse Calvin’s metaphor) and the fully “associated” code (a master committee) are achieved by certain types of “corticocortical projections” which go beyond the localized connectivity responsible for supporting triangular arrays and involve links which “can go long distances, as from one hemisphere to another...though most only make a U-shaped passage through the white matter of one gyrus and then terminate in a nonadjacent patch of cortex that’s only a few centimeters away” (Calvin 1996a, 131). Because such links are able to reconstitute the hexagonal plating of one area of cortex in another, Calvin terms them a “faux fax” and, writing in the mid-1990s, likens them to hyperlinks in the then-nascent internet (Calvin 1996a, 125, 131). While this copying is often error-free, miscopying of a hexagon established in the connectivity of the “sending” area as a result of the distorting effect of different attractors in the “receiving” area is a further mutational scenario, to add to those outlined in Section 4.1.2.

[95] The faux fax allows a mechanism for the coding of hierarchical structure in music, in that “the links may be reciprocal, allowing a distributed ‘data base’ [of features such as the sequence of allele-class musemes constituting a musical structure] to activate the elements of a centrally-located category [schema] representation” (Calvin 1996a, 135). As suggested, this model of representation appears capable, via recursive embedding (Calvin 1996a, 194), of accounting for commonality- and structure-abstraction at many levels in music, including that underpinning the perception, cognition, and memorization of correspondences between local-level melodic musemes (such as that linking the patterns articulating Museme b in Example 2), between intermediate-level structures (such as phrase-length schemata like the Romanesca), and between high-level formal patterns (Narmour 1999).

[96] The mechanism for structural-hierarchic abstraction is illustrated in Figure 13, in which, for clarity of exposition, a hypothetical three-element structure is shown. Three instantiations of the structure are represented in quadrants A, B, and C, each eventually connected via reciprocal faux-fax linkage (shown as dotted, double-headed arrows) to the “centrally-located representation,” hereafter “CLR,” in quadrant D, which corresponds to association cortex.

[97] The curved arrows represent the progression from one pattern of hexagonal paving to another, as different embedded attractors are cycled through during the Darwinian competitions of listening or recall, certain attractors being strengthened during repeated rehearings or recallings as a more detailed and stable model of the music is encoded. The paving patterns x, y, and z represent the florescence of particular features abstracted from the musical surface on such criteria as salience or repetition. They may be striking and/or recurrent foreground-level musemes (Deliège and Mélen’s cues), or (as is intended here) they may be more abstract shallow-middleground-level musemes. In the case of the latter, the foreground-level musemes generating them are perhaps more extensively cloned across cortex during listening or recall than their more conventional neighbors.

[98] The multiply recursive-hierarchic nature of this process is represented by the nine faux-fax links converging on xA (for clarity only these nine connections are shown at this level) from other hexagons to the north-west of quadrant A (not shown), which represent those pitches of foreground-level musemes selected to constitute the shallow-middleground-level musemes. The process is reductive, in that the three triangles of xA connect back to (and, in effect, select) a subset of elements, perhaps (as here) only one pitch, from a <7±2-element foreground-level museme. In this regard, Calvin speaks of a “hash” or “message digest,” which is a “unique short-form identifier, a ‘fingerprint’ of something more complicated” (Calvin 1996a, 17, 207; see also 123, 138). A potential further hierarchic level (which might encode the commonalities shared by different structural schemata) is suggested by the link from the CLR of quadrant D to its south-east, which leads, together with others, to an even higher-level representation (not shown).

[99] The designations xA, xB, xC, etc., represent membership of a museme allele-class (y and z are separate classes). Table 2 illustrates this principle with some hypothetical four-note musical exemplars. Boxed elements in the first two sub-columns (level n + 3) are those above-mentioned “pitches of foreground-level musemes selected to constitute the shallow-middleground-level musemes” which are represented in the next two sub-columns (level n + 2, quadrants A–C), these then being connected to the hexagons encoding the “structural” sequence of the last column (level n, quadrant D).

[100] In this example, xA (together with xB...xn) might outline the tonic chord with a prominent upper-voice $\hat{3}$; yA...yn might be based upon a dominant chord with upper-voice $\hat{2}$; and zA...zn might return to a tonic chord, prolonging $\hat{1}$ in the upper voice. In this way, a piece expressing the structure xA–yA–zA is analogous to others expressing, via different foreground-level musemes, the structures xB–yB–zB and xn–yn–zn; and all exemplars may be represented using the unitary coding x{A...n}–y{A...n}–z{A...n} shown in quadrant D. This representation may be spatial (recalled as a synchronic structure, via synchronous firing of the triangular arrays within the CLR hexagon) or spatiotemporal (recalled, fast-forward, diachronically, via sequential firing), the distinction perhaps accounting in part for the differences between semantic and episodic memory respectively.

[101] The CLR is a Memesatz because it (or an invariant subset of it) is almost certainly reconstituted as patterns of attractor embedding in the brains of all those listeners who have heard pieces A...n. While it is not possible to determine this directly, and while no two listeners will form an identical representation of the same piece of music or of a set of related movements, the recurrence across composers of certain specific features within common structural schemata is strong supporting evidence that (in skilled listeners) a Memesatz is encoded. That is, there are recurrences which go beyond the generic descriptors of the form and which manifest themselves as specific ways of implementing it.

[102] One such hashed or indexed feature is a telltale contrapuntal-harmonic marker regularly found in association with the sonata-form end-transitional V/V (V/III in minor-key sonata forms) which, because it confirms the dominant of the new key unambiguously via V/V/V, has a salience and importance well beyond its often very fleeting duration.⁽¹⁴⁾ Three examples of this museme are shown in Example 6, followed by an abstract of its underlying structure. All three passages are composed of a number of foreground-level musemes situated at a level corresponding to n + 3 in Table 2 and represented in absentia by the links to xA in Figure 13. Example 6 iv corresponds to the shallow-middleground-level n + 2, that of xA, etc. A level n CLR might abstract just one element of this three-element structure, the terminal V/V being the most likely candidate for hashing.

[103] As suggested in Section 4.1.2, indexation/ hashing is capable of accounting for the encoding of pitch sequences in relative (intervallic and scale-degree) terms. The same principle allows a CLR to encode multiple instantiations of a Memesatz in different keys, in that (to adapt the formulation of that earlier section) the CLR may encode the Memesatz as both an interval pattern (by quantifying the frequency differentials between its arrays) and a scale-degree sequence (in conjunction with connections to brain regions encoding conceptual information about these higher-level pitch representations). It might be connected to myriad other minicolumns, such that basins of attraction are set up which create ghost images of the Memesatz at the other eleven transpositional levels. These could then be cued on the fly when a form of the Memesatz occurs at other than the original transpositional level.

[104] Lastly, and beyond the purely structural dimension of music, the concept of the faux fax allows us to theorize, at least in principle, how a museme encoded primarily in auditory cortex (the perceived and remembered sound of the museme) may be brought together with the graphical memes (the representation of the museme in the form of symbolic notation) and the verbal-conceptual memes (the ideas associated with the museme, either as technical description or as semantic/affective adjunct, and taking the form of internal sound-images, of speech, of written text, and of the motor actions required to externalize them) associated with it.

5. Conclusion: Calvin’s Theory and ART Neural Network Models of Perception, Cognition, and Memory

[105] Computational models have been used as a means of testing a range of hypotheses on music perception, cognition, and memory, on the grounds that a successful simulation based upon a particular theory offers evidence in support of it being a true reflection of brain/mind function. Nevertheless, Temperley urges caution, in that

the mere fact that a model performs a process successfully certainly does not prove that the process is being performed cognitively in the same way. However, if a model does not perform a process successfully, then one knows that the process is not performed cognitively in that way. If the model succeeds in its purpose, then one has at least a hypothesis for how the process might be performed cognitively, which can then be tested by other means (Temperley 2001, 6; emphases in the original).

[106] One subfield of such studies is neural network modeling (Todd and Loy 1991; Tillman et al. 2003). Because several decades’ work in this area has suggested that simulations based upon relatively basic anatomical and physiological representations of neuronal interconnection are capable of replicating complex perceptual, cognitive, and memory operations, we can say, apropos Temperley, that “one has at least a hypothesis for how the process might be performed cognitively.” In turn, the results of simulations allow models to be refined and subsequently “tested by other means.” More specifically, certain models align closely with aspects of the HCT, offering support for—or rather not falsifying—Calvin’s hypotheses and my extension of them.

[107] Neural network models simulate connections of various strengths between populations of virtual neurons. Connections model sensitivity to inputs which represent a feature of the environment (perception), and they may be strengthened by repeated exposure (learning), becoming relatively stable features of the system (memory). Often, the connections are organized in multilayered hierarchies, which allow the system to abstract schemata from regularities in the input. Gjerdingen has used such models to simulate aspects of the psychology of musical pattern categorization and schema abstraction (Gjerdingen 1989a, 1989b, 1990, 1992). He employed an Adaptive Resonance Theory (ART) architecture, a type originally developed by Stephen Grossberg (1987). Despite certain differences between their implementation and the fine details of Calvin’s model, ART networks are broadly consonant with the HCT. Perhaps this is not surprising, given the general convergence of neurobiology and the computer simulation of neurobiological processes on hierarchic and Darwinian models in the 1990s.

[108] In one of Gjerdingen’s simulations the resonating units are groups of four cells, not the three minicolumnar vertices of the Calvinian triangular array; and they are visualized as vertical layers with each layer coding for a specific pitch event, not horizontal interdigitating triangles (Gjerdingen 1990, 343, Figure 2; 350, Figure 5). Despite the difference in structure—an anatomically incorrect one, as Calvin would see it—the same functionality is implemented. That is, a pattern of activation is set up in an area of a field (a layer of cell-groups) in response to some aspect of the external (input) or internal (feedback) environment, which after a period of competition then comes to dominate the field—in the HCT by extent, in Gjerdingen’s model by amplitude of resonance—at the expense of less “fit” patterns.

[109] In an analogue to Calvin’s SFP among coordinated triangular arrays encompassed by a hexagon, Gjerdingen argues that “[a] recency effect sufficient to encode temporal order can in fact be achieved without any reliance on decay. In place of the passive decay of individual cells, one substitutes the dynamic interaction of multiple groups of cells, each small group forming a feedback loop” (Gjerdingen 1990, 342). He represents a sequence of three such events abstractly as ▲–●–■ (Gjerdingen 1990, 341, Figure 1); these correspond to Millerian pitch sequences such as the boxed pattern (a–b–c♯¹) in the bass line of measure 42 of Example 6 i. Accuracy of firing order is facilitated by the suppression of an event by a subsequent input owing to the action of inhibitory interneurons, a functional AGC, which cap the level of activation across the field and therefore enforce a Darwinian selection for matching input to activation (Gjerdingen 1990, 342–3).

[110] Figure 14 shows Gjerdingen’s summary of the structure and function of one of his networks (Gjerdingen 1990, 365, Figure 12; see also 353, Figure 6; reproduced with permission). While his model implements four hierarchic levels, more are surely involved in real brain processes (1990, 353), as is also suggested in the layout of Figure 13 and Table 2. Consequently, the following attempt to translate Gjerdingen’s mapping of type of musical material to hierarchic level into Calvinian-musemic terms is necessarily only indicative.

[111] At level F[ield of neurons]₁, the network is tuned to respond to “a bundle of features.” That is, it attends to (among other things) single pitches and verticals and therefore corresponds to lower levels of the FE/PB stage of perception, the melding of simultaneous frequencies into a discrete pitch or chord. Level F₂, termed a “concept” by Gjerdingen, corresponds to gestalt-chunked clusters of F₁ features,⁽¹⁵⁾ and is the level of the particulate, Millerian, single-unit museme, the fundamental building block of musical culture. From a sample of six of Mozart’s earliest compositions, level F₂ reduced numerous such patterns to 25 schematic representations—rather, it was permitted to form a maximum of 25 categories, which it proceeded to fill with different abstracted schemata. One of these, pattern no. 13, is shown to the right of level F₂ in Figure 14 (Gjerdingen 1990, 360, Figure 8). These categories correspond to the sub-foreground level, in that each represents the voice-leading framework of a set of broadly similar figures; each might therefore be regarded as defining a museme allele-class (Section 4.3.1).

[112] The assemblage of such particles into longer “sequences of concepts” is coded by level F₃ and represents chains formed by the parataxis of perceptually and evolutionarily distinct unit musemes. Level F₄ encodes “higher-level” commonalities in the museme-sequences of level F₃, giving rise to phrase-schemata built upon sequences of superficially different but allelically analogous musemes. It therefore corresponds to the level of the memeplex (Jan 2007, 80–96). Note that the relationship between levels F₁ and F₂ (uniparametric/atomic museme-elements–multiparametric/molecular museme; Snyder: event–(chunked) event sequence; Narmour: style shape–style structure) is paralleled by levels F₃ and F₄ (unit-museme sequence–higher-order category/memeplex).

[113] Connections between layers are analogous to those implemented in cortex by Calvin’s faux-fax links. To clarify the similarities, Gjerdingen’s level indicators are added to Figure 13 and Table 2. The CLR of Figure 13’s quadrant D is, as suggested, situated several hierarchic levels above the F₄ level of Figure 14, as befits structures much more extended than the phrase-length schemata coded for by F₄. As with the faux-fax-linked hexagons of Figure 13, “Grossberg networks accomplish this process of segmentation, often called chunking [in my terminology, coindexation-determined segmentation, not FE/PB gestalt-determined segmentation], by combining different neural fields in a multilevel hierarchy...a single group of cells in the upper level is capable of categorizing an entire pattern of activation at the lower level” (Gjerdingen 1990, 344). That is, F₂ and F₄ extract from F₁ and F₃ respectively a minimum schematic structural description, Calvin’s hash or unique short-form identifier. Accordingly,

particular F₂ [and F₄] populations become closely associated with various aspects of F₁ [and F₃] populations [respectively]. For each F₂ population, the learned pattern of strong and weak inputs stored in its synapses forms the neural equivalent of a long-term memory. And the set of all the long-term memories in F₂ defines the categories that the field ‘knows’ and can recognize (Gjerdingen 1990, 348).

[114] Beyond this similarity, however, Gjerdingen’s network implements a feature which is not explicitly accounted for in the HCT and which by adaptive resonance mediates between the “feedforward” from F_1/3 to F_2/4 (F_1/3 features contributing to the definition of an F_2/4 schema) and the feedback from F_2/4 to F_1/3 (an F_2/4 schema contextualizing and predicting forthcoming F_1/3 features).⁽¹⁶⁾ In this “orienting subsystem,” specialized “comparator cells” executing a “vigilance parameter” prevent a novel sequence of features becoming erroneously shoehorned into an extant schema, which would prevent the formation of new schemata (Gjerdingen 1990, 348–51). The subsystem connects the comparator cells to the upper layer of F_1/3 and to an interposed additional layer of cells between the upper and lower layers of F_1/3, allowing comparison of the excitation of the bottom layer (input to F_1/3) with that of the top layer (feedback to F_1/3 from F_2/4). “The magnitude of total comparator-cell activation...is thus a measure of the degree of match between input and feedback patterns” (Gjerdingen 1990, 351).

[115] A similar subsystem might operate in cortex and, while speculative, could be implemented by a “vigilance array” within the hexagons located at each end of a faux fax. A specialized triangle within a hexagon encoding a museme might compare the excitation for that museme with that of its CLR in order to assess the “degree of match” between the particular and the general, severing the link should there be a significant divergence between instantiation and category. For illustration, one such pair of vigilance arrays is indicated on Figure 13, the triangles shown with dotted lines (other arrays are implied at F₂/n + 3). Such a system might therefore verify the accuracy of mapping between a set of allelic foreground-level (F₂) musemes and their shallow-middleground-level (F₃) framework, and between this and the deep-structural CLR (F_n).

[116] Finally, and moving beyond the details of implementation,⁽¹⁷⁾ the choice of an ART architecture by Gjerdingen aligns closely with the broad tenor of Calvin’s theory in that, to identify another virtue of such models,

a Grossberg network is not continually informed of the right answer to each problem of categorization. The network itself must decide which [higher-level] population is the right one to respond to each [lower-level] pattern of activation. And the network itself must decide whether [a lower-level] pattern of activation is a variant of an established category or a completely new pattern. For the purposes of modeling the cognition of musical phenomena, these are highly desirable traits. After all, the average listener receives no instruction in categorizing musical phenomena. And even trained musicians intuitively abstract and categorize most musical phenomena long before they begin the formal study of music theory. When it comes to the perception of music, we seem to lift ourselves by our own bootstraps (Gjerdingen 1990, 345).

[117] This aspect, fundamental to both ART models and the HCT, indicates the power of algorithmic Darwinian processes to create patterning from an amorphous substrate, to shape meaning through replication, and—as a “crane” not a “skyhook” (Dennett 1995, 74–5)—to “bootstrap” quality and complexity (Dawkins 1991). Transcending the primary evolutionary realm of biological life on earth, the secondary evolutionary realm of memetic replication builds complexity on the foundations of memory and challenges music theory to address the nature, operation, and impact of the museme.

Steven Jan
University of Huddersfield
Department of Music and Drama
Queensgate
Huddersfield HD1 3DH
United Kingdom
s.b.jan@hud.ac.uk

Works Cited

Adkins, Mathew. 2007. “Schaeffer est Mort! Long live Schaeffer!” Proceedings of the Electroacoustic Music Studies Conference, 12–15 June 2007. http://www.ems-network.org/IMG/pdfAdkinsEMS07.pdf.

—————. 2009. “The Application of Memetic Analysis to Electroacoustic Music.” Sonic Ideas, 1/2: 34–41.

Berz, William L. 1995. “Working Memory in Music: A Theoretical Model.” Music Perception, 12/3: 353–64.

Blackmore, Susan J. 1999. The Meme Machine. Oxford: Oxford University Press.

Borges, Jorge L. 1970. Labyrinths: Selected Stories and Other Writings, eds D.A. Yates and J.E. Irby. London: Penguin.

Brattico, Elvira. 2006. “Cortical Processing of Musical Pitch as Reflected by Behavioural and Electrophysiological Evidence.” PhD diss., University of Helsinki.

Bregman, Albert S. 1990. Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT Press.

Brodmann, Korbinian. 1909. Vergleichende Lokalisationslehre der Grosshirnrinde. Leipzig: Barth.

Calvin, William H. 1996a. The Cerebral Code: Thinking a Thought in the Mosaics of the Mind. Cambridge, MA: MIT Press.

—————. 1996b. How Brains Think: Evolving Intelligence, Then And Now. New York: Basic Books.

—————. 1998. “Competing for Consciousness: A Darwinian Mechanism at an Appropriate Level of Explanation.” Journal of Consciousness Studies, 5/4: 389–404.

Campbell, Donald T. 1974. “Evolutionary Epistemology.” In The Philosophy of Karl Popper, ed. P.A. Schilpp. La Salle, IL: Open Court.

—————. 1990. “Epistemological Roles for Selection Theory.” In Evolution, Cognition, and Realism: Studies in Evolutionary Epistemology, ed. Nicholas Rescher. Lanham, MD: University Press of America.

Cohn, Richard L. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and their Tonnetz Representations.” Journal of Music Theory, 41/1: 1–66.

Cope, David. 2003. “Computer Analysis of Musical Allusions.” Computer Music Journal, 27/1: 11–28.

Cross, Ian. 2003. “Music, Cognition, Culture, and Evolution.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Dawkins, Richard. 1983a. “Universal Darwinism.” In Evolution from Molecules to Men, ed. D.S. Bendall. Cambridge: Cambridge University Press.

—————. 1983b. The Extended Phenotype: The Long Reach of the Gene. Oxford: Oxford University Press.

—————. 1989a. The Selfish Gene, 2nd edition. Oxford: Oxford University Press.

—————. 1989b. “The Evolution of Evolvability.” In Artificial Life: Proceedings of the Interdisciplinary Workshop on the Synthesis and Simulation of Living Systems, ed. Christopher G. Langton. Santa Fe Institute Studies in the Sciences of Complexity. Redwood City, CA: Addison-Wesley.

—————. 1991. The Blind Watchmaker. London: Penguin.

Deliège, Irène. 2000. “Listening to a Piece of Music: A Schematization Process based on Abstracted Surface Cues.” In Musicology and Sister Disciplines: Past, Present, Future. Proceedings of the 16th International Congress of the International Musicological Society, London, 1997, ed. David Greer. Oxford: Oxford University Press.

Deliège, Irène and Marc Mélen. 1997. “Cue Abstraction in the Representation of Musical Form.” In Perception and Cognition of Music, ed. Irène Deliège and John A. Sloboda. Hove: Psychology Press.

Delius, Juan D. 1991. “The Nature of Culture.” In The Tinbergen Legacy, ed. M.S. Dawkins, T.R. Halliday, and Richard Dawkins. London: Chapman and Hall.

Dennett, Daniel C. 1993. Consciousness Explained. London: Penguin.

—————. 1995. Darwin’s Dangerous Idea: Evolution and the Meanings of Life. London: Penguin.

Deutsch, David. 1997. The Fabric of Reality: The Science of Parallel Universes – and Its Implications. London: Allen Lane.

Deutsch, Diana. 1999. “Grouping Mechanisms in Music.” In The Psychology of Music, 2nd Edition, ed. Diana Deutsch. San Diego, CA: Academic Press.

Dunsby, Jonathan. 2010. “Memory, Memorizing.” Grove Music Online. Oxford Music Online.
http://www.oxfordmusiconline.com/subscriber/article/grove/music/42568, accessed 14 May 2010.

Fux, Johann Joseph. 1965. The Study of Counterpoint. From Johann Joseph Fux’s Gradus ad Parnassum, trans. Alfred Mann and John Edmunds. Revised edition.

Gjerdingen, Robert O. 1988. A Classic Turn of Phrase: Music and the Psychology of Convention. Philadelphia: University of Pennsylvania Press.

—————. 1989a. “Meter as a Mode of Attending: A Network Simulation of Attentional Rhythmicity in Music.” Integral, 3: 67–92.

—————. 1989b. “Using Connectionist Models to Explore Complex Musical Patterns.” Computer Music Journal, 13/3: 67–75.

—————. 1990. “Categorization of Musical Patterns by Self-Organizing Neuronlike Networks.” Music Perception, 7/4: 339–70.

—————. 1992. “Learning Syntactically Significant Temporal Patterns of Chords: A Masking Field Embedded in an ART 3 Architecture.” Neural Networks, 5/4: 551–64.

—————. 2007. Music in the Galant Style. New York: Oxford University Press.

Grossberg, Stephen. 1987. “Competitive Learning: From Interactive Activation to Adaptive Resonance.” Cognitive Science, 11/1: 23–63.

Halpern, Andrea R. 2003. “Cerebral Substrates of Musical Imagery.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Hebb, Donald O. 1949. The Organization of Behavior: A Neuropsychological Theory. New York: Wiley.

Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, MA: MIT Press.

Hyer, Brian. 1995. “Reimag(in)ing Riemann.” Journal of Music Theory, 39/1: 101–38.

Jan, Steven B. 2007. The Memetics of Music: A Neo-Darwinian View of Musical Structure and Culture. Aldershot: Ashgate.

—————. 2010. “Memesatz contra Ursatz: Memetic Perspectives on the Aetiology and Evolution of Musical Structure.” Musicae Scientiae, 14/1: 3–50.

—————. 2012. “Evolutionary Thought in Music Theory and Analysis: A Corrective to “Babelization”?” In Proceedings of the Conference L’analyse musicale aujourd’hui: crise ou (r)évolution?, Université de Strasbourg, 19–21 November 2009, ed. Mondher Ayari, Jean-Michel Bardez, and Xavier Hascher. Strasbourg: University of Strasbourg Press.

Juslin, Patrik N. and John A. Sloboda, eds. 2009. Handbook of Music and Emotion: Theory, Research, Applications. Series in Affective Science. Oxford: Oxford University Press.

Knopoff, Leon and William Hutchinson. 1981. “Information Theory for Musical Continua.” Journal of Music Theory, 25: 17–44.

Laland, Kevin N. and Bennett G. Galef. 2009. The Question of Animal Culture. Cambridge, MA: Harvard University Press.

Langrish, John Z. 1999. “Different Types of Memes: Recipemes, Selectemes and Explanemes.” Journal of Memetics—Evolutionary Models of Information Transmission, 3 (2). http://cfpm.org/jom-emit/1999/vol3/langrish_jz.html, accessed 28 May 2010.

Lartillot, Olivier. 2009. “Taxonomic Categorisation of Motivic Patterns.” Musicae Scientiae, Discussion Forum 4B, Musical Similarity: 25–46.

Lartillot, Olivier and Petri Toiviainen. 2007. “Motivic Matching Strategies for Automated Pattern Extraction.” Musicae Scientiae, Discussion Forum 4A, Similarity Perception in Listening to Music: 281–314.

Leech-Wilkinson, Daniel. 2009. The Changing Sound of Music: Approaches to Studying Recorded Musical Performances. London: CHARM.

Leman, Marc. 1995. Music and Schema Theory: Cognitive Foundations of Systematic Musicology. Berlin and Heidelberg: Springer.

Leng, Xiaodan and Gordon L. Shaw. 1991. “Toward a Neural Theory of Higher Brain Function Using Music as a Window.” Concepts in Neuroscience, 2/2: 229–58.

Leng, Xiaodan, Eric L. Wright, and Gordon L. Shaw. 1990. “Coding of Musical Structure and the Trion Model of Cortex.” Music Perception, 8/1: 49–62.

Lerdahl, Fred. 1992. “Cognitive Constraints on Compositional Systems.” Contemporary Music Review, 6/2: 97–121.

Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge, MA: MIT Press.

Lynch, Aaron. 1998. “Units, Events and Dynamics in Memetic Evolution.” Journal of Memetics—Evolutionary Models of Information Transmission, 2 (1). http://jom-emit.cfpm.org/1998/vol2/lynch_a.html.

McKay, John Z. 2009. “The Problem of Improbability in Music Analysis.” Paper presented at the Conference L’analyse musicale aujourd’hui: crise ou (r)évolution?, Université de Strasbourg, November 19–21.

Meyer, Leonard B. 1956. Emotion and Meaning in Music. Chicago: University of Chicago Press.

—————. 1973. Explaining Music: Essays and Explorations. Chicago: University of Chicago Press.

—————. 1989. Style and Music: Theory, History, and Ideology. Philadelphia: University of Pennsylvania Press.

Miller, George A. 1956. “The Magical Number Seven, Plus or Minus Two: Some Limits on Our Capacity for Processing Information.” Psychological Review, 63/2: 81–97.

Mountcastle, Vernon B. 1957. “Modality and Topographic Properties of Single Neurons of Cat’s Somatic Sensory Cortex.” Journal of Neurophysiology, 20/4: 408–34.

—————. 1978. “An Organizing Principle for Cerebral Function: The Unit Module and the Distributed System.” In The Mindful Brain: Cortical Organization and the Group-Selective Theory of Higher Brain Function, ed. Gerald M. Edelman and Vernon B. Mountcastle. Cambridge, MA: MIT Press.

—————. 1997. “The Columnar Organization of the Neocortex.” Brain, 120: 701–22.

Mozart, Wolfgang Amadeus, Herbert von Karajan, and William Kempff. 1956/2008. Piano Concerto no. 20, Symphony no. 41 (‘Jupiter’). Audite 95.602.

Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago: University of Chicago Press.

—————. 1999. “Hierarchical Expectation and Musical Style.” In The Psychology of Music, ed. Diana Deutsch. 2nd edition. San Diego, CA: Academic Press.

Nattiez, Jean-Jacques. 1990. Music and Discourse: Toward a Semiology of Music, trans. Carolyn Abbate. Princeton, NJ: Princeton University Press.

Nigrin, Albert. 1993. Neural Networks for Pattern Recognition. Cambridge, MA: MIT Press.

Ockelford, Adam. 2009. “Similarity Relations Between Groups of Notes: Music-Theoretical and Music-Psychological Perspectives.” Musicae Scientiae, Discussion Forum 4B: Musical Similarity: 47–98.

Papineau, David. 1995. “Science, Problems of the Philosophy of.” In The Oxford Companion to Philosopy, ed. Ted Honderich. Oxford: Oxford University Press.

Parsons, Lawrence M. 2003. “Exploring the Functional Neuroanatomy of Music Performance, Perception, and Comprehension.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Plotkin, Henry C. 1995. Darwin Machines and the Nature of Knowledge: Concerning Adaptations, Instinct and the Evolution of Intelligence. London: Penguin.

Prinz, Wolfgang. 2003. “Experimental Approaches to Action.” In Agency and Self-Awareness: Issues in Philosophy and Psychology, ed. Johannes Roessler and Naomi Eilan. New York: Oxford University Press.

Ryle, Gilbert. 2000. The Concept of Mind. London: Penguin.

Samson, Séverine and Nathalie Ehrlé. 2003. “Cerebral Substrates for Musical Temporal Processes.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Schenker, Heinrich. 1979. Free Composition, ed. and trans. Ernst Oster. New York: Longman.

Schoenberg, Arnold. 1970. Fundamentals of Musical Composition, ed. Gerald Strang and Leonard Stein. London: Faber.

Seeger, Charles. 1960. “On the Moods of a Musical Logic.” Journal of the American Musicological Society, 13: 224–61.

Shennan, Stephen. 2002. Genes, Memes, and Human History: Darwinian Archaeology and Cultural Evolution. London: Thames and Hudson.

Snyder, Bob. 2000. Music and Memory: An Introduction. Cambridge, MA: MIT Press.

—————. 2009. “Memory for Music.” In The Oxford Handbook of Music Psychology, ed. Susan Hallam, Ian Cross, and Michael Thaut. Oxford: Oxford University Press.

Solomon, Maynard. 1991. “The Rochlitz Anecdotes: Issues of Authenticity in Early Mozart Biography.” In Mozart Studies, ed. Cliff Eisen. Oxford: Clarendon Press.

Stafford, William. 1991. The Mozart Myths: A Critical Reassessment. Stanford, CA: Stanford University Press.

Stainsby, Thomas and Ian Cross. 2009. “The Perception of Pitch.” In The Oxford Handbook of Music Psychology, ed. Susan Hallam, Ian Cross, and Michael Thaut. Oxford: Oxford University Press.

Stevens, Catherine and Tim Byron. 2009. “Universals in Music Processing.” In The Oxford Handbook of Music Psychology, ed. Susan Hallam, Ian Cross, and Michael Thaut. Oxford: Oxford University Press.

Tagg, Philip. 1999. “Introductory Notes to the Semiotics of Music, Version 3.” http://www.tagg.org/xpdfs/semiotug.pdf, accessed 13 May, 2010.

Temperley, David. 2001. The Cognition of Basic Musical Structures. Cambridge, MA: MIT Press.

—————. 2007. Music and Probability. Cambridge, MA: MIT Press.

Tillmann, Barbara, Jamshed J. Bharucha, and Emmanuel Bigand. 2003.“Learning and Perceiving Musical Structures: Further Insights from Artificial Neural Networks.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Todd, Peter M. and D. Gareth Loy. 1991. Music and Connectionism. Cambridge, MA: MIT Press.

Tovey, Donald F. 1935. Essays in Musical Analysis, Vol. 1: Symphonies. London: Oxford University Press.

Važan, Peter. 2000. “Memory for Music: An Overview.” Systematic Musicology, 7/1–2: 7–31.

Warnock, Mary. 1987. Memory. London: Faber.

Zatorre, Robert J. 2003. “Neural Specializations for Tonal Processing.” In The Cognitive Neuroscience of Music, ed. Isabelle Peretz and Robert J. Zatorre. Oxford: Oxford University Press.

Footnotes

1. An analytical grammar (Ockelford 2009, 88) formalizes a model of music coherent within the terms of a particular theory (but needs, however, to remain vigilant for the specter of apophenia (seeing patterns where none exists) (McKay 2009)). Compositional and listening grammars (Lerdahl 1992) make their appeal for coherence to the impulses of creativity and to the constraints of psychology respectively.
Return to text

2. He lists “five other factors...known to be important to the evolution of species” on 23–5.
Return to text

3. I borrow this term from Tagg (who takes it from (Seeger 1960)), retaining the signifier while changing the signified. That is, while Tagg defines the museme as “a minimal unit of musical discourse that is recurrent and meaningful in itself within the framework of any one musical genre,” I simply employ it as a contraction of “musical meme.” Nevertheless, a trace of Tagg’s original meaning remains even as I omit, for present purposes, questions of musical signification and referentiality (Tagg 1999, 32). See also (Jan 2007, 100–105).
Return to text

4. See Dunsby 2010 for a general overview of memory as it applies to music.
Return to text

5. Snyder’s indication of the ambit of WM is represented by the dotted-line oval overlaid at the top of my Figure 2 (Snyder 2000, 49, Figure 4.1). See also (Berz 1995).
Return to text

6. The term “orientation column” (Calvin 1996a, 205) refers to the fact that, in the visual cortex, certain minicolumns respond optimally to stimuli orientated in a certain spatial plane, the topography of the cortex closely mapping perceptual input from the visual field. The analogous (tonotopic) organization of auditory cortex is discussed in Section 4.1.2.
Return to text

7. In Calvin’s diagrams, the “raised [grey] hexagons” represent “[a] complete active set of triangular arrays ... sustained by a basin of attraction in the underlying connectivity.” A “flat [white] hexagon” represents “[a] complete active set, merely sustained by recruitment [mis]copying from neighboring hexagons” (Calvin 1996a, 62).
Return to text

8. See (Calvin 1996a, 99–102) for a detailed mapping of the “six essential aspects of the creative darwinian process that bootstraps quality,” plus the “five other factors,” to the HCT.
Return to text

9. In this sense the HCT accords with the precepts of “common coding theory,” the idea that “somewhere in the chain of operations that lead from perception to action, the system generates certain derivatives of stimulation and certain antecedents of action that are commensurate in the sense that they share the same system of representational dimensions” (Prinz 2003, 171). In contrast, the “classical sensorimotor framework” “relies entirely on separate coding” and requires “a mapping device that translates stimulus codes into movement codes” (Prinz 2003, 171; emphasis in the original).
Return to text

10. LTP is “[a] sustained (minutes to days) change in [inter-neuronal] connection strength, largely synaptic, that follows some priming events—such as a barrage of impulses...LTP is thought to provide the physiological scaffolding for slowly making (during memory consolidation) the anatomical changes that more permanently increase the synaptic strength” (Calvin 1996a, 209, 207).
Return to text

11. At a still lower level, the sub-atomic dimension of protons, neutrons, and electrons maps on to the individual, simultaneous frequency components (harmonics) which are fused in perception to create an event. See also (Bregman 1990).
Return to text

12. For the application of gestalt psychology to questions of musical segmentation and grouping, see Diana Deutsch 1999 and Snyder 2000, 39–43. For post/neo-gestalt theories, see Lerdahl and Jackendoff 1983, Narmour 1990 and Temperley 2001. See also Stevens and Byron 2009).
Return to text

13. The minicolumnar grid upon which the triangular arrays are placed in this and subsequent examples is taken from http://williamcalvin.com/Demo2.htm (accessed 5 March 2010).
Return to text

14. This museme is the sixth in a recurring sequence of eight expositional “nodes” in Jan 2010, 22–5. In Gjerdingen’s terms, it constitutes an instance of a (here short) Indugio plus “Converging cadence” schema (Gjerdingen 2007, 274; see also 464), although this conjunction of formulae was not confined to this structural locus.
Return to text

15. The fields of such a simulation may correspond to different locations in the human nervous system. Those at levels F₁ and F₂, attending to lower-level phenomena, represent more peripheral regions of the auditory system whereas levels F₃ and F₄ are implemented by cortical processes.
Return to text

16. F₂ is connected to F₃ by “simple [one-way] feedforward links,” not the “symbolic [two-way, feedback-implementing] synapses” which link F₁ with F₂ and F₃ with F₄ (hence the network’s designation as of the ART-2 type) (Gjerdingen 1990, 352). Real faux-fax links may well be “symbolic.”
Return to text

17. Certain limitations of the ART architecture are addressed by Gjerdingen’s employment of a “masking field” in later studies (Gjerdingen 1992), and in subsequent work by others (see Nigrin 1993).
Return to text

Copyright Statement

Copyright © 2011 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Michael McClimon, Editorial Assistant
Number of visits: