Review of Dmitri Tymoczko, A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice (Oxford University Press, 2011) *
Julian Hook
KEYWORDS: Tymoczko, geometry, chords, voice leading, scales, tonality, chromaticism, style, common practice, jazz
Copyright © 2011 Society for Music Theory
[1] Near the beginning of his book Style and Music, Leonard Meyer repeats a parable told by the American philosopher John Searle, describing what might happen when an intelligent observer who knows nothing of American football watches a game for the first time.(1) To paraphrase somewhat, the observer watches a quarter or two of the game and eventually declares, “I have figured out football. Football consists of a statistically regular alternation of circular clustering, linear clustering, and random interpenetration.”
[2] The observer’s description of football is not wrong: the players on the field do arrange themselves in statistically predictable ways as described. Clearly, though, this explanation misses the point of football in important ways. The statistical phenomena it details are nothing more than incidental byproducts of the things that football is really about: the objectives, the rules, and the strategies of the game, about all of which our observer remains blissfully clueless. In Searle’s terms, the observer has noted some superficial brute facts, but has failed to account for the deeper institutional facts, which create constraints that shape the brute facts in essential ways.
[3] In my more cynical moments, I find myself suspecting (and this is Meyer’s point as well) that the understanding of music displayed in much of what is said and written on the subject is ultimately not much better than this observer’s understanding of football. We make many observations about music, and while these observations are usually correct in some sense, they often seem to miss important points: we observe brute facts while remaining oblivious to more fundamental principles that underlie, motivate, and explain those facts.
[4] Dmitri Tymoczko evidently harbors such suspicions as well, perhaps more often and more strongly than I do. While there are some brute facts in Tymoczko’s new book A Geometry of Music (henceforth AGOM), the book is set apart by its aspirations to unearth deeper institutional facts that others have overlooked. Tymoczko is unafraid to question conventional wisdom, spurn the beaten path, and seek new viewpoints on familiar landmarks, and AGOM does not lack for bold claims with far-reaching consequences. It promises nothing less than a rational foundation for tonality; a set of common principles that unify the music of not just one or two centuries but broad swaths of music history spanning the better part of a millennium; new perspectives on (among other things) scales, modulation, functional harmony, chromaticism, and the place of jazz in music history; and a powerful, overarching geometric model that ties it all together.
[5] The reader who suspects that a book of 450 pages cannot possibly deliver on such a sweeping array of promises may be surprised by the remarkable extent to which it succeeds. The geometric model that takes pride of place in the title is a monumental achievement in its own right, and is brought to bear revealingly on fundamental aspects of harmony, voice leading, consonance, tonality, and style, aptly illustrated through hundreds of figures and musical examples in a wide range of styles. The upshot of it all is a book that occasionally vexes but more often illuminates, inspires, and exhilarates: a treasury of big ideas, by any reasonable standard a major treatise for our field.
[6] The essential features of the geometric model are developed in the third of AGOM’s ten chapters, “A Geometry of Chords.” The chord spaces described here have variously been dubbed “CQT spaces” (after the groundbreaking article by Callender, Quinn, and Tymoczko, published in Science in 2008, expanding upon Tymoczko 2006), “OPTIC spaces” (after the five kinds of symmetries the theory admits, defined by equivalence under octave shifts, permutation of notes within a collection, transposition, inversion, and cardinality change), and “orbifold spaces” (after the mathematical name for the topological structures formed by these spaces, which in general are non-Euclidean and include singularities of various kinds). These spaces may be thought of as adding a geometric component to pitch-class set theory, situating chords of n notes in a continuous space (not a discrete lattice) in n dimensions, while taking into account any desired combination of the OPTIC symmetries: for example, the notion of “pitch-class set” presupposes the O, P, and C symmetries, while the notion of “set class” presupposes all five. Many of Tymoczko’s applications of the model depend crucially on its ways of measuring distance: a voice leading is a path through an appropriately chosen OPTIC space, and the distance between any two chords in that space reflects the potential to connect them via smooth voice leading. As such, the OPTIC spaces use sophisticated techniques from contemporary mathematics to pull together many threads from musical scholarship of the last half-century, including set theory, scale theory, neo-Riemannian theory, and an assortment of work on voice leading and geometric representations.(2)
[7] To say that the geometric model lies at the heart of the book would be accurate, but also misleading in at least two ways. First, AGOM offers neither the first nor the most complete presentation of this model. Chapter 3 limits its scope to a few of the most musically useful spaces in two, three, or four dimensions, and Appendix B provides only tantalizing glimpses of the more general theory and some of the new considerations that arise in higher dimensions. Readers looking for coverage of the OPTIC spaces in their full generality still have no alternative to the technical presentation in Science. Secondly, A Geometry of Music is not a book about geometry; it is a book about music. More exactly, it is about the ways in which geometry can shape and inform our understanding of music—ways that are many and varied indeed. Anyone who finds diagrams like the pitch-class circle, the circle of fifths, or the neo-Riemannian Tonnetz useful for visualizing aspects of musical structure should, upon learning to navigate the OPTIC spaces, come to appreciate the varied perspectives and novel musical insights that these spaces provide.
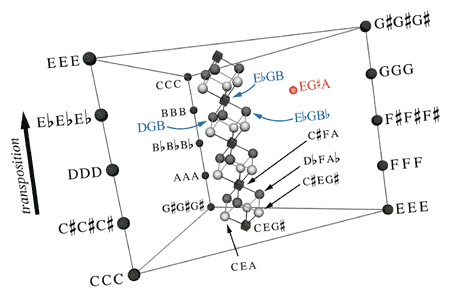
Figure 1. A section of three-note chord space (A Geometry of Music, page 86, Figure 3.8.2; color annotations added)
(click to enlarge)
[8] An easily described example of such an insight—one of many that could be chosen for illustrative purposes—concerns a relationship between voice leading and nearly equal divisions of the octave. Three-dimensional chord (OP) space, described in Section 3.8, forms a triangular prism. Augmented triads, equal divisions of the octave into four-semitone intervals, lie on the central axis of this prism, and major and minor triads, which divide the octave nearly equally, are grouped near this central axis (see Figure 1).(3) It is a consequence of this geometry that every major or minor triad lies near several others, and in particular lies near its T4 and T8 transpositions. For example, an
[9] In four-note chord space, the same reasoning shows that dominant and half-diminished seventh chords (minimal perturbations of the diminished seventh, the four-part equal division of the octave) offer the greatest potential for voice-leading connections with other chords of the same type, and particularly with their transpositions by three semitones. The repercussions of this difference for the way composers use triads and seventh chords are explored in section 3.10, titled “Triads are from Mars; seventh chords are from Venus.” The claim here, supported by a table showing the frequencies of root motions of triads and seventh chords in works by Schubert and Chopin, is that because of the voice-leading properties just described, triads are more likely to be connected by major-third root movement, while seventh chords are more likely to be connected by minor thirds.(4)
[10] The musical ideas that Tymoczko draws from geometric inspiration are not limited to the ways chords move in chromatic space. The role of a chord in the above examples may be played instead by a scale, or more generally by what Tymoczko calls a macroharmony, a collection of notes controlling the pitch content of music over a period of time. Studying movement from one scale to another in an appropriate space provides a new way of thinking about modulation in traditional tonal music (a modulation from C major to G major is a move from one seven-note collection to another nearby one),(5) or of thinking about relationships between different types of scales in the music of Debussy, Shostakovich, or Reich.(6) In Chapter 7 there is a proposed grammar of functional harmony based on the diatonic circle of thirds, which is roughly a diatonic version of Figure 1’s graph of nearly even trichords.
[11] The musical examples that Tymoczko offers usually illustrate his points well, and it is enjoyable (and not too difficult) to find more examples to supplement them.(7) Most of the examples are short, and the book does not claim to offer a comprehensive methodology for analysis of complete works, or even to recapture all that traditional analytical approaches might tell us (nothing in the geometry, for example, differentiates the resolution of a tendency tone from any other stepwise voice leading), but broader implications are not in short supply. If you are a composer, Tymoczko says, and if you want to write music featuring a limited variety of chord types, connected by smooth voice leading, you will have more success if you choose to use nearly-even triads or seventh chords than if you try to use uneven sets like 015. Precepts about compositional strategy permeate the book, and while it is reasonable to wonder how many composers deliberately formulate their objectives in such ways, the precepts reveal constraints that inevitably shape musical works whether composers are conscious of them or not. It is only a small step from compositional strategies to broad pronouncements about style: it is no coincidence, in Tymoczko’s view, that triads and seventh chords form the harmonic stock-in-trade of so much of our music.
[12] The music in which we most often encounter triads and seventh chords is, of course, tonal, and Tymoczko’s generalizations apply mainly to music that is “tonal” at least in the broadest sense of the word. As early as page 4 of AGOM, he identifies five features characteristic of “tonality” taken broadly. (These should be relatively uncontroversial; harmonic consistency and smooth voice leading are two of them.) He revisits these features throughout the book, describing how their interactions are constrained by geometry, and postulating that in various manifestations and combinations they characterize an “extended common practice” that stretches from eleventh-century polyphony through contemporary jazz and delineates the repertoire that is most compellingly illuminated by the geometric model. Music by Stravinsky, Glass, and Bill Evans, for example, falls comfortably within this compass, thus addressing what Tymoczko perceives as a failing of his own musical education, in which these composers were marginalized.(8)
[13] Every book is shaped by its author’s prejudices. Those who have followed Tymoczko’s career know that he has at times been openly critical of some approaches to composition and musical scholarship, sometimes pointedly enough to discomfit even those of us who share some of his reservations. AGOM’s attitude toward these topics ranges from entertaining barbs (see the discussion of “atonal food” on page 392) to polite agnosticism (as in the discussion on pages 264–267 of the compatibility between the geometric approach and “pluralist Schenkerianism”) to benign neglect (David Lewin, transformation theory, and group theory are barely mentioned). Appendix C, “Discrete Voice-Leading Lattices,” criticizes the neo-Riemannian Tonnetz as a voice-leading graph; the criticism is apt, but ignores the many other applications that interpret the Tonnetz and related graphs more abstractly, as depictions of intervallic or transformational structure in an algebraic sense, more or less independent of voice leading.
[14] There is more than a little irony in some of these criticisms and omissions, as they involve some of the very giants on whose shoulders Tymoczko is standing for his panoramic view. To the extent that the geometric model grows from set theory, it traces a fairly direct lineage to the work of Babbitt and Schoenberg, leading proponents of some of the only important Western musical styles of the last several centuries that fall outside Tymoczko’s “extended common practice” (and atonal music, after all, lives in the OPTIC spaces too). Four of the five OPTIC symmetries can be elegantly described in terms of orbits of group actions, and it is hard to imagine that Tymoczko’s work could have unfolded as it did had David Lewin not introduced transformation groups (and, more broadly, rigorous mathematical thinking) into American music theory in his own idiosyncratic way. Though AGOM is in many ways meticulously documented—Tymoczko is generous with citations of opinions that differ from his own, and the bibliography fills ten small-print pages—it occasionally gives the impression of disowning its own heritage, and therefore perhaps of being even more iconoclastic than it actually is. The level of originality in this work is remarkable enough already, and hardly needs exaggerating.(9)
[15] Readers who may be inclined to bypass AGOM in the expectation that it will be forbiddingly technical should be assured that it is not. Tymoczko confronts with apparent relish the daunting challenge of selling his ideas to a broad audience of theorists, composers, musicians, and students, and his ability to capture the intricacies of complex material while presenting it clearly and comprehensibly is praiseworthy. Some parts of the book are difficult, to be sure, but the level of abstraction subsides fairly quickly after peaking in Chapter 3. Appendix F provides some pedagogically valuable exercises, most of them pertaining to the most technical material in Chapters 2–4.
[16] In fact, the book has been taken to task in some quarters on the opposite grounds, for sweeping essential details under a rug of too-casual narration. In a forum devoted to AGOM at the international conference of the Society for Mathematics and Computation in Music (Paris, June 2011), a few attendees lamented the book’s lack of axioms, definitions, theorems, and proofs in a formal mathematical style.(10) There are many pictures but almost no equations, and there are certainly times when group-theoretic considerations might have offered valuable alternative perspectives.(11) The discussion of the geometric spaces falls far short of the full generality of the OPTIC spaces, and a formal definition of orbifolds is nowhere to be found. Tymoczko responded to such objections by saying that his exposition is modeled less on a mathematics textbook than on writings in physics or other applied sciences, where authors routinely eschew the formal axiomatic style and present only as much mathematics as is needed for the applications at hand. It is clear in any case that the sometimes opposing demands of scope, technical accuracy, and readability require some balances to be struck in a book of this nature, and though I sometimes find myself craving more detail, the author’s decisions are surely defensible.
[17] AGOM is enriched by two other ambitious undertakings on Tymoczko’s part. He makes available a custom-designed software tool enabling visualization of chords in several geometric spaces; one can easily display the chords shown in Figure 1, for example, and rotate the picture in three dimensions to view it from different angles.(12) (There are also several ways to view four-dimensional chord space, which not surprisingly is considerably harder to grasp.) Also, various points are supported by statistical analyses estimating the frequencies with which certain characteristics appear in the works of certain composers or eras—a valuable if time-consuming technique that is slowly gaining a foothold in music theory scholarship.(13)
[18] The book as a whole is attractively produced, but in a work of this complexity some errors are inevitable. Fortunately, most of the errors I spotted are of the sorts that many readers will likely pass over without notice or will correct with little difficulty: missing words, incorrect note names, small mismatches between example and description.(14) With a few exceptions, the musical and graphic examples are clearly and accurately rendered.(15)
[19] The potential audience for A Geometry of Music is as wide-ranging as the book itself. It was clear at the aforementioned forum that Tymoczko’s work has earned great respect within the international community of mathematical music theorists. It has also attracted the attention of at least a few composers, cognitive scientists, and psychologists, and Tymoczko has apparently taught the material with some success to Princeton undergraduates. But the substance of the book is harmony, counterpoint, tonality, scales—the stuff of music theory—and it is music theorists who stand to benefit the most from it. The indefinite article in the title perhaps tacitly acknowledges that no book can truly stake a claim to being the last word on its subject, but this one provides the most definitive answers now available to many questions that music theorists have asked and to many more that we didn’t know we had. If the author’s way of doing music theory or promulgating his results is not quite like most of the music theory that we have learned and taught, that is hardly a sufficient reason why we should not give his powerful ideas the attention they deserve.
Julian Hook
Jacobs School of Music
Indiana University
1201 East Third Street
Bloomington, IN 47405
juhook@indiana.edu
Works Cited
http://mtosmt.org/issues/mto.04.10.3/mto.04.10.3.callender.pdf (accessed 16 September 2011).
Callender, Clifton. 2004. “Continuous Transformations.” Music Theory Online 10.3.
http://mtosmt.org/issues/mto.04.10.3/mto.04.10.3.callender.pdf (accessed 16 September 2011).
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320: 346–348.
http://www.mtosmt.org/issues/mto.03.9.4/mto.03.9.4.cohn_frames.html (accessed 16 September 2011).
Cohn, Richard. 2003. “A Tetrahedral Graph of Tetrachordal Voice-Leading Space.” Music Theory Online 9.4.
http://www.mtosmt.org/issues/mto.03.9.4/mto.03.9.4.cohn_frames.html (accessed 16 September 2011).
Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42: 241–263.
Meyer, Leonard B. 1989. Style and Music: Theory, History, and Ideology. Philadelphia: University of Pennsylvania Press.
Morris, Robert D. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20: 175–208.
Quinn, Ian. 2006. “General Equal-Tempered Harmony (Introduction and Part I).” Perspectives of New Music 44 (2): 114–159.
—————. 2007. “General Equal-Tempered Harmony: Parts 2 and 3.” Perspectives of New Music 45 (1): 4–63.
Quinn, Ian, and Panayotis Mavromatis. 2011. “Voice-Leading Prototypes and Harmonic Function in Two Chorale Corpora.” In Mathematics and Computation in Music, Proceedings of the Third International Conference of the Society for Mathematics and Computation in Music, Paris, June 2011, edited by Carlos Agon, Emmanuel Amiot, Moreno Andreatta, Gérard Assayag, Jean Bresson, and John Mandereau (Berlin: Springer), pages 230–240.
Roeder, John. 1987. “A Geometric Representation of Pitch-Class Series.” Perspectives of New Music 25: 362–409.
Searle, John R. 1969. Speech Acts: An Essay in the Philosophy of Language. Cambridge, UK: Cambridge University Press.
Straus, Joseph N. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25: 305–352.
Tymoczko, Dmitri. 2004. “Scale Networks and Debussy.” Journal of Music Theory 48: 219–294.
—————. 2006. “The Geometry of Musical Chords.” Science 313: 72–74.
—————. 2008a. “Lewin, Intervals, and Transformations: A Comment on Hook.” Music Theory Spectrum 30: 164–168.
—————. 2008b. “Scale Theory, Serial Theory and Voice Leading.” Music Analysis 27: 1–49.
Footnotes
* The reviewer thanks Emmanuel Amiot, Scott Murphy, and Steven Rings for helpful conversations.
Return to text
1. Meyer 1989, 11–12, quoting Searle 1969, 52.
Return to text
2. The theory of orbifolds was developed by William Thurston in the late 1970s. The significant work on voice leading and musical geometry includes, among others, Roeder 1987, Morris 1998, Douthett and Steinbach 1998, Straus 2003, Cohn 2003, and notable contributions by the CQ portion of the CQT triumvirate, such as Callender 2004 and Quinn 2006 and 2007.
Return to text
3. To form the complete space, the two triangular ends of the prism in Figure 1 must be glued together with a twist, so that the two corners representing the triple unison CCC are superimposed. The space is thus a higher-dimensional analog of a Möbius strip; indeed, the analogous two-note chord space is precisely a Möbius strip (AGOM Figure 3.3.1).
Return to text
4. Of course, real music is messier than elegant theory. While it does show a statistical preference for chord connections of the sorts Tymoczko describes, the table (p. 99) also confirms the presence in the literature of many other chromatic progressions, including Martian-Venusian hybrids in which triads move by minor thirds or seventh chords by major thirds: maximally smooth voice leading, evidently, is not always the paramount consideration in chord choice.
Return to text
5. In theory, diatonic scales inhabit a seven-dimensional OP space; fortunately, lower-dimensional spaces can capture the essential features when only a few scale types are involved.
Return to text
6. Some of these insights were introduced in Tymoczko’s earlier work on scales (2004, 2008b), newly contextualized by the OPTIC spaces.
Return to text
7. While reading AGOM I happened simultaneously to be renewing my acquaintance with the piano music of Gabriel Fauré, and found time and again that the geometric perspective shed light on Fauré’s chromatic adventures. The middle section of the Fourth Barcarolle, op. 44, modulates down repeatedly by semitone, tracing a clear path that winds down around the central axis of Figure 1’s three-note chord space (
Return to text
8. This failing is addressed most provocatively in the Introduction (page xvii): “The music I encountered [in college] was the music my teachers knew how to talk about. Unfortunately, this was not the music I had come to college wanting to understand.” More disturbing is the preceding paragraph’s suggestion that these eminent teachers “knew nothing about” the music that most appealed to Tymoczko. Significantly, of the five features of tonality, the one that most sharply discriminates the traditional “common practice” of the eighteenth and nineteenth centuries from the remainder of Tymoczko’s “extended common practice” is centricity, which is also the feature about which the geometric model seems to tell us the least (although the “pitch-class profiles” introduced in section 5.6 offer an interesting take on centricity).
Return to text
9. In some cases, an apparent tendency on Tymoczko’s part to exaggerate the radical nature of his accomplishments may have less to do with self-promotion than with a low threshold of radicalism. He has at times described as “radical” work by various other people, including myself (Tymoczko 2008a), that I would not necessarily describe in that way. Oxford’s publicity for the book perhaps does not help by suggesting that Tymoczko has finally explained “what makes music sound good.” A promotional blurb on the dust jacket unwittingly contributes a further hyperbole by describing Tymoczko as the only member of “the intersection of those who are distinguished composers and those who have published in Science,” overlooking Clifton Callender’s membership in that elite group.
Return to text
10. One commenter went so far as to describe the book’s style as “anti-intellectual.” (“I have been called many things,” Tymoczko said in response, “but this is the first time I have ever been called anti-intellectual.”) Those who voiced such reservations were, I believe without exception, European; some noted that a formal mathematical style of exposition is better tolerated in Europe than in America.
Return to text
11. For example, an exercise in Appendix F asks the reader to explain why there are five efficient voice leadings that permute three closely clustered notes in a four-note chord. The intended geometric explanation, involving paths reflecting off the boundaries of four-dimensional chord space, is somewhat hard to visualize (though a good exercise, to be sure), but algebraically the reason is obvious: there are six permutations of three objects, including the identity.
Return to text
12. The ChordGeometries program is available at the author’s website (http://dmitri.tymoczko.com). Additionally, the book has a companion website (http://www.oup.com/us/ageometryofmusic), where audio files corresponding to many of the musical examples may be heard. The audio may be beneficial to those who have difficulty playing or aurally imagining the examples, but the synthesized sound will be off-putting to many listeners, and there are occasional mismatches between printed examples and their audio counterparts.
Return to text
13. Corpus studies are widely used in some other disciplines, notably linguistics, where it is widely recognized that the results sometimes force scholars to challenge their assumptions and confront phenomena that might otherwise escape their notice. A number of corpus-based studies of music have appeared in recent years; for example, Quinn and Mavromatis 2011 use corpus-based analysis to shed light on syntactic differences between Bach chorales and a corpus of Lutheran chorales from a century earlier. Tymoczko does not describe the methodology underlying his computer analyses in detail, and admits that it is sometimes “simplistic but hopefully unbiased” (249). Occasional oddities in the results betray a lack of discernment in these analyses. A table of modulation frequencies (251), for example, suggests that the major subtonic is one of the most common goals of a modulation from a minor key; one suspects that most of these “modulations to VII” would be analyzed by most theorists as tonicizations of V/III.
Return to text
14. Apologies are owed to Richard Rodgers and Gabe Fankhauser, whose names are misspelled, and perhaps to the girl of Debussy’s eighth Prelude, whose title appears on page 324 as “La fille aux cheveaux de lin,” leaving us uncertain whether she is in possession of flaxen hair or flaxen horses.
Return to text
15. In Figure 9.3.6 on page 328, the
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: