Total Voice Leading

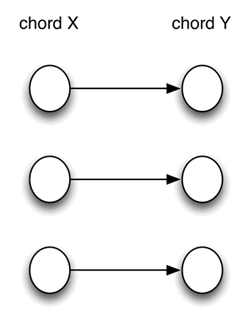
[1] People usually think about voice leading as in Example 1, with each note in Chord X moving to a destination in Chord Y.⁽¹⁾ I propose to think of it instead as in Example 2, taking into account all the possible destinations in Chord Y of each note in Chord X. A bit more formally, I define the total voice leading between sets X and Y as the complete collection of ordered pc intervals formed between the pcs in X and the pcs in Y.⁽²⁾ Instead of concerning ourselves with the behavior of individual tones, we will focus on the overall voice-leading gesture, the sound envelope, the sonic environment created by the motion from X to Y.

[2] Among the intervals formed between two sets in any particular context, some will be more marked for attention than others, but all are at least potentially in play. The less marked ones create a nimbus within which the more marked ones are heard. Taken together, they create a total sonic package in which all intervals play a role. It is the same as in hearing the sonic identity of a single chord—one may be more aware of some intervals than others, but it is the total package of intervals that characterizes the chord. Indeed, the interval content of Chord X is equivalent to the total voice leading from Chord X to itself. In that sense, the interval content of a harmony is a special case of total voice leading X→Y, where X=Y. Total voice leadings are thus roughly equivalent to the interval content of a single chord, generalized and horizontalized, with some of the same conceptual and perceptual advantages and challenges.

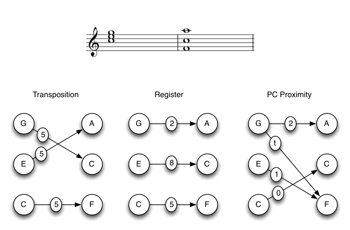
[3] It is easy to trump up a context in which one is invited and almost compelled to attend to all of the voice-leading intervals simultaneously. In Example 3, for instance, one simultaneously hears the intervals formed within each instrumental part (flute, violin and trumpet), within each register (high, middle, and low), and among the similarly articulated notes (sustained whole notes, tremolo half notes, and staccato eighth notes). But even in a much simpler, more conventional progression like the one in Example 4, most of the intervals that comprise the total voice leading are near the forefront of musical consciousness, or can easily be summoned there.

[4] If x is the cardinality of X and y is the cardinality of Y, the number of intervals in the total voice leading between X and Y will be xy. In Example 2, for instance, there are nine arrows connecting the three pcs in X with the three pcs in Y. Similarly, the total voice leading between two tetrachords would be 4 x 4 = 16. If the perceptual task is understood to be the direct perception of all sixteen intervals simultaneously, this might seem a daunting proposition. But, at least in principle, the task is no different from recognizing the identity of a particular hexachord, and it’s not all that different in quantity either. A hexachord contains fifteen intervals, and recognizing it would seem to depend more on the perception of the total package of intervals than on the discrete discernment of each one individually. The same is true of the total voice leading between two tetrachords, or between two sets of whatever size. In any case, total voice leading, like total interval content, is probably best thought of as an underlying potential in the relationship between two sets (which may be the same set), with local contextual factors inevitably emphasizing some intervals more than others, and probably doing so in different ways.

IFUNC and imultisets

[5] My concept of total voice leading represents a slight reorientation of David Lewin’s IFUNC(X, Y)(i), which tells us “in how many different ways the interval i can be spanned between (members of) X and (members of) Y” (Lewin 1987, 88).⁽³⁾ As i ranges over the twelve possible ordered pc intervals (0 through 11), we can gather the values into a twelve-place IFUNC-vector (see Example 5). The first entry in the IFUNC-vector indicates the number of times the ordered pc-interval 0 is found between X and Y; the second entry indicates the number of times the ordered pc-interval 1 is found between X and Y; and so on.

[6] The contents of the IFUNC-vector can be arranged as a set (or multiset) of intervals, which I call an imultiset. An imultiset is the collection of ordered pc intervals spanned between X and Y, that is, the total voice leading between X and Y. Just as a pcset or pcmultiset contains pcs, an imultiset contains ordered pc intervals. These imultisets can be treated and understood somewhat in the manner of pcsets or pcmultisets.⁽⁴⁾

[7] Like pcsets and pcmultisets, imultisets can be placed in a usable normal form, following a standard algorithm. When there is more than one occurrence of one or more intervals in an imultiset, I follow the procedure described in Robinson (2009): eliminate the doublings; put the simple set into normal form in the usual way; reinstate the doublings.

Equivalence relations (imultiset and imultiset-class)

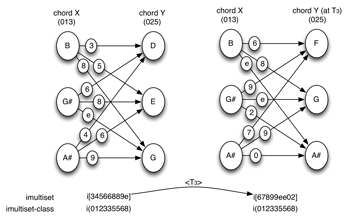
[8] Order permutation and imultiset inversion. If the order of X and Y is reversed (that is, if we are concerned with the voice leading Y→X instead of X→Y), each interval in the imultiset will be replaced with its complement mod 12. In other words, reversing the order of the generating pcsets has the effect of inverting the imultiset formed between them.⁽⁵⁾ Two imultisets related by inversion will be said to be I-equivalent members of a shared imultiset-class. Imultiset prime forms will be the member of the imultiset class with the lowest numerical value (see Example 6).⁽⁶⁾ The idea that the total voice leading from X to Y and the total voice leading from Y to X could be understood as equivalent, to within inversion, does not seem to me to pose any particular conceptual or perceptual problem. Each interval in one total voice leading is simply replaced by its complement mod 12 (i.e., its inversion) in the other. What went up now goes down, and vice versa.

[9] Transposition. When Set Y is transposed by T_n with respect to Set X, the imultiset is also transposed at T_n.⁽⁷⁾ Two imultisets related by transposition, will be said to be T-equivalent members of a shared imultiset-class (see Example 7). I will designate the transposition of an imultiset as <T_n>, to be read as “hyper- T_n.” <T_n> is a transposition of transpositions or, to put it slightly differently, an interval between intervals.⁽⁸⁾ The possibility of <T_n> arises when we are comparing two imultisets (i.e., collections of intervals). If each interval in the second imultiset is n semitones larger than a corresponding interval in the first multiset, then the two imultisets are related at <T_n>.

[10] In Example 8, each interval in the second imultiset is 3 semitones larger than the corresponding interval in the first imultiset (interval 4 becomes interval 7, interval 10 becomes interval 1, and so on). The two imultisets are thus related at <T3>. We could also talk in the same way about hyper-hyper-T <<Tn>>—that would be the interval between the intervals between intervals.

[11] Compared to inversion, the transposition of an imultiset poses serious conceptual and perceptual issues. It requires one to attend to the shape of the total voice leading rather than to the qualities of the intervals. For example, if the total voice leading from X to Y has three 5s and zero 6s, the total voice leading from X to T₁(Y) will have three 6s and zero 7s: everything has shifted one place over. The intervallic profile (the intervals among the intervals) will stay the same, but the intervals themselves will change. With reference to Example 7, one might listen for <T₃> by attending to the repeated intervals in the first voice leading: two 6’s (G♯–D and A♯–E) and two 8’s (G♯–E and B–G), differing in size by 2. In the second voice leading, we find two 9’s (A♯–G and G♯–F) and two 11’s (G♯–G and B–A♯), again differing in size by 2. The actual interval sizes have changed, but a distinctive feature of the total voice leading—repeated intervals that differ in size by 2—remains recognizably the same. The optimal ear-training strategy would thus involve attending to the distinctive features of the imultiset that mark its contour or shape.⁽⁹⁾

[12] Inversion. The inversion of pcset Y with respect to X has no consistent effect on IFUNC(X, Y), or on the total voice leading (imultiset) between X and Y.⁽¹⁰⁾ However, inverting both X and Y about the same axis does have a predictable effect, and it is the same effect as reversing the order of X and Y, namely inverting the imultiset at <I₀> (see Example 9).

[13] I will designate the inversion of an imultiset as <I_n>, to be read as “hyper-I_n.” <I_n> is a way of thinking about the axis of inversion around which two intervals might be heard to balance. Interval 3 and interval 7, for example, could be thought of as lying equidistant on either side of interval 5, which lies halfway between them. In that sense, interval 3 and interval 7 are related at <I₁₀>, and their axis of inversion is 10/2 = 5. In comparing two imultisets, if each interval in one imultiset is as far below some midpoint as each corresponding interval in the other imultiset is above it, then the two imultisets are related at <I_n> (see Example 10). We could talk in the same way about hyper-hyper I <<In>>—that would indicate the point of inversional balance between two points of inversional balance.⁽¹¹⁾

[14] Imultiset-class and prime form. If two imultisets are related by either transposition or inversion, they may be considered members of the same imultiset-class. All the members of an imultiset-class, like all the members of a pcset-class, have the same total interval content. However, when speaking of imultiset-class, we are now talking about the invariance of the intervals between intervals. An imultiset-class contains total voice leadings that are related by transposition or inversion and that thus share a particular shape or arrangement or dispersion of intervals. As noted above, imultiset-classes can be identified with a representative (prime) form.

Inversional Symmetry (IS)

[15] X and Y are pc identical. When X and Y are pc identical (i.e., related at T₀), the imultiset that results from the total voice leading between them will correspond to the traditional twelve-place interval vector for scX (and scY) (what I referred to above as an IFUNC-vector): the number of 0’s in the vector will correspond to the cardinality of the set, and each non-zero interval will be balanced by its complement mod 12. The voice-leading imultiset is thus inversionally symmetrical (see Example 11). In an inversionally symmetrical imultiset, the intervals balance above and below a central pair (inversional axis) of tritone-related intervals. When pcset X and pcset Y are identical, the intervals in the imultiset are distributed equally around intervals 0 and 6 (for every interval n, there is another interval 0-n). The imultiset is thus I-symmetrical at <I₀>.

[16] X and Y are related by transposition. If X and Y are members of the same T_n-type (i.e., related by T_n), the imultiset that results from the voice leading between them will be inversionally symmetrical at <I_2n> (see Example 12). When the pcsets are related at T₀, the imultiset is self-inversional at <I₀>, as just noted. When the pcsets are related at T₂ (as in the left side of Example 12), the imultiset is self-inversional at <I_2×2> = <I₄>. In such an imultiset, the intervals are distributed equally around intervals 2 and 8 (for every interval n, there is another interval 4-n).

[17] If we reverse the order of X and Y, the imultisets of X→Y and Y→X will be related by inversion at <I₀>, as noted above. But because X and Y in this case are related by transposition, and their imultiset is thus self-inversional, the imultisets of X→Y and Y→X will also be related by transposition.

[18] X and Y are related by inversion. If X and Y are related by inversion, however, the voice-leading imultiset is generally not inversionally symmetrical (see Example 13).

[19] X and Y are both inversionally symmetrical. If both X and Y are inversionally symmetrical pcsets, then the imultiset that results from the total voice leading between them will also be inversionally symmetrical (see Example 14). In that sense, there is something in common between two sets related by transposition and two sets that are pc-symmetrical: both produce total voice leadings that are inversionally symmetrical.⁽¹²⁾

Transpositional Combination (TC)

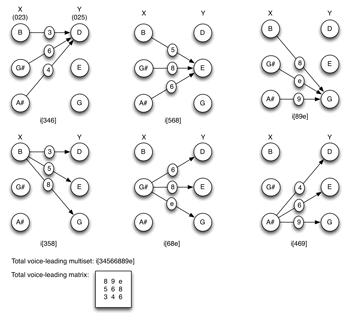
[20] All imultisets produced as the total voice leading between two pcsets will have the TC-property. According to Cohn, “Any pitch- or pc-set has the TC-property if it may be disunited into two or more transpositionally related subsets” (1988, 23). A set (or set class) with the TC-property may be understood as generated by the transposition of one of its operands to the transpositional levels of the other: “TC is a binary operation which takes as its operands two set-classes, and adds the value of each element in the prime form of the first operand to that of each element in the prime form of the second operand. The result is a larger set which bears the TC-property” (27–28).⁽¹³⁾

[21] In the case of the imultisets under discussion here, the operands are the generating pcsets, X and Y. But because of the difference between TC (with X transposed to the level of the pcs in Y) and total voice leading (where the notes in X move to the notes in Y), the imultiset will be equivalent to I(X)*Y rather than X*Y. Nonetheless, because I(X) has the same interval content as X, it is still true to say that the total voice leading from X to Y bears the imprint of the generating sets, and that X and Y are always embedded in the total voice leading they jointly generate.

[22] When X and Y are trichords, for example, the nine-element imultiset will embed three I(X)-type trichords (related by transposition by the intervals in Y) and three Y-type trichords (related by transposition by the intervals in I(X)) (see Example 15). The TC property can be easier to visualize if the imultiset is written as a matrix.⁽¹⁴⁾ The columns are all the T_n-type of Y and the rows are all the Tn-type of I(X). For the first pair of pcsets in Example 15 ([G♯, A♯, B] → [D, E, G]), the columns of the matrix contain forms of (025) related at T₀, T₁, and T₃while the rows of the matrix contain forms of (013) related at T₀, T₂, and T₅.⁽¹⁵⁾ I will use this matrix notation occasionally, when the TC property of an imultiset is at issue.

[23] The I(X)-type trichords are the subsets of the total voice leading that have arrows from all three of the pcs of X to the same single pc of Y (these are found in the rows of the array). The Y-type trichords are the subsets of the total voice leading that have arrows from one single pc of X to all three of the pcs of Y (these are found in the columns of the array). Example 16 demonstrates with reference to the first pair of pcsets in Example 15.

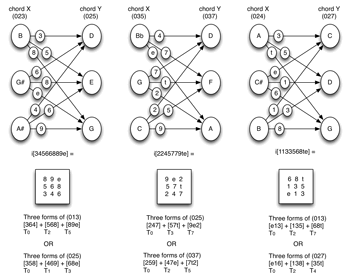
[24] If both X and Y are inversionally symmetrical, as in the third pair of chords in Example 15 (024 and 027), I(X)*Y and X*Y are equivalent. Example 17 examines the effect of TC on the voice-leading imultiset between two pairs of inversionally symmetrical pcsets. If X is a member of sc(03) and Y is a member of sc(04), the total voice leading between them will be the imultiset-class i(0347), which is equivalent to (03)*(04). If X is a member of sc(05) and Y is a member of sc(024), the total voice leading between them will be the imultiset-class i(024579), which is equivalent to (05)*(024).

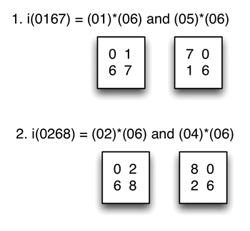
[25] Multiple parentage. Just as pcsets and pcsc may have the TC-property in more than one way, imultisets can be produced by different pairs of generating sets.⁽¹⁶⁾ Interestingly, the multiple parentage of imultiset i(02468t) plays a central role in Lewin’s (Lewin 1987) description of IFUNC. Example 18 offers a reconfiguration of Lewin’s Figure 5.1, with some additional information added.

[26] As Lewin shows, there are three different ways to produce the same total voice leading. He doesn’t explore this aspect of the situation, but I think the clear implication is that the larger gesture here is substantially and audibly the same in all three cases, despite the differences in the generating sets. This is the place where the present concept of total voice leading can make a particularly valuable contribution: showing that disparate scs may be connected by effectively the same voice leading.

X and Y are both dyads (2x2)

[27] When X and Y are both dyads, their total voice leading can be represented by a four-element imultiset. Because dyads are inversionally symmetrical, the voice-leading imultiset between any pair of dyads will always be I-symmetrical. All of the imultisets have the TC property X*Y, where X and Y are the generating dyads. The chart in Example 19 identifies the imultiset-classes resulting from the total voice leading between any two two-element pcset-classes.⁽¹⁷⁾

[28] Among the four-element imultisets produced by the voice leading from a dyad to another dyad (2 x 2), two have multiple parentage (see Example 20). Example 21 provides a simple schematic realization of these two multiply parented total voice leadings.

Musical examples with dyads

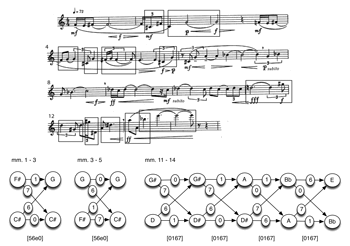
[29] We look now at three short passages to get a sense of how total voice leading (including imultisets, hyper-T, and multiple parentage) might play out in a musical context. In Example 22, the opening measures of “Diminished Fifth,” from Bartók’s Mikrokosmos, the multiple parentage of i(0167) is at issue. Five simultaneities are identified in Example 22a (the fourth of these is a theoretical reconstruction—A♭ and A belong together, but the A♭ has moved on by the time A arrives). Because there is an alternation of (06) and (01), the total voice leading in every case is i(0167), represented by either i[56e0] or i[0167].

[30] In Example 22b, the harmonic tritones are heard in relation to the melodic perfect fourths. Once again, the total voice leading is i(0167) represented by i[56e0] and i[0167]. To put it in a slightly different way, the melodic fourths bear the same relation to the harmonic tritones that the harmonic semitones do. The hyper-transpositions of the imultisets reflect the principal transpositions (i.e., intervals) among the pcs, namely 1 and 5. That is, the voice-leading intervals (mostly 1s and 5s) are recursively recalled in the shift of the total voice leading (hyper-T) by 1 or 5. In this case, <T₁> is equivalent to <T_-5> (or <T₇>). The choice of label is intended to emphasize the recursive relationship between the intervals and the intervals-between-the-intervals.

[31] There are obviously significant perceptual issues in hearing total voice leading, including multiple parentage and especially recursion. Let us begin to address these issues by focusing on the first progression in Example 22a (E♭-A to E♭-D) in comparison with the first progression in Example 22b (E♭-A to A-D). In both cases, the total voice leading is i[56e0], but produced in different ways. In the first progression, the move from A to D (5) is extremely prominent, filled in with passing tones, and it is equally easy to hear the E♭ as sustained (0). Hearing E♭ as going to D (11) is also not much of a challenge: the lowest note is drawn upward to the highest note. The connection between A and E♭ (6) is also perfectly audible, although in this case one hears more an association of two tones than any sense of directed motion from one to the other: it is more a case of “hearing with” than of “going to.” Thus all the intervals in this particular total voice leading are fully present to any willing listener, although the intensity of the presence, and the nature of the association, necessarily varies.

[32] In the first progression of Example 22b, it is easy to hear E♭ going to A (6) and A going to D as in Example 22a (5). E♭ goes to D, the lowest note drawn up to the highest, as in Example 22a (11). Hearing the A as retained (0) is perhaps a bit more of a stretch, but its recurrence on the second beat of the following measure reinforces any attempt to do so. As in the first progression of Example 22a, the four intervals that comprise the total voice leading are all fully accessible to any willing listener, but the intensity of their presence varies: some are experienced as simple, directed motions; others are experienced more as associations that provide a context for these simpler motions. A bit of extra effort is required to bring all four intervals to consciousness, but the effort is rewarded by the ability to hear one total voice leading, [56e0] in this case, produced by different dyads. Such multiple parentage becomes a distinct and unifying feature of the passage.

[33] Stravinsky’s Epitaphium begins with a duet for flute and clarinet (Example 23). The harmonic dyads are all members of ic1, ic2, and ic3, and I wish to make three observations about their succession from the point of view of their total voice leading. First, the progression from ➂ to ➃ (C♯-E to C♯-C) and the progression from ➅ to ➆ (E♯-F♯ to E♯-D) have the same total voice leading, shown in the example as <T₀>. Second, the relationship that ➄–➅ bears to ➃–➄ is the same as the relationship that ➇–➈ bears to ➄–➅, namely <T₇>. In both cases, the intervallic profile of the total voice leading has shifted over to the same degree: each interval in the second imultiset is 7 semitones larger than in the first imultiset. Third, the relationship that ➁–➂ bears to ➀–➁ is the same as the relationship that ➇–➈ bears to ➅–➇, namely <I₃>. This is true even though the sizes of the dyads are different in the two cases. Hyper-relations thus permit comparison of progressions among pc sets of different types.

[34] The perceptual challenges involved with hearing recursive relationships are worth exploring in a bit more detail. We focus on a specific instance, namely the <T₇> produced by the comparison between the progressions of ➃–➄ and ➄–➅. In the first of those progressions (C♯-C to B-C), the total voice leading is i[tee0]. C is retained as a common tone (0) while C♯ moves to B (10). (C♯ is followed by C in attack order (11) and C is then followed by B (11). We can think of the total voice leading as involving two intervals of the same size (11), produced by attack order, flanked by one slightly smaller interval (10) and one slightly “larger” interval (0). In the following progression (B-C to E♯-F♯), the total voice leading has the same contour: two intervals of the same size (6), produced by the motion within each instrumental part (C-F♯ and B-E♯), flanked by one slightly smaller interval (5 and 7, both produced by attack order).

[35] To hear both of these total voice leadings, and to hear that they share the same distribution of intervals, strikes me as a perfectly attainable goal of focused attention. Recognizing that this distribution has been shifted up seven semitones <T₇> is obviously a bit harder to produce as an immediate feature of aural experience. Even more problematic is the notion that the 7 in <T₇>, which measures the interval between the intervals, is in some sense the same as the 7 in, for example, T₇ that associates B with F♯. I think it is possible to make this connection, both conceptually and experientially (I base this assertion on quiet, sustained introspection), and that effort is worth it, because the recursive relationship adds an enriching and unifying dimension to my hearing of the passage. But deciding whether the rewards are worth the effort takes us into the realm of personal preferences, which may vary a great deal.

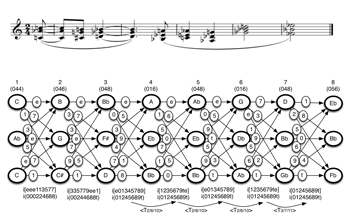
[36] In the opening of Varèse’s Density 21.5 (Example 24), the first phrase (measures 1–2) approaches its concluding tritone (C♯-G) from a perfect fourth (C♯-F♯), via the total voice leading i[0167]. In the second phrase (measures 3–5), the same tritone is approached from a minor second (F♯-G), via the same total voice leading, i[0167]. To put it in a slightly different way, approaching or leaving a tritone from a perfect fourth or semitone with which it shares a tone will produce the same total voice leading. In the music that follows, the same total voice leading binds together all of the melodic dyads.

[37] As noted earlier, the extent to which the four intervals of these total voice leadings are directly experienced aurally necessarily varies. In the first progression (C♯-F♯ to C♯-G), F♯-G (1) and C♯-C♯ (0) are the registral lines, while F♯-C♯ (7) and C♯-G (6) are produced by the attack order. One might imagine that 1 and 0 are something akin to a more traditional idea of voice leading while 6 and 7 provide a contextual penumbra for them. The intervals are not all equally vivid or functionally the same, but they all participate in creating the color of the progression. In the second progression (F♯-G to C♯-G), the situation is slightly different: now 0 and 7 comprise the registral lines (G-G and F♯-C♯) while 1 and 6 result from attack order (G-C♯ and F♯-G). But that the same total voice leading is involved in both cases, namely i[0167], and that it results from two different types of dyad pairs, namely (05)*(06) and (01)*(06), strike me as an experientially immediate and enriching way of hearing the passage.

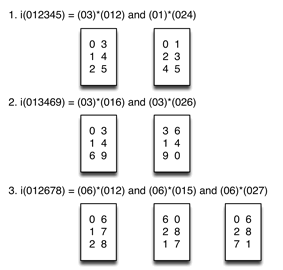
[38] When X is a dyad and Y is a trichord (or vice versa), their total voice leading can be represented as a six-element imultiset (see Example 25). Among these six-element imultisets, seven have multiple parentage, and the number of different generating pairs ranges from two to four (see Example 26).

[39] Example 27 contains a chord progression that exploits the multiple parentage of i(013679), which results from the combination of a tritone (06) with one of four possible trichords: (013), (014), (025), (037).⁽¹⁸⁾ Despite the variety of the chords, each adjacent pair of chords expresses the same total voice leading. There are also interesting patterns of recurrence among the hyper-T and hyper-I relations.

Musical examples with dyads and trichords

[40] The total voice leading explored abstractly in Example 27, involving the multiple parentage of i(013679), is realized throughout the opening measures of Crawford’s Diaphonic Suite No. 1, second movement (see Example 28). The melodic line is frequently punctuated with tritones, and these are typically followed by or overlapped with (013), (014), or (037) to produce a consistent total voice leading amid the harmonic diversity. If we look more closely at the first phrase of the melody (delimited by the double bar at the end of the fourth measure), we can hear it as two related gestures in which a single tritone (E♭-A or A-(E♭) is followed by two different trichords (C-C♯-E and (E♭-G♭-F). Within these two pairs of chords, the second total voice leading is related to the first at <T_-1>. In other words, all of the intervals in the first total voice leading have shrunk by semitone. That larger gesture is reflected at the melodic surface by the descending semitone, G♭-F, which concludes the phrase. Something similar happens in the varied repeat of the opening music, beginning in measure 8. There, the two voice leading gestures are related at <T₊₃>, which is reflected in the ascending minor thirds that conclude each of the constituent trichords.

[41] Something similar happens in the first two phrases of the first movement of the same work (see Example 29). In the first phrase, combinations of (012) and (03) produce a total voice leading represented by i(012345). In the second phrase, combinations of a different pair of scs, (01) and (024), produce the same total voice leading. As before, the analysis offers a way of hearing a single class of total voice leading, i(012345), as remaining the same even as the harmonies that produce it vary. The intervals involved are not all experienced with the same degree of immediacy—some are registral lines, some are produced by successive attacks, and some are more associations than directed motions, providing a context or atmosphere for the others. But taken together, these intervals comprise a single voice-leading gesture that unifies and enriches a hearing of the passage.

X and Y are both trichords (3x3)

[42] When X and Y are both trichords, their total voice leading can be represented as a nine-element imultiset (see Example 30). Five of these imultisets have multiple parentage (see Example 31).

Musical examples with trichords

[43] In three passages of music by Schoenberg, from the Book of the Hanging Gardens and Pierrot Lunaire, the augmented triad plays a prominent role within a prevailing trichordal texture (see Examples 32, 33, and 34). Approaching and leaving an augmented triad from these particular trichords involves the same total voice leading. It might be possible to make a recursive argument about these passages—that the hyper-T involved reflect aspects of the intervallic surface of the music—but they would seem a bit forced to me. I would prefer to conclude with the observation that the augmented triad in these passages functions as something like a universal solvent—it can be approached from different places and left in different directions, but the total voice leading remains the same, imparting a sense of gestural uniformity amid the harmonic diversity.

Joseph N. Straus
Graduate Center, City University of New York
365 Fifth Avenue
New York, NY 10016
jstraus@gc.cuny.edu

Works Cited

Buchler, Michael. 2007. “Reconsidering Klumpenhouwer Networks.” Music Theory Online 13, no. 2.

Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice Leading Spaces.” Science 320: 346–48.

Cohn, Richard. 1986. Transpositional Combination in Twentieth-Century Music. PhD diss., Eastman School of Music.

—————. (1988). “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 10: 19–42.

—————. 1991. “Properties and Generability of Transpositionally Invariant Sets.” Journal of Music Theory 35, no. 1–2: 1–32.

Klumpenhouwer, Henry. 1991. “A Generalized Model of Voice-Leading for Atonal Music.” PhD diss., Harvard University.

—————. 2007. “Reconsidering Klumpenhouwer Networks: a Response.” Music Theory Online 13, no. 3.

Lewin, David. 1959. “Re: Intervallic Relations Between Two Collections of Notes.” Journal of Music Theory 4, no. 1: 298–301.

—————. 1977a. “Forte’s ‘Interval Vector,’ My ‘Interval Function,’ and Regener’s ‘Common-Note Function.’” Journal of Music Theory 21, no. 2: 194–237.

—————. 1977b. “A Label-Free Development for 12-Pitch-Class Systems.” Journal of Music Theory 21, no. 1: 29–48.

—————. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.

—————. 1990. “Klumpenhouwer Networks and Some Isographies That Involve Them.” Music Theory Spectrum 12, no. 1: 83–120.

—————. 1998. “Some Ideas About Voice-Leading Between Pcsets.” Journal of Music Theory 42, no. 1: 15–72.

Lundberg, Justin. 2012. A Theory of Voice-leading Sets for Post-tonal Music. PhD diss., Eastman School of Music.

Morris, Robert. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20, no. 2 (1998): 175–208.

Robinson, Thomas. 2009. Pitch-Class Multisets. PhD diss., Graduate Center of the City University of New York.

Roeder, John. 1985. “A Theory of Voice Leading for Atonal Music.” PhD diss., Yale University.

—————. 1994. “Voice Leading as Transformation.” In Musical Transformation and Musical Intuitions: Essays in Honor of David Lewin , ed. Raphael Atlas and Michael Cherlin, 41–58. Roxbury, MA: Ovenbird Press.

Straus, Joseph. 1997. “Voice Leading in Atonal Music.” In Music Theory in Concept and Practice, ed. James Baker, David Beach, and Jonathan Bernard, 237–74. Rochester: University of Rochester Press, 1997).

—————. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25, no. 2: 305–52.

—————. 2005. “Voice Leading in Set-Class Space.” Journal of Music Theory 49, no. 1: 45–108.

Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.

Wilson, Andrew. 2012. “Voice Leading as Set.” Paper presented at the annual meeting of the Music Theory Society of the Mid-Atlantic.

Footnotes

1. There has been an upsurge of scholarly interest in atonal voice leading in recent years, including Roeder 1985; Klumpenhouwer 1991; Roeder 1994; Straus 1997; Lewin 1998; Morris 1998; Straus 2003; Straus 2005; Callender, Quinn, and Tymoczko, 2008; and Tymoczko 2011. All of these sources, in one way or another, take the view of voice leading enshrined in Example 1. I am grateful to Julian Hook, Philip Lambert, Drew Nobile, Richard Cohn, and two anonymous reviewers for this journal for valuable comments on earlier drafts of this article. Some of the initial impetus for this study, and all of the extensive computational work associated with it are attributable to Will Orzo.
Return to text

2. I take the phrase and the concept of “total voice leading” from a brief discussion in Morris 1998: “Given two pcsets A and B, the total voice-leading from A to B includes any and all moves from any pcs of A to any pcs of B—that is, all the ways one can associate the pcs of A with those of B in as many voices as necessary or desired” (178). Morris is primarily interested in restricting the total voice leading by parsing it into the more usual sorts of voices (as in Example 1). The present study, in contrast, focuses on the total package of intervals formed between pcsets A and B, without restrictions and without traditional parsing.
Return to text

3. Lewin 1959 introduces the concept of “interval function” and Lewin 1977a explores it in considerable detail. In a particularly revealing passage, and one that directly engages the topic of the current study, Lewin calls attention to the “contrapuntal” nature of his conception—he is concerned about the intervals formed between two harmonies rather than those formed within a single harmony: “Forte’s interval vector is a rigorously harmonic concept. My interval function, from which I derive my “interval content” is as rigorously contrapuntal in conception. Given pcsets X and Y, and an interval i, INTF(X, Y, i) is the number of distinct ways in which the interval i can be spanned from a member of X to a member of Y; that is, the number of distinct pairs of pcs (x, y) such that x is a member of X, y is a member of Y, and the interval from x to y is i. The concept is a useful model for the following situation. Imagine yourself improvising at the keyboard, using only notes of X in your left hand and only notes of Y in your right hand. How many different ways can an interval of i occur in the resulting counterpoint? In this connection, one needs all the intervals from 0 through 11, since X and Y may have common notes, the number of possible contrapuntal 7’s may be different from the number of contrapuntal 5’s, etc.” (1977a, 201–2 ). Similarly, Lewin 1977a refers to the potential for IFUNC to reflect the “total potential counterpoint” between two harmonies: “The interval function is a useful tool for conceptualizing such musical phenomena as the ‘total potential counterpoint’ between a hexachord X and its complement X’” (203). In the same spirit, Lewin 1977b speaks of the way in which his interval function can reflect the “‘overall sound’ of the counterpoint” between two pitch-class sets (40).
Return to text

4. Lundberg 2012 and Wilson 2012 independently develop the concept of what they both call a “voice-leading set” or vlset. This is a set of intervals formed between two pcsets and, like pcsets, a vlset may be understood as part of a larger class of sets related by transposition or inversion. For both Lundberg and Wilson, voice leading is understood in the traditional manner of my Example 1, not in terms of the total voice leadings discussed here.
Return to text

5. Compare Lewin’s (1987) Theorem 5.1.4, which asserts: IFUNC(Y, X)(i) = IFUNC(X, Y)(i^-1). In other words, however many occurrences of some interval i there are in the first IFUNC-vector, there will be exactly that number of occurrences of the complement of i in the second IFUNC. In this sense, IFUNC(Y, X) and IFUNC(X, Y) are inversions of each other.
Return to text

6. This differs from the procedure in Robinson 2009: eliminate doublings; put the set in prime form following the standard algorithm; replace the doublings.
Return to text

7. Compare Lewin’s (1987) Theorem 5.1.6A and 5.1.6B which assert: IFUNC(T_n(X), Y)(i) = IFUNC(X, Y)(ni) and IFUNC(X, T_n(Y))(i) = IFUNC(X, Y)(in^n-1). In other words, when X is transposed by n semitones with respect to Y (or vice versa), the IFUNC-vector will rotate clockwise or counterclockwise by n places.
Return to text

8. My concept of hyper-T and hyper-I (to be discussed below) are obviously derived from and related to the use of these terms and concepts in relation to Klumpenhouwer networks—see Klumpenhouwer 1991 and Lewin 1990. In both cases, we are talking about the transposition of transpositions (intervals) or the inversion of inversional axes (sums). For more recent assessments of hyper-T and hyper-I in the context of Klumpenhouwer networks, see Buchler 2007 and the numerous responses in Music Theory Online 13/3 (2007), especially Klumpenhouwer 2007.
Return to text

9. In the related context of the transposition of what they call “voice-leading sets,” both Wilson (2012) and Lundberg (2012) consider the perceptual challenges of the transposition of intervals (what I am calling hyper-Tn).
Return to text

10. As Lewin (1987) observes, “There is not much to be said in general about the effect of applying an inversion operation to X, Y, or both, so far as IFUNC is concerned” (101). The last part of Lewin’s assertion (“or both”) appears to be incorrect.
Return to text

11. As with hyper-T, the perceptual issues associated with hyper-I are discussed in the K-net literature cited above.
Return to text

12. What I am calling the inversional symmetry of the imultiset (representing the total voice leading between two sets), Lewin (1977a) thinks of as enabling a kind of “invertible counterpoint,” i.e., a counterpoint whose intervals are not changed by reversing the order of the two sets: “We can conceptualize the counterpoint as being ‘invertible,’ in this context, if an exchange of pcsets between left and right hand does not affect the total distribution of intervallic possibilities. Formally, we can call the interval function from X to Y ‘invertible’ if, for every interval i, INTF(Y, X, i) = INTF(X, Y, i) (202). Lewin goes on to say, “It would be interesting to find what general relations between X and Y would be necessary and sufficient for their interval function to be invertible. Such general relations have as yet not been found.” I believe that the preceding section of the present study does identify these general relations. In my terms, the imultisetclass that represents the total voice leading between pcsetX and pcsetY will remain the same when X and Y are reordered if X and Y are identical, or if X and Y are related by transposition, or if X and Y are both inversionally symmetrical.
Return to text

13. See also Cohn 1986, which includes a list of the 137 set classes that bear the TC-property, along with the operands that generate them.
Return to text

14. Cohn 1988 uses matrices for precisely this purpose. Morris 1998 describes the use of “t-matrices” in describing total voice leading: “The t-matrix constructed from two pcsets A and B lists all the intervals from A to B. . . . Since it contains all of the possible intervals from A to B, it registers the total voice-leading from A to B” (203). Morris is primarily interested in subsets of the contents of these matrices.
Return to text

15. The matrix notation also makes it easy to grasp the traditional (one-to-one) voice leadings embedded within the total voice leading. If one extracts from one of these matrices a group of intervals such that no two occupy the same row or column, the result will be one of the ways of mapping the three pcs of X onto the three pcs of Y. In the first of the matrices in Example 15, there are six ways of extracting three numbers such that no two are in the same row or the same column: 3-6-e; 3-8-9; 4-5-e; 4-8-9; 6-6-8; and 6-5-9. These are the six traditional, one-to-one ways of voice leading from Set X to Set Y (Morris 1998).
Return to text

16. “Multiple parentage” is a coinage of Cohn 1988: “Most of the 137 TC-set-classes are the product of several or even many different operations” (28).
Return to text

17. Cohn 1988 Example 9, presents the same information in staff notation, including the multiple parentage of (0167) and (0268), but excluding the multisets with pc duplication.
Return to text

18. Cohn 1991 explains why the transpositional combination of these four trichord-types under tritone transposition produces the imultiset 013679. See Cohn’s Table 3 (p. 11) and surrounding discussion.
Return to text

Copyright Statement

Copyright © 2014 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.