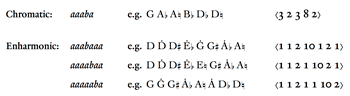Genus, Species and Mode in Vicentino’s 31-tone Compositional Theory
Jonathan Wild
KEYWORDS: Vicentino, enharmonicism, chromaticism, sixteenth century, tuning, genus, species, mode
ABSTRACT: This article explores the pitch structures developed by Nicola Vicentino in his 1555 treatise L’Antica musica ridotta alla moderna prattica. I examine the rationale for his background gamut of 31 pitch classes, and document the relationships among his accounts of the genera, species, and modes, and between his and earlier accounts. Specially recorded and retuned audio examples illustrate some of the surviving enharmonic and chromatic musical passages.
Copyright © 2014 Society for Music Theory
Table of Contents
- Introduction [1]
- Tuning [4]
- The Archicembalo [8]
- Genus [10]
- Enharmonic division of the whole tone [13]
- Species [15]
- Mode [28]
- Composing in the genera [32]
- Conclusion [35]
Introduction
[1] In his treatise of 1555, L’Antica musica ridotta alla moderna prattica (henceforth L’Antica musica), the theorist and composer Nicola Vicentino describes a tuning system comprising thirty-one tones to the octave, and presents several excerpts from compositions intended to be sung in that tuning.(1) The rich compositional theory he develops in the treatise, in concert with the few surviving musical passages, offers a tantalizing glimpse of an alternative pathway for musical development, one whose radically augmented pitch materials make possible a vast range of novel melodic gestures and harmonic successions. In this article I begin with an acoustic derivation of the 31-tone scale, a derivation that is not entirely explicit in L’Antica musica. I go on to examine the aesthetic rationales Vicentino proposes for his tuning system, and to investigate, through close reading of the treatise, the modal and generic frameworks that he develops within it, while considering their historical antecedents. Finally I consider to what extent these pre-compositional pitch structures are realized in the surviving compositions by performing some preliminary analysis on the works excerpted in the treatise. I shall not attempt an exhaustive account of Vicentino’s advice for composers, which encompasses rhetoric, text setting, and affect; my focus will remain on the novel pitch structures his theories generate.
[2] One difficulty in working with a repertoire such as this is the inability of the modern musician to recreate, mentally or in performance, the sound and affect of the unfamiliar intervals from the enharmonic genus. In my own experience I found I needed to hear what Vicentino intended before fully grasping what was at stake in his theorizing or appreciating the import of the musical possibilities. Renderings accomplished via synthesis remained musically unsatisfying. And so with the help of my colleague Peter Schubert I have created aural illustrations of the musical examples by retuning, in post-production, specially recorded performances by professional singers to match precisely the intonational stipulations in L’Antica musica.(2) Some of these recordings appear as audio examples in this article.
[3] I reserve for a follow-up article to this one, to be published separately, a more thorough analysis of the surviving compositions, not restricting myself to the theoretical approaches suggested by Vicentino’s own writings in L’Antica musica. Additionally, in this second article I shall venture beyond Vicentino’s compositions and investigate the results of applying the practices demonstrated in his enharmonic works to some carefully selected music by a near-contemporary, Luzzasco Luzzaschi.
Tuning
[4] As was well known by Vicentino’s lifetime, the compound major 3rd derived by stacking four perfect 5ths is too wide when compared to the major 3rd of just intonation, now known to be derived from the harmonic series. The discrepancy between the two, 21.506 cents, is the syntonic comma.(3) For keyboard instruments the practical solution to the incommensurability of 5ths and 3rds, if pure major 3rds were desired, was to narrow each perfect 5th by a small amount—one quarter of the syntonic comma—causing a stack of four 5ths to yield a pure major 3rd. The resulting temperament is called ¼-comma meantone—or often simply meantone—due to the size of its whole tone, which is the mean of the 9:8 and 10:9 whole tones first described in Ptolemy’s syntonic diatonic and proposed in several earlier sixteenth-century treatises.(4)
[5] If this temperament is extended to a chain of 12 pitches, all related by meantone 5ths of 696.578 cents, some pitches near the ends of the chain will not be suitable as triadic roots, since the triad’s third or fifth, or both, will be noticeably mistuned. As an example, if the chain runs from
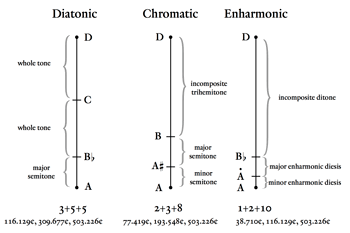
Figure 1. Intervallic makeup of the whole tone and the diatonic semitone in Vicentino’s 31-tone system
(click to enlarge)
[6] The tuning system Vicentino intended for his vocal compositions is founded on a fortuitous coincidence: in ¼-comma meantone temperament, the discrepancy between the pitches
[7] The preceding paragraph gave one derivation for the 31-fold division of the octave, beginning with the near correspondence of the enharmonic diesis to one fifth of a meantone whole tone. But we can make use of a different principle, that of the quasi-closed cycle of 5ths, to reach the same result. A set of twelve pitches generated by iterating meantone-tempered 5ths does not “wrap around” with a usable 5th: the interval between the end of the chain and its beginning, a so-called “wolf 5th,” is too wide at about 737 cents. If we search for longer chains, generated by iterating the meantone 5th more than twelve times, that also wrap around with a 5th-like interval, we shall find that after 19 pitches a narrow wolf 5th of about 661 cents is left over. Concatenating the two chains, we find that the opposite errors of the 12-note and 19-note chains neatly cancel out, and the 31-note chain of meantone 5ths results in a very nearly closed cycle with a wrap-around 5th of 702.65 cents—not what we would typically call a wolf, as it is considerably closer to a pure 5th (701.955 cents) than is the meantone 5th used to generate the rest of the cycle! (11)
Figure 2. An octave span of the two manuals of the archicembalo
(click to enlarge)
[8] To within the small errors discussed in note 10, then, Vicentino’s system circulates; that is, a complete circle of 31 keys may be traversed without encountering any unusable, out-of-tune triads. He writes of the archicembalo—the special harpsichord he invented, which includes all 31 pitches in each octave—that it is “the foremost and perfect instrument, in that none of the keys lacks any consonances” (315).(12) While Vicentino thus recognizes the circulating nature of an entire 31-tone system, this does not seem to have been his foremost rationale for proposing it. In the surviving musical excerpts he never uses triads or keys from opposite ends of the 31-tone chain of 5ths in close proximity to one another, and so the tuning does not need to circulate and no potential “wolf” intervals arise. This renders moot the question of whether he intended his 31-tone tuning to be exactly equal, or merely to yield a good approximation of equality.(13)
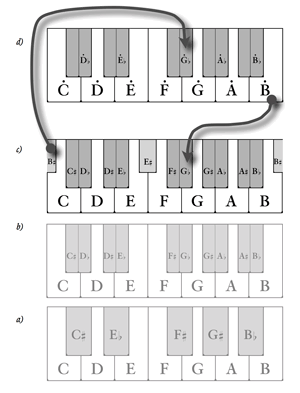
The Archicembalo
[8] The archicembalo as it is described in L’Antica musica has 36 pitches per octave spread across two manuals, the lower with 19 keys per octave and the upper with 17.(14) The lower manual includes the common meantone gamut (
[9] The remaining five black keys on the upper manual of the archicembalo (not labeled in Figure 2 as they do not play a part in the present discussion) are tuned as pure 3:2 5ths, rather than meantone 5ths, above the lower-manual pitches F, G,
Genus
[10] Some of the intervals belonging to the genera of antiquity, transmitted to Vicentino’s time principally through Boethius, would have been unfamiliar to many musicians in sixteenth-century Italy.(17) One of Vicentino’s aims in L’Antica musica was to reacquaint contemporary listeners with intervals like the enharmonic diesis, the smallest step of the enharmonic genus. In so doing not only would he increase the variety of intervals available to composers—in itself a beneficial outcome, in his view—but the smaller intervals introduced would also have the desirable attribute of unfamiliarity. Thus he hoped to make it possible for composers to recreate the powerful effects on listeners that were claimed in the accounts of Greek antiquity.
[11] On intervallic variety in composition and its potential for moving the listener, he writes: “Compared to the ancient ratios, ours are not only more numerous but more sonorous. But why, then, in our times do we not observe musicians producing those effects that authors claim were made in antiquity?” (20). Another reason for composers to seek variety is given in Chapter 2 of Book I on Music Practice; after discussing the differing degrees of musical experience a listener might have, Vicentino writes: “Because of the great diversity between the hearing of one person and that of another, composers must create as much diversity in their compositions as there are listeners’ opinions if they want to satisfy all judgments based on the sense of hearing” (21–22). On the importance of novelty for producing an effect on listeners he writes that the reason for the diminished effects of modern music “is the overabundance and profusion of music today. However good an impression these effects may make, they no longer move people as they did when they were first discovered. For novelty, insignificant though it may be, earns much more admiration than what is commonplace and later magnified” (20). Both principles, variety and novelty, are constant themes in his writing on compositional aesthetics, and can be seen as primary reasons for his espousal of the genera of antiquity and the expanded gamut of 31 pitches.
Figure 3. The three genera as they are embedded in Vicentino’s 31-tone tuning
(click to enlarge)
Figure 4. The subdivision of a natural whole tone proper to the enharmonic genus
(click to enlarge)
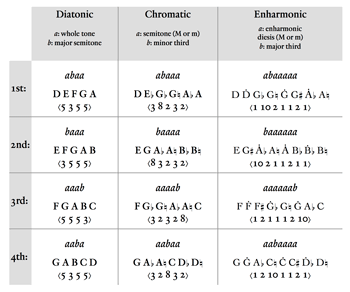
[12] Figure 3 depicts the three genera as they are embedded in Vicentino’s scale and labels the intervals according to his terminology. A perfect 4th spans 13 scale steps in the 31-tone system, and it may be divided as 3+5+5 (diatonic genus), 2+3+8 (chromatic genus), or 1+2+10 (enharmonic genus).(18) Among ancient sources, Vicentino’s particular shadings of the genera come closest to Ptolemy’s—not surprising, as Ptolemy’s divisions favor the 5:4 major 3rd of just intonation, which is accurately represented in ¼-comma meantone.(19)
Enharmonic division of the whole tone
[13] Chapters 5 and 11 of Book I on Musical Practice prove valuable in deciphering certain decisions later in the treatise. In these two sections, Vicentino illustrates how the natural whole tone should be divided in the enharmonic genus.(20) While Figure 1 above showed the underlying division of the whole tone into five parts, all of them minor dieses, Vicentino explains that it is characteristic of the enharmonic to include one major diesis as part of the division of the whole tone, yielding four unequal parts. Figure 4 shows the two admissible divisions of the G–A whole tone according to this “four-fold rule”: both ascending and descending, the whole tone is divided into a major and minor semitone by using either a flat or a sharp pitch in the central position, at the composer’s choice. The two semitones produced must then each be divided into two dieses by inserting enharmonically inflected pitches, one adjacent to each of the natural notes. The minor semitone is consequently found to comprise two minor dieses, while the major semitone comprises one minor and one major diesis, with the minor diesis abutting the natural note.(21) Each of the two permissible divisions in Figure 4 therefore includes Ġ and Ȧ
Figure 5. Chart of enharmonic subdivision schemes for whole tones and semitones
(click to enlarge)
Figure 6. Chart depicting admissible divisions of different kinds of whole tone
(click to enlarge)
Figure 7. The three species of 4th in each genus
(click to enlarge)
[14] In Book V on Musical Practice, Chapters 48–52, Vicentino prescribes different divisions for four kinds of non-diatonic whole tones: “chromatic” whole tones written with sharps (e.g.,  ,
,  ,
,  ,
,  ,
,
Species
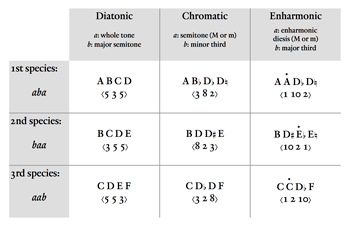
[15] The most important theoretical innovation Vicentino made in L’Antica musica was to combine the nuanced intervallic structures of the Greek genera—not generally considered part of modern compositional practice by his contemporaries—with the permutational relationships that characterize the species of 4ths and 5ths, a fixture of medieval and Renaissance music theory. Figure 7 shows how this merging of two systems is accomplished in the case of the 4th. Key to Vicentino’s generalization of the species to other genera are first, his retention of the same abstract pattern of step sizes for a given species—for example, aba for the first species of 4th—and second, his replacement of the smallest intervals in the diatonic arrangement by the largest in the new genus, and vice-versa. What the first species of 4ths in all three genera have in common, then, is that the step interval that is substantially different from the others in that genus—the different step interval being the semitone (diatonic), the minor 3rd (chromatic), or the major 3rd (enharmonic)—occurs second in the sequence of step sizes within the 4th, surrounded by the genus’s two intervals that are of equivalent (not necessarily identical) size. In the second species of 4th the unique interval is in the lowest position, and in the third species, it is in the highest position. This all makes for a conveniently tidy way of mapping species from one genus to another, but Vicentino’s stated reasons for exchanging large and small steps when passing from the diatonic genus to the others have more to do with respecting the contrasting aesthetic qualities of the genera. He writes of the chromatic genus:
The chromatic fourth has all its steps placed differently and contrary to the sound of the diatonic steps. For the diatonic steps produce a harsh sound, whereas the chromatic steps restore a gentle sound to the ear. . . . Where there were small diatonic steps, there are now placed large steps on the same degree in the chromatic fourth. And where there were large diatonic steps, I now place small chromatic ones. (186)(25)
[16] As can be seen in the table, the two identical whole tones of the diatonic genus have been replaced by the non-identical major and minor semitones of the chromatic genus.(26) The sizes of semitone required in the species of chromatic 4th depend on the spelling of the “incomposite trihemitone”, the step in the chromatic genus that spans three semitones. Spelling the trihemitone as an augmented 2nd (i.e., seven steps of the 31-tone scale) would have required the other two steps to both be major semitones, and allowed the 4th to be written using each letter name only once—for example, B–C–
[17] Similarly, in the three enharmonic species of 4th shown in the right-hand column of Figure 7, the whole tones of the diatonic are transformed into major and minor enharmonic dieses, and the semitone step is transformed into an incomposite ditone. The incomposite ditone usually appears as a major 3rd, but is occasionally spelled as a diminished 4th narrowed by an enharmonic dot, for example Ȧ to
Figure 8. The four species of 5th in each genus
(click to enlarge)
[18] Greek writers on musical scales did not directly explore the subdivision of the 5th as a structural scalar component; the composite 5th arose only as the combination of a structural tetrachord plus the tone of disjunction. Vicentino, following the practice of more recent theorists, wished to include the 5th on equal footing to the 4th in his theoretical system. But incorporating the medieval species of 5th in the context of the non-diatonic genera presents a particular difficulty: there is no obvious way to map the patterns of step sizes in a diatonic 5th to the other genera. For example, the first-species 5th in the diatonic genus has the ascending pattern abaa—a whole tone, a semitone, then two more whole tones. But it is not possible to find a combination of the intervals characteristic of the chromatic genus—the minor 3rd and the major and minor semitones—that will sum to a perfect 5th consisting of four steps, as occurs in the diatonic. That sum will require an extra semitone, and thus a perfect 5th consisting of five steps: a minor 3rd and four semitones. Such being the case, Vicentino must have decided that the step pattern that most resembles the diatonic first species abaa is the pattern that retains the unique interval in second position: abaaa. Likewise, the second species of 5th retains the unique interval in first position: baaa ↦ baaaa, and the fourth chromatic 5th retains the unique interval in last position: aaab ↦ aaaab. Finally the pattern of the third diatonic 5th, aaba, could be interpreted in two different ways resulting in two different chromatic patterns: we could think of it either as “the unique interval is in the third position,” or as “the unique interval is in the second-to-last position.” Vicentino chose the former interpretation, and so his third chromatic 5th has the pattern aabaa with the minor 3rd in the central position.(29) The table in Figure 8 shows the chromatic species of 5th in the central column. As with the chromatic 4ths, the species of 5th are not strict rotations of one another when we distinguish major semitones from minor. Rather than accept the conclusion that any arrangement is permitted, we can account for Vicentino’s decisions about which semitones to place where by the following implied rule for constructing chromatic 5ths: prefer major semitones above natural pitches (i.e., use pitches written with a flat) to maximize contrast with the enharmonic.
Figure 9. Unused permutations of intervals comprising the 5th in the chromatic and enharmonic genera
(click to enlarge)
[19] The species of 5th in the enharmonic genus are even more problematic than in the chromatic: ideally, the three whole tones and one semitone of the diatonic could be transformed straightforwardly into three enharmonic dieses and a ditone—unfortunately, though, these four steps do not sum to a perfect 5th. Vicentino’s enharmonic 5ths, then, use a total of six dieses and one ditone; the resulting templates are shown in the right-hand column of Figure 8 along with their pitch realizations.(30) The fourth species of enharmonic 5th is constructed, as was the case in the chromatic genus, so as to have its unique interval in third position rather than in second-to-last position, which—with so many trailing dieses required to make up the 5th—means its step pattern aabaaaa appears quite dissimilar to that of its diatonic cousin aaba. The patterns aaabaaa, aaaabaa and aaaaaba do not occur in Vicentino’s account of the species of 5th.(31) I have included them in Figure 9, with corresponding pitch realizations, for the sake of being able to see a complete set of permutations.
[20] As we did for the chromatic 5ths above, we can infer some preference rules that would account for Vicentino’s choices in distributing the enharmonic dieses, whose quality—major or minor—is not specified by a pattern such as abaaaaa. For instance, depending on whether the first interval is taken as a minor or major diesis, the pattern abaaaaa could have begun either D–Ḋ–
- Prefer a minor over a major diesis at the beginning.
- Prefer to place the major 3rd such that one or both of its endpoints fall on natural notes.
- Divide a whole tone that lies between natural notes according to the “four-fold” rule of Section 4 above.
- Prefer
B♭ overA♯ ; otherwise, given a choice between writing a flat or a sharp pitch, prefer the one that does not appear in the corresponding chromatic 5th.(32)
Such a set of rules obviates the need to ascribe to Vicentino the intention that all permutations of major and minor dieses should be equally valid.
[21] Now, it is true that in one passage Vicentino indicates that composers may consider other possibilities for distributing the dieses. In the discussion of the third enharmonic species of 5th he writes: “It begins its ascent with six steps of major and minor dieses. The first step is minor, the second minor, the third major, the fourth minor, the fifth minor, and the sixth major. However, a composer may at his good pleasure arrange the order of these major and minor dieses, as well as the major and minor semitone, in any way he sees fit” (200).(33) Here the extended run of dieses occurs between the bounds of a natural whole step, which we already know can be divided different ways (see the discussion of the “four-fold rule” in Section 4): the primary division of a natural whole tone into major and minor semitones can be made in two ways by using a sharp or flat, each way requiring a particular subdivision into major and minor enharmonic dieses. I believe Vicentino wrote “in any way the composer sees fit” as shorthand for “in any of the ways previously explained as admissible that the composer sees fit,” and he never intended the reader to break the “immutable rule” of Book I, Chapter 11, that requires a minor diesis to be the first encountered, whether ascending or descending, when a natural whole tone is to be enharmonically subdivided (54). Below when we encounter the octave species we shall find Vicentino making use of this very restricted freedom to slightly redistribute the dieses within the natural whole tone, as he rewrites the first 5th so the whole tone G–A is divided at
[22] Armed now with three species of 4th and four species of 5th in each genus, Vicentino is ready to proceed to the octave species resulting from their combinations—but which combinations should he use? In the diatonic genus there was of course an existing set of arrangements of 4ths and 5ths long accepted by musicians: the seven diatonic octave species commonly enumerated by theorists since Boethius. Vicentino cannot simply present these as axiomatic, however—he needs to reverse-engineer a system of constructing them, in order to be able to generalize the system to the other genera, which have no conventional lists of octave species of their own.(34) There must be seven species, which he derives from the three species of 4th and four species of 5th by allowing each to begin an octave species, paired with its corresponding 5th or 4th placed conjunctly above, finally recycling the first 4th to accompany the fourth 5th in the absence of a fourth 4th (138). The resulting sequence of combinations is as follows:
| First 8ve (A–a): | first 4th | placed below | first 5th |
| Second 8ve (B–b): | second 4th | placed below | second 5th |
| Third 8ve (C–c): | third 4th | placed below | third 5th |
| Fourth 8ve (D–d): | first 5th | placed below | first 4th |
| Fifth 8ve (E–e): | second 5th | placed below | second 4th |
| Sixth 8ve (F–f): | third 5th | placed below | third 4th |
| Seventh 8ve (G–g): | fourth 5th | placed below | first 4th |
[23] While these seven octaves would have been familiar to all musicians, Vicentino’s derivation of them is original in that it appears to make the octave species dependent on, and therefore subordinate to, the species of 4ths and 5ths. His explanation obscures the fact that many other arrangements of these 5ths and 4ths might be possible; should we pursue this line of thinking we find that of the 24 implied combinations (three species of 4th × four species of 5th × two ways of ordering each combination), just 12 result in familiar diatonic octave species.(35) Of the remaining combinations of diatonic 4ths and 5ths, eight result in modes of the ascending melodic minor (e.g., first 4th placed below a third 5th) and four result in modes of a “whole-tone plus one” collection, Forte 7-33 [012468a] (e.g., second 4th placed above a third 5th).(36)
Figure 10. Vicentino’s seven chromatic octaves
(click to enlarge)
Figure 11. Vicentino’s enharmonic octave species
(click to enlarge)
[24] Having shown how to construct the diatonic octave species, Vicentino can now move on to the chromatic species, following an analogous procedure. For example, the first chromatic octave (A–a) should conform to the pattern of the first diatonic octave, and is thus formed by the first chromatic 4th below the first chromatic 5th. The result is a scale of eight notes: A
[25] When it comes to the enharmonic octaves, Vicentino’s process established in the other genera breaks down in the fourth octave and never recovers. Figure 11 shows the details, with Vicentino’s octaves as they are given in L’Antica musica in the highlighted cells of the table.(39) In the left-hand column are the seven species as they would have been constructed following the procedure for the diatonic and chromatic: three plagal and four authentic species. None of Vicentino’s last four combinations of enharmonic 4ths and 5ths correspond in the expected way to the diatonic and chromatic genera, whose fourth through seventh octave species were constructed with a 5th below a 4th. But the last four enharmonic octaves as given by Vicentino can be explained, for the most part, in another way. The D–d, E–e and G–g diatonic octaves have alternative plagal descriptions: E–e, for example, could be construed as the second diatonic 4th below the first diatonic 5th, instead of the second 5th below the second 4th. Such plagal descriptions for the diatonic octaves on D, E, and G, when transformed into the enharmonic, are shown in the central column and correspond quite closely to Vicentino’s suggestions.(40) It appears, then, that without mentioning the change in strategy, he has employed exclusively the plagal descriptions of the diatonic octave species as the basis of his generalization to the enharmonic, instead of the expected authentic descriptions in the case of the fourth, fifth, and seventh octave.(41) One consequence of this decision—probably a desirable consequence, given Vicentino’s predilection for variety—is that these octaves are thereby given contrasting structures to those of the odd-numbered modes, discussed in the following section.(42)
[26] How, though, ought we to explain what surely must be errors in the sixth octave? The F–f octave is divided neither plagally nor authentically: neither a
[27] These seven enharmonic octaves form quite a heterogeneous set. Recall that the seven diatonic octaves were rotations of one another; likewise, six of the seven chromatic octaves fell into two groups of three, each group internally related by rotation. Here, though, only two of the seven enharmonic octave species are related to each other by rotation: the third and seventh octaves, when appropriately rotated, produce the same series of step intervals (in fact the two octaves have exactly the same pitch-class content). When we apply the level of scrutiny of the last few paragraphs to Vicentino’s octave species, it is easy to have our impression reinforced that Vicentino is always thinking of pitch structures at their specific transpositional level rather than as abstract strings of intervals—these are apparently not structures he finds it natural to transport indiscriminately around the 31-tone system, even if the circular nature of the system makes such transpositions conceivable in theory.
Mode
[28] The octave species are not the final word in theoretical pitch structures in L’Antica musica. Vicentino goes on to discuss the eight modes of each genus; again, the rationale for setting out these modes is explicitly concerned with compositional variety, and he invokes the equal status he wishes the modes of the chromatic and enharmonic to share with the diatonic:
Today one should not be astounded by such inventions. For if the diatonic genus has opened the way to composing the eight diatonic modes, why should the chromatic and enharmonic genera not have their own eight modes to serve each genus? When a composer has the freedom to write in the first mode of the diatonic or of the chromatic or of the enharmonic orders, he will have compositional resources of such richness, so many steps and various species adorned with so varied a set of procedures, that his compositions, on account of their great diversity of mixed steps, will be marvelous things to hear. (205–6)
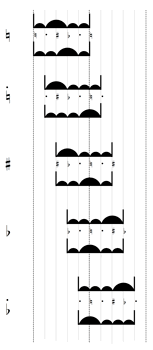
Figure 12. The eight modes of the enharmonic genus
(click to enlarge and listen)
[29] Like most other theorists of his time, Vicentino notes there is one more mode than octave species.(45) His enumeration follows the standard pattern of paired authentic and plagal structures on each of the finals D, E, F, and G. Melodic examples are provided for the eight modes in each genus, but here I shall discuss the enharmonic modes only. They appear below in Figure 12 and may be heard in the embedded audio files, performed using solmization syllables assigned to the pitches of the mode following Vicentino’s solmization system for the enharmonic genus.(46) For the odd-numbered modes (i.e., authentic), the examples share the following approach: they ascend stepwise to cover their entire octave range using the appropriate species of 5th and 4th, then return relatively rapidly to their final, via leaps and enharmonic decoration of the final, the 5th, and other suitable turning points.(47) In the portion of each modal example that follows the completion of the authentic ambitus, Vicentino usually treats the line quite freely, using pitches from outside the mode as contrast. For example, the third mode initially covers its range using second-species 5ths and 4ths, whose large ditone step is at the bottom. But once the example has attained the modal final at the top of its octave span, the high E is decorated with an enharmonic upper-neighbor figure, a filled-in semitone that is not properly part of the mode. Immediately afterwards, the fifth degree, B, is similarly decorated, creating an upper tetrachord B–Ḃ–C–E, whose small steps clustered at the bottom of the tetrachord contrast with the “correct” second-species tetrachord for that mode, B–
[30] The plagal modes are presented even more freely. The second mode begins not on its final D, but ascends from A through A. The fourth and eighth modes, before ascending to the top of their range, set out downwards from their final—although the eighth mode does not include the expected first-species 4th (G–
Figure 13. Examples of “unruly” division of the 4th of 5th
(click to enlarge)
Figure 14. The ending of Vicentino’s motet Musica prisca caput
(click to enlarge and listen)
[31] No sooner have all these modes and species been set out so laboriously for the reader than Vicentino goes on to exhort musicians to use instead “mixtures among the species of the three genera, so that every student can use in his music every sort of step found in the three genera. Just as it is possible to write eight pure modes in each of the diatonic, chromatic, and enharmonic systems, so it is also possible to compose steps mixed from the species and systems of the genera” (202). He laments that other composers “do not understand how this mixture of various steps and leaps, accompanied gracefully by consonances, can make a fine harmonic consensus. Nor do they realize that the more the steps are altered in a composition, the more attentive and moved will be the listener, in contrast to a composition that proceeds by always arranging its steps and leaps in one way” (203). He gives several examples of 4ths and 5ths that have been subdivided according to these “unruly” (confusi) steps, pointing out that despite the conflicting genera within their boundaries, they remain true 4ths and 5ths. His examples (Maniates’ exx. 48.1–48.3) are reproduced here in Figure 13, annotated with the number of fifth-tones between adjacent notes.(49) A passage from the very end of the composition Musica prisca caput (Figure 14) illustrates a beautifully unruly division of the ascending perfect 4th, A–D in the soprano, involving 11 distinct pitches in a very similar arrangement to the fourth unruly division of the ascending 4th shown in Figure 13.(50) The A–D 4th is initiated by the tenor’s A before being transferred to the soprano as she moves to Ȧ; the soprano line has been isolated for the listener in the second audio file.(51)
Composing in the genera
Figure 15. Vicentino’s chromatic composition Hierusalem
(click to enlarge, see the rest, and listen)
Figure 16. Chromatic species in the second tenor part of Hierusalem
(click to enlarge)
[32] If we asked a modern musician to create a composition using a genus, we might expect him or her to treat the genus as a source collection from which to draw all or almost all pitches, either in one voice or in all voices. In this approach, writing “in the enharmonic” would be analogous to writing in, say, an octatonic mode: there would be a fixed gamut of admissible notes for a piece, or a section of a piece. Clearly, though, this is not what Vicentino has in mind. The composition in Figure 15, Hierusalem, is given in L’Antica musica explicitly as an example of pure chromatic writing; in fact the opening of this piece is the only passage in Vicentino’s surviving compositions that convincingly demonstrates a clear relationship to any of the generic species described at such length in the treatise. The imitative entries spell out chromatic species of 4ths, including ascending and descending third-species tetrachords and descending second-species.(52) After the opening section, though, none of the voices are consistent with a single chromatic species for any more than a few notes at a time. Instead, Vicentino’s aim was that each voice be restricted to the intervals available in the chromatic genus: the major and minor semitone and the incomposite trihemitone (minor 3rd).(53) This restriction on intervals will give rise to an unrestricted set of pitches, even in a “pure chromatic” composition, as eventually any pitch (uninflected enharmonically) may be reached from any other via some chain of chromatic intervals. Figure 16 demonstrates an analysis of the pitches of the second tenor line of Figure 15 that remains “in the chromatic genus” by continually modulating from one chromatic species to another, so that every melodic succession smaller than a 4th is interpreted as a step interval of a chromatic species of 4th or 5th, suitably transposed.(54) The segmentation suggested here after the initial imitative section should not be taken as indicative of any real succession of species of 4ths and 5ths; there are many equally valid ways of parsing the voice into chromatic segments. The point is that some such modulation between chromatic species must be implicitly present if we are to understand each melodic interval as functioning as a single step of some chromatic species, and not as part of one of the “unruly” divisions that dominate the non-pure chromatic and enharmonic works.
Figure 17. Successions of major triads wholly in the chromatic genus
(click to enlarge)
[33] This constraint on melodic succession renders the harmonic aspect of composition quite difficult when applied to multiple voices simultaneously. Consequently the range of harmonic successions in Figure 15 above is quite impoverished compared to what we might expect to encounter in chromatic works by roughly contemporaneous composers like Lassus or Gesualdo. Although surprisingly many triadic successions are possible in abstract—despite the restriction that voice-leading may only contain intervals proper to the chromatic genus—most of these successions are quite awkward to pull off, requiring voice-crossings, anti-parallel leaps, forced ![]()
Figure 18. Vicentino’s composition Soav’e dolc’ardore
(click to enlarge and listen)
Figure 19. Ending of Vicentino’s composition Dolce mio ben
(click to enlarge and listen)
[34] The situation is worse still in the enharmonic. A moment’s experimentation will show that it is possible to write very few triadic successions whose voice-leading comprises exclusively major and minor enharmonic dieses, major 3rds, and 4ths and 5ths.(55) And indeed each of the voices in Vicentino’s example of enharmonic composition, Soav’e dolc’ardore (Figure 18), includes intervals foreign to the enharmonic genus. What, then, can he have meant by describing Soav’e dolc’ardore as enharmonic, rather than as a mixture of the genera—which is how he describes other pieces that feature some enharmonic inflection but are not wholly restricted to melodic intervals from the enharmonic genus? I believe the answer is that in this excerpt, every succession of triads involves at least one voice that moves by an enharmonic diesis (major or minor), as demonstrated in Figure 18.(56) Thus the excerpt necessarily belongs to the enharmonic genus, since melodic motion by enharmonic dieses cannot occur in either the chromatic or the diatonic.(57)
Conclusion
[35] In essence, by invoking the possibility of mixing genera or species at will, Vicentino has allowed himself to write any melodic line conceivable—as long as it is “accompanied gracefully by consonances, [making] a fine harmonic consensus,” i.e., triadic harmony (203).(58) This certainly removes some of the explanatory power that might otherwise have devolved to the genera in any analytic account of the surviving enharmonic compositions, and spending any time with these works is sufficient to convince oneself that Vicentino’s enharmonic inflections generally appear to be carried out with no obvious relationship to a framework of generic species. Figure 19 illustrates the concluding measures of the piece Dolce mio ben. After a lengthy passage entirely without enharmonic inflections the final sonority hovers insistently, one fifth-tone higher than the expected
[36] Given the lack of recognizable generic segments of any significant length in the compositions, and the extent to which we must invoke mixture of genera and frequent modulation of species in order to fit melodic lines to genera at all, it is reasonable to ask why Vicentino devoted so much attention in his treatise to the apparatus of classifying genera and species. We might simply chalk it up to the music theorist’s irresistible urge to systematize: Vicentino the systematic theorist appears not to have wished to allow Vicentino the unruly composer sole responsibility for his reboot of the Greek genera. Another possible contributing factor is the prestigious pedigree conferred by a theoretical system akin to that of Boethius; Vicentino’s system even surpasses Boethius’s in its greater complexities. By placing his compositional innovations in that particular intellectual lineage, Vicentino ensured his writing, and hopefully his compositions too, would be widely read and discussed.
[37] In a follow-up to this article I shall look at other ways to approach Vicentino’s 31-tone music, ways that are not solely focused on the genera and species that form the basis of the theoretical approaches of L’Antica musica. The pitch systems of L’Antica musica and their complex set of interrelationships differ from anything in the theoretical writings of Vicentino’s contemporaries, in that they are largely synthetic: his pitch systems do not attempt to codify an existing musical practice that has evolved naturally over many generations, nor do they simply transmit or reexamine received wisdom from previous theorists. In this respect L’Antica musica is startlingly modern: it is experimental compositional theory that, despite the treatise’s title, owes less to antiquarianism and more to avant-gardism; surely there is no sixteenth-century musician of more radical inventiveness in the area of melodic materials.(60) Vicentino certainly anticipates antipathy towards his unfamiliar notions, complaining that:
some singers and musicians, who believe themselves knowledgeable, show their amazement to everyone whenever they encounter a novelty in musical signs that has been introduced for the sake of some sort of consonance. Straight away they begin by saying, ‘It is not good, it is not easy to sing,’ and conclude that ‘it will not endure,’ citing the example of past composers to prove that if the practice in question were good those composers would have used it. (35)
[38] This appraisal of the likelihood of acceptance for his novel procedures was sadly too accurate, as borne out in these words from a detractor, Vincenzo Galilei, written after Vicentino’s death:
Don Nicola had some students, who, while he played, especially in the enharmonic genus, sang this sort of music composed by him. He had this music performed in all the principal cities of Italy and I have heard it often, in various times and places. Let it be the sign of whether this music pleased or not that after his death it was practiced neither by his students nor by anyone else. . . . If by misfortune one of the singers lost his way while singing, it was impossible to put him back on the right track. Thus this kind of music necessarily required an instrument that could guide the voices of the singers through unknown tracts (not to say through precipitate cliffs), not letting them proceed according to the nature of singing and through a straight path. These particular sounds of the enharmonic . . . could only be unpleasant to the senses. . . . After Don Nicola’s death the music was not sung any more; the instruments were no longer played in that manner and his students completely abandoned the enharmonic, not finding anyone who wished to listen to it.(61)
[39] I suspect that the easily imaginable difficulties in rendering favorable performances would have played the greatest role in the negative reactions to Vicentino’s musical practice recorded by Galilei and other contemporaries. For my part, having spent some time on producing faithful recordings of the few surviving works, I have found Vicentino’s 31-tone system was certainly able to accommodate beautiful, compelling music—music that is for the most part impossible to recreate outside the 31-tone system. Even if we estimate generously that he may have written as many as a few dozen 31-tone works in his lifetime, Vicentino still could barely have scratched the surface of the possibilities offered in a compositional world of such wealth. I hope this initial investigation, along with the longer excerpts to be presented in the second part of the article, will make it easier to treat the notion of 31-tone music in the sixteenth century not merely as a misguided novelty or an evolutionary dead-end, but as a window briefly opened on a foreign landscape of strange allure and unexpected treasures.
Jonathan Wild
McGill University
Department of Music Research, Schulich School of Music
555 Sherbrooke West
Montreal, Qc H3A 1E3
Canada
wild@music.mcgill.ca
Works Cited
Barker, Andrew, ed. 1989. Greek Musical Writings II: Harmonic and Acoustic Theory. Cambridge: Cambridge University Press.
Barnes, J. 1971. “The Specious Uniformity of Italian Harpsichords.” In Keyboard Instruments: Studies in Keyboard Organology, ed. E.M. Ripin, 1–9. Edinburgh: Edinburgh University Press.
Berger, Karol. 1980. Theories of Chromatic and Enharmonic Music in Late 16th-Century Italy. Ann Arbor: UMI Research Press.
Bertrand, Anthoine de. [1578] 1927. Second livre des Amours de Ronsard. In Monuments de la musique française au temps de la Renaissance vol. 4, ed. Henry Expert. Paris: Maurice Sénart. Originally published in Paris: Adrian Le Roy et Robert Ballard.
Chalmers, John H. Jr. 1993 The Divisions of the Tetrachord. Hanover, New Hampshire: Frog Peak Music.
Fogliano, Lodovico. [1529] 1969. Musica Theorica. In Monuments of Music and Music Literature in Facsimile. Ser.. 2. 93. New York: Broude Brothers. Originally published in Venice.
Glarean, Heinrich. [1547] 1950. Dodecachordon. Ed. and trans. Clement Miller. PhD diss., University of Michigan.
Kaufmann, Henry William. 1966. The Life and Works of Nicola Vicentino. Rome: American Institute of Musicology.
Huygens, Christiaan. [1691] 1986. “Lettre touchant le cycle harmonique.” In Tuning and Temperament Library vol. 6, ed. Rudolf Rasch, Utrecht: Diapason Press. Originally published in Histoire des ouvrages des Sçavans, 78–88. Rotterdam: Reinier Leers.
Lindley, Mark. 1982. “Chromatic systems or non-systems from Vicentino to Monteverdi: Review of Theories of Chromatic and Enharmonic Music in Late 16th Century Italy by Karol Berger.” Early Music History 2: 377–404.
Marchetto da Padova. [1318] 1978. Lucidarium. In “The Lucidarium of Marchetto of Padua: A Critical Edition, Translation, and Commentary,” trans. Jan Herlinger. PhD diss., University of Chicago.
Palisca, Claude V. 1954. “The Beginnings of Baroque Music; Its Roots in Sixteenth Century Theory and Polemics.” PhD diss., Harvard University.
Ramos de Pareja, Bartoloméo. [1482] 1901. Musica Practica. In Publikationen der internationalen Musikgesellschaft 2. Trans. Clement A. Miller in Musicological Studies and Documents 44, 1993. Originally published in Bologna.
Schubert, Peter N. 1991. “The Fourteen-Mode System of Illuminato Aiguino.” Journal of Music Theory 35, no. 2: 174–210.
Tinctoris, Johannes. [1477] 1961. Liber de arte contrapuncti. Trans. Albert Seay. Rome: American Institute of Musicology.
—————. [1476] 1976. Liber de natura et proprietate tonorum. Trans. Albert Seay. Colorado Springs: Colorado College Music Press Translations.
Vicentino, Nicola. [1555] 1996. L’Antica musica ridotta alla moderna prattica. Rome: Antonio Barrè. Translated as Ancient Music Restored to Modern Practice by Maria Rika Maniates. New Haven: Yale University Press.
—————. 1959. L’Antica musica ridotta alla moderna prattica. In facsimile, ed. Edward E. Lowinsky. Kassel: Bärenreiter Verlag.
—————. 1990. Four Enharmonic Madrigals, ed. Alexander Silbiger. Utrecht, Netherlands: Diapason Press.
Wild, Jonathan and Peter Schubert. 2008. “Historically Informed Retuning of Polyphonic Vocal Performance.” Journal of Interdisciplinary Music Studies 2, nos. 1&2, 121–39.
Woodley, Ronald. 2006. “Sharp Practice in the Later Middle Ages: Exploring the Chromatic Semitone and its Implications.” Music Theory Online 12, no. 2.
Zarlino, Gioseffo. 1558. Istitutioni Harmoniche. Venice.
Footnotes
1. Vicentino [1555] 1996. Page numbers cited in the present article refer to the 1996 translation by Maria Rika Maniates. As Maniates’ translation is the principal means of access many readers will have to the treatise, I shall record in the notes of this article certain corrections to her examples, to avoid any confusion for readers cross-referencing my work with hers.
Folio numbers cited in the present article refer to the widely available facsimile edition of L’Antica musica (1959). This edition suffered from a number of mistaken “amendments”: some of the markings present in the musical notation on the scanned manuscript—markings whose meaning is explained later in this article—were thought to be flyspecks or other unintended blemishes, and “cleared up” before reproduction. This discovery by British musicologist David Gallagher is recounted in an as-yet unpublished manuscript, “Vicentino’s Lost Dieses” (personal communication), which also contains a great deal of supplementary material about the treatise, its context, and its reception.
For a book-length study of Vicentino’s life and works, see Kaufmann 1966. The collections of enharmonic vocal compositions Vicentino is known to have published are currently lost to musicology; the surviving excerpts from L’Antica musica have been transcribed by Maniates and by Kaufmann in the publications just mentioned, and also by Alexander Silbiger in his edition Nicola Vicentino: Four Enharmonic Madrigals (Vicentino [1555] 1990), which also includes a brief discussion of the theoretical system and some analytic commentary.
Research for this article was supported by SSHRC grant 608-2011-0048. Space and equipment were provided by CIRMMT, the Centre for Interdisciplinary Research in Music Media and Technology. Some of the content was first presented in a talk at the 2008 Society for Music Theory conference in Nashville, titled “Through ‘unknown tracks and precipitate cliffs’: Analysis and performance of an enharmonic madrigal by Nicola Vicentino.”
Return to text
2. The technological challenges, and approaches to solving them, are described in Wild 2008. See also note 51 below for a summary of the process. I thank Peter Schubert for his contribution to the recordings, for many discussions on this project, and for his feedback on the present article. I am grateful too for the participation of recording engineers Nick Squire and Brett Leonard from McGill University’s Sound Recording Program.
Return to text
3. I shall extend the representation of intervals in cents to three decimal places to avoid the accumulation of rounding errors. Just intonation and meantone tunings yield irrational fractions of the octave, and their interval sizes cannot be expressed precisely in decimal notation of finite length. The syntonic comma has the ratio 81:80.
Return to text
4. Since the whole tone of ¼-comma meantone is the mean of the 9:8 and 10:9 whole tones, which sum to a pure 5:4 major 3rd, it follows that this whole tone is also the mean between the unison and the pure major 3rd. The earlier Renaissance theorists who had followed Ptolemy in proposing the just ratios 9:8 and 10:9 for the whole tones of the diatonic scale include Ramos (1901), Fogliano (1969) and Zarlino (1558).
The designation “meantone” is often extended to encompass a broader family of temperaments—including for example 1/3-comma, 1/5-comma, and 1/6-comma—which temper the perfect 5th by lesser or greater amounts and render different intervals purely; in these temperaments the whole tone is still the mean of their major 3rd and the unison, though it is no longer the mean of the traditional just intonation whole tones. For keyboard instruments (though not for vocal music) Zarlino famously advocated 2/7-comma meantone, which tempers major and minor 3rds by equal (but opposite) amounts.
Return to text
5. Vicentino mentions the existing practice of providing a split-key between G and A in order to allow a perfect 5th below
Return to text
6. Vicentino’s writings do not make explicit whether he believes this difference to correspond exactly to one fifth of his whole tone. See note 10 below for the detailed intervallic calculations.
Return to text
7. A typographic detail: while in this manuscript the dot is centered above the “E”, and not above the entire note name “
Return to text
8. I include the double-sharp and double-flat synonyms in Figure 1 for the convenience of the modern reader; Vicentino never uses them. Their correspondence to Vicentino’s dotted pitches is clear when we consider the fact a double-sharp must be twice as far removed from the natural note it affects than is a single sharp; that is, twice as far as 2/5s of a tone, i.e., 4/5s of a tone. Thus
Return to text
9. Earlier theorists—for example Tinctoris, in his Liber de arte contrapuncti of 1477, or Marchetto, in his Lucidarium of 1318—had also implied a fivefold division of the whole tone; however, their systems use a wider 5th than that of ¼-comma meantone, with the result that
Return to text
10. Specifically, the fifth-tone corresponds to the minor enharmonic diesis; as is shown in Figure 1, the diatonic semitone may be considered as divisible into two uneven parts, the minor and major enharmonic dieses, such that the major diesis is equivalent in size to two minor dieses.
The ¼-comma whole tone is 193.157 cents; 1/5 of this is 38.631 cents. This is within 0.1 cents—one thousandth of a semitone!—of the step size of 31-tone equal temperament, 38.710 cents. For all practical purposes we may consider, as I believe Vicentino did, the ¼-comma whole tone to be subdivided evenly into five parts and the diatonic semitone into three, yielding a 31-tone octave. To be absolutely thorough: in a ¼-comma meantone gamut constructed as an extended chain of 5ths, the interval between the pitches
Return to text
11. This relationship between 12-tone, 19-tone, and 31-tone chains of 5ths can also be understood by examining the size of 5th in the corresponding equal temperaments, where the 12-tone 5th is too wide and the 19-tone 5th too narrow compared to the meantone target. When adding the cardinalities of equal temperaments, the resulting approximation to a given interval is given by the weighted average of its approximation in the two systems, where the weighting is proportional to the cardinalities of equal temperament. So the 31-tone perfect 5th is 19/31sts of the way between the 12-tone perfect 5th and the 19-tone perfect 5th; or, equivalently, 12/31sts of the way between the 19-tone perfect 5th and the 12-tone perfect 5th.
Return to text
12. There is a very similar statement on p. 54. I shall discuss the effects of the archicembalo design on Vicentino’s harmonic language at length in Part 2 of the article.
Return to text
13. Additional reasons to use 31-tone equal temperament have been proposed since Vicentino’s time; here I shall mention only its very good approximation of the seventh partial of the harmonic series, corresponding to the augmented 6th of ¼-comma meantone, first noted by Christiaan Huygens in 1691.
Return to text
14. Detailed and illustrated instructions for constructing, tuning, and playing an archicembalo appear in Book V on Music Practice, a substantial portion of the entire treatise.
Return to text
15. Accidental pitches written with sharps inflected by an enharmonic dot do not appear on either manual; they would be superfluous because they are equivalent to the (uninflected) flat accidentals already present on the lower manual.
Return to text
16. A second, alternative tuning of the archicembalo that extends this principle of tuning pure 3:2 5ths on the upper manual is given in L’Antica musica. In this second tuning the lower keyboard is tuned as before, i.e., as a 19-note chain of tempered 5ths from
Return to text
17. For a thorough account of the ancient genera, the reader is referred to Andrew Barker’s introduction to Greek Musical Writings II: Harmonic and Acoustic Theory (Barker 1989).
Return to text
18. Excepting the ditone of 10 dieses, we might notice that the other interval sizes in Vicentino’s tuning form a Fibonacci series: 1, 2, 3, 5, 8, and 13 dieses. This is due to the way intervals that are adjacent in size to each other combine to make larger intervals: a minor and major enharmonic diesis combine to form a major semitone, which combines with a minor semitone (the same size as a major enharmonic diesis) to form a whole tone, which combines with a major semitone to form a minor 3rd, which combines with the whole tone to form a perfect 4th.
Return to text
19. The consecutive ratios of Ptolemy’s enharmonic, all superparticular, are 46/45, 24/23 and 5/4, yielding a perfect 4th of 498.045 cents with movable pitches 38.051 cents and 111.732 cents above the lowest pitch; a comparison with Figure 3 reveals the closeness of Vicentino’s approximation. In John Chalmers’ book The Divisions of the Tetrachord (1993) the author gives over 700 ways to divide the perfect 4th into three intervals according to various historical, theoretical, and speculative principles, including 88 divisions consistent with an enharmonic genus. For the sake of comparison, after Ptolemy’s enharmonic (no. 104 in Chalmers’ main catalogue), the most similar to Vicentino’s enharmonic are: 56/55 × 22/21 × 5/4, also found in Ptolemy but thought to be a later scribal addition (Chalmers’ no. 107); 40/39 × 26/25 × 5/4, found in Avicenna (no. 108); and a “Neo-Aristoxenian” genus (no. 600) based on a tempered 4th of 500 cents divided into 30 equal parts, where the movable pitches are placed at 7/3rds, and at 7 of these parts (38.889 cents and 116.667 cents) above the lowest pitch.
As for the chromatic genus as embedded in the 31-tone system, it most closely resembles Ptolemy’s soft chromatic, 28/27 × 15/14 × 6/5, whose movable pitches are 62.961 cents and 182.404 cents above the lowest note.
Return to text
20. The natural whole tone is one occurring between two notes written as naturals.
Return to text
21. It was perhaps Vicentino’s emphasis on the four-fold rule that caused later writers to believe he advocated quarter-tones; Anthoine de Bertrand is one such example. In the Avertissement au lecteur placed at the beginning of his Second livre des Amours de Ronsard (1927), in which he borrows Vicentino’s superscript dot notation, Bertrand writes that the enharmonic dots in one of his works raise the pitch of a note by a quarter-tone (he adds that those who are unable to perform them accurately may ignore them!).
Return to text
22. On the archicembalo, the two divisions of a natural whole tone admissible under the four-fold rule display identical patterns of distribution, alternating between the upper and lower manuals. This is one of several cases that I shall claim is indicative of the influence of the archicembalo’s design on Vicentino’s compositional theories.
The adjacency
Return to text
23. Vicentino does not discuss whole tones like B–
Return to text
24. The examples in this section of Maniates’ translation (392–98) contain several mistakes. In her ex. 48.1, system 3, m. 2, the second note (E) should be dotted. Ex. 49.1, sys. 2, m. 3, Ġ
Return to text
25. In Chapter 7 of Book I on Music Practice, Vicentino cites Boethius as the authority for the statement that “chromatic” signifies the transformation of the whole tone and semitone steps of the diatonic into the semitones and trihemitone of the chromatic. See p. 48 and Maniates’ footnotes 54–56.
Return to text
26. Vicentino sometimes refers to the major and minor variants of the semitone or the diesis collectively, without distinction; other times he is careful to specify which of the major or minor variant he intends. He treats the two whole tones of the diatonic tetrachord similarly: while they are identical in size in any meantone temperament, he sometimes refers to the major and minor whole tone—terms which only make sense in tunings based on just intonation where both 9:8 and 10:9 whole tones are present. For example, in Book I Chap. 6 he writes: “You must realize that in contemporary practice we form the diatonic genus out of one major semitone, one sesquinonal [10:9] whole tone, and one sesquioctaval [9:8] whole tone. This inequality of tones affords us the advantage of being able to use the consonances of the third and sixth, both major and minor” (44). Elsewhere he concedes that in practice this is not quite true; for example in Book I Chap. 24 he states that the natural whole tone is both sesquioctaval and sesquinonal in nature, i.e., partakes of both the 9:8 and the 10:9 ratios (67). Since when speaking of his own tuning he has no need to differentiate between the major and minor whole tone of the syntonic diatonic, he recycles these terms elsewhere in the treatise to refer to the quasi-whole-tone intervals that exceed, and that fall short of, the whole tone by 1/5 of a tone—6/5ths and 4/5ths of a tone, respectively.
Return to text
27. Vicentino writes that his chromatic 4th displays “the opposite arrangement from that of Boethius,” a statement that requires some explanation. Boethius’s chromatic ascends, exactly like Vicentino’s, with a diatonic semitone followed by a chromatic semitone then a minor 3rd (see Chapter 7 of Book I on Music Theory). The sense in which the two theorists describe “opposite arrangements” becomes apparent when we rewrite their divisions in terms of major and minor semitones. In Boethius’s chromatic, tuned using Pythagorean intervals, the diatonic semitone is smaller than the enharmonic semitone, and so his division begins with a minor semitone.
The three chromatic 4ths are not strict circular rotations of one another when we take into account the difference between the major and minor semitone: the third 4th presents a different arrangement from the others in that it is the minor (chromatic) semitone that precedes the minor 3rd. Berger 1980 points this out and suggests the implication is that while Vicentino only shows us one possibility, we should consider there to be two equally valid versions for every species of chromatic 4th, related to each other by exchanging the positions of the major and minor semitone (9). I disagree, since elsewhere (Chap. 6 of Book I on Music Theory) Vicentino points out that 4ths in the chromatic genus should have a chromatic semitone placed adjacent to their minor 3rd, completing a ditone. The alternative second-species B–D–
Return to text
28. A similar situation to the chromatic arises in that Berger (1980) considers equally legitimate those variants of the enharmonic 4ths, unmentioned by Vicentino, whose major and minor enharmonic dieses have been exchanged (9). But some of the variants that would be admitted by Berger—second-species B–
Return to text
29. Berger (1980) appears not to consider Vicentino’s step pattern aabaa for the fourth chromatic species of 5th as a legitimate option: he simply labels it a mistake and corrects it to G–
Return to text
30. Of the six dieses, four must be minor and two major. It would theoretically be possible for an enharmonic 5th to comprise two minor dieses and three major alongside the required major 3rd—but this would not allow the characteristic enharmonic division of the whole tone into four parts.
Vicentino makes two mistakes in his prose description of the second enharmonic 5th (200). Maniates corrects one (her footnote 68); the other mistake is that the final diesis must be minor.
Return to text
31. Berger 1980 suggests aaaaaba should be the correct pattern for the fourth enharmonic species of 5th. Just as in the discussion of the fourth chromatic species of 5th, the natural mapping of the diatonic species aaba to a pattern of six “a”s and one “b” is open to interpretation; he reads it as “b is in second-to-last position” rather than “b is in third position” (12). Berger’s 5th produces a regular 8ve species in combination with the first 4th, and I suspect this is why he prefers it over Vicentino’s.
Additional differences between Berger’s and my account of Vicentino’s enharmonic derive from the fact that Berger believes the enharmonic must be considered the result of transformation and subdivision of the chromatic (which is itself a result of transformation and subdivision of the diatonic), and not at all a direct transformation of the diatonic (1980, 14–15). But Vicentino writes (Book III, Chap. 45): “I begin with the formation of the three enharmonic fourths, arranged in the same way as the chromatic fourths—by putting the big step in the location of the small diatonic one, and the small steps in place of the big diatonic ones” (198). Thus no intermediate chromatic is required for the passage from diatonic to enharmonic. Berger’s understanding, contradicted in the passage just quoted and not supported elsewhere in the treatise, leads to a system of considerably greater complexity and admits many variant species, variants which are not alluded to in L’Antica musica save in one ambiguous passage which I discuss below. I also find that Berger’s rules for dividing and subdividing the diatonic 5ths, explained at the bottom of p. 11, fail to produce the required chromatic and enharmonic species. Remapping the tones and semitones of the diatonic species into intervals characteristic of the chromatic and enharmonic genera, using the abstract patterns that correspond most closely to the diatonic originals, is a more parsimonious recipe than Berger’s obscure process of subdivision.
Return to text
32. This last preference is not expressed explicitly; generally, though, Vicentino clearly values strong differentiation between chromatic and enharmonic. The exception for
Return to text
33. In the original, f63: “Hora la terza quinta terrà quest’ ordine, che prima caminerà con sei gradi de Diesis maggiori & minori; Il primo grado sarà minore, . . . et il sesto maggiore; avuenga che nell’ ordine di questi Diesis Enarmonici, il Compositore può ad ogni suo beneplacito mettere i maggiori, & i minori secondo ch’ à egli verrà piu commodo; & coso anchora de i semitoni maggiori & minori”.
Return to text
34. It is possible of course to extract octave species from the conjunct and disjunct arrangements of tetrachords found in the Greater and Lesser Perfect Systems of Greek harmonics (described in detail in the Introduction of Barker 1989), scale systems which encompassed all three genera. However, since these octave species were not generally understood as combining species of 4th and 5th, and since they may include a tone of disjunction not characteristic of the step sizes available in the chromatic or enharmonic genus, they are not useful precedents for Vicentino’s theoretical program.
Return to text
35. The F–f and B–b species appear once each; all others have two possible constructions (e.g., the E–e species, comprising the second 5th below the second 4th, could also be described as the second 4th below the first 5th). Vicentino’s derivation, which indicates which species are constructed plagally and which authentically, allows his seven species to be identified with seven of the eight traditional modes; only the hypomixolydian (first 4th below fourth 5th) is absent.
Return to text
36. Precisely this program of exploration was carried out in Glarean’s Dodecachordon, Chapter III of Book II. I quote the passage at length to illustrate the author’s remarkably systematic approach. Glarean writes: “The following fact troubles some exceedingly—and formerly it also kept me in anxiety—namely: how it could happen that only seven octave species arise from the connection of twenty-four fourths and fifths (for there are that many if, for instance, we connect the individual species of fourths above and below the individual fifth species . . . for both can occur). In order that it may appear in a clearer light to the reader, we have placed the entire matter before him in a very plain manner, so that he is then able to judge at a single glance how these species arise and sprout forth, as it were, and then to judge which may be useful and which must be rejected in the diatonic system. . . . The diatonic genus accepts twelve and rejects the same number. . . . The twelve are rejected for four reasons”—and he describes some disqualifying successions that occur, such as four whole tones in a row, or two semitones in a row—“And so twelve connections are left. . . . And among them, six are divided arithmetically [i.e., plagally] and six harmonically [i.e., authentically]” (1950, 172–74).
In her introduction to the translation of L’Antica musica, Maniates points out that Vicentino appears to show his awareness of Glarean’s treatise, without naming its author, in his negative appraisal of “some people” who would have us believe there are more than eight modes (xxvi; see also 139n8).
Return to text
37. Maniates has omitted the flat on the B in this mode (her example 38, 189).
Return to text
38. This seventh chromatic 8ve of Vicentino’s qualifies as a mode of limited transposition (disregarding the difference between major and minor semitones for now): transposing it by a half-octave leaves it invariant; stated equivalently, we can shift the starting point of the cycle aabaaaba forward or backwards by four positions, and the resulting scale is unchanged.
Using Berger’s amended fourth 5th (see note 31 above) to construct the seventh 8ve, as shown in the bottom row of the table, would result in a rotation of the same scale as the first six 8ve species. We now see one advantage of Berger’s amendment: when combined with a first 4th, his fourth 5th produces an 8ve whose minor-3rd steps are separated by a 4th/5th, like the other accepted combinations of 4ths and 5ths. Still, one rotation of the scale (aabaabaa, the only mirror-symmetrical rotation) would remain missing, and Vicentino does not ever give reason to believe that all 8ve species in a given genus should be modes of the same scale.
Return to text
39. Maniates’ Example 47 erroneously labels the fourth 8ve as third 8ve, and the ordinals for all the remaining 8ves are off by one (202). She omits four flat signs (the mistakes are in the second, fourth, and sixth 8ves). More seriously she writes a bass clef for the sixth 8ve (‘fifth 8ve’, in her labelling), but places the notes (originally in the alto clef) in what would be their correct staff positions for a treble clef, thus misattributing to this 8ve an ambitus of A–a.
Return to text
40. For the sake of completeness I have also shown in the central column the alternative authentic divisions for the first and third 8ves, A–a and C–c, which Vicentino treats plagally in all genera.
Return to text
41. Berger 1980 dismisses the last four enharmonic octaves as they appear in L’Antica musica, suggesting they are all simply mistakes, and that Vicentino meant to continue with a sequence of combined 5ths and 4ths exactly analogous to the one he used for the other genera (13). It is Vicentino’s octaves’ near correspondence to a logical set of alternative arrangements of 4ths and 5ths that suggests otherwise to me, and leads me to believe that many of the changes to the pattern expected by Berger may well have been intentional on Vicentino’s part.
Return to text
42. There are two discrepancies that remain unexplained in the fourth 8ve: Vicentino writes a Ḃ instead of an
There are other unexpected changes to be found in the first 5th, which appears as the upper portion of the first and fifth 8ves. Here too, as in the fourth 8ve, Vicentino has interpolated a Ġ
Finally as mentioned earlier in the discussion of the enharmonic 5ths, Vicentino has taken advantage of the possibility of rewriting the first 5th—still following the “four-fold rule”—so that the enharmonically subdivided whole tones G–A and D–E feature a flat rather than a sharp (first and fifth 8ves).
Return to text
43. Perhaps this is why Maniates reads Vicentino’s sixth 8ve as a clef mistake (see note 39 above): if displaced on the staff (without altering any of the notated accidentals) to begin on any other natural note, Vicentino’s sixth 8ve would be properly plagally divided, like the others in the series. In Maniates’ revision, which turns it into an A–a 8ve, the upper 5th is a recognizable enharmonic species: it is a first 5th, at its “native” pitch level, D–A. But the lower 4th would not be properly enharmonic: its leap falls on a minor 3rd, from Ḃ
Return to text
44. The lower tetrachord of this F–f 8ve has its characteristic major 3rd in the fourth interval from the bottom, distinguishing it from the three species of enharmonic 4th enumerated in the earlier section. The upper 5th has the major 3rd in second position, like the first species of 5th—but with two fewer trailing dieses, due to the diminished quality of the B–F 5th. The unusual nature of both these structures could be seen as analogous to the non-traditional arrangements of tones and semitones in the augmented 4th and diminished 5th found in a “plagal” diatonic F–B–f species.
Return to text
45. Like others he misattributes the invention of the additional mode to Ptolemy. See Maniates, 144–45.
Return to text
46. Figure 12 is transcribed from L’Antica musica (f66). I have corrected mistakes in the original in the Fourth Mode, where Ė
For reasons of space I shall not elaborate on Vicentino’s solmization system in the present article; it is set out in L’Antica musica in Book 1 on Music Practice, Chapters 5 and 11 (40–43 and 53–54). Daniel Donnelly assisted with the assignation of solmization syllables.
The performance here is by tenor Nils Brown, retuned in the studio as discussed below in note 51.
Return to text
47. The modal melodies invite comparison with similarly motivated examples in treatises by writers such as Tinctoris (1476) and Illuminato Aiguino (see Schubert 1991).
Return to text
48. When the eight chromatic modes are presented (191–93) Vicentino is similarly casual about the lower tetrachords in the plagal modes, not attempting to fill them with 4ths of the species earlier claimed to be required—“these [i.e., chromatic] modes are formed by arranging their fourths and fifths exactly in the same way as the diatonic modes” (190)—but instead simply decorating the various turning points of the modes with typical chromatic gestures.
Return to text
49. The 5ths are notated in the tenor clef in L’Antica musica. There are two curiosities: the fifth descending 4th is not entirely in descending order (see the note marked *), and the last descending 5th fails to end on the expected D (see the end, marked **).
Return to text
50. The antepenultimate and penultimate pitches of the soprano line form the pair
Return to text
51. The recording of a real soprano, whose original performance did not take into account the enharmonic dots, has been adjusted in post-production using the software Melodyne (published by Celemony), to yield precisely the pitches demanded in the score. Since the adjusted version retains all the vibrato and richness of the original vocal timbre, only transposing the pitch center of each note and leaving all other audio “information” intact, the results are particularly naturalistic and compelling. For the ensemble recordings this adjustment was carried out on each voice part individually; the singers had to be recorded in isolation, each listening through headphones to a reference recording that we had them make as the first step of the process. While rerecording their own part singers also watched a synchronized video of the reference performance to obtain timing and expressive cues, so they could recapture as much of the nuances of the reference performance as possible. In this way we hoped to achieve a convincing musical result when recombining the rerecorded parts. The isolated recordings had to be anechoic (dry) for the pitch-correction process to work; convolution reverb was added as the final step, to simulate a suitable performance space.
Return to text
52. The first-species 4th, absent in this composition, whose two semitones are separated by a minor 3rd or augmented 2nd, could also easily be accommodated in the kind of sixteenth-century chromatic idiom Vicentino’s work belongs to; for example a line of D–
Return to text
53. Covering a combination of these intervals in one step or leap—for example, writing a diminished 5th (conceived as two trihemitones) or a whole tone (conceived as the composite of an adjacent major and minor semitone) in the chromatic—was equally inacceptable, although the perfect 4th and 5th were apparently acceptable as neutral, appearing as they did in every genus. This was at the root of Vicentino’s famous debate with Lusitano: Vicentino claimed that music could not be considered diatonic when it included, for example, a melodic interval of a major 3rd, since the “incomposite ditone”, i.e., one not broken by an intervening pitch, exclusively indicates the presence of the enharmonic genus. (History records the claim was not found persuasive by the adjudicators: Vicentino lost the debate.)
Return to text
54. There are a small number of rogue intervals in the piece that do not properly belong to the chromatic: for example, in the second tenor part shown in Figure 16, the major 6th A–C after the two statements of the tetrachord figure, and the D–C whole tone near the end, each straddling a rest. (Both of these can appear as composite intervals in a broader chromatic span: the whole tone appears in two of the three species of 4th and any species of 5th, and the major 6th appears in every chromatic 8ve—but this should not grant them independent validity as direct or incomposite melodic intervals of the chromatic genus, according to Vicentino.) About the situation in another purportedly pure chromatic composition, Alleluia, Haec dies, where Vicentino acknowledges retaining a small number of foreign melodic intervals for their suitably intense character, see Maniates’ Introduction, lii and n92.
Melodic 4ths and 5ths are apparently judged neutral; as they do not specifically indicate the presence of some other genus, they may be used in pure chromatic and enharmonic compositions without causing the music to leave its genus.
Return to text
55. In Part 2 of this article (forthcoming) I shall examine more thoroughly the voice-leading characteristics of all triadic transformations available in a 31-tone universe.
Return to text
56. Vicentino points out that the entrances are imitative, in that each voice begins with an enharmonic diesis, whether ascending or descending (223). We may conclude that it is admissible for enharmonic imitation to alter the quality of the diesis, as some voices have a minor diesis and others major.
Return to text
57. Near the end of the excerpt (which breaks off abruptly in L’Antica musica as shown in the example) Vicentino does include one succession without an enharmonic diesis anywhere in the voice-leading, spanning the bar line between the second-to-last and last completed measures. But even here there is a feint to enharmony: in the (non-enharmonic) progression of triads Ȧ minor to Ė major, the soprano is given Ȧ to
Return to text
58. The original reads: “di maniera che questa commistione de varij gradi & salti, che con bell’ ordine di consonanze accompagnati sono, fanno buono concento d’armonia” (f65). Also relevant is this passage on p. 207: “[A pupil] should know how to match and accompany with harmony all sorts of disproportioned and irrational intervals, and also how to sing them so as to show the world that he is exceptional and can accomplish with artifice that which cannot be done by reason.”
Return to text
59. The composition begins on folio 67v of L’Antica musica. The entire text reads: “Dolce mio ben, son quest’i dolci lumi che tanto dolcemente mi consumi.”
Return to text
60. Other writers may have shown greater innovation in dissonance treatment and in harmonic practice; my claim relates only to pitch structures expressed melodically. It is curious that for all Vicentino’s strongly professed interest in novelty, he never explores innovation in other musical elements than melody. Vocal textures are unremarkable throughout the surviving excerpts, and rhythm and meter are treated in an orthodox manner. He restricts his harmonic palette almost entirely to major and minor triads; as for the exceptions, other than conventional dissonance treatment like suspensions, I have found only the odd augmented triad in passing, and one dubiously treated diminished triad (at the end of the second verse of Musica prisca caput). David Gallagher’s unpublished article “Vicentino’s Lost Dieses” (see note 1) proposes that in fact some of Vicentino’s improbable verticalities, easy to dismiss as printing errors, were actually intended as experimentally dissonant sonorities; musically I find it difficult to agree with these conclusions.
Return to text
61. Vincenzo Galilei, Discorso intorno all’uso dell’Enharmonio, c. 1586, quoted in Palisca 1954.
Return to text
Folio numbers cited in the present article refer to the widely available facsimile edition of L’Antica musica (1959). This edition suffered from a number of mistaken “amendments”: some of the markings present in the musical notation on the scanned manuscript—markings whose meaning is explained later in this article—were thought to be flyspecks or other unintended blemishes, and “cleared up” before reproduction. This discovery by British musicologist David Gallagher is recounted in an as-yet unpublished manuscript, “Vicentino’s Lost Dieses” (personal communication), which also contains a great deal of supplementary material about the treatise, its context, and its reception.
For a book-length study of Vicentino’s life and works, see Kaufmann 1966. The collections of enharmonic vocal compositions Vicentino is known to have published are currently lost to musicology; the surviving excerpts from L’Antica musica have been transcribed by Maniates and by Kaufmann in the publications just mentioned, and also by Alexander Silbiger in his edition Nicola Vicentino: Four Enharmonic Madrigals (Vicentino [1555] 1990), which also includes a brief discussion of the theoretical system and some analytic commentary.
Research for this article was supported by SSHRC grant 608-2011-0048. Space and equipment were provided by CIRMMT, the Centre for Interdisciplinary Research in Music Media and Technology. Some of the content was first presented in a talk at the 2008 Society for Music Theory conference in Nashville, titled “Through ‘unknown tracks and precipitate cliffs’: Analysis and performance of an enharmonic madrigal by Nicola Vicentino.”
The designation “meantone” is often extended to encompass a broader family of temperaments—including for example 1/3-comma, 1/5-comma, and 1/6-comma—which temper the perfect 5th by lesser or greater amounts and render different intervals purely; in these temperaments the whole tone is still the mean of their major 3rd and the unison, though it is no longer the mean of the traditional just intonation whole tones. For keyboard instruments (though not for vocal music) Zarlino famously advocated 2/7-comma meantone, which tempers major and minor 3rds by equal (but opposite) amounts.
The ¼-comma whole tone is 193.157 cents; 1/5 of this is 38.631 cents. This is within 0.1 cents—one thousandth of a semitone!—of the step size of 31-tone equal temperament, 38.710 cents. For all practical purposes we may consider, as I believe Vicentino did, the ¼-comma whole tone to be subdivided evenly into five parts and the diatonic semitone into three, yielding a 31-tone octave. To be absolutely thorough: in a ¼-comma meantone gamut constructed as an extended chain of 5ths, the interval between the pitches D♯ and E♭ (a doubly-diminished 2nd, generated by twelve ¼-comma 5ths) would be 41.059 cents. The interval between E♭♭ and D♯ (a triply-diminished 2nd, generated by nineteen ¼-comma 5ths) would be 34.990 cents. It is the weighted mean of these (three of the former, two of the latter, as found in the succession D–E♭♭–D♯–E♭–D𝄪–E) that corresponds so closely to 1/31st of an octave. A similar calculation, one that also shows the near-exact correspondence of this temperament to 31-equal, is possible starting from the threefold division of the ¼-comma diatonic semitone of 117.108 cents.
As for the chromatic genus as embedded in the 31-tone system, it most closely resembles Ptolemy’s soft chromatic, 28/27 × 15/14 × 6/5, whose movable pitches are 62.961 cents and 182.404 cents above the lowest note.
The adjacency C♯–D♭ does occur in one composition, Musica prisca caput, discussed in Fig. 14 below.
The three chromatic 4ths are not strict circular rotations of one another when we take into account the difference between the major and minor semitone: the third 4th presents a different arrangement from the others in that it is the minor (chromatic) semitone that precedes the minor 3rd. Berger 1980 points this out and suggests the implication is that while Vicentino only shows us one possibility, we should consider there to be two equally valid versions for every species of chromatic 4th, related to each other by exchanging the positions of the major and minor semitone (9). I disagree, since elsewhere (Chap. 6 of Book I on Music Theory) Vicentino points out that 4ths in the chromatic genus should have a chromatic semitone placed adjacent to their minor 3rd, completing a ditone. The alternative second-species B–D–E♭–E and third-species C–C♯–D–F, both legitimate according to Berger, would contravene this guideline by placing a diatonic semitone adjacent to the minor 3rd. This causes the occurrence of the composite diminished 4ths, B–E♭ and C♯–F respectively, formed of a minor 3rd and a diatonic semitone, rather than the ditones B–D♯ and D♭–F, which contain a minor 3rd and a chromatic semitone. In the case of the first 4th, whose trihemitone falls in the middle and must be surrounded by one each of the minor and major semitones to complete the perfect 4th, both arrangements, A–A♯–C♯–D and A–B♭–D♭–D, contain a composite major 3rd and, in interlocking fashion, a composite diminished 4th. I believe Vicentino preferred the latter arrangement because in ascent it begins with a major (i.e., diatonic) semitone; in fact, none of the chromatic species of 4th, 5th, or 8ve begins with a minor semitone. This maximizes the contrast—always an important consideration for Vicentino—between the chromatic and enharmonic species: in the enharmonic species that begin with an enharmonic diesis, it is always a minor diesis, never a major diesis. Thus Vicentino’s 4ths, 5ths, and 8ves as they appear in L’Antica musica allow the listener to distinguish the chromatic from the enharmonic genera as early as their very first interval.
Vicentino makes two mistakes in his prose description of the second enharmonic 5th (200). Maniates corrects one (her footnote 68); the other mistake is that the final diesis must be minor.
Additional differences between Berger’s and my account of Vicentino’s enharmonic derive from the fact that Berger believes the enharmonic must be considered the result of transformation and subdivision of the chromatic (which is itself a result of transformation and subdivision of the diatonic), and not at all a direct transformation of the diatonic (1980, 14–15). But Vicentino writes (Book III, Chap. 45): “I begin with the formation of the three enharmonic fourths, arranged in the same way as the chromatic fourths—by putting the big step in the location of the small diatonic one, and the small steps in place of the big diatonic ones” (198). Thus no intermediate chromatic is required for the passage from diatonic to enharmonic. Berger’s understanding, contradicted in the passage just quoted and not supported elsewhere in the treatise, leads to a system of considerably greater complexity and admits many variant species, variants which are not alluded to in L’Antica musica save in one ambiguous passage which I discuss below. I also find that Berger’s rules for dividing and subdividing the diatonic 5ths, explained at the bottom of p. 11, fail to produce the required chromatic and enharmonic species. Remapping the tones and semitones of the diatonic species into intervals characteristic of the chromatic and enharmonic genera, using the abstract patterns that correspond most closely to the diatonic originals, is a more parsimonious recipe than Berger’s obscure process of subdivision.
In her introduction to the translation of L’Antica musica, Maniates points out that Vicentino appears to show his awareness of Glarean’s treatise, without naming its author, in his negative appraisal of “some people” who would have us believe there are more than eight modes (xxvi; see also 139n8).
Using Berger’s amended fourth 5th (see note 31 above) to construct the seventh 8ve, as shown in the bottom row of the table, would result in a rotation of the same scale as the first six 8ve species. We now see one advantage of Berger’s amendment: when combined with a first 4th, his fourth 5th produces an 8ve whose minor-3rd steps are separated by a 4th/5th, like the other accepted combinations of 4ths and 5ths. Still, one rotation of the scale (aabaabaa, the only mirror-symmetrical rotation) would remain missing, and Vicentino does not ever give reason to believe that all 8ve species in a given genus should be modes of the same scale.
There are other unexpected changes to be found in the first 5th, which appears as the upper portion of the first and fifth 8ves. Here too, as in the fourth 8ve, Vicentino has interpolated a Ġ♭ between G and G♭ (transposed to a Ḋ♭ between D and D♭ in the fifth 8ve). All three interpolated notes, marked with asterisks in Figure 11, occur after a leap up to a flatted note, where Vicentino would otherwise have continued directly to the natural note. I believe Vicentino has subdivided these steps to remove any potential ambiguity with the minor semitone of the chromatic genus: the step of two fifth-tones is indeed properly enharmonic (for example Ġ to A♭, a major diesis), but when transposed to begin on a flat (for example G♭ to G♮) it resembles a chromatic step: the minor semitone. By the addition of these interpolated notes Vicentino has corrected all steps of his enharmonic 8ve species whose notation could be construed as chromatic—except one, D♭–D♮, in the first 4th at its native pitch level in the first 8ve (though he does include the interpolated Ḋ♭ in the First and Second Enharmonic Modes, discussed below). I do not believe, as Berger does, that all major enharmonic dieses are subject to an optional subdivision into minor dieses—only those whose notation allows them to be confused with chromatic steps of a minor semitone. Supporting this reading are passages like the following, discussing enharmonic division: “It is possible to make a major diesis at the beginning and ending of a whole tone; this step, however, is also a minor semitone. In order to distinguish the enharmonic from the chromatic, it is necessary always to put a minor diesis at the start and at the finish” (54).
Finally as mentioned earlier in the discussion of the enharmonic 5ths, Vicentino has taken advantage of the possibility of rewriting the first 5th—still following the “four-fold rule”—so that the enharmonically subdivided whole tones G–A and D–E feature a flat rather than a sharp (first and fifth 8ves).
For reasons of space I shall not elaborate on Vicentino’s solmization system in the present article; it is set out in L’Antica musica in Book 1 on Music Practice, Chapters 5 and 11 (40–43 and 53–54). Daniel Donnelly assisted with the assignation of solmization syllables.
The performance here is by tenor Nils Brown, retuned in the studio as discussed below in note 51.
Melodic 4ths and 5ths are apparently judged neutral; as they do not specifically indicate the presence of some other genus, they may be used in pure chromatic and enharmonic compositions without causing the music to leave its genus.
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial assistant
Number of visits:
50955