The Concept of Mutability in Russian Theory
Ellen Bakulina
KEYWORDS: Mutability, peremennost’, tonality, tonal pairing, Russian music theory, Iavorskiĭ, Mazel, Berkov, Sposobin, Kholopov, Miasoedov
ABSTRACT: In the last several decades, some important studies, such as those by Christopher Lewis, Harald Krebs, William Kinderman, and William Rothstein, have explored alternatives to monotonality in tonal music. In this paper, I discuss the concept of peremennost’ (mutability), which addresses the same problem from a Russian perspective. Mutability is generally defined as a fluctuation between two diatonically related tonal centers, usually a third apart. However, this somewhat narrow definition does not capture the notion in all its richness; the concept of mutability evolved significantly over the course of the last century. I explore this concept in the writings of six twentieth-century Russian theorists: Boleslav Iavorskiĭ, Lev Mazel, Viktor Berkov, Igor Sposobin, Iuriĭ Kholopov, and Andrei Miasoedov.
Copyright © 2014 Society for Music Theory
Example 1. Example of a mutable folk song (taken from Kholopov 1988, Ex. 114a)
(click to enlarge and listen)
[1] Mutability, or peremennost’, generally defined as a fluctuation between two or more diatonically related tonal centers, has been a central concern in Russian music theory that deals with folk and church music, as well as folk-inspired Russian classical music. A typical example of what is often understood to be mutability is given in Example 1 (a Russian folk song), in which the melody implies a motion from C major to A minor. Though the concept of mutability is usually tied to a specific body of repertoire, its conceptualization brings to the fore some crucial features of Russian theoretical thought in the twentieth century, such as a growing concern with tonal centricity and a focus on diatonic church modes.
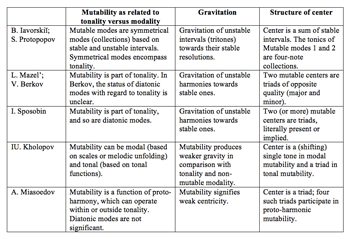
Example 2. Summary of the concept of mutability in the writings of Iavorskiĭ, Protopopov, Mazel, Berkov, Sposobin, Kholopov, and Miasoedov
(click to enlarge)
[2] In this paper, I explore the concept of mutability in the writings of six twentieth-century Russian theorists, all of whom except one (Mazel) apply it to folk and folk-like music: Boleslav Iavorskiĭ, Lev (Leo) Mazel, Viktor Berkov, Igor Sposobin, Iuriĭ Kholopov, and Andrei Miasoedov.(1) I show that the notion of mutability has traversed a path from a very specific idea involving concrete pitch relationships to a considerably more abstract idea involving a weakening of tonal center. In my discussion, I concentrate on three major theoretical issues: modality and tonality, gravitation, and centricity. All of these aspects are summarized in Example 2, which the reader may consult as needed.(2)
[3] In his recent dissertation on Glinka’s A Life for the Tsar, Daniil Zavlunov (2010) asserts that the theorists who wrote about mutability after Boleslav Iavorskiĭ, the pioneer of the concept, distorted and simplified Iavorskiĭ’s ideas.(3) The Iavorskiĭ and post-Iavorskiĭ writings are indeed quite different; but, rather than speaking of a distortion, I wish to speak of a changing theoretical context and paradigm shifts. I claim that mutability as a concept underwent two such paradigm shifts: a functionality shift, from a tritone-based to a key-based understanding; and later a centricity shift, from a notion of specific key relationships to a more abstract notion of centricity versus decentralization.(4)
Example 3. BoleslavIavorskiĭ’s (1908) symmetrical systems
(click to enlarge)
[4] The writer who first introduced the notion of mutable mode was Boleslav Iavorskiĭ, a theorist, composer, and pedagogue. In his treatise Stroenie muzykal’noĭ rechi (The structure of musical speech) (1908), Iavorskiĭ presents his theoretical system known as teoriia ladovogo ritma (the theory of modal rhythm), and this was later developed by his student and follower Sergei Protopopov (1930).(5) The Iavorskiĭ/Protopopov system rests on the concept of gravitation of unstable tones to stable ones, related by a semitone. On this principle, two basic musical structures are built: the single symmetrical system (SSS) and the double symmetrical system (DSS), both of which are presented in Example 3. A single symmetrical system is a tritone that resolves inwards to a major third or outwards to a minor sixth. A double symmetrical system, in its complete form, is a perfect fifth that resolves inwards through a doubly diminished fifth to a minor third. The principle of centricity here operates through the gravitation of unstable tones of the tritone (see the black note heads in the examples) to stable ones of the resolution (white note heads).(6)
Example 4. Iavorskiĭ’s symmetrical systems and mutable modes
(click to enlarge)
[5] On this basis, Iavorskiĭ builds his simple symmetrical modes, all of which represent combinations of single and double symmetrical systems. Example 4 presents two mutable modes, the first and second, both of which belong to the category of simple symmetrical modes. Each mutable mode contains three symmetrical systems, where the three stable intervals—the thirds—together form a tonic. In the first mode, the tonic is a four-note combination (which Protopopov explicitly calls a seventh chord), a major third surrounded by two minor thirds. In the second mutable mode, the tonic is a minor third surrounded by two major thirds.(7)
[6] It is crucial to note that Iavorskiĭ and Protopopov never mention triadic implications of melodic notes in these modes. Instead, they concentrate on the functions and behavior of single tones. The defining characteristic of the mutable mode is the changeable nature of tone function depending on its registral position. In mutable mode 1, for instance, the tones G and A occur twice. The lower G is unstable and it gravitates upwards toward the stable A. The upper A is unstable and it gravitates downwards toward G. This means that, at least in theory, the Iavorskiĭ/Protopopov system rejects octave equivalence of function in folk music.(8) Though pitch classes may be the same in any octave, the function of every pitch class (its stability or instability) differs depending on the register.
Example 5a. Example of Iavorskiĭ’s mutable mode 2 (from Protopopov 1930, 2:51). Russian folk song “Solntse zakatalos’,” from the song collection of M. Balakirev
(click to enlarge and listen)
Example 5b. Formation of the mode in “Solntse zakatalos’” according to Protopopov
(click to enlarge and listen)
[7] Example 5, from Protopopov 1930 (2:51), illustrates one of the mutable modes (mode 2). Protopopov observes that four tones are melodically emphasized in the folk song (Example 5a):
[8] Iavorskiĭ’s ideas were quickly adopted by other theorists, some of whom began to use the term “mutable mode” in a different sense and in relation to other kinds of repertoire. In 1937, the term was adopted by Lev Mazel, who applied it in his analysis of Chopin’s piano music (see Zavlunov 2014). In the section on the modulatory plan of Chopin’s Fantasia in F minor, Mazel writes: “The main mode-tonality [i.e., key] of the Fantasia may be naturally considered not merely F minor or
Of course, it is necessary to take into account the fact that there is no mutable mode in the strict sense: there are no phrases and progressions that we would need to consider being in such a mode by assigning stable and unstable properties alternately to certain tones. We are only faced with a certain oscillation between F minor and
A♭ major. . . . The term “mutable mode” is used here, therefore, in a broader sense than it is used by the author of the theory of modal rhythm [i.e., Iavorskiĭ]. (Mazel’ [1971] 2008, 38)
[9] The wording of this passage is remarkably similar to modern English-language discussions of tonal duality in Romantic music and specifically the concept of tonal pairing, which originated in the work of Robert Bailey (1985).(10) Therefore, a comparison between Iavorskiĭ’s and Mazel’s concepts of the mutable mode reveals a crucial change, a paradigm shift in the understanding of mutability, which I would like to call a functionality shift. This means that Mazel brings the notion of mutability into the realm of conventional tonal music and therefore tonal theory and tonal functions.(11) The functionality shift happens due to a difference in repertoire: while Iavorskiĭ’s mutable modes are intended for European folk and liturgical music, Mazel deals with the music of a nineteenth-century composer.
Example 6. Comparison of stable and unstable tones in Iavorskiĭ’s and Mazel’s mutable modes. Stable tones are shown as open note heads. The scheme is reconstructed from Iavorskiĭ’s, Protopopov’s, and Berkov’s writings
(click to enlarge and listen)
[10] Although Mazel specifies that by mutability he does not mean a changing function of specific tones, in fact such a changing function does exist in his mutable mode, though not in Iavorskiĭ’s sense. Example 6 presents my summary of the two views (here, Mazel’s column has been transposed from the four-flat system of Chopin’s Fantasia in F minor to the natural system). The example shows Iavorskiĭ’s four-note tonic of mutable mode 1 and the A–G pair (the black note heads), in which the stable/unstable relationship depends on register. Mazel partitions Iavorskiĭ’s single four-note tonic into two interlocked triads that alternate as tonal centers in the course of a composition. The tones A and G can each be stable and unstable in Mazel’s system as in Iavorskiĭ’s. But for Mazel this function depends on which tonic currently dominates in a musical passage, i.e., on the tonal plan of a work, and not on the note’s registral position.
Example 7. Berkov’s example of a mutable excerpt (Berkov 1948, 60–61). Mikhail Glinka, A Life for the Tsar, act 1, chorus
(click to enlarge and listen)
[11] Approximately a decade after Mazel, Victor Berkov (1948) brings up the mutable mode in his book on Mikhail Glinka. As with Mazel, Berkov’s subject is a nineteenth-century composer. Therefore, Berkov also explains mutability as a kind of tonality, more specifically a tonality in which the classical modulatory motion from a major key to its dominant is replaced with a third-related motion to a minor key (most often relative). Example 7 presents a mutable mode from Berkov’s book. Unlike Iavorskiĭ and Protopopov, and like Mazel, Berkov discusses the mutable mode as a fluctuation between two different tonics. Here is an excerpt from his discussion:
At the beginning, this song is given as monophonic, later—with orchestral accompaniment. This way, later in the song, we can compare our own unintentional inward harmonization of the monophony with Glinka’s harmonization. The basis of this song’s harmony is the mutability between C major and A minor, the fluctuation between the two relative tonics. The song ends with the dominant of C major. (Berkov 1948, 61)
[12] Later, he says about another similar example: “After the appearance of the relative minor (in the form of a one-measure-long tonicization), a concluding modulation to the key of the opening major’s dominant follows” (1948, 61). These excerpts clearly show that (1) a single tone, even in a monophonic passage, always presumes potential harmonization, and therefore a mutable center (or tonic) is a harmony, usually a triad, and not a tone; (2) the mutability of third-related centers participates in the functional dynamics (T, S, and D) and modulatory motions of tonal music; and (3) third-related and fifth-related tonal centers are categorically different kinds of relationships. The concept of mode so important to Iavorskiĭ is still important for Berkov, but for Berkov, only two modes exist: major and minor.(12) In sum, Berkov’s view of mutability is conceptually akin to Mazel’s, but it is somewhat more specific with regard to chordal implication and the contrast between third- and fifth-relations.
Example 8. Types of mutability in Sposobin (1951, 142–49)
(click to enlarge)
Example 9. Instances of mutability from Sposobin (1951). Russian folk song from Rimski-Korsakov’s collection
(click to enlarge and listen)
Example 10. Iuriĭ Kholopov’s modality-type and tonality-type modes: a comparative overview (Kholopov 1988, Chapter 9)
(click to enlarge)
Example 11. Classification of modal and tonal mutability in Kholopov: comparative table
(click to enlarge)
Example 12a. Kholopov (1988): an instance of modality (weak tonal gravity), which borders on relative mutability due to the almost equal status of the two tonics, expressed in Riemannian functional analysis in both keys
(click to enlarge and listen)
Example 12b. Sergei Rachmaninov, All-Night Vigil, movement 12, measures 123–26
(click to enlarge and listen)
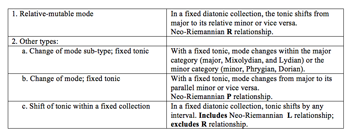
[13] Another theorist who adopted the term mutable mode was Igor Sposobin, in his textbook Elementarnaia teoriia muzyki (Elementary theory of music) (1994).(13) In a general sense, Sposobin’s idea is very close to Mazel’s and Berkov’s: all these writers share a reliance on tonality and tonal functions and the view of mutability as a change of tonic (usually multiple times) in the course of a piece.(14) This is not the same as the Western concept of modulation; changes in a mutable mode most often occur back and forth between two diatonically related tonal centers, while modulation embraces many more possibilities.(15) For both Berkov and Sposobin, the center of a mode, including a mutable mode, is a major or minor triad, even if harmonies and tonal motion are only implied by a monophonic melody (as opposed to a total absence of triadic implication in Iavorskiĭ).
[14] Sposobin’s major innovation as regards mutability is his classification of it into two main types (see Example 8): (1) relative mutability, or relative-mutable mode (parallel’no-peremenny lad), the type that Berkov deals with almost exclusively, and (2) mutability “of other types.” These other types include not only a shift of tonal center in a fixed diatonic collection, but also a change of collection with a fixed tonic. The latter situation may involve a change of mode (from major to minor or the reverse) or a change of mode subtype (i.e., the diatonic modes), which he considers special types of major and minor. For example, Phrygian is minor with a lowered .(16) Just such a change of mode, from A natural minor to A Phrygian minor, occurs in Example 9. Finally, the last row in the table in Example 8 is similar to the relative type (the pairing of relative keys), except that the tonic shifts by an interval other than a third. Thus, notwithstanding the conceptual proximity between Berkov’s and Sposobin’s mutability, Sposobin has a more refined classification and a more clearly expressed view of mode.
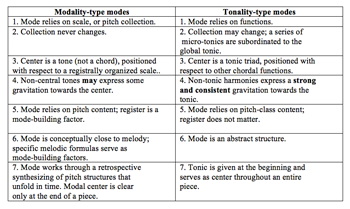
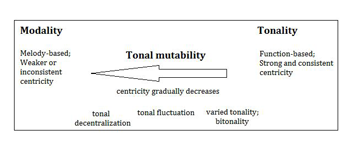
[15] Mutability becomes a more abstract concept, which references the weakening of centricity in general rather than any specific tonal relations, in the work Sposobin’s student Iuriĭ Kholopov. Kholopov’s textbook Garmoniia: teoreticheskii kurs (Harmony: A theoretical course) (1988), intended as a theoretical counterpart to his two-volume Garmoniia: Prakticheskiĭ kurs (Harmony: A practical course) (2003), is our next focus.(17) It is once again pertinent to begin with Kholopov’s views of mode. Kholopov classified mode into two categories: lady modal’nogo i tonal’nogotipa, which I translate as modality-type and tonality-type modes (see Example 10, my summary of Kholopov’s Chapter 9).(18) Modality relies on specific melodic formulae and pitch collections, organized in register, with a single tone serving as a center, toward which there may or may not be gravitation. Tonality relies on a system of gravitation, with a triad serving as center, toward which other harmonies show consistent gravitation. The strength of gravitational pull, together with the melody-versus-functionality aspect, is the kernel of the distinction.(19)
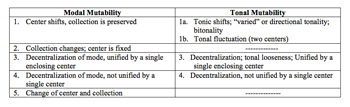
[16] In accordance with the distinction between modality and tonality, Kholopov classifies mutability into the same types: modal and tonal, which I summarize in Example 11. Each type presumes multiple shifts or ambiguity of center. According to Kholopov, “The main difference between these two types of mutability [modal and tonal] resides in that modal mutability is linked to pitch collections and tone-centers [zvukami-ustoiami], whereas tonal mutability is linked to tonal gravitations and the interactions between tonic chords” (1988, 176). A further classification of mutability references the degree of decentralization, i.e., the degree to which the tonic is weakened. The last three rows of Example 11 feature decentralized tonics (the fifth row is an extreme case).(20) Examples 12a and 12b present two instances of tonal mutability (the relative type), one from Kholopov 1988 and the other my own analysis of a passage from Sergei Rachmaninov’s Vsenoschnoe bdenie (All-Night Vigil). In both instances, the structural equality of relative tonics is expressed in functional or Roman-numeral analysis in both keys simultaneously.(21)
[17] Although both types of mutability, modal and tonal, have different degrees of decentralization (see Example 10), Kholopov ultimately conceives of tonal mutability as a conceptual mediating phase between tonality and modality. He writes: “The weaker the force of tonal centricity, the stronger the mutability of modes [ladovaia peremennost’] expresses itself in different ways” (1988, 173).(22) In this sense, the further down we move within the left column of Example 11, the closer we approach modality-type modes, since these modes by definition exhibit attenuation of center. Accordingly, Example 13 rearranges Kholopov’s classification of mutability to highlight the continuum between modality and tonality. (If we were to include modal mutability in this scheme, it would be situated on the far left side of the box.) Kholopov's mutability therefore references the principle of decentralization in general. This principle marks another paradigm shift in the history of the concept: the centricity shift. Unlike earlier theorists, for whom mutability always involves specific kinds of key relationships, for Kholopov it is a more abstract idea—the idea of a weak tonal or modal center. Significantly, Kholopov’s concept is the broadest of all in terms of repertoire: his examples include both Russian and Western music, both folk- and art-music examples, the latest of which belong to the twentieth century (Rimsky-Korsakov and Reger; see Kholopov 1988, 175–76).
Example 13. Kholopov’s tonal mutability as a measure of relative centricity (click to enlarge) | Example 14. Andrei Miasoedov’s (1998) proto-harmony as (a) a pitch collection, (b–e) the collection doubled in consonances and (f) a chord progression (click to enlarge) |
[18] The notion of a shifting or ambiguous tonal center is also important in the work of Andrei Miasoedov, professor of the Moscow Conservatory who recently retired (in 2009). His treatise O garmonii russkoĭ muzyki (On the harmony of Russian music) (1998) explores what it is that makes Russian music harmonically unique. In this work, he introduces the notion of pra-garmoniia (proto-harmony), which, in his view, is the structural foundation of Russian music. Proto-harmony, presented in Example 14, is built on four diatonically related harmonies whose roots can be ordered by perfect fifths. The example shows a gradual historical evolution of proto-harmony from four fifth-related tones, which in ancient Russian folk music were most probably doubled in octaves and fifths (according to Miasoedov), to triads.
[19] For Miasoedov, mutability occurs when the chords of proto-harmony are experienced as tonal centers that compete for predominance in the course of a piece. The result is what he calls equality of status between the chords of the proto-harmony (19). Miasoedov writes:
In the harmonic progression, or, more precisely, among the four given chords, any one of them may take the role of “tonic.” For Russian harmony, this is fundamentally important. . . . It must be said that the perception of these triads as “tonics” is sufficiently relative. In all the schemes given above, it is very easy to undermine their stability. This is natural, because the notion of stability and instability are very relative in two-, three-, or four-chord diatonic systems, on which the triadic combinations given here are based. (Miasoedov 1998, 19)
Proto-harmony, almost always in connection with “mutability of modes,” i.e., a shifting center, appears in his discussion of music by Bortniansky, Glinka, Dargomyzhsky, and other Russian composers.(23)
[20] Even though proto-harmony is Miasoedov’s own innovation, the notion of a shifting or ambiguous tonal center (which might comprise more than two centers, as in Kholopov’s model) brings Miasoedov’s mutability into conceptual proximity with Kholopov’s tonal mutability. Both notions refer to tonality with a weakened tonic, or to multiple tonics that coexist at the same level of structure in the same piece.
[21] As a summary of the notion of mutability explored here, I refer the reader once again to the table in Example 2. The table shows that the concept of mutability has moved gradually from a tritone-based definition and concrete pitch relationships, through a contextualization in functional tonality, through interaction between major/minor keys and diatonic modes, to a general notion of weakened gravity. It needs to be stressed that even though contemporary English-language writers often limit their understanding of mutability to a single type—the relative type—the idea of mutability cannot be expressed in a single definition.(24) Any such definition would oversimplify the array of meanings that various theorists have attached to it, as well as preclude one from seeing many implicit connections with past and present Western theories of tonality.
[22] By offering a chronologically arranged table of mutability’s conceptual development, I do not mean to argue that the authors developed the idea in a conscious effort to produce a unified theory of mutability, or that the historical trajectory shown here was intentional. Rather, mutability is a sort of recurrent theme that comes to light at points where tonal unity is questioned in some way, usually though not always in connection with folk music. An analysis of this recurrent theme, however, reveals the implicit trajectory of the concept and its uses through the course of the twentieth century.
Ellen Bakulina
The Graduate Center, City University of New York
New York, NY 10016
obakulina@gc.cuny.edu
Works Cited
Bailey, Robert. 1985. “An Analytical Study of the Sketches and Drafts.” In Wagner, Richard, Prelude and Transfiguration from “Tristan and Isolde”, ed. Robert Bailey, 113–46. New York: W.W. Norton & Co.
BaileyShea, Matt. 2007. “The Hexatonic and the Double Tonic: Wolf’s ‘Christmas Rose’.” Journal of Music Theory 51, no. 2: 187–210.
Bazayev, Inessa. 2014. “The Expansion of the Concept of Mode in Russian Music Theory.” Music Theory Online 20, no. 3.
Berkov, Viktor. 1948. Garmoniia Glinki [Glinka’s harmony]. Moscow-Leningrad: Muzgiz.
Carpenter, Ellon DeGrief. 1988. “The Theory of Music in Russia and the Soviet Union, ca. 1650–1950.” PhD diss., University of Pennsylvania.
—————. 1995. “Russian Theorists on Modality in Shostakovich’s Music.” In Shostakovich Studies, ed. David Fanning, 76–112. Cambridge: Cambridge University Press.
Dahlhaus, Carl. 1990. Studies on the Origin of Harmonic Tonality. Translated by Robert Gjerdingen. Princeton: Princeton University Press.
Dubovsky, Iosif, et al. 1987. Uchebnik garmonii [A Textbook of Harmony], commonly known as Brigadnyi uchebnik [The team textbook]. 4th edition. Moscow: Muzyka.
Ewell, Philip. 2012. “Rethinking Octatonicism: Views from Stravinsky’s Homeland.” Music Theory Online 18, no. 4.
Fétis, François-Joseph. [1844] 2008. Complete Treatise on the Theory and Practice of Harmony. Translated by Peter M. Landey. Hillsdale, NY: Pendragon Press.
Johnston, Blair. 2009. Harmony and Climax in Late Works of Sergei Rachmaninoff. PhD diss., University of Michigan.
Hyer, Brian. 2002. “Tonality.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 726–77. Cambridge: Cambridge University Press.
Iavorskiĭ, Boleslav. 1908. Stroenie muzykal’noĭ rechi [The structure of musical speech]. Moscow.
Kholopov, Iuriĭ. 1988. Garmoniia: Teoreticheskiĭ kurs [Harmony: A theoretical course]. Moscow: Kompozitor.
—————. 2003. Garmoniia: Prakticheskiĭ kurs. [Harmony: a practical course]. 2nd edition. Moscow: Kompozitor.
—————. 2008a. “Ladoperemennost’ kak svoistvo modal’nykh ladov.” [Modal mutability as a characteristic of modality-type modes]. In Idei IU.N. Kholopova v XXI veke: K 75-letiiu so dnia rozhdeniia [The ideas of IU.N. Kholopov in the 21st century: in celebration of his 75th birthday], ed. T.S. Kiuregian, 101–4. Moskva: Muzizdat.
—————. 2008b. “K probleme lada v russkom teoreticheskom muzykoznanii.” [Towards the question of mode in Russian music-theoretical thought.] In Idei IU.N. Kholopova v XXI veke: K 75-letiiu so dnia rozhdeniia [The ideas of IU.N. Kholopov in the 21st century: in celebration of his 75th birthday], ed. T.S. Kiuregian, 79–100. Moskva: Muzizdat.
Mazel’, Lev. [1971] 2008. Issledovaniia o Chopine [Chopin Studies]. Moscow: Kompozitor.
McQuere, Gordon. 1978. “‘The Elements of the Structure of Musical Speech’ by S.V. Protopopov: A Translation and Commentary.” PhD diss., The University of Iowa.
—————. 1983. “The Theories of Boleslav Yavorsky.” In Russian Theoretical Thought in Music, ed. Gordon McQuere, 109–64. Ann Arbor, Mich.: UMI Research Press.
Miasoedov, Andrei. 1998. O garmonii russkoĭ muzyki (korni natsionalnoĭ spetsifiki) [On the harmony of Russian music (the origins of national characteristics)]. Moscow: Prest.
Powers, Harold. 2001. “Mode.” The New Grove Dictionary of Music and Musicians, ed. Stanley Sadie, 2nd edition, vol. 16, 775–823. London: McMillan Publishers.
Protopopov, Sergei. 1930. Elementy stroeniia muzykal’noĭ rechi [The elements of the structure of musical speech], 2 vols. Moscow: Gosudarstvennoe izdatel’stvo. Muzykal’nyĭ Sektor.
Sposobin, Igor. [1951] 1994. Elementarnaia teoriia muzyki [Elementary music theory]. Moscow: Kifara.
Straus, Joseph. 1982. “Stravinsky’s ‘Tonal Axis’.” Journal of Music Theory 26, no. 2: 261–90.
Taruskin, Richard. 1997. Defining Russia Musically: Historical and Hermeneutical Essays. Princeton, NJ: Princeton University Press.
Van Der Merwe, Peter. 1989. Origins of the Popular Style. New York: Oxford University Press.
Zavlunov, Daniil Yakov. 2010. “M.I. Glinka’s A Life for the Tsar (1836): A Historical and Analytic-theoretical Study.” PhD diss., Princeton University.
—————. 2014. “The ‘Tselostnyĭ Analiz’ (Holistic Analysis) of Zuckerman and Mazel.” Music Theory Online 20, no. 3.
Discography
Discography
Glinka, Mikhail. 1836. A Life for the Tsar (Ivan Susanin), Act 1, Chorus of Oarsmen. Conducted by Alexander Melik-Pashaev. 1947 (1998). Preiser Records 90365, 2 compact disks.
Mussorgsky, Modest. 1868 and 1873. Boris Godunov, Act 1, Scene 1, Chorus of Hermits. Conducted by Alexandr Lazarev. 1987 (2005). Long Branch, NJ: Kultur D2852. DVD.
Rachmaninoff, Sergei. 1915. All-Night Vigil, movement 12. Conducted by Nikolai Kornev. 1994. Philips 442 344-2. 1 compact disc.
Footnotes
1. In English-language scholarship, mutability has been mentioned by Richard Taruskin (1997, 13, 29, and 133), Blair Johnston (2009, 165–88), and Daniil Zavlunov (2010, 423–67). Only Zavlunov has a more or less complete discussion of the topic; I compare my approach to his below. Gordon McQuere (1983, 117) mentions the variable (or mutable) modes in Iavorskiĭ’s theory.
Return to text
2. This table and those that follow are my summaries of explanations that, in the writings that I explore, mostly take several pages and sometimes up to an entire chapter.
Return to text
3. “As many of Iavorskiï’s ideas and formulations were absorbed into mainstream theory, they became distorted, either because individual theorists chose to disregard the original meaning and context of the constructs, or they chose to reconfigure the constructs to suit their needs” (Zavlunov 2010, 429). Zavlunov also offers a brief overview of the concept of mutability.
Return to text
4. A note on terminology: Peremennost’, a noun, originally appeared in the adjectival form peremennyi (changeable or mutable) in the writings of Iavorskiĭ; the term was made into a noun only by later theorists. The term peremennyi has been translated into English as variable (in McQuere 1978 and 1983) and mutable. The expression “mutable center,” which I am introducing, is similar to tonic in Western tonal theory.
Return to text
5. For sources of Iavorskiĭ’s ideas and a bibliography, see Zavlunov 2010, 423. A good summary of Iavorskiĭ’s theory is also found in Ewell 2012.
Return to text
6. Iavorskiĭ, having been introduced to the writings of François-Joseph Fétis (2008) in the 1890s, was greatly influenced by the Belgian scholar’s notion of the centrality of the tritone and its resolution (Carpenter 1988, ch. 17).
Return to text
7. The Iavorskiĭ/Protopopov four-note mutable tonic is related to a few recent theoretical notions. The first is Robert Bailey’s (1985) double-tonic complex, which also includes the notes of two third-related triads, but is more concretized in a given piece’s voicing and texture. The second is Joseph Straus’s (1982) tonal axis, which is structurally equivalent and conceptually extremely close to Iavorskiĭ’s tonic. Finally, Peter van der Merwe (1989, 177–83) offers a similar concept called a “ladder of thirds,” which, just like Iavorskiĭ’s four-note tonic, is understood melodically (a “modal frame”), rather than vertically.
Return to text
8. Regarding the significance of register, Protopopov writes: “If the melody exceeds an octave, the pitch collection of a folk song cannot be determined based on the pitches that occur within one octave” (1930, 2:3). This statement, however, refers to actual pitches, rather than to their modal functions.
Return to text
9. An analysis more consistent with the abstract modal structure, with its differentiation of function based on register, would posit that the tonic is F4,
Return to text
10. In particular, Mazel’s definition corresponds nearly word-for-word with a definition of tonal pairing by Matthew BaileyShea (2007, 195), who explains it as a “piece [that] consistently vacillates between two keys, usually third related.”
Return to text
11. Mazel does not pay any particular attention to the notion of tonal functions, but he uses functional terms (tonic, subdominant, and dominant) in their conventional sense. Although Iavorskiĭ and Protopopov operate with these terms as well, their meaning in most symmetrical modes, including mutable modes, strongly differs from traditional tonal theory. For more on the meaning of subdominant and dominant in Iavorskiĭ, see McQuere 1983 (113–15).
Return to text
12. The term mode is somewhat problematic in the present context, because the Russian word lad (mode) is broader than any potential English-language equivalent. Ellon Carpenter (1995, 76–77) stresses the breadth of the notion of lad in Russian theory; see also Bazayev 2014 (in the present volume). For recent notions in English-language literature, similar in scope though somewhat different in meaning, see Powers on mode (2001, 776; part I.3 of the article on mode, especially paragraph 6) and Hyer’s fourth meaning of tonality, as a generic term encompassing the church modes as well as major-minor tonality (2002, 727–28). “Tonality” in this usage can often be translated in Russian as “ladovaia struktura,” literally “modal structure.”
Return to text
13. Sposobin also discussed mutability in other works, such as the textbook he co-authored with three other writers (Dubovsky et al. 1987). Sposobin was the first to use the word peremennost’ (mutability) as a noun.
Return to text
14. Berkov does not actually use the word function, but he operates with functional terms, such as tonic and dominant, in a conventional tonal way.
Return to text
15. Even when the two mutable centers or tonics relate to each other as I and V, a conventional modulatory plan in tonal works, Sposobin emphasizes that the V-functioning side is a Mixolydian mode, rather than a key of V with a raised leading tone ( in the original key). This idea has to do with the repertoire, for the folk songs Sposobin considers almost never feature accidentals “tonicizing” a new key. In this separation of the mutable mode from modulation with changing pitch collections, Sposobin is extremely close to Berkov.
Return to text
16. Sposobin’s whole discussion of tonal and harmonic concepts is firmly rooted in the major/minor distinction, which he calls “color” (okraska), and which is also the basis of his understanding of tonality (Sposobin [1951] 1994, 89). In contrast, Berkov mentions diatonic modes but never describes them as major or minor.
Return to text
17. Other sources that expound Kholopov’s views on mutability include his articles from 1986 and 1996, which were later reprinted in Kholopov 2008a and 2008b. There, his fundamental idea of mutability as a characteristic of modality (meaning weakness of center) is confirmed, though the classification is slightly different.
Return to text
18. My translation of his terms here is necessarily inexact. The exact equivalent of his “lad modal’nogo tipa” would be “mode of modal type,” which is tautological. Therefore, instead of “mode of modal and tonal types” I have chosen “modality-type and tonality-type modes,” a translation that avoids tautology, at least in part.
Return to text
19. Kholopov explicitly relies on Hugo Riemann’s theory of harmonic functions, which was incorporated into Russian music theory in the 1920s and 1930s (Carpenter 1988, chs. 21 and 29). Moreover, Kholopov’s view of tonality and modality exhibits a remarkable affinity with a similar discussion in another Riemann-influenced theorist, Carl Dahlhaus, who states that modes (in the Renaissance) are constructs based on relationships of tones, whereas keys rely on functions, and therefore chords (Dahlhaus 1990, 154).
Return to text
20. Sposobin’s typology of mutability, discussed above, occupies the two upper lines, without distinction between the left and right columns; as we have seen, he does not differentiate between tonality and modality.
Return to text
21. It is significant that both examples bear a relationship to church music (Mussorgsky’s passage, though taken from an opera, is a stylization of church chant). Weakness of tonal center is very typical for Russian liturgical music.
Return to text
22. A similar idea of mutability as a general principle of attenuated tonal center, and therefore as being in conceptual proximity to modality-type modes, is found in a different work of Kholopov’s (2008a, 101): “Mutability reflects the most important feature of modality-type mode. The modal center [ustoi] lacks the strength of the tonal center, i.e. the tonic.”
Return to text
23. For more on the connection between mutability and proto-harmony, see Miasoedov 1998, 50–52.
Return to text
24. For example, Taruskin (1997, 13 and 29) mentions the “mutable mode,” referring to the relative type, as a notion used by ethnomusicologists. Later, however (pages 133 and 138), he also mentions cases where the two tonics are related by a whole tone. Johnston (2009, ch. 5) concentrates mostly on relative-mutable situations, but includes one exception, where the two centers are E minor and C major (in Rachmaninoff’s “Three Russian Songs,” op. 41).
Return to text
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Senior Editorial Assistant
Number of visits:
24667