Sergei Taneev’s Vertical-Shifting Counterpoint: An Introduction

I. Inverse and Direct Shifts

[1] Sergei Taneev’s Podvizhnoi kontrapunkt strogogo pis’ma (Movable counterpoint in the strict style) (1909) initiated the Russian study of counterpoint as an independent discipline.⁽¹⁾ The treatise deals with two phenomena: vertical-shifting (vertikal’no-podvizhnoi) and horizontal-shifting (gorizontal’no-podvizhnoi) counterpoint. Both concern the relation of an original combination (pervonachal’noe soedinenie) of two of more voices to a derivative combination (proizvodnoe soedinenie) created by adjusting the voices in pitch or time. In vertical-shifting counterpoint, which includes invertible counterpoint, the voices are diatonically transposed higher or lower. In horizontal-shifting counterpoint, the voices enter earlier or later relative to one another.

[2] Example 1 illustrates both kinds of movable counterpoint.⁽²⁾ The original combination of voices is shown on the top staff, and three derivatives appear beneath it. The first and second derivatives involve vertical shifting, and the third involves horizontal shifting. (The example’s annotations are explained below in paragraphs [5]–[6].) The first derivative demonstrates invertible counterpoint at the tenth: the lower voice has shifted up a tenth, so that it crosses above the higher voice. In the second derivative, the voices do not cross; instead, the distance between them increases. With the third derivative the voices have been adjusted temporally, so that the upper voice enters half a measure later. All derivatives observe the rules of strict-style counterpoint. Weak-beat dissonances arise through passing motions (neighbor notes and cambiatas are also permitted); strong-beat suspensions are prepared and resolved down by step.

[3] One of Taneev’s insights is that the fundamental element of invertible counterpoint is not the registral swapping of the voices, but rather the vertical shift involved. He distinguishes the inverse shift (perestanovka protivopolozhnaia) from the direct shift (perestanovka priamaia). With the inverse shift, the voices cross to create invertible counterpoint, as with the first derivative of Example 1. With the direct shift, the voices do not cross, as with the example’s second derivative.⁽³⁾ Taneev is the first theorist to identify direct shifting as distinct from invertible counterpoint.⁽⁴⁾

[4] A second insight of Taneev’s is that both inverse and direct shifting operate according to the same principles. Taneev developed a mathematical system that efficiently generates the rules for vertical shifting at any interval. (Horizontal shifting is not approached in the same systematic way and will not be discussed in the remainder of this paper.⁽⁵⁾) The present essay introduces the system, explaining the process by which such rules can be generated, and extends it analytically. An introduction to Taneev’s method is necessary because the existing English translation contains copious errors.⁽⁶⁾ This article serves in part as a guide to help interested English-speaking readers navigate Taneev’s treatise.

II. The Rules of Vertical-Shifting Counterpoint

[5] Taneev’s system is grounded in mathematics. In prose Taneev retains the traditional interval names, but he assigns them numerical values one less than the names imply. A second is interval 1, a third interval 2, and so on (Example 2).⁽⁷⁾ This allows for simple addition and subtraction. The equation 2 + 2 = 4 recognizes that two thirds form a fifth. Taneev conventionally refers to the upper and lower voices of an original combination as voices I and II, respectively. Negative interval values, as shown on the left side of Example 2, indicate that voice I has descended below voice II.

[6] To form a derivative, each voice either stays on pitch or shifts higher or lower. The symbol v measures the interval of the shift, using positive values for outward shifts (voice I up, voice II down) and negative values for inward shifts (voice I down, voice II up), as schematized in Example 3. The vertical index, symbolized Jv, is the sum of the two v values.⁽⁸⁾ Adding Jv to each vertical interval of the original combination yields the size of the corresponding derivative interval. Example 4 illustrates this with Jv = −9, or invertible counterpoint at the tenth. There are multiple combinations of v values that sum to −9. All produce the same resultant vertical intervals; only the pitch level differs.⁽⁹⁾

[7] To determine the rules for vertical-shifting counterpoint at a given Jv, three factors must be taken into account: suspensions, the interval of the shift, and variable intervals.

Suspensions in Simple Counterpoint

[8] Dissonance treatment is tightly regulated in the strict style. Strong-beat suspensions must be prepared and resolved down by step. Suspensions can appear in voice I or II, but there are two exceptions. First, a second may not resolve to a unison, although a ninth may resolve to an octave. Second, a seventh may not resolve in the lower voice to an octave. Both exceptions prevent the note of suspension from sounding simultaneously against the note of resolution (§§81–82).

[9] Taneev uses suspension symbols (znaky sviazki) to symbolize restrictions on dissonant intervals (Example 5).⁽¹⁰⁾ Symbols above and below interval numbers represent restrictions on voices I and II, respectively. The symbol “—” means that a suspension is permitted; the symbol “(—)” means that a suspension is forbidden. Negative intervals have the same suspension symbols as their positive equivalents, but with the voices swapped.

Interval of the Vertical Shift

[10] Dissonances must be treated properly in both original and derivative combinations. At a given shift, each original interval that becomes dissonant in the derivative must adopt the restrictions of the latter interval. If both original and derivative intervals are dissonant, the strongest restriction in each voice must be followed.

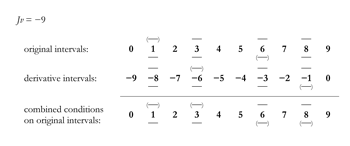
[11] To calculate the restrictions for a given Jv, Taneev constructs an interval table, aligning original with derivative intervals in columns. The conditions for each original interval are found by selecting the strongest restriction for each voice within each column. Example 6 illustrates this with Jv = −9. Each original interval must fulfill both its own conditions and those imposed on its corresponding derivative interval. These combined conditions, summarized in the table’s bottom row, indicate which suspensions can be used at Jv = −9. Example 7 is a musical setting employing all possible suspension types.⁽¹¹⁾ Each suspension in the original, labeled in the example, produces correct counterpoint in the derivative.⁽¹²⁾

Variable Intervals

[12] Taneev distinguishes fixed intervals (intervaly ustoichivye) from variable intervals (intervaly neustoichivye). Fixed intervals are either original consonances that yield derivative consonances or dissonances that yield dissonances. Variable intervals are consonances that yield dissonances or vice versa. Variable intervals reverse the dissonance-to-consonance trajectory of suspension resolutions, as shown in Example 8. In the example’s original combination, the two notes marked with X resolve dissonant suspensions. But at Jv = −12, the consonant resolutions become dissonant. Because the notes marked with X become dissonant in the derivative, they are treated like passing tones in the original: they continue down by step after resolving the suspensions. In general, when a variable interval resolves a dissonant suspension, the note of resolution must be treated as a passing tone, neighbor note, or cambiata, or else it may function as the free note to a new suspension (§167).⁽¹³⁾

[13] Taneev adds an X to the suspension symbol “—” for variable intervals, indicating that the note of resolution must be treated as a dissonance. All variable intervals require the X wherever “—” appears, except below interval 4 and above interval 5.⁽¹⁴⁾ A dotted line is added in place of a suspension symbol to track this exception. Example 9 presents the interval table for Jv = −11, or invertible counterpoint at the twelfth.⁽¹⁵⁾ The variable intervals are 5 and 6; an X is added to the suspension symbol for each. Example 10 demonstrates the use of intervals 5 and 6 as suspensions at Jv = −11. The notes of resolution are consistently treated as passing tones.

Multiple Derivatives

[14] In order to determine the restrictions on vertical-shifting counterpoint at a given Jv, the following three-step process is used:

1. Construct an interval table, aligning original with derivative intervals.
2. Identify the strongest restriction for each voice within each column.
3. For variable intervals, add an X to the symbol “—”, except where the dotted line appears.

[15] With Taneev’s system, the rules for any vertical shift, or combination of shifts, can be efficiently calculated. For counterpoint that produces multiple derivatives through multiple shifts, the rules can be determined by expanding the interval table to accommodate each additional Jv. Example 11 illustrates with the multiple index Jv = 3, −8. Only interval 4 is fixed; the remaining intervals are variable and the symbol X is required (except above interval 5).⁽¹⁶⁾ Example 12 uses these conditions in an original combination employing various suspension types. The example provides derivatives both at Jv = 3 (direct shift at the fourth) and at Jv = −8 (inverse shift at the ninth).

III. Taneev’s Counterpoint in Practice

[16] Taneev’s interest in counterpoint is evident in his compositions, although his turn-of-the-century fugal writing sounds nothing like the vocal polyphony examined in his treatise. Podvizhnoi kontrapunkt is not primarily concerned with analysis, but it offers occasional comments on music of the eighteenth and nineteenth centuries. Several features distinguish the tonal free style from the earlier strict style according to Taneev: abundant chromaticism (§236), unprepared dissonances (§274), and the privileging of harmonic considerations over contrapuntal rules (§498). The availability of accented passing tones and incomplete neighbor notes seemingly imperils the relevance of strict-style restrictions. Because of this, Taneev’s comments on tonal excerpts tend to merely identify the Jv used, without expounding on dissonance treatment. Yet tonal practice frequently encourages the resolution of dissonances down by step, allowing the suspension symbols to retain some potency.

[17] In what follows, I investigate passages from two of Taneev’s own compositions. In a fugue from the String Quintet No. 1, Taneev produces three vertical shifts from an original combination, maintaining proper downward resolution of dissonances. In an early string trio, an entire scherzo is flipped upside down, inviting a Taneevan investigation of reversible counterpoint.

String Quintet No. 1 in G major, op. 14 (1903), III, Variation 9

[18] The quintet’s Finale features a triple fugue. The first two subjects combine in vertical-shifting counterpoint and produce three derivatives, at Jv = −11, 4, and −12. The conditions on this triple index explain how Taneev deploys such a combination of shifts. Example 13 provides the interval table; Example 14 presents the score excerpts for the original and derivative combinations, accompanied by additional voices.

[19] Intervals of the original combination are labeled, using suspension symbols from the interval table. First, observe that interval 7 is a fixed consonance, yielding consonant intervals in all three derivatives. Its placement on the first downbeat ensures that each combination can begin from a point of stability.⁽¹⁷⁾ Second, the suspension symbols on intervals 2, 3, and 4 motivate the gradual stepwise descent in the upper voice. The symbol “—” requires that voice I proceed down by step; the symbol X requires that the line continue down by step, as if the note of resolution were dissonant. In measure 14, a downward leap interrupts voice I’s descent, delaying the expected motion from E♭ to D, which arrives on the downbeat of measure 15. On beat 2 of measure 15, the voices form interval 5, which takes the symbol “—” with X below, necessitating a downward stepwise motion in voice II. From this point on, each note of resolution becomes the free note to a new suspension, and the two voices proceed in staggered descent. Third, although interval 6 participates in this staggered suspension chain, it is available as a suspension only at Jv = −11 and 4. In the third derivative, which uses Jv = −12, Taneev alters the ending of voice I to avoid parallel octaves.⁽¹⁸⁾ The suspension symbols explain several features of the contrapuntal writing, accounting for Taneev’s use of the compound index Jv = −11, 4, −12.

String Trio in D major, op. posth. (1879–80), II: Scherzo in contrapunto alla riversa

[20] In the early String Trio in D major, Taneev recapitulates a 93-measure A major scherzo upside down in F♯ minor. The music is inverted around F4 in pitch space, so that the three original parts, top to bottom, are performed bottom to top in melodic inversion, as if a mirror had been placed on the score.⁽¹⁹⁾ As shown in Example 15, flipping the counterpoint upside down preserves all interval sizes between adjacent voices; no vertical shifting is involved.⁽²⁰⁾

[21] Taneev designates the phenomenon counterpoint alla riversa in the score and reversible counterpoint (obratimyi kontrapunkt) in his treatise.⁽²¹⁾ Reversible counterpoint is mentioned briefly in the Introduction, where Taneev states that it lies outside the scope of his study.⁽²²⁾ Although he develops no mechanism to approach it mathematically, his suspension symbols can be adapted for such a purpose. In the tonal free style, chordal sevenths resolve down by step. This poses a problem in reversible counterpoint. As Example 16a shows, in alla riversa form, the upper-voice seventh remains unresolved, whereas the lower voice ascends by step.⁽²³⁾ Example 16b presents a solution. At the moment that the upper voice descends, the lower voice ascends. The dissonance resolves through a stepwise wedging motion preserved alla riversa. This solution is available only in the free style; in the strict style, both voices I and II would have to be prepared and suspended simultaneously, impossible in two-voice counterpoint.⁽²⁴⁾

[22] Example 17 shows the six dissonance resolutions, modified for reversible counterpoint. The symbol “—” above the interval number requires an inward wedging motion; the symbol “—” below requires an outward wedging motion. The symbol X indicates that the following interval is itself dissonant. Wedging motions permit the use of dissonances in reversible counterpoint.⁽²⁵⁾

[23] In the String Trio, Taneev uses the seventh-to-fifth inward resolution, shown in Example 16b, in tonal harmonic contexts, incorporating the intervallic motion into progressions that move from a seventh chord on $\hat{7}$ to the tonic triad. Example 18a presents an excerpt from an interior theme of the original scherzo. The reduction of Example 18b shows a bracketed motion from vii^∅ to I⁶ in four voices.⁽²⁶⁾ Example 18c isolates the constituent two-voice dissonant intervals and their resolutions through wedging motions.⁽²⁷⁾ Alla riversa, the dissonances resolve in the same way; in the derivative, VII⁷ embellishes a local F minor tonic (Example 19). The progression V⁷–I being unavailable in reversible counterpoint, the scherzo uses motions from seventh chords on $\hat{7}$ to local tonics, ensuring proper dissonance resolution.⁽²⁸⁾

IV. Conclusion

[24] Taneev’s approach to vertical-shifting counterpoint is comprehensive in the range of shifts it treats, the subtleties of the rules it generates, and the efficiency by which different index values can be combined. Many prior theorists restricted themselves to the most common intervals of invertible counterpoint, listing new sets of rules for each index.⁽²⁹⁾ By contrast, Taneev demonstrates that the same principles underlie every index, including those exploited less often by composers. Some prior theorists missed nuances uncovered by Taneev’s system. For instance, Zarlino (1968, 159) forbade the use of strong-beat sixths and sevenths in invertible counterpoint at the twelfth. Taneev’s suspension symbols—in particular the conditions stipulated by the symbol X—suggest how such intervals can be used. Other writers provided rules for various combinations of index values. In this regard Taneev (§190) singles out Habert (1899), whose treatise enumerates individual sets of conditions for forty-six combinations of invertible counterpoint index values. (Needless to say, the combination Jv = −11, 4, −12 does not appear.) Taneev’s work answers most completely the questions that have concerned theorists of counterpoint for centuries.

Christopher Segall
College-Conservatory of Music
University of Cincinnati
Box 210003
Cincinnati, OH 45221
segallcr@ucmail.uc.edu

Works Cited

Arzamanov, Fedor. 1956. “Zavety S. Taneeva (k 100-letiiu so dnia rozhdeniia)” [Taneev’s testaments (on his 100th birthday)]. Sovetskaia muzyka, no. 11: 27–39.

Bogatyrev, Semen. 1960. Obratimyĭ kontrapunkt [Reversible counterpoint]. Moscow: Muzgiz.

Carpenter, Ellon D. 1983. “The Contributions of Taneev, Catoire, Conus, Garbuzov, Mazel, and Tiulin.” In Russian Theoretical Thought in Music, ed. Gordon D. McQuere, 253–378. Ann Arbor: UMI Research Press.

Franck, Peter. 2010. “‘A Fallacious Concept’: Invertible Counterpoint at the Twelfth within the Ursatz.” Music Theory Spectrum 32, no. 2: 121–44.

Grove, Paul Richard, II. 1999. “Sergei Ivanovich Taneev’s Doctrine of the Canon: A Translation and Commentary.” Ph.D. diss., University of Arizona.

Habert, Johannes Evangelista. 1899. Die Lehre von dem doppelten und mehrfachen Kontrapunkte. Leipzig: Breitkopf und Härtel.

Kuznetsov, Igor’. 2006. “Sovremennye aspekty taneevskoi teorii prostogo i slozhnogo kontrapunkta” [Contemporary perspectives on Taneev’s theory of simple and complex counterpoint]. In Ot Gvido do Keidzha: Polifonicheskie chteniia; Po materialam nauchnoi konferentsii, 24 fevralia 2005 goda [From Guido to Cage: Polyphonic readings; From the materials of a scientific conference, February 24, 2005], ed. N. I. Tarasevich, 155–70. Moscow: Prima.

Marpurg, Friedrich Wilhelm. 1754. Abhandlung von der Fuge, vol. 2. Berlin: Haude und Spener.

—————. 1843. Abhandlung von der Fuge, vol. 2, ed. Simon Sechter. Vienna: Diabelli.

Parker, Beverly Lewis. 1981. “Direct Shifting and Mixed Shifting: Important Contrapuntal Techniques or Taneev’s Oddities?” South African Journal of Musicology 1: 1–27.

Plotnikova, Natal’ia. 2011. “Trudy S. I. Taneeva po teorii kontrapunkta” [Taneev’s writings on the theory of counterpoint]. In Muzykal’no-teoreticheskie sistemy 20 veka [Musical theoretical systems of the 20th century], ed. M. G. Aronovskiĭ, 4–54. Moscow: Muzizdat.

Prout, Ebenezer. 1891. Double Counterpoint and Canon. London: Augener.

Starostin, Ivan. 2010. “K istorii prepodavaniia muzykal’no-teoreticheskikh distsiplin v Moskovskoi konservatorii” [Toward a history of music theory instruction at the Moscow Conservatory]. Nauchnyi vestnik Moskovskoi konservatorii [Scientific bulletin of the Moscow Conservatory] 1: 44–56.

Taneev, Sergei. 1909. Podvizhnoi kontrapunkt strogogo pis’ma [Movable counterpoint in the strict style]. Leipzig: Beliaev.

—————. 1959. Podvizhnoi kontrapunkt strogogo pis’ma, ed. Semen Bogatyrev. Moscow: Muzgiz.

—————. 1962. Convertible Counterpoint in the Strict Style. Translated by G. Ackley Brower. Boston: Bruce Humphries.

Weinberg, Jacob. 1958. “Sergei Ivanovitch Taneiev.” Musical Quarterly 44, no. 1: 19–31.

Zarlino, Gioseffo. 1968. The Art of Counterpoint: Part Three of Le Istitutioni harmoniche, 1558. Translated by Guy A. Marco and Claude V. Palisca. New Haven: Yale University Press.

Footnotes

1. Podvizhnoi kontrapunkt was originally published in Moscow and Leipzig in 1909, six years before Taneev’s death. In 1959, Semen Bogatyrev oversaw the publication of a new edition with modernized spellings. Within the Russian conservatory tradition, Taneev was the first to bring systematic methods to the study of music theory, to that point considered an aspect of composition (Starostin 2010, 44–49). Taneev’s work has had a lasting influence on contrapuntal theory; on the extension of his ideas and methods by subsequent theorists, see Grove 1999, 349–444; Kuznetsov 2006; and Plotnikova 2011.
Return to text

2. The example comes from the Introduction to Podvizhnoi kontrapunkt. Both Weinberg (1958) and Carpenter (1983) use the same example to demonstrate movable counterpoint.
Return to text

3. Taneev also identifies a mixed shift (perestanovka smeshannaia), in which the voices transpose so that they overlap. Derivatives using the mixed shift can be analyzed as being derived partially from the inverse shift and partially from the direct shift, depending on which voice is higher at any given moment.
Return to text

4. Parker (1981, 8–11) surveys dozens of historical contrapuntal treatises, noting that most authors either do not identify direct shifting, do not name it, or do not conceive of it as distinct from invertible counterpoint. She names Ebenezer Prout (1891) as representative of the last category, as he identified direct-shifting counterpoint as “re-inverted” counterpoint, that is, as counterpoint that has been inverted first at one interval (e.g., the octave) and then again at a different interval (e.g., the tenth).
Return to text

5. Kuznetsov characterizes Taneev’s approach to vertical-shifting counterpoint as a scientific system and his approach to horizontal-shifting counterpoint as a practical method. He further points out that the mathematical basis of vertical-shifting counterpoint affords the realization of new contrapuntal possibilities (Kuznetsov 2006, 155). The equations used in horizontal-shifting counterpoint primarily offer a labeling method.
Return to text

6. At the instigation of Serge Koussevitzky, an English-language edition was published in 1962, using for its text a translation completed in 1932 by G. Ackley Brower, an American composer. As decades of readers have unfortunately discovered, Brower’s pidgin English is nearly unreadable, a problem compounded by the innumerable errors in the prose, in the ubiquitous mathematical formulas, and in the musical examples.
Return to text

7. In the example captions and the main text, references to Taneev’s treatise are by section number instead of page number, so that they remain consistent for all three editions cited here (Taneev 1909, 1959, 1962).
Return to text

8. In horizontal-shifting counterpoint, the symbol h indicates the number of measures voice I shifts to the left and voice II shifts to the right. The index Jh is the sum of the h values. Taneev uses the symbols h and Jh to describe the size of the horizontal shifts, but a given Jh does not systematically generate a set of contrapuntal rules in the way that a given Jv does.
Return to text

9. Intervals are measured by size, not by quality. At pitch levels where interval 4 or −4 would be represented as a dissonant diminished fifth instead of a consonant perfect fifth, Taneev advises adding an accidental (as in the second derivative of Example 4) or changing the overall key signature (§69).
Return to text

10. In the English translation, Brower renders znaky sviazki as “tie-signs.”
Return to text

11. Invertible counterpoint at the tenth, or Jv = −9, has other well-known rules not accounted for by the suspension symbols. The symbols do not, for instance, affirm the common injunction against parallel thirds and parallel sixths, which in the derivative become parallel octaves and fifths, respectively. Taneev addresses this by prohibiting similar and parallel motion to all consonances, perfect and imperfect, at any Jv corresponding to an interval that can be major or minor in quality (§101).
Return to text

12. At Jv = −9, each original suspension produces a new suspension in the derivative. But at other index values, suspension–resolution patterns may produce other configurations, such as those involving tied consonant intervals proceeding to dissonances. This possibility is taken up in the discussion of variable intervals, which follows immediately below (paragraphs [12]–[13]).
Return to text

13. The free note is the note against which a suspension is dissonant, impelling the latter to resolve.
Return to text

14. Most variable consonances proceed by step to dissonances, necessitating the X. But fifths and sixths, both consonances, can proceed to each other by step. In the case of sixth-to-fifth and fifth-to-sixth motions, therefore, the note of “resolution” need not be treated as a dissonance (§135). Thus an X is not added to the symbol “—” for sixth-to-fifth motions (above interval 5 or below interval −5) or for fifth-to-sixth motions (below interval 4 or above interval −4).
Return to text

15. The dotted line appears below interval 11 and above interval −11, as 11 (the twelfth) is a compound interval 4 (the fifth).
Return to text

16. Interval 1 takes the X below in spite of the dotted line on the interval 4 in its column; the X is necessitated by the absence of a dotted line on interval −7. Interval 8 takes the X below for the same reason.
Return to text

17. This possibility is not always actualized, as in the first and second derivatives Taneev subverts the consonant interval with a dissonant harmony through the addition of other voices.
Return to text

18. The third derivative duplicates voice II, so that its line sounds in syncopated parallel tenths between the viola (v = −12) and second cello (v = 4). On the duplication of voices in vertical-shifting counterpoint, see §§195–228.
Return to text

19. The inversion maps the A major scale onto C♯ Phrygian. In dualist terms, the prime, A, of the original upward-generated tonic triad maps onto the prime, C♯, of the downward-generated tonic triad in the derivative.
Return to text

20. Taneev uses the term mirror counterpoint (zerkal’nyi kontrapunkt) to refer to upside-down counterpoint that does not involve vertical shifting (Introduction; see also Bogatyrev 1960, 25).
Return to text

21. Reversible counterpoint has not been previously named in English. Writing in German, Marpurg named it Contrapunkt in der Gegenbewegung (Marpurg 1754, 26). Referring to an instance of reversible counterpoint in Bach (WTC II, Fugue in D minor), Peter Franck writes that “technically speaking” it is invertible counterpoint at the octave (Franck 2010, 134n23). He cites Zarlino, who identifies reversible counterpoint as a “mode of double counterpoint” (Zarlino 1968, 165–70). Presumably both writers are responding to the registral swapping of voices that occurs in both invertible and reversible counterpoint. The compositional technique involved, however, is different: interval sizes change in invertible counterpoint but stay the same in reversible counterpoint. In his book on reversible counterpoint, Bogatyrev distinguishes the process of melodic shifting (peredvizheniia), the transposition that occurs in vertical-shifting counterpoint, from that of melodic generation (obrazovanie), which forms new lines by inverting the melodic contour (Bogatyrev 1960, 26–27).
Return to text

22. In the English translation, Brower renders obratimyi kontrapunkt as “metamorphosed counterpoint.” Evidently Taneev intended to write a separate book on reversible counterpoint, but it was never completed (Arzamanov 1956, 31; Carpenter 1983, 360n6). Bogatyrev’s Obratimyi kontrapunkt (1960) takes up the challenge, employing Taneev’s method to study reversible counterpoint. Because Bogatyrev limits his investigation to the strict style, the system he develops is quite different from my analysis of wedging motions here.
Return to text

23. I borrow Bogatryev’s (1960) notation for voices transformed through melodic inversion. Voice I^∞ in the derivative is a melody with the same rhythm but opposite contour as the original voice I.
Return to text

24. Because of this, Bogatyrev altogether precludes the use of suspensions in two-voice reversible counterpoint (Bogatyrev 1960, 27–28).
Return to text

25. Marpurg and Sechter were the first to make this point. In volume 2 of Abhandlung von der Fuge, Marpurg listed five intervals that could be used in Contrapunkt in der Gegenbewegung: the augmented second, diminished seventh, augmented fourth, diminished fifth, and perfect fourth—all of which resolve through stepwise wedging motions (Marpurg 1754, 29). In his gloss on Marpurg’s treatise, Sechter described wedging motions more explicitly, writing that any dissonance could be used, if at the moment that one voice resolves down by step, the other voice moves up (Marpurg 1843, 34). As the intervals in Example 17 are arbitrary with respect to quality, accidentals may be added to yield Marpurg’s permissible dissonances and their resolutions.
Return to text

26. Throughout the excerpt, the viola oscillates in eighth notes between two different contrapuntal voices; in the reduction the viola’s pitches are stemmed down in the treble clef. The bracketed progression contains apparent parallel octaves between soprano and tenor (G–F), but because of the way the viola unfolds its pitches, the parallels are not heard as such.
Return to text

27. Between alto and tenor, a dissonant second expands outward to a perfect fourth. This fourth is consonant because it does not involve the bass—and as it does not involve the soprano, which will become the bass alla riversa, it will remain consonant in the derivative.
Return to text

28. Besides the vii^∅7 and VII⁷ chords identified in Examples 18 and 19, Taneev also uses vii°⁷. The retransition to the A major main theme concludes with a motion to V (E major) from an applied vii°⁷ (measures 65–68). In the F♯ minor scherzo alla riversa, the inverted retransition concludes with a motion to iv (B minor) from its applied vii°⁷ (measures 203–6).
Return to text

29. In his Translator’s Preface, Brower notes that of eighteen counterpoint texts surveyed, most deal with invertible counterpoint only at the octave, tenth, and twelfth, and moreover some are dismissive of invertible counterpoint at other intervals. In total the eighteen texts deal with invertible counterpoint at only nine different intervals (Taneev 1962, 10).
Return to text

Copyright Statement

Copyright © 2014 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.