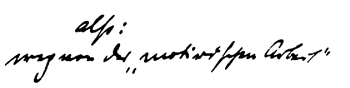“Away with Motivic Working?” Not So Fast: Motivic Processes in Schoenberg’s op. 11, no. 3
Jack F. Boss
KEYWORDS: Schoenberg, motive, motivic process, intuitive aesthetic
ABSTRACT: Schoenberg’s third Piano Piece op. 11 has given rise to an international controversy regarding whether its melodic materials, harmonies and rhythms are carefully worked out according to larger patterns or are by-products of expression and improvisation. Articles and books in English use Schoenberg’s writings, particularly one of his 1909 letters to Busoni, to support the claim that op. 11, no. 3 was among the first of his pieces to exemplify an “intuitive aesthetic,” and is relatively free from overarching formal, harmonic, rhythmic or motivic patterns. Meanwhile, German-language studies focus on detailed analysis of the piece, describing networks of motivic and harmonic relationships.My article maintains the latter point of view; but it also goes beyond existing analyses to describe a large motivic process that gives op. 11, no. 3 coherence as a whole. It takes two motivic progressions that characterize op. 11, no. 1, “expanding” and “explanatory” processes, and sets them against one another in a conflict, but with no resolution—the first process simply takes over at the end. In addition, the “expanding” process can be heard as becoming more abstract as the first piece progresses, and as moving back from abstract to concrete through the third piece. This motion from concrete to abstract and back is illustrated in another way by considering the piece’s motivic progressions from the viewpoint of “minimal offset voice-leading” as described by Straus 1997 and Straus 2005.
Copyright © 2015 Society for Music Theory
[1] Arnold Schoenberg’s third Piano Piece op. 11 is at the heart of an international controversy about whether its melodies, harmonies and rhythms are carefully worked out according to larger patterns or, alternatively, are sheer by-products of expression and (perhaps) improvisation. Does op. 11, no. 3 manifest “amotivicism,” a complete avoidance of motivic recurrence, or does it continue to use motivic relations and processes to create long-range coherence in ways similar to the first two pieces in op. 11? I believe a case can be made for the latter, if we keep two principles in mind, both of which are consistent with Schoenberg’s own statements about “motive” in his mature work, Fundamentals of Musical Composition (1967). First, motives can appear in a wide variety of parameters—pitch, interval, contour, or rhythm (among others)—and can be of any size, though relatively small units are more typical.(1) We will be concerned in this article with small pitch-interval successions (two intervals, three pitches) and small set classes (with a cardinality of 3). Second, my main criterion for recognizing a motive as such in Schoenberg’s music is that it be repeated or varied in such a way that the sequence of motive forms participates in some kind of directional process, which Schoenberg characterized as “development” or “growth.”(2) In Schoenberg’s atonal music, this directional process does not normally include every possible melodic segment or simultaneity in a passage (this allowance for intervening material parallels Schoenberg’s motivic analyses of tonal music in Fundamentals, in which the segments are generally well-founded but do not include every possible legitimate segmentation). But as long as a proposed process accounts for a majority of possible motives, I believe that both motives and process are worthy of recognition.(3) I will discuss specific examples of this phenomenon in the latter part of my article.
[2] Before I present my own analysis of the Piano Piece op. 11, no. 3 to illustrate my argument for motivic processes therein, it is important to review the literature that has sprung up around this piece, to get a better understanding of the “international controversy” I referred to at the beginning of this article. Much of the literature in English tends to rely on Schoenberg’s early writings and those of his students to support the claim that op. 11, no. 3 was among the first of his pieces to exemplify an “intuitive aesthetic,” and is therefore free from overarching formal, harmonic, rhythmic or motivic patterns. Supposedly, it shares those characteristics with other works Schoenberg composed in the late summer of 1909: the fifth of the Orchestral Pieces op. 16, and Erwartung op. 17. Among the authors who take this stance are Joseph Auner, in the 1989 article in the Journal of the Arnold Schoenberg Institute that coined the term “intuitive aesthetic,” and Áine Heneghan, in a more recent article in Musical Currents from the Left Coast (2008) that describes a “volte-face” in Schoenberg’s compositional philosophy after op. 11, no. 3 and works similar to it. Their articles characterize op. 11, no. 3 and the other pieces of its era as lacking motives, motivic variation and motivic development.
Example 1. Part of a letter from Arnold Schoenberg to Ferruccio Busoni, dated August 13, 1909 (translated by Antony Beaumont; a larger excerpt may be found in Beaumont 1987, 389)
(click to enlarge)
[3] The principal source to which these authors appeal is Schoenberg’s August 1909 letter to Ferruccio Busoni that includes the phrase paraphrased in my title, “away with motivic working out” (according to the typical English translation).(4) This phrase comes in the midst of a passionate description of (and argument for) the young composer’s new avant-garde aesthetic, directed at a well-known pianist and fellow composer who had already shown some sympathy to Schoenberg’s ideas, and whom Schoenberg was desperately trying to convince to perform the three pieces of op. 11. See Example 1, excerpted from Antony Beaumont’s collection of letters to and from Busoni (1987, 389).
[4] Schoenberg advocates getting away from a number of the features of past music that restrict free expression, including form and the kind of harmony that functions to build form, in addition to “motivic working out.” He also claims in the letter that complete freedom of expression is best achieved when a piece is brief and “concise!” Now, concision is certainly an important characteristic of some of Schoenberg’s music from around this time period (the op. 19 piano pieces come to mind), but one could argue that some of his most successful “intuitive” music is actually rather long (such as Erwartung). Op. 11, no. 3 itself runs to 35 measures, which is only slightly shorter than average for a Schoenberg piano piece. This suggests that perhaps it is dangerous to take the Busoni letter too literally as a guide to analyzing these pieces; some of the other problems with using it for that purpose will be considered in paragraphs [10] and [11].
[5] A second source supporting the “intuitive” argument is Anton von Webern’s rather brief commentary about the third Piano Piece, made in his contribution to a Festschrift published for Schoenberg in 1912, which echoes some of his teacher’s language in describing op. 11, no. 3. Webern tells us that the first two pieces of op. 11 relied to some degree on older conceptions of form and motive, but with the third piece, Schoenberg “abandons motivic working” completely (Webern [1912] 1999, 224).
[6] Other writers in English give more attention to detailed analyses of op. 11, but nevertheless insist that the third piece is amotivic, in a way that neither of the preceding pieces in op. 11 were. Ethan Haimo in Schoenberg’s Transformation of Musical Language gives a prominent place to Schoenberg’s letter to Busoni, and asserts in the strongest possible terms that the letter accurately describes the style of op. 11, no. 3 (Haimo 2006, 348):
Nothing could highlight more clearly the suddenness of the transformation in Schoenberg’s compositional approach than this letter. Schoenberg’s rapturous description of his new compositional philosophy is a remarkably precise portrayal of his compositions, beginning with op. 11, no. 3. . . There is no “motivic working out. . . ”
[7] Haimo’s sense of a “sudden transformation” between the first and third pieces gives rise to two widely disparate motivic analyses. He creates a painstakingly detailed dialectical analysis of op. 11, no. 1 that shows how motives after m. 12 are introduced as antitheses to the ones featured in mm. 1–11, and then after m. 19, both kinds of motives are brought together in different kinds of syntheses (Haimo 2006, 297–307). This is followed, after a few pages, by an analysis of op. 11, no. 3 that labels a few motives in the opening three measures, but then claims that those elements are never repeated or developed in the subsequent measures (Haimo 2006, 338):
The opening ideas do not give way temporarily to other ideas; they give way permanently to those ideas, which—in turn—have their own fleeting moment on center stage only to disappear forever.
[8] Thus Haimo’s interpretation of Schoenberg’s letter to Busoni influences his analysis of the third piece, pointing him in a particular direction: toward deemphasizing the repetition and development of motives. But I would like to offer a contrasting analytic approach that does not treat Schoenberg’s letter as a “remarkably precise portrayal of his compositions,” but instead adapts concepts of motivic coherence and development that Schoenberg formulated more clearly later in his career, and adds my own ideas about kinds of motivic transformation to them. I believe that such an approach will provide a satisfying and convincing account of op. 11, no. 3 as a whole.
[9] In making this argument, I need to assure the reader that I am not claiming to reconstruct Schoenberg’s own thoughts as he composed the piece. As I have written before, “it is impossible to know all the details of Schoenberg’s thought process in composing” (Boss 2014, 3). Instead, I am claiming, as I have done elsewhere (Boss 2014, 2–3; Boss 2009, 226–28), that an analysis that is guided by the composer’s written comments about motivic coherence, and that ties them to observations made in the piece itself, enables me to make a worthwhile account of it for myself—which may (or may not) convince my reader.
Example 2. Two lines from Schoenberg’s original handwritten letter to Busoni (reproduced from a photocopy held by the Arnold Schönberg Center, finding element 1909.08.13, SatColl D2, folder 2). Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
[10] I will present analytical evidence, provided by others as well as myself, for my contention that op. 11, no. 3 can and should be described in terms of carefully worked-out motivic processes, later on in this article. But before that, it will be useful to bring up a few problems with the way Schoenberg’s letter to Busoni is used to make an argument for the “intuitive aesthetic” in the literature that has just been discussed. First, Schoenberg’s original German does not read “Weg mit der ‘motivische Arbeit’,” as the usual translation “Away with motivic working out” would lead us to believe. Schoenberg’s actual phrase, as indicated by a photocopy of the letter held in the collection of the Arnold Schönberg Center, is “weg von der ‘motivischen arbeit’.” See Example 2, which reproduces the pertinent lines in Schoenberg’s handwriting from the photocopy. Daniel Raessler renders it in what I think is a more accurate way in his 1983 study of the Schoenberg-Busoni correspondence: “Let’s get away from motivic working out” (14). Considering the larger context of Schoenberg’s exclamation, one might go even further and read it this way: “In my most recent music (including the three pieces of op. 11) I’ve been trying to get away from motivic working out, but I haven’t been completely successful yet.” In the two paragraphs of the letter immediately preceding Example 1’s excerpt, Schoenberg admits as much (translated in Raessler 1983, 13–14):
I have not attained in either [of the first two pieces of op. 11] what I conceived. Perhaps, even certainly not even in the third, which will be finished during these days. Several orchestral pieces [op. 16?], which I wrote recently, have led me closer in one respect, but farther away in another from what I had already considered achieved. Perhaps it is still not within reach. Perhaps I still need longer in order to write the kind of music that I feel compelled to write, music that for several years has hovered elusively before me and which I, for the time being, cannot grasp.
[11] Rather than a confident assertion that he had already done away with motivic processes in the third piece of op. 11, then, it may be safer to interpret “Weg von der ‘motivischen arbeit’” as an attempt to convince Busoni that Schoenberg, though he hadn’t gotten there quite yet, was striking out in a new, more “intuitive” direction, one that Busoni himself was beginning to espouse in his own writings.(5) Both Raessler 1983 and Theurich 1976 remind us that the main purpose of Schoenberg’s correspondence with Busoni in 1909 was to convince him to perform the three op. 11 pieces, which Schoenberg had just sent to him. But Busoni’s initial reaction to the pieces was not to agree to perform them as is. Instead, he made an arrangement of the second piece that made it conform a bit more to typical late nineteenth-century piano textures. (Raessler 1983, 10 gives a short, representative excerpt of the Busoni arrangement.) Schoenberg’s placing himself on the path away from “motivic working” was not so much an artist’s manifesto as a plea to a famous pianist from a young composer to consider performing the op. 11 pieces without edits, because Schoenberg’s music as originally conceived was beginning to take a new direction that Busoni himself was known to support.
[12] But back to the “international controversy” to which I alluded at the beginning of this article. We encounter a starkly different view of op. 11, no. 3 from that associated with the “intuitive aesthetic” if we consider the recent German-language literature on the piece. There, if quotations from the writings of Schoenberg or Webern about abandoning motivic working in this piece are presented, it is only for the purpose of challenging them as “one-sided” or even “inaccurate,” as Christian Raff does in his study of Schoenberg’s atonal music (Raff 2006). The basis of the assertions in the German literature is thorough and detailed motivic, formal and harmonic analysis, which follows more closely Schoenberg’s ideals of “developing variation” and Grundgestalt. He formulated these concepts later in his career, but I am asserting that it is possible, and even desirable, to understand his earlier music (tonal and pre-twelve-tone atonal) in terms of them. In my understanding, “developing variation” calls for motives, as they are varied, to create local successions that transform the motive incrementally, away from or toward the original. These successions should delineate and characterize sections of the musical form. (See note 2 for one of Schoenberg’s own definitions of the term, from Fundamentals of Musical Composition; see also Boss 1992, 130.) As for Grundgestalt, it constitutes the “basic shape,” the initial motive, phrase, or theme (or later, twelve-tone row) that provides intervallic and rhythmic material for the rest of the piece to develop, and also indicates the outline of the development.(6)
Example 3. Reprinted from Examples 68–70 of Brinkmann (1969)
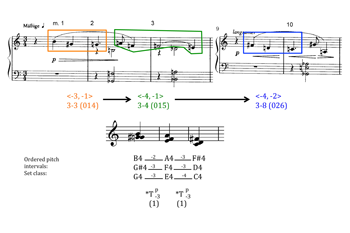
(click to enlarge)
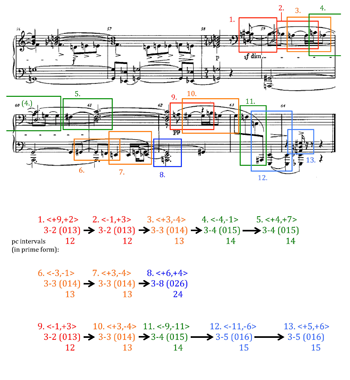
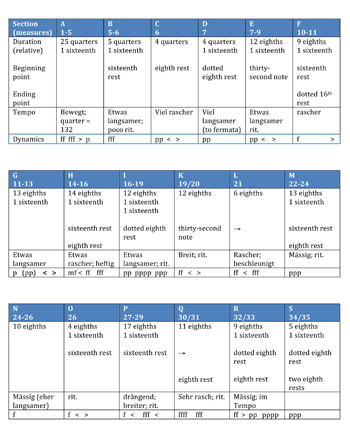
[13] The general consensus among German-speaking authors seems to be that op. 11, no. 3, though it certainly does not follow tradition with respect to its musical form, is suffused with long- and short-range motivic and harmonic networks that give it coherence in lieu of the form. An illustration of such networks is provided by Reinhold Brinkmann’s well-known 1969 treatise on all three piano pieces; see my Example 3, reprinted from his Examples 68–70 on page 121.
[14] Brinkmann’s analysis of op. 11, no. 3 begins with a description of the piece as loose in form, a series of contrasting episodes that he calls Satzzonen (and labels alphabetically from A to S). In that sense, it differs from the first two pieces in the set, which both resemble classical forms in certain ways. But, as his discussion progresses, he begins to call the reader’s attention to motivic successions within some of the Satzzonen (Brinkmann 1969, 112–13), then to motives that link the end of one Satzzone to the beginning of the following one (114). Finally (120–22) comes the discussion accompanying my Example 3, after a section of the text where he acknowledges the “remnants of motivic working” (Reste motivischer Arbeit) within this unusual formal layout.
[15] The upper left corner of Example 3 illustrates motivic connections between Satzzonen A, L, and P, separated by multiple measures. The opening left-hand motive of the first section A, <-1,-6> in ordered pitch intervals, is developed in both hands 27 measures later at the onset of P: <-2,-4> in the left hand, <-1,-4> in the right, with similar rhythmic settings to the original. And at the beginning of L, 21 measures after the onset of A (thus prior to P), an even more thoroughgoing motivic connection includes a variation of A’s left-hand motive <-1,-3,-1>, together with a right-hand chord quite similar to that which had opened A’s right-hand succession: unordered pitch intervals <9,4> instead of the <11,4> of A, but a member of the same set class, 3-3 (014).
[16] The upper right corner of Example 3 considers interval successions that are more distant variations of the opening of A, within Satzzonen K (m. 20) and H (mm. 15–16). The passage from K seems to be derived from the alto voice of A: <+2, +3, +2, +6, -1> in A transforms into <+2, +3, +7, -5, -5> in K, both expressed as groups of six sixteenth notes. The passage from H seems more closely related to the bass voice at A’s beginning: A’s <-1,-6,-2> is altered and surrounded by other intervals to yield <(+4) -2, -5, -1 (-6)>.
[17] The bottom half of Example 3 shows, in detail, a richly varied motivic network within the opening 5 measures of section A itself. Within this passage, a number of strands exhibit incremental development away from the original motive, exemplifying developing variation. The bass line presents a succession of varied forms of its initial three-sixteenth, dotted-eighth motive, highlighted in blue: <-1, -6, -2>, <0, +11, -16>, <+3, -9, +1> (the colors are my addition to Brinkmann’s original example, but the boxes, brackets and arrows are his). Likewise, the alto voice’s opening six sixteenths (highlighted in red) give rise to a motivic succession: they first undergo a liquidation to four sixteenths, then repeat on different pitches, and then extend and augment themselves to three sixteenths and three eighths, with contours and some ordered pitch intervals kept intact. Three repetitions of what is commonly called the “Viennese Trichord,” a vertical combination of unordered pitch intervals 5 and 6 (with the tritone below the perfect fourth), forming set class 3-5 (016), are circled and bracketed, as is its close transformation consisting of pitch intervals 6 and 7, with the tritone below the perfect fifth (highlighted in green). Other melodic and chordal motive successions are circled as well, highlighted in orange, purple and brown. The brown succession progressing from the last sixteenth of m. 2 to m. 5 could perhaps be reconceived; its two boxed elements at the beginning are identical in pitch, though spelled enharmonically, but the large bracketed chords starting with the final chord of m. 3 seem to me to fit better on the “Green Line” of Viennese Trichord transformations, since the left hand of both chords either consists of or contains <
[18] To be sure, Brinkmann’s early (1969) study does not make use of either ordered pitch interval or set-class terminology, but the segments he circles and brackets do indeed form motivic networks that include both long-range connections and local “developing” successions, and they suggest that the piece contains other such motivic links as well. All this motivic activity happens in the context of what Brinkmann considers to be a loose conglomeration of contrasting episodes at the beginning of his analysis; but nevertheless, he acknowledges its motivic coherence increasingly as the analysis progresses.
[19] Other German-language authors focus on the large patterns formed by harmonic progression in op. 11, no. 3. Christoph Neidhöfer’s interpretation, for example, draws together a number of the harmonies of op. 11, no. 3 into Lewinian transformational networks (Neidhöfer 2008). These networks consist of transpositions and a group of contextual inversions that Neidhöfer devises specifically for op. 11. He demonstrates that these transformations, while they may be unique to op. 11, are nevertheless shared by the first and third pieces of the set, a point that resonates with many of the observations about motives and motivic process I will make below.
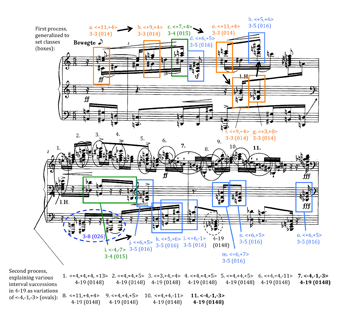
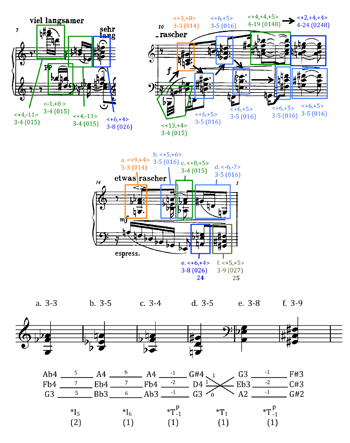
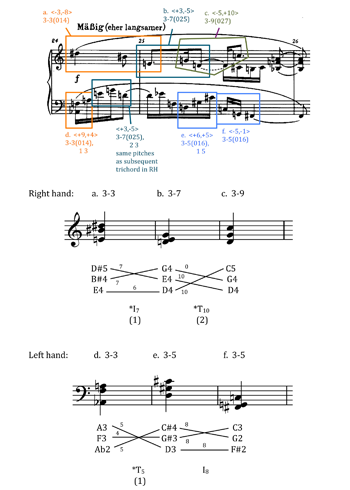
[20] One more account of op. 11, no. 3 deserves mention before moving on to my own reading—that of Bryan Simms in The Atonal Music of Arnold Schoenberg 1908–1923 (2000, 66–71). Simms, like other writers in English, quotes Schoenberg’s letter to Busoni, discusses it in some detail, and makes many of the same deductions from it, labelling op. 11, no. 3 as “athematic” (together with op. 16, no. 5 and Erwartung). He further argues that neither “traditional thematic development” nor “development of motives” occurs in this piece (page 67). But at the same time, he raises the possibility of another way that op. 11, no. 3 and works of its time might be able to create large-scale coherence: patterns consisting of “motivic particles” (Simms 2000, 67):
But the principle of recurrence is not entirely eliminated. It is relegated instead to a technique. . . of the free and sporadic return of motivic particles, that is, small and usually nondistinctive figures that lack a memorable rhythm or shape. These can be single intervals, minute rhythmic gestures, or even single durations, cells that encompass a few tones, or other minuscule figures that the composer could instantaneously call on in a headlong act of composing.
[21] Simms’ notion that a “cell that encompasses a few tones” (as opposed to themes or motives consisting of pitch intervals and rhythms) could be the subject of developmental processes is reminiscent of George Perle’s characterization of Schoenberg’s “free” atonality in Perle 1981, 9–39. Simms explores the notion himself a little further in his more detailed analysis of the beginning of the third Piano Piece:
The return of motivic particles begins even in the two opening measures of Piece No. 3 [see my Example 7a, which reproduces mm. 1–3]. Among the most prominent of them are two three-note figures that are introduced in the incomplete first measure: the chordC♯ , C, E in the right hand and the line A–G♯ –D in the left. Their tones return in free variants in every measure of the work, but the figures do not retain their original rhythmic profiles or intervallic shapes as in motivic development. For example, the trichord A–G♯ –D returns in the left-hand line of m. 1 as the succession D–C♯ –A–G♯ , reordered and expanded by the additional toneC♯ ; it next reappears verticalized, inverted, and transposed as A,D♯ ,G♯ in m. 2 (middle staff). This technique of detaching motivic development from rhythm would prove to be of immense importance in Schoenberg’s later development of the atonal style. (Simms 2000, 67)
[22] My own position in the international debate about large-scale coherence in op. 11, no. 3 takes its cue from Simms in one way, but in another way takes a step beyond both his work and the Central European authors discussed earlier. I do not believe that it is sufficient to speak of networks of motivic particles that span multiple measures in this music while limiting the study of developmental processes to the local level. Instead, I want to demonstrate that, together with op. 11, no. 1, the third piece creates a large-scale developmental process that begins with ordered pitch-interval successions (at the beginning of the first piece) but later generalizes the same process to set classes (at the end of the first piece and throughout the third piece), and ends with unordered pitch-interval collections. Opus 11’s generalization from ordered pitch-interval processes to set-class processes also can be understood in terms of what Joseph Straus (1997 and 2005) has described as “near-transposition,” “near-inversion,” or “minimal-offset voice-leading,” first in pitch space, then, as the first and third pieces progress, in pitch-class space, returning again to pitch space near the end of piece no. 3.(7)
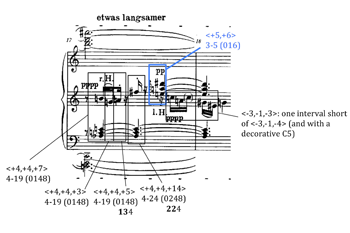
[23] A further comment about my use of Allen Forte’s concept of “set class” is appropriate here. Though Haimo (1996) has claimed that Schoenberg “did not compose with set classes,” Forte’s notion nevertheless lines up quite well with one of Simms’ conceptions of motivic particles—that is, figures or cells that do not retain their original rhythmic profiles or intervallic shapes in the process of development. For this reason among others, my own sense is that Schoenberg probably did have some conception of “set class,” but that he called it by a different name. As I have argued elsewhere (Boss 2014, 2; Boss 2009, 228–29), he likely understood what we call set class as that property of a motive (the total interval content) that remains after it has had its ordered interval succession, contour and rhythm obscured through extensive development; i.e., the one property that would tie such a remote transformation back to the original motive. Nevertheless, whether Schoenberg did or did not intentionally compose with set classes, the notion of set class is still indispensable to my account of coherence in op. 11 that harmonizes in some ways with the composer’s own statements.
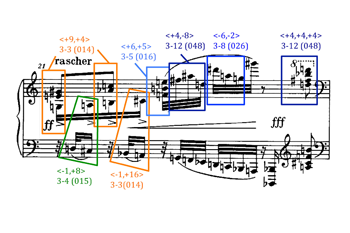
[24] The large developmental process that spans and connects the first and third pieces of op. 11 can be understood as involving a dialectical relationship between two sub-processes: op. 11, no. 3 takes up two kinds of motivic progressions that first occur and play crucial roles in op. 11, no. 1, and sets them against one another in a conflict, but with no resolution—the first process simply takes over and “wins” at the end. For that reason, I would be reluctant to characterize the third piece as a Schoenbergian “musical idea,” though I believe other pieces from the “atonal” period can be understood that way, including op. 11, no. 1. Op. 11, no. 3 seems to build itself around the introduction and elaboration of a conflict or problem, but the conflict ends with the disappearance of one of the opposing forces, rather than a synthesis of the two.
Example 4. The first motivic process from op. 11, no. 1, an incremental ordered pitch-interval expansion at the piece’s opening. Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
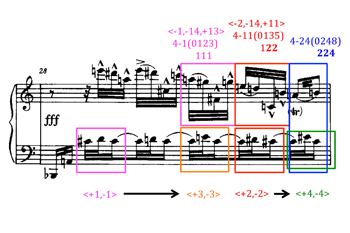
[25] I would describe the two motivic processes from the first piece that are placed in conflict by the third piece as follows. The first process is an incremental expansion of ordered pitch intervals in three-note (or two-interval) motives, which is then generalized to a succession of set classes whose prime forms expand their ordered pitch-class intervals incrementally. In Example 4, from the first 10 measures of op. 11, no. 1, the ordered pitch interval -3 from the first motive expands to -4 in the second, and subsequently in the third motive, the second ordered pitch interval also expands by a half step to -2. I represent the interval expansions by warmer colors for the smaller pitch intervals and cooler colors for the larger pitch intervals. Alternatively, we can read this progression in terms of “minimal-offset voice-leading in pitch space,” as discussed in Straus 2005, 45–46. The bottom half of Example 4 shows that the pitch set created by the first motive, reinterpreted vertically, relates to the second motive’s pitch set through “fuzzy” transposition down by three semitones. The “fuzziness” is caused by the top voice, which only moves down by two semitones. This creates an “offset” of 1 (shown in parentheses below the transposition label). Likewise, the second motive’s pitch set moves to that of the third motive through fuzzy transposition down by three semitones. In this latter voice leading, the bottom voice moves down four semitones to create the fuzzy quality. The resulting set classes progress down through Allen Forte’s list of trichords (1973, 179): 3-3 (014), 3-4 (015), 3-8 (026).
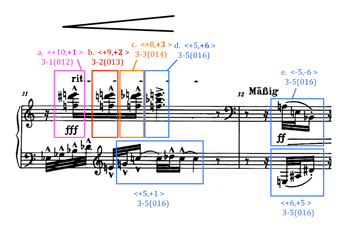
Example 5a. The first motivic process from op. 11, no. 1, generalized to successions of set classes at the piece’s ending, mm. 58–64 (chords are read as ordered pitch-interval successions from the bottom up). Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
Example 5b. A motivic segmentation from Schoenberg’s Fundamentals of Musical Composition, the analysis of the opening of Beethoven’s op. 2, no. 1 (Schoenberg 1967, 63). Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
[26] Example 5a, the end of op. 11, no. 1, can be understood as replicating the gradual opening up of intervals in Example 4, but in a more abstract way—the ordered pitch intervals themselves do not expand incrementally with any consistency, but the adjacent ordered pitch-class intervals in the prime forms of the set classes do. As I suggested back in paragraph 1, in my segmentation I am taking an approach similar to the one espoused by Schoenberg in his motivic analyses of tonal music: it is possible to leave certain segments out of the reckoning, so long as most of the possible segments are still accounted for. Example 5b reproduces a well-known instance of a Schoenbergian motivic analysis, the illustration of sentence structure in the opening of Beethoven’s Piano Sonata op. 2, no. 1, from Fundamentals of Musical Composition (Schoenberg 1967, 63). Note that numerous pitch successions that could have been bracketed as motives are ignored here: for example, the F5–
[27] If we allow ourselves to read Example 5a, then, according to processes created by most (but not all) of its sets, we clearly have three set-class expansions, represented by warmer colors for the set classes with smaller pitch-class intervals this time, and cooler colors for the sets with larger pc intervals. In the top line, five sets project a progression from 3-2 (013) to 3-3 (014), then to 3-4 (015). In the second line, three sets create a process that starts back on 3-3 (014), and opens all the way out to 3-8 (026) with adjacent pitch-class intervals 2 and 4. Finally, in the third line five sets trace a progression from 3-2 (013) to 3-3 (014), then to 3-4 (015), followed by 3-5 (016) at the cadence. It is interesting to notice that the first two lines of Example 5a’s set-class succession trace the same path through the set classes as all of Example 4: essentially, from 3-3 to 3-4 and ultimately to 3-8. But the third line of the latter example adds another expanding sequence that reaches only to 3-5.
[28] A question could be brought up at this point as to whether it is possible to hear the successions of ordered pc intervals in prime forms I have just described as “expansions” in any meaningful sense. For example, in one case (sets 3 and 4), one of the pitch intervals that represent set class 3-3 (014) moving to 3-4 (015) grows smaller, in another (sets 10 and 11), the pitch intervals representing 3-3 and 3-4 grow larger, but not incrementally. The answer I would give to this question is that even though the ordered pitch intervals of sets such as these do not expand incrementally, there are indeed audible differences between the set-classes 3-2, 3-3, 3-4, 3-5, and 3-8, which depend on the understanding of their intervals as relatively small or large in pitch-class space. Many of us have participated in post-tonal aural skills exercises in which our instructor asked us to distinguish between the various trichordal set-classes, suggesting that we reduce what we hear to a normal form by transposing and reordering the pitches, and then considering whether the intervals between the resulting notes are half steps, whole steps, minor or major thirds, perfect fourths, etc. After a while, without doing the mental work of transposing and reordering, we begin to hear 3-2 in any voicing as more “compressed” than 3-3 or 3-8, because of the characteristic interval-class 1 dissonance of one of the trichord’s intervals, be it half-step, major seventh, or minor ninth, and the interval-class 2 dissonance of one of the others. My assertion is that the set-class expansions I describe in this article can be heard in much the same way: as progressions from chords more dependent on smaller interval classes (such as seconds and sevenths) to those featuring larger interval classes (thirds, sixths, fourths and fifths, and tritones).(8)
Example 5c. The progressions between sets from Example 5a reinterpreted as voice leadings in pitch or pitch-class space
(click to enlarge)
Example 6. The second motivic process from op. 11, no. 1, explaining other interval successions in set-class 4–19 in terms of an overlap of the first two stages in Example 4. Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
[29] Example 5c reinterprets the expansions of adjacent pitch-class intervals from Example 5a as voice-leadings in Straus’s sense. From the alternative perspective of voice leading, it is interesting that the three parts of the progression described above generalize progressively. The first part (sets 1–5) begins and ends with “crisp” inversion and transposition of pitch classes (meaning that all three voices invert their pitch classes by the same sum or transpose by the same pc interval). In between, sets 2–4 relate by fuzzy pitch transposition down one semitone, recalling the progression from Example 4. Sets 6–8 combine a crisp pitch transposition (again, down one semitone) with a fuzzy inversion in pitch-class space. Finally, sets 9–13 are linked primarily by transpositions and inversions in pitch-class space, two of them fuzzy with offsets of 1, the last one a crisp pitch-class inversion. As we progress through Examples 4 and 5c, the voice-leadings gradually shift from pitch space to pitch-class space, preparing us for the circumstances found at the beginning of op. 11, no. 3.
[30] The second process from op. 11, no. 1 that plays an important (but steadily diminishing) role in my understanding of the third piece is what I have elsewhere called an “explanatory” process (Boss 2008, 267). In this process, presentations of set class 4-19 (0148) containing various kinds of interval sequences that seem remote from the opening motives of the piece are followed by presentations of that same set class as an overlap of the first two stages in the ordered pitch interval expansion process, <-3,-1,-4> or <-4,-1,-3>. The latter interval sequences “explain” how the former, remote, ones could arise from op. 11, no. 1’s initial motives, <-3,-1> and <-4,-1>, by overlapping and reordering. Example 6 provides an illustration, which is adapted from Examples 13-3, 13-4 and 13-16 of Boss 2008. The two passages in my Example 6a come from the beginning of op. 11, no. 1’s first contrasting section, mm. 12 and 14. The top four notes of the run in m. 12 and the piano harmonic chord in m. 14 both project set class 4-19, using intervals that seem quite foreign to the motives that opened the piece, <+4,+4,+9> and <+4,+4,+3>. The strange nature of these interval combinations is reinforced by the drastic change in rhythm and dynamics to 32nd-note runs and ppp that occurs at the beginning of m. 12, and the new timbre, piano harmonics, in m. 14. The listener may well ask at this point: “How does this music relate intervallically or motivically to the opening motives?”
[31] As I argued in Boss 2008, a passage near the end of op. 11, no. 1 can be understood as explaining the previous 4-19 chords, by setting 4-19 somewhat prominently as an overlap of <-3,-1> with <-1,-4> interval successions identical or closely related to the motives that opened the piece. To be sure, this line is hidden behind the surface of the music in the manner of a Schenkerian middleground (hence the stems and beams in my example), but F5 and D5 are highlighted as beginning and ending points of a chromatic descent in mm. 54–56 (and repeated with accents an octave lower in the following measure).
[32] As I mentioned earlier, I understand op. 11, no. 3 as taking the “expanding” and “explanatory” processes from the first piece and setting them against one another, in an alternation of different procedures that signifies a conflict. Unlike many of Schoenberg’s pieces that appear to create a synthesis or resolution of such conflicts, ultimately enabling one opposing element to function productively in a context controlled by the other, this piece simply allows the “explanatory” process to grow weaker as the piece progresses, and the “expanding” process to become more and more predominant. I would now like to discuss a number of passages from the third piece that illustrate the inverse trajectories of the work’s motivic processes.
[33] Let us begin with Example 7a, the opening 3¼ measures. This passage begins by projecting the “expanding” process in set-class space. It contains three set-class successions whose prime forms expand their intervals incrementally, from 014 to 015 to 016. In the first succession, letters a–d, two 3-3 chords move to 3-4 and then on to 3-5.(10) In the second, letters e–h (middle of m. 1), the right hand returns to 3-3 and the left hand repeats it twice as the right hand expands again to 3-5. The third expansion, letters i–o, begins in m. 2, where the middle stave presents 3-4, followed by a whole series of 3-5s in the middle and lower staves of mm. 2 and 3. As Example 7b shows, reinterpreting the expanding process that begins op. 11, no. 3 in terms of minimal-offset voice-leading reinforces the idea that op. 11, no. 1’s opening expansions are being generalized here into the pitch-class realm. The first succession in mm. 0–1a translates into a crisp inversion and two fuzzy transpositions in pitch-class space; as in the opening measures of the first piece, the offsets of the transpositions reflect the incremental interval expansions. Likewise, the second succession in m. 1b features mostly pitch-class transformations, ending with a fuzzy transposition up by 28 half steps. The third succession in mm. 2–3 incorporates pitch transformations to a larger degree, including a pitch inversion around B3 between letters j and k, but still includes three successive crisp inversions in pitch-class space from k to n.
|
Example 7a. The second process “following on the heels” of the first in the opening section of op. 11, no. 3. Used by permission of Belmont Music Publishers, Los Angeles (click to enlarge) |
Example 7b. The progressions between sets from Example 7a reinterpreted as voice leadings in pitch or pitch-class space (click to enlarge) |
Example 8. Reinhold Brinkmann’s form chart for op. 11, no. 3, translated from pp. 110–11 of Arnold Schönberg: Drei Klavierstücke op. 11: Studien zur Frühen Atonalität bei Schönberg (1969)
(click to enlarge)
Example 9. Three sections in which variations of the first process dominate (Brinkmann’s D, F and first measure of H). Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
Example 10. The second, explanatory process fails under a sustained 3–5 (endpoint of the first process). Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
[34] While the third expanding succession, letters i–o, is running its course in the left hand, however, its competitor the explanatory process enters in the right hand near the beginning of m. 2, becoming the dominant strand in the texture for a short while, and drawing the listener’s attention away from the prolongation of the expansion’s end point, 3-5, going on beneath it. In the bottom half of Example 7a, six chords present 4-19 as an augmented triad plus some note a half-step away in pitch-class space—sonorities that are not related in any obvious way to the opening motives of op. 11, no. 1, just like the interval collections at mm. 12–14 in the first piece. Then, at circle number 7 in Example 7a, <-4,-1,-3> appears, a close relative of the set in Example 6b that “explained” 4-19 as an overlap of the opening motives. Chords 8, 9 and 10 return to the structure of an augmented triad plus a half step, and then at number 11 the same “explanatory” succession, <-4,-1,-3>, shows up again. So, set-class 4-19 is explained not once, but twice in mm. 2–3 of the right hand.
[35] Reinhold Brinkmann, in the form chart of op. 11, no. 3 mentioned earlier (Brinkmann 1969, 110–11), includes the passage we just discussed in his opening Satzzone, A, which ends on the downbeat of m. 5. Example 8 shows my translation of Brinkmann’s chart. Brinkmann divides the next 12 measures into 7 sections, which he calls B through H, and every one of them except for B features some kind of set-class expansion process. (Section B is best characterized as chromatically ascending major thirds, which are re-voiced and transposed to form a descending movement. Thus its characteristic interval remains constant rather than expanding.) The “explanatory” process, meanwhile, disappears completely in sections B–H. I chose m. 7, mm. 10–11a and m. 14 to illustrate; these correspond to Brinkmann’s sections D, F, and the first measure of H, and they are shown in Example 9.
[36] Measure 7, at the top left corner of the example, presents three interval successions in the same rhythm of two bound sixteenths, all belonging to set-class 3-4 (015), followed by the expansion 3-8 (026) at the fermata. As for mm. 10–11a, an interval succession belonging to 3-4 in the left hand and a 3-3 chord in the right give way to a whole series of 3-5 chords in both hands, while in the right hand at the end of the passage, 4-19 (0148) progresses to 4-24 (0248), expanding the first pitch-class interval in 0148 while contracting the second. In m. 14, the right hand begins by expanding from 3-3 to 3-5 (a path it has taken in several of the previous examples), and then goes from a 3-4 chord to a 3-5 melodic segment at the end of the measure. Meanwhile, the left hand in the second half of m. 14 reaches the furthest extent of ordered pitch-class interval expansion we have heard to this point: it begins at 3-8 (026) and expands the second ordered pitch-class interval of that prime form from 4 to 5 to attain 3-9 (027).
[37] The correspondence we have already seen between expansion of adjacent intervals in set classes and minimal-offset voice-leading in pitch-class space continues with the three passages illustrated in Example 9, and is particularly well illustrated by the last of them, m. 14. The voice-leading graph directly below the score of m. 14 shows that the first expansion from 3-3 to 3-5 is accomplished through a fuzzy inversion with an offset of 2, but every chord after that relates to the one before it or above it (in the case of chord e) through transpositions or inversions having an offset of 1. The second and fourth transformations are pitch-class transpositions and inversions, and the third and fifth are fuzzy pitch transpositions of -1, which to my ear recall similar voice-leadings in the final measures of op. 11, no. 1 (illustrated in Example 5c). This allusion to the sound-world of the first piece, perhaps, prepares us for what is to come in m. 17.
[38] After seven straight set-class expansions in mm. 5b–16a, the following section, mm. 16b–19, which Brinkmann calls I, allows the explanatory process to rear its head one more time, briefly (and very quietly). See Example 10. It is important to note that section I enters at an extremely soft dynamic, pppp, after the immediately preceding measures, mm. 14–16, had created a large crescendo from mf to fff. The impression this gives the listener is that section I is an afterthought. But within this little addendum, we hear a series of three set class 4-19s, all of them consisting of an augmented triad (which is sustained) plus a note a half-step away in pitch-class space, similar to chords 1–6 of Example 7a. Before the explanatory interval succession follows this group of 4-19s, however, a 4-24 chord occurs, a simultaneous expansion and contraction of the ordered pc intervals of 4-19. Then a 3-5 chord, <+5,+6>, intervenes in the top register of the middle staff at a slightly louder dynamic, pp—reminding us of the endpoints of the “expanding process” in several of the previous passages. As if it were disrupted in its explanatory function by the 3-5, the following music starts to present <-3,-1,-4>, but breaks down two-thirds of the way through, after -3 and -1, and gasps out another -3 instead, almost as if the explanatory process was trying to express something with its last breath but could not quite get it out.
Example 11. In Brinkmann’s section L, 3-3 and 3-4 (in a setting that recalls the piece’s opening) expand to 3-5 and then subsets of the whole-tone scale. Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
Example 12. In Brinkmann’s section N, 3-3 leads to expansions 3-7 (025) and 3-9 (027), in a similar rhythm to that of the opening measures of op. 11, no. 1. Used by permission of Belmont Music Publishers, Los Angeles
(click to enlarge)
[39] After the explanatory process’s last gasp in Section I, we never hear from that process again. From m. 19 to the end of the piece, there is a series of nine Satzzonen, several of which project set-class expansions. Three of these are illustrated in Examples 11, 12, and 13, corresponding to Brinkmann’s sections L, N, and the middle measure of P. Section L, in m. 21, begins in a way that recalls the piece’s opening, with 3-3 chords in the right hand against a descending bass line that forms set classes 3-4 and 3-3 with some of the tones in the middle voice. Then the right hand offers a series of trichord set classes whose prime-form adjacent intervals expand quickly: 3-5 (016), 3-12 (048), 3-8 (026), and finally another 3-12 chord at the end of the measure.
[40] Section N, 2½ measures later, expands its set classes in a different way, not in the direction of whole-tone subsets like 3-8 and 3-12, but rather towards trichord subsets of the diatonic scale. The right hand begins on a 3-3 set class like many of the other sections previously discussed, then that set overlaps by one note with a 3-7 (025), and the 3-7 overlaps in turn with a 3-9 (027). This passage reminds us of the opening of op. 11, no. 1, the original incremental interval expansion of the three Piano Pieces, not only because of its set classes and gradual expansion of their adjacent pitch class intervals, but also on account of its rhythm, which for the most part divides the note values of the opening two measures of the first piece in half. But the voice-leading graph of the right hand’s interval collections (reinterpreted as verticalities) in the middle of Example 12 shows that the minimal-offset voice-leadings that characterized the beginning of the first Piano Piece are still being projected on the more abstract level of pitch-class space. This will change in a few measures to a more directly audible version of the expanding process.
[41] The left hand during mm. 24b–25 begins with a different 3-3 from the right hand’s set (a transposition up 5 in pc space), then expands to 3-7 with not only the same intervals but also the same pitches as the following 3-7 in the right hand, a very brief canon at the unison. It then finishes with a pair of 3-5 sets. The voice-leading graph at the bottom of Example 12 skips over the left hand’s 3-7 to go directly from 3-3 to 3-5 (considering the left hand 3-7 to be a preview copy of the one in the right hand, and thus more pertinent to the process going on in the upper voice). Without that collection, 3-3 in d progresses to 3-5 in e through a fuzzy pitch-class transposition by 5 with an offset of 1, and then the 3-5 is prolonged by a crisp pitch-class inversion.
[42] In m. 28, we hear the passage illustrated in Example 13, the middle measure of Brinkmann’s section P. Here, the right hand’s thirty-second-note groups end with three set classes whose prime-form ordered pitch-class intervals expand quickly, 4-1 (0123) with three half steps, 4-11 (0135) with a half step and two whole steps, and finally 4-24 (0248) with two whole steps and a major third. To make the passage’s direction towards larger intervals more salient, the piano’s left hand plays a pair of ordered pitch-interval expansions by which a half step grows out to a minor third, then a whole step grows out to a major third. This turn in m. 28 from the more abstract expansion of adjacent intervals in prime forms towards progressive expansion of unordered pitch intervals prepares the listener for the most obvious and salient presentation of the expanding process, which will occur three measures later.
|
Example 13. The middle measure of Brinkmann’s P, m. 28. An expansion of ordered pitch-class intervals in prime forms in the right hand is paired with two ordered pitch-interval expansions in the left. Used by permission of Belmont Music Publishers, Los Angeles (click to enlarge) |
Example 14a. The last half of Brinkmann’s section Q and first part of his section R. The expansion process projects itself more audibly (and forcefully) through an incremental expansion of pitch intervals, creating a recognizable wedge shape. Used by permission of Belmont Music Publishers, Los Angeles (click to enlarge) |
[43] All the interval expansions in the last part of op. 11, no. 3, including the three we just described, seem to culminate in the closing three Satzzonen of the piece, Brinkmann’s Q, R and S. In the last half of Q, just before the final cadence, we hear an interval expansion that is less abstract and more salient than any we have heard before (see Example 14a). This final, culminating expansion involves not only adjacent pitch-class intervals in prime forms like those that came before it, but in addition there is an incremental expansion involving the upper pitch intervals of the four chords. <+10,+1> goes to <+9,+2>, which is followed by <+8,+3> and finally <+5,+6>, a pitch-interval pair belonging to set class 3-5 that has already become familiar as the endpoint of expansions in a number of previous examples. The motion from 1 to 2 to 3 to 6 in the top two voices forms not only an audible outward-expanding wedge, but one marked with heavy accents, a dynamic of fff, and a gradual ritard, as if to impress upon the listener that this shape is most definitely the source for and culmination of all the set-class expansions that came before it. Once we reach the interval pattern <+5,+6> at the end of this wedge, on the third beat of m. 31, both hands continue to repeat the same pattern, both in the inversion <-5,-6> and in the retrograde inversion <+6,+5>, four times over the next two measures (the first one is shown at the end of Example 14a). The expansion process asserts itself as strongly as can be imagined, while the “explanatory” process has been silent since m. 19. This is a clear victory for the expansion process at the end of the piece, but not one that creates a synthesis by allowing the “explanatory” process to coexist and support expansion somehow.
Example 14b. Voice-leading graph of the right hand of Example 14a
(click to enlarge)
[44] Example 14b presents the right hand of Example 14a from the voice-leading perspective, and, as one might imagine, the progression from chords a–d, the salient pitch interval expansion just described, translates into a series of fuzzy pitch transpositions at t = 0. The interval expansion in the top two voices corresponds to offsets of 1 for the first two transformations, and then the offset rises dramatically to 3 to approach the final, accented chord in the high register, the peak of the progression. In the realm of voice-leading as well as those of pitch intervals vs. pitch-class sets, op. 11, no. 3 brings the expanding process down from the level of abstraction on which it had resided to something more concrete (and more directly audible), just as the first piece had pushed the expanding process from a more concrete presentation towards higher levels of abstraction.
[45] I think it is accurate and justifiable to make a distinction between op. 11, no. 3 and the previous two pieces in the set on the basis of its musical form, as almost all the writers quoted at the beginning of my article do. Both of the earlier pieces present modified tonal forms: for example, the first piece of op. 11 could be heard as a sonata-rondo with an abbreviated recapitulation. The third piece does seem closer to the “moment” form label Brinkmann suggests for it, because its small Satzzonen are much harder to group into something resembling a recognizable tonal form. However, since they can be understood as connecting to each other via large motivic processes, as I have just demonstrated, the label “moment form,” at least in the sense Stockhausen conceived it, is entirely inappropriate.(11)
[46] Despite the unique qualities of the third piece’s form, it seems to me that English-language scholars go too far when they take Schoenberg’s hopeful protests about his new direction to Busoni, and Webern’s similarly motivated characterizations of his teacher’s work, too literally, and use them as evidence for their claim that motivic relations and processes are completely absent in the piece. Instead, it is my strong sense that an analyst can argue for motivic processes that span all of op. 11, no. 3, the “expanding” and “explanatory” processes, acting on set classes as well as pitch-interval motives. Further, one can claim that these processes grow out of similar processes in op. 11, no. 1, and thus create a motivic connection between the two pieces, that the “expanding” process becomes stronger over the course of the third piece and obliterates the “explanatory” one, and that the “expanding” process’s motion from abstract set-class expansions to concrete interval expansions in the third piece reverses a trend from concrete to abstract in op. 11, no. 1. Finally, I would like to argue that it is these processes themselves that give op. 11, no. 3 its undeniable long-range coherence, since it lacks a clear, tonally derived musical form. As I stated above, such an analytic argument may not follow exactly the outlines of the composer’s thought process, whatever that may have been. But I believe it enables me to make a convincing description of op. 11, no. 3 that harmonizes in some ways with Schoenberg’s published remarks about motivic coherence.
Jack F. Boss
School of Music and Dance
1225 University of Oregon
Eugene, OR 97403–1225
jfboss@uoregon.edu
Works Cited
Auner, Joseph. 1989. “Schoenberg’s Aesthetic Transformations and the Evolution of Form in Die glückliche Hand.” Journal of the Arnold Schoenberg Institute 12 (2): 103–28.
Beaumont, Antony. 1987. Ferruccio Busoni: Selected Letters, trans., ed., and with an introduction by Antony Beaumont. Columbia University Press.
Boss, Jack. 1992. “Schoenberg’s op. 22 Radio Talk and Developing Variation in Atonal Music.” Music Theory Spectrum 14 (2): 125–49.
—————. 2008. “The ‘Musical Idea’ and Motivic Structure in Schoenberg’s op. 11, No. 1.” In Musical Currents from the Left Coast, ed. Jack Boss and Bruce Quaglia, 256–81. Cambridge Scholars Publishing.
—————. 2009. “The ‘Musical Idea’ and the Basic Image in an Atonal Song and Recitation of Arnold Schoenberg.” Gamut 2 (1): 223–66.
—————. 2014. Schoenberg’s Twelve-Tone Music: Symmetry and the Musical Idea. Cambridge University Press.
Brinkmann, Reinhold. 1969. Arnold Schönberg: Drei Klavierstücke op.11: Studien zur frühen Atonalität bei Schönberg. Beihefte zum Archiv für Musikwissenschaft, vol. 7. Franz Steiner Verlag.
Christensen, Thomas. 1987. “Schoenberg’s op. 11, No. 1: A Parody of Pitch Cells from Tristan.” Journal of the Arnold Schoenberg Institute 10 (1): 38–44.
Forte, Allen. 1973. The Structure of Atonal Music. Yale University Press.
—————. 1981. “The Magical Kaleidoscope: Schoenberg’s First Atonal Masterwork, Opus 11, Number 1.” Journal of the Arnold Schoenberg Institute 5 (2): 127–68.
—————. (1988). “New Modes of Linear Analysis.” Unpublished paper presented at the Oxford University Conference on Music Analysis.
Gostomsky, Dieter. 1976. “Tonalität—Atonalität: Zur Harmonik von Schönbergs Klavierstück Op. 11, Nr. 1.” Zeitschrift für Musiktheorie 7 (1): 54–71.
Haimo, Ethan. 1996. “Atonality, Analysis and the Intentional Fallacy.” Music Theory Spectrum 18 (2): 167–99.
—————. 2006. Schoenberg’s Transformation of Musical Language. Cambridge University Press.
Heneghan, Áine. 2008. “Schoenberg’s Compositional Philosophy, the Three Piano Pieces, and his Subsequent Volte-Face.” In Musical Currents from the Left Coast, ed. Jack Boss and Bruce Quaglia, 299–314. Cambridge Scholars Publishing.
Lewin, David. 1982–83. “Transformational Techniques in Atonal and Other Music Theories.” Perspectives of New Music 21 (1–2): 312–71.
Maegaard, Jan. 1972. Studien zur Entwicklung des dodekaphonen Satzes bei Arnold Schönberg, 3 vol. Wilhelm Hansen Musik-Forlag.
Neidhöfer, Christoph. 2008. “Atonalität und Transformational Analysis: Zu einigen verborgenen (und nicht so verborgenen) Strukturen in Schönbergs Klavierstück op. 11, 3.” In 100 Jahre Atonalität: Herausforderung für Musiktheorie, 53–73. Staatlichen Instituts für Musikforschung Preussischer Kulturbesitz.
Ogdon, Will. 1981. “How Tonality Functions in Schoenberg’s Opus 11, Number 1.” Journal of the Arnold Schoenberg Institute 5 (2): 169–81.
Perle, George. 1981. Serial Composition and Atonality: an Introduction to the Music of Schoenberg, Berg and Webern, 5th rev. ed. University of California Press.
Raessler, Daniel M. 1983. “Schoenberg and Busoni: Aspects of Their Relationship.” Journal of the Arnold Schoenberg Institute 7 (1): 7–27.
Raff, Christian. 2006. Gestaltete Freiheit: Studien zur Analyse der frei atonalen Kompositionen A. Schönbergs—auf der Grundlage seiner Begriffe. Sinefonia, vol. 5, 233–65. Wolke-Verlag.
Roig-Francolí, Miguel A. 2001. “A Theory of Pitch-Class-Set Extension in Atonal Music.” College Music Symposium 41: 57–90.
Schoenberg, Arnold. 1967. Fundamentals of Musical Composition. Faber and Faber.
—————. 1984. Style and Idea: Selected Writings of Arnold Schoenberg, ed. Leonard Stein, trans. Leo Black. University of California Press.
Simms, Bryan. 2000. The Atonal Music of Arnold Schoenberg, 1908–1923. Oxford University Press.
Straus, Joseph N. 1997. “Voice Leading in Atonal Music.” In Music Theory in Concept and Practice, ed. James M. Baker, David W. Beach, and Jonathan W. Bernard, 237–74. University of Rochester Press.
—————. 2005. “Voice-Leading in Set-Class Space.” Journal of Music Theory 49 (1): 45–108.
Theurich, Jutta. 1976. “Der Briefwechsel zwischen Arnold Schönberg und Ferrucio Busoni.” In Arnold Schönberg—1874 bis 1951: Zum 25. Todestag des Komponisten, ed. Mathias Hansen and Christa Müller, 55–58. Akademie der Künste der DDR.
Webern, Anton von. [1912] 1999. “Schoenberg’s Music.” In Arnold Schönberg, R. Piper, 1912. Trans. Barbara Z. Schoenberg as part of Schoenberg and his World, ed. Walter Frisch, 210–30. Princeton University Press.
Footnotes
1. See the paragraph on “What Constitutes a Motive” in Schoenberg 1967, 9. It begins: “Any rhythmicized succession of notes can be used as a basic motive, but there should not be too many different features.” After describing rhythmic, intervallic and contour “features” of a motive, Schoenberg ends the paragraph: “Every element or feature of a motive or phrase must be considered to be a motive if it is treated as such, i.e. if it is repeated with or without variation.”
Return to text
2. Schoenberg 1967, 8: “Homophonic music can be called the style of ‘developing variation.’ This means that in the succession of motive-forms produced through variation of the basic motive, there is something which can be compared to development, to growth.”
Return to text
3. This article will not address the related issue of whether op. 11, no. 3 is “athematic” as well as “amotivic,” although the literature we are about to survey asserts a lack of themes as well as motives. My understanding of “theme” again depends on Schoenberg’s Fundamentals of Musical Composition, in this case the pertinent passages in Chapter 11, “Melody and Theme.” To summarize, Schoenberg defines themes as relatively large single units consisting of chains of motives, designed to create imbalance or “problems” deep enough that the rest of the piece is necessary to restore balance (1967, 101–04). Such an entity calls for multiple measures, and op. 11, no. 3 indeed does not have multiple-measure “themes” that return as wholes in succeeding measures, or set up problems that are solved later. Therefore I am happy to agree with labeling the third Piano Piece as “athematic”; this article only argues against the “amotivic” label.
Return to text
4. The letter can be found on the Schönberg Center website at http://www.schoenberg.at/letters/search_show_letter.php?ID_Number=108 (Accessed January 17, 2014). Its “filing element” is the supposed date, 1909.08.13. The English translation of it that has been passed down in most of the secondary literature comes from Beaumont 1987, 389.
Return to text
5. For example, Theurich 1976, 57 provides this quotation from Busoni regarding his 1909 Berceuse élégiaque (translation mine): “With this piece, I succeeded for the first time in creating a unique sound of its own, and dissolving form in feeling (italics mine).”
Return to text
6. Schoenberg defines Grundgestalt in “Linear Counterpoint” (1931), reprinted in Schoenberg 1984, 290, as follows:
‘Whatever happens in a piece of music is nothing but the endless reshaping of a basic shape.’ Or, in other words, there is nothing in a piece of music but what comes from the theme, springs from it, and can be traced back to it; to put it still more severely, nothing but the theme itself. Or, all the shapes appearing in a piece of music are foreseen in the ‘theme’. (Italics are Schoenberg’s.)
Return to text
7. Straus (1997, 268–70, n31) has acknowledged earlier works by Allen Forte and David Lewin as sources for these concepts: Forte 1988, which introduces the notion of a “unary voice-leading transformation,” and Lewin 1982–83, which discusses what patterns would (or do) occur if the “wrong” notes in near-transpositions and near-inversions were made right.
Return to text
8. One study that makes a similar distinction between incremental expansions of ordered and unordered pitch intervals on the one hand, and expansions of adjacent ordered pitch-class intervals between elements of prime forms on the other hand is Roig-Francolí 2001. Roig-Francolí calls the former, more concrete kind of expansion “chromatic intervallic expansion” and the latter “linear transformation of set classes,” and claims that both play roles in “pitch-class set extension.” He presents an analysis of Webern’s op. 5, no. 3 (72) that expands incrementally through the same group of set classes we just encountered in Schoenberg’s op. 11, no. 1: 3-2, 3-3, 3-4, 3-8. But he does not place the same emphasis on patterns created by moves from intervallic expansion to set-class expansion and back, understanding the changes in level of abstraction as process-defining, as I do.
Return to text
9. To depict the first piece of Schoenberg’s op. 11 as a juxtaposition of expanding processes involving trichord motives or pitch-class sets with “explanatory” processes involving tetrachords, as I have just done, constitutes a departure from earlier set-class or “cell”-based approaches to the piece; for example, Forte 1981 and Perle 1981, 10–15. Forte’s analysis is remarkable for its focus on large sets: mostly hexachords and pentachords, but some larger sets as well. He refers to the trichords I have mentioned, as well as set class 4-19, frequently, but comprehends these elements as subsets of and intersections between the larger sets that are his main concern. He is not interested in describing processes that connect smaller sets. Perle 1981, on the other hand, does focus his attention on “cells” of three or four notes, as I do; and in certain cases he even discusses the long-range development of these cells. His comment on how mm. 58–63 consist of “non-literal imitations of [mm. 1–2’s] original melodic pattern [that] lead to a restoration of the original notes, but in a new permutation” (10–11) is a good example. But he seems to understand the piece more in terms of multiple, loosely-related developmental strands, as opposed to narrowing the development down to only two competing processes. My approach differs even more sharply from other analytic treatments of op. 11, no. 1 (such as Brinkmann 1969, 60–96; Gostomsky 1976; Ogdon 1981; and Christensen 1987) that hear in it elements of functional tonal syntax, either lifted from their context and rearranged (Christensen) or more or less kept in context, which is then blurred almost beyond recognition by the addition of dissonance, the absence of important tonality-defining notes, and reference to multiple tonalities simultaneously (Brinkmann, Gostomsky and Ogdon). Rather than placing the piece’s interval collections into their possible tonal contexts, I prefer to put tonal context aside and focus simply on the patterns they form when compared with one another, showing that those patterns participate in global processes that produce their own coherence.
Return to text
10. The level of abstraction to which the expansion underlying the opening succession of op. 11, no. 1 has been subjected in no. 3 is made clearer when we notice that the bottom unordered pitch interval of chords a–d actually shrinks successively: 11, 9, 7, 6. But other obvious features reinforce the sense of growth during these four chords —the rise in register, crescendo to sf, and progression of the upper unordered pitch interval from 4 to 5.
Return to text
11. Brinkmann himself seems to recognize this (1969, 114), when he proposes, later in his analysis than the suggestion of “moment form” (110), a grouping of the Satzzonen into larger sections. These are an opening section consisting of A–D (mm. 1–7), two middle sections consisting of E–G (mm. 8–13) and H–O (mm. 14–26), and a closing section, P–S (mm. 27–35).
Return to text
Copyright Statement
Copyright © 2015 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Tahirih Motazedian, Editorial Assistant
Number of visits:
28988