Review of The Analysis and Cognition of Basic Melodic Structures and The Analysis and Cognition of Melodic Complexity by Eugene Narmour

Introduction

[1] “There is at present virtually no viable conceptual framework for the analytical criticism of melody.”⁽¹⁾ Thus wrote Leonard B. Meyer in 1973 before setting out to expound his theory of implication in tonal melody in his volume Explaining Music. A paragraph later Meyer went on to add,

Schenker’s theories are primarily concerned to explain the middleground and background organization of tonal music—the large-scale structure. My concern will be to explain the foreground and its adjacent levels.⁽²⁾

This quotation might also serve as a manifesto for the two recent volumes by Meyer’s colleague and one-time student, Eugene Narmour, which build on the foundation laid in Explaining Music.⁽³⁾ The model presented in Narmour’s books, the implication-realization model, constructs a quite radical conceptual framework for melody analysis, and, following in Meyer’s rather than Schenker’s footsteps, takes as its central focus the foreground note-to-note relationships between tones.

[2] The two volumes reviewed here complement each other to a large extent, although, taken sequentially, the second provides some minor modifications of the first. Volume 1, The Analysis and Cognition of Basic Melodic Structures: the Implication-Realization Model (hereafter called “Vol 1”) explicates the basic building blocks of the theory, and concentrates on note-to-note relations in melody cognition and analysis. Volume 2, The Analysis and Cognition of Melodic Complexity: the Implication-Realization Model (hereafter called “Vol 2”), explores relations within larger groups of notes and relations between non-contiguous tones. Given that Narmour’s theory, at least in its present manifestation, is relatively new, this review will attempt to provide a precis of it before offering any critical appraisal.

[3]Taking the theory as a whole, several overarching goals may be identified. Firstly and most generally, Narmour aims to explain the “‘genetic code’ of melody” (Vol 1, p. xiv), to provide a taxonomy of archetypal melodic shapes. The implication-realization model thus strives for parsimony in that it tries to classify the infinite number of possible melodies according to a short list of melodic archetypes.

[4] Secondly, Narmour’s approach is bottom-up. Although, in the analysis of melody, considerations of style, culture, and the listener’s previous experience (various types of memory) come into play, the theory largely parses melodies from note to note on the basis of the raw parameters of musical sound. These parameters include interval size, direction, rhythmic duration, dynamic accent and so on. Thus, even quite low-level culturally specific cognitive constructs such as scale degree, are regarded as secondary in importance to the theory.

[5] Thirdly, theword “cognition” alongside the word “analysis” in the titles of both volumes signals the theory’s strong perceptual and cognitive leanings. That is to say, although Narmour develops a sophisticated symbology in order to perform analyses on the score, his ultimate aim is to describe how listeners hear melody. To this end the implication-realization model rests on hypotheses substantiated or suggested by the research literature of music perception and cognition. In this respect at least, Narmour’s orientation is similar to that of Lerdahl and Jackendoff.⁽⁴⁾ In line with this psychological bias, at the end of the first volume reviewed here, Narmour proposes a number of experimental studies intended empirically to test the validity of his theory.

[6] Fourthly, and perhaps most importantly, the words “implication-realization” betoken the theory’s concern with tracing the listener’s changing expectancies over time, and the extent to which those expectancies are realized or denied. Thus, based on bottom-up implications in the various parameters of musical sound, the theory measures listeners’ ongoing levels of surprise as an aesthetic response to music as well as listeners’ ongoing perceived structural closure.

Basic Archetypes

[7] As intimated above, the most far-reaching aspect of Narmour’s theory is that it postulates a set of principles of melodic analysis and cognition that work on individual parameters of musical sound from the bottom up. These principles are wholly divorced from any influences of style, culture or musical ability/training on the part of the listener. As such they are presumed to be universal to all listeners and therefore, from an analytical point of view, universally applicable to all types of melodies, regardless of historical or geographical provenance.

[8] Narmour’s primary hypothesis is that any two successive pitches (i.e. one melodic interval) imply a third pitch (a second interval). Thus, at the most basic level, melodies can be divided up into elemental building blocks of three pitches, with pitches one and two of each block forming the antecedent interval of “implication,” and pitches two and three forming the consequent interval of “realization.” Whether the antecedent implicative interval is completely realized, only partially realized or denied depends on size and registral direction of the consequent interval. These two parameters, interval size and direction, lie at the heart of Narmour’s theory, yet are envisaged as working independently in melody cognition.

[9] The parameter “interval size,” designated in Narmour’s symbology by the abbreviation “I,” is for most purposes dichotomized into small and large intervals. Small intervals range from the unison to the perfect fourth, and large intervals comprise the perfect fifth and wider. The tritone is an ambiguous interval that can be counted as either small or large, depending on the context.

[10] In addition, the relationshipbetween successive intervals is characterized by calculating the difference between them (for example a major 3rd followed by a perfect 5th have a difference of three semitones or a minor 3rd). Depending on their intervallic difference, antecedent and consequent intervals are “equal” (difference of a perfect unison between two intervals), “similar” (difference of less than a minor or major 3rd) or “different” (difference of more than a minor or major 3rd). Whether the difference limen between two intervals is a minor or a major third depends on the shape of the three-pitch structure in question (see Vol 1, pp. 85–88 for the reasoning behind choosing particular difference limens).

[11] The parameter “registral direction,” designated by the abbreviation “V” (from the word “vector”), has three categories: up, down and lateral (or a repeating pitch). Up followed by up, down followed by down or lateral followed by lateral are counted as continuations of registral direction, and any other combinations are counted as changes of registral direction.

[12] By applying the Gestalt principles of good continuation, similarity and proximity to the parameters of interval size and registral direction, Narmour posits two basic three-pitch melodic archetypes. Narmour hypothesizes that if a listener hears an initial small interval (i.e. narrower than a tritone), that interval will imply a second similarly small interval continuing in the same registral direction. If this implication is realized by the third pitch, giving an up-up or down-down motion comprised of two small intervals, then the resultant melodic shape is a “Process” (designated by the symbol “P”). Examples of Processes would be C4–D4–E♭4 (assuming now and hereafter that C4 is “middle C”), or A♯3–F♯3–D3. If the interval of implication is a unison (giving lateral motion between the two pitches) then the listener will expect a second interval in the lateral direction, giving a shape of three repeated pitches. When this implication is fully realized the result is what Narmour calls a “Duplication” (designated by the symbol “D”). An example of a Duplication is D♯2–D♯2–D♯2.

[13] The structures P and D arise, therefore, from the realization of melodic implications generated by Gestalt laws. However, Narmour also posits the operation of an opposite, counterbalancing law, namely reversal. It should be stressed that no “law” of traditional Gestalt psychology embodies reversal, and thus it is not so solidly grounded in accepted perceptual principles as are P and D. Rather, evidently influenced by Meyer’s notion of “gap-fill melodies,” the author seems to have included reversal for theoretical completeness.⁽⁵⁾

[14] In contrast to the implication of a small antecedent interval, when an initial large interval (i.e. larger than a tritone) is heard, it implies a small consequent interval changing direction. In other words a large antecedent interval implies both a change in interval size and a change in direction. If the implications in both the parameters of interval size and registral direction are realized, then a third basic melodic archetype is generated, namely a “Reversal” (designated by the symbol “R”). Examples of Reversals are A3–F4–E♭4, C♯5–F♯4–A4 or D4–C♯5–C♯5. (Note that the last example involves lateral motion between the second and third pitches, up-lateral being a change in direction.)

[15] The three-pitch structures P, D and R, the primal structures of Narmour’s theory, are generated when melodic implications in both parameters of interval size and registral direction are realized. However, a further group of three-pitch structures are possible when an implication in only one or the other of the two parameters is realized. As mentioned above, a small antecedent interval (other than a unison) implies a similarly small interval continuing in the same direction. If the interval-size parameter implication alone is realized, i.e. small-small but involving a change of direction, then the resultant three-pitch structure is called an “Intervallic Process”, or “IP.” Examples of IPs are C4–E4–D♯4 or B♭3–F3–G3. If only the direction parameter implication is realized, i.e. up-up or down-down but moving from small to large, then the resultant structure is called a “Registral Process,” or “VP.” Examples of VPs are D4–E4–C♯5 or G3–E3–A2.

[16] Corresponding types of partial realizations are also possible with large antecedent intervals. Thus, as mentioned above, a large antecedent interval implies a change of interval size and registral direction. If, however, just the interval-size parameter implication is realized, i.e. large-small but evincing no change in direction, then the resultant structure is an “Intervallic Reversal,” or “IR.” Examples of IRs are C3–B3–C4 or D♯5–G♯4–F♯4. If, on the other hand, just the direction parameter implication is realized, i.e. a change in direction but the second interval is larger than the first, the resultant structure is a “Registral Reversal,” or “VR.” Examples of VRs are E♭3–B♭3–C3 or D5–E4–G♯5.

[17] The last type of partial realizations to be considered are those derived from the Duplication. Firstly in this regard, Narmour argues that a “Registral Duplication” [VD] does not exist, since one cannot have realization of a lateral registral direction (unison-unison) without also repeating the antecedent interval and therefore realizing the intervallic implication. Therefore the only remaining derivative of the Duplication is the “Intervallic Duplication,” or “ID.”

[18] In the opinion of this reviewer, Narmour’s use of term Intervallic Duplication is inconsistent given the logic of the other structures so far identified. Narmour identifies any pitch structure consisting of any two identical small intervals moving in opposite directions as an ID. A defining characteristic of an ID is therefore that the first and third pitches are identical. Thus, examples of IDs would be C4–D4–C4 or B♭3–F3–B♭3. The reason given by Narmour for calling this type of structure an Intervallic Duplication seems to be that the antecedent interval size is replicated exactly in the consequent interval, but the registral direction of the antecedent is denied by the registral direction of the consequent. However, this argument treats the structure as a complete whole, in retrospect, whereas all other structures hitherto have been derived by considering the realization prospectively. For example, with the C4–D4–C4 structure, when the listener hears the antecedent interval between C4–D4, according to Narmour’s theory he/she will expect a small consequent interval that continues upward (with a third pitch of E4 or F4, for example). When the third pitch, C4, occurs, admittedly the implication is partially realized (interval size is realized and direction is denied), but why is it a Duplication that has been partially realized? Why, on the basis of the first two pitches, would the listener expect a Duplication rather than a Process? This quirk is made more confusing by the fact that structures such as C4–C4–D4, whose antecedent interval is in fact a unison, are labelled as Intervallic Processes or IPs (see Narmour Vol 1, p.358, Ex. 21.7). In this latter case, with the antecedent unison (C4–C4), the listener might reasonably expect the lateral registral direction to be repeated in the consequent interval (resulting in C4–C4–C4), so that when the D4 sounds the prospectively implied lateral motion is denied. This type of structure seems to me to be a more logical candidate for the title “ID,” than does a structure such as C4–D4–C4. My argument is one of nomenclature and ultimately, if accepted, does no great damage to Narmour’s theory. However, the reader interested in pursuing Narmour’s theory further may find it helpful to remember the ID as a specific subset of IP, an ID being an IP where the first and last pitches are identical.

[19] The structures so far summarized, in which the implication in at least one parameter is realized, Narmour calls “prospective” because at least one of the listener’s unconscious expectations is fulfilled. In contrast, a third group of structures in which both interval-size and registral-direction implications are denied, Narmour dubs “Retrospective”. They are thus called because it is only on the completion of the three-pitch structure that the true contour of the structure becomes apparent; in prospect, on the basis of the antecedent interval, the listener expects something quite different. For example, if the listener hears a large antecedent interval, this implies a small consequent interval in the opposite direction. If, however, what actually follows is a similarly large interval in the same direction, then implications in both parameters have been denied. The resultant structure is here a “Retrospective Process” since, like a Process, the structure contains two similarly sized intervals in the same direction, but, unlike a Process, the initial interval is large. An example of a Retrospective Process would be C4–A4–F♯5.

[20] In Narmour’s theory, every prospective structure has a retrospective counterpart, with retrospective structures being designated by the symbol for their prospective counterpart in parentheses. Thus, for example, a Retrospective Process is symbolized by “(P).” Generally, retrospective structures have the same directional characteristics and the same relationship between the antecedent and consequent intervals (same, similar, or different) as their prospective counterparts. Retrospective structures differ from their prospective counterparts, however, in the size of their antecedent interval. Therefore, if a prospective structure has a small antecedent interval, then its retrospective counterpart will have a large antecedent interval, and vice versa. An exhaustive account of the logic behind every retrospective structure is beyond the scope of this review. Those interested readers should consult Vol 1, pp. 195–198, and ch. 14.

[21] Forthe sake of convenience, Table I summarizes all the prospective and retrospective structures with their intervallic and directional characteristics. For a summary of these structures in a different order with additional information, see Narmour Vol 1, Appendix 2, pp. 435–436.

[22] The“Category” column divides the structures into Processes, Duplications and Reversals. The abbreviations for all the structures are given in the second column. Intervallic information is divided into three columns. The “Ant” column describes the size of the antecedent interval, where “sm” = “small”, “la” = large and “uni” = “unison” according to the criteria outlined earlier in this review. The “Con” column describes the size of the consequent interval using the same abbreviations as the “Ant” column, as well as “v.sm” and “v.la” which stand for “very small” and “very large” respectively. The adverb “very” indicates an interval that is even smaller or even larger than the small or large antecedent interval. The column “Ant-Con” describes a comparison between the antecedent and consequent intervals, and provides two pieces of information. The first piece of information compares the size of the antecedent and consequent intervals as “=” (exactly equal) “sim” (similar) or “dif” different. The second piece of information in the Ant-Con column gives the requisite absolute difference between the antecedent and consequent intervals for these intervals to be classified as a particular structure. Here “m” = “minor,” “M” = “major” and “P” = “perfect.” Thus, for example, for the antecedent and consequent intervals to be counted as similar in a Process structure, the difference between these intervals must be less than or equal to a minor third. The final column, “Direction” compares the registral direction of the antecedent and consequent intervals, with “contin” signifying a directional continuation and “change” signifying a change of direction.

Structures arising from Parametric Interaction

[23] All of the structures summarized in Table I are derived purely from implications and realizations in the pitch domain. However, one of the great strengths of Narmour’s theory is that it also incorporates other parameters of musical sound as centrally important determinants of analysis. Thus, in naming particular melodic structures, the analyst must also take into account note durations, dynamic accent, consonance and so on. In the parameter of duration, for instance, Narmour identifies three types of relationships that may inhere between successive note values, namely “additive” (isochronous repetition of the same note duration), “countercumulative” (longer to shorter) and “cumulative” (shorter to longer). Cumulative rhythms may serve to suppress the melodic implication between two pitches if the second note is greater than or equal to 1.5 times the duration of the first note. If this durational relationship is present, for example in the rhythm quarter->dotted-quarter or quarter->half, then the interval between the pitches having these rhythmic values is simply identified as a dyad. A dyad is thus a disconnected interval whose implication fades because the listener has to wait too long for the realization. Note that this type of suppression of an implication is to be distinguished from a denial; in a denial the implication is still pending when the unexpected tone of realization sounds. In Narmour’s symbology a dyad is simply labelled with a numeral indicating the width of the interval, e.g. “6” for a major or minor sixth, “4” for a diminished, perfect or augmented fourth and so on. (Vol 1, pp. 391–410).

[24] Rests (silences) can also function to suppress implications and therefore perceptually isolate particular pitches. For example the rhythm quarter->quarter->quarter-rest will isolate the pitches of the first two quarters as a dyad. Again, whatever consequent interval may have been implied by the interval between the first two pitches is suppressed by the silence that follows this interval. Rests may also serve to isolate single notes so that no continuation is even implied. These single-note structures are called “Monads” and symbolized on the score by the letter “M” (Vol 1, pp. 410–414).

[25] Returning to Table I, all the structures listed here consist of three pitches in their most basic format. Thus if one imagines the rather artificial situation of a perfectly isochronous monophonic series of pitches, undifferentiated as to dynamic and timbre, and with no meter suggested, then this melody would be analyzed as a series of linked three-pitch structures where the third and final pitch of one structure becomes the first pitch of the next structure. Such a sequence is analyzed after Narmour in Example 1. However, if the series of pitches in Example 1 were also marked by durational, metric, dynamic, harmonic and articulative accents, then, insofar as these accents coincided, Narmour’s analytical methodology would attempt to reflect the grouping suggested by these accents. I have already noted how durational cumulation or use of rests can cause individual pitches or pairs of pitches to be isolated and thus form Monads or Dyads. By the same token, if metric accent, change of harmony, articulation or whatever suggests a grouping of more than three pitches, then Narmour makes use of two further structure types: “combinations” and “chains.”

[26] A combination is simply the interlinking of two basic melodic structures so that the consequent interval of realization of the first structure is also the antecedent interval of implication of the second structure. A combination therefore consists of three intervals (four pitches) that cohere owing to the operation of parameters other than interval size or direction. Consider Example 2. In this example the three pitches C4–B3–D4 form an Intervallic Process [IP], while the pitches B3–D4–F4 form a Process [P]. However, because B3 and D4 are dissonant with the underlying harmony (Narmour uses an X to indicate dissonance), and because of the change of harmony on the F4, the most stable and salient pitches in this pattern are C4 and F4. the boundary pitches. To reflect this four-pitch structure the analysis shows the combination IPP rather than two separate structures. Notice also that, whereas in Example 1 adjacent structures share only one pitch in common, the two structures that make up a combination share two pitches (one interval) in common. Combinations can occur in numerous situations where four pitches are naturally grouped together, and those readers interested in extensive examples should consult Vol 2, chs. 2–7. Narmour identifies 217 possible archetypal combinations, all of which are listed and exemplified in Vol 2, Appendix 5, pp. 391–396.

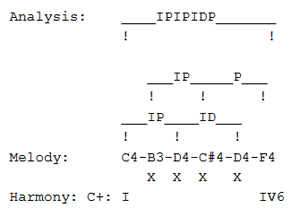
[27] Having briefly described combinations, chains take the process of expanding the basic melodic structures one stage further. A chain is the interlinking of three or more basic melodic archetypes. As is the case with combinations, each archetype within a chain shares two pitches (one interval) with its immediate neighbours. Example 3 shows a modification of Example 2 to give the chain IPIPIDP. Since chains can be any number of pitches greater than or equal to four in length, the number of possible chains is theoretically limitless. However, the vast majority of the chains that Narmour identifies when he expands on the subject at length in chapters 8 through 10 of Volume 2, are no longer than four or five pitches. Again, as was the case with combinations, it should be stressed that chains frequently arise from the operation of parameters other than interval size or direction.

[28] It will be recalled that one of the purposes of Narmour’s theory is to record the ebb and flow of melodic closure as a series of notes is unfolded in time. All of the structures introduced thus far embody different, and quantifiable degrees of melodic closure according to Narmour’s theory. In fact, Narmour proposes that closure can occur in one or more of six parameters (see Vol 1, pp. 11–12):

1. when a rest or repetition interrupts and therefore suppresses an implication, e.g. a dyad;
2. on a metrically strong beat;
3. on a harmonically consonant tone, following a harmonically dissonant tone (a resolution);
4. on a long duration following a short duration (cumulative rhythm);
5. when a large melodic interval moves to a small melodic interval (the pitch concluding the small interval is closural—if the reverse occurs, namely a small interval followed by a large one, then non-closure is the result);
6. when registral direction changes (the pitch concluding the change is closural—lateral to lateral is neutral so far as closure is concerned, and up to up or down to down are non-closural).

As might be expected, several of these parameters allow multiple gradations of closure. Harmonically, the greater the difference in consonance between a dissonance and its resolution, the stronger the resolution (Vol 1, pp. 288–289). In his analyses, Narmour makes use of three gradations of dissonance, and three gradations of consonance or resolution, “weak,” “moderate” and “strong” in each case (see Vol 2, Appendix 2, p. 375 for definitions and symbology of each). Incidentally, although this is regrettably not made explicit, Narmour seems to treat dissonance and consonance as psycho-acoustic phenomena, and thus maintains that they act from the bottom-up rather than being stylistically determined. Durationally, the greater the ratio of the long duration to the short duration, the greater the closure of the cumulation (Vol 1, pp. 292–293 & p. 314). Intervallically, the greater the difference between the large and the small intervals, the greater the closure (Vol 1, pp. 283–284 & p. 308).

[29] In addition to the multiple gradations of closure along several of the parameters, it is also important to realize that points of closure in different parameters may or may not coincide with each other (what Narmour calls “parametric congruence” and “parametric non-congruence” respectively). The greater the number of parameters that evince closure on a particular note, the greater the overall closure of that note. Taking the gradations of closure on one parameter together with the varying degrees of parametric non-congruence, one can see that Narmour’s theory posits a wide range of types and degrees of closure, allowing for many subtle gradations of closure on a particular tone.

[30] For the purposes of analysis, however, Narmour divides degrees of closure into three categories: “articulation,” “formation” and “transformation.” Articulation occurs when closure among the parameters is completely non-congruent. Formation is a stronger form of closure than articulation, and it occurs when closure among the parameters is partially non-congruent. Transformation occurs when closure among the parameters is sufficiently congruent for a note to be labelled as the beginning or end of a structure, that structure being a basic archetype [P, D, R, IR, VP etc.], a combination or a chain. As was intimated earlier with the C4 and F4 in Example 2, for instance, another way of conceptualizing transformational tones is as the stable boundary tones of a coherent melodic grouping.

[31] Asa theory of melodic perceptual grouping, I think the implication-realization model is very successful. Previous theories, those of Cooper and Meyer and Lerdahl and Jackendoff being the most eminent, have viewed groups as temporally contiguous yet mostly self-contained chunks;⁽⁶⁾ only in the case of elision do successive groups share a tone or chord. However, one problem with such self-contained groups is the often arbitrary placement of an accented tone as either a group-initiating or group-ending accent. To be sure, some perceptual research indicates that, for instance, dynamic accents tend to initiate groups whereas durational accents tend to end groups.⁽⁷⁾ That being said, the experimental jury is still out on the sort of grouping likely to result from parametric interaction. What happens, say, when dynamic and durational accent coincide, as in Example 4? Are the dynamically accented half notes group-initiating (analysis a) or group-ending (analysis b)? Narmour’s solution (what would be analysis c) felicitously circumvents the problem. By simply labelling the longer and louder tones as the group boundaries he recognizes their greater salience and stability while remaining agnostic as to their position within a group. Also, to the extent that a graphic analysis on paper can ever be analogous to the aural experience of sounds in time, analysis c better captures the balance between continuity and segmentation that is surely so central to melodic perception. Analyses a and b visually chop up the flow of the rhythm in a manner that does not accord with perception. Narmour’s conception of grouping, then, is a novel and welcome departure from previous theories.

[32] Correct recognition of the transformational boundary tones is necessary in Narmour’s model because it allows the analyst to begin to build a hierarchical analysis of a melody. The pitches of transformational tones are the pitches that “survive” the winnowing out process of analysis, and are consequently those that are left at the next level up in a reductional hierarchy. Example 5 reproduces the rather simple series of pitches from Example 1 giving higher level analyses. Lest, on the basis of Example 5, any reader should draw the erroneous conclusion that tracing transformations from one hierarchical level to the next simply consists of selecting every second note, remember that the melody here exhibits no combinations or chains. Since only those pitches at the beginning or end of a square bracket would be found in the analysis at the next level up, in combinations or chains the reductional process would remove all the pitches that lie within a bracket (i.e. more than every second pitch). For a richer example involving varying degrees of durational, harmonic and metrical closure see Vol 2, p. 32, Ex. 1.8.

[33] With regard to this Example 1.8, Narmour states that the ability to extrapolate higher hierarchical levels from note-to-note structures is desirable primarily for the sake of analytical completeness:

The extent to which listeners actually transform structural tones to such levels remains an open question. The main point for the reader to observe is that, despite the simplicity of the theory and the apparent paucity of available structures, the analysis generates from the bottom up a sophisticated hierarchical accounting of every melodic tone.⁽⁸⁾

Despite the hierarchical component in the implication-realization model, then, Narmour’s primary interest in these two volumes is still note-to-note relations. This predilection is reflected in the fact that the vast majority of musical examples in both volumes show solely surface-level analyses.

[34] All of the structures, whether archetypes, combinations or chains, and whether considered on the note-to-note level or on a higher hierarchical level, are hypothesized as resulting from bottom-up processes. However, Narmour is also ready to admit the influence of top-down (learned or style-specific) processes on melodic implication. One example that immediately springs to mind is the strong pull that scale-step implications will have for enculturated listeners of Western tonal music (e.g. the leading-tone tending towards the tonic). Symbologically Narmour accounts for such learned or style-specific influences by appending the abbreviation “(xs)” (for “extra-opus style”) whenever these are deemed to affect melodic implication. Similarly, when motivic references or simple repetitions within a piece may be assumed to mold a listener’s expectations, Narmour uses the abbreviation “(os)” (for “intra-opus style”).

[35] Recognition of the influence of tonality (xs) is particularly necessary in these volumes since many of Narmour’s examples are of tonal, common-practice period melodies. The author’s reasons for relegating style-specific influences to secondary variables in the theory are laid out lucidly and at some length in Chapters 2 and 3 of Volume 1. However, given that the theory does try to model perception of an “educated” listener, one has to wonder whether the top-down influences might not be more powerful than the bottom-up processes in many of Narmour’s examples. It is quite possible that the effect of bottom-up implications would be more tangible in music for which the average listener has not developed sophisticated schemata. For this reason, not only is the implication-realization model pan-stylistic, but it may actually be better suited for analyzing music outside the (Western) common-practice period. Interestingly, Narmour offers analyses of excerpts of pre-tonal music in Appendix 3 of Volume 2, and analyses of non-Western melodies in Appendix 4 (presumably as heard by a naive cultural outsider). One other repertoire where listeners’ top-down schemata are likely less developed is 20th-century post-tonal music. Therefore, given its ability to generate reductional hierarchies using only bottom-up principles, Narmour’s theory may offer another useful perspective on the thorny problem of post-tonal prolongation.

Streaming and Tempo

[36] One type of melodic texture that requires special attention is pseudopolyphony, or what Berry calls a “compound line.”⁽⁹⁾ As the reader will recall, pseudopolyphony occurs when an ostensibly monophonic line gives the illusion of tracing two or more polyphonic voices through rapid change of register, or rapid intervallic leaps. This type of writing is the hallmark of Bach’s solo ’cello suites, for instance.

[37] In fact, pseudopolyphony is one of the most studied types of pitch pattern in experimental perceptual research, coming under the general heading of “Auditory Stream Segregation” or simply “streaming.”⁽¹⁰⁾ A number of converging experimental studies suggest that the occurrence of streaming in the pitch domain is dependent on two parameters: interval size and rate of occurrence (tempo). In a now classic experiment, van Noorden showed that the faster the tempo, the narrower must be the interval between two pitches for those two pitches to form one coherent stream.⁽¹¹⁾ If the tempo is faster than about ten tones per second and the interval between these tones is a minor third or wider then the two pitches will always form separate streams. At a tempo of five tones per second stream segregation always occurs at an interval of about a major ninth or wider. At the other extreme, two tones separated by the interval of a major second or smaller always cohere as one stream regardless of the tempo. Between these extremes, van Noorden identified a perceptually ambiguous region where most musical melodic patterns would lie. Despite this ambiguity, however, it is possible to derive measures of streaming for melodic patterns that estimate how many perceptual streams are likely to occur at a given point.⁽¹²⁾

[38] What is important to emphasize with regard to Narmour’s theory is that streaming is an automatic perceptual process that occurs regardless of the style of music in which it is embedded.⁽¹³⁾ Therefore streaming is exactly the sort of phenomenon that Narmour’s bottom-up perceptual model should capture. To be fair, Narmour is evidently aware of much of the literature on streaming (see Vol 1, p. 352, footnote 5); however, his recognition of the importance of streaming in melodic analyses is somewhat inconsistent. For instance, Narmour’s Example 14.18 (Vol 1, p. 276), an extract from Handel’s violin sonata in G minor, HWV 368, contains the following pitches (all eighth notes in groups of three) analyzed as combinations (see Example 6). To be sure, the upper-level analysis captures the Process, P, that is present between the E♭4, E4 and F4 that sound on the beat. Unfortunately the lines that also emerge in the “middle” and “upper voices” (B♭4–C5–C5 and G5–G5–A5 respectively) are not reflected at all. In my opinion, in this case, Narmour’s concern with the note-to-note implications and realizations overshadows the perceptually more salient stream segregation that is likely to occur at this point.

[39] By Volume 2, Narmour’s treatment of streaming is more finely honed. With Example 3.5 (Vol 2, p. 77) Narmour introduces the idea of concurrent overlapping structures caused by streaming. Here, he allows multiple analyses of a compound line: one analysis traces the note-to-note structures while other analyses trace the structures that arise from non-contiguous yet registrally proximate pitches. This, I feel, captures quite neatly the perceptual ambiguity that is inherent in many passages of pseudopolyphony. However, Narmour is not always so vigilant in this regard, there being a number of examples throughout the two volumes where the stream segregation that would likely result from abrupt changes of register (and return) is left by the analytical wayside in favor of note-to-note implications and realizations (Volume 1: Examples 8.17a p. 175; 10.10, p. 204; 14.17, p. 275; 21.3, Vol 1, p. 353. Volume 2: Examples 8.8, p.183; 9.9, p. 195; 10.11, p. 227).

[40] My contention that streaming should figure more centrally in a bottom-up theory of melody perception and cognition, foreshadows a more general refinement that I shall offer, namely consideration of tempo. The extent to which intervallic relationships between contiguous pitches are registered by the human auditory apparatus, and therefore the extent to which implications based on interval size and direction can be generated, will depend on the absolute rate at which those pitches sound.

[41] At one extreme, as the streaming research cited above suggests, if notes sound too rapidly the intervallic and temporal relationship between them becomes blurred. At the other extreme, if notes sound too slowly, owing to the limitations of short-term auditory store the brain is not able to integrate the separate pitches into one coherent whole.⁽¹⁴⁾ Between these two extremes, tones are most readily grouped together when separated between about 250 and 900 milliseconds, that is between metronome markings 240 and c. 70.⁽¹⁵⁾ A reasonable hypothesis might then be that melodic implications are more compelling within this range than outside it. Of course, for an analytical system that takes the musical score as its source, tempo does not immediately present itself as a vital parameter. Tempo is one of the least well defined parameters in a score and probably the one that varies the most within one performance and between different performances. However, this problem is far from insurmountable— one might take the tempi from “classic” or “benchmark” recordings, for example—and some consideration of the range of tempi at which a passage might be presented to a listener would be a welcome addition to the model.

Conclusion

[42] Despite some minor inconsistencies, Narmour’s ideas merit wide dissemination. Unfortunately Narmour is not always his own best evangelist; his presentation and ordering of concepts often obfuscates rather than elucidates, with many of the principles of the model being introduced piecemeal via numerous musical examples throughout the two volumes. Also, possibly in an effort to reveal the multifaceted nature of the theory as quickly as possible, Narmour sometimes presents concepts in musical examples before these concepts have been given more than a very cursory introduction in the text. In this regard, Chapter 1 of Volume 1, for example, makes a rather discouraging beginning to what is ultimately a rewarding read.

[43] On a more positive note, the model offers a wealth of experimental hypotheses for researchers in music perception and cognition. Indeed, if the 1995 Society for Music Perception and Cognition annual conference in Berkeley is any indication, Narmour’s ideas are currently the object of favorable attention among many music psychologists. Also, partly in response to Narmour’s own list of experimental questions posed at the end of his first volume, there is now a small but ever-burgeoning literature of empirical studies that have tested aspects of the model.⁽¹⁶⁾ While in the interests of internal validity these experiments have generally used short and simple melodic stimuli, their converging results tentatively support many of Narmour’s principles.⁽¹⁷⁾

[44] Overall, my complaints notwithstanding, the implication-realization model is surely a highly impressive undertaking. In drawing together the numerous parameters of musical sound it fastidiously reflects much of the richness of the note-to-note experience of melody. Yet, despite its attention to detail, the theory provides a parsimonious taxonomy of melodic shapes. This classification system could well prove invaluable in such analytic enterprises as tracing a composer’s stylistic evolution or comparing melodic styles among two or more different composers. Some may feel that style-specific top-down processes are given rather short shrift; however, the author promises further coverage of such matters as well as the treatment of counterpoint and large-scale tonal structures in future volumes. In the meantime, Narmour should be credited for going much of the way towards addressing the complaint by Meyer that was quoted at the beginning of this review—with the implication-realization model, Narmour has offered an extremely viable conceptual framework for the analytical criticism of melody.

Matthew S. Royal
University of Western Ontario
Faculty of Music
Talbot College
London, Ontario, Canada, N6A 3K7
mroyal@julian.uwo.ca

Works Cited

Berry, Wallace. Structural Functions in Music. New York: Dover, 1987; reprint, Englewood Cliffs, NJ: Prentice Hall, 1976.

Bregman, Albert S. Auditory Scene Analysis: The Perceptual Organization of Sound. Cambridge, MA: MIT, 1990.

Cooper, Grosvenor W., and Leonard B. Meyer. The Rhythmic Structure of Music. Chicago: University of Chicago, 1960.

Cowan, Nelson. “On short and long auditory stores.” Psychological Bulletin 96 (1984): 341–70.

Hartmann, William M., and Douglas Johnson. “Stream segregation and peripheral channeling.” Music Perception 9 (1991): 155–84.

Huron, David. “Voice Segregation in Selected Polyphonic Keyboard Works of Johann Sebastian Bach.” Ph.D. diss., University of Nottingham, U.K., 1989.

Krumhansl, Carol L. “Music psychology and music theory: Problems and prospects.” Music Theory Spectrum 17 (1995): 53–80.

Lerdahl, Fred, and Ray Jackendoff. A Generative Theory of Tonal Music. Cambridge, MA: MIT, 1983.

McAdams, Stephen, and Albert S. Bregman. “Hearing musical streams.” Computer Music Journal 3 (1979): 26–43, 60, 63.

Meyer, Leonard B. Explaining Music Berkeley, CA: University of California, 1973.

Michon, John A. “The making of the present: A tutorial review.” In Attention and Performance VII, ed. Jean Requin. Hillsdale, NJ: Lawrence Erlbaum, 1979.

Thompson, William F. Review of The Analysis and Cognition of Basic Melodic Structures and The Analysis and Cognition of Melodic Complexity, by Eugene Narmour. Journal of the American Musicological Society, in press.

van Noorden, Leon P.A.S. “Temporal Coherence in the Perception of Tone Sequences.” Ph.D. diss., The Institute of Perception Research, Eindhoven, The Netherlands, 1975.

Woodrow, Herbert. “The role of pitch in rhythm.” Pychological Review 18: (1911): 54–77.

Footnotes

1. Leonard B. Meyer, Explaining Music (Berkeley, LA: University of California, 1973), 109.
Return to text

2. Meyer, Explaining Music, 109–110.
Return to text

3. Eugene Narmour, The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model (Chicago and London: University of Chicago, 1990); Eugene Narmour, The Analysis and Cognition of Melodic Complexity: The Implication-Realization Model (Chicago and London: University of Chicago, 1992).
Return to text

4. Fred Lerdahl and Ray Jackendoff, A Generative Theory of Tonal Music (Cambridge, MA: MIT Press, 1983).
Return to text

5. Meyer, Explaining Music.
Return to text

6. Grosvenor W. Cooper and Leonard B. Meyer, The Rhythmic Structure of Music (Chicago and London: University of Chicago, 1960); Lerdahl and Jackendoff, Generative Theory.
Return to text

7. Herbert Woodrow, “The role of pitch in rhythm,” Psychological Review 18 (1911): 54–77.
Return to text

8. Narmour, Vol 2, 32.
Return to text

9. Wallace Berry, Structural Functions of Music (New York: Dover, 1987; reprint, Englewood Cliffs, NJ: Prentice Hall, 1976).
Return to text

10. Albert S. Bregman, Auditory Scene Analysis: The Perceptual Organization of Sound (Cambridge, MA: MIT, 1990); Stephen McAdams and Albert S. Bregman, “Hearing Musical Streams,” Computer Music Journal 3 (1979): 26–43, 60, 63.
Return to text

11. Leon P.A.S. van Noorden, “Temporal Coherence in the Perception of Tone Sequences” (Ph.D. diss., The Institute of Perception Research, Eindhoven, The Netherlands, 1975).
Return to text

12. David Huron, “Voice Segregation in Selected Polyphonic Keyboard Works of Johann Sebastian Bach” (Ph.D. diss., University of Nottingham, UK, 1989), ch 14.
Return to text

13. William M. Hartmann and Douglas Johnson, “Stream segregation and peripheral channeling,” Music Perception 9 (1991): 155–84.
Return to text

14. For a review of the literature on the low-level auditory store see Nelson Cowan, “On short and long auditory stores,” Psychological Bulletin 96 (1984): 341–70.
Return to text

15. John A. Michon, “The making of the present: A tutorial review,” in Attention and Performance VII, ed. Jean Requin (Hillsdale, NJ: Lawrence Erlbaum, 1979).
Return to text

16. For a good list of recent empirical investigations of Narmour’s theory see William Forde Thompson, review of The Analysis and Cognition of Basic Melodic Structure and The Analysis and Cognition of Melodic Complexity, by Eugene Narmour, in Journal of the American Musicological Society (1995): in press.
Return to text

17. For example Carol L. Krumhansl, “Music psychology and music theory: Problems and prospects,” Music Theory Spectrum 17 (1995): 53–80.
Return to text

Copyright Statement

Copyright © 1995 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.