Issues in the Study of Similarity in Atonal Music

Introduction

[1] A number of recent studies have considered the measurement of similarity between pcset classes.⁽¹⁾ The similarity measures proposed in these studies all relate set classes. Yet such measures are of practical value only if they are used in connection with instances of these set classes, whether they be created compositionally or identified analytically.⁽²⁾ The context in which a pcset is presented, however, can distort the features of a set in numerous ways. Furthermore, pitch is only one of several aspects of music in which similarity can affect our judgment of musical meaning. As David Lewin notes in comments broadcast to mto-list in response to an article published in this journal by Thomas Demske, the word “similarity” is being overworked these days in music analytic settings.⁽³⁾ Lewin objects, for example, when two musical segments are called “similar” when in the most perceptually immediate fashions they may be quite dissimilar. While I would not go so far as to suggest banning the word from our discourse (a possibility Lewin grudgingly admits would likely be impossible), it is certainly the case that invoking the term “similarity” without further qualification is problematic, because any two things will be similar in some ways and dissimilar in others. Though I would argue that there is nothing wrong with the word, per se, it is clear that we need to be more specific about what we mean when we say two musical gestures are similar. Furthermore, we should acknowledge that we have a poorly developed understanding of the roles similarity plays in music, and are therefore using crude tools in a crude fashion. Refining these tools will require getting acquainted with the theoretical and experimental literature on similarity in cognitive science and psychology. Recent work by Robert Goldstone would provide a good jumping-in point.⁽⁴⁾ Further exploration of this literature lies outside my intended scope here.

[2] It is the concern with the effects of context on similarity judgments that motivates this paper. The paper begins first, however, with a critical examination of the state of research in the area of set-class similarity. Specifically, it articulates some unresolved issues surrounding this narrowly focussed aspect of similarity. After this close-up shot on set-class similarity, the paper begins to zoom out, considering next how we might take musical context into account when considering similarity of this sort. Zooming further out, it will look at how set class similarity might interact with similarity in other dimensions through an analysis of Schoenberg’s Op. 19, No. 4. Finally, the paper looks at some more general issues relating to context-sensitive similarity, and briefly considers the place of these fairly limited notions of similarity in the larger context of human cognition.

Some Questions

[3] We begin by considering the measurement of similarity between uninstantiated pitch-class sets, or set classes. “Similarity measures” here will mean those functions which propose to measure similarity of interval-class or other subset content. I believe that Rahn’s view remains viable: that an effective context-sensitive measure of pcset similarity (what Rahn calls a “theory of harmony”) will need to be based on a suitable context-free similarity measure.⁽⁵⁾

[4] There are some unresolved questions pertaining to such measures, however, and we begin by exploring these. First, what does it mean for two set classes to be maximally or minimally similar? This is important because the various similarity measures described in the literature do not fully agree about what constitutes maximum and minimum similarity. For example, under Lewin’s REL, Rahn’s ATMEMB, and Castren’s RECREL,⁽⁶⁾ all set-class pairs having no common subsets are considered minimally similar. My IcVSIM, on the other hand, measures the extent of “skewedness” of two set classes’ difference-vector entries, not the extent of their shared ic content. No skew means maximum similarity; maximum skew (within the possibilities of the 12-pc SC universe) indicates minimum similarity. The extent of shared subset content thus only indirectly affects the similarity value. For example, the dyads 2-1 and 2-2 have an IcVSIM value of 0.577, in the 95th percentile of all IcVSIM values.⁽⁷⁾ But 3-1 (0,1,2) [210000] and 3-10 (0,3,6) [002001], which also have no common ics, have a value of 1.291 (39%; increasing IcVSIM values indicate decreasing similarity). The contrast between these two views seems somewhat Orwellian: all disjoint SCs are equally dissimilar (according to one set of functions), but some are more equally dissimilar than others (according to other functions). Nevertheless, there is a certain sensibility to both views. The first group of functions says that sets with no common features cannot be viewed as having any more than absolute minimum similarity. IcVSIM, on the other hand, takes the view (though not explicitly) that, for example, dyad pairs are more likely to be non-intersecting than trichord pairs. Thus, the fact that a pair of trichords is non-intersecting is more striking than the fact that a pair of dyads is.⁽⁸⁾

[5] At the other end of the scale, does it make sense for non-identical set classes to be judged maximally similar? All measures which base their similarity rating only on interval-class content necessarily judge Z-related set classes to be maximally similar. My IcVSIM also considers sets to be maximally similar whenever their ic-vector entries differ by a constant value, the vectors thus having the same “contour.” Set classes 5-11 (0,2,3,4,7) [222220] and 8Z15 (0,1,2,3,4,6,8,9) [555553] form such a pair, since adding 3 to each entry of 5-11’s ic vector yields the vector for 8Z15. Measures based on the proportional distribution of the vectors’ contained elements, such as Castren’s RECREL, find pairs like the whole-tone set class 6-35 (0,2,4,6,8,10) [060603] and its lone pentachordal subset 5-33 (0,2,4,6,8) [040402] to be maximally similar. Lewin’s REL_2_ function—that is, REL using the dyads as the TEST sets—also finds these set classes maximally similar. REL where TEST contains all set classes does not, however, because 6-35 contains an instance of 6-35 which 5-33 does not. The REL value of 0.97 (99.1%) reflects the subtle dissimilarity of these set classes. There is no question that this latter pair of set classes is particularly closely related, but it would seem desirable to judge non-identical set classes to be less than maximally similar. This is not possible when considering only ic content.

[6] Another question is how similarity should correlate with inclusion. In their study of musical contour, Marvin and Laprade assert that “one of the most intuitively satisfying ways of judging similarity in csegs [contour segments] of differing cardinalities is to count the number of times the smaller cseg is embedded in the larger”.⁽⁹⁾ Given that they go on to propose a number of measures of cseg similarity based on parallel constructions in pcset theory, I take the authors to suggest that the embedding of one set in another would also be a suitable measure of the similarity of those sets. This would be akin to using Lewin’s embedding function (EMB) as a similarity measure for pcsets.⁽¹⁰⁾ This assertion is unsatisfying for two reasons. First, since same-sized sets cannot be embedded in one another, two different criteria for measuring similarity are required—one for same-sized and one for different-sized sets. Further, the potential for embedding increases as the difference in the sets’ sizes grows. A six-note set contains only six five-note subsets, but twenty three-note subsets. According to this view, a three-note set would,on average, be more similar to a six-note set than would a five-note set. Yet my intuition suggests that, on average, we would expect five- and six-note sets to be more closely related than three- and six-note sets because they tend to have more common features. The embedding number between two sets tells us something quite different than does their shared subset content. The embedding number sets up a dependent relationship—set X is contained in set Y n times. But in measuring their similarity, we need to examine the objects on the same basis.

[7] Metaphorically, we might consider how the relationship between a set and its (perhaps multiply embedded) subset parallels the relationship between a daughter and her mother. To judge the similarity of a daughter and her mother, we compare their features: hair color, nose shape, laugh, temperament, and so on. Though similarity in any of these features may result from their genetic lineage, lineage is not the same as similarity. After all, there are certainly instances in which one pair of unrelated people is more similar in appearance than another pair with shared genes (consider Jay Leno’s Dancing Itos, or the world’s overabundance of Elvis look-alikes, for example!). Likewise, multiple embedding of set class X in set class Y may make X and Y similar, but not necessarily more similar than Y and a third set, Z. Thus, while the similarity between musical objects may correlate with an embedding relationship—and often does to a large, if not perfect extent—it need not.

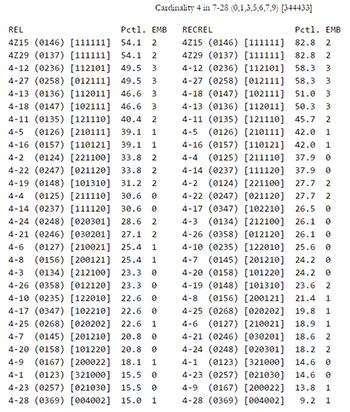
[8] One such case is illustrated in Table 1. The table shows the relationship between the embedding number (EMB) and two similarity measures, REL (with all set classes in TEST) and RECREL (the former of which is based explicitly on the embedding number), for set class 7-28 and the tetrachords. The choice of similarity functions here is insignificant; other functions yield similar results. For each function, the tetrachords are sorted according to their similarity to 7-28. Nineteen four-note set classes are subsets of 7-28, with four set classes (4-12, 4-13, 4-18, and 4-27) occurring as many as three times. Ten tetrachordal set classes are not subsets of 7-28. If the embedding number and the similarity values were maximally correlated, the embedding numbers would decrease as one moves down the list. While those set classes occurring as subsets of 7-28 three times are among those set classes most similar to 7-28, a number of 7-28 subsets are found far down both lists, including set-class 4-28, which is the tetrachord least similar to 7-28 according to both functions. On the other hand, set classes not found in 7-28 can be found as high as the thirteenth position in the REL list and tenth in the RECREL list.

[9] Another issue is whether all instances of an interval class (or other embedded subset) contained in a set class should be considered equivalent. Existing measures of ic similarity, for example, treat the fourth instance of an ic as having the same “value” as the first. Yet the difference between having one instance compared to zero of some ic is proportionately more dramatic than the difference between having four compared to three.⁽¹¹⁾ With each additional instance of an ic, the collection becomes increasingly saturated with that ic and changes are (presumably) less noticeable. Lewin’s REL takes this into effect to some extent. At the core of REL is the summing of the geometric means of corresponding subset vector entries: SQRT(X_i_ * Y_i_). If both sets being compared contain two instances of some interval class, SQRT(2 * 2) = 2 is added to the summation. But if set X has half as many instances of that ic, 1, set Y must have twice as many, 4, to achieve the same result: SQRT(1 * 4) = 2. In other words, instances 3 and 4 of set Y are effectively equal in value to instance 2 of set X.

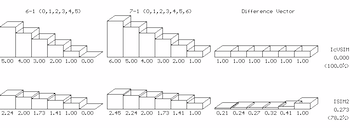
[10] Any of the similarity measures based on difference vectors, such as Morris’s SIM ⁽¹²⁾ and my IcVSIM, could be modified to work with a scaled ic vector which gives less value to each additional ic instance. There are many ways one might scale vector entries. One would be to replace each ic-vector entry with its square root. The vector for set class 6-32 (0,2,4,5,7,9) [143250] would become [1.00 2.00 1.73 1.41 2.24 0.00]. The first instance of an ic is therefore worth 1.0, the second is worth SQRT(2) - SQRT(1) = 0.41, the third is worth SQRT(3) - SQRT(2)=0.32, and so on. A pair of vectors scaled in this way could then be supplied as input to the IcVSIM function (which calculates the standard deviation of the difference vector entries). I will call the measure that uses this scaling function ISIM2.⁽¹³⁾ Example 1 illustrates how scaling the ic vector in this way affects the similarity rating between the chromatic six- and seven-note collections. The first row of graphs shows the ic vectors for the two sets and their difference vector. Since the entries in the difference vector are all 1, IcVSIM judges the sets to be maximally similar (IcVSIM=0.0). The second row of graphs shows the vector entries scaled by the square root function. The difference vector at the lower right shows that the extra ic1 in 7-1 is much less significant (0.21) than the extra ic6 (1.0). The difference vector is no longer level and the similarity value of 0.273 puts these two sets at the 78th percentile of all ISIM2 values, compared to the 100th percentile under IcVSIM.

[11] Another factor not taken into account in the existing similarity literature is the qualitative differences between the interval classes. For example, do we hear ic1 and ic2 as equal in dissimilarity to, say, ic1 and ic5? Might their similarity be affected by factors such as relative consonance or dissonance? (Interval-classes 1, 2, and 6 are relatively dissonant, for example, while ics 3, 4, and 5 are relatively consonant⁽¹⁴⁾. Or perhaps we might also hear ic4 as more similar to ic2 than to ic1, for example, because ic4 sounds more “whole-tone” than “chromatic.” To take this into account, we might create a scaled ic vector along the lines of the previous paragraph in which each instance of an interval-class would evoke a weaker sense of the other ics according to some empirically determined formula.

[12] Having now backed into the issue of perception, let us now consider it more explicitly. There is a sometimes unstated, and always unsubstantiated, claim among the authors of similarity measures that there is a correlation between theoretical and actually perceivable similarity. Morris, for example, suggests his measure would provide “a rationale for the selection of sets that insure predictable degrees of aural similitude.”⁽¹⁵⁾ I have been more cautious, saying only that a correlation between similarity measures in the abstract and the music as heard would be “interesting.”⁽¹⁶⁾ Castren goes furthest, perhaps. Through informal and, by his own admission, unscientific testing, with himself as the lone subject, Castren found that “chords derived from set-class pairs with RECREL values approximately up to 20 seemed to cause an impression of similarity.”⁽¹⁷⁾ (RECREL values range from 0 to 100, with 0 indicating maximum similarity. A value of 20 represents approximately the 90th percentile.) The lack of any published work which confirms or refutes the perceptual validity of the similarity measures found in the literature makes all such claims speculative, however.

[13] Stepping back a little further, we can now consider this more interesting and more difficult question: How does musical context affect our judgment of similarity? Measures of set-class similarity must assume that all pcs in a set are equally “connected” and implicitly treat the intervals found between them as perceptually equivalent. But once a set class is instantiated, the salience of its members will vary, and the connection strength between those pitches will likewise vary, influencing our aural picture of a musical segment’s interval-class content. Factors that affect the relative salience of pitches include their registral placement, dynamics, duration, and timbre. Lerdahl includes these and other salience conditions in an engaging article in which he proposes an extension of his and Jackendoff’s theory of tonal prolongational structure to the atonal repertoire.⁽¹⁸⁾ Morris, in his presentation of a contour reduction algorithm, grants greater salience status to the first and last pitches of a melodic line and to registral maxima and minima.⁽¹⁹⁾ The salience of the interval-classes formed by those variously salient pitches is also based on a number of factors, including at least the relative registral, temporal, and order proximity of the pitches. (Our reliance on the artificial partitioning of the musical surface into discrete analytical objects is another complex issue that is discussed briefly below. It is an area which merits further discussion in another forum.)

[14] Consider Examples. 2A and B, which show two instances of the segment [D-F♯-G]. In Example 2A, the pitches are in a similar register and have equal durations and dynamics. All three pitches are relatively equal in salience and the interval classes found between them (1, 4, and 5) would seem to be represented approximately equally. In Example 2B, the middle pitch is dropped an octave and its dynamic level reduced. Here the salience of ics 1 and 4 would seem to be reduced relative to that of ic 5.

[15] Consider now Examples 2C-E which show three realizations of the chromatic hexachord, set class 6-1, whose ic vector is [543210]. The version in Example 2C—the set in its “prime” form—emphasizes the set class’s chromatic features, though I think we would be inclined to hear the other ics in roughly the same proportion as they are found in the ic vector. In Examples 2D and E, rhythmic differentiation is introduced. Because their attack points are closer together, we are inclined to group a short note with a following rather than a preceding long note. Thus, in Example 2D, the semi-tonal connections, indicated on the example by slurs, would be heard more strongly than the whole-tone connections. This is reversed in Example 2E, where the temporally more proximate pitches are related by whole step. We might thus expect a contextually derived interval-class vector for Example 2D to weight ic1 more than a similar vector for Example 2E. Likewise, Example 2E’s vector would reflect the greater emphasis on ic2, relative to Example 2D. The issue of ic weighting in large vertical structures is explored by Robison, who suggests that the greater the registral distance between two pitches, the less the interval-class between those pitches should count in the ic vector.⁽²⁰⁾

[16] We have been concerned to this point with a narrowly defined notion of “similarity”—the intervallic or subset similarity of pitch-class sets. As noted at the beginning of this paper, however, in most Western music musical meaning derives substantially from the manipulation of similarity and dissimilarity in various musical dimensions. Frequently, musical objects being compared will be similar in some ways and dissimilar in others. This is clearly central to such concepts as “motivic development” and “theme and variations,” but it plays a role in many other ways. There are numerous other dimensions along which we might measure similarity. These would include, but certainly not be limited to, contour, rhythm, metric orientation, register, distribution in pitch-space, textural deployment (vertical versus horizontal), location within the overall texture, articulation, dynamics, and timbre. Similarity in some non-pitch parameters has been the formal subject of recent studies. For example, Marvin and Laprade, and Morris, discuss contour similarity, and Marvin discusses rhythmic contours in the music of Varese.⁽²¹⁾ Orpen and Huron discuss how similarity in various parameters might be measured quantitatively (giving examples from J. S. Bach) through a single mechanism, the Damerau-Levenshtein metric for measuring edit distances between data sets.⁽²²⁾

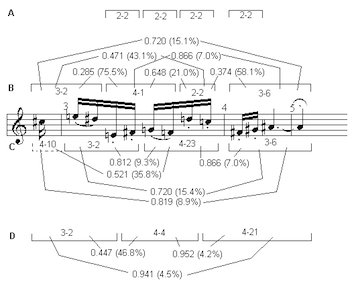
Analytic Implications

[17] We will focus here specifically on the interaction between pcset similarity and similarity in other dimensions. Though means of quantifying similarity in some of these other dimensions either exist or could be proposed, my approach is sufficiently informal to allow a more informal approach. Examples 3 through 8 are excerpts from Schoenberg’s Kleine Klavierstuck, Op. 19, No. 4. In each example, musical segments are labeled with Forte numbers, while similarity ratings of various segment pairs are shown using the ISIM2 function described above. The ISIM2 value is followed by the percentile ranking placing that value in the context of ISIM2 values for all set-class. The percentile ranking makes it unnecessary to interpret the ISIM2 values (which, incidentally, range from 0 to 1.54). I should note further that, although the various similarity measures do not always agree so nicely, all the points I will be making hold, save one or two, which are noted, if Lewin’s REL or Castren’s RECREL functions are used instead.

[18] In the opening bars of Op. 19, No. 4 (Example 3), a melodic fragment is interrupted by a short, accented dyad. These two gestures are dissimilar in many ways: one is melodic, the other harmonic; one extends over two bars, the other lasts just a 32nd note; the melodic gesture is marked piano, while the dyad is forte (dynamics are not shown on the example). The gestures are also dissimilar intervallically. The melodic line, set-class 5Z17 (0,1,3,4,8) [212320], lacks only a tritone; the dyad with which it is juxtaposed is exactly that interval class, set-class 2-6. The ISIM2 value for these sets is at just the 5th percentile, reflecting strong dissimilarity. These contrasts in various dimensions establish a theme for the rest of the piece.

[19] The following phrase, shown in Example 4, is like the first in many ways. A melodic line—with more notes than that of the first phrase, but with an obviously derivative general contour—is again interrupted by a shorter harmonic gesture, marked with a contrasting articulation (legato versus staccato). The example shows the melodic line divided into two segments based on the recovery of the initial register upon the leap up to D5. As in the first phrase, the contrasting parts of the texture also contrast with respect to their intervallic similarity. The ISIM2 percentile values for the first melodic segment compared to the two harmonic segments are 8.0% and 12.7%, while those for the second melodic segment compared to the harmonic segments are 0.3% and 0.8%. Consider now, however, the relation between the two melodic segments. Although they are clearly similar in many ways—rhythm, register, general contour, articulation—intervallically they are quite dissimilar (2.9%). Likewise, the two components of the harmonic gesture at the end of the phrase are also very dissimilar (2.5%). This becomes a pattern in this piece. With one exception, adjacent musical segments which are similar in one or more ways are made up of distinctly dissimilar set classes.

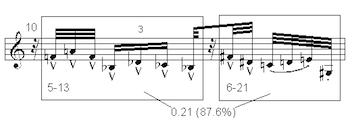
[20] Examples 5 and 6 show this for two of the three remaining phrases of the piece. In Example 5, the chords in measure 6 have an ISIM2 value below the 10th percentile, while the ISIM2 percentile for the two melodic segments is 4.0%.⁽²³⁾ Finally, in Example 6, the two chords that accompany the closing melodic gesture have an ISIM2 value below the 10th percentile. Each of the phrases shown in these examples seems to contain a sense of progression through a change in intervallic content within segments that are otherwise similar in one or more “surface” ways. Though I am not sure that my hearing isn’t being affected by my analysis, I am certain that I hear the piece going this way.

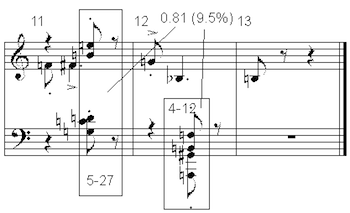
[21] The one exception to this pattern occurs in the rapid figure played between the previous two examples (Example 7). The melody here divides into two segments which are similar in overall contour, register, rhythm, and, uniquely in this piece, ic content (87.6% according to ISIM2). This measure goes by very quickly, and again I may be imagining this, but I do not hear the sense of progression or contrast that I hear in the earlier examples.

[22] This is a natural point to discuss the crucial role segmentation plays in analysis of this sort. The identification of musical segments can have a powerful effect on similarity relations. Adding one note to a five-note segment, for example, increases the number of interval classes by 50%. Depending on the circumstances this can sometimes change substantially the intervallic makeup of that segment and thereby affect the relations between that and other segments. The extent of the effect, however, depends on what interval classes are actually added.

[23] This issue is explored in Example 8, which reconsiders the melodic line of measures 3–5, a passage originally examined in Example 4. As shown in Example 8A, this melodic line includes four non-overlapping major seconds (set class 2-2), with an additional M2 between the last two notes. The saturation of this interval provides considerable unity to the melodic line. Yet combining these dyads in different ways, or segmenting the notes in ways which do not preserve this feature, reveals dissimilarities on a larger-scale. In Example 4, for example, this line was divided into two segments based on recovery of the higher register, 6-2 and 5-33, strongly dissimilar sets (their ISIM2 value ranks at 2.9%).

[24] Examples 8B-D show three other possible segmentations.⁽²⁴⁾ ISIM values and their respective percentiles are shown for each pair of sets in each segmentation. In Example 8B the phrase is divided into four segments based on registral proximity. Here, segments 1 and 2 are fairly closely related (76%), as are segments 3 and 4 (58%). The apparent dissimilarity between segments 2 and 3 (21%) is exaggerated by the fact that similarity ratings involving dyads tend to be quite low for most similarity functions because of the paucity of interval-classes. Nevertheless, segment 3 is notably more similar to segment 4 than to segment 2. Considering non-adjacent segments, segments 1 and 3 are as similar as a dyad could be to 3-2, but segments 2 and 4 are decidedly dissimilar (7%), suggesting again a 2+2 grouping of these segments. Finally, segments 1 and 4 are also quite dissimilar (15%). Though there are some changes in the particulars, the segmentation in Example 8B bears out the relations shown in Example 4.

[25] The three-segment partitioning of the melody in Example 8C is based on the underlying metric framework, the similarity in articulation between beats 1 and 2 in measure 3, and the quasi-contour inversion (high dyad—low dyad → low dyad—high dyad) in those same beats. The resulting melodic set classes, 3-2, 4-23, and 3-6, are again highly dissimilar to one another, with the closest relation, that between segments 1 and 3, reaching only 15%. Including the anacrusis C♯ in the first segment seems justified, given the parallel with the opening of the movement. Doing so, however, changes things somewhat. In particular, the new melodic segment 1 (including the C♯) and segment 2 are more closely related, having reached the middle third of ISIM2 values (36%). Lewin’s RELt function, in fact, rates these sets at the 71st percentile among RELt values. (This is so because 4-10 (0235) and 4-23 (0257) each contain two (025) subsets.) On the other hand, including the C♯ anacrusis increases the dissimilarity between segments 1 and 3—in agreement with the other segmentations considered so far. What segmentation 8C shows that the others do not is the repetition, not just of set class, but pitch-class content as well, between melodic segment 2 and the first left-hand segment of measure 4, 4-23 (see Example 4).

[26] One last segmentation, Example 8D, divides the twelve pitches into three groups of four notes, each beginning with a 16th-note anacrusis. Though this segmentation is perhaps more salient visually than aurally, it shares with the others a notable dissimilarity between the earlier segments and the final segment—a dissimilarity which persists despite unity within dimensions such as rhythm, articulation, and small-scale intervallic organization. It agrees nicely, however, with the contour relations among the three segments. Segments 1 and 2, which could be termed “neutrally” similar (47%), share a contour feature in which their “downbeats” are approached from below and “resolve” downward in the manner of an appoggiatura. Segment 3, which is strongly dissimilar to the other segments, is approached from above and “resolves” upward.

Conclusions

[27] In the examples cited above, musical segments with very similar surface features were often quite dissimilar in terms of their intervallic makeup. On the other hand, it is equally likely that in a given composition musical segments which are similar in an abstract sense may be realized in very dissimilar ways in the music. Just as people have features which may or may not be similar (mouth and nose shape, eye and hair color, height and weight, sense of humor, style of laughter, political leanings, ethnic background, and so on), the similarity of musical segments will vary across various musical features. So how should we deal with the conflicts found in the various musical parameters with regard to similarity? We should probably revel in those conflicts since the tension between similarity and contrast is central to the way much western art music works.

[28] This argues for continuing to consider similarity on an individual parameter basis, rather than looking for a generalized similarity index. In the detailed study of individual works, a generalized index would sacrifice much interesting information. (Deciding which parameters to include and how to weight them seems like a impossible task, as well.) But comparing similarity in two or more selected dimensions as above might be useful sometimes. Specific types of similarity relationships could be used in defining musical features. Klangfarbenmelodie, for example, could be defined as a negative correlation between textural stratum and timbre. And observations such as those made above in connection with Op. 19, No. 4, help us understand more about the musical “vectors” at work in a piece. On the other hand, there are undoubtedly times when a generalized notion of similarity would be useful, too. The music history course exercise of distinguishing the music of Mozart and Haydn is a categorization problem in which, through a sometimes (but not always) unconscious comparing of various musical parameters against remembered features of each composer and his music, students attribute a piece to one or the other composer.

[29] To these ends, continued work at developing and refining meaningful similarity measures for different musical parameters would be useful. Similarity of various sorts is implicated in such varied musical concepts as motive, phrase, theme, contrast, variation, development, recapitulation, cadence, meter, form, pitch class, interval, set class, instrument families, and register. It would be fruitful to evaluate more systematically the relative significance of the various parameters for evoking musical meaning, since it is through the manipulation of similarity in various of these domains that composers communicate meaning. In which parameters do similarities and differences help create structural boundaries in a piece? Which help to relate sections to one another? Which help us understand more local organizational levels? Which help to define a particular composer’s style? Do some seem to work in combination with others? The role of context in listening needs more explicit attention as well. Goldstone, for example, discusses five types of context which can influence experiments on similarity judgment (not musical similarity specifially): cultural context, perspectival context, recent (laboratory) context, concurrently displayed information, and “context that is created by subjects when there is none.”⁽²⁵⁾ Though some of these questions may be more interesting to psychologists, we in the music theory community would do well to keep them in mind as well.

Eric J. Isaacson
Indiana University
Department of Music Theory
Music Department
Bloomington
Indiana 47405
isaacso@indiana.edu

Footnotes

1. Critical reviews of this literature appear in the most recent of these: see Eric Isaacson, “Similarity of Interval-class Content Between Pitch-class Sets: The IcVSIM Relation,” Journal of Music Theory 34 (1990): 1–28; Isaacson, “Similarity of Interval-class Content Between Pitch-class Sets: The IcVSIM Relation and Its Application” (Ph.D. diss., Indiana University, 1992), esp. pages 12–135; and Marcus Castren, “RECREL: A Similarity Measure for Pitch-classes” (Ph.D. diss., Sibelius Academy (Helsinki), 1994), esp. pages 16–100.
Return to text

2. Robert Morris comments on the compositional potential of similarity relations in “A Similarity Index for Pitch-class Sets,” Perspectives of New Music 18 (1979–80): 446. In his dissertation, James Bennighof bases a composition on John Rahn’s similarity function, ATMEMB. See James M. Bennighof, “A Theory of Harmonic Areas Defined by Pitch-class Sets” (Ph.D. dissertation, University of Iowa, 1984); and John Rahn, “Relating Sets,” Perspectives of New Music 18 (1979–80): 483–497.
Return to text

3. Thomas R. Demske, “Relating Sets: On Considering a Computational Model of Similarity Analysis,” Music Theory Online 1.2 (1995). Lewin’s remarks were broadcast to mto-talk, the electronic discussion forum associated with Music Theory Online, on 30 March 1995. The comments are available in the MTO archive under the filename mto-talk.march95 (ftp://societymusictheory.org/pub/mto/mto-talk/mto-talk.march95).
Return to text

4. See http://cognitrn.psych.indiana.edu/rgoldsto/papers.html for a list of Goldstone’s papers.
Return to text

5. John Rahn, “Toward a Theory of Chord Progression.” In Theory Only 11/1–2 (1989): 9.
Return to text

6. David Lewin, “A Response to a Response: On Pcset Relatedness,” Perspectives of New Music 18 (1979–80): 498–502; John Rahn, “Relating Sets,” Perspectives of New Music 18 (1979–80): 483–497; and Castren, “RECREL,” pages 101–125.
Return to text

7. Throughout this paper, similarity values are often given with a percentile figure. The percentile indicates where that particular value falls in the context of all values produced by that similarity function. For all functions, a percentile of 0 indicates minimum similarity, while a 100 indicates maximum similarity.
Return to text

8. Having invoked intuition, we must acknowledge that this is a sticky area, since what we call intuition is largely subjective. There will always be situations where people’s intuitions differ, sometimes because of differences in musical experience, sometimes because of different choices from among multiple possible hearings. But while it seems somewhat slippery to insist, “Well, that’s how I hear it,” absent some objective measure—whatever that would be—it will have to do.
Return to text

9. Elizabeth West Marvin and Paul Laprade, “Relating Musical Contours,” Journal of Music Theory31 (1987): 237.
Return to text

10. David Lewin, “Forte’s Interval Vector, My Interval Function, and Regener’s Common-note Function,” Journal of Music Theory 21 (1977): 194–237. The embedding number counts the number of members of an equivalence class contained in some specific set and forms the basis for Lewin’s REL function. For any set classes X and Y, REL(X,Y) is based on the suitably scaled summation, as Z ranges over the sets in TEST, of SQRT(EMB(/Z/,X) times EMB(/Z/,Y)), where TEST might be the dyad classes to measure intervallic similarity, or all set classes to measure total subset similarity (Lewin, “A Response to a Response”).
Return to text

11. This point was raised by Michael Friedman in response to a paper I read at the 1992 meeting of the Society for Music Theory.
Return to text

12. Robert Morris, “A Similarity Index for Pitch-class Sets.”
Return to text

13. This and other ISIM measures using different scaling functions are included in my WinSIMS and DosSIMS computer programs. These programs are available for download from my World-Wide Web home page (http://ezinfo.ucs.indiana.edu/~isaacso/). Descriptions of the scaling functions are also available there.
Return to text

14. David Huron, “Interval-Class Content in Equally Tempered Pitch-Class Sets: Common Scales Exhibit Optimum Tonal Consonance,” Music Perception 11 (1994): 289–305.
Return to text

15. Morris, “A Similarity Index for Set Classes,” page 446.
Return to text

16. Isaacson, “Similarity of Interval-Class Content,” Ph.D. diss., page 251.
Return to text

17. Castren, “RECREL,” page 148.
Return to text

18. Fred Lerdahl, “Atonal Prolongational Structure,” Contemporary Music Review 4 (1989): 65–88; Fred Lerdahl and Ray Jackendoff,A Generative Theory of Tonal Music (Cambridge: MIT Press, 1983).
Return to text

19. Robert D. Morris, “New Directions in the Theory and Analysis of Musical Contour,” Music Theory Spectrum 15/2 (1993): 205–228.
Return to text

20. Brian Robison, “Modifying Interval-Class Vectors of Large Collections to Reflect Registral Proximity Among Pitches,” Music Theory Online 0.10 (1994).
Return to text

21. Marvin and Laprade, “Relating Musical Contours”; Robert Morris,Composition with Pitch-Classes (New Haven: Yale University Press, 1987), esp. Ch. 2; Elizabeth West Marvin, “The Perception of Rhythm in Non-Tonal Music: Rhythmic Contours in the Music of Edgard Varese,” Music Theory Spectrum 13 (1991): 61–78.
Return to text

22. Keith R. Orpen and David Huron, “The Measurement of Similarity in Music: A Quantitative Approach for Non-parametric Representations,” Computers in Music Research 4 (1991): 1–44.
Return to text

23. An alternate segmentation associating the anacrusis with the downbeat chord rather than the following melodic line, and dividing that melodic line into two 5-note segments, yields very similar results, except that the melodic segments are more similar to the chords than in the segmentation used here. I have not shown the inter-textural relations to reduce visual clutter in the example, except the relation between the second melodic segment, 7-34, and the chord which is heard in measure 8, 4Z29. This is the only pair of sets from different dimensions of the texture that are closely related in this piece. The question of alternate segmentations is addressed below.
Return to text

24. The effects of various musical factors on grouping, the resulting possibility of multiple segmentations, and choosing among these, is explored effectively in Christopher Hasty, “Segmentation and Process in Post-Tonal Music,” Music Theory Spectrum 3 (1981): 54–73.
Return to text

25. Robert. L. Goldstone, “Mainstream and Avant-garde Similarity,” Psychologica Belgica 35 (1995): 145–165.
Return to text

Copyright Statement

Copyright © 1996 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.