Review of Christopher F. Hasty, Meter as rhythm
New York and Oxford: Oxford University Press, 1997.

[1.1] Rhythm and meter are difficult to theorize—not only to formalize but also simply to discuss—because of their elusive and variegated nature. For twenty years Christopher Hasty has explored fundamental questions about musical time. In a series of important articles in the 1980’s,⁽¹⁾ he developed some conceptually and analytically productive ways to conceive of temporal processes in music. Although the topics of his articles were not explicitly linked, one would naturally expect a book-length study to follow.

[1.2] After a decade of suspenseful silence, the anticipated book has indeed appeared. Its processive perspective is familiar from the earlier articles, but its topic, the music it discusses, and its grounding in philosophy, psychology, and music theory are fresh. For the importance of its subject, for the quality, consistency, and depth of its theoretical insight, and for the wisdom and clarity of its exposition, Meter as Rhythm should be read and appreciated. It requires a willingness to engage with seemingly small musical details, with diverse musics, and with a speculative, philosophical mode of exposition, but the reader’s persistent efforts will be well rewarded.

2. A New View of Meter as Projection

[2.1] Many modern conceptions of rhythm and meter place them in opposition. Rhythm is often defined to consist of the actually sounding durations of music, while meter is the alternation of strong and weak beats, or the interaction of pulse strata, that are inferred from the rhythm. Rhythm is thus conceived as emerging and active— a “concrete” patterning that is measured by, and heard to work with or against the “abstract,” deterministic, rigid metrical grid. These contrasting conceptions are ingrained deeply into much theorizing and into most practical communication about rhythm.

[2.2] Hasty problematizes this opposition on both perceptual and logical grounds. As an alternative, he defines meter simply, without reference to accent or pulse, as the potential of a duration to be immediately reproduced. This potential arises in connection with sensations that we gather about events as they “become,” or unfold in time. To describe meter from the perspective of an active listener, Hasty appropriates concepts and terminology from Alfred North Whitehead’s Process and Reality. From this perspective, he says, meter is “a process in which the determinacy of the past is molded to the demands of the emerging novelty of the present.” (168). It is thus “rhythmic” in the sense that it, too, is emerging, active, creative and perpetually novel.

[2.3] The essence of meter, in Hasty’s theory, is the process of “projection.” Specifically, as an event becomes, its duration accumulates “projective potential,” or the potential to condition our expectations about the duration of future events. In the simplest case, the duration’s projective potential is “realized” when “there is a new beginning whose durational potential is determined by the now past first event.” We perceive this realization when we project that the second event will replicate the duration that it makes past. The second event’s duration may or may not actually realize this projection, and the parity or disparity that is manifest at its end (at the beginning of a third event) corresponds to musical perceptions of “too short” or “too long” that may be expressively and analytically significant.

[2.4] Hasty illustrates metrical projection with graphical diagrams that (he ruefully notes) necessarily rely on the very spatial metaphors that he is striving to avoid. To gain a better understanding, and a more truly temporal representation of the nature of projection, please examine the Java applet in Example 1.⁽²⁾ It allows the user to determine, in sequence, the beginnings and ends of three line segments, representing events, and to examine the resulting projections and other metrical effects, such as speeding up, slowing down, and hiatus. Click the mouse to define the beginning of the event, then move the mouse to the right to define the duration of the event, then click to end the event. Up to three events of any length may be so determined; however, to keep the demonstration focused on Hasty’s theory, the applet will not permit the user to define events that do not involve metrical projections. The scale of time in the example is calibrated by a constant “Lim” signifying the maximum duration that can be projective, which Hasty speculates to be about two seconds in this highly simplified monophonic texture. Try defining events of various lengths, and observe how the projections accumulate, disappear, and changes accordingly, as explained in the running commentary. (I’m sorry that the current version of the Java programming language does not offer a practical method for playing the sound sequences.)

3. Consequences for Metrical Theory

[3.1] Although the concept of projection is simple, Hasty uses it to develop detailed and enlightening readings of durational patterns. His readings address many fundamental musical issues, for example: the metrical nature of beginning, ending, and continuation; the differences among various patterns ostensibly having the “same” meter; and metrical effects that have been observed by many other analysts.

[3.2] Chapter 9 reworks some traditional conceptions of meter in terms of projection. Metrical accent is defined as “the accent of beginning”; this resembles Jonathan Kramer’s definition (The Time of Music, Schirmer, 1988, p. 86), but has substantive differences. “Beginning” itself is a function that is determined processively—that is, the function of beginning is only perceived as a duration that is begun becomes. The significance of a beginning depends on whether the duration of interest is that of a single event, or of a harmony, or of a series of associated successive durations. In the last case, the later durations in the series contribute to the continuation of the duration of the whole group.

[3.3] Accordingly the distinction between strong and weak (metrical) accent is replaced with a functional distinction between beginning and continuation, as shown in Example 2 (Hasty’s 9.2).

Each small vertical stroke above a note head symbolizes not a beat but to the “becoming” of the entire mensurally determinate duration that is begun by the attack of the note. The larger vertical stroke over the first notehead refers to the becoming of entire duration of two quarter notes; because the half note duration is continued through a series of briefer durations, its onset is called a “dominant beginning.” The slanted stroke over the second notehead indicates that, even while its duration begins, the earlier beginning (of the two-note group) is still actively becoming, so the second event’s becoming is a “continuation” of that duration.

[3.4] The functions of beginning and continuation are not immutable. They may be reassessed as later events modify the listener’s sense of what has begun. For instance, anacrusis is understood in this context as a continuation that becomes “detached” from a beginning.

[3.5] Hasty first employs the concepts of projection, beginning and continuation to analyze the meter of common brief durational patterns. The analyses show how patterns with the same meter signature are actually quite different in projective action. They also permit some original and interesting distinctions, such as between acceleration and increased activity of division. Other effects, such as “silent beginning,” are also explained as results of projection.

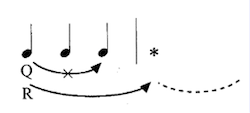
[3.6] Since meter entails the projected reproduction of a duration, duple meter is privileged in the theory. (Indeed the duple bias is reflected frankly in the two-column layout of the book’s text.) Triple meter can nevertheless be explained, however, in the manner shown in Example 3 (Hasty’s 9.18f).

This shows a half-note projection Q, corresponding to a potential duple meter, that is denied by events starting at the asterisk that favor (say, by motivic repetition) a dotted-half projection R. The third quarter note in this situation is then regarded as a “deferral”–it functions to delay the next dominant beginning. More complex meters are also analyzed in similar terms.

[3.7] The traditional terms “beat” and “measure” take on novel connotations in this context. A “beat” is a beginning—not a time point, but a function that is evaluated as the event becomes. “Beats” need not recur at equal time intervals: “the flexibility of mensural determinacy frees projective activity from the narrow confines of ‘precise’ equality” (277). “Measure” refers not to the notated bar, but to any duration that is mensurally determinate. Any projection is therefore a “measure.” Measures “are not given—they are created under the pressure of antecedent events and are creative for present and future events.” A given passage of music may present a polyphony of “measures,” some reinforcing regular meter, and others possibly acting against it.

4. Analytical Applications

[4.1] Chapter 10 initiates a move from the general to the particular by applying the theory in analysis. Meter, as projection, is always specific to the given musical context. For example, Hasty demonstrates, identical durational patterns may have different metrical interpretations depending on their pitches and tempi.

[4.2] Analyzing the meter of a musical passage in these terms entails identifying its projections, and distinguishing beginnings, continuations, and anacruses at the beat and measure level. The theory allows one to explain how, in many cases, the basic projection-functions are modified subtly and richly by denials, overlappings, and contractions. A complete analysis thus explains the continuity or discontinuity in a passage, locates certain common types of projections that execute such formal functions as closure, and identifies certain common metrical processes such as the “contraction of projective focus.”

[4.3] The emphasis on beat and measure does not preclude a consideration of longer excerpts. A whole chapter is devoted to examining how projection—which is perceived only in relatively brief time spans up to a few seconds—may be “simulated” over larger time spans by means of grouping parallelisms and mutually reinforcing briefer projections. Indeed, in the analyses of common-practice tonal music, the focus is not so much the smaller patterns (which generally accord with the notated meter signature) but on the varieties of larger-scale “hypermetrical” contractions and elisions, and their effect onmus ical continuity. To further clarify how he regards this “simulated” meter, Hasty compares his readings to Schenkerian-oriented analyses by Schachter and Rothstein.

[4.4] One of the most impressive aspects of the book is the variety of music that is analyzed. The tonal works analyzed in depth include the first movement of Beethoven’s First Symphony and the Trio of Mozart’s Symphony No. 35. But there are also quite convincing accounts of meter in non-tonal modernist music by Wolpe and Carter, showing what thwarts larger-scale projections, and explaining how various denials and deferrals of dominant beginnings facilitate continuity and the sustaining of energy. With reference to the Webern Saxophone Quartet Hasty explains how hiatus contributes to the creation of a “phrase” built of successive projective “consituents,” each of which possesses varying degrees of openness or closure. He also provides detailed and exciting readings of vocal polyphony by Monteverdi and Schütz, readings that convincingly connect the observed metrical effects to the syntax and semantics of the poetry. No one has succeeded better in expressing verbally the rhythmic nature of these musics.

5. Strengths, Evidences, and a Few Weaknesses

[5.1] Hasty’s theory verges on the systematic, even on the programmable, as Example 1 begins to demonstrate, but he constantly eschews the temptation and dangers of system building. He is frank about the speculative nature of his concepts, and very clear about the intensely personal nature of hearing rhythm and meter. It seems that he is less interested in providing a basis for “verifiable” analyses (however that quality might be defined) than he is in provided a clear language for discussing musicians’ possibly disparate metrical intuitions. He acknowledges, even celebrates, the interaction of composer, performer, listener in creating meter, and shows how tempo, the listener’s attention, and various performance decisions affect the perception of projection— for instance comparing Boulez’s and Craft’s recordings of Boulez’s le marteau sans maître.

[5.2] It is also remarkable that this carefully elaborated theory—in sharp contrast to some contemporary theories of pitch—emphasizes sensation over structure and feeling over logic. The analyses treat not quantities but qualities of (to cite a few examples) “breadth and spaciousness,” “suspense and elasticity,” “urgency,” “mobility,” “relaxation,” “focus,” and getting “lost in a moment of ending.” Style, in this view, “is above all an environmentally (culturally and personally) specific manner of feeling duration.” Such statements may appear foreign to some theorists, but Hasty makes them meaningful through a carefully reasoned and clearly expressed theory of how such feelings arise from a single, intuitively plausible principle.

[5.3] Although the content of his projective theory is primarily speculative, Hasty grounds it by telling references to a variety of psychological studies. Further important precedents for his ideas are revealed in the original glosses and interpretations he provides of earlier music theory. Heinrich Koch, for example, is cited to describe meter “as a creative act of attention, not bound by law, but arising from the exercise of our cognitive or imaginative powers.” Mattheson’s conception of Bewegung–movement through time–is also cited as an early recognition of the essentially processes aspects of rhythm. The 19^th-century theorist who most anticipates Hasty’s theory is Hauptmann, who clearly discusses meter as a process whereby duration is created, a process grounded in an innate perceptual disposition for measure.

[5.4] Hasty also gives due consideration to recent rhythmic theories—Cooper and Meyer, Lerdahl and Jackendoff, as well as Schachter and Rothstein—finding a basis for dialogue even with those that maintain an opposition of meter and rhythm. Other supporting references range widely through twentieth-century philosophy, science, German music theory, and musicology.

[5.5] One important antecedent is inexplicably omitted. There is no mention of Wallace Berry’s Structural Functions in Music (Prentice-Hall, 1976), which is perhaps the most explicit previous treatment of music in terms of process, as it is notably attuned to “the musical work transpiring in time”(25). Berry anticipates Hasty’s terminology: “metric units are initiated by . . . impulses of relatively strong projection” (317). He hears impulses to have different functions, and represents impulse functions with vertical and slanting arrows and lines on scores, as Hasty does. He regards these impulses as functional at different “levels of metric structure,” and also allows for functional “dualities,” “as when the final impulse of a metric unit is both conclusive and anticipative at the same level” (328). Since Hasty spends so much effort at acknowledging tangential theories, it would have been enlightening to read his comments on a theory that is a perhaps distant but nevertheless distinctive precursor of his own. (Perhaps he or others will now consider how his work relates to this and to more recent treatments of meter as process.⁽³⁾

[5.6] Some other minor negligences also bother me. The book suffers from a few production problems: a smattering of typographical mistakes in the text, and, more seriously, some rhythmic errors in the musical examples (Ex. 15.2, an excerpt from le marteau, is an especially egregious and by no means solitary instance). More substantively, many analytical decisions about interpreting the onset of an event as a dominant beginning or a continuation hinge on questions of segmentation that are not addressed directly by the theory. Hasty gives the impression that these questions are impossible to address systematically, but a more explicit discussion of segmentation would help justify some of his analytical decisions.

[5.7] This book is not an easy read. The concepts are original and their author is thorough, so their exposition is long, detailed, and philosophical. Since the theory does not assume any of the common ways of thinking about meter and rhythm, it may not fall into most reader’s comfort zones. Indeed it demands sustained concentration—and a good memory, since the brief index provides little help. But I found it absolutely compelling. It is a vital contribution that has broad potential to affect how we listen, value, and teach music of all styles—potential that will be realized to the extent that we attend to the insights it contains.

John Roeder
University of British Columbia
School of Music
6361 Memorial Road
Vancouver, B.C. V6T 1Z2 CANADA
jroeder@unixg.ubc.ca

Footnotes

1. Hasty’s articles include:

• “Rhythm in Post-tonal Music: Preliminary Questions of Duration and Motion,” Journal of Music Theory 25.2 (1981): 183–216.
• “Segmentation and Process in Post-tonal Music,” Music Theory Spectrum 3 (1981) 54–73
• “Phrase Formation in Post-tonal Music,” Journal of Music Theory 28.2 (1984): 167–90.
• “On the Problem of Succession and Continuity in Twentieth-century Music,” Music Theory Spectrum 8 (1986): 58–74.

2. I gratefully acknowledge Tom Roeder for realizing my design of this example in the Java programming language.
Return to text

3. For instance, Justin M. London, “Loud Rests and Other Strange Metric Phenomena (or, Meter as Heard),” Music Theory Online 0.2 (1993): 0–16; and John Roeder, “Formal Functions of Hypermeter in the ‘Dies irae’ of Verdi’s Messa da Requiem,” Theory and Practice 19 (1994): 83–104.
Return to text

Copyright Statement

Copyright © 1998 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.