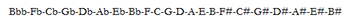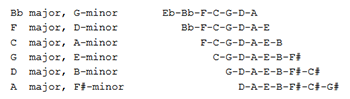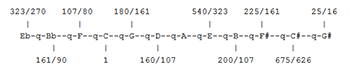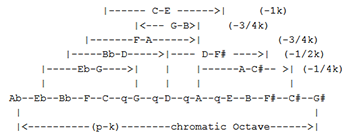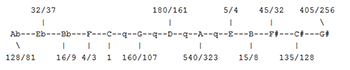Algorithms for Mapping Diatonic Keyboard Tunings and Temperaments
Kenneth P. Scholtz
KEYWORDS: Algorithm, chain of fifths, diatonic scale, equal temperament, enharmonic, just intonation, meantone, Pythagorean tuning, schisma, syntonic comma
ABSTRACT: Diatonic keyboard tunings in equal temperament, just intonation, meantone and well tempered scales are derived from Pythagorean tuning using algorithms whose operations involve combinations of pure fifths and syntonic commas. Graphic diagrams of the line of fifths are used to show the harmonic and mathematical relationships between common tunings and temperaments. Four modes of just intonation are derived from Pythagorean tuning by an algorithm that narrows each major third by one syntonic comma. Equal temperament is approximated with imperceptible error by algorithms that narrow Pythagorean and justly tuned enharmonic intervals by one or more syntonic commas.
Copyright © 1998 Society for Music Theory
Table of Contents
5. The Four Modes of Just Intonation
8. Algorithms for Schismatic and Syntonic Equal Temperment
1. Introduction
[1.1] This article describes algorithms that map the traditional harmonic tunings and temperaments for the keyboard: Pythagorean tuning, equal temperament, just intonation, and historical variations on meantone temperaments. Keyboard tuning is used because it has been worked out in detail over hundreds of years and is understood to give a reasonable approximation of the pitch choices made by performers on instruments without fixed pitches. I have excluded analysis of multiple divisions of the octave into more than twelve notes because they were not commonly used temperaments. Working from the chain of fifths, we will demonstrate how the intervals in any tuning or temperament can be mapped from Pythagorean tuning by algorithms that combine pure fifths and syntonic commas.(1) The algorithms that map the tunings and temperaments into one another are not purely mathematical, but are derived from the harmonic structure of the chain of fifths and enharmonic relationships between notes.
[1.2] This article is not concerned with generating diatonic scale tuning from prime numbers or otherwise deriving its form from physical or mathematical principles. We will use the historic definition of a diatonic scale as two tetrachords plus one additional tone that completes the octave. The diatonic octave is divided into five whole tones and two semitones in all tunings and temperaments. The convention of assigning letter names to notes in a 12-note chromatic keyboard for diatonic scales will be observed. The chain of fifths will be introduced and used as the defining feature common to all scales without initially assuming any particular tuning.
[1.3] Several modern theorists, including Mark Lindley(2) and Easley Blackwood(3) have applied algebraic techniques in describing the tonal relationships which form traditional diatonic scales. Others have developed diagrams to compare the differences in pitch for a note in various tunings.(4) Although such techniques have their uses, I did not personally find them particularly helpful in visualizing the overall difference between one tuning system or temperament and another. For my own analysis, I prefer to diagram the chain of fifths and use rational fractions to express the size of the intervals.(5) Differences between tuning systems are indicated by placing commas or fractional commas between adjacent fifths. This provides a visual comparison between the separate diatonic tunings and temperaments of a complete scale and makes it easier to demonstrate the mathematical and musical relationships between them.
[1.4] Theorists classify tuning systems as either cyclic, generated by a reiterative sequence of fifths, or divisive, tunings that subdivide the octave.(6) Historically, this division is somewhat arbitrary. Euclid and Boethius derived the Pythagorean tuning that we now associate with a sequence of fifths by dividing a monochord into two octaves.(7) Methods based upon the overtone series or other systems which attempt to derive just intonation from acoustic phenomena are often considered to be divisive in nature. The typographical diagrams utilized in this article interpret tunings and temperaments in terms of the line of fifths.
2. The Chain of Fifths
[2.1] It is well known that every diatonic scale can be reordered into a sequence of fifths. For the C-major scale, the sequence of fifths is F–C–G–D–A–E–B, renumbering the notes of the scale in the order 4–1–5–2–6–3-7. This is the sequence of notes produced when one starts with C and then tunes a keyboard alternately down a fourth and up a fifth until the last note of the scale is reached. For consistency of metaphor, I call the sequence of fifths a “chain” in which the fifths are “links,” without assuming any specific tuning system.
Figure 1. A Section of the Chain of Fifths
(click to enlarge)
Figure 2. Six Diatonic Scales in a Chromatic Chain From
(click to enlarge)
[2.2] The chain of fifths has its origin at C and extends to the
sharp notes on the right and the flat notes on the left. The
chain is theoretically endless, neither closing nor repeating, so
that each note in the chain is musically unique.(8) Figure 1
shows the central 21 links in the chain, with C at the origin.
All the notes in the chain are considered to be within a single
octave bounded by two C’s. Since fifths and fourths are
inversions, each note is a fifth above the note to its left and a
fourth above the note to its right. As a matter of convention,
it is useful to consider the links to the right of C to be
ascending fifths and the those to the left to be ascending fourths. The same seven letter names repeat themselves over and over in
the same invariant sequence of the C-major scale—F–C–G–D–A–E–B—with each repetition augmented by sharps to the
right and flats to the left. Any group of six adjacent links
defines a major diatonic scale whose tonic note is one link from
the left end of the group, and a natural minor scale which starts
two links from the right end. Horizontal movement of any
six-link group is the equivalent of transposition of the scale
into a new key as exemplified by Figure 2. A twelve-note
chromatic keyboard commonly contained the notes from
[2.3] The chain of fifths can be used to rationally order the
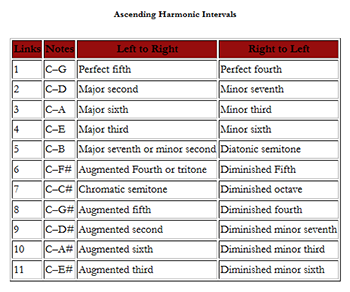
harmonic structure of the diatonic scale. Figure 3 lists the
harmonic intervals available on a twelve-note chromatic keyboard
for each pairing of links in the chain of fifths. The pairs of
notes listed are examples that start with C. Any interval can be
horizontally transposed along the chain of fifths. Figure 3 classifies harmonic intervals by the number of links and
their direction on the chain of fifths. Each pair of intervals
are inversions of one another. Chromatic intervals have more
than six links, diatonic intervals have six or fewer. Generally
speaking, major intervals and augmented intervals ascend from
left to right, while minor intervals and diminished intervals
ascend from right to left. The perfect fourth is the only
consonant interval that ascends from right to left, which may
reflect its harmonic ambiguity. Intervals that ascend to the
right from a flat to a natural are always major, such as
3. Pythagorean Tuning
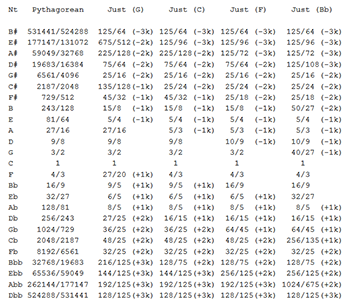
[3.1] Tuning the diatonic scale with pure fifths, now known as
Pythagorean tuning, was the norm for nearly 2,000 years. The
Pythagorean tuning of twelve notes in a standard
[3.2] Although
[3.3] A wolf fifth, “w,” occurs at the end of the line when
4. Equal Temperament
[4.1] Equal temperament has been commonly used for the past 150 years to tune pianos and organs and, before that, was used for fretted instruments such as guitars and lutes. Equal temperament flattens the fifths (and sharpens the fourths) by 1/12 of a Pythagorean comma, “p,” as shown in Figure 5. This is just enough to give a true octave from a chain of 12 links. In musical terms, the 12 fifths in the chromatic line are made exactly equal to 7 octaves. As can be seen from Figure 5, the term “equal temperament” only applies to the fifths. The other intervals are not tempered equally with respect to Pythagorean tuning. In Figure 5, the Pythagorean comma is indicated by the upper-case “P” and 1/12 of the Pythagorean comma by the lower-case “p.” The direction of the arrow indicates the ascending harmonic interval. Reversing the arrow would invert the interval and change the sign of the fraction, as illustrated by the fifth (-1/4p) and the fourth (+1/4p).
[4.2] Since equal temperament makes every thirteenth note the
same, it makes all enharmonic pairs equal; for example,
[4.3] We can easily demonstrate from the chain of fifths that
equal temperament makes both the tuning and the musical function
of each pair of enharmonically equivalent notes equal, using the
12 links from C to
Figure 7. Equal Temperament
(click to enlarge)
Figure 8. Dissonant Internal Intervals in Just Intonation Scale
(click to enlarge)
Figure 9. Just scales in
(click to enlarge)
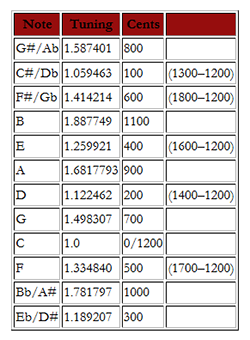
[4.4] Calculating the tuning of an equally tempered scale generates irrational numbers,(14) because the rational fraction that measures the Pythagorean comma must be divided into twelve roots. One equally tempered semitone equals the twelfth root of 2, an irrational number whose value is normally given in a decimal approximation as 1.05946 (100 cents.) The tuning of the chain of equal tempered fifths in six place decimals is given in Figure 7. Using the diagram in Figure 5, the 700-cent logarithmic tuning of an equally tempered fifth is narrower than a 702 cent perfect fifth by 2 cents, 1/12 of the 24-cent Pythagorean comma. The last column in Figure 7 displays this pattern; the pitch of each note in the vertical chain is 700 cents above the note below it before subtracting out the octave.
5. The Four Modes of Just Intonation
[5.1] In Pythagorean tuning, only the fifths and fourths are tuned as consonant intervals. The thirds and sixths generated by a sequence of perfect fifths are not generally considered consonant by comparison to the most consonant major third which is 5/4, a minor third of 5/6 and their inversions, a major sixth of 5/3 and a minor sixth of 8/5. The diatonic tuning that includes both consonant thirds and pure fifths is known as just intonation. One traditional method of forming a C-major scale in just intonation is to combine consonant tonic, dominant and subdominant triads, F–A–C, C–E–G and G–B–D. This tunes the just diatonic scale shown in Figure 8. The D–A link is narrowed by a syntonic comma indicated by the “k.” Since the other links are pure, the pitch of A, E and B will also be lower than Pythagorean by a syntonic comma. Even though each note has its optimum tuning relative to C, just intonation is a theoretical scale which is unsatisfactory for tuning an instrument with fixed pitch because the narrow D–A results in the unjust intervals shown in Figure 8. The narrow D–A sounds much the same as a Pythagorean wolf fifth. The Pythagorean minor third and its inversion, the major sixth between D and F also sound badly out of place in an otherwise just scale.
[5.2] Tuning a chromatic octave in just intonation creates
further difficulties since alternate tunings are required for
each note. A theoretical scale of just intonation can be
calculated for four diatonic major scales in the chromatic octave
by replicating the procedure used to form the scale of C-major.
A scale of
[5.3] It is helpful at this point to introduce the concept of an algorithm, which is a set of instructions for making a series of calculations. Each of the tunings we have discussed so far can be derived from an algorithm for tuning the chain of fifths into one 12-note chromatic octave on a keyboard. The Pythagorean tuning algorithm has four steps:
- C is tuned to an arbitrary unit pitch of 1.
- Tune the pitch of each note to be a perfect fifth (3/2)
from the notes immediately adjacent to it. - If the pitch of any note is greater than 2, divide the
pitch by 2 to keep it within the same octave. - Stop after the 12 notes from
E♭ toG♯ have been tuned.
The equal temperament algorithm is the same as the Pythagorean algorithm except that the interval in step 2 is 1/12 of a Pythagorean comma narrower than a pure fifth. Although justly tuned scales often have been considered to represent a different species from the Pythagorean or the equally tempered scale, we will show in Figure 10 how an algorithm can be derived that maps Pythagorean tuning into just chromatic scales.
[5.4] The scale in Figure 10 has a syntonic comma at every
fourth link. This produces a chromatic scale in which the
diatonic scale of C-major is just and the maximum number of major
thirds are a consonant 5/4. This scale is generated by an
algorithm in which (1) the fourth link of a Pythagorean C-major
scale is narrowed by a syntonic comma and (2) every fourth link
above and below that link is also narrowed by a syntonic comma.
The tuning of the just chromatic scale from
F-major: major fourth broadened by a syntonic comma.
C-major: fifth of the II chord narrowed by a syntonic comma.
G-major: fifth of the dominant triad narrowed by a comma.
D-major: fifth of tonic triad narrowed by a syntonic comma.
A-major: major fourth broadened by a syntonic comma.
It is, thus, amply clear that just scales with consonant thirds cannot be meaningfully used on a chromatic keyboard.
[5.5] Since the scale in Figure 10 was created by an algorithm
that narrowed every fourth link by one syntonic comma, one can
generate four chromatic modes of just intonation, one for each of
the scales shown in Figure 9. These are the only just chromatic
scales that are possible when C has the relative tuning of 1,
since the pattern of the algorithm repeats after the fourth
link.(16) Figure 11 presents the tuning of the four modes of
just intonation along a chromatic scale from
[5.6] F. Murray Barbour listed 22 historical scales of just
intonation dating from 1482 to 1776 in his historical survey of
tuning and temperament.(18) Barbour defined just intonation more
broadly than we have done, including within the concept any
12-note chromatic scale that possessed some pure fifths and at
least one pure third. Barbour described a late 18th-century
tuning by Marpurg which is the same as Figure 10 as “the
model form of just intonation.”(19) Two scales which correspond
to the F-major mode shown in Figure 11 were described by Barbour
as “the most symmetric arrangement of all.” The first was an
early 17th century scale by Salomon de Caus which started with
[5.7] It is also interesting to compare the actual tuning of
notes in Figure 11 with Ellis’s “Table of Intervals not exceeding
One Octave” in his appendix to Helmholtz.(22) Figure 11 gives
new significance to intervals whose names as given by Ellis imply
a diatonic origin. Thus Ellis’s list includes the following
varieties of fourths: “acute,” 27/20, a “superfluous,” 25/18 and
another “superfluous,” 125/96. Figure 11 shows that the
“acute” fourth is the just fourth in the G-major mode, the first
“superfluous” fourth is an augmented fourth,
[5.8] We can now appreciate why the chain of fifths is useful for evaluating the harmonic consequences of alternate tunings of a diatonic scale embedded in a chromatic keyboard. It is not possible to arbitrarily change the pitch of one note without altering its relationship with all other notes in the chromatic space. The interdependence of tuning is not limited to instruments with fixed pitch. For example, a string quartet could not play passages containing a sequence of triads in just intonation without altering the melodic intervals and, possibly the overall level of pitch.(23) The problems of tuning harmonic intervals can only be solved by dynamic ad hoc adjustments of pitch to obtain optimum consonance while preserving the melodic line and stability of pitch.(24) This is one of the reasons why it is so difficult for inexperienced musicians to achieve good ensemble intonation.
[5.9] The syntonic comma is not an independent variable; the independent variables are the tuning ratios for the consonant fifth and major third as determined by psychoacoustic measurements, which are 3/2 and 5/4. The syntonic comma, even though it has been known and separately named for two thousand years is merely derived from the difference between the consonant or just major third and the Pythagorean major third generated by four consecutive fifths. However, one would not intuitively expect that this single dependent variable could be used to measure all the differences in tuning between Pythagorean and just scales, including intervals that are not generated by major thirds.(25) The just intonation algorithms provide a coherent framework for this ancient and well respected dependent variable known as the syntonic comma. As was noted above, just intonation and Pythagorean tuning are commonly thought of as different species of tuning. The just intonation algorithms demonstrate that just intonation can more completely be understood in terms of the chain of fifths and syntonic commas than if considered independently.
6. Meantone Temperament
[6.1] Meantone temperament is a keyboard tuning that makes a
chromatic scale with consonant major thirds playable in diatonic
scales in a few closely related keys. It does so by equally
dividing the syntonic comma over the four links of each
major third. This results in a whole tone that is exactly half-
way between the alternate 9/8 and 10/9 found in just scales. The
name “meantone” is derived from the resulting mid-size interval
for the whole tone even though the division of the whole tone was
only a by-product of distributing the syntonic comma. Dividing
the comma into four “quarter commas” and distributing the
quarter-commas so that every fifth was tempered by one
quarter-comma also smooths out the three narrow fifths created by
the undivided comma in the just scale, replacing them with a
sequence of tempered fifths that are far more tolerable to
the ear. The earliest generally accepted meantone scale was
described by Pietro Aron in the early sixteenth century for a
chromatic scale from
[6.2] The quarter-comma (4q = 1k) narrowing of each link in the chain of fifths is shown in Figure 12, which also depicts the resulting alteration of other intervals from Pythagorean tuning. Compared to Pythagorean tuning, it is evident that the fifths to the right of C are all tuned a quarter-comma flat, while the fourths to the left of C become a quarter-comma sharp. As before, Figures 10 and 12 allow us to measure the difference between the just and meantone scales without using arithmetic. As an example, a mean-tone chromatic semitone is narrowed by 7/4 syntonic commas compared to Pythagorean tuning and 3/4 of a syntonic comma compared to just intonation.
[6.3] Meantone temperament and its variations was the established mode for tuning keyboards for nearly three centuries. English pianos and organs were tuned this way until the middle of the nineteenth century.(27) As Thurston Dart explained in his treatise on early music:
Thus mean-tone provides the player with a group of about a dozen ‘central’ keys in which all the important chords are more in tune than they are in the modern piano. . . . Mean-tone is admittedly imperfect as a tuning for chromatic music; for diatonic music, however, it cannot be bettered, as the musicians of earlier times knew very well.(28)
For a time, organs were built with more than twelve keys per
octave in order to utilize more of the extended chromatic scale.
The keys could be split or other devices used to enable the
performer to play either note of an enharmonic pair such as
[6.4] Since a syntonic comma is 81/80, a quarter-comma, its fourth root, is an irrational number. However, rational fractions that closely approximate the size of a quarter-comma and which cumulatively equal a full syntonic comma can be derived by arithmetically dividing a syntonic comma of 324/320 into four parts as follows:
324/320 = 321/320 x 322/321 x 323/322 x 324/323
Therefore, a quarter-comma fifth may calculated as being:
3/2 x 320/321 = 160/107
Rational fractions approximating each of the other meantone intervals may be calculated in a similar manner, using the other fractions in the expansion. A chromatic meantone tuning for a keyboard is shown in Figure 13 for a chain of fifths tempered by a quarter-comma (q).(31) Logarithmic values for a meantone scale can be easily calculated by subtracting one-fourth of a syntonic comma (22/4 = 5.5 cents) from every pure fifth. Thus each meantone fifth will be 696.5 cents.
7. Well Temperament
[7.1] The term well temperament includes a family of temperaments that modified meantone temperament to eliminate wolves and to expand the range of playable keys by taking advantage of the small difference between the Pythagorean comma and the syntonic comma. The difference between the two commas is an interval of 32805/32786 (2 cents), which is called the schisma. If only four links of a chromatic keyboard scale are tempered by a quarter-comma, with the remainder being tuned pure, the chromatic scale will exceed an acoustic octave by only a schisma and the wolf fifth will be thereby minimized to the point of nonexistence.
Figure 14. Schematic of Well Temperament
(click to enlarge)
Figure 15. Well Temperament
(click to enlarge)
[7.2] Figure 14 illustrates a simplified form of well temperament
in which all but the central four links are Pythagorean and the
major thirds vary from just (C–E) to fully Pythagorean (
8. Algorithms for Schismatic and Syntonic Equal Temperament
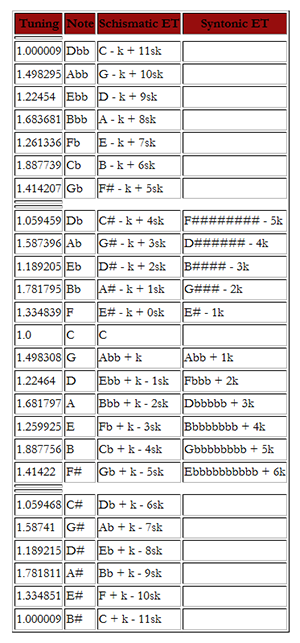
[8.1] We will develop and expand upon the method advocated by Kirnberger in the eighteenth century for deriving a scale of equal temperament from Pythagorean intonation.(32) A scale obtained by the first procedure is schismatic equal temperament and a scale obtained by the second procedure is syntonic equal temperament. The tuning of schismatic ET is exactly equal to the tuning for syntonic ET, the only difference being in their algorithms. Both match the tuning of equal temperament to several decimal places as shown in Figure 16.
[8.2] Schismatic and syntonic equal temperament is derived by
extending a well-tempered scale eleven links to the left and
right of C. When the eleventh note to the left of C is raised by
one syntonic comma and the eleventh note to the right of C is
lowered by one syntonic comma the results are tunings for
| E#-1k | = | 10935/8192 | = | 1.334839 | F(ET) | = | 1.334840 | |
| = | 16384/10935 | = | 1.498308 | G(ET) | = | 1.498307 |
This strategy works because a syntonic comma is very nearly 11/12
of a Pythagorean comma, expressed as k = 11/12P. Therefore a
schisma, defined as sk = P-k = 32805/32786, is very nearly 1/12
of a Pythagorean comma “p,” the amount by which each link is
narrowed in equal temperament. The pitch of
As shown in Figure 5, F+p is the pitch of F in equal temperament.
Since the precise value of a schisma is 1.954 cents and 1/12 of a
Pythagorean comma is 1.955 cents, the error is only 1/1000 of a
cent. One can then obtain decimal tunings for equal temperament
by reiterating the proportions for
[8.3] We will now derive and apply two algorithms which map
Pythagorean tuning into equal temperament. The algorithm based
upon the schisma produces schismatic ET. As with ordinary equal
temperament, this procedure equates the tuning of enharmonic
pairs, substituting G for
- Starting with C, move 10 links to the left to
A♭ ♭ +1k. Substitute G enharmonically forA♭ ♭ +1k. - Move 1 link to the right 5 times, adding 1 schisma to the width of each interval. Rename each note enharmonically.
- Returning to C, move 10 links to the right to
E♯ -1k. Substitute F enharmonically forE♯ -1k. - Move 1 link to the left 4 times, subtracting 1 schisma from the width from each interval. Rename each note enharmonically.
Figure 16. Schismatic and Syntonic Equal Temperament
(click to enlarge)
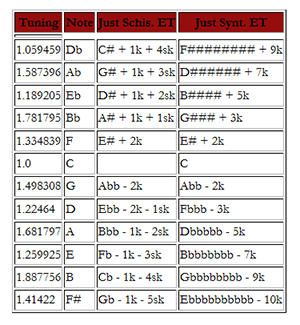
Figure 17. Just (C-Major mode) Schismatic and Syntonic Equal Temperaments
(click to enlarge)
[8.4] The algorithm that produces syntonic equal temperament
also starts with the intervals C–
- Starting with C, move 10 links to the left to
A♭ ♭ + k. Substitute G enharmonically forA♭ ♭ +1k. - Reiterate the action 5 more times, adding 1 syntonic comma to the width of each 10-link interval. Rename each note enharmonically.
- Returning to C, move 10 links to the right of C to
E♯ -1k. Substitute F enharmonically forE♯ -1k. - Reiterate the action 4 more times, subtracting 1 syntonic comma for each 10-link interval. Rename each note enharmonically.
[8.5] We can now go a step further and derive the algorithm that
maps just intonation into syntonic ET from the algorithms
previously used to map Pythagorean tuning into just intonation.
For example,
[8.6] Of course, neither syntonic nor schismatic ET are
precisely equal. They do not merge all enharmonically equivalent
notes, as shown by the outer sections of Figure 16 which contains
notes from
9. Concluding Thoughts
[9.1] This article has explored the relations between keyboard tunings based upon the chain of fifths. We began by accepting the historical definition of a diatonic scale embedded in a 12-note chromatic keyboard. We demonstrated that the terms used to name diatonic and chromatic intervals can be rationally ordered according to the number of links between the intervals on the chain of fifths. We then derived algorithms that map Pythagorean tuning into just intonation and equal temperament and map just intonation into equal temperament. Pythagorean tuning and just intonation have traditionally been classified as distinct tuning strategies, while Pythagorean tuning and equal temperament have been related only by the Pythagorean comma. This article has shown that the three tunings can be related using algorithms that utilize combinations of pure fifths and syntonic commas.
Appendix I
Historical Scales of Just Intonation Listed by Barbour
The numbers in the left hand margin correspond to the number used by Barbour. The table lists the author of the temperament, the date of its publication, the chromatic compass of the tuning on the chain of fifths, and the number of intervals which are pure or are altered by one or more commas, starting at the left end of the chain.
81. Ramis, 1482. Ab-F# Ab-G, 8=0, 4=-1k.
82. Erlangen, 15c. Ebb, Bbb, Gb-B, 2=+1k, 8=0, 2=-1.
83. Erlangen revised, Eb-G#, 7=0, 3=-1k.
84. Fogliano 1529 Eb-G#, 1=+1k, 4=0, 4=-1k, 3=-2k.
85. Fogliano 1529 Eb-G#, 2=+1k, 4=0, 3=-1k, 3=-2k.
86. Fogliano 1529 Eb-G#, 1=+1k, 1=+1/2k, 3=0, 1=-1/2k,
3=-1k, 3=-2k.
88. Agricola 1539. Bb-D#, 8=0, 4=-1k
89. De Caus 17c. Bb-D#, 4=0, 4=-1k, 4=-2k
90. Kepler 1619 Eb-G#, 2=+2, 5=0, 5=-1
91. Kepler 17c. Ab-C#, 3=+1, 5=0, 4=-1
92. Mersenne 1637 Gb-B, 4=+1, 4=0, 4=-1
93. Mersenne 1637 Bb-D#, 4=0, 4=-1, 4=-2
94. Mersenne 1637 Gb-B, 5=+1, 3=0, 4=-1
95. Mersenne 1637 Gb-B, 5=+1, 4=0, 3=-1
96. Marpurg 1776 Eb-G#, 2=+1, 4=0, 4=-1, 2=-2
97. Marpurg 1776 Eb-G#, 1=+1, 6=0, 2=-1, 2=-2
98. Marpurg 1776 Eb-G#, 2=+1, 3=0, 4=-1, 3=-2
99. Malcolm 1721 Db-F#, 3=+1, 5=0, 4=-1
100. Rousseau 1768 Ab-C#, 3=+1, 4=0, 3=-1, 2=-2
101. Euler 1739 F-A#, 4=0, 3=-1, 5=-2
102. Montvallon 1742 Eb-G#, 1=+1, 5=0, 6=-1
103. Romieu 1758 Eb-G#, 1=+1, 5=0, 4=-1, 2=-2
Appendix II.
Ellis’s Table of Intervals not Exceeding an Octave
This chart lists the intervals identified by Ellis as being
formed from pure fifths and major thirds. It provides the
inverted proportions used by Ellis and his name for the interval
along with the Pythagorean equivalent of the interval from Figure
11.
24:25 Small semitone C#-2k
128:135 Larger limma C#-1k
15:16 Diatonic or just semitone Db+1k
25:27 Great limma Db+2k
9:10 The minor tone of just intonation D-1k
125:144 Acute diminished third Ebb+3k
108:125 Grave augmented tone D#-3k
64:75 Augmented tone D#-2k
5:6 Just minor third Eb+1k
4:5 Just major third E-1k
25:32 Diminished fourth Fb+2k
96:125 Superfluous fourth E#-3k
243:320 Grave fourth (F-1k)
20:27 Acute fourth F+1k
18:25 Superfluous fourth F#-2k
32:45 Tritone, augmented fourth F#-1k
45:64 Diminished fifth Gb+1k
25:36 Acute diminished fifth Gb+2k
27:40 Grave fifth G-1k
16:25 Grave superfluous fifth G#-2k
256:405 Extreme sharp fifth (G#-1k)
5:8 Just minor sixth Ab+1k
3:5 Just major sixth A-1k
75:128 Just diminished seventh Bbb+2k
125:216 Acute diminished seventh Bbb+3k
72:125 Just superfluous sixth A#-3k
128:225 Extreme sharp sixth A#-1k
5:9 Acute minor seventh Bb+1k
27:50 Grave major seventh B-2k
8:15 Just major seventh B-1k
25:48 Diminished octave Cb+2k
64:125 Superfluous seventh B#-3k
Kenneth P. Scholtz
2821 Anchor Ave.
Los Angeles, CA 90064-4605
kscholtz@earthlink.net
Footnotes
1. The syntonic comma is defined as the difference between the
Pythagorean tuning and just tuning of the major third. The
difference between the just third (5/4) and the Pythagorean third
(81/64) is 81/80, calculated as follows: 81/64 x 4/5 = 81/16 x
1/5 = 81/80. The syntonic comma is also the difference between
the Pythagorean and just tunings for all diatonic intervals other
than the fourth and fifth, which are the same in both tunings.
The reason for the repeated appearance of the syntonic comma will
be apparent from the discussion of the four modes of just
intonation in section 5.
Return to text
2. Mark Lindley and Ronald Turner-Smith, “An Algebraic Approach
to Mathematical Models of Scales,” Music Theory Online 0.3
(1993), which is a commentary based upon their book,
Mathematical Models of Musical Scales (Bonn: Verlag fuer
Systematische Musikwissenschaft, 1993).
Return to text
3. Blackwood, The Structure of Recognizable Diatonic Tunings,
(Princeton: Princeton University Press, 1985).
Return to text
4. See, for example, L. L. Lloyd’s diagrams in his articles in
the 1954 Grove’s Dictionary of Music and Musicians on “Just
Intonation” and “Temperaments.”
Return to text
5. Intervals measured by rational fractions can be converted
into cents using the following approximate values: octave = 1200
cents, perfect fifth = 702 cents; Pythagorean comma = 24 cents;
syntonic comma = 22 cents.
Return to text
6. See Lindley and Turner-Smith, “An Algebraic Approach,”
paragraph 4.
Return to text
7. In modern terminology, dividing the string in half gives two
octaves, in thirds gives a fifth and an eleventh, and in fourths
gives a fourth, octave and double octave. The other diatonic
notes are then determined by calculating intervals of a fifth
from these intervals. This produces two diatonic octaves in
Pythagorean tuning.
Return to text
8. Perfect fifths do not combine to produce a perfect octave.
The nth fifth in a sequence of n fifths is defined mathematically
by the expression (3/2)(n), which can never be an exact multiple
of 2 since every power of 3 is an odd number. The mathematical
proof that no sequence of fourths can ever produce an octave is
less obvious since every even number can be expressed as a
fraction with an odd denominator, and every power of 3 can be
associated with an infinite sequence of even numbers, such as
18/9, 36/9,
Return to text
9. In logarithmic measure, a perfect fifth is 702 cents.
Therefore twelve perfect fifths equals 8424 cents while seven
octaves is 8400 cents. The difference, the Pythagorean comma, is
therefore equal to 24 cents.
Return to text
10. Euclid (attrib.), Section of the Canon, in Barker, Greek
Musical Writings, vol. 2 (Cambridge: Cambridge University
Press, 1989), 199. Twelve links on the chain of fifths can be
interpreted as 12 fifths, 6 whole tones, 4 minor thirds and 3
major thirds. Thus, the Pythagorean comma is also equal to the
difference between three major thirds or four minor thirds and an
octave. In Pythagorean tuning, a Pythagorean comma is the
interval between any two notes separated by 12 links on the chain
of fifths.
Return to text
11. Blackwood, Recognizable Diatonic Tunings, 58.
Return to text
12. The development of the 12-tone school of composition was a
logical consequence of accepting the 12-semitone model of equal
temperament in place of a chain of harmonic fifths.
Return to text
13. These stacked rows appear in Helmholtz’s On the Sensations
of Tone (London: Longman, 1885; New York: Dover, 1954; orig.,
4th ed., Braunshweig: Verlag von Fr. Vieweg u. Sohn, 1877), 312,
where it is used to illustrate the enharmonic relation between
notes in Pythagorean intonation.
Return to text
14. An irrational number, such as pi or the square root of two,
is one that cannot be expressed as the ratio of two integers. An
irrational number includes a nonterminating decimal written to
the number of decimals needed for practical accuracy.
Return to text
15. Rossing, The Science of Sound (Reading, Mass: Addison Wesley,
1982), 161. This is a general textbook on acoustics. Rossing’s
chart lists the equally-tempered, just and Pythagorean tunings for a
22-note chromatic scale in cents and decimals. The just scale
corresponds to the “C” scale in Figure 10.
Return to text
16. It is possible to generate an infinite number of chromatic just scales by allowing the four adjacent links in Pythagorean tuning to freely slide along the chain of fifths. Whenever C is not part of the Pythagorean notes, it will necessarily be raised or lowered by one or more syntonic commas and no note in the chromatic scale will be tuned to 1. However, changing the absolute tuning of the notes in this manner does not change their relative tuning. Therefore, all of the just chromatic scales generated in this manner can be transposed into one of the four modes listed in Figure 11. The major and minor scales available in each of the four modes are the following:
G-mode: Cb, Eb, G, B, D# E-minor mode: Fb, Ab, C, E, G# C-mode: Fb, Ab, C, E, G# A-minor mode: Bbb, Db, F, A, C# F-mode: Bbb, Db, F, A C# D-minor mode: Gb, Bb, D, F#, A# Bb-mode: Ebb, Gb, Bb, D, F# G-minor mode: Cb, Eb, G, B, D#
Return to text
17. The algorithm used to construct just chromatic scales can be
used to illustrate why intervals generated by the prime 7 cannot
be systematically included in diatonic keyboard tunings. Pleasant
sounding intervals can include sevens. Examples which are
commonly cited are a 7/4 minor seventh, a 7/5 diminished fifth,
both of which are part of a diminished seventh chord in which the
notes C, E, G,
Eb- Bb-s-F--C--G-s-D----A
7/6 7/4 4/3 1 3/2 7/4 21/16
However, temperaments based on 7’s or factors of 7 do not produce a usable family of chromatic keyboard scales from the chain of fifths, which would have the desired ratios for the diminished seventh chord. The “septimal” comma which produces a 7/4 minor seventh and an 8/7 major second on the second link of the chain of fifths is 64/63 (27 cents). Therefore, reiteration of the septimal comma, “s”, in an algorithm which tunes every minor seventh to 7/4 produces two modes of septimal chromatic scales in which E is 64/49, not the desired 5/4.
Mode 1 (F) Mode 2 (G)
G# 4096/2041 (+4s) 4096/2041 (+4s)
C# 8192/7203 (+4s) 348/343 (+3s)
F# 512/343 (+3s) 512/343 (+3s)
B 2048/1029 (+3s) 96/49 (+2s)
E 64/49 (+2s) 64/49 (+2s)
A 246/147 (+2s) 12/7 (+1s)
D 8/7 (+1s) 8/7 (+1s)
G 32/21 (+1s) 3/2
C 1 1
F 4/3 21/16 (-1s)
Bb 7/4 (-1s) 7/4 (-1s)
Eb 7/6 (-1s) 147/128 (-2s)
Ab 49/32 (-2s) 49/32 (-2s)
Db 49/48 (-2s) 1029/1024 (-3s)
Gb 343/256 (-3s) 343/256 (-3s)
Cb 343/192 (-3s) 7203/4096 (-4s)
Fb 2401/2048 (-4s) 2401/2048 (-4s)
These septimal modes are worse than the just modes because the
septimal comma is broader than the syntonic comma by five cents.
The deviation from just intonation is further aggravated because
septimal commas increase the pitch of notes to the right of C and
decrease the pitch of notes to the left of C, contrary to the
action of the syntonic comma. Thus, compared to just intonation,
the pitch of notes to the right of C will be painfully sharp and
notes to the left will be dismally flat. For example, the major
third necessary for the diminished seventh chord will be 2s+1k
(76 cents) broader than in a just scale while the minor sixth
will be 2s + 1k (49 cents) narrower.
Return to text
18. Barbour, Tuning and Temperament: A Historical Survey
(East Lansing, Michigan: Michigan State College Press, 1953),
90–102.
Return to text
19. Ibid., 100.
Return to text
20. Ibid., 97–98.
Return to text
21. Ibid., 94.
Return to text
22. Helmholtz, On the Sensations of Tone, 453. A similar
list of “Extended Just Tuning” is found in Blackwood,
Recognizable Diatonic Tunings, 116–119.
Return to text
23. Blackwood, Recognizable Diatonic Tunings, 74, demonstrates
that in a common progression of C-major triads from II to V, just
intonation would require that D as the root of the II chord be
one syntonic comma lower in pitch than D as the fifth of the V
chord. In The Science of Musical Sound (Scientific American
Books, 1983, 67), John Pierce shows a five chord
progression, I, IV, II, V, I, in which the just tuning of C drops
by a syntonic comma from the first chord to the last.
Return to text
24. It is for this reason that Lloyd in his article on Just
Intonation in the 1954 Grove Dictionary adopted the position that
instruments without fixed pitch and vocalists use a flexible
scale in which the size of the intervals vary according to the
context and part of the reason that Lindley and Turner-Smith
introduced the concept of “leeway” into their algebraic tuning
theory.
Return to text
25. Inspection of the chain of fifths tells us that a major
third can only generate one-quarter of the infinite series of
chromatic notes that are generated by the fifth. This is why the
tuning of the major third is a subsidiary factor in the
generation of diatonic scales.
Return to text
26. Barbour, Tuning and Temperament, 26.
Return to text
27. Grove’s Dictionary of Music and Musicians (1954),
“Temperaments” (380).
Return to text
28. Dart, The Interpretation of Music (New York: Harper & Row,
1963), 47.
Return to text
29. Barbour, Tuning and Temperament, 108–9. Since the first
reference to split keys found by Barbour goes back to 1484, this
device must have been used for both Pythagorean and meantone
tunings.
Return to text
30. Grove’s Dictionary of Music and Musicians,
“Temperaments” (379).
Return to text
31. Barbour’s table 24 gives a monochord mean-tone tuning derived by Gibelius in 1666 by arithmetic division of the comma which is the same tuning shown in Figure 12. Gibelius’s monochord is divided into an octave between 216000 and 108000, in which G = 144450, D = 193200 and A = 129200. The equivalence of these monochord tunings to Figure 12 is calculated as follows:
G = 216000/144450 = 4320/2889 = 480/321 = 160/107
D = 216000/193200 = 540/483 = 180/161
A = 216000/129200 = 540/323
Barbour states that these approximations “check closely with
numbers obtained by taking roots,” with the G being off by
0.000003. Barbour, Tuning and Temperament, 29.
Return to text
32. Barbour, Tuning and Temperament, 64.
Return to text
Copyright Statement
Copyright © 1998 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Jon Koriagin and Rebecca Flore, Editorial Assistants