The Role of Set-Class Identity in the Estimation of Chords
Tuire Kuusi
KEYWORDS: set-class, trichord, pentachord, aural estimation, chord categorization
ABSTRACT: The study examined the role of set-class identity for the subjects’ estimations of chords. Additionally, the study examined what factors other than the set-class identity were guiding the subjects’ estimations. In the test the subjects (professional musicians, amateurs, and non-musicians) heard sequences of five chords. Four chords were derived from one set-class and one chord from another set-class. The subjects were asked to rate which chord did not belong to the same group as the others. It was found that the subjects selected the chord according to the set-class identity in approximately 61% of the cases. The chordal factors guiding the subjects’ estimations were also analyzed. Among these factors were the register of the chords and the arrangement of the pitches within the chords.
Copyright © 2003 Society for Music Theory
INTRODUCTION
[1] Pitch-class set theory was originally developed to provide a theoretical framework for describing pitch organization of post-tonal music. Among important pioneers were Milton Babbitt, Allen Forte, and David Lewin. Babbitt applied concepts of mathematical set theory to music, and many pitch-class set-theoretical concepts are based on Babbitt’s ideas. A general theory using these concepts was formulated by Forte. Since then, the theory has been developed by many researchers.(1)
[2] Pitch-class set theory is most often applied to analysis. Instead of the analytical application of the theory, this study is focused on one concept of the theory, namely, the set-class.(2) Set-class is an abstract concept: a complex of a number of entities sharing certain properties according to which they can be classified. As an abstract concept, the set-class is not directly observable. Since it is not possible to make perceptual estimations of set-classes, these estimations must be done from observable entities (pitch sets) representing the set-classes. Every set-class can be represented by an infinite number of pitch sets, and the properties of a set-class are always present in the pitch sets representing it. Many authors of pitch-class set-theory have—directly or indirectly—discussed the connection between set-classes and the pitch sets derived from them.(3) Generally, they state that there is a connection between the set-class and the pitch sets derived from it in some circumstances. However, they also state that the realization of the pitch sets involves many factors some of which are independent from the set-class (factors mentioned by different authors are, for example, the arrangement of the pitches as chords or as melodies, the registral placement of the pitches, the octave duplications, counter, rhythm, timbre, articulation, and dynamics).
[3] The number of studies on the connection between set-classes and perception of pitch sets derived from them is small. Most of these studies have analyzed the connection between certain pitch-class set-theoretical resemblance models and the perception of closeness or similarity between pitch sets. Some of these studies have also analyzed the factors involved in the closeness estimations.(4) Further, Kuusi has shown that there is a connection between some factors guiding the estimations and the properties of the set-classes.
AIM
[4] The aim of this study was to test the subjects’ ability to discriminate between selected set-classes. In this study, the set-classes were represented by block chords played using the piano sound. Each set-class was represented by a number of chords. The idea was to test how well the subjects could discriminate chords derived from a certain set-class from chords derived from some other set-class and what factors other than the set-class identity were guiding the subjects’ estimations.
[5] A new testing regime was used. The subjects were played sequences of chords. These sequences were formed of five chords: four ‘standard’ chords from the ‘standard’ set-class forming the context and one ‘deviant’ chord from the ‘deviant’ set-class. The subjects were asked to rate which chord did not belong to the same group as the others. Hence, another aim of the study was to test this testing regime.
THE SET-CLASSES, THE TEST CHORDS, THE TEST, AND THE SUBJECTS
[6] As it was possible to test only a rather small number of items, the author first decided to use only triad and pentad classes. The number of triad classes was four: 3-1 {0, 1, 2} (the 3-pc chromatic class), 3-2A {0, 1, 3}, 3-8A {0, 2, 6} (the set-class from which the dominant seventh chord without the fifth can be derived), and 3-11B {0, 4, 7} (the set-class from which the major chord can be derived). The number of pentad classes was five: 5-1 {0, 1, 2, 3, 4} (the 5-pc chromatic class), 5-4A {0, 1, 2, 3, 6}, 5-33 {0, 2, 4, 6, 8} (the 5-pc whole-tone class), 5-34 {0, 2, 4, 6, 9} (the set-class from which the dominant ninth chord can be derived), and 5-35 {0, 2, 4, 7, 9} (the pentatonic class).
[7] The consonance values for the set-classes were calculated using the Huron model of consonance for set-classes (Huron 1994).(5) According to the Huron values, the most dissonant set-class of the nine set-classes of the study was 3-1 with value -1.146, and the most consonant one was 3-11B with value 0.740 (see Table 1). The other dissonant set-classes were 5-1 (-0.588), 3-2A (-0.472), and 5-4A (-0.309), and the other consonant set-classes were 5-35 (0.479) and 5-34 (0.224). There were two set-classes close to the middle point of the range of the values (the middle point was -0.203). These were 3-8A (-0.216) and 5-33 (-0.169).
[8] The location of set-class 3-8A in the middle of the range of consonance values needs closer examination. As stated earlier, the dominant seventh chord without the fifth can be derived from set-class 3-8A. The dominant seventh chord is usually considered to be a rather consonant chord, at least by musically trained subjects, and the absence of the (perfect) fifth does not affect the character of the chord. However, the absence of the fifth affects the consonance value: the three intervals between the fifth and the other pitches of the dominant seventh chord (perfect fifth and two minor thirds) would increase the consonance value. Hence, set-class 3-8A will be included in the ‘consonant’ set-classes.
Figure 1. The chords derived from the four triad classes
(click to enlarge)
Figure 2. The chords derived from the five pentad classes
(click to enlarge)
[9] Each of the triad classes was represented by two chordal settings. The span of the chordal settings varied between 13 and 16 semitones, that is, the interval between the lowest and highest pitch varied between the minor ninth and the major tenth. Additionally, each chordal setting was played on three to six transpositional levels in middle register (between A3 and Eb5). Hence, each triad class was represented by seven to twelve chords. The chords derived from the triad classes are in Figure 1.
[10] Three chordal settings with the span of 14 semitones (the major ninth) were derived from each pentad class. Each chordal setting was played on five transpositional levels in middle register (between A3 and Eb5). Hence, each pentad class was represented by 15 chords. The chords derived from the five pentad classes are in Figure 2.
[11] The properties of the set-classes are always present in chords derived from them. Hence, to some extent the set-class properties determine the characteristics of the chords representing it regardless of the chordal setting. For example, all chords derived from set-class 3-11B are always major chords, and chords derived from set-class 5-1 have dissonant intervals between the pitches. It seems likely that the familiarity of chords derived from set-class 3-11B and the dissonance of the chords derived from set-class 5-1 are characteristics guiding aural perception of them, but it should be remembered that these characteristics are due to the set-class properties. Naturally, the audibility of these characteristics can to some extent be enhanced or concealed by aspects of chordal setting. A limited number of chord spans and the middle register were used in this test in order to diminish the effect of chordal factors (that is, factors independent from the set-class).
[12] The chords were first made using the Finale 2000 program. On the program the pitches of each chord were made to start and stop in perfect simultaneity by quantifying the note values. In addition, each pitch was given the same objective dynamic level. A grand piano sound Bösendorfer from the Nemesys Gigastudio piano sample library was used when the chord sounds were played.(6)
[13] There were 42 items in the test. Each item consisted of a sequence of five chords played three times. As already stated, in each sequence, four of the five chords were derived from the standard set-class and one from the deviant set-class. Every triad class was paired with every other triad class and every pentad class with every other pentad class, but triad classes were not paired with pentad classes. This made altogether 12 triad-class items and 20 pentad-class items. Additionally, there were ten controls (4 items using triad classes and 6 items using pentad classes). All 16 items using triad classes (played in random order) were presented first, followed by the 26 items using pentad classes (again in random order). The test items are in Figure 3.
[14] Each chord lasted one second and the three sequences were separated by a two-second silence. Hence, one item lasted 3*7 = 21 seconds. Two items were separated by a seven-second silence. The whole test lasted approximately 20 minutes. Two items can be heard in the sound files Item 1 and Item 2.
[15] The subjects were asked to rate which one of the five chords did not belong to the same group as the others. The subjects were not told any principles of the criteria according to which they should make their ratings; hence, they were allowed to define for themselves their own criteria. During a short practicing session before the test, the subjects were able to familiarize themselves with the material to be used. The ratings were made on a test form in which numbers from 1 to 5 represented the five chords of each sequence. The subjects’ task was first to aurally select one chord not belonging to the group and then to circle the number representing that particular chord. After the test the subjects filled out a questionnaire with questions about their age, sex, music studies, and listening habits.
[16] Eighty-two subjects participated. They were not paid for participating. Twenty subjects were rejected because of their poor performance in the control chord test. The remaining 62 subjects were divided into four subgroups according to their music studies:
- music theorists and composers (theorists/composers, N = 14)
- professional musicians or music students (professionals, N = 27)
- subjects who have studied music but not professionally (non-professionals, N = 11)
- subjects who have never studied music (non-musicians N = 10)
[17] The subjects of group 1 (theorists/composers) were teachers or professional students from the Department of Composition and Music Theory at the Sibelius Academy. Seven of them were female and seven male. Their ages varied from 20 to 53 years, the average being 33.21. The total years of music studies (both non-professional and professional) varied between 12 and 40 years, and the average was 20.86. They reported that they listen to or play or compose post-tonal music from 2 to 43 hours per week (the average was 7.46 hours). Two of the subjects reported having absolute pitch.
[18] The subjects of group 2 (professionals) were professional musicians or professional music students from various departments of the Sibelius Academy. Eight of them were female and nineteen male. The average age was 24.44, and the range was from 18 to 41 years. The average of all music studies (both non-professional and professional studies) was 14.96 years, the range being from 10 to 21 years. These subjects reported that they listen to or play post-tonal music from 0 to 32 hours per week, the average being 4.39 hours. The number of subjects with absolute pitch was seven.
[19] The subjects of group 3 (non-professionals) were teachers or students from Helsinki University, Department of Psychology. Nine of them were female and two male. Their ages varied between 20 and 46 years, the average being 28.18. The average time of non-professional music studies was 11.36 years, the range being from 5 to 20 years. These subjects reported that they listen to or play post-tonal music from 0 to 10 hours per week, the average being 2.18 hours. The number of subjects with absolute pitch was one.
[20] The subjects of group 4 (non-musicians) were teachers or students from Helsinki University, Department of Psychology. Five of them were female and five male. Their ages varied from 20 to 42 years, the average being 24.70. They reported that they listen to or play post-tonal music from 0 to 5 hours per week (the average was 1.00 hour). None of them reported having absolute pitch.
RESULTS
[21] As already stated, there were originally 42 items in the test. However, a mistake was discovered in one item when the chords were played to the first group of subjects. The item 24 {5-4A, 5-1} was incorrect (it was actually {3-10, 5-1}), and the subjects’ ratings of this item were excluded from analyses. Hence, the total number of items to be analyzed was 41.
[22] The total number of cases was 2542 (41 items rated by 62 subjects). The total number of cases in which no selection was made was 30, hence, very small (1.18%). This can be interpreted to indicate that the subjects were motivated to make the test and that they were able to operate with the testing regime.
Table 2. The averages and the standard deviations (in parentheses) of ratings that were made according to the pitch-class set-theoretical paradigm
(click to enlarge)
[23] The connection between the pitch-class set-theoretical paradigm and the subjects’ estimations was analyzed first. In total, the deviant chord was selected in 1547 cases, that is, in 60.9% of all cases. The averages of ratings in which the subjects selected the deviant chord were also calculated separately for each group (see Table 2). As can be seen, these averages differed clearly from one group to another. The theorists/composers made their ratings most often according to the pitch-class set-theoretical paradigm, even though only a few of them were familiar with the paradigm. The professionals made more ratings according to the paradigm than the non-professionals, and the non-professionals more than the non-musicians.
[24] The differences between the average by theorists/composers and the averages by other groups of subjects were statistically very significant (p < .001) in most cases (the value p < .001 indicates that the result could have occurred by chance in fewer cases than 1 in 1000). The exceptions of this were the differences between theorists/composers and professionals: the averages were 12.64 and 9.93 respectively for the triad classes (p < .010), and 19.07 and 17.00 for the pentad classes (this difference was not statistically significant, p > .050). Additionally, the differences between the averages of non-musicians and the averages of the other subject subgroups were statistically very significant (p < .001) in all but two cases: the averages of non-professionals and non-musicians were 7.91 and 4.60 for the triad classes (p < .010), and 13.82 and 9.07 for the pentad classes (p < .050).
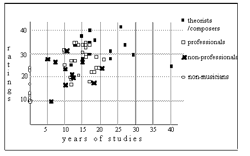
Figure 4. The ratings made according to the pitch-class set-theoretical paradigm (Y-axis) plotted against the years of music studies (X-axis)
(click to enlarge)
[25] The results of the first analysis indicated that the subjects were rather well able to aurally discriminate chords according to the set-class from which the chords were derived. Naturally the aural perception was guided by the audible characteristics of the chords (for example, the degree of consonance or the familiarity of the chords), but, as already stated, these characteristics are due to the set-class properties. Additionally, the results indicated that the connection between pitch-class set-theoretical paradigm of set-classes and subjects’ ratings of chords was higher for subjects who were musically highly trained than for subjects without musical training. This result was expected and reasonable. However, the number of years of music study alone could not explain the ratings. This can be seen from the scatter diagram (Figure 4) in which the ratings made according to the pitch-class set-theoretical paradigm are plotted against the years of music study. The correlation between these ratings and the years of study was 0.57 (p < .001), indicating that the years of study explained the ratings only to some extent. The scatter diagram shows that the type of musical studies is important as well.
[26] In the questionnaire the subjects were asked how many hours per week they listen to or play post-tonal music. Even though this kind of question cannot be considered a very exact one, it was hypothesized that there might be some connection between the ratings and the familiarity with the chord material. The correlation was calculated between the reported hours and the ratings made according to the pitch-class set-theoretical paradigm. The correlation was very low (r = 0.26, non-significant), indicating that the results of the test cannot be explained by the listening habits.
[27] The second analysis aimed at identifying and categorizing the chordal factors that were guiding the subjects when they selected one of the standard chords instead of the deviant chord. These factors were connected with chordal setting and they were independent of the set-class identity. In this analysis the focus was on those chords that were selected by an especially high proportion (25% or higher) of subjects. Ten such cases were found. In four of these cases the most often selected standard chord was chosen more often than the deviant chord (items 4, 11, 16, and 33) and in one case they were selected equally often (item 25).
Example 1. The five chords of items 4 and 14. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
[28] In item 4, chords 1, 2, 3, and 5 were derived from the standard set-class 3-1, and chord 4 was the deviant derived from set-class 3-2A (see Example 1 for the item). Hence, the whole item consisted of dissonant chords. In this item, 41.9% of the subjects selected chord 3. It was selected especially by the non-professionals, the professionals, and the non-musicians. As can be seen, this chord was neither the highest nor the lowest one. Yet it was the only chord of this item with a small interval (the major second) between the two highest pitches; the other chords had a small interval (the major second in the standard chords and the minor third in the deviant chord) between the two lowest pitches. Hence, the difference in the arrangement of the pitches seemed to affect the ratings. When the same item was played again as a control (item 14), similar ratings were made: altogether 37.1% of the subjects selected chord 3. This time this chord was selected especially by the non-professionals and the professionals.
Example 2. The five chords of items 7 and 15. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
Example 3. The five chords of items 11 and 16. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
Example 4. The five chords of items 25 and 42. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
Example 5. The five chords of items 29 and 38. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
Example 6. The five chords of item 33. The percentiles indicate how often each chord was selected in the test
(click to enlarge)
[29] In item 7, chords 1, 3, 4, and 5 were derived from the standard set-class 3-8A, and chord 2 from the deviant set-class 3-1 (see Example 2). As stated earlier, the dominant seventh chord without the fifth can be derived from set-class 3-8A, and the chords can be considered consonant. And as can be seen, this chord was twice in root position (chords 1 and 4) in this item. When ratings were made of item 7, 29.0% of the subjects selected chord 1, the higher one of the two chords in root position. Interestingly, chord 4 was selected by 0% of the subjects. Chord 1 was selected most often by the non-musicians. When this item was played again as a control (item 15), 21% of all subjects selected chord 1 and 0% chord 4. Again chord 1 was selected most often by the non-musicians.
[30] In item 11and its control item 16, the standard chords were 1, 2, 4, and 5 (derived from set-class 3-2A) and the deviant chord was 3 (set-class 3-1). Hence, the set-classes were the same as those in items 4 and 14 (see above), and all chords of these items were dissonant. The chords of items 11 and 16 are in Example 3. As can be seen, chord 1 and chord 5 were similar chordal settings on different transpositional levels, and so were chords 2 and 4. When ratings were made of these items, the lower one of the two similar chordal settings was selected more often that the higher one: chord 5 was selected more often than chord 1, and chord 4 was selected more often than chord 2.
[31] In item 25 and its control item 42, the standard chords were 1, 2, 3, and 5 and they were derived from set-class 5-35. Hence, the context was rather consonant. The deviant chord was number 4 and it was derived from set-class 5-33. The chords are in Example 4. When the subjects made their ratings, 40.3% of them selected chord 5 in item 25 and 32.3% of them in item 42. As can be seen, chord 5 was the highest in register. There were subjects from all subgroups, the fewest being theorists/composers and the most being non-professionals and non-musicians.
[32] In item 29 and its control item 38, the standard set-class was 5-34 and the chords derived from it were 2, 3, 4, and 5. Hence, the context was rather consonant. The deviant set-class was 5-33, and the deviant chord was number 1 (see the chords in Example 5). As can be seen, the dominant ninth chord was in root position twice in these items (chords 3 and 4). In both cases chord 3, the higher one of the root-position chords, was selected by 25.8% of the subjects. There were subjects from all subgroups, yet this chord was most often selected by the professionals and least often by the non-musicians. Chord 4 (the lower of the root-position chords) was selected by 11.3% of the subjects in item 29 and by 12.9% of the subjects in item 38. Those who selected chord 4 were most often non-professionals and non-musicians.
[33] In item 33, the set-classes were 5-35 (standard) and 5-34 (deviant), and the whole item was rather consonant. The standard chords were 1, 2, 3, and 4, and the deviant chord was number 5. The chords are in Example 6. As can be seen, two of the standard chords had the major chord formed of the three lowest pitches (chords 1 and 4). Of the standard chords, the highest chord (chord 2) was selected by 30.7% of the subjects, especially by the theorists/composers and the professionals. Chord 4, which was the higher one of the two having the major chord, was selected by 21% of the subjects, most often by the professionals. Hence, it seems that within this item, both the register and the arrangement of pitches were factors guiding the ratings.
CONCLUSIONS
[34] The study has examined the subjects’ ability to categorize chords according to their set-class identity. Additionally, the study has examined the importance of chordal factors for the categorization. In the test the subjects were played a five-chord sequence successively three times and they were asked which chord does not belong to the same group as the other chords. It seemed to be rather easy for the subjects to make their ratings in this new testing regime.
[35] The test was made in pitch-class set-theoretical paradigm. In each five-chord sequence, the four standard chords were derived from the standard set-class and the deviant chord from the deviant set-class. It was found that in approximately 61% of all cases the subjects selected the deviant chord; hence, they made their ratings according to the pitch-class set-theoretical paradigm. Additionally, a clear connection was found between the years and the type of music study and the number of ratings made according to the paradigm. The highly trained subjects from the Department of Composition and Music Theory from the Sibelius Academy made their ratings most often according to the paradigm, even though only a few of them were familiar with pitch-class set theory. The subjects with no music study made their ratings most often according to factors other than those connected with set-class identity. These other factors were chordal: the register and the chordal setting of the chords.
[36] The analyses of the cases in which one of the standard chords was selected instead of the deviant chord revealed some tendencies. First, the register of the chord seemed to affect the ratings. If the context was consonant or rather consonant, the subjects tended to select the highest chord. But if the context was dissonant, they tended to select the lowest chord. There were altogether 20 cases in the test in which this tendency could be seen, but only two cases with the opposite tendency. Second, certain aspects of chordal setting seemed also to guide the subjects. These were the placement of a small interval (in triads), and the arrangement of the pitches so that they formed the root position of a familiar tonal chord (both in triads and pentads). Altogether ten cases were found in which these kind of chordal aspects seemed to guide the subjects’ estimations, while the opposite was found in only one case.
[37] The results of this study showed that the estimations of chords are based on a number of simultaneous factors. Set-class identity seems to be one of them, the other ones being chordal. The factors revealed in this study were closely related to those revealed in earlier studies as well (7). This was the case even though the earlier studies have used totally different kinds of testing regimes and even though only some of the earlier studies have used pentachords.(7)
[38] The present study has evoked need for additional study. The new testing regime used in the study needs to be tested using other set-classes. The relative importance of set-class identity and the relative importance of chordal factors should be examined in varying set-class and chord contexts. The finding that the subjects tend to select the highest chord in a consonant context and the lowest chord in a dissonant context is worth further examination.
Tuire Kuusi
Sibelius Academy
Department of Composition and Music Theory
PL 86
00251 HELSINKI
FINLAND
tuire.kuusi@siba.fi
Footnotes
1. The reader interested in the basic concepts, objectives,
and background of pitch-class set theory can find a general discussion in, for
example, these: Allen Forte, The Structure of Atonal Music (New Haven and
London: Yale University Press, 1973); John Rahn, Basic Atonal Theory (New
York: Schirmer, 1980); Robert Morris, Composition with Pitch-Classes (New
Haven and London: Yale University Press, 1987); Joseph Straus, Introduction to Post-Tonal Theory (New Jersey: Prentice Hall, 1990).
Return to text
2. A pitch-class set is a collection of pitch-classes
without duplications, and a set-class is a collection of pitch-class sets
mutually related by a transformation or by a group of transformations. The
transformation used in this study is transposition (Tn;
transpositional classification).
Return to text
3. See, for example, Robert Morris, “A Similarity Index for
Pitch-Class Sets,” Perspectives of New Music 18/2
(1979/80): 447; John Rahn, “Relating Sets,” Perspectives of New Music 18/2
(1979/80): 494; Mark Hoover, “Set Constellations,” Perspectives of New Music
23 (1984): 165–166; Fred Lerdahl, “Atonal Prolongational Structure,”
Contemporary Music Review 4 (1989): 66; Thomas Demske, “Relating Sets: On
Considering a Computational Model of Similarity Analysis,” Music Theory Online
1.2 (1995): 16, 17; Richard Hermann, “Towards a New Analytical Method for
Post-Tonal Music: A Response to Thomas Demske,” Music Theory Online 1.3
(1995): 15, 16, Footnote 2; Eric Isaacson, “Issues in the Study of Similarity in
Atonal Music,” Music Theory Online 2.7 (1996): 16; Isaacson, “Neural Network
Models for the Study of Post-tonal Music,” in Mark Leman (ed.), Music,
Gestalt, and Computing: Studies in Cognitive and Systematic Musicology (Berlin:
Springer-Verlag, 1997): 237–238; David Rogers, “A Geometric Approach to Pcset
Similarity,” Perspectives of New Music 37 (1999): 78; Marcus Castrén, “Pairs of Chords as Objects Illuminating Set-Class Similarity: Some Viewpoints and a
Computer-Assisted Procedure to Create test Material for Listener Experiments,”
Electronic Journal of Music Theory and Analysis 1/1 (2000).
Return to text
4. Cheryl Bruner, “The Perception of Contemporary Pitch
Structures,” Music Perception 2 (1984):
25–39; Don B. Gibson, “The Aural Perception of Nontraditional Chords in Selected
Theoretical Relationships: A Computer-Generated Experiment,” Journal of
Research in Music Education 34 (1986): 5–23; R.C. Lane, A Multidimensional
Scaling Study of Seven Theoretical Indexes of Intervallic Similarity and
Musicians’ Perceptions Among Twenty-One Pitch-Class Sets (Ph.D. diss.,
University of North Carolina, 1997); Virginia Williamson and Panayotis
Mavromatis, “Categorizing Atonal Sonorities: Multidimensional Scaling,
Tree-Fitting and Clustering Compared,” (Paper presented at the Society for Music
Perception and Cognition Conference, Evanston, Illinois, 1999); Arthur Samplaski,
A Comparison of Perceived Chord Similarity and Predictions of Selected
Twentieth-Century Chord-Classification Schemes, Using Multidimensional
Scaling, and Cluster Analysis (Ph.D. diss., Indiana University, 2000); Tuire
Kuusi, Set-Class and Chord: Examining Connection between Theoretical
Resemblance and Perceived Closeness (Helsinki: Sibelius Academy, 2001); Kuusi,
“Semantic Differential as a Method for Collecting Estimations of Chords,” (in
the Fifth Triennal ESCOM Conference: Proceedings, 2003). Two closely related
studies by Gibson examine the effect of octave equivalence (or pitch class) in
chord perception: Gibson, “The Aural Perception of Similarity in Nontraditional
Chords Related by Octave Equivalence, Journal of Research in Music Education
36 (1988): 5–17; Gibson, “The Effects of Pitch and Pitch-Class Content of the
Aural Perception of Dissimilarity in Complementary Hexachords,” Psychomusicology
12 (1993): 58–72.
Return to text
5. David Huron, “Interval-Class Content in Equally Tempered
Pitch-Class Sets: Common Scales Exhibit Optimum Tonal Consonance,” Music Perception
11 (1994): 289–305. When the Huron consonance values were calculated, the
indexes for interval-classes were summed up and the resulting value was divided
by the total number of interval-classes in the set-class. In each triad class
the total number of interval-classes was 3, and in each pentad class it was 10.
Return to text
6. I would like to thank Mr. Santtu Valve from the
department of Music Technology, Sibelius Academy, for helping to prepare the
sound data.
Return to text
7. Bruner, “The Perception of Contemporary Pitch
Structures” (1984); Samplaski, A Comparison of Perceived Chord Similarity and
Predictions of Selected Twentieth-Century Chord-Classification Schemes, Using
Multidimensional Scaling, and Cluster Analysis (2000); Kuusi, Set-Class and
Chord: Examining Connection between Theoretical Resemblance and Perceived
Closeness (2001), “Semantic Differential as a Method for Collecting
Estimations of Chords” (2003).
Return to text
Copyright Statement
Copyright © 2003 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Tahirih Motazedian, Editorial Assistant