Just Intonation in Renaissance Theory and Practice
Ross W. Duffin
ABSTRACT: Just intonation has a reputation as a chimerical, theoretical system that simply cannot work in practice. This is based on the assessment of most modern authorities and supported by misgivings expressed during the Renaissance when the practice was supposedly at its height. Looming large among such misgivings are tuning puzzles printed by the 16th-century mathematician, Giovanni Battista Benedetti. However, Renaissance music theorists are so unanimous in advocating the simple acoustical ratios of Just intonation that it seems clear that some reconciliation must have occurred between the theory and practice of it. This article explores the basic theory of Just intonation as well as problematic passages used to deny its practicability, and proposes solutions that attempt to satisfy both the theory and the ear. Ultimately, a resource is offered to help modern performers approach this valuable art.
Copyright © 2006 Society for Music Theory
Introduction |
Theoretical Background |
Benedetti's Puzzles | Problematic Passages
| Is Just Tuning Possible?
A New Approach | Problem Spots
in the Exercises | Rehearsal Usage
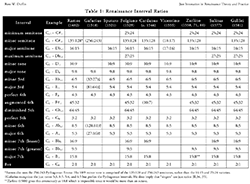
| Conclusion
Introduction
The idea. . . that one can understand the ratios of musical consonances without experiencing them with the senses is wrong. Nor can one know the theory of music without being versed in its practice.
[1] So begins the first of two letters sent by the mathematician Giovanni Battista Benedetti to the composer Cipriano de Rore in 1563. Subsequently publishing the letters in 1585,(1) Benedetti was attempting to demonstrate that adhering to principles of Just intonation, as championed most famously by Gioseffo Zarlino,(2) would, in certain cases, cause the pitch of the ensemble to migrate. This, of course, raises questions about whether Just intonation can work in practice. His letters were discussed at length by the late Claude Palisca,(3) and I am greatly indebted to his work. However, there remain many misconceptions about the subject of Just intonation, then and now, so Benedetti’s evidence will form one crucial part of this re-examination of its theory and practice in Renaissance music.
[2] In modern times, the use of acoustically pure intervals in musical performance—Just intonation—has not had a very positive reputation. J. Murray Barbour, whose book, Tuning and Temperament (1951 remains a standard reference more than half a century after its publication, and whose 1958 recording, The Theory and Practice of Just Intonation (1958 Musurgia A-3), has been one of the few resources available to anyone interested in the subject, referred to pure major and minor thirds as boring and insipid, and to anyone advocating a certain form of Just intonation as insane.(4) It is difficult to imagine an opinion on tuning more powerfully expressed, and it makes the consignment of Just intonation to the dustbin of history seem, as it were, all the more justified. But there was a fundamental flaw in Barbour’s conception of Just intonation, as may be seen in these two statements:
The characteristic features of Just intonation in its practical application, are demonstrated best and most precisely on keyboard instruments. [emphasis original]
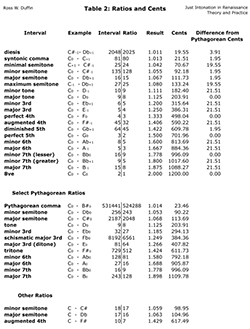
Of course, it is the severe limitation of just intonation to twelve notes in the octave, with enharmonically equivalent notes forbidden, that has caused its outright rejection by musicians.(5)
[3] These things caused Barbour, in his words, to “present just intonation more because of its significance for the history of musical theory than as a tuning system that was ever of importance in the world of practical Western music.”(6) It is a grievous misunderstanding of Just intonation to think that it is meant to work in a twelve-note octave as found on modern keyboard instruments, however. Nor does the theory of Just intonation as described by many writers in the Renaissance ever suggest that a choice must be made between enharmonics. Barbour’s error caused him to offer recordings of supposedly Just chords that were nothing of the kind. To give one example, his version of the triad on the second degree of the “Just” major scale, presented a 9:8 whole tone, a 4:3 fourth, and a 5:3 major sixth above the “tonic.” In such a chord, the “third” is not a pure minor third and the “fifth” is not a pure fifth above the root. There are ways to create a pure minor triad on the second degree of the scale—using a 10:9 rather than a 9:8 whole tone, for instance—but such solutions are not explored because they violate Barbour’s arbitrary twelve-note octave rule. Unfortunately, generations of students and scholars have depended on his flawed exposition as the last word on the issue.
[4] Another burden that Just intonation has had to bear are the studies from the 1930s by Carl Seashore and others, showing the supposed preference of musicians and listeners for “unjust” intervals, including wide major thirds and narrow diatonic semitones. As Barbour summarized:
All of these experiments prove conclusively that singers and instrumentalists have no predilection for the so-called natural intervals, and that the same is valid for the majority of listeners.(7)
[5] This has been “gospel” in the psychology of music field for decades. I suggest, however, that much of a person’s preference for intervals depends not on biological predilection but on aural conditioning, and in the 1930s through the 1950s, singers and violinists (the usual subjects of such experiments) had probably never heard Just intervals nor knew any sort of context where their use would make musical sense. This is not to say that most musicians and listeners today would react any differently: the stranglehold of equal temperament in our musical culture has seen to that. But it does not diminish the value of Just intervals in general, and particularly not in the culture of the Renaissance.
[6] Some writers have also cast doubt on whether singers, especially, could sound frequencies to the kind of tolerances necessary to achieve intentional tuning choices.(8) Performances and recordings by modern early music groups, such as the Hilliard Ensemble recording used below, refute that supposition utterly in my opinion, presenting highly trained voices with minimal vibrato and a level of accomplishment in tuning accuracy that Seashore, Barbour and their colleagues probably never imagined.(9)
[7] It is one thing, however, for a group of singers to have talent and good ears, and another for the theory behind a complicated tuning system to be understood, assimilated, and realized in performance. Refuting the notion that Just intonation is merely a theoretical system without any practical value will take a precise, note-by-note analysis of several relevant passages—the kind of rigorous examination that, to my knowledge, only theorist and composer Easley Blackwood has attempted before. But even Blackwood concluded, echoing Barbour, that “just tuning is of no practical use with regard to the existing Western repertoire.”(10)
[8] The aim of this article is to show that view to be erroneous. To do so, it will be necessary to establish the remarkable level of agreement among Renaissance theorists on the subject of intervals, to deal with misgivings about Just intonation expressed during the Renaissance, and finally, to demonstrate how singers could have accomplished—and may today accomplish—Just intonation in the context of Renaissance polyphony.
Theoretical Background
[9] Beginning with Ramos de Pareja in 1482,(11) the simple ratios of Just intonation began to be cited by theorists and used in their divisions of the monochord. Before that, the 3:2 ratio of the pure fifth and its resulting musical system—a whole tone derived from two pure fifths and a major third derived from four pure fifths (in other words, Pythagorean tuning)—comprised the almost universal theoretical model. The ratios of the Pythagorean system, after the 2:1 octave and the 3:2 fifth, were mathematically complex, however, so Ramos’s identification of intervals with simple harmonic ratios was greeted with near-unanimous acceptance. Just intonation was easy to support from both a scientific and practical standpoint because the intervals not only had simple mathematical ratios, they sounded demonstrably better than those derived from the Pythagorean system.
[10] Table 1 shows the interval ratios promulgated by a selection of prominent Renaissance musical theorists. The one famous “hold-out” who continued to favor the old Pythagorean system was Gafurius, although he did acknowledge that the simple ratios were used by practical musicians.(12) As may be seen, there is not much disagreement as to what constituted the correct ratios for intervals: for each theorist I have given those ratios that are either mentioned explicitly in the text, or can be deduced by the writer’s recommended combination of ratios to create other intervals.
[11] Many of the basic interval ratios are superparticular, where the first number exceeds the second by one. Thus, an octave is 2:1, a fifth is 3:2, a fourth is 4:3, a pure major third is 5:4, a pure minor third is 6:5. These “six-limit” ratios—the senarius, or senario, as Zarlino calls them—are the basic harmonic intervals. Zarlino attributed almost mystical significance to the senario in the same way that Pythagoras apparently did to the tetractys—the first four numbers. But the intervals represented in the senario cannot be the only ones in the system because they do not fully account for stepwise motion. The 9:8 whole tone is in common with the Pythagorean system, but Just intonation also possesses a 10:9 “minor tone” which is the difference between a 5:4 (that is, 10:8) major third and a 9:8 major tone. Like the common harmonic intervals, those smaller intervals are also part of the harmonic series (the series of overtones of any naturally produced sound), so the 10:9 ratio, for example, is simply the distance from the 9th to the 10th harmonic in the overtone series and thus, in itself, a natural acoustical phenomenon.
[12] Other intervals can be deduced by inversion: the 5:4 pure major third inverts to an 8:5 pure minor sixth. The 6:5 pure minor third similarly inverts to a 5:3 pure major sixth, the 9:8 major tone to the 16:9 lesser minor seventh, the 10:9 minor tone to the 9:5 greater minor seventh.
[13] It is perhaps surprising to see ratios for the tritone and the diminished fifth given by Renaissance theorists. Some of these are given explicitly as numerical ratios; others were derived by specified combinations of intervals, such as the tritone as a pure major third plus a major tone (5:4 + 9:8 = 45:32), or a pure fifth minus a major semitone (3:2 - 15:16 = 45:32). The diminished fifth (or semi-diapente) is the inversion of that at 64:45, but was also derived as a pure fourth plus a major semitone (4:3 + 16:15).
[14] The semitone with the lowest ratio in the system, 16:15, can be derived as the difference between the 4:3 fourth and the 5:4 major third, but of course, it also exists as that interval in the harmonic series, as the distance between the ascending overtones gets smaller and smaller. Regarding the other semitone sizes, two of them consist of differences between the 16:15 major semitone and the two different sizes of whole tone: Subtract a 16:15 major semitone from a 10:9 minor tone and the 25:24 semitone remains (10:9 - 15:16 = 25:24); subtract it from a 9:8 major tone and the 135:128 semitone remains (9:8 - 15:16 = 135:128).
[15] That accounts for most of the ratios in Table 1, with the exception of the semitones given by Vicentino, and the 10:7 ratio given for the tritone by Cardanus. Vicentino’s semitones seem a simple arithmetical way to divide the 9:8 (18:16) major tone, and the 18:17 ratio, in particular, found some use, at least, in lute fretting schemes in the Renaissance. The idea of dividing the whole tone in this way stems from Boethius's early sixth-century De Institutione Musica I.16.(13) So-called septimal ratios—those using the seventh harmonic, like 10:7—are often considered by modern theorists as part of the Just scale, but with the exception of Cardan’s citation, they were clearly avoided by Renaissance theorists and, indeed, I believe they were not normally part of the Renaissance harmonic and melodic vocabulary.
Table 2. Ratios and Cents
(click to enlarge)
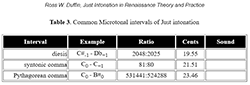
Table 3. Common Microtonal Intervals of Just intonation
(click to enlarge and listen)
Table 4. Just intervals with their sounds
(click to enlarge and listen)
[16] Table 2 gives the ratios and cents values for Just intervals, along with a selection of other intervals for comparison. One characteristic of the differences between Pythagorean-derived notes and notes in Just intonation is that they are separated by a syntonic comma. The syntonic comma is a microtonal interval which is the difference between the Pythagorean major third, or ditone, at 81:64—that is, two consecutive 9:8 whole tones—and the pure major third at 5:4, or 80:64. Thus, the syntonic comma has the ratio 81:80. This small interval can thus be recognized as the difference between a major tone and a minor tone, and between Just intervals and their Pythagorean equivalents. Modern theorist and composer Easley Blackwood’s comma-variant notation of C0, C+1, and so on, is extremely useful, both for discussions and charts of intervals, as in Tables 1 & 2, as well as in annotating musical scores.(14) Briefly, octaves, fifths, fourths, and major tones that are pure to one another have the same annotation; major thirds, major sixths, and minor tones are all narrow by one comma; minor thirds and minor sixths are wide by one comma. I will use Blackwood’s system for analyzing Benedetti’s problematic progressions, as well as the difficult passages he himself culled from the works of Orlando di Lasso.
[17] First, I
need to mention some other very small intervals in Table 2. One is the
Pythagorean comma, which is the difference between 12 pure fifths and 7 pure
octaves. It is larger than the syntonic comma by a miniscule interval called a
schisma. This is also the amount by which a pure fifth exceeds an equal-tempered
fifth, as well as the amount by which a syntonic comma exceeds the diesis in the
Just system—the diesis being the discrepancy between diatonic versions of
[18] These kinds of discrepancies and, indeed, the whole system of Just intervals may seem arcane to modern musicians (and even to musicologists), but, as shown by Table 1, these ratios constituted the essence of intervallic relationships in the Renaissance. The principal intervals of Just intonation are given in Table 4, along with sound files with consecutive and simultaneous demonstrations of the intervals.
[19] The remarkable degree of agreement among Renaissance theorists, particularly with regard to the most common harmonic intervals, leads inexorably to the conclusion that Just intervals were preferred in both theory and—as even the theoretically objecting Gafurius confirms—in practice. The “sounding number” of these pure ratios, furthermore, would be experienced by singers—reinforced, in a live acoustic, by various combination tones—as sonorous, beatless, tranquil chords which, I believe, would have been the constant goal of performers. At the very least, from the historical evidence, it may reasonably be inferred that Just intonation represents an aesthetic preference over other systems on the part of Renaissance musicians generally, and that attempts should be made to explore Just intonation as a way of understanding that preference. However, Benedetti’s shrewdly conceived progressions, discussed below, as well as the complaints of Zarlino’s erstwhile pupil Vincenzo Galilei,(16) have led modern scholars to believe that the use of these Just intervals as recommended by the theorists was unsustainable, and that temperament—even equal temperament—was the necessary result. I hope to show that such a conclusion is not inevitable.
Benedetti’s Puzzles
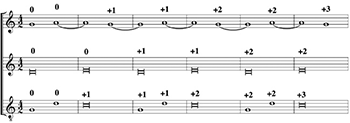
[20] In his second letter to Cipriano de Rore, Benedetti gave the progression shown in Example 1a, and demonstrated, as illustrated here in Blackwood-style numeric annotations, that using Just ratios would cause the pitch to rise by a comma for each repetition of the two-measure pattern. I use the term “puzzle” for this and Benedetti’s other progression since we are clearly left to wonder what the “solution” is if these passages are not to migrate microtonally. (The sound of all migrating examples is set to loop so that listeners can hear again where the passage started in terms of pitch.)
[21] This ascent results because the singer of the bottom voice tries to make the C at the beginning of bars 2, 4, and 6, pure as a minor third (or major sixth) against the A tied over from the previous bar in the top voice. This necessitates raising the C by one comma, which necessitates raising the G in the top voice in order to be pure to the sustained C in the bottom, and so forth. There is no question that the consistent application of the theoretical ratios to the notes in this passage would result in the comma ascent described by Benedetti and the presumptive conclusion that Just intonation is impractical. It did not go away, however, so the problem of comma migration continued to plague theorists for a long time. Christian Huygens, at the end of the 17th century, noted:
For if you ask any of our Musicians, why two or more perfect fifths cannot be us’d regularly in composition; some say ’tis ... because when you pass from one perfect fifth to another, there is such a change made as immediately alters your Key, you are got into a new Key before the Ear is prepared for it, and the more perfect Chords you use of the same kind in Consecution, by so much the more you offend the Ear by these abrupt Changes....I say therefore, if any Persons strike those Sounds which the Musicians distinguish by these Letters, C, F, D, G, C, by these agreeable Intervals, altogether, perfect, interchangable, ascending and descending with the Voice: Now this latter sound C will be one Comma, or very small portion lower than the first sounding of C [as shown in Figure 1:]
Therefore we are compell’d to use an occult Temperament, and to sing these imperfect Intervals, from doing which less offence arises.(17)
[22] The comma descent occurs, of course, because of the wide pure minor third from F to D. In the 18th-century, the theorist Robert Smith cited Huygens’ comments on comma migration, along with a revealing story printed in France in 1707. It refers to a real situation like the theoretical one described by Benedetti in his second example below:
This is also confirmed by what we are told of a monk, who found, by subtracting all the ascents of the voice in a certain chant from all its descents, that the latter exceeding the former by two commas: so that if the ascents and the descents were constantly made by perfect intervals, and the chant were repeated but four or five times, the final sound, which in that chant should be about the same as the initial, would fall about a whole tone below it. But finding that the voices in his quire did not vary from the pitch assumed, he concluded that the musical ratios, whereby he measured those successive ascents and descents were erroneous.(18)
[23] The monk’s example appears to be a strophic piece which, technically, should have migrated downward by two commas each time through. Thus, “four or five times” through the music, starting each stanza on the ending pitch of the previous one, would cause the piece to drop a total of eight or ten commas respectively (the whole tone being made up of nine commas). Since the piece didn’t descend as predicted, the monk decided that the harmonic ratios must have been erroneous, but we know they were not: it was some basic “homing instinct” on the part of the singers to maintain their original pitch level. Frequently in the Renaissance, furthermore, choirs sang in alternatim with organ, making a stable pitch not just desirable but necessary.
[24]
Indeed,
Benedetti notes that the migration problem does not occur on keyboard
instruments, and recommends a tuning system with tempered fifths ascending to
Benedetti did not say that his tuning was an equal temperament, but since his demonstrations show that all semitones and whole tones should be equalized, this would have been a logical goal. Indeed, his tuning method is not unlike that proposed by Giovanni Lanfranco in 1533, which J. Murray Barbour has interpreted as equal temperament.(19)
[25]
The method
of tempering fifths up to
[26] Meantone is certainly one possible “solution” to these tuning puzzles, although all of the fifths are quite narrow in anything approaching the quarter-comma variety, and that’s why people continued to look for “just” solutions that provide at least some places of repose. Example 1b gives Benedetti’s passage in a succession of meantone temperaments.(25)
[27] Any choice of meantone temperament is a trade-off between musical quality and convenience. The most extreme form given here—1/3 comma—has pure minor thirds, which means that it sounds especially good in modes and pieces that emphasize minor triads. It can also be used in a 19-note octave to create an extended meantone system. Its drawbacks, however, include a major third that is narrower than pure, and a fifth that is extremely narrow. Listeners can hear in the 1/3 comma version how the odd-numbered measures sound sour since they contain only open fifths, whereas the even-numbered measures are somewhat better. The 2/7 comma version sounds similar but slightly better with the improved fifths and major thirds, and the version in 1/4 comma meantone sounds better still in the open fifths (though not actually pleasant) and very euphonious in the triads. In 1/5 comma meantone, the fifths and major thirds are about the same distance from pure (though the third is wide and the fifth narrow), which means that they beat at a similar rate and create a kind of “vibrato” effect that some listeners find attractive. The 1/6 comma version is slightly better in the fifths but slightly worse in the major thirds, though they are still quite acceptable--a good compromise, perhaps. (The virtues of 1/6 comma meantone become evident with more complex harmonies.)(26) Finally, the equal tempered version exhibits excellent odd-numbered measures because its fifths are almost pure, but its major thirds are excruciatingly wide, causing the even-numbered measures to sound very sour and “jangly.”
[28]
While the
use of any temperament would solve the migration problem, and while singers can
learn to adjust to meantone when they are obliged to sing with a keyboard, it
seems very unlikely that these are systems that Renaissance singers, left to
their own devices and singing unaccompanied, would conceive for themselves.
Furthermore, I have yet to discover a single Renaissance pedagogue recommending
such temperaments for singers. Even Benedetti’s recommendations, given after
pointing out the difficulty of maintaining Just intonation, are for tempering
“in organis & clavicymbalis.”(27)
And it is difficult to imagine that singers would look at his temperament recipe
and say, “Oh dear, I won't be able to sing that
Plate 1. Benedetti’s two tuning puzzles, from Diversum, pp. 279, 280
(click to enlarge)
Example 1c. Benedetti’s first passage in a Blackwood version
(click to enlarge and listen)
[29] One thing about the use of Just tuning in Example 1 is that Benedetti assumes that the pitch of any note would not change throughout its duration and, while this seems like a reasonable supposition, we don’t know for sure, and Benedetti’s score (see Plate 1) with tied notes like modern notation, could be interpreted to invite that possibility.
[30] Such changing pitches have been the basis for the Just tuning solutions of Easley Blackwood.(28) With apologies to Prof. Blackwood, I think he would try to resolve Benedetti’s tuning puzzle as shown in Example 1c.
[31] As may be seen, Blackwood’s approach is to allow the pitch of a note to change, so that it starts at one pitch but adjusts by a comma part way through. Thus, the A in the top part starts at 0 in order to be pure to the D0 below it, but it changes to -1 in order to make a pure minor third (or rather, major sixth) to the C0 at the beginning of bar 2. Meanwhile, the E is at -1 to make a pure major third above the C. All of this allows the G in the top part in bar 2 to stay at 0 against the C0 and thus prevents the microtonal modulation of Benedetti’s version.
[32] I think the mere fact that Benedetti pointed out complications in the use of Just intonation and gave examples actually supports the case for the its use in Renaissance polyphony generally. Since he was aware of where the system is vulnerable, he must have been very familiar with it. I also recognize the theoretical correctness of Benedetti’s version, but in general I agree with Blackwood that while such microtonal modulation may be unavoidable in some cases, it is undesirable in most situations. It is especially hard to imagine real musicians being tempted to adopt a solution that results in progressive departure from the starting pitch.
[33] While the monk’s singers in the story given above help to confirm that microtonal modulation is undesirable (and additionally confirm that choirs were still thinking about Just intonation in the eighteenth century), I actually find Easley Blackwood’s solutions using mid-note adjustments to be extremely awkward for performers and strange for listeners. Because of his comma shifts on suspended notes, it is frequently some harmonically and rhythmically prominent chord that becomes the conspicuous focus of the adjustment. This raises the question of whether there is a “quasi-just” solution that would maintain the overall pitch level but sacrifice the perfection of certain less prominent harmonic intervals in order to accomplish that. There are, in fact, two such possibilities in this passage. One is to sacrifice the purity of the syncopated D-A fifth in the second half of the first measure, as in Example 1d. This allows the impure D0-A-1 fifth to occur in a rhythmically weak position, and then follows that sonority with pure first inversion and root position triads. It also allows the syncopated canon between the top two voices to use the same size of whole tone (the minor tone), so this solution has some melodic logic as well, even though the offending D0-A-1 fifth, albeit brief and unaccented, is extremely unpleasant.
[34] In fact, I chose the timbre for these examples because it actually seems to exaggerate the effect of the tuning. Just to show that voices in a live acoustic with vibrato would sound significantly better, I have included an alternative rendering of Example 1d using a voice-like timbre with vibrato and reverb.
[35] This kind of tuning subtlety is not at all worthwhile when an extensive amount of vibrato is used, but a pitch variance of 22 cents is negligible for vibrato anyway. Moreover, using vibrato to cover up imperfections in tuning is something that happens all the time in performances today, even where the goal is Equal Temperament.
[36] An alternative and perhaps more appealing quasi-Just solution is to sacrifice the purity of the suspended note in the second measure (see Example 1e). Since that note resolves downward to form a triad, it is treated like a suspended dissonance, so harmonic impurity may seem less of an issue even though the variance from the pure interval is also one comma. And in spite of the fact that the impurity occurs on a strong beat, it is not as difficult for the performer nor so jarring for the listener as Blackwood’s comma shift.
[37]
Benedetti’s
second puzzle (see Example
2a) shows downward migration of the pitch level, comma by
comma, in the repetition of a different two-measure pattern. In Benedetti’s
version, the E in the bottom part must be at -1 to be pure to the G0
in the middle part, and the
Example 2a. Benedetti’s second passage in his own version (click to enlarge and listen) | Example 2b. Benedetti’s second passage in Duffin version (click to enlarge and listen) |
[38] This passage appears to have a more obvious alternative solution than Benedetti’s first example (see Example 2b). Since the E in the bottom voice is dissonant with the top voice when it enters, that dissonance overshadows the need for purity in the G-E minor third. Thus, the impurity of that minor third occurring with a dissonance is inconsequential, and the rest of the notes can stay stable in pitch.
[39]
It also
happens that G0 to
Problematic Passages
[40] Benedetti’s puzzles were designed expressly to show potential difficulties in using Just intonation. Perhaps more relevant to Renaissance music in general is whether the principles of Just intonation can be made to work on "real" music from the period—especially passages that have been identified as problematic from a tuning standpoint.
[41]
The first
example for this purpose actually comes from a reference by Benedetti himself,(29) although he did not explain how the tuning was problematic, as he did for the
puzzles. It is the end of Rore’s own chanson Hellas, comment which is the
secunda pars of En vos adieux. It is not hard to see what
Benedetti was referring to (see Example
3a). A succession of pure chords will
require the
Example 3a. Rore’s Hellas, comment (ending) in Benedetti’s presumed version (click to enlarge and listen) | Example 3b. Rore’s Hellas, comment (ending) in Duffin version (click to enlarge and listen) |
[42] Furthermore, this passage is a petite reprise, so its wholesale repetition would mean an ascent of four commas if Just ratios were maintained throughout. If, on the other hand, the singers were required to stay stable in pitch and find a quasi-Just solution, what could they do? One possibility is shown in Example 3b.
[43]
The
hinge-points here occur at the beginning of bar 3 and the beginning of bar 5. In
both cases, the
[44] Another source for Renaissance musical passages that are problematic from a Just tuning standpoint is The Structure of Recognizable Diatonic Tunings, where theorist and composer Easley Blackwood introduces two examples (see chapter 7, pp. 129–53), both from a single motet: Orlando di Lasso’s four-voice Ave regina caelorum. The first passage begins with a problematic circle of fifths, with suspensions from chord to chord. Example 4a shows Blackwood’s interpretation of what the passage must have been like if strict Just ratios were applied.
Example 4a. Lasso’s Ave regina caelorum excerpt in Blackwood’s presumed “Just” version (click to enlarge and listen) | Example 4b. Lasso’s Ave regina caelorum excerpt in Blackwood’s own “Just” version (click to enlarge and listen) |
[45] Describing the apparently inevitable downward “modulation” by two commas in five measures as “a distortion of the intent,” however, he prefers the version in Example 4b as an alternative.
Example 4c. Blackwood’s first Lasso example in Duffin version
(click to enlarge and listen)
Example 5a. Blackwood’s second Lasso example in his own version
(click to enlarge and listen)
Example 5b. Blackwood’s second Lasso example in Duffin version
(click to enlarge and listen)
[46] While Blackwood avoids microtonal modulation with this version, I personally find both of these solutions unsatisfactory. They both include wrenching shifts from the third to the fourth measure that simply cannot be practical, even for musicians whose main aim is to perform in Just intonation. In the Renaissance, of course, performers did not have musical scores for calculating possible comma shifts in the middle of a note, so a wholesale modulation like that at mm. 3–4 seems impossible. If these solutions are what Easley Blackwood regards as plausible realizations of this passage, it is no wonder people have little faith in the practice of Just tuning.
[47] My own solution, shown in Example 4c, begins the same as Blackwood’s preferred version, but avoids microtonal modulation by allowing two impure intervals. In bar 3, the alto’s G-1 is impure against the C0 in the tenor and bass, and in bar 4, the A-1 in the top voice is impure to the D0 in the alto and bass. In both cases, these impure fifths occur as suspensions against notes a major second or minor seventh away. Thus, the impurity is masked to a large degree by the dissonant interval that occurs simultaneously, and there is no other microtonal awkwardness.
[48] Blackwood’s second example is the last nine measures of Lasso’s same Ave regina caelorum motet (see Example 5a).
[49] Blackwood essentially starts a comma lower than he ends (with D at -1, for example) but keeps a smoothly consistent pitch throughout until he has to “pay the piper” and raise the pitch two measures from the end in order to finish at 0. One highly unusual aspect of his version—really a side-issue here—is his choice of tuning for the second note in the sixth measure of the Alto part. I have represented it as -x since it is outside the usual comma units of the Just system. What Blackwood says in his discussion of this passage is that, since the chord is like a dominant seventh, he wants a note at the 7th harmonic over G. This note is lower by about 27 cents (1.25 comma) than the note we expect, which is F0. Here, I personally think Blackwood’s choice is vertical priority run amok, especially since the note doesn’t even resolve like it should in a dominant seventh progression. Placing that note in a melodic context is something no performer of Renaissance music would find intuitive or gratifying.
[50] My own solution, shown in Example 5b, relies on what I perceive to be the most likely placement of the notes in certain modes. Since the passage starts by firmly outlining the A mode, the positions of the notes correspond most closely to the tendencies in that mode, including F and C at +1. The beginning of the third measure begins a transition to G mode. The A mode flickers again briefly in the second measure of the second line before G mode settles in once and for all.
[51] Whereas Blackwood delays the comma ascent to the final until the second last measure, my version manages to maintain a more stable pitch throughout by fudging the transition from A mode to G mode in the middle of bar 3. The problem there is that the C wants to be pure to the G in the middle of the measure, but also wants to be pure to the A at the beginning. What I have done is to make the C pure to the A at the beginning of the measure and allow the C to be impure against the G in the middle. This choice is made because the latter C is a dissonant suspension, so its impurity is more easily tolerated. The second awkward moment in my version occurs at the beginning of bar 6, where there is a shift to G at +1, and the tenor part even has to raise a consecutive B. The problem here is that the modal orientation is unstable and the temporary focus on A requires C at +1, necessitating G+1 when the two overlap. The B and E at the beginning of bar 6 could be kept at -1, as in Blackwood’s solution, but sooner or later the texture must rise by a comma, whether at the beginning of bar 7, or bar 8 (as in Blackwood's version). Example 5b seems to me the best solution.
Is Just Tuning Possible?
[52] Benedetti’s puzzles have reinforced the modern view that Just tuning is impossible in practice—that the theory of pure intervals was not transferable to the real world of musical sound even though the ratios were set forth so unanimously by theorists of the Renaissance. It is true that Zarlino, perhaps the most conspicuous champion of Just tuning, had to endure criticism from colleagues at the time. But even Vincenzo Galilei, Zarlino’s “most outspoken and severest critic,”(30) in 1589 had to admit that, in practice, singers do use pure intervals rather than tempered ones:
. . . truly, voices sing musical intervals in their true and perfect ratio, whereas most artificial musical instruments play them more or less distantly from their true form.(31)
[53] Among modern critics, Palisca and others implicitly or explicitly call for some form of temperament as the only solution. As Palisca says:
In [Benedetti’s] examples, the performance will continue on an even keel only if the true intervals of the senario recommended by Zarlino are abandoned through judicious adjustments by the singers. A system of temperament thus becomes a necessity.The solution to the problem is obviously equal semitones and tones, or what is called equal temperament.(32)
[54] Without endorsing temperament, other critics simply discount the utility of Just intonation, as in Blackwood’s comments cited in the Introduction above,(33) and Mark Lindley’s characterization of Zarlino’s flexible Just system based on the senario as “metaphysically inspired nonsense.”(34)
[55] The fact is, the evidence suggests that Renaissance singers did try to follow the precepts of Just intonation, using simple ratios for both melodic and harmonic intervals wherever possible, and since they did not seem to migrate in pitch as would have been inevitable with strict adherence to Just ratios, it behooves us, I believe, to try to figure out what they did. As I hope I have shown, it is possible in problematic passages, and even in Benedetti’s puzzles, to devise solutions that follow principles of Just tuning but that modify only one or two pure intervals, rather than the entire system, as does temperament. This is a compromise, certainly, but I don't believe it invalidates the whole concept of Just intonation nor necessitates the total replacement of Just tuning with some form of temperament. Moreover, most Renaissance choral works do not contain many tuning problems, if any at all, and thus allow the singers to pursue a goal of Just intonation without the kind of severe difficulty encountered in the Benedetti examples.
Example 6. Thomas Tallis, Lamentations of Jeremiah (end of the 1st part)
(click to enlarge and listen)
[56] As a demonstration of this, I have chosen part of a piece apparently composed around the time Benedetti was writing to Rore—the end of the first part of the Tallis Lamentations (see Example 6)—and have annotated an untexted score with the notes as they appear, and changes as necessary. The sound examples include an electronic performance to demonstrate the Just ratios under controlled circumstances, a recording by the Hilliard Ensemble (Thomas Tallis: Lamentations of Jeremiah, ECM 1341 833 308–2 (1987), trk 1 excerpt), used with the kind permission of ECM Records, and lastly, for comparison, an electronic version in equal temperament. While there are one or two notes in the human performance that may not be absolutely perfect (I’m thinking in particular of the top part in mm. 132–34), it still illustrates, overall, that the ideals of Just intonation can be achieved in practice with stunning effect.
[57] The members of The Hilliard Ensemble managed to solve the tuning problems successfully and create a version that approaches Just intonation, and my annotated score—buttressed by my electronic re-creation of a Just version—shows how I think that was accomplished. There are actually no tuning problem spots at all, which is why on the annotated score I’ve basically shown only where notes change from their previous positions. The entire passage is mostly in the A mode although it moves briefly to the G mode at m. 129. At m. 136, overlap with G+1 in the lower voices requires D to be at +1 in the top voice, but the excursion is brief and there is no awkwardness in getting back to D0. The essential point, of course, is how astonishing the live performance sounds with this kind of tuning. The final chord in the Hilliard Ensemble performance is one of the most extraordinary examples of perfect tuning I have ever heard, and once when I played it for a performance practice class, one student wrote afterwards that Just tuning was “shocking.” Indeed, it is shocking that the effect of Just intonation in performance is so striking, and shocking also that we don't get to hear it more often!
[58] Remembering Benedetti’s epigrammatic comment about experiencing the ratios with the senses, I don’t think anyone would argue that such a performance would be improved by the use of tempered fifths and thirds, and I trust the electronic ET version makes that amply clear. In fact, such vivid practical demonstrations help us understand that music students in the Renaissance had good reason to reconcile their teachers’ basic theory of Just intonation with their own practice of it, and rather than abandoning it all for the compromise of temperament, they must have found a way to make it work. The answer to the question “Is it possible?” must therefore be a resounding “Yes!” The next question must be: “How can we begin to reconstruct such a practice in our own time?”
A New Approach
[59] Ensemble music from the Renaissance (as well as from the later Middle Ages) and less complex later music can work in Just intonation and is much enhanced by its use. And even if the exact theoretical ratios are not achieved, it is still possible for performers to make conscious adjustments that will help to “justify” the tuning and make the music sound better acoustically and closer to a Renaissance ideal. Most performers, however, have no idea how to begin. As may have been evident in my discussion of the problematic passages cited by Blackwood, the theory that I have developed over the last few years is that the practice of Just intonation is based on the prevailing mode of the music. I have elsewhere written at length about the theory behind it.(35) What modern performers need to understand first of all, is that notes have certain placement tendencies in each of the modal centers: F, C, G, D, and A/E (I consider the latter pair of finals together since, in my experience, they seem to use an almost identical scale). In order to approach Just intonation, then, performers need to gain a fair idea of where the notes are likely to be found in each mode, and how to find alternatives when problems arise, or when the modal center shifts within a section or passage.
[60] It’s easy enough to look at an individual chord and say, “Oh yes, these intervals need to be pure.” The difficulty comes in figuring out how a perfectly tuned chord is approached and succeeded by other perfectly tuned chords. For example, is the major 3rd of some triad pure because the third is low, or because the root is high? Both solutions can work but each requires a microtonally distinct interval of approach and departure for the root and third of the chord, and one solution is usually better than another depending on the mode and the context. At the point of making the choice between possible solutions, the vertical/harmonic puzzle of Just intonation becomes a horizontal/melodic one for the individual performer. This is the crux of the issue. Notes in Just intonation are certainly not found along the Equal Tempered scale, and they are not always in the same place. Thus, the precise placement of the pitches and the various sizes of melodic intervals are not always predictable, especially to someone reading a single musical line. Performers need to develop the ability to use different sizes of the same written interval, along with a sense of melodic tendencies in each mode that can help them make choices depending on the harmonic and melodic context. Low sharps, high flats, and wide leading tones are a good place to start, but there is more to it than that.
[61] Refining the different sizes of semitone is the most difficult part of Just intonation for performers, although in practice the semitones are mostly 112 cents (0 up to +1, or -1 up to 0, as in typical leading tones) or 92 cents (0 up to -1, or +1 up to 0, as in typical chromatic alterations of a note). The largest and smallest semitones do occur in chromatic passages, however. Practice in recognizing and differentiating the different sizes of whole tone and semitone is crucial to achieving Just intonation.
[62] To enable performers to explore the harmonic and melodic requirements of performing in Just intonation, and to learn this skill by practice, I composed five Just tuning exercises which accompany this discussion. The point of these exercises is to familiarize musicians with the kinds of adjustments necessary to sing or play in Just intonation, and to help them to recognize similar situations in the music they perform. The exercises are sometimes highly chromatic, but in a way that reflects harmonies and progressions found in music from the later 16th and early 17th centuries. (Students of the era will no doubt enjoy tracing the echoes of familiar passages in the various progressions.) Performers who can negotiate Just tuning in the complicated progressions given here should have little problem with most ensemble music in these modes!
[63] The exercises were composed originally in the year 2000 for the use of the Early Music Singers at Case Western Reserve University. The sound is organ-like, with a blendable timbre and stable pitch (although the computer clearly wrestles with playing dissonant cross relations, suspensions, and even second inversions, despite the Just tuning). Performers can practice the exercises by playing or singing along with all voices at once, with a single voice part alone, or in a "music minus one" situation with the computer omitting one part. Three different speeds can be selected (M.M. = 30, 55, or 80). To listen to the individual exercises, click here. To view or download a PDF file of the five exercises, click here.
[64] Mastery of these exercises has proven effective in teaching performers
- to be aware of pure intervals in the harmony
- to make informed guesses as to where to place the notes melodically
- how to make conscious adjustments so the tuning will be better
[65] These are significant achievements for the members of any ensemble performing Renaissance music. Moreover, returning to the exercises again and again, and wrestling with their problems, can deepen the understanding and improve these skills still further.
Problem Spots in the Exercises
[66] Although tuning problems are somewhat exaggerated in the Benedetti and Blackwood examples, “real music” often does contain isolated passages that have no solution satisfying every requirement of pure tuning. The most common case occurs where a note carries over from one chord to another and simply cannot be pure in both. While most of the progressions in the Exercises work beautifully, I have allowed problematic passages to stand, typically with a choice of note that seems to fit best within the mode but that may be momentarily unjust. As noted above, this often means choosing to compromise the minor 3rd, frequently at some point that also includes a dissonance which helps to cover the impurity.
[67] Table 5 shows some of the tuning problem spots in the five exercises. I discuss each one briefly to illustrate where the problem lies and how I decided to resolve the situation.
[68] With more experience and expertise, singers can perhaps experiment with different solutions from the ones given here, including “mid-note” alterations like those used by Easley Blackwood. Used subtly, with discreet sliding rather than abrupt changes in pitch, and covered by a softer dynamic, such adjustments might well represent a possible compromise between his approach and mine. Nevertheless, I suppose the very existence of such problem spots allows skeptics to continue to maintain that Just intonation is, after all, a merely theoretical system that cannot work in practice. However, I believe a serious attempt to master the approach represented by these exercises will bear fruit, and further, that the overwhelming beauty of works performed in this way—even with occasional problem spots—will amply reward performers and listeners alike, and “justify” the effort. And even if singers are unable to match the exact theoretical positions of the notes in Just intonation, the fact that they are aware of the system and come somewhat closer to Just ratios should still make their singing “better in tune” according to the criteria expressed so unanimously during the Renaissance.
Rehearsal Usage
[69] In using these tuning exercises with performers in a rehearsal situation, conductors might first wish to indicate each chord, holding some longer than others until they settle into tune. Eventually, the exercises should move along at a more even and flowing pace. Especially when first beginning to work with these exercises, singers may wish to sing “ah” as a basic vowel sound, with “ee” for +1 annotations and “oh” for -1 annotations. This helps to raise and lower the pitches of the notes by the kinds of small increments necessary. Eventually, this extra help shouldn’t be needed to find the pitches (which is obviously good because “real” texted music has its own vowel requirements). Conductors might also wish to try transposing up or down from the written pitch, although opening unisons in some of the exercises will preclude anything but a short distance in either direction.
Conclusion
[70] There has been a tendency among modern writers to view Just intonation as impossible in Renaissance musical practice in spite of the overwhelming theoretical evidence in its support. This study has presented an alternative view, namely, that Renaissance performers would have preferred solutions that favor Just intonation wherever and whenever possible, and that deviations from it would have been momentary adjustments to individual intervals, rather than wholesale adoption of temperament schemes. This would have allowed them to follow the prevailing theoretical precepts of simple acoustical ratios as much as possible, while avoiding such pitfalls as progressive transposition, comma by comma, in passages with circles of fifths in overlapping sonorities. This conclusion is based on careful analysis and reinterpretation of some of the most problematic passages that have been put forward to demonstrate the supposed impossibility of Just intonation.
[71] The Renaissance system of tuning for non-fixed instruments and voices (as well as the late-medieval system, for that matter), according to this new conclusion, was based on certain note placement tendencies within each of the modal centers. As a demonstration of that, and to provide practical examples for performers wishing to explore this approach, a series of highly chromatic Just Tuning Exercises in each of the modal centers has been provided in score and in sound, and the problematic passages within them discussed. These Exercises are intended for both private practice (using the sound versions) and rehearsal usage using the scores in an ensemble setting. They are proving to be effective in furthering the understanding and skill of performers in the use of Just intonation for Renaissance music.
Ross W. Duffin
Case Western University
rwd@case.edu
Works Cited
Aaron, Pietro. 1523. Toscanello. Venice.
Barbour, Murray. 1951. Tuning and Temperament. East Lansing.
—————. 1958. The Theory and Practice of Just Intonation. Musurgia A-3.
Benedetti, Giovanni Battista. 1585. Diversarum speculationum mathematicarum & physicorum liber. Turin.
Blackwood, Easley. 1985. The Structure of Recognizable Diatonic Tunings. Princeton.
Boethius, Anicius Manlius Severinus. 1989. Fundamentals of Music, trans. Calvin M. Bower, ed. Claude V. Palisca.
Brues, Austin M. 1927. Studies from the Harvard Psychological Laboratory.
Duffin, Ross W. 2000. “Tuning.” In A Performer’s Guide to Medieval Music, ed. Ross W. Duffin. Bloomington.
—————. 2006. “Baroque Ensemble Tuning in Extended 1/6 Syntonic Comma Meantone.” Digital Case.
—————. 1992. “The Musica Practica of Bartolomeo Ramos de Pareia: a critical translation and commentary.” Ph.D. diss., University of North Texas.
Gafurius, Franchinus. 1518. De harmonia musicorum instrumentorum opus. Milan.
—————. 1589. Discorso particolare intorno all’unisono. Florence.
—————. 2003. Dialogue on Ancient and Modern Music, in Music theory translation series. Yale University Press.
Greene, Paul C. 1936. “Violin Performance with Reference to Tempered, Natural, and Pythagorean Intonation.” Psychology of Music 4: 232–51.
Guthrie, E.R. and H. Morill. 1928. Studies from the University of Washington.
Huygens, Christian. 1698. Cosmotheoros.
—————. 1707. “Méthode genérale pour former les Systèmes temperés de musique.” Memoires de l’Académie des Sciences.
Lindley, Mark. 1974. “Early 16th-Century Keyboard Temperaments.” Musica Disciplina 28: 149–50.
Lusitano, Vicente. 1553. Introduttione facilissima. Rome.
Miller, Clement A. 1993. Bartolomeo Ramis de Pareia, musica practica: commentary and translation. Musicological studies & documents, 44. Hänssler.
Nickerson, James F. “Intonation of Solo and Ensemble Performance of the Same Melody.” Journal of the Acoustical Society of America 21: 593–95.
Palisca, Claude V. 1986. Humanism in Italian Renaissance Musical Thought. Yale University Press.
—————. 1994. Studies in the History of Italian Music and Music Theory. Clarendoess.
Pareja, Ramos de. 1482. Musica Practica. Bologna.
Salinas, Francisco de. 1577. De Musica Libri Septem. Salamanca.
Schlick, Arnolt. 1511. Spiegel der Orgelmacher und Organisten. Speyer.
Seashore, Carl E, ed. 1936. Objective Analysis of Musical Performance. University of Iowa Studies in the Psychology of Music 4.
Seashore, Harold G. 1936. An Objective Analysis of Artistic Singing. In Objective Analysis of Musical Performance, ed. Carl E. Seashore. University of Iowa Studies in the Psychology of Music, 12–171.
Smith, Robert. 1759. Harmonics, or the Philosophy of Musical Sounds, second edition.
Ternström, Sten and Johan Sundberg. 1986. “Acoustics of choir Singing.” In Acoustics for Choir and Orchestra. Kungliga Musikaliska Akadamien.
—————. (1988). “Intonation Precision of Choir Singers.” Journal of the Acoustical Society of America 84: 59–69.
Ternströ, Sten and Duane Richard Karna. “Choir.” In The Science and Psychology of Music Performance: Creative Strategies for Teaching and Learning, ed. Richard Parncutt and Gary E. McPherson, 269–84. Oxford.
Vicentino, Nicola. 1555. L’Antica Musica Ridotta alla Moderna Prattica.
—————. 1571. Dimonstrationi Harmoniche. Venice.
Zarlino, Gioseffo. 1558. Le Instituioni Harmoniche. Venice.
—————. 1588. Sopplimenti Musicali. Venice.
Footnotes
1. Benedetti 1585 Diversarum speculationum mathematicarum & physicorum liber (Turin, 1585), pp. 277–83.
Return to text
2. Zarlino 1558 Istitutioni Harmoniche (Venice, 1558), especially the seconda parte; Zarlino 1571 Dimostrationi Harmoniche (Venice, 1571), especially ragionamento secondo and quarto; Zarlino 1588 Sopplimenti Musicali (Venice, 1588), libro quarto.
Return to text
3. Palisca 1986 See his Humanism in Italian Renaissance Musical Thought (New Haven, 1986), pp. 257–65; and Palisca 1994 Studies in the History of Italian Music and Music Theory (Oxford, 1994), pp. 213–23.
Return to text
4. The comment about the thirds is from the insert to Barbour 1958, p. 31, and the sanity comment is from Barbour 1951, p. 105.
Return to text
5. Both of these quotations are from the insert to Barbour 1958, the first on p. 3, and the second on p. 31.
Return to text
6. Barbour 1958 Musurgia A-3, p. 31.
Return to text
7. Barbour 1958 Musurgia A-3, p. 31. The studies Barbour cited include those from the Psychological Laboratory at the University of Iowa, such as C. Seashore 1936 (see in particular, Greene 1936; studies from the Harvard Psychological Laboratory by Brues 1927; studies from the University of Washington by Guthrie 1928; Nickerson 1949, 593–95.
Return to text
8. See H. Seashore 1936, especially “The
Accuracy of Intonation and Intervals,” pp. 48–57. More recent studies from the
Department of Speech Communication and Music Acoustics at the Royal Institute of
Technology in Stockholm, include Ternström and Sundberg 1986, 12-22; Ternström and Sundberg 1988. Most recently, Ternström and Duane Richard Karna opine that “there should
be no inherent advantage of using just intonation in choir music,” although this
does seem to imply that it is possible. See their chapter, Ternström and Karna 2002.
Return to text
9. Seashore and Barbour maintain that scooping and pitch wandering make it
impossible for singers to come reliably closer to a certain frequency than about
a fifth of a semitone. See H. Seashore 1936, pp. 25–77, and Barbour 1958, pp. 197–98. But the Hilliard Ensemble recording excerpt given below, in a sampling of major
chords at eleven points throughout, gives an average major 10th (the most common
voicing for the third) with a ratio of 2.507 above the root. This compares with
the pure ratio of 2.500 and the ET ratio of 2.520, and represents a predilection
for thirds that are twice as close to pure as they are to ET, as well as a
tuning accuracy six times closer to the intended frequency than that predicted
above. The excerpt also ends with a chord sustained with astonishingly pure
tuning over a full eight seconds duration. It takes remarkable precision and
extraordinary vocal control to maintain such a beautifully tuned chord for so
long, but this recording shows that it is possible, and that our expectations
for ensemble singing should be adjusted accordingly. Indeed, even Ternström and
Karna acknowledge that “vocal groups that perform close harmony with one voice
to a part
Return to text
10. Blackwood 1985, p. 153.
Return to text
11. Pareja 1482. See commentary and translation by Miller 1993, and by Fose 1992.
Return to text
12. Gafurius 1518, Book II, ch. 34, 35.
Return to text
13. Boethius 1989, p. 26.
Return to text
14. Blackwood 1985, pp. 67–68.
Return to text
15. Lusitano 1553, p. 4. The practice of referring to the diesis as a comma, in fact, persisted into the 19th century.
Return to text
16. See his Galilei 1581; Galilei and Palisca 2003, pp. 10–134.
Return to text
17. Huygens 1698, pp. 88–90. As his preferred tuning method, Huygens, in fact, recommended 31-note Equal Temperament, a system which is almost identical to extended quarter-comma meantone. Quarter-comma and other meantone temperaments are discussed below.
Return to text
18. Smith 1759, pp. 229, citing Huygens 1707, p. 263.
Return to text
19. Palisca 1986, p. 264.
Return to text
20. Lindley 1974, 149-50.
Return to text
21. Schlick 1511, ch. 8.
Return to text
22. Aaron 1523, Book II, ch. 41.
Return to text
23. Salinas 1577, book 3.
Return to text
24. See Vicentino 1555, Book V; Vicentino, Maniates, and Palisca 1996, Book V, 315–443. This is a long and complicated discussion, but on pp. 432–433, for example, he describes his whole tone as made up of five “dieses” or commas, of which three belong to the major semitone and two to the minor semitone. Thus, an octave consists of seven major semitones (7 x 3 = 21) plus five minor semitones (5 x 2 = 10), or of five whole tones (5 x 5 = 25) plus two major semitones (2 x 3 = 6), both of which methods give a total of thirty-one equal parts.
Return to text
25. It is not sufficiently recognized, I believe, that each of these meantone temperaments possesses one or more Just intervals. Pythagorean tuning is known to contain pure 5ths and 4ths, of course, but each of the regular meantone temperaments given in Example 1b has some purity as well.
|
Regular Meantone version
|
Pure interval
|
Ratio
|
|
1/3 Comma
|
minor 3rd
|
6:5
|
|
Major 6th
|
5:3
|
|
|
2/7 Comma
|
minor semitone
|
25:24
|
|
1/4 Comma
|
Major 3rd
|
5:4
|
|
minor 6th
|
8:5
|
|
|
1/5 Comma
|
Major semitone
|
16:15
|
|
Major 7th
|
15:8
|
|
|
1/6 Comma
|
tritone
|
45:32
|
|
diminished 5th
|
64:45
|
The fact that each of these systems found adherents in the Renaissance may
have been due, in part, to the presence of these pure intervals and the
consequent enhancement to certain modes and progressions.
Return to text
26. See my forthcoming article and practice resource Duffin 2006, "Baroque Ensemble Tuning in Extended 1/6 Syntonic Comma Meantone."
Return to text
27. Benedetti 1585, p. 281.
Return to text
28. See Blackwood 1985, especially ch. 7.
Return to text
29. Benedetti 1585, p. 278.
Return to text
30. So characterized in Palisca 1994, p. 224.
Return to text
31. “
Return to text
32. Palisca 1994, p. 222.
Return to text
33. Barbour 1958, p. 153.
Return to text
34. New Grove 2, “Just intonation.”
Return to text
35. For a detailed explanation of how Just intonation works in late-medieval
polyphony, see my chapter, Duffin 2000, 545–62.
Return to text
|
Regular Meantone version
|
Pure interval
|
Ratio
|
|
1/3 Comma
|
minor 3rd
|
6:5
|
|
Major 6th
|
5:3
|
|
|
2/7 Comma
|
minor semitone
|
25:24
|
|
1/4 Comma
|
Major 3rd
|
5:4
|
|
minor 6th
|
8:5
|
|
|
1/5 Comma
|
Major semitone
|
16:15
|
|
Major 7th
|
15:8
|
|
|
1/6 Comma
|
tritone
|
45:32
|
|
diminished 5th
|
64:45
|
The fact that each of these systems found adherents in the Renaissance may have been due, in part, to the presence of these pure intervals and the consequent enhancement to certain modes and progressions.
Copyright Statement
Copyright © 2006 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Andrew Eason, Editorial Assistant