Glenn Gould’s “Constant Rhythmic Reference Point:” Communicating Pulse in Bach’s Goldberg Variations, 1955 and 1981

[1] If the average person knows anything about the Canadian pianist Glenn Gould (1932–82), it is that he was an eccentric performer as well as an eccentric human being. He disliked most of the common practice piano repertoire, he abruptly left the concert stage in 1964—only nine years after his successful international debut in New York—and for the remainder of his career he maintained an active but extremely buffered public persona as a recording artist, radio producer, essayist, and critic. If one knows anything further about his eccentricities in performance, it is that he relished unusual tempi. In his late 1960s recording of Mozart’s K. 331 Piano Sonata, for instance, Gould begins at such a slow rate ( = ca. 60 bpm) that it may difficult for some listeners to feel a pulse at all.

[2] Were we to listen to the entire movement, however, we would find that the main beat of each of this movement’s variations is slightly faster than the previous. This plan, which Gould explicitly acknowledged, mirrors the piece’s increasing amount of beat division and subdivision, creating increasing rhythmic activity with each subsequent variation.⁽¹⁾ The surface rhythms and the tempo of the main beat reinforce one another, propelling the listener from the theme through the final variation. Thus while Gould’s tempi often seem peculiar, they are often chosen in the service of a broader musical plan, chosen in order to communicate his conception of a work to his audience.

[3] Gould commented specifically on this general tempo plan for Mozart’s K. 331 in a 1976 interview, and in his remaining years he continued to discuss and develop ideas about tempo and rhythmic continuity in performance. Gould discussed in great detail his tempo choices for one of his very last studio recordings, Bach’s Goldberg Variations, recorded in 1981. To the extent that any artistic decision by this unpredictable personality had the power to surprise, this recording project did; Gould had launched his career with what many considered a definitive recording of the Goldberg Variations in 1955, not to mention that he rarely recorded any composition twice. The relative wealth of public comments concerning his 1981 version, then, is due in no small part to his perceived need to justify, or at least explain it. These recorded, filmed, and written comments, combined with the two studio recordings, provide a rare opportunity to investigate an artist’s theoretical musings and a performance that are explicitly connected.

[4] There are two main sources for Gould’s comments on the 1981 recording: first, the film made by Bruno Monsaingeon in the studio during the recording process, and second, a radio interview conducted by CBC music critic Tim Page just after the public release of the recording in 1982. These comments can be collected into a loose theory of temporal relations—a theory that provided Gould’s motivation for returning to the studio to re-record the Goldberg Variations, and one that also provides a framework for listening to the recording itself.

[5] In the opening minutes of Monsaingeon’s film, Gould responds to the filmmaker’s question “why do it again?”:

GG: I wasn’t motivated to do it until rather recently, when it occurred to me, on one of my rare re-listenings to that early recording, that it was very nice, but that it was perhaps a little bit like thirty very interesting but somewhat independent-minded pieces going their own way . . .

GG: [I thought that] if I looked at it again, I could find a way of making some sort of almost arithmetical correspondence between the theme and the subsequent variations, so that there would be some sort of temporal relationship—I don’t want to say just exactly two, four, eight, sixteen, thirty-two, that kind of correspondence, but—you know what I mean, that there would be a sense in which—substituting for the fact the Bach has absolutely no melodic design that is continuous but rather a base harmonic design that is continuous—there would be at least a rhythmic design that was continuous and a sense of pulse that went through it. And that seemed to me sufficient justification . . . to do it all over again.⁽²⁾

[6] Gould clearly felt that his contribution to the coherence of the work was to be in the time dimension, controlling the periodicities in the score and creating “a sense of pulse” that spanned the entire work. Gould fleshed out these ideas in the 1982 radio interview:

GG: I’ve come to feel over the years that a musical work, however long it may be, ought to have basically—I was going to say ‘one tempo’ but that’s the wrong word—one pulse rate, one constant rhythmic reference point. Now obviously there couldn’t be anything more deadly dull than to exploit one beat that goes on and on and on indefinitely —that’s what drives me up the wall about rock, you know, and . . . about minimalism . . .

TP: Oh-ho! I think we should argue that one another time.

GG: Yeah, probably so. Anyway, I would never argue in favor of an inflexible music pulse, you know, that just destroys any music. But you can take a basic pulse and divide or multiply it, not necessarily on a scale of two, four, eight, sixteen, thirty-two, but often with far less obvious divisions, I think, and make the result of those divisions or multiplications act as a subsidiary pulse for a particular movement or section of a movement . . .

GG: So in the case of the Goldberg, there is in fact one pulse, which—with a few very minor modifications—mostly modifications which I think take their cue from ritards at the end of the preceding variation, something like that—one pulse that runs all the way throughout.⁽³⁾

[7] Here Gould expands on the idea of an unchanging but flexible pulse rate using the term “constant rhythmic reference point.” This concept allows him and his audience to follow larger shifts in the tactus rate, as long as new pulses bear a roughly integral relation to the constant rhythmic reference point. These comments no doubt remind many readers of David Epstein’s work with proportional tempo.⁽⁴⁾ Like Gould, Epstein presumes that tempo relationships in simple ratios like 1:2 or 2:3 are perceptible. Because of their musical intuitions about perception, however, both author and pianist shy away from more complex ratios such as 3:5. Epstein does so explicitly,⁽⁵⁾ while Gould simply never discusses connections in his Goldberg Variations that are more complex than 2:3. Nevertheless, both make allowances for ritardandi and rubato that will make any rational relationship inexact. These intuitions correspond well with theories of categorical perception, which hold that humans will assign any rhythmic relationship to one of a very few simple-ratio categories. Despite the expressive imprecision often involved in performing a rhythm, we tend to hear rhythmic relationships as 1:1, 1:2, or 1:3.⁽⁶⁾

[8] That Gould did not want his pulse relationships to be obvious is clear from the following exchange with Page:

GG: Well, you know, when one describes a process this way, it sounds just so relentlessly clinical, so ruthlessly sterile and anti-musical, really. And it is at that level, it’s almost embarrassing, I . . . I’m sorry . . .

TP: Well, don’t . . . please don’t be embarrassed, because I think you’ve given us a remarkable insight into your working method.

GG: Well, thank you. But you know what I mean. On the face of it, it’s exactly like analyzing a particular tone row of Schoenberg, for example, and saying ‘well this is a wonderfully symmetrical tone row, and therefore it must inevitably lead to a wonderfully symmetrical work.’

TP: I’ve heard that talk before.

GG: Exactly, and it ain’t necessarily so. I think it’s a technique—the idea of rhythmic continuity—that’s really only useful if everybody does ‘feel it in their bones’, you know, to use your words; experiences it subliminally, in other words, and absolutely nobody actually notices what’s really going on.

[9] As part of a larger empirical study on tactus choice in recorded music, I conducted a comparative investigation into the effect of Gould’s tempo relationships in his 1955 and 1981 recordings of the Goldberg Variations. The primary challenge to such a project is hinted at in the quote immediately above. How does one quantify a “feeling in the bones?” For this reason I did not attempt to establish that study participants were actively perceiving (or not perceiving) the relationships that Gould discusses for the 1981 version. Instead I measured physical responses to the time dimension of Gould’s recordings and took these responses as evidence of perceptions that may or may not have been conscious. The methodological problem was to evaluate the communicative power of Gould’s proportional tempo connections without telegraphing the ideas themselves to participants in the study. The study sessions could not, for instance, include follow-up questions after each excerpt asking if and which proportion the listener just heard. If so, listeners would begin listening for proportions and would focus their attention on finding them—certainly not a typical mode of engagement with live or recorded music.

[10] A brief prose summary of the study’s method is given here along with its results; a full version of the method is included as Appendix A. I used three transitions between variations in the study, chosen in part because Gould had commented on them specifically. The segments of music (the conclusion of one variation and beginning of the next) were chosen to represent Gould’s own recording procedure during the 1981 session; immediately before recording a variation he took his tempo cue by listening to the playback of the end of the previous variation. Example 2 shows one such transition, the end of Variation 16 and the beginning of Variation 17. 28 participants heard this section of music in a controlled lab environment; half heard the 1955 version, the other half heard the 1981 version. Participants were asked to tap with their finger(s) or hand along with the music at a steady and comfortable rate. This rate is a listener’s primary beat level or tactus, and it will normally correspond to some layer of a piece’s metric structure.

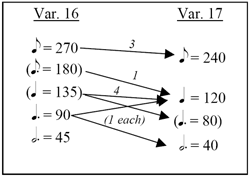
[11] The metric levels that were possible tactus candidates in the 1955 performance are shown in Figure 1. Bach’s note values and Gould’s performance tempi are given in the left column for Variation 16, and in the right column for Variation 17. The notes and tempi in parentheses indicate pulses that are hemiolic with respect to the notated meter. The connections between tactuses that participants made across this transition are shown with arrows, and the number of individuals who took each path is shown in italics near those arrows. The responses are quite diverse, and the amount of attention given to hemiolas by this group of listeners is especially noteworthy.

[12] Gould spoke with Page about his reconception of this transition for the 1981 recording:

GG: . . . instead of using the dotted quarter from the fughetta [Variation 16] as my yardstick for Variation 17, I took two-thirds of it, two-thirds of a bar from the fughetta, and used the actual quarter note which that two-thirds represents. The new beat gave three for the price of two, and that applied to Variation 17 allowed, you know, for a much more effervescent tempo [he sings the opening rhythms of Variation 17].

[13] Returning to Figure 1 for a moment, we should note that the hemiolic relationship Gould discusses was already the most popular response to his 1955 version of this transition. Five of the eleven participants chose the hemiolic 135 bpm pulse as tactus in Variation 16, and carried that pulse rate more or less directly across the break to the 120 bpm quarter note pulse. This result indicates that a hemiolic quarter note is not difficult to hear in Variation 16, even if Gould wasn’t consciously thinking about it in 1955. While the rhythmic gestures of the end of this variation are clearly based in three, the very consistent density and rapidity of attacks does makes it possible, even easy, to feel a quarter note pulse.

[14] Figure 2 reproduces Figure 1 and adds the analogous information for the 1981 performance. Gould’s constant rhythmic reference point is evident in his intended pulse connection, 105 to 108 bpm. This connection will be perceived as 1:1, and was followed by all three participants who chose the 105 bpm pulse as their initial tactus. What Gould does not mention when discussing this hemiolic pulse link, however, is that it maintains a continuous eighth note pulse between movements. Since these eighth notes are clear in the notated meter of each variation, we would expect this connection to be very attractive to listeners as well. In Figure 2 we can see that this was indeed the case—the perceived 1:1 eighth note connection from 210 to 216 bpm was followed by six out of the eight participants who chose 210 bpm as their initial tactus. The remaining two participants followed a 2:1 path, from 210 to 108 bpm, the notational path indicated by Bach’s meter signatures for the two variations. Only a single participant followed a path (70 to 108 bpm) that did not have a continuous or half-time feel. While Gould certainly intended the constant rhythmic reference point between these two movements to be the quarter note, the connections that most listeners actually made could be characterized as “subsidiary pulses,” related to his intended connection by simple ratios, 1:1 or 2:1.

[15] More generally, we can see in Figure 1 increased clarity in the responses to the 1981 performance, manifested in fewer paths between variations, as well as by a solid majority of 1981 responses following the two 1:1 paths that are implied by Gould’s comments. Kevin Bazzana uses the term “metrical counterpoint” to describe Gould’s emphasis on dissonant rhythmic interpretations: “Gould’s fondness for metrical counterpoint in part explains his fondness for relatively stable tempos, [because] the impact of cross-rhythms is heightened where the basic rhythmic profile is strict.”⁽⁷⁾ If we apply this idea to these two variations, we see that while there were more hemiolic pulses felt in the 1955 version, only the hemiola that Gould explicitly mentions was chosen in response to the 1981 recording. His 1981 conception of Variation 16’s 3/8 meter includes an emphasis on the dissonant quarter note pulse, which feeds into the quarter note of Variation 17. Contrast this relative clarity with his 1955 performance of this transition, which he implied was less planned—a difference that is indeed reflected in participant responses.

[16] Gould exercises similar influence over an audience’s perceived beat in the transitions between Variations 18, 19, and 20, influence that here also creates a more general effect of perceived speed when moving from one movement to the next.

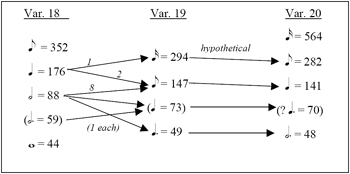
[17] Only the first of these two transitions was used in the study, since tactus responses to the Variation 19 into 20 transition in both performances seemed predictable. Figure 3a shows the pulses, performance tempi, and responses to the 1955 performance of these variations. Listeners from Variation 18 into 19 most often chose the to connection that the respective meter signatures indicate as the tactus. Like the 1955 version of Variation 16 into 17, there is a surprising diversity of paths chosen here. The hypothesized paths from Variation 19 into 20 shown in Figure 3a represent the most likely paths given the responses from 18 into 19; other paths are plausible but less probable.

[18] In response to the 1981 performance (Figure 3b), there were only three paths chosen between Variations 18 and 19; while neither the 1955 nor the 1981 performance elicited only one path, the 1981 performance elicited far fewer. The most frequently chosen transition between 1981’s Variations 18 and 19 was 96 to 90 bpm, and in the film of this recording, it is this path that one sees Gould conduct across the break between movements. Finally, all three paths chosen in response to the 1981 performance have a 1:1 or 2:1 relationship, where there are no paths chosen in response to 1955 that are likely to be felt as either continuous or half-time. With these 1981 responses from 18 into 19, it is a reasonable prediction that listeners would follow the inverse paths between Variations 19 and 20.

[19] With respect to the overall affect of Gould’s tempo choices, Bazzana states, “Most of Gould’s wide departures from given tempo markings suggest a desire to exaggerate the affect implied by the composer—to take it further in the indicated direction.”⁽⁸⁾ Bazzana is explicitly referring here to a composer’s own tempo markings, which are absent from the Goldberg Variations. The characteristic tempo of each movement is derived instead from general dance and instrumental genres of Bach’s day, as well as from the overall metrical structure present, and it is the latter feature that we can see Gould taking into account with his performance tempi. In Variations 18–20, it is clear from the score and both performances (see Figures 3a and b) that there is faster rhythmic activity in Variations 18 and 20 relative to that in Variation 19. While these compositional factors are evident even at Gould’s 1955 performance tempi, Gould exaggerates the structural differences with his 1981 tempo choices. As the very fast subdivision is subtracted going from Variation 18 into 19 (see Figure 3b), Gould slows the overall tempo, and as a fast subdivision is added back in going from Variation 19 into 20, he increases the overall tempo. Listeners to the 1981 performance clearly felt these tempo changes, seen in their chosen paths across the transitions. Thus the structural features of the music, combined with Gould’s tempo choices, create an inescapable impression of slowing from Variation 18 into 19, and speeding up from Variation 19 into 20. This uniformity of impression is certainly absent in the 1955 performance.

[20] While it is unlikely that any single performance could elicit the same tactus response from every individual in an audience, or that any two individuals would follow an identical tactus path throughout an entire set of variations, thus far Gould’s 1981 performance of the Goldberg Variations do limit and direct those responses. Variations 18–20 were an example of a performer working with, even exploiting a composed musical structure, and yet that same structure can also limit a performer’s influence. To demonstrate this point we turn to one more transition, from Variation 14 into 15. Gould singled out this transition in the Page interview as one that particularly benefited from a constant rhythmic reference point, and in so doing he reiterated portions of the argument made to Monsaingeon the previous year:

GG: Think of Variation 15 . . . It’s the most severe, and rigorous and beautiful canon . . . , and a movement like that is preceded by Variation 14, logically enough, which is certainly one of the giddiest bits of neo-Scarlatti-ism imaginable . . . Quite simply, the trap in this work, in the Goldberg, is to avoid letting it come across as thirty independent pieces, because if one gives each of those movements their head, it can very easily do just that.

[21] How does Gould use tempo to bridge this stylistic gap in 1981 differently than 1955? Figure 4 compares Gould’s two performances and their respective listener responses. It is immediately evident that the same paths were taken across the transition in both performances, despite the markedly different tempi for Variation 15. It is also noteworthy that no participant who heard the 1981 performance traversed the break at the most logical tempo connection, 96 to 90 bpm, which would be perceived as a 1:1 relationship. But as Gould was quoted above, a variation’s initial tactus may be influenced by ritardandi at the end of the previous variation. In this situation, the noticeable ritardando at the end of Variation 14 probably influences listener perception of the transition. Structural factors come into play as well, however; the 96 bpm pulse is not the fastest pulse present in Variation 14, while the 90 bpm pulse is the fastest pulse present in Variation 15. In this and a previous empirical study I have found that certain people prefer not to tap along with the fastest available pulse, and I would predict that these individuals, if they chose 96 bpm in Variation 14, would move to the quite slow 45 bpm pulse in Variation 14, even though a seemingly simpler transition to 90 was possible.⁽⁹⁾ In both performances of Variation 14 into 15, then, the very different metric structures of these adjacent variations force listeners into a slower Variation 15 pulse, regardless of their tactus in Variation 14. Only in the 1981 performance, however, was this slower pulse a subsidiary pulse, perceptually related to the previous tactus as 2:1 or 4:1, simple ratios that do not exist in listeners’ experience of the 1955 performance.

* * *

[22] The type of data presented in this study can serve as a springboard from which to initiate close analytic readings of both a score and performances of it. Once we have gathered listener responses to multiple performances of a piece, we can more easily identify differences in responses that are influenced by performance factors against the backdrop of an invariant structure. For Wallace Berry, tempo and articulation are “the essential categories of [a performer’s] interpretive intervention,”⁽¹⁰⁾ and I have attempted to engage at least the first of these here. From a performer’s standpoint, Gould’s constant rhythmic reference point is perhaps best seen, again in Berry’s terms, as “a reasoned basis from which to make interpretive choices.”⁽¹¹⁾ Indeed, much music theory has been and continues to be created and taught for precisely this reason.

[23] Structural features of music limit performers’ and listeners’ options over and above basic psychological or kinesthetic constraints such as extreme pulse rates⁽¹²⁾—this is Bach’s degree of control over our experience of his Goldberg Variations. In performing the set (for either recording), Gould was able to shape and direct an audience’s perception of time and pulse in the work while acknowledging and accepting the composer’s agency. Gould’s interpretive choices are based in Bach’s structures, in his own ideas about creating coherence within and between those structures, and, for all his self-aware rumination, in his own intuitive expression. We have seen that these factors combine more effectively in Gould’s 1981 performance to control listeners’ apprehension of pulse within sections of music and across transitions. Yet the composer and/or performer cannot dictate a uniform tactus no matter how clear we might find a performance in this respect—individual listeners also retain a degree of agency as part of this exchange. The perception of time in music is both a bottom-up and top-down process, and we will create richer analyses when our methods embrace the full network of communication between composer, performer, and audience.

* * *

Postscript on methodology

[24] In the course of this study I have approached musical objects as well as experimental data as creatively and subjectively as any music analyst. Theorists who tend to see music and empiricism as at best strange bedfellows may not see the point in basing the above conclusions on empirical observation, while psychologists may be put off by the absence of significance claims due to the small number of participants, or even by the methods section appearing as an appendix. It is my hope that, for the sake of healthy disciplinary cross-pollination, all readers are willing to embrace aspects of less familiar research models while forgoing aspects of those that are most familiar: that trained scientists can appreciate a rich musical discussion flowing from an approach that may be viewed as insufficiently rigorous, and that theorists can appreciate how formal experimentation might contribute to an essentially analytical project. Music theory can borrow methods and modes of discourse from experimental science without trying to become part of it,⁽¹³⁾ and without insulating itself in the process from the type of critical response that has long motivated disciplines in the humanities.

* * *

APPENDIX A: Study Method

Stimuli:

40 musical excerpts were drawn from a variety of repertories, focusing on the broadly defined body of Western classical music. The excerpts were taken from readily available commercial recordings, and ranged from 15–45 seconds in length. 25 of the 40 excerpts contained a shift in metric structure, ranging in disruptiveness from the addition/subtraction of (a) consonant pulse(s) to the complete cessation of an initial meter and the establishment of a new meter. The Gould excerpts were part of this group of 25.

The 40 excerpts were organized into two lists of 29 excerpts each (Lists 1 and 2), with 18 excerpts appearing identically in both lists. The remaining 11 excerpts in each list were paired across lists based on the following two comparisons:

1. Different performances of an identical section of music were paired (e.g. the Gould recordings).
2. A section of music containing a metric shift was paired with the same recording, but beginning after the metric shift had occurred.

The pieces and performances were chosen for a high degree of structural and performed temporal regularity during their opening 5–8 seconds, and during the 5–8 seconds following a metric shift. Excerpts were manipulated prior to the experiment in AIFF format to roughly equalize amplitudes across all excerpts and bring them within the range of comfortable hearing.

Each excerpt was followed by a recorded voice that instructed participants to complete a speed rating task which will be described below. This prompt was followed by approximately 4 seconds of silence, which was itself followed by a 10-second chunk of a distractor stimulus. These stimuli were musical or non-musical sounds free of metric content or regular pulse, but nonetheless aurally engaging. These were identical to those used in Study 1, and were drawn from commercial recordings of free jazz, Eastern European folk music, ‘sounds of nature’, or high-quality home recordings of the author’s then 9-month-old daughter striking various toy percussion instruments while vocalizing. Any components of these recordings that involved a steady pulse (i.e. two or more successive IOIs) were removed or rendered unsteady via computer editing.

Apparatus:

All stimuli were played back using a program written in MAX/MSP through Sennheiser HD 570 stereo headphones. Participants responded to the stimuli by tapping their dominant hand on an 8” by 11” piece of white Plexiglas placed on a desktop. Underneath this Plexiglas was another of the same size, with an Infusion Systems I-Cube Touchstrip piezoelectric sensor placed between the two layers. This sensor has a minimum activation force of approximately 25 grams, and a mechanical response time of 1–2 ms. Participants were not instructed to tap in any particular fashion; they could tap with one or more fingers, entire hand, fist, etc. Output from this sensor was fed into a MAX program and the time interval between each tap was recorded in milliseconds and beats per minute. The MAX program only accepted input from the I-Cube sensor once every 4 ms, so this was the necessary quantization of the tapping data. Nevertheless, the apparatus allowed consistent data to be collected regardless of individual tapping style, and was able to obtain uniform within-subjects data for participants who altered their tapping style during the study.

Participants:

The participants were 28 adult volunteers, 25 of whom were graduate or undergraduate students at the University of Chicago, 3 of whom were members of the community. The group was balanced in terms of gender, with an age range of 18–58, mean of 24, and median of 21. Most had responded to a campus advertisement and were part of the Psychology Department’s subject pool; some graduate students and community members were recruited as acquaintances of the author. They represented a wide range of musical training, musical performance experience, and listening habits, but were relatively uniform in overall educational level in that all had were pursuing or had completed at least an undergraduate degree program.

Procedure:

The participants came for a single session, which began with them completing a questionnaire on their musical training, performance experience and habits (both formal and informal), classroom training in music, dance training, experience and habits (both formal and informal), and their habits and experience in the consumption of music, whether live or recorded. They were then seated at the testing station and briefly allowed to become comfortable tapping on the 8” by 11” surface. They were then given verbal instructions to tap on the pad at a steady, comfortable, medium rate, that seemed to them neither fast nor slow (spontaneous tempo). Next, the tapping task was explained, including the directive to “tap at a comfortable and steady rate” along with the excerpts. They were then directed to don the headphones, and a warm-up excerpt that contained a clear metric shift was presented.

After the warm-up excerpt, participants were then asked to remove the headphones, and the speed rating task was explained. They were asked to rate the speed of the second part of the excerpt compared to the speed of the first part, using the following scale: 1=very much slower, 2=slower, 3=a little slower, 4=the same/no change, 5=a little faster, 6=faster, 7=very much faster.

The battery of 29 excerpts was then administered in random order. The sequence of stimuli was excerpt-speed rating prompt-distractor stimulus. When a speed rating had been made and the distractor stimulus had ceased, I determined that the participant was ready to move on and began the next excerpt, allowing a minimum of 5 seconds to elapse between the end of the distractor stimulus and the subsequent excerpt.

14 participants responded to the List 1 excerpts, 14 responded to List 2. After all excerpts had been presented, participants were asked to produce spontaneous tempo a second time.

Peter A. Martens
Texas Tech University
School of Music
Box 42033
Lubbock, TX 79410
peter.martens@ttu.edu

Footnotes

1. Tim Page (ed.), The Glenn Gould Reader (New York: A. Knopf, 1984), 40. As Gould also acknowledged, this tempo plan completely disregards Mozart’s Adagio indication for Var. V.
Return to text

2. Bruno Monsaingeon, The Goldberg Variations [film], (Glenn Gould Plays Bach, 3; CBC-Casart co-production, 1981) [Video release: Sony Classical, GGC xv, 1994].
Return to text

3. Tim Page, Recorded interview with Glenn Gould, Aug. 1982 [released as disc 3 of A State of Wonder containing the 1955 and 1981 recordings of the Goldberg Variations. Originally released as CBS LP M3X38610, 1984].
Return to text

4. Epstein, Beyond Orpheus (Cambridge, Mass.: MIT Press, 1979) and Shaping Time (New York: Schirmer Books, 1995).
Return to text

5. Epstein, Shaping Time, 125 and 505, fn 15.
Return to text

6. See e.g. summary in Eric Clarke, “Rhythm and Timing in Music,” in The Psychology of Music, 2nd ed., ed. D. Deutsch (San Diego: Academic Press, 1999); Categorical perception will occur even if listeners are aware of the imprecision, and thus this concept supercedes perceptual thresholds for exactness based on Weber’s Law, within which listeners will not even detect rhythmic imprecision.
Return to text

7. Kevin Bazzana, The Performer in the Work (Oxford: Clarendon Press, 1997), 179 (paraphrasing Joanne Rivest).
Return to text

8. Bazzana, 165.
Return to text

9. Peter Martens, “Beat-Finding, Listener Strategies, and Music Meter.” PhD diss. (University of Chicago, 2005).
Return to text

10. Wallace Berry, Musical Structure and Performance (New Haven: Yale University Press, 1989), 2–3.
Return to text

11. See Berry, 7.
Return to text

12. See Justin London, Hearing in Time (Oxford: Oxford University Press, 2004).
Return to text

13. Robert Gjerdingen, “An Experimental Music Theory?” in Rethinking Music, ed. N. Cook and M. Everist (Oxford: Oxford University Press, 1999), 169.
Return to text

Copyright Statement

Copyright © 2007 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by Brent Yorgason, Managing Editor and Stefanie Acevedo and Tahirih Motazedian, Editorial Assistants
Number of visits: