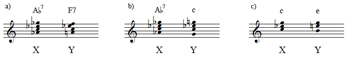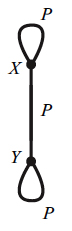Birdcage Flights: A Perspective on Inter-Cardinality Voice Leading *
Joti Rockwell
REFERENCE: http://www.mtosmt.org/issues/mto.03.9.4/mto.03.9.4.cohn.php
KEYWORDS: Voice leading, transformation, neo-Riemannian theory, parsimonious graphs
ABSTRACT: This study explores connections between trichords and tetrachords from a voice-leading perspective. It begins with a definition of a voice-leading relation that draws from the work of Callender, Douthett, and Steinbach and uses a matrix to account for parsimonious voice leading. Given specific matrix values and chord-type constraints, networks arise that integrate both trichords and tetrachords, and both inter- and intra-cardinality relations can be modeled by the resulting “birdcage” graphs.
Copyright © 2009 Society for Music Theory
[1] After more than a decade of work in neo-Riemannian and transformational theory, music theorists now have a strong handle on how to get from one consonant triad to another. Like a seasoned urbanite describing the quickest or most interesting route between two city locations, today’s trained music theorist can rattle off a bevy of moves one can make to get from one triad to the next.(1) Recently, this knowledge of the harmonic terrain has been extended to include trichords other than major and minor triads, trichordal set-classes, seventh chords, tetrachordal set-classes, and chords and set-classes of other cardinalities.(2) As theorists become increasingly skilled at mapping musical spaces, the pitch universe seems to be on the verge of being completely charted.
[2] With much of this theory resting on an epistemological foundation of voice leading, though, there are a number of challenges to the project of charting pitch space. Perhaps the most significant of these is the problem of characterizing voice leading between pitch-class sets of different cardinalities. In situations such as these, the question of accounting for an added pitch manifests itself as a mathematical uncertainty since a function, strictly speaking, cannot be used to model the motion both to and from each pcset. David Lewin, for example, calls attention to this issue in analyzing passages from Wagner containing both triads and seventh chords: “it would be impossible to express any of the voice leadings [of Lewin’s musical excerpts] as formal mathematical functions” (Lewin 1998, 67).
[3] One solution to the challenge of function-based models of inter-cardinality voice leadings, proposed by Julian Hook as a “cross-type transformation,” involves considering chords as individual objects rather than collections of pitch classes.(3) Functions can then be used to map a set of chords to and from another set of chords of different cardinality, provided that the respective chord-sets are of equal size. This approach retains the algebraic clarity and coherence of intra-cardinality transformations by being a model of chord progression rather than voice leading.
[4] Incorporating inter-cardinality voice-leading relationships, however, can be a messy task. Joseph Straus has noted that with regard to a voice-leading graph, inter-cardinality moves among set classes can be “too numerous and intertwined” (Straus 2003, 63), and such moves have introduced a variety of complications into more recent spatial models of voice leading. In a later study by Straus, for example, the inclusion of sets of different cardinality results in set-class redundancies within his space, as well as rules prohibiting any type of move within the space that violates his definition of a shortest voice-leading path (Straus 2005, 57–59). For Tymoczko 2006, an inter-cardinality move manifests itself either as a shift from one multi-dimensional space to another space of different dimensions—a seemingly extreme form of spatial transportation—or as a move nearing a boundary of the higher-dimensional space, in which case the intra-cardinality voice-leading properties of the lower-cardinality chord are less revealingly organized.(4) Perhaps this issue is, as Tymoczko 2007 argues, less a problem with the models than it is a reasonable interpretive and conceptual challenge to the theorist or analyst using them. Either way, the question remains as to whether musical spaces that incorporate both inter- and intra-cardinality voice leading can match the cogency, suggestiveness, and analytic applicability of the successful single-cardinality models. The present study, which can be viewed as an exploration of subspaces of the more generalized studies of Straus 2005, Tymoczko 2006, and Callender, Tymoczko, and Quinn 2008, suggests that there may be some promise in this regard.
[5] This study examines connections between trichords and tetrachords from a voice-leading perspective. Drawing from the work of Callender 1998 and Douthett and Steinbach 1998, it begins with a definition of a voice-leading relation that uses a 2×2 matrix as a way of accounting for parsimonious voice leading for both inter- and intra-cardinality moves. Given specific matrix values and chord-type constraints, networks arise that integrate both trichords and tetrachords. One such network proves to be a successful model for the “omnibus” progression, illustrating the pattern’s unique voice-leading properties. After formalizing these types of networks as “birdcage” graphs, this study finds all other such graphs for all types of parsimonious voice leading as given by the initial definition. Focusing on voice leadings as framed by particular chords, rather than chords as related by particular voice leadings, this study ultimately addresses the topic of inter-cardinality voice leading by answering the following questions: what parsimonious voice leadings allow for a trichordal set class and a tetrachordal set class to map both to themselves and to one another, and what are the set classes for which this situation can be met?
1. Modeling voice leading with the P-matrix
[6] In a footnote to their investigation of parsimonious graphs, Jack Douthett and Peter Steinbach suggest a way in which their relation definition might be extended to accommodate pcsets of different sizes: motion from a larger pcset to a smaller one can be modeled as a “surjective” or “onto” map acting on each of the pitch classes in the larger set (Douthett and Steinbach 1998, 261). Example 1 illustrates the idea of such a model for two cases. In Example 1a, τ is the function moving G,B,D, and F to G,C,C, and E, respectively. This function contains no inverse: there is no single-valued way of moving the C major chord to the G7 chord, since the pitch class C splits into two other pitch classes. In Example 1b, however, the function τ′ does have an inverse since the two pcsets have the same cardinality. The function is thus not just a surjection or “onto” mapping but a bijection, i.e., a mapping that is both “one to one” and “onto.”
[7] Given that composers move seamlessly within and among harmonies of various sizes, theories of voice leading do well to include both types of motion shown in Example 1. The present study thus models voice leading with a “parsimonious voice-leading matrix,” in which the pcsets under consideration need not be of the same cardinality. As Example 2 illustrates, this P-matrix is of the form
| u1 | u2 | d1 | d2 |
, where u1 and u2 each represent the number of voices moving up by semitone and whole tone, respectively, while d1 and d2 represent the number of voices moving down. Example 2a shows how a progression of G7→C corresponds to a P-matrix where u1 = 1, u2 = 0, d1 = 1, and d2 = 1 according to the motions given in Example 1a. Note that the term “matrix” is not used here to employ all the mathematics of linear algebra—the determinant of P and matrix multiplication with P, for example, would seem to have little musical utility—but to represent voice leading as a combination of vectors, one type of which corresponds to motions by a given number of semitones and the other of which tallies the voice-leading moves in a given direction. In other words, P is best considered as a combination of its row and column vectors.
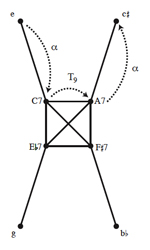
[8] P-matrices can be defined formally by invoking the surjective τ function from Example 1, thus allowing for “fusing” (and, indirectly, “splitting”) as introduced by Callender 1998. Definition 1 presents such a construction in which a chord X is greater than or equal to another chord Y in size, τ maps each pc in X to each pc in Y, and P indexes downward motion with the bottom row of the matrix and upward motion with the top row.(5) Though this definition is limited to voice leading involving only one or two semitones, it can straightforwardly be extended to accommodate all sizes of voice-leading moves by expanding P into a 2 × z matrix, where the largest move is the size of z semitones. This generalized definition of voice leading is given as an Appendix and is not needed for the present purposes.
Definition 1: Given pcsets X and Y where the cardinality #X ≥ #Y, the two sets are related by a P-matrix
u1 u2 d1 d2 (written X
u1 u2 d1 d2 Y ) if there exists a surjection τ: X → Y and a set {xk}
such that X\Y (the set of pcs in X that are not in Y) = {xk}
#X-1 k = 0 , and
d1 + d2 + u1 + u2 - 1 k = 0
[9] The present voice-leading model, as illustrated by the first two examples and formalized in Definition 1, warrants two observations. First, P-matrices are not unique to a given harmonic progression, since the voice leading can occur in a number of different ways. It is convenient to assume that the voice leading is as smooth as possible; that is, each voice in chord X moves to the nearest pc in chord Y.(6) Given this constraint, P will still not necessarily be unique for any given progression (e.g., P for Example 2a could also be given as
| 1 | 1 | 1 | 0 |
if τ maps D to E), but the sum of all dn and un for any of the matrix possibilities will remain the same. Second, as shown by Example 2b and 2c, a given P can represent moves that both alter and preserve the cardinality of the chords. A matrix that corresponds to a cardinality-changing move, however, is subject to an “intervallic closure” condition. Restricting the condition to chords of cardinality 4 and 3, closure entails that for a tetrachord X to move to a P-related trichord Y, the voice-leading moves corresponding to one or two pcs in X must sum to some interval in X. Voice leading between tetrachords and trichords can easily satisfy this condition: consider, for example, that in cases involving only one voice-leading move (where the sum of all P-matrix values equals 1), the only tetrachordal set-class for which this condition cannot be met is set class [0369], the diminished seventh chord. This unique case results from the fact that only whole-tone or semitonal motion is involved, neither move of which is large enough to “close” any of the minor-third intervals in a diminished seventh chord.
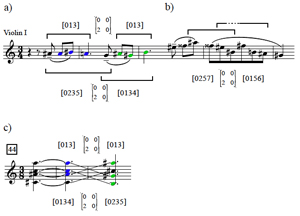
[10] In addition to the flexibility of accounting for both inter- and intra-cardinality moves, an advantage of characterizing voice leadings with P- matrices is that while they can provide sums for total voice leading, they do not classify relationships by the sums alone. It seems overly general, for example, to consider the “hexatonic pole” transformation LPL to be the same type of voice leading as a T1 transformation on a triad.(7) At the same time, P-matrices are not so specific as to relate only to a single Tn or TnI set class, as most of the common transformational labels do. An analytic benefit from this perspective is that musical works can be interpreted according to voice-leading equivalences—a type of motivic unity—when the harmonic palette is otherwise varied.(8) For instance, Example 3 illustrates how
| 0 | 0 | 2 | 0 |
can serve as a unifying device at two key moments in Bartók’s Third String Quartet. The first phrase of the piece is framed by an [013] self-mapping via
| 0 | 0 | 2 | 0 |
, and including the G4 in the hearing gives a tetrachordal mapping from [0235] to [0134] (Example 3a). If one hears the ![]()
![]()
![]()
![]()
| 0 | 0 | 2 | 0 |
[0156] occurs (Example 3b).(9) At 44 of the Seconda parte, in what is to that point the most striking texture of the quartet, all four instruments glissando from {C, ![]()
![]()
![]()
![]()
![]()
[11] As yet we have not accounted for motion from a smaller pcset to a larger one; since P involves the opposite scenario such motion is given by the “mirror” of P as given in Definition 2. A result of Def. 2 is that the relation given by P is non-commutative, since X P Y implies Y (MIR(P)) X. Furthermore, if a given nonzero P is the same as its mirror, some type of contrary motion is at work.(10)
Definition 2: For P =
u1 u2 d1 d2 , MIR(P) =
d1 d2 u1 u2
[12] With the voice-leading definitions now in place, various types of voice-leading parsimony can be explored, nine of which are proposed in Example 4. These types correspond to all P-matrices in which the total voice leading is equivalent to three semitones or less. There is also one addition, type IX, which corresponds to the smoothest voice leading involved in a move between a tonic major triad and its dominant-seventh chord (Examples 1a and 2a). Though this sort of motion is not especially parsimonious, strictly speaking, this voice-leading type appears in this study due to its frequency in the musical literature. The mirrors of each matrix in Example 4 are not included in the list, since they are grouped as part of the same voice-leading type. This consideration follows from the fact that common transformations correspond to both a P-matrix and its mirror; e.g., the L-transformation is represented by either
| 1 | 0 | 0 | 0 |
or
| 0 | 0 | 1 | 0 |
, depending on the mode of the triad.
2. “Birdcage” graphs
Example 5.
| 1 | 0 | 1 | 0 |
(click to enlarge)
Example 6.
Tn{0,3,7}}, P =
| 1 | 0 | 1 | 0 |
(click to enlarge)
Example 7.
{Tn{0,4,7,10}, Tn{0,3,7}}, P =
| 1 | 0 | 1 | 0 |
(click to enlarge)
Example 8. Omnibus subgraph
(click to enlarge)
Example 9. Brahms, third symphony, Poco Allegretto, measures 150–154
(click to enlarge)
[13] As an initial case, consider the second type of voice leading from Example 4, in which two voices move in contrary motion, each by a semitone. This type stands out from the others in that it is the only one with mirror symmetry. Allow also the constraint in which the two chords involved are either minor triads or dominant seventh chords. We thus have P =
| 1 | 0 | 1 | 0 |
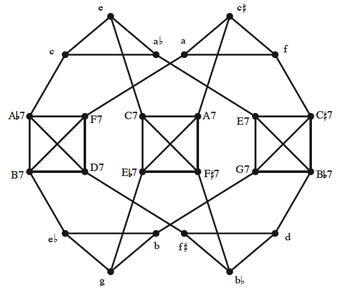
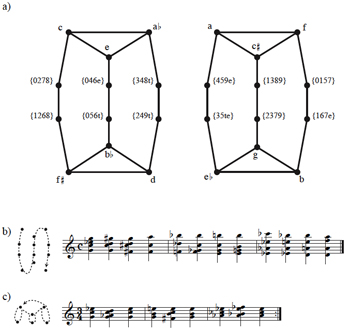
where X,Y ∈ {Tn {0,4,7,10}, Tn{0,3,7}} (mod12). As Example 5 illustrates, there are three scenarios corresponding to these matrix and set-class conditions. Expressed tonally, these scenarios are: a) a dominant seventh chord moves to another dominant seventh chord whose root is a minor third up, a minor third down, or a tritone away; b) a dominant seventh chord moves to a minor triad whose root is a major third up; or c) a minor triad moves to another minor triad whose root is a major third up or down.
[14] If we represent this scenario as a “parsimonious graph,” in which vertices represent pcsets and edges represent voice-leading relations, we obtain the figure given in Example 6, which this study names a “birdcage graph.” Some familiar structures from transformational theory are immediately apparent in this graph: each of the four outer triangles connecting the minor triads represents a subgroup of the neo-Riemannian LP group (a cyclic group of order 3 which can be represented by its generators as 〈LP〉 or 〈T4〉), while the inner squares connecting the seventh chords can also be considered as a subgroup of the group of transformations on dominant seventh chords (a cyclic group of order 4 given by 〈T3〉 or, with the transformations of Douthett and Steinbach, 〈L2*P2*〉 (Douthett and Steinbach 1998, 249–252)). The union of the pc’s of any triangle connecting minor triads is a hexatonic set, while the union of the pc’s of any square is an octatonic set.(11)
[15] What is perhaps most interesting about this graph, though, is that the only case in which the P-matrix
| 1 | 0 | 1 | 0 |
can be considered a transformation is the one involving a change in cardinality. Specifically, given chords X ∈ Tn{0,4,7,10} and Y ∈ Tn{0,3,7}, the P-relation
| 1 | 0 | 1 | 0 |
can be regarded as a bijection mapping one chord to another. In other words, though the voice leading for this matrix involves a surjective mapping of four voices in chord X to three in chord Y, the result of this voice leading for the two set types in question is to map each chord in the {0,4,7,10} transposition class bijectively to each chord in the {0,3,7} transposition class. With regard to the graph, if we color the edges according to the three voice-leading scenarios shown in Example 5, the cardinality-changing edges are the only ones not adjacent to an edge of their own color (see Example 7).(12) This result occurs because there is only one interval in X that can be closed by P (ic2) and only one way of closing it. The function corresponding to this cardinality-changing move is an involution due to P having mirror symmetry.(13)
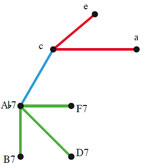
[16] The birdcage graph of Example 6 gains particular relevance when we use it to model the “omnibus” progression of the type explored by the theorist Georg Vogler around the turn of the nineteenth century.(14) There are a number of ways of discerning a group structure from the graph, most of which involve combining the cardinality-changing transformation with some of the known groups that act on triads and seventh chords.(15) For the present purposes, though, we will restrict ourselves to the cardinality-changing P-matrix transformation discussed above, labeled here as α, along with transposition. As Example 8 illustrates, beginning with any of the minor triads and repeatedly applying an <α, T9, α> sequence of transformations induces one of three possible “omnibus subgraphs,” around which the omnibus progression follows a clockwise path.
[17] Though many omnibus patterns can be heard in common-practice music, composers can navigate the space of
Example 6 without recourse to a continuously descending chromatic line. Brahms, for example,
can be heard to utliize the symmetry of this space toward the end of the third movement of his third symphony. As
Example 9 illustrates, E7 and ![]() 7
7![]()
![]()
[18] The combination of inter- and intra-cardinality relationships in Example 9 addresses an issue arising in the multiset voice-leading approach presented in Tymoczko 2006 and Callender, Tymoczko, and Quinn 2008. Their work renders collections of pcsets such as those of
Example 6 as one of their “quotient spaces,” in which some combination of five types of equivalence is applied to an n-dimensional space with real coordinates (![]() n), with the coordinates designating ordered
pitch sets of cardinality n. Chord spaces form as a result of octave and permutation equivalence (e.g., “gluing together”
n), with the coordinates designating ordered
pitch sets of cardinality n. Chord spaces form as a result of octave and permutation equivalence (e.g., “gluing together” ![]() 4
4![]() 5
5![]() n/Sn, an n-dimensional torus acted on by the symmetric group Sn.
n/Sn, an n-dimensional torus acted on by the symmetric group Sn.
[19] The issue is n. In the case of intra-cardinality moves, chords relate to one another in the same orbifold, and the geometry of the orbifold can lead to observations about both the chords and the voice leadings involved. One can define transformations as paths in the space, thus combining geometrical and group-theoretic approaches (indeed, group actions have already been used to create the orbifold); one can use the geometry of the space to measure voice-leading distance; and one can, as the present study does, render points and paths in the space as a mathematical graph, thus focusing solely on chords and voice-leading relationships. In the case of inter-cardinality moves, though, the two types of chords are in two different orbifolds, each of which has a different number of dimensions.
[20] The authors present three ways of handling this issue. First, glue together the various spaces by means of “cardinality equivalence” and use the resulting “C space” to model inter-cardinality progressions. Such an operation distorts the geometry of the orbifolds, though, such that the resulting space is impractical for examining voice leading (Callender, Tymoczko, and Quinn 2008, supporting materials, 14). Second, treat the smaller chord as a multiset in the higher- dimensional orbifold. In many cases, this is a productive approach. The omnibus progression, for example, achieves a particularly revealing interpretation this way: the chords of
Example 8 appear in the 4-dimensional orbifold as the sequence ![]() as {4,8,11,2}→{3,8,11,3} and the fourth move of A
as {4,8,11,2}→{3,8,11,3} and the fourth move of A![]() 7→c as {8,0,3,6}→{7,0,3,7}, thus producing the “wrong” triads since the distance between {3,8,11,3} and {7,0,3,7} in this space does not represent double-semitonal voice leading.(17) A third option that avoids this problem is to simply employ the various spaces as appropriate (Tymoczko 2007), using the 3-dimensional space to model trichordal relations and the 4-dimensional space to model tetrachordal and tetrachord↔trichord relations. The third approach is closest to that of the present study, except that here the various relations are integrated into a single graph.
7→c as {8,0,3,6}→{7,0,3,7}, thus producing the “wrong” triads since the distance between {3,8,11,3} and {7,0,3,7} in this space does not represent double-semitonal voice leading.(17) A third option that avoids this problem is to simply employ the various spaces as appropriate (Tymoczko 2007), using the 3-dimensional space to model trichordal relations and the 4-dimensional space to model tetrachordal and tetrachord↔trichord relations. The third approach is closest to that of the present study, except that here the various relations are integrated into a single graph.
[21] With the structure of Examples 6–9 in mind, Definition 3 presents a formal conception of a birdcage graph. Essentially, the definition states that for a graph to be a birdcage graph, the voice-leading relation given by P must allow both cardinality-changing and cardinality-preserving moves. It also rules out the voice-exchange relation in which a pcset is mapped to itself, such as {0,1,4,7}→{1,0,4,7} for P =
| 1 | 0 | 1 | 0 |
Definition 3: Given a P-matrix and a graph with vertex set V = {v: v ∈ X ∪ Y} where X and Y are TnI set classes of cardinality 4 and 3, respectively, and edge set E = {e: e ∈ (va, vb)} such that va P vb, the graph is a “birdcage” graph if there exist edges eX, eY, and eX,Y such that:eX = (x1, x2) where x1 ≠ x2 and x1, x2 ∈ X
eY = (y1, y2) where y1 ≠ y2 and y1, y2 ∈ Y
eX,Y = (x,y) where x ∈ X and y ∈ Y
Example 10. Birdcage set-class pseudograph
(click to enlarge)
Example 11. a) Graph for X,Y ∈ {Tn{0,3,6,10}, Tn{0,4,7}}
b) “Ziehn Inverted Omnibus”
(click to enlarge)
Example 12. Near-birdcage for X,Y ∈ {Tn{0,3,7,10}, Tn{0,4,8}}
(click to enlarge)
Example 13. a) Graph for X,Y ∈ {Tn{0,1,5,7}, Tn{0,3,7}}
b) and c) paths through the graph
(click to enlarge)
Example 14. a) Opening to Berg’s Piano Sonata, Op. 1
b) Op. 4, no. 1, measure 9
(click to enlarge)
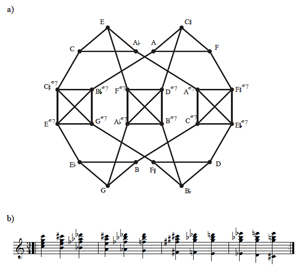
Example 15. All birdcage possibilities for all 9 voice-leading types (I-IX in Example 4)
(click to enlarge)
Example 16. Slice of graph for X∈[0124], Y∈[013], P =![]()
(click to enlarge)
Example 17. Opening of Bartók’s Sixth String Quartet
(click to enlarge)
Example 18. a) Graph for X∈[0247], Y∈[037], P = ![]()
b) [1:52] of U2’s “With or Without You”
(click to enlarge)
Example 19. a) Graph for X∈[0258], Y∈[037], P =![]()
b) jazz chord possibilities
(click to enlarge)
Example 20. a) opening and
b) [2:13] of Miles Davis’s “Freddie Freeloader”
(click to enlarge)
[22] Example 10 visualizes the definition with a birdcage “set-class pseudograph,” which contains two vertices connected by an edge and a self-loop (hence the prefix “pseudo”) at each vertex. The pseudograph of any combination of X, Y, and P that satisfies Def. 3 will have the form of Example 10, since both set classes have the ability to self-map and map to one another via P. By including TnI set classes, Def. 3 leaves open the possibility for birdcage graphs to have multiple components that partition the tetrachordal and trichordal families, provided that each component connects at least two chords of each cardinality. With the precise definition in place, two questions arise: first, do birdcage graphs exist that include chords other than minor triads and dominant sevenths if P =
| 1 | 0 | 1 | 0 |
? Second, what types of birdcage graphs exist for P-matrices other than P =
| 1 | 0 | 1 | 0 |
, and what set-classes are involved?
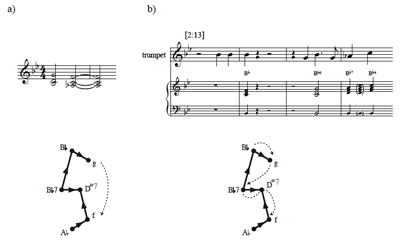
[23] Since birdcage graphs involve TnI set classes, the most logical initial move in searching for graphs in addition to that of Example 6 is to invert each of the chords in the example. This transformation produces an identical structure that relates major triads and half-diminished seventh chords. Example 11 illustrates such a graph along with a corresponding progression labeled here as a “Ziehn Inverted Omnibus” after Bernhard Ziehn, who included this progression in his Canonical Studies.(18) Since Example 6 and Example 11 contain all the chords of each transposition class for X = [0258] and Y = [037], they combine to form the complete birdcage graph for the two set classes.
[24] The harmonic progression of Example 11 is not employed nearly as frequently in the musical literature as the uninverted form, most likely because it is considerably more difficult to integrate within a tonal context. Telesco (2001, 134) suspects that “at least some instances exist,” but even Wagner, whose interest in both parsimonious voice leading and the dramatic potential of the half- diminished seventh chord would in principle lead him to such a progression, seems not to use it in any extended capacity. It is absent, for example, in Gauldin’s 2001 and 2004 studies of double-semitonal voice leading and wedge progressions in Wagner’s music. Nonetheless, Hunt 2007 has traced a number of motivic correspondences in the Ring cycle that utilize the
| 1 | 0 | 1 | 0 |
mapping between half-diminished chords and major triads.
Furthermore, it was a striking harmonic pattern in measures 101–2 of the prelude to Parsifal—B![]()
![]() 7,
7, ![]() 7
7![]() maj7
maj7![]() 7
7![]() 7—
7—![]() 7 to A
7 to A![]() (a triadic resolution that Wagner thwarts in
measure 102 with a G suspension, which prevents a premature return to tonic in an otherwise quite dissonant passage), as well as D
(a triadic resolution that Wagner thwarts in
measure 102 with a G suspension, which prevents a premature return to tonic in an otherwise quite dissonant passage), as well as D![]() 7 to F
7 to F![]() 7,
can be modeled with the Example 11 graph.
7,
can be modeled with the Example 11 graph.
[25] Another possibility for a birdcage graph would invoke the minor seventh chord’s abilities to move parsimoniously among its members. The resulting graph connects these seventh chords with augmented triads, though it is technically not a birdcage graph since there are no two augmented triads that can be related by P. Example 12 illustrates this graph, which has fewer edges and vertices in part because of the symmetry of its pcsets: augmented chords have only four unique transpositions, while the inversionally invariant minor sevenths (unlike dominant and half-diminished 7ths) are not related to fully diminished seventh chords by a semitone, resulting in fewer P connections to other members of their own set class.
[26] Computing all voice-leading possibilities for P =
| 1 | 0 | 1 | 0 |
leads to the result that only one other type of tetrachord—set class [0157]—and no other types of trichords can produce a birdcage graph for this particular voice-leading type.(19) This result is mainly due to the first two edge requirements in Def. 3, since examples of tetrachords fusing into trichords are plentiful but the ability of chords to self-map via P is rare. [0157] tetrachords have this voice-leading property because of their closeness to the transpositionally invariant [0268]: pc0 in {0,1,5,7} can move down, creating an [0268] tetrachord, while pc5 can move up, restoring [0157].(20)
[27] Example 13a presents a birdcage graph that includes minor triads and {0,1,5,7} transpositions, which lead to a rather different structure than that of Examples 6, 11, and 12. Unlike the previous examples, this graph is planar and consists of two components (four for the complete birdcage graph when all [037] and [0157] members are included), and it is possible to walk through each of the vertices of each component graph without crossing the same vertex twice. As the musical realization of
Example 13b suggests, though, such twelve-chord “Hamiltonian” paths lack the voice-leading consistency of the omnibus progression, despite the fact that they can be built on a descending chromatic bassline.(21) The subgraph realization of
Example 13c is more like the omnibus progression since it utilizes inter-cardinality involutions, but the lack of the chromatic voice exchange (e.g., the ![]()
[28] The desultory upper voice leading of Example 13b and the static nature of Example 13c would appear to make such patterns less desirable to composers than would the omnibus progression, and indeed they are not extensively used in the literature. Nonetheless, the graph of Example 13a proves useful in considering the music of Alban Berg, whose use of both parallel and contrary (“wedge”) semitonal voice leading is well-documented (Headlam 1996, DeVoto 1991, and Schmalfeldt 1991). In Berg’s case, steadily progressing chromatic lines do not tend to maintain set-class consistency as they do for the omnibus progression, such that voice leading is often more of a unifying factor than harmonic type. Notwithstanding local harmonic variety, set classes [037] and [0157] seem to play a consistently important role in his works, most likely due to their usefulness in contexts that combine tonality and atonality. Example 14 gives two important instances in which Berg utilizes the parsimonious relations between these set classes.(22) In the opening of his Piano Sonata, Op. 1, numerous instances of descending double-semitone motion give way to the mirror voice leading for a V→i cadence in B minor. The opening tetrachord {11,1,6,7}, which is a particularly significant sonority in this work and others (Schmalfeldt 1991, 92–94), connects to B minor, the key of the sonata, via contrary double semitonal motion. As Example 14b shows, this same motion along with an [0157] self-mapping generates a motive that appears frequently in the Altenberg Lieder.(23) This self-mapping corresponds to Lewin’s RICH transformation, which maps an ordered pcset to its retrograde inverted form that begins with the initial set’s final two pcs (1987, 180–188).
[29] We have now exhausted all the birdcage possibilities for the type-II matrix (P =
| 1 | 0 | 1 | 0 |
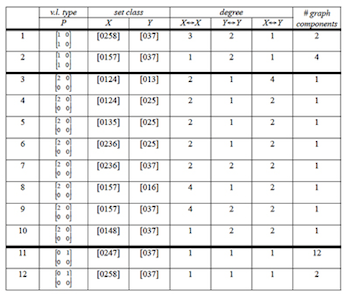
). Considering all other types of voice leading from Example 4, as well as all trichordal and tetrachordal set classes (excluding voice crossings), results in the possibilities given in Example 15. This table lists all birdcage possibilities, twelve in number, and gives an sense of the structure and connectedness of each graph. For a given chord X or Y, the number of other chords it relates to in set class X or Y via P or MIR(P) is called the degree, which corresponds directly to the degree of the respective vertex in the colored parsimonious graph. Birdcage graphs are thus graphs for which all three degree columns are nonzero, and in cases of degree 1, the P-relation can be regarded as a bijection.
[30] Since P-matrices other than
| 1 | 0 | 1 | 0 |
do not have mirror symmetry, birdcage graphs 3 through 12 are directed graphs in which arrows distinguish between P and its mirror. Voice-leadings in the direction of the arrow correspond to matrices as given in Example 4, while moves in the opposite direction correspond to the mirrors. As Example 16 shows, birdcage graphs for P =
| 2 | 0 | 0 | 0 |
are more densely woven than the ones observed thus far.
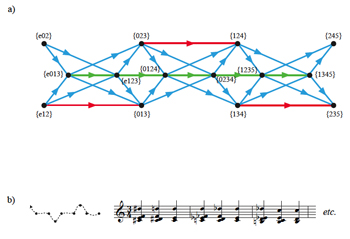
[31] Example 16a gives a section of the birdcage graph for [0124] and [013] using the P-matrix
| 2 | 0 | 0 | 0 |
. To visualize the entire graph, extend both the edges outward and wrap the graph in a circle so that it looks something like a braided loop or wreath. The coloring of
Example 16a allows one to verify the degree values charted in Example 15. The graph is organized such that there is a line of trichords on the top and bottom while tetrachords run through the middle. Intra-cardinality moves correspond to horizontal lines in this figure, with trichord→trichord moves having degree 1 and tetrachord→tetrachord moves having degree 2. Inter-cardinality moves are at an angle and involve vertices of degree 4. This graph has only one component (it is connected) because, unlike the voice leading from the previous graphs, this type of P-matrix can link inversionally related pcsets. Musical progressions that move consistently through this graph via a chromatically descending bass cannot employ all of the
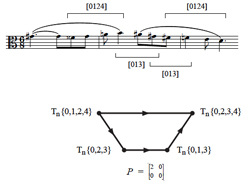
[32] The graph of Example 16 recalls Bartók’s dense motivic chromaticism as analyzed in Example 3, which illustrated how the Third String Quartet begins with an [013] self-mapping via
| 0 | 0 | 2 | 0 |
. More abstractly, the opening of the Sixth String Quartet (which is the opening theme for each of the quartet’s movements) is constructed according to the “transposition class” birdcage graph of Example 17. Here,
| 2 | 0 | 0 | 0 |
voice leading, in combination with transposition, maps each of the bracketed pcsets to one another while also accounting for the overall progression of {7,8,9,11}→{2,4,5,6}.(24) Notably, all the arrows of the graph correspond to the temporal progression of the pcsets in the passage, meaning that in an abstract sense, this melody is built on repeated applications of
| 2 | 0 | 0 | 0 |
and not its mirror.
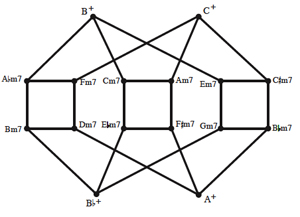
[33] Example 18a gives the first of the two birdcage graphs corresponding to P =
| 0 | 1 | 0 | 0 |
, both of which have tonal implications. This graph consists of twelve component subgraphs, each of which links two [0247] pentatonic subsets with two consonant triads. Since each major triad and its [0247] superset is connected in the subgraph to a “relative” pair a minor third down, it is convenient to order the components in the manner of a circle of fifths that includes minor keys. Arrows do not appear in the inter-cardinality edges because both
| 0 | 1 | 0 | 0 |
and
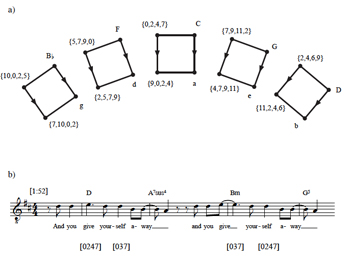
| 0 | 0 | 0 | 1 |
can map the chords to one another. The musical result of this graph is the observation that 9-8 motion with a major triad and 4-3 motion with a minor triad (retaining the chordal third) connect two types of chords, each of which can self-map via a single whole-tone move. The sonorities on the words “give yourself” in U2’s “With or Without You” (1987) trace these relationships (Example 18b), such that the ateleological feel of the passage arises not only out of melodic and textual repetition but also out of harmonic/voice-leading consistency.
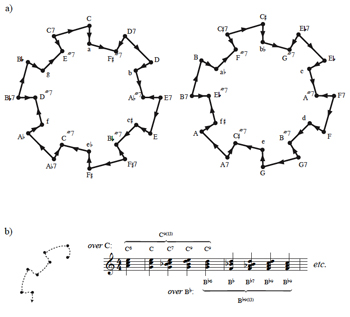
[34] Example 19a presents the latter of the two birdcage graphs that incorporate consonant triads and major-minor/half-diminished seventh chords. The graph partitions the four transposition classes of the 48 chords into whole-tone-related sets, due in part to the whole-tone voice leading that generates it. While the components of this graph could be represented as circles rather than gear-like structures, the current rendering makes it easier to visualize how “major” and “minor” chords are each connected: major triads and their tetrachordal supersets occupy the outer rings of the graph, while minor triads and their tetrachordal supersets occupy the inner rings.
[35] Chained 5-vertex subgraphs of Example 19a give a useful family of jazz chords over a common bass note. As
Example 19b illustrates, the minor triads at the edges of these subgraphs form incomplete “add6” and “9” chords over the root of the two “major” chords in the segment.(25) The five vertices thus comprise a set of possible chords that a pianist can play with her right hand over a left-hand foundation corresponding to the major triad in the set. The union of these five chords forms a 13 chord in which the 9th is included. As Example 20 illustrates, Miles Davis’s “Freddie Freeloader” (1959) begins by moving between the outer chords of this collection, and the beginning of his trumpet solo suggests a more complete path. The great staff below the trumpet line in
Example 20b charts chords that Miles Davis’s melodic tones initiate, and the end of the phrase skips through ![]() 7
7![]()
![]() 7
7
[36] The results of this study can be summarized as follows:
- The original birdcage graph that models the omnibus is the only one involving splitting and fusing in the strict sense. In other words, it is the only graph in which the changing trichordal pc splits into two different pcs (or, conversely, the only one in which two voices in the tetrachord move to create the fused pc in the trichord). Thus, the omnibus progression and its inverse are unique from a voice-leading perspective.
- None of the set classes in any birdcage graph has inversional symmetry, which means that each complete graph has 48 vertices representing the four transposition classes of the trichords and tetrachords.
- Despite the absence of these set classes, all pcsets that can form birdcage graphs are minimal perturbations of inversionally invariant sets. In other words, each of the sets in a birdcage graph can be connected to an inversionally invariant set by a single semitonal move. For example,
{0,2,5,8} {0,3,7}1 0 0 0 {0,2,6,8};
0 0 1 0 {11,3,7}; and {0,1,6}
0 0 1 0 {11,1,6}.
- The high degree of interconnectedness for
2 0 0 0 voice leadings (birdcages 3–10) results in graphs that have only one component, while the limited voice-leading possibilities of the other two voice-leading types result in various partitions of the 48 chords.
- In providing the conditions under which birdcage graphs exist, this study demonstrates how pcsets can map to members of their own set class, a phenomenon that has been privileged in the neo-Riemannian literature.(26) These results can help in judging the extent to which diatonic collections are indeed “over-determined.” The consonant triad, for
example, has one degree of “hex-pole”-type connectedness (e.g.
{0,3,7} , while [026] has two (e.g. {0,2,6}2 0 1 0 {11,4,8})
1 0 2 0 {11,3,5}, and {0,2,6}
1 0 2 0 {11,1,7}).
- Birdcage graphs can be used in the analysis of both tonal and atonal literature. Still, as with the other spatial models that relate to this study, the full extent to which birdcage graphs are musically practicable will be borne out through further analytic study.
- The mathematical concepts employed here, namely surjective mappings and graphs, intersect but are not coextensive with group-theoretic and geometrical approaches to music theory. Again, analysis, perhaps along with composition and studies in the psychology of music, will be critical in determining the degree to which the various mathematical metaphors hold.
Appendix: Generalized Voice-Leading Definition
Definition 1a: Given pcsets X and Y where the cardinality #X ≥ #Y, the two sets are related by a P-matrix
u1 u2 ... uz d1 d2 ... dz if there exists a surjection τ: X → Y and a set {xk}
such that X\Y = {xk}
#X-1 k = 0 , psum =
psum-1 k = 0 (dn + un), and
z ∑ n = 1
Joti Rockwell
Pomona College
Department of Music
340 N College Ave, Claremont, CA 91711
joti.rockwell@pomona.edu
Works Cited
Callender, Clifton. 1998. “Voice-Leading Parsimony in the Music of Alexander Scriabin.” Journal of Music Theory 42, no. 2: 219–234.
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320, no. 5874: 356–348.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26, no. 2: 177–199.
Childs, Adrian. 1998. “ Moving Beyond Neo-Riemannian Triads: Exploring a Transformational Model for Seventh Chords.” Journal of Music Theory 42, no. 2: 181–194.
Cohn, Richard. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations.” Journal of Music Theory 41, no. 1: 1–66.
—————. 1998. “Square Dances with Cubes.” Journal of Music Theory 42, no. 2: 283–296.
—————. 2003. “A Tetrahedral Graph of Tetrachordal Voice-Leading Space.” Music Theory Online 9.4 (2003).
Devoto, Mark. 1966. “Some Notes on the Unknown Altenberg Lieder.” Perspectives of New Music 5, no. 1: 37–74.
—————. 1991. “Alban Berg and Creeping Chromaticism.” In Alban Berg: Historical and Analytical Perspectives, ed. David Gable and Robert P. Morgan, 57–78. Oxford: Clarendon Press.
Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2: 241–264.
Gauldin, Robert. 2001. “The DOUTH2 Relation as a Dramatic Signifier in Wagner’s Music Dramas.” Music Analysis 20, no. 2: 179–192.
—————. 2004. “The Theory and Practice of Chromatic Wedge Progressions in Romantic Music.” Music Theory Spectrum 26, no. 1: 1–22.
Gollin, Edward. 1998. “Aspects of Three-Dimensional Tonnetze.” Journal of Music Theory 42, no. 2: 195–206.
Headlam, Dave. 1996. The Music of Alban Berg. New Haven: Yale University Press.
Headlam, Dave and Matthew Brown. 2007. “Comment on ‘The Geometry of Musical Chords.’” Science 315, no. 5810 (19 January): 330.
Hook, Julian L. 2002a. “Uniform Triadic Transformations.” Ph.D. dissertation, Indiana University.
—————. 2002b. “Uniform Triadic Transformations.” Journal of Music Theory 46, no. 1 and 2: 57–126.
—————. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29, no. 1: 1–39.
Hunt, Graham G. 2007. “David Lewin and Valhalla Revisited: New Approaches to Motivic Corruption in Wagner’s Ring Cycle.” Music Theory Spectrum 29, no. 2: 177–196.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.
—————. 1998. “Some Ideas About Voice-Leading between Pcsets.” Journal of Music Theory 42, no.1: 15–72.
Pau, Andrew. 2007. “Voice Leading as Harmonic Determinant in Atonal Music.“ Paper presented at the annual meeting of the Society for Music Theory, Baltimore.
Santa, Matthew. 2003. “Nonatonic Progressions in the Music of John Coltrane.” Annual Review of Jazz Studies 13: 13–25.
Schmalfeldt, Janet. 1991. “Berg’s Path to Atonality: The Piano Sonata, Op. 1.” In Alban Berg: Historical and Analytical Perspectives, ed. David Gable and Robert P. Morgan, 79–109. Oxford: Clarendon Press.
Shimbo, Amy. 2001. “Some Transformations Between Triads and Seventh Chords.” Presented at the Symposium in Neo-Riemannian Theory (Buffalo, NY).
Straus, Joseph. 2003. “Uniformity, Balance, and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25, no. 2: 305–352.
—————. 2005. “Voice Leading in Set-Class Space.” Journal of Music Theory 49, no. 1: 45–108.
—————. 2008. “Motivic Chains in Bartók’s Third String Quartet.” Twentieth-Century Music 5, no. 1: 25–44.
Strunk, Steven. 2003. “Wayne Shorter’s Yes and No: An Analysis.” Tijdschrift voor muziektheorie 8: 40–56.
Telesco, Paula. 1998. “Enharmonicism and the Omnibus Progression in Classical-Era Music.” Music Theory Spectrum 20, no. 2: 242–79.
—————. 2001. Review of The Omnibus Idea, by Victor Fell Yellin. Music Theory Spectrum 23, no. 1: 129–136.
Tymoczko, Dmitri. 2006. “The Geometry of Musical Chords.” Science 313, no. 5783 (7 July): 72–74.
—————. 2007. “Response to Comment on ‘The Geometry of Musical Chords’.” Science 315, no. 5810 (19 January): 330.
Yellin, Victor Fell. 1998. The Omnibus Idea. Warren, MI: Harmonie Park Press.
Ziehn, Bernhard. 1912. Canonical Studies: A New Technic in Composition. Milwaukee: W.A. Kaun Music Co.
Footnotes
* I would like to thank Richard Cohn, Joseph Straus, Dmitri Tymoczko, and the anonymous reviewers at
MTO for helpful feedback on this research. I would also like to thank Jack Douthett for providing detailed comments on an earlier draft.
Return to text
1. Of these possible triadic moves—usually referred to as “transformations,” “operations,” or “voice leadings”—the most commonly cited are the canonical twelve-tone operators of transposition and inversion, along with the more recently formalized neo-Riemannian operations of L (Leittonwechsel), P (Parallel), and R (Relative). These five moves hardly exhaust the possibilities, though, since there are 620 × 1021 ways (i.e., 24 factorial) of mapping the set of 24 consonant triads onto itself. This unwieldy group of possibilities is tamed by Hook 2002a, which integrates a variety of commonly referenced triadic transformations into his “UTT” formalism.
Return to text
2. See Callender, Tymoczko, and Quinn 2008, Tymoczko 2006, Straus 2005, Cohn 2003, Gollin 1998, and Childs 1998.
Return to text
3. Hook 2002b, further expanded in Hook 2007.
Return to text
4. Headlam 2007 has raised a similar issue regarding the geometric position of relatively small-cardinality pcsets in higher dimensional spaces. A later section of the present
study addresses the topic of Callender, Quinn, and Tymoczko’s multidimensional spaces in more detail.
Return to text
5. Readers may wish to skip the latter portion of Definition 1, since an understanding of the material to follow is not contingent upon knowing the specifics of how τ is defined.
Return to text
6. <Straus 2003 calls this the “smoothest” or “most efficient” voice leading. Cohn 1998 considers voice-leading efficiency as a function VLE which sums all the minimal voice-leading distances in a given progression. In terms of P-matrices, the sum of all the matrix values for X→Y
Return to text
7. Examples of these neo-Riemannian and twelve-tone transformations are ![]()
![]()
Return to text
8. Andrew Pau (2007) has shown evidence of this type of voice-leading unity in a number of works by Schoenberg and Berg.
Return to text
9. As this second phrase is more complex than the first, other hearings are eminently plausible, including ![]() , F
, F![]() , A
, A![]() , B
, B![]() }
}
| 1 | 0 | 2 | 0 |
| 2 | 0 | 1 | 0 |
Return to text
10. Admittedly, the notion of a “mirror” is a way of working around the fact that the surjective nature of τ precludes an inverse function for inter-cardinality mappings. A common solution to this issue is to work with multisets, in which case voice leadings are always bijective. Analytically, however, multisets pose the problem of “phantom doublings” in which the size of a chord cannot be ascertained from the number of pcs it possesses. Splitting and fusing are viable musical concepts that avoid such a problem. This study thus
explores the surjective model, notwithstanding the fact that in the case of splitting, the frequently used Lewinian metaphor between musical motion and mathematical functions breaks down.
Return to text
11. I would like to thank Jack Douthett for this observation about pc unions.
Return to text
12. In graph-theoretic terms, this is not a proper coloring because two or more edges of the same color are adjacent to one another for the intra-cardinality cases. The familiar problem in graph theory of finding minimal edge colorings is thus similar but not identical to the question of finding unique voice-leading types within a voice-leading graph.
Return to text
13. This function is the “S2” split transformation of Shimbo 2001 (described in Hook 2002a, 117). Hunt 2007 refers to it as a “Leittonwechsel split” (“S*L”), since a neo-Riemannian L transformation is contained within it. Hunt’s conception is thus similar to that of Hook (2002b, 117–118 and 2007, 2–3), who connects the same types of chords (e.g., c→A![]() 7) through the combination of L and a cross-type “inclusion transformation” that maps [037] triads to their unique [0258] supersets. Unlike the other authors, Hook avoids defining his cross-type transformation as an involution, since having a transformation acting on a set of 48 triads and seventh chords leads to algebraic complications (2007, 5, footnote 8).
7) through the combination of L and a cross-type “inclusion transformation” that maps [037] triads to their unique [0258] supersets. Unlike the other authors, Hook avoids defining his cross-type transformation as an involution, since having a transformation acting on a set of 48 triads and seventh chords leads to algebraic complications (2007, 5, footnote 8).
Return to text
14. Hence the motivation for the term “birdcage graph.” For an examination of Vogler’s relationship to this progression, as well as numerous musical examples invoking omnibus progressions, see Telesco 1998 and Yellin 1998.
Return to text
15. See Hook 2002b, 116–118 and Hook 2007, 1–3, both studies of which argue that the examination of the group actions he defines quickly leads to realizations about the omnibus progression’s voice-leading efficiency. The present study has made the opposite point: exploring parsimonious voice leading between triads and seventh chords leads in this case to an algebra of harmonic transformation for which Hook’s cross-type and GIS homomorphism theory is the foundation.
Return to text
16. Callender, Quinn, and Tymoczko 2008 demonstrate how the omnibus progression forms a line in their 4- dimensional chord space, while also relating the progression to the geometry of K-nets (supp. mat., 16–19 and 39–44). The 2-dimensional graph in Tymoczko’s Fig. 2 (2006, 73), though, suffices to illustrate the phenomenon of reflection via contrary semitonal motion.
Return to text
17. In this space, {0,3,3,7} and {11,3,3,8} are the triadic multisets that preserve the contrary semitonal motion between a![]() and c. Not all examples afford such a possibility, since if one is interested in double-semitonal motion for dyads, the 2-dimensional space needs to be used; e.g.,
and c. Not all examples afford such a possibility, since if one is interested in double-semitonal motion for dyads, the 2-dimensional space needs to be used; e.g.,
Return to text
18. <Ziehn 1912, as described in Yellin 1998, 9–13.
Return to text
19. The voice-leading calculations were done with a computer program written in Python.
Return to text
20. Voice-leading efficiency for [0157] self-mappings is in keeping with long-held observations in neo-Riemannian theory that link a chord’s ability to parsimoniously self-map to its closeness to inversional symmetry, transpositional symmetry, and/or equal division of the octave. See Cohn 1997, 1–6; Callender 1998, 221; Tymoczko 2006; and Callender, Tymoczko, and Quinn 2008, supp. mat.,10–13.
Return to text
21. The descending chromatic line of Example 11b can be completed, thus rendering the overall progression as a cycle, by moving from d to ![]()
Return to text
22. The one type of relation not given in Example 14, that of parsimonious voice leading between consonant triads, belongs more to the music of Berg’s predecessors than it does to his compositions.
Return to text
23. DeVoto 1966 identifies this motive, labeling it α, in three of the five songs. Schmalfeldt (1991, 93–94, footnote 26) notes that it contains “interlocking presentations” of [0157].
Return to text
24. Alternatively, following Straus 2008 and Lewin 1987, one can draw serial mappings between melodic fragments of equal cardinality. Excluding the first two notes, the passage would then constitute an chain of four overlapping trichords related by inversion, retrograde inversion, and retrograde inversion: (8,9,11) →(11,10,8)→(8,6,5)→(5,4,2).
Return to text
25. The add6 chord lacks a chordal fifth, while the add9 chord lacks a chordal third. Jazz players routinely omit chord tones according to taste, although leaving out the chordal fifth is far more common than omitting the chordal third, which plays a more important role in defining the sonority. For studies that explore parsimonious voice leading in jazz, rock, and pop music, see Strunk 2003, Santa 2003, and Capuzzo 2004.
Return to text
26. See Cohn 1997, who attributes the “over-determined” quality of consonant triads to their ability to self-map via parsimonious voice leading.
Return to text
| 1 | 0 | 2 | 0 |
| 2 | 0 | 1 | 0 |
Copyright Statement
Copyright © 2009 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by William Guerin, Mitch Ohriner, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: