Dyadic TC Lattices: Revisiting the TC/IS Relationship
Donald G. Traut
REFERENCE: http://www.mtosmt.org/issues/mto.02.8.3/mto.02.8.3.scotto.php
KEYWORDS: Voice leading, transformation, neo-Riemannian theory, parsimonious graphs
ABSTRACT: This short study builds on Richard Cohn’s work by illustrating that dyadic transpositional combination alone accounts for the majority of noteworthy set-classes with the TC-property. It presents six lattices of scs all related by TC and then analyzes the results as they relate to the 94 scs with IS.
Copyright © 2009 Society for Music Theory
[1] In an article from 1988, Richard Cohn explores the relationship between inversional symmetry and transpositional combination, especially as it relates to Bartók analysis (Cohn 1988). He argues that while it is well known that many of the pitch collections most important to Bartók’s music are inversionally symmetric, it is also significant that they can all be explained using transpositional combination (TC). He makes this clear in the illustration shown in Example 1. Here we see both the inversional axis (represented with a dotted line) and the TC-property (shown beneath each figure) of several noteworthy collections. Indeed, collections such as Antokoletz’s “x” and “z” cells, along with the diatonic, whole-tone, and octatonic collections, all parse into two transpositionally related pitch-class sets. As Cohn argues, while these collections are all inversionally symmetric, the presence of the TC-property is not a mere coincidence that can be ignored.
[2] While the crux of Cohn’s article is analytic in nature, he also mentions some of the more abstract elements of TC. Some of this comes in the form of simple statistics. As he writes:
Of the 223 set-classes, 137 bear the TC-property. Of particular interest for the present purposes is the relationship of the contents of this group to the contents of the group of ninety-four bearing the IS-property. Seventy-two set-classes bear both properties; that is, about three-quarters of all IS-set-classes are also TC-set-classes (Cohn 1988, 24–25).
He goes on to explain that the list of set-classes containing both IS and TC includes most of the important set-classes for Bartók analysis:
These include the thirteen tetrachord-types which can be realized as inversionally-symmetric structures of exactly four pitches; all of the partial and complete interval-cycles, including chromatic, diatonic, and whole-tone sets; and all of the Tn-invariant sets such as the octatonic collection and the “1:3 model” (Cohn 1988, 25).
Since his goals for the article are primarily analytic, Cohn stops short of traveling further down this abstract path. But for those interested in this topic, there are still worthwhile questions to ask. Just what are the set-classes that have IS but not TC? Also, are there any distinctions among those sets that do have both IS and TC?
[3] Cohn answers some of these questions in his dissertation (Cohn 1987). In this exhaustive study, he provides the theoretic groundwork for TC and illustrates its analytic importance in contemporary music. In addition to defining the operation and showing its role in music, this document contains appendixes listing various TC properties of all 223 scs. Of primary interest here are the categories into which Cohn places set-classes based on their TC properties.(1) He uses four categories: 1) prime; 2) semi-prime; 3) fully factorable; and 4) semi-factorable. Prime scs—such as 4-12 (0236)—do not possess the TC-property at all, while fully factorable scs—such as 4-17 (0347)—have a TC path stemming from a “simple operation” (TC3 of (04) in the case of 4-17). Semi-factorable scs have TC, but their generative path traces back to a “mixed operation,” meaning one of the initial operands is a trichord or larger. The example Cohn gives is 6-19 (013478), which comes from TC1 of 3-11 (037). Finally, semi-prime sets are those whose TC operands are both trichords or larger, resulting in a “complex operation.” This is the case for 6-31 (014579), which is generated when 3-11 (037) is transpositionally combined with itself.
[4] Armed with further information about the role TC plays in the set universe, we may ask even more questions regarding the relationship between TC and IS. As stated earlier, it will certainly be interesting to know exactly which sets have IS but not TC. Further, now that we know that scs can be categorized based on their TC properties, it will be useful to see if there are differences among those sets that do have both IS and TC. With these points in mind, this paper adds to our understanding of the TC/IS relationship in two main ways. First, it presents lattices that contain all of the fully factorable set-classes. These are referred to as dyadic TC lattices because all set-classes produced can be traced back to a pair of dyads. This approach was first suggested by Robert Morris’s work, which used lattices to illustrate how small sets combine to generate larger sets (Morris 2001, 23). Second, it analyzes the results for the IS sets. While all sets produced on the lattices will be IS, we will see that not all of the possible IS sets appear; that is, they are not fully factorable. The paper concludes with a discussion of these remaining set-classes.
[5] There are several things that need explanation in order to understand the lattices:
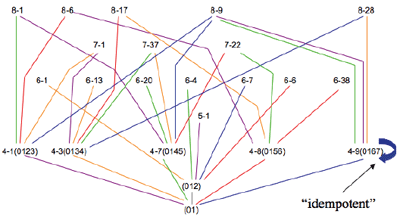
Colors: | Each TC operation is assigned a color as follows: TC 1 = black; TC 2 = purple; TC 3 = orange; TC 4 = green; TC 5 = red; TC 6 = blue. (This color scheme is shown in the lower right-hand corner of each illustration.) A colored line then connects a smaller set with the larger set that results when the smaller set undergoes a TC operation. For example, TC 3 (orange) of (01) results in (0134). Thus, an orange line will connect (01) to (0134). |
Recursion: | As Cohn states, “Since the input and output of an operation are entities of the same type, it follows that the result of one operation can serve as an operand for a subsequent one, and that TC is capable of recursion” (Cohn 1988, 29–30). Thus, each new sc is itself subjected to the six TC operations. This is done to all new members until all unique scs for that lattice have been produced. |
Pruning: | At each cardinality, only those TC operations producing new scs are shown.(2) For example, TC 1 of (012) would result in (0123). However, this relationship is not shown since (0123) was already produced at an earlier cardinality level (i.e., TC 2 of (01)). The only exceptions to this pruning practice are those scs that turn into themselves at any TC level. These “idempotent” scs (as Cohn calls them) are represented with a curved arrow. |
Order: | Set-classes of the same cardinality are all on the same horizontal plane. Aside from that, there is no method to the order of presentation. |
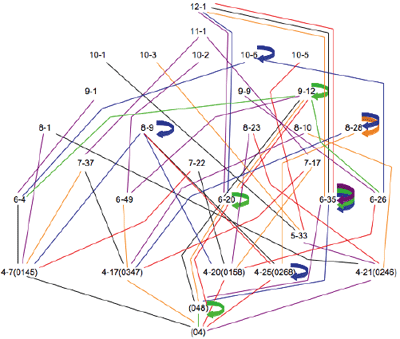
Example 2. Beginning of Lattice 1
(click to enlarge)
Example 3. Middle stage of Lattice 1
(click to enlarge)
Example 2 shows the beginning of Lattice 1. The six TC transformations result in six new sets, each of which is connected to (01) via the appropriate colored line. Example 3 shows the next set of transformations, which operate on the one trichord and the five tetrachords. Finally, Example 4 shows the final round of operations and thus presents the completed lattice for the (01) dyad.
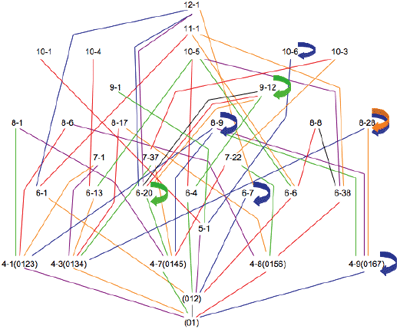
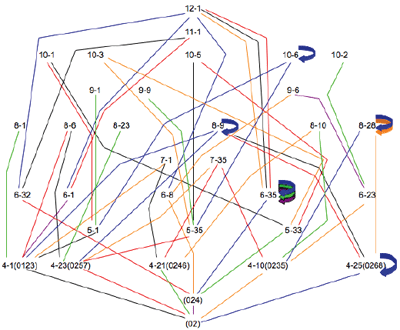
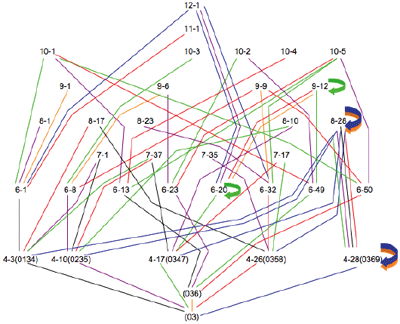
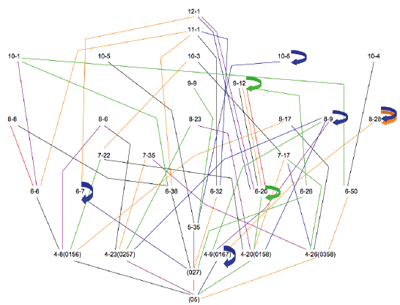
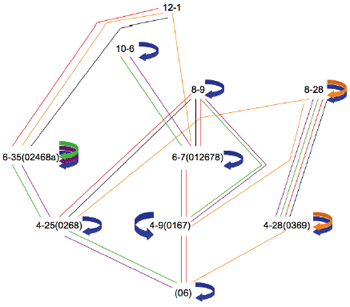
[6] Examples 5-9 present lattices for the remaining dyads. While the pruning process described above does not allow for illustrations of all TC paths, the individual lattices do reveal some relationships worth mentioning. For example, Lattice 1 (Example 4) shows a single path to 6-20 (the hexatonic collection), which then blossoms with three different paths to 9-12 (i.e., three augmented triads), two paths straight to the aggregate, and one idempotent transformation. In Lattice 2 (Example 5), TC 2 then TC 6 generates the whole-tone collection (6-35), which then maps onto itself at the three even TC levels and straight to the aggregate at the odd TC levels. Each of the five tetrachords generated in Lattice 3 (Example 6) has at least one mapping that leads to the octatonic collection (8-28). Not surprisingly, Lattice 4 (Example 7) is dominated by the clear path from the augmented triad, to the hexatonic collection (6-20), and on to 9-12, with its three augmented triads. And finally, Lattice 6 (Example 9) generates only collections that are idempotent on at least one TC level.
Example 10. Debussy, String Quartet, IV
(click to enlarge)
Example 11. Crumb, Five Pieces For Piano
(click to enlarge)
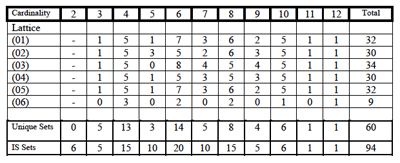
Table 1. Totals from dyad lattices
(click to enlarge)
Table 2. Roster of inversionally symmetric set classes
(click to enlarge)
Table 3. “Prime” SCs with IS
(click to enlarge)
Table 4. “Semi-factorable” SCs with IS
(click to enlarge)
Example 14. Nonochord “none” sets
(click to enlarge)
[7] Generating these lattices can provide more context for analyses that incorporate TC. This is especially true when discussing the relationship between TC and fully chromatic or aggregate formations, as Mark McFarland has done recently (McFarland 2005). As McFarland shows, Debussy often transposed the same pc-set numerous times to create fully chromatic collections. Thus, McFarland explains the first measure of Example 10 as four transpositions of a minor third, which when taken together, form SC 7-1. However, the analysis seen beneath the score illustrates another way of achieving this. Since the passage clearly stems from a dyad—(03) in this case—it is possible to show the generative path from the dyad to the larger sets. This is confirmed by referring to Lattice 3 (Example 6) and following the path from the dyad, through the tetrachord, and on to the septachord. Measure three of the same excerpt shows a similar situation. Here, three TC transformations generate aggregate completion from an initial tritone. Since the initial dyad is (06), this transformational path appears on Lattice 6 (Example 9).(3) For one more example, consider the passage shown in Example 11, taken from George Crumb’s Five Pieces for Piano.(4) Here, three successive transformations of TC 3 generate the aggregate from the opening (012) collection. While this passage does not begin with a dyad, the transformational path is easy to follow on Lattice 1 (Example 4).(5) As in the Debussy examples, the lattice illustrates at a glance how the smaller set becomes a larger one. Further, in each case, the lattices place the scs involved in a larger context, adjacent to other scs related by TC, thus illustrating how the unique path chosen by the composer achieved the desired result.
[8] While studying each individual lattice is useful for several reasons, we must take them as a whole to learn about their relationship to IS. Table 1 presents tallies from the lattices. The six rows devoted to each of the lattices show the number of set-classes generated at the twelve cardinalities. For example, Lattice 3 produces eight hexachords (the most for that cardinality), but it does not produce any pentachords. In the “Total” column, we see that Lattice 3 does in fact generate the most set-classes overall, while Lattice 6 generates the least by far. Table 1 also shows the total number of unique sets at each cardinality. It superimposes this on the total number of IS sets at each cardinality. For example, it is clear that Lattices 1–5 each produced one trichord. The “Unique Sets” entry shows that all five of these trichords were different. The “IS Sets” entry tells us that there are only five trichords with IS. Since we know that all the sets produced on our lattices are IS, we can safely state that dyadic TC generates all five of the IS trichords. By contrast, we can also see that dyadic TC generates only three of the ten possible pentachords with IS.
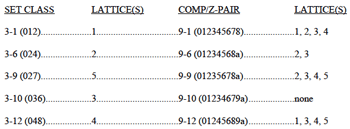
[9] Table 2 provides even more detailed information regarding the IS sets and TC. Listed here are all 94 scs with IS. Also listed are the lattices (if any) on which these scs appear. For example, 4-7 (0145) appears on Lattices 1 and 4. Its complement, however, does not appear on any (i.e., it is not fully factorable).(6) Perhaps the most striking fact here is that, other than 11-1 and 12-1 (which are not shown in Table 2), the octatonic collection (8-28) is the only set-class that appears on all six lattices. This makes sense, given the collection’s many tetrachordal parsings.(7) Interestingly, Lattice 5 is the only lattice to show only one path to the octatonic collection: TC 6 of (05), then TC 3 of (0167).
[10] At this point, we can return to a question posed at the outset: Will these dyadic lattices generate all of the IS scs? We know now that the answer is “no.” As Cohn points out, there are 94 scs that have the IS-property. As Table 1 shows, the lattices generate only 60 of these.(8) Add to that the six dyads themselves and we can account for 66 of the IS scs. Thus, of the 94 scs with IS, 28 are not represented on any of the lattices. They have an entry of “none” in Table 2.
[11] These 28 “none” sets divide into two groups, shown here in Tables 3 and 4. The first group (Table 3) includes the 17 scs that have the IS-property, but cannot be generated by TC of any kind; they are “prime.”(9) The second group (Table 4) consists of the remaining “none” scs, which can be generated by TC, but are not fully factorable and thus do not appear on any of the lattices presented herein.(10)
[12] Examples 12–14 illustrate one way each of these eleven scs can be generated using TC. While there are several TC possibilities for each of these examples, the goal here is to find one of the more explicit equations where at least one of the operands is a dyad.(11) As the examples show, this is possible for all eleven of the scs. In most cases, a tetrachord combines (and partially overlaps) with a transposed version of itself to generate the larger set. This is the case for all three of the septachords (Example 12), which can derive from TC 2 of prime tetrachords. Of the seven octachords (Example 13), all but one derives in similar fashion: a tetrachord combines with a transposed version of itself (this time sans overlap, of course). Once again, all of the tetrachords used here are prime. Set-class 8-24 does not factor into two tetrachords, but instead reveals T4-related versions of 5-8, with two members overlapping.
|
Example 12. Septachord “none” sets (click to enlarge) |
Example 13. Octochord “none” sets (click to enlarge) |
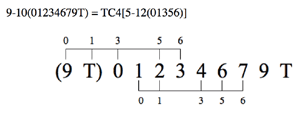
[13] The one nonachord, 9-10, is curious. Example 14 illustrates how it divides into two versions of 5-12. But this is not what is interesting here. As shown earlier, there are exactly five nonachords with the IS-property: 9-1, 9-6, 9-9, 9-10, and 9-12. Of these five, all but 9-10 are fully factorable and thus appear on at least one of the dyad lattices. Remarkably, 9-10 stands out from its IS brethren even further. Not only is it the lone IS nonachord that is not fully factorable, but it is also the only IS nonachord that cannot be derived from non-overlapping versions of 3-10 (036). Indeed, 9-1, 9-6, 9-9, and 9-12 all appear on Lattice 3, which features (036) as its lone trichord.(12)
[14] This interesting point about 9-10 is just one of the many tidbits gained by viewing dyadic TC via these lattices. Not only are we able to see many of the specific TC paths that generate specific scs, but we can also quickly view the families of sets produced on each of the lattices. They have not been formalized in that fashion for this particular study, but such an approach could prove fruitful.
[15] Several new points can be made regarding the relationship of TC to IS as well. As Cohn pointed out, of the 223 scs, 137 have the TC-property. Of these, only 60 are from dyadic TC (and thus appear on one of the lattices presented herein). The remaining 77 scs get their TC-property from non-dyadic TC. Thus, dyadic TC does not generate even half of the total scs that possess the TC-property. However, of the 94 scs with IS, close to two-thirds are fully factorable. Moreover, all but five of the scs with both TC and IS are present on the lattices (when we include the six dyads themselves). Further, the dyadic TC lattices include all of the scs Cohn cited as being important for Bartók analysis, including the interval cycles, the “x” and “z” cells, and the chromatic, diatonic, whole-tone, and octatonic collections. But the role of dyadic TC goes beyond that. In addition to collections important to Bartók, we can add all six of the all-combinatorial hexachords, which of course includes the hexatonic collection, 6-20. These insights seem to suggest that while TC in general is indeed an important complement to IS, dyadic TC in particular warrants our closest attention.(13)
Donald G. Traut
University of Arizona
School of Music
1017 N. Olive Road
P.O. Box 210004
Tucson, AZ 85721-0004
dgtraut@email.arizona.edu
Works Cited
Cohn, Richard. 1987. “Transpositional Combination in Twentieth-Century Music.” Ph.D. dissertation, Eastman School of Music.
—————. (1988). “Inversional Symmetry and Transpositional Combination in Bartók.” Music Theory Spectrum 10: 19–42.
—————. 1991. “Bartók’s Octatonic Strategies: A Motivic Approach.” Journal of the American Musicological Society 44/2: 262–300.
McFarland, Mark. 2005. “Transpositional Combination and Aggregate Formation in Debussy.” Music Theory Spectrum 27/2: 187–220.
Morris, Robert D. 2001. Class Notes for Advanced Atonal Music Theory. Lebanon, NH: Frog Peak Music.
Scotto, Ciro G. 2002. “Transformational Networks, Transpositional Combination, and Aggregate Partitions in Processional by George Crumb.” Music Theory Online 8/3: 1–15.
Footnotes
1. These categories are defined on pp. 94–99 of Cohn 1987.
Return to text
2. The curious reader can refer to Appendix 4 of Cohn’s dissertation, which lists all possible TC derivations for all 137 scs with the TC-property.
Return to text
3. While the first two TC operations are easily followed on Lattice 6, the final one is not shown on the lattice due to the pruning process.
Return to text
4. Many thanks to Aaron Templin, a graduate student at the University of Arizona, for bringing this passage to my attention. For other analyses involving TC and Crumb, see Scotto 2002.
Return to text
5. Again, the motion from 6-1 to 9-1 and from 9-1 to 12-1 is not represented in the lattice due to the pruning process. Still, it should be clear that TC 3 generates those paths.
Return to text
6. This is obviously not entirely unusual. There are several complement pairs where one member is fully factorable and the other is not. Conversely, there are a few scs that map directly to their complement by some TC operation. These are indicated with an asterisk (*).
Return to text
7. This certainly overlaps with Cohn’s observations about the “fertility” of the octatonic collection. See Cohn 1991.
Return to text
8. In his dissertation, Cohn listed these “fully-factorable” scs in Table IV of Appendix 6 on p. 616.
Return to text
9. The 17 sets listed here are all included on Cohn’s complete list of prime scs, found on p. 616 of his dissertation.
Return to text
10. The 11 sets listed here are all included on Cohn’s complete list of semi-factorable scs, found on
p. 616 of his dissertation. However, the careful reader will notice that, when added to the 60 collections generated by the lattices, the total number of scs with both TC and IS comes to 71, a slight difference from Cohn’s total of 72 cited above.
Return to text
11. The curious reader can refer to Appendix 4 of Cohn’s dissertation, which lists all possible TC derivations for all 137 scs with the TC-property.
Return to text
12. While some of the operations that lead from (036) to the nonachords fell prey to the pruning process and do not appear explicity on the (03) lattice, a quick study of the five nonachords reveals this statement’s validity.
Return to text
13. I would like to thank Bob Morris, Evan Jones, Matthew Shaftel, and the anonymous readers for their helpful comments.
Return to text
Copyright Statement
Copyright © 2009 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by William Guerin, Mitch Ohriner, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: