How to Perform Impossible Rhythms
Julian Hook
KEYWORDS: rhythm, meter, metric conflict, triplets, piano, 19th century, Brahms, Scriabin
ABSTRACT: This paper investigates a fairly common but seldom-studied rhythmic notation in the nineteenth-century piano literature, in which duplets in one voice occur against triplets in another, and the second duplet shares its notehead with the third triplet—a logical impossibility, as the former note should theoretically fall halfway through the beat, the latter two-thirds of the way. Examples are given from the works of several composers, especially Brahms, who employed such notations throughout his career. Several alternative realizations are discussed and demonstrated in audio examples; the most appropriate performance strategy is seen to vary from one example to another. Impossibilities of type
Copyright © 2011 Society for Music Theory
I
[1.1] As an ex-mathematician, I do not use the word “impossible” lightly. When a mathematician says that something is impossible, it means the thing involves some inherent logical contradiction. Adding two even numbers and getting an odd number, for example, is impossible, no matter how much one practices one’s addition. This paper, accordingly, is not about rhythms that are merely very difficult, as might be encountered in the music of Elliott Carter or Brian Ferneyhough. Rather, it is about rhythms with the curious property that, no matter how faultless a performer’s mental metronome and digital dexterity may be, it is logically, mathematically, absolutely impossible to play exactly what the composer wrote.(1)
Example 1. Brahms, Variations on an Original Theme, Op. 21, No. 1, Variation 5 (Breitkopf & Härtel)
(click to enlarge and see the rest)
Example 2. Rhythmic notation in left hand of Example 1
(click to enlarge)
Example 3. Possible realizations of Example 1, measures 3–4, left hand
(click to enlarge, see the rest, and hear the audio examples)
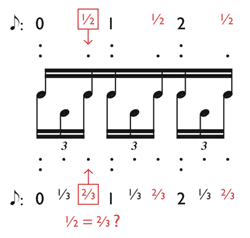
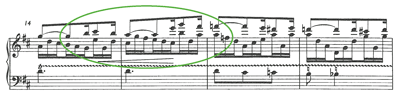
[1.2] Example 1 is full of impossible rhythms. The trouble starts in measure 3, where two voices are notated on the lower staff. One voice, written with stems up, moves in sixteenth notes, duple subdivisions of the beat in the moderately slow
[1.3] Several proposed interpretations of this rhythm are given in Example 3. The only way to achieve mathematically accurate subdivisions in both voices is shown in 3a: the troublesome note must simply be played twice. The added keystroke is pianistically ungraceful at best, and the audio example should be sufficient to convince the reader that 3a is not what Brahms intended, and not a realistic option in performance. The example is nevertheless instructive as a sort of unrealizable ideal, a paradigm of the two-against-three polyrhythm implied by the notation. If the final notes of the duplet and triplet groups did not coincide—if, say, the third triplet were B instead of E—then a strict polyrhythmic performance analogous to Example 3a would be unproblematic; it would, in fact, be the only rhythmically “correct” way to play the passage. It is only the shared note that makes this performance infeasible and forces the pianist to seek other options.
[1.4] Example 3b and its slight variant 3b′ depict a performance with triplet priority: the triplets are played strictly in time and the duplets are “swung” in a 2-to-1 proportion to conform to the triplets. The remaining options give priority to the duplets, forcing the third triplet to arrive early, on the half-beat. At 3c the middle triplet is positioned midway between the first and third, so it too arrives early. At 3d the middle triplet is restored to its proper triplet position, creating an incomplete triplet in counterpoint with the duplet. Example 3d thus resembles 3a, but lacks the rearticulation of the duplicated note. Aurally, the incomplete triplet in 3d may be difficult to perceive as a triplet; this attack rhythm is perhaps more likely to be perceived as shown in 3d′, where a 32nd-note triplet subdivision within the first duplet implies a sixfold subdivision of the beat.
[1.5] Brahms’s use of a self-contradictory notation for this rhythm is enigmatic in several ways. Brahms customarily took great care with his notation, and lavished considerable detail on this score in particular: notice, in Example 1, the copious explicit performance instructions written just in the opening measures of this variation. All of the alternative notations in Example 3 are clear and consistent, and all these notations were readily available to Brahms. In fact, Examples 4–7 show notations similar to 3a–d as employed by Brahms in other works—or even, in one case, elsewhere in this same work.
Example 4. Brahms, “Wie rafft ich mich auf,” Op. 32, No. 1, measures 27–29 (compare Example 3a)
(click to enlarge)
Example 7. Brahms, “Es liebt sich so lieblich im Lenze!”, Op. 71, No. 1, measures 37–39 (compare Example 3d)
(click to enlarge)
[1.6] Although Example 3a was dismissed as pianistically infeasible, such a pattern becomes a reasonable option when the two voices are performed by two different musicians. In Example 4 the eighth notes play the role of the sixteenths in the previous examples. Several times in this example the third note of a piano triplet shadows the same note sounding a fraction of a beat earlier in the second of a pair of duplets in the voice, a heterophonic effect similar to Example 3a.
[1.7] Example 5, from the final variation in the same set as Example 1, features triple subdivisions only, including an explicit indication of triplets against “swung duplets,” notated just as in 3b.
[1.8] In Example 6, the piano part closely resembles a textural inversion of Example 1, but there are no triplets: the rhythmic notation in the right hand is written unambiguously in a way much like Example 3c, privileging the duplets.
|
Example 5. Brahms, Variations, Op. 21, No. 1, variation 11, measures 14–17 (compare Example 3b) (click to enlarge) |
Example 6. Brahms, Sonata for Cello and Piano, Op. 38, mvt. II, Trio, measures 1–5 (compare Example 3c) (click to enlarge) |
[1.9] Finally, the piano part in Example 7 features a recurring pattern that includes duplets against incomplete triplets, rather like 3d.
[1.10] It is reasonable to suppose that Brahms’s preferred way of performing Example 1 must have resembled Example 3b (and therefore Example 5), Example 3c (and 6), or Example 3d (and 7)—but in that case it is also reasonable to wonder why he chose the notation of Example 1 rather than the unambiguous alternative. Above all, it is reasonable to ask what a pianist should do when playing this variation. On the evidence of op. 21, no. 1’s modest discographic record, the path of least resistance seems to be that of Example 3b: take the fastest notes—the triplets—at face value, letting the duplets fall where they may. As justification for this reading, one might say that the duplet notation is to be read not as a strict metrical prescription, but only as an indication of grouping or voice leading involving a subset of the triplets. Furthermore, because the right hand plays only duplets, it could be argued that the left hand must project the triplets accurately in order for the basic two-against-three conflict to be heard. Some might suggest also that instead of reading too much into Brahms’s choice of note values we should be reading the visual alignment of the score: in Example 1 the second duplet in each right-hand pair, rather than aligning with the second duplet (third triplet) in the left hand, typically falls instead between the second and third triplets, consistent with a triplet-priority performance of the left-hand rhythm. Indeed, of the alternatives in Example 3, it is 3b that most closely approximates the way this rhythm is played in every recorded performance of which I am aware. Wilhelm Backhaus’s 1935 performance, sans repeats, is offered as an example (listen to Audio Example 1a).
Audio Example 1. Brahms, Op. 21, No. 1, Variation 5
link to score (Example 1)
a. performance by Wilhelm Backhaus 1935 | b. performance by the author |
Example 8. Brahms, Variations, Op. 21, No. 1, Variation 5 (Simrock, 1861)
(click to enlarge and see the rest)
[1.11] While the consensus triplet-priority reading is certainly defensible, I believe that the duplet-priority readings (Examples 3c and 3d) merit consideration as well, for several reasons. First, as Brahms tells us, the variation is a canone in moto contrario, a canon in inversion, and it is the left hand’s duplets, not the triplets, that imitate the subject in the right hand (which also moves in duplets). Occasionally, as in measure 4, the canonic voices proceed in parallel tenths, and so presumably should move in the same note values. Scrutiny of Simrock’s 1861 first edition of the work, shown in Example 8, is revealing. Although essentially the same impossible notation appears in the Simrock as in the more recent Breitkopf edition of Example 1, the alignment of the notes is distinctly different: in most cases Simrock’s right-hand duplets align closely with the left-hand duplets (and therefore with the third triplet in each group) rather than falling between the triplets as in Example 1.(2)
[1.12] Perhaps the strongest argument for a duplet-priority performance is that the duplets carry more integrity as an independent voice than the triplets. Structurally, the two voices in the left hand are not the lines indicated by the stems and beams at all: rather, the duplets form one voice, and the other is the bass line, consisting of the middle triplets only, as accompaniment to the canon. (Reading the duplets and triplets as independent voices results in a great number of dubious parallel unisons.) Backhaus’s performance, like most others, accentuates the right-hand melody over a continuous carpet of relatively undifferentiated triplets. In practice, the more one wishes to bring out the imitating voice in the canon (the upper voice in the left hand), the more one would like to hear that voice moving in a rhythm of equal duplets.
[1.13] The performance in Audio Example 1b takes advantage of the variation’s two-reprise structure to present two alternative interpretations of the contentious left-hand rhythm. The first time through each half of the variation, the performance resembles Backhaus’s (and Example 3b), bringing out the right hand and giving metric priority to the triplets in the left. The repeats, in contrast, give prominence to the imitating voice in the canon, now played in duplets. In the repeats the placement of the middle triplets approximately as in Example 3d highlights the independence of this third voice and forces the bass notes to be short, perhaps conjuring the image of a pizzicato cello accompanying the canon.
II
[2.1] The expanding literature on rhythm and meter, notably Krebs 1999 and London 2004, offers many insights about metric conflicts of various sorts. Studies of performance practice such as Rosenblum 1988 and Brown 1999, meanwhile, have much to tell us about historically appropriate interpretations of various notational conventions, rhythmic and otherwise. The literally impossible nature of a notation such as that in Example 1, however, seems to have escaped scholarly attention. This neglect is perhaps attributable in part to the admittedly fussy nature of the subject, which may appear to depend on a literal-minded reading of notation at the most microscopic scale. The conundrum for the performer is nevertheless a real one—literal-minded or not, one must somehow decide what to play—and the general disregard for the question becomes more remarkable with the realization of just how common such notations actually are in the Romantic piano literature. A rather cursory scan through this repertoire turned up examples of impossible rhythms in works by Schubert, Mendelssohn, Chopin, Robert and Clara Schumann, Liszt, Franck, Brahms, Fauré, MacDowell, Debussy, Sibelius, Amy Beach, Rachmaninov, Ravel, Ernő Dohnányi, Nicolas Medtner, and Karol Szymanowski. The examples are impressive not only for their number but also for their variety, which the whirlwind tour presented here can only begin to suggest.(3)
[2.2] The impossibilities in Examples 9–13 are all of the same general
[2.3] In Example 10, duplet priority seems more suitable. Mendelssohn’s melody features duple sixteenth-note subdivisions throughout the piece, only occasionally sharing a notehead with the accompanying triplets (as in measures 3, 4, 9, 11, and 12, marked in the example). Melodic coherence demands that the duplets be played evenly in these locations as elsewhere.(4)
|
Example 9. Brahms, Ballade in B Major, Op. 10, No. 4, measures 56–59 (click to enlarge) |
Example 10. Mendelssohn, Song without Words in F Major, Op. 85, No. 1, measures 1–12 (click to enlarge) |
Example 11. Clara Wieck (Schumann), Concerto in A Minor, Op. 7, mvt. II, measures 37–39
(click to enlarge)
[2.4] In many other cases the most appropriate rhythm in performance might be a matter of some debate. In Example 11, the impossible rhythm occurs in the right hand of the piano. The triplets maintain an established pattern as in Example 9, but the duplet voice is the primary melody and is doubled in the solo cello, suggesting that the duplets too should be even.(5)
[2.5] These examples suggest, then, that the shared note is best played as a triplet in some instances and as a duplet in others, while in still other cases an argument may be made for either reading. In some situations it may be possible to persuade listeners that they are hearing both duplets and triplets played accurately. One can, of course, play a note that is neither halfway through a beat nor two-thirds of the way, but somewhere in between; it may be possible for listeners to hear such a note as either a duplet or a triplet depending on various contextual and cognitive considerations, in a sort of auditory illusion comparable to many well-known optical illusions that can be perceived in two distinct ways. A case for such a compromise placement might be made even in Examples 9 and 10 above, notwithstanding the preferences indicated previously for these examples.(6)
Example 12. Brahms, Intermezzo in A Major, Op. 76, No. 6, measures 17–28
(click to enlarge and hear the audio example)
Example 13. Liszt, Concerto in E-flat Major, mvt. III, measures 28–39 (solo part only)
(click to enlarge)
Example 14. Brahms, “Regenlied,” Op. 59, No. 3, measures 53–56
(click to enlarge and see the rest)
[2.6] In any case, a small fractional difference between two theoretically distinct attack points may in some circumstances be subsumed by rhythmic flexibility on the part of the performer. The difference between
[2.7] In Example 13 we see a composer apparently changing his notational mind. In measures 31–33 Liszt writes a series of
[2.8] A slightly more complicated pattern combining impossibilities of two different types turns up in several works by Brahms. In Example 14, the stems-up voice in the right hand is notated in triplets, the stems-down voice in duplets; the initial eighth-note rest in each half-measure simultaneously fills the space of a triplet in one voice and a duplet in the other. In each five-note group the last duplet coincides with the last triplet, forming a
[2.9] A desire for notational clarity may bear upon impossible rhythms in various ways. Examples 15 and 16 illustrate a common Schumann trait: a melody that hovers around the beat without quite being on it. The top-voice melody in Example 15 is written in ordinary quarter and eighth notes, but many of these notes must arrive a bit late in order to accommodate the waves of accompanying sextuplets; numerous 1⁄2 = 2⁄3 impossibilities occur as a result. A similar sort of melodic displacement arises in Example 16, where again many melody notes seem to fall a sixth of a beat late. Here, however, Schumann notates the rhythm of the melody without contradiction, the more exact notation perhaps necessitated by the slower tempo, which makes the sixth-beat discrepancies more apparent. The notation of the melody in Example 15 looks simpler than that in Example 16, suggesting that some impossible rhythms may be notated as they are only because the impossible notation is visually simpler than a theoretically correct notation would be.
|
Example 15. Robert Schumann, Romanze, Op. 28, No. 1, measures 33–44 (click to enlarge) |
Example 16. Robert Schumann, Dichterliebe No. 12, “Am leuchtenden Sommermorgen,” measures 23–30 (click to enlarge) |
Example 17. Franck, Prelude, Chorale, and Fugue, Prelude, measures 1–4
(click to enlarge and see the rest)
Example 18. Schumann, Bunte Blätter, Op. 99, No. 2 (“Stücklein II”)
(click to enlarge and see the rest)
Example 19. Impossible rhythm in Example 18, measure 3
(click to enlarge and see the rest)
[2.10] The same principle could apply in a case like Example 17, where each accented quarter note in measures 1 and 3 must fit impossibly into the space of seven-eighths of a beat (and the whole notes in measures 2 and 4 into slightly less than four beats). Theoretically Franck might have written double-dotted eighth notes and ties as needed in these locations, but his use of full-beat note values is simpler, is probably clearer, and better conveys a desire for continuity in the melody formed by the accented notes. It also suggests the possibility that the right-hand notes, rather than falling slightly after the beat, instead define their own “beats,” not precisely aligned with those in the left hand.(8)
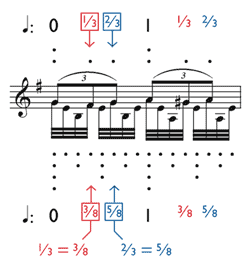
[2.11] A higher degree of complexity appears in measure 3 of Example 18, where a triplet melody must share its notes with a pattern of 32nd notes. As detailed in Example 19a, Schumann’s notation implies the impossible equations
Audio Example 2. Schumann, Op. 99, No. 2, measures 1–22
link to score (Example 18)
a. performance by Maria João Pires 2002 | b. performance by Sviatoslav Richter 1968 |
[2.12] Sviatoslav Richter, in a concert performance of the same work, somehow makes the triplets more equal. The first triplet in measure 3 is somewhat distorted, but the remaining triplets proceed at a very uniform pace. The rhythm of Richter’s 32nd notes is difficult to hear precisely, but must be something approximating Example 19c. At measure 19, Richter brings out the lower doubling of the triplets considerably more than Pires does; we might suppose that the evenness of Richter’s triplets makes this voicing more acceptable (listen to Audio Example 2b).
[2.13] As measured on a stopwatch, the differences among the various proposed realizations of impossible rhythms are small, but a comparison of the above two performances should be sufficient to dissuade anyone from the suspicion that the differences may be so small as to be inconsequential. In each of the impossible equations
[2.14] Neither Pires nor Richter performs Example 18 in a rigid, unvarying tempo. Evidently, projecting the distinctions between the various realizations of these rhythms does not require absolute metronomic regularity on the part of the performer. Adopting the common metaphor of meter as a grid, we may distinguish between the flexibility of the grid and the fine resolution of the grid points: as a whole the grid may be elastic, allowing the tempo to tighten and relax at the performer’s discretion, even while the individual points marking beats and subdivisions at all levels of the metric hierarchy are microscopically small pinpoints, so that differences among interpretations such as those discussed above remain clearly discernible despite the flexible tempo.(11)
III
Example 20. Schumann, Noveletten, Op. 21, No. 1, measures 29–32
(click to enlarge)
Example 21. Brahms, “Ständchen,” Op. 106, No. 1, measures 25–26
(click to enlarge)
Example 22. Chopin, Nocturne in F-sharp Major, Op. 15, No. 2, measures 25–28
(click to enlarge)
Example 23. Chopin, Prelude in E Major, Op. 28, No. 9, autograph, measures 1–4
(click to enlarge)
Example 24. Schubert, Winterreise No. 4, “Erstarrung,” measures 79–81
(click to enlarge)
Example 25. Schubert, Trio in B-flat Major, D. 898, mvt. I, measures 37–40
(click to enlarge)
Example 26. Schubert, Winterreise No. 6, “Wasserflut,” measures 1–4
(click to enlarge and see the rest)
[3.1] In addition to the triplet conflicts discussed above, Example 18 includes another notational curiosity at measures 14 and 16: a dotted rhythm in which the dotted eighth note seems to occupy only five-eighths of a beat, suggesting the impossible equation
[3.2] In Examples 20 and 21, the dotted eighths apparently take up two-thirds of a beat (slightly less than three-quarters) and five-sixths of a beat (slightly more than three-quarters), respectively; numerous other examples could be cited for both of these notations. Example 22 shows a more exotic type: here the dotted notes in the top voice last four-fifths of a beat if the quintuplets are played evenly. Another distinctive feature of Example 22, found occasionally in Chopin and some other composers, is the proliferation of extra stems and beams indicating fragmentary inner voices. Often the note values in these surplus voices do not add up to whole beats in any coherent way. It seems clear that the purpose of the extra beams is to underline the transitory voices, not to show precise metrical positioning, so the note values must not be read too literally—an observation that could have some bearing on some other impossible-rhythm examples as well.(12)
[3.3] Although impossible rhythms may have attracted little scrutiny, a related question involving dotted rhythms has been the subject of some study and even controversy. This is the matter of what has been called “triplet assimilation”: when dotted rhythms occur opposite triplets in another voice, should the dotted rhythms be performed in 2:1 proportion to match the triplets? The alignment of the notes in Chopin’s well-known autograph of the E-major Prelude, shown in part in Example 23, has led many people to conclude that Chopin expected the dotted rhythms to be assimilated to the triplets. Close examination of this autograph shows that some noteheads are double-stemmed, shared between the two conflicting rhythms, thus qualifying them as impossible rhythms of the
[3.4] This is not the place to rehash the triplet-assimilation controversy in detail. The question arises in music as early as the sixteenth century, and in a number of works by J. S. Bach (for instance the E-minor Fugue from Book II of The Well-Tempered Clavier), and relates as well to a few other notations employed by Bach from time to time (such as ![]() in the D-major Fugue from Book I). The matter has been disputed in print at least since the time of C. P. E. Bach; here it will suffice to say that no single solution to the problem has ever been universally accepted.(14)
in the D-major Fugue from Book I). The matter has been disputed in print at least since the time of C. P. E. Bach; here it will suffice to say that no single solution to the problem has ever been universally accepted.(14)
[3.5] Much of the recent triplet-assimilation controversy has centered on the music of Schubert. Assimilators claim support for their position in the very existence of notations such as that in Example 24, where the
[3.6] The nineteenth-century examples of impossible rhythms presented in the earlier sections of this article are not unrelated to the triplet-assimilation problem, but in some ways they present a fundamentally different and more peculiar sort of quandary, one not addressed by a single decision about the length of a dot. Noteheads shared between two voices played by a single musician are an essential feature of these examples, essentially limiting their scope to music for the keyboard, and indeed, the repertoires in which the two problems arise are nearly complementary. The assimilation problem is generally supposed by those on all sides of the controversy essentially to end with Schubert, excepting only an occasional slightly later example such as the Chopin Prelude. Brown gives several examples intended to show that later composers such as Mendelssohn, Schumann, Berlioz, and Brahms differentiated their note values more scrupulously (Brown 1999, 616–21). Impossible rhythms of the shared-notehead variety, on the other hand, really pick up steam only after the time of Schubert. As the examples above suggest, I have found more such notations in the music of Brahms than in any other composer, spanning his career from the Sonata, op. 1, to the very last page of the Vier ernste Gesänge, op. 121. Some of the characteristics for which Brahms is celebrated seem ideally suited to the formation of impossible rhythms: he was fond of polyrhythms and contrapuntal textures, and often wrote multiple voices on one staff. Brahms’s scores might be described as being denser in information content than those of many other composers of his time, and an impossible rhythm is essentially a case of too much information—so much, in fact, that some of it becomes contradictory. Notational complexity is hardly surprising in an era when rhythmic notation bears greater burdens than ever before, but it is remarkable in this climate of notational “precision” that this complexity so often produces instructions whose precise observance is theoretically unattainable.
IV
[4.1] Admitting vertical alignment as a potential source of impossibility in rhythmic notation broadens the scope of our inquiry considerably, not only by eliminating the restriction to keyboard music but also by allowing for superposed rhythms of increased complexity. Example 27, although it involves only the piano part of Franck’s Quintet, suggests that even a composer may at times be misled by a deceptive alignment.
[4.2] At the end of measure 371, a four-against-three polyrhythmic texture gives way to more straightforward duple subdivisions in what must be described as a rather clumsily handled seam. The two sixteenth notes at the end of this measure initiate a motive derived from the movement’s primary theme, which continues in the piano for the next two measures. Evidently these two notes, like those that follow, are intended to sound in octave doubling, played by both hands in the same rhythm. But this alignment is at odds with Franck’s note values: the sixteenth notes in the left hand, as part of a larger triplet, are theoretically shorter than those in the right. The alignment implies the impossible equations
Example 28. Stravinsky, Petrushka (1911), Tableau I, measures 23–37 (condensed score)
(click to enlarge and see the rest)
[4.3] A curious passage in the First Tableau of the original 1911 version of Stravinsky’s Petrushka is shown in Example 28.(17) The score presented here is considerably condensed, but its rhythmic complexities capture those in the full score. At measure 25, a melody enters in ![]() =
= ![]() seems an odd choice, inasmuch as the half note does not define a primary pulse in either the
seems an odd choice, inasmuch as the half note does not define a primary pulse in either the ![]() =
= ![]() or
or ![]() =
= ![]() .
.
[4.4] The same instruction appears also on the piccolo-oboe melody, where it proves thornier. The meter change here is from
Example 29. Stravinsky, Petrushka (1947), Tableau I, measures 23–37 (condensed score)
(click to enlarge and see the rest)
[4.5] When Stravinsky revised Petrushka in the 1940s, he reconsidered this notation as shown in Example 29. There are many small changes in details of orchestration and articulation, and the general accelerando has been eliminated (perhaps a change of little consequence: acceleration is barely discernible, if at all, in most performances of the original version, and it leads in any case to a new section at measure 42 at essentially the same tempo as before). More significantly, the impossible aspects of the notation have also been removed, for the time signatures
[4.6] The revised notation is surely more precise, and makes the changing note lengths in the woodwinds explicit. On the other hand, it is plausible that Stravinsky wanted the woodwinds’ eighth notes, floating above the pulsations in the rest of the ensemble, to sound more or less steady throughout the passage—an intent implicit in the original notation but relinquished in the revision. Two recorded performances, both of the 1911 version, are revealing. Pierre Boulez
(Audio Example 3a) meticulously controls the subdivisions in the woodwind melody as detailed above and as codified in the more punctilious 1947 notation. The varying speeds of eighth notes are clearly audible, especially in the
Audio Example 3. Stravinsky, Petrushka (1911), Tableau I, measures 23–39
link to score (Example 28)
a. performance by the Cleveland Orchestra, conducted by Pierre Boulez 1991 | b. performance by the Columbia Symphony Orchestra, conducted by Igor Stravinsky 1960 |
V
Example 30. Scriabin, Prelude in C Major, Op. 11, No. 1 (Izdatel’stvo Musyka, Moscow)
(click to enlarge and see the rest)
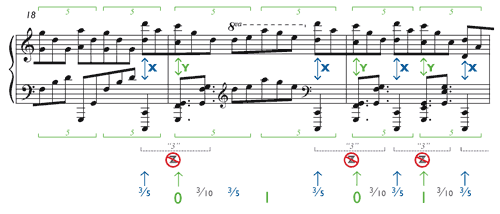
[5.1] An especially perplexing dilemma is posed by Scriabin’s Prelude, op. 11, no. 1, shown in Example 30. The eighth notes running throughout the piece in the right hand are actually quintuplets, five in the time of four, ten notes in every
[5.2] The left hand often plays the same quintuplet rhythm as the right, but quarter notes appear in the left hand as well: briefly in measure 8, and almost continuously from measure 19 to the end. Three quarter notes occupy the time of five quintuplets, so the quarter notes must be triplets, three in the time of two, though Scriabin’s notation does not make this explicit. Like the quintuplets, the triplet groups are displaced from the beats, the first triplet in each group falling before the beat.
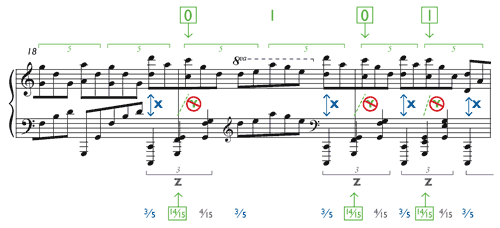
[5.3] The stream of quintuplets is uninterrupted from the beginning of the piece to the end. What is in question is where the triplets fall relative to the quintuplet stream. The published score shows small inconsistencies in alignment from measure to measure, but in general, as Example 32 shows, the notation suggests three things about this alignment, which I shall call conditions X, Y, and Z:
- Condition X: The two kinds of groupings apparently begin simultaneously, as the first triplet in each group aligns with the first quintuplet. Consequently the first triplet in each group must fall at the
3⁄5 point. - Condition Y: Whenever a triplet crosses a barline, the notation shows that the second triplet in the group falls on the downbeat, coinciding with the third quintuplet in the concurrent right-hand group. Similarly, in the mid-measure triplets in measures 20, 22, 23, and 24, the second triplet in the group appears to align with the quintuplet on the second beat of the measure (the beat labeled “1” in Example 32).
- Condition Z: The three triplets in each group are evidently equal in duration. The quarter notes all look the same; there is nothing to indicate that any of them should be longer or shorter than the others.
[5.4] The problem, of course, is that X, Y, and Z cannot all be true. If X and Y are true, then the first triplet takes up the time of two quintuplets—two-fifths of a beat rather than one-third—so the three triplets cannot be equal.
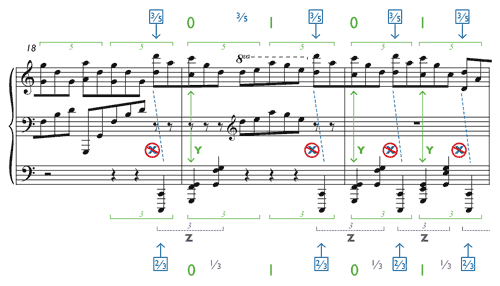
[5.5] Although satisfying the three conditions simultaneously is impossible, it is possible to satisfy any combination of two of them. Examples 33–35 show the three possible pairings, beginning with the combination “X and Y but not Z” in Example 33. Here the groupings align at the
Example 33. First possible realization of Op. 11, No. 1, measures 18–20: X and Y but not Z
(triplet and quintuplet groups aligned; downbeats aligned; unequal triplets)
(click to enlarge)
[5.6] Example 34 is a rather clumsy attempt to show “X and Z but not Y.” Here again the groupings begin together at the
Example 34. Second possible realization of Op. 11, No. 1, measures 18–20: X and Z but not Y
(triplet and quintuplet groups aligned; equal triplets; downbeats misaligned)
(click to enlarge)
[5.7] Finally, in Example 35 (“Y and Z but not X”), the triplets remain equal (Z), but the alignment now occurs on the downbeats (Y) rather than at the beginning of the groups (not X). This puts the first triplet at the
Example 35. Third possible realization of Op. 11, No. 1, measures 18–20: Y and Z but not X
(downbeats aligned; equal triplets; triplet and quintuplet groups misaligned)
(click to enlarge)
[5.8] What is a performer to do in the face of these conflicting indications? Which two conditions should be respected, and which one violated? Recorded evidence in this case shows significant differences of opinion. Audio Example 4a below is a performance by Ruth Laredo that fairly closely matches Example 33. When the triplets enter in measure 19, one can hear that the groupings align and the downbeats align, but the triplets are noticeably unequal in duration.
Audio Example 4. Scriabin, Op. 11, No. 1, measures 13–25
link to score (Example 30)
a. performance by Ruth Laredo 1971 | b. performance by Mikhail Pletnev 1997 |
[5.9] The difficulty of notating Example 34 precisely may be taken in a roundabout way as evidence in support of this reading: perhaps, unable to write exactly what he wanted, Scriabin had to settle for a simpler approximation. The performance by Mikhail Pletnev (Audio Example 4b) resembles Example 34 more closely than Example 33: Pletnev’s triplets are appreciably more uniform than Laredo’s, and at least most of the time the middle triplet falls distinctly before the beat defined by the right hand’s quintuplets.
[5.10] Most available recordings of this Prelude conform broadly to one or the other of the above two approaches, respecting condition X and violating either Y or Z. The alternative in Example 35, “Y and Z but not X,” seems to have been rejected by most performers, or not to have entered their minds. This combination, however, has much to recommend it, starting with the evident deficiencies in the two readings just considered: the odd proportions of the quarter notes in Example 33 and the non-alignment of the second triplet with the beat in Example 34. The half-note beats are projected with some clarity in the right hand, reinforced by details such as the tenuto marks near the beginning of the piece and octave doublings near the end. In measure 20 and again in measure 22, a prominent 4–3 inner-voice resolution in the left hand seems to warrant a position of metric strength; this inner-voice motion has been heard since measure 2, where the same F and E, embedded in the left-hand quintuplets, fell clearly on the beats. The low C in the final measure of the piece will be heard as a downbeat no matter what, but this is simply the next quarter note in line, so if it falls on a beat, presumably other notes in corresponding locations should be similarly positioned. Finally, the misalignment of the triplet and quintuplet groups (“not X”) in Example 35 is defensible: the slight delay between the right- and left-hand attacks represents the most common kind of asynchrony in piano performance (called a “melody lead” in Palmer 1996), and allows the player a little more time to negotiate the large leaps in the left hand at the end of measures 18, 19, and 21 without disrupting the flow of quintuplets in the right.
[5.11] One recorded performance at least vaguely resembling Example 35, remarkably, is a performance by the composer himself, recorded on a piano roll in Moscow in 1910 (Audio Example 5a). There is more tempo variation in Scriabin’s performance than in any modern recording; the difference in tempo from the beginning of the piece to the end may come as a shock to twenty-first-century ears. Scriabin’s technique is hardly a model of clarity, and exact note placements are difficult to judge, but at least a few times one can hear the right-hand quintuplet groups starting before the left-hand triplet groups (“not X”), as in Example 35.
Audio Example 5. Scriabin, Op. 11, No. 1
link to score (Example 30)
a. performance by the composer ( Scriabin 1910) | b. performance by the author |
[5.12] As a vindication of my preference for Example 35, Scriabin’s performance is admittedly nebulous. My own effort is provided as Audio Example 5b.
VI
[6.1] What to make of impossible rhythms? Do they represent mere carelessness on the part of the composer? A bad edition? An attempt to simplify a notation that would otherwise be inordinately complex? A deliberate attempt at provocation, by stretching the limits of conventional musical notation? An approximate representation of an imaginary ideal, a desired auditory illusion, rather than a precise timing instruction? A hint to nuances of expressive timing that the composer expects of the performer? An indication not of temporal matters at all but of grouping or voice leading? Does this study amount to little more than a finicky obsession with distinctions so minute as to be insignificant—or at least to be camouflaged in the mists of the rubato playing appropriate to most of the examples considered here?
[6.2] One or a few of the above examples might be adduced in support of each of these hypotheses, but I have come to believe that no single explanation adequately accommodates all the examples. An impossible rhythm was described earlier as a case of too much information. From the performer’s point of view, paradoxically, too much information is very like too little information: it means that one has to make a choice. Or, perhaps better, one gets to make a choice. At the outset I adopted the stance of a mathematician, but it is as a performer faced with making practical decisions about every detail of a score that I find myself most tantalized by impossible rhythms. Performers are accustomed to making choices about many things, but the basic meaning of rhythmic notation is not usually among them. This exceptional freedom of interpretive choice is one of the things that I find appealing about these rhythms, and ultimately it may be the best answer to the question of what they mean.
Julian Hook
Indiana University
Jacobs School of Music
1201 East Third St.
Bloomington, IN 47405
juhook@indiana.edu
Works Cited
Badura-Skoda, Paul. 1992. “Triolenangleichung bei Schubert: ein noch ungelöstes Problem.” Üben und Musizieren 4: 8–14.
Bilson, Malcolm. 1994. “Triplet Assimilation in the Music of Schubert—A Reply.” Historical Performance 7: 27–31.
Brown, Clive. 1999. Classical and Romantic Performing Practice, 1750–1900. Oxford: Oxford University Press.
Byrd, Donald A. 1984. “Music Notation by Computer.” PhD diss., Indiana University.
Clarke, Eric F. 1987. “Categorical Rhythmic Perception: An Ecological Perspective.” In Action and Perception in Rhythm and Music, edited by Alf Gabrielsson, 19–33. Stockholm: Royal Swedish Academy of Music.
Friberg, Anders, and Johan Sundberg. 1995. “Time Discrimination in a Monotonic, Isochronous Sequence.” Journal of the Acoustical Society of America 98: 2524–31.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. Cambridge, MA: MIT Press.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. New York: Oxford University Press.
London, Justin. 2004. Hearing in Time: Psychological Aspects of Musical Meter. Oxford: Oxford University Press.
Montgomery, David. 1993. “Triplet Assimilation in the Music of Schubert: Challenging the Ideal.” Historical Performance 6: 79–97.
Neumann, Frederick. 1987. “Conflicting Binary and Ternary Rhythms: From the Theory of Mensural Notation to the Music of J. S. Bach.” Music Forum 6: 93–127.
Palmer, Caroline. 1996. “Anatomy of a Performance: Sources of Musical Expression.” Music Perception 13: 433–53.
Rosenblum, Sandra P. 1988. Performance Practices in Classic Piano Music: Their Principles and Applications. Bloomington: Indiana University Press.
Yorgason, Brent. 2009. “Expressive Asynchrony and Meter: A Study of Dispersal, Downbeat Space, and Metric Drift.” PhD diss., Indiana University.
Discography
Discography
Backhaus, Wilhelm. 1935. Concerto for Piano and Orchestra No. 2 in B flat major, Op. 83. Johannes Brahms. Allegro CDO 3034.
Boulez, Pierre (conductor). 1991. Stravinsky: Petrouchka / Le Sacre du printemps. The Cleveland Orchestra. Deutsche Grammophon 435 769-2.
Laredo, Ruth. 1971. Scriabin: 24 Preludes, Op. 11. Phoenix PHCD 114.
Pires, Maria João. 2002. Artist Portrait. Warner Classics 0927-49141-2.
Pletnev, Mikhail. 1997. Scriabin: Sonata No. 4, Op. 30. Virgin 7243 5 45247 2 1.
Richter, Sviatoslav. 1968. Schumann: Bunte Blätter, Op. 99. BBC Legends 4103-2.
Scriabin, Alexander. 1910. The Composer as Pianist. Pierian 0018.
Stravinsky, Igor (conductor). 1960. Works of Igor Stravinsky. Disc 2. Columbia Symphony Orchestra. Sony 88697103112-02.
Footnotes
1. Earlier versions of this paper were presented at the Indiana University Graduate Theory Association Symposium (2008), the Society for Music Theory conference (Nashville, 2008), and colloquia at the University of Washington, the University of Iowa, and Florida State University. I am grateful for the many insightful comments received on those occasions, which have testified time and again to the extraordinary variety of perspectives and interpretations that sensitive musicians and listeners bring to the rhythmic phenomena discussed in this paper. Thanks also to Justin London for a thorough reading and several valuable suggestions, and to Ira Braus and Donald Byrd for some especially thought-provoking correspondence.
Return to text
2. No autograph of op. 21, no. 1 survives. Eusebius Mandyczewski, editor of the Breitkopf edition (1927), cites the Simrock edition as his primary source. A few other differences between the two editions are worth mentioning, though they bear less significantly, if at all, on the analysis here. In the Simrock, the left-hand triplets are beamed in groups of nine, spanning an entire measure, rather than in groups of three as in Breitkopf. (Nine-measure phrases with nine notes to the bar, as in the triplet voice in this variation, are an extraordinarily rare circumstance.) In some measures Simrock reverses the stem directions in the left hand, stemming the triplets upward and the duplets downward. In measure 5, Simrock gives the 32nd-note subtriplet to the triplet voice while in Breitkopf it belongs to the duplet voice. (This subtriplet imitates the grace notes of measure 3, though not in inversion.) After measure 11 Simrock abandons the left hand’s duplet beams entirely, but even after that point the third triplets nearly align with the right hand’s duplets. Finally, the Breitkopf score shows an incorrect placement of the first ending in the variation’s final system; this has been corrected in Example 1 to match Simrock.
Return to text
3. The present study is inevitably incomplete. In addition to rhythm/meter and performance practice there are many other angles from which the problem of impossible rhythms might be approached. Cognitive considerations are given short shrift here, as are historical precedents for the phenomenon. In some cases, a study of autographs and sketches might prove helpful in disentangling the roles of the composer and engraver.
Return to text
4. A 1939 edition of the Songs without Words, “revised and edited” by Stewart Macpherson and published by the Associated Board of the Royal Schools of Music, contains (among numerous editorial interventions that may seem overindulgent by today’s standards) a rare example of explicit editorial commentary on an impossible rhythm, seemingly in disagreement with the performance strategy I have advocated in op. 85, no. 1. In a footnote at measure 3, Macpherson writes:
The direction (in several places in this movement) that the half-beat semiquaver in the melody should coincide with the third note of the triplet in the accompaniment is Mendelssohn’s own. This departure from the exact mathematical division of the beat is so conducive to smoothness that the Editor has ventured to adopt the same plan wherever the Right hand has to play at the same time notes both of the melody and of the accompaniment.
The second sentence refers to spots such as measure 8, where in Macpherson’s edition the first and last sixteenth notes in the melody are both shifted slightly rightward to align with the final notes of the concurrent triplet groups (played here also by the right hand). Because no such realignment is shown when the duplets and triplets are played by separate hands, the “smoothness” that the editor so admires is apparently a function not only of timing but of ease of performance. I thank David Lewis of the Department of Computing at Goldsmiths, University of London, for bringing this edition to my attention.
Return to text
5. The passage in Example 11 is discussed by Krebs, who describes the “superposition of the cello’s duplet eighth notes on the piano’s triplets,” implying a triplet-priority reading on the part of the pianist but without noting that the duplet notation is also present in the piano (Krebs 1999, 210).
Return to text
6. Clarke 1987 shows that perception of rhythmic patterns is categorical: an ambiguous two-note pattern is typically heard either as a duplet or as a triplet, not as a member of some indeterminate middle category. Moreover, the boundary between the two categories shifts according to the musical context, perception of triplets becoming more likely in the presence of other triplets in the music. In the absence of other cues, Western-enculturated listeners are known to show a preference for binary metric groupings (Huron 2006, 195–96), so that a note placement that is mathematically closer to a triplet may nevertheless be perceived as a duplet.
Return to text
7. Paired impossibilities like those of Example 14 appear also in “Die Mainacht,” op. 43, no. 2; “An die Tauben,” op. 63, no. 4; “Wenn ich mit Menschen- und mit Engelzungen redete,” op. 121, no. 4; and the finale of the Cello Sonata in E Minor, op. 38. The duplet beams in Example 14 are absent from the first edition of this song (Simrock, 1873), but the impossible notations appear in the first editions of all of the other works just mentioned.
Return to text
8. Detailed performance studies show that pianists’ hands are rarely perfectly synchronized, nor is such synchronization necessarily considered desirable, even when (as is usually the case) the score contains no suggestion of asynchrony. See, for example, Palmer 1996, 441–42.
Return to text
9. Estimating the “just noticeable difference” (jnd) in the time domain—the smallest variation in timing that listeners are able to perceive—is a complex subject. London reports the results of studies showing that “the lower limit for meter, that is, the shortest interval that we can hear or perform as an element of a rhythmic figure, is about 100 milliseconds” (0.1 seconds)—approximately the length of the 32nd notes in Example 18—but that separate tones can be discerned, and variation in interonset intervals between two sounds can be discriminated, with much finer precision, heavily dependent on musical context London 2004, 27). Friberg and Sundberg 1995 show that in the context of a steady stream of pulses, the jnd is about 2.5 percent of the interonset interval between pulses, down to a minimum jnd of about 6 milliseconds (0.006 seconds). A listener hearing one performance at a time cannot directly judge an offset between attack points in two separate performances of an excerpt such as Example 18, but the variation in the lengths of triplets performed in a 3:2:3 ratio as in Example 19b, even at the rapid tempo of this example, is significant enough to be perceived with little difficulty.
Return to text
10. Ira Braus, in personal communication, has expressed a preference for still another performance strategy in measure 19: he suggests playing the right hand in even 32nd notes and the left in even triplets, so that the melodic doubling is not precisely synchronized.
Return to text
11. There are, to be sure, some circumstances in which by the composer’s design a beat is not a microscopic pinpoint at all, but is dispersed over a period of time. These situations, which include rolled chords, some grace notes, and unsynchronized attacks such as those in Example 17 above, have been studied in detail by Brent Yorgason (Yorgason 2009), but are generally distinct from the examples considered in this article.
Return to text
12. Example 22 is discussed in Byrd 1984, 57–58. Byrd’s dissertation, one of the few sources to mention explicitly the impossible nature of some rhythmic notations, confronts the problem for its implications on the design of music-notation software, which tends to resist attempts by users to do impossible things.
Return to text
13. The Stichvorlage autograph of the Preludes is in the National Library in Warsaw. The E-major Prelude autograph is reproduced in full in the front matter to the 1949 Paderewski edition of the Preludes.
Return to text
14. See Montgomery 1993 for an extensive bibliography on the subject of triplet assimilation, and Neumann 1987 in particular for examples in Bach and implications for earlier music.
Return to text
15. Montgomery 1993 was written in direct response to Badura-Skoda 1992, and prompted a counter-response from Malcolm Bilson (Bilson 1994). The Winterreise excerpts in Examples 24 and 26 appear in Brown 1999, 617, and Montgomery 1993, 90, respectively, and other examples similar to these are discussed in both sources.
Return to text
16. Errors of alignment are not uncommon in published scores, even when the note values are not in question. Undoubtedly many such errors are introduced during the engraving process. They may cause a performer momentary distraction even when the rhythms are simple, and can be seriously confusing in more complex situations. Several examples of the latter occur in the Schirmer editions of the piano works of Samuel Barber, for instance in the third of the Four Excursions, op. 20, measures 17 and 55, and the first movement of the Sonata, op. 26, measure 16.
Return to text
17. I am grateful to Michael Cuthbert for calling the Petrushka example to my attention.
Return to text
18. Chopin’s C-major Prelude, op. 28, no. 1, features five-note groupings also; this similarity is one of many ways in which the twenty-four Preludes of Scriabin’s op. 11 pay homage to Chopin’s op. 28.
Return to text
19. Astute readers may note a fourth premise lurking in this discussion, namely the supposition that the five quintuplets in each group are equal. An alternative reading to those considered here is theoretically possible, in which conditions X, Y, and Z are all satisfied but the quintuplets are distorted so that the first two quintuplets together occupy only one-third of a beat. This interpretation strikes me as less viable than any of the other options proposed: to alter the rhythm of the quintuplets beginning at measure 19 seems bizarre, and to distort it in this way from the beginning of the piece stranger still. If anything, most performers tend to lengthen the first notes of each quintuplet group, not to shorten them.
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by John Reef, Editorial Assistant
Number of visits: