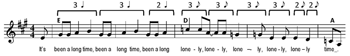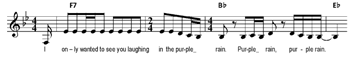Formal Functions of Metric Dissonance in Rock Music *
Nicole Biamonte
KEYWORDS: meter, rhythm, form, phrase structure, rock music
ABSTRACT: This article explores the interactions of metric dissonance with phrase structure and form in rock music, offers categorization schemes for common formal functions of metric dissonance, and presents several corpus studies of metric dissonance in the works of single artists and bands as well as in a cross-section of rock songs. These data allow for comparative analyses of the metric profile of a given artist or band, suggest genre correlations with particular metric patterns, and demonstrate a trend of increasing metric dissonance throughout the history of rock.
Copyright © 2014 Society for Music Theory
Introduction
[1.1] Pop and rock music are frequently generalized as being in 4/4 meter throughout.(1) Like most generalizations, this is substantially true, but—also like most generalizations—on closer examination the reality proves to be more complicated. Numerous examples of rock songs that deviate from the 4/4 norm through asymmetrical or changing meters, either temporarily or on a large scale, are offered by Everett (2009a, 308–9), Rosenberg (2010, 64–69), Moore (2012, 66–68), and Stephens (2013). Recent studies have shown that listeners readily entrain to a regular meter and readily perceive disruptions of the metric hierarchy (Ladinig et al. 2009, Honing 2012, Fitch 2013). This study explores the functions of such disruptions, focusing on the interactions of metric dissonance with phrase structure and form in Anglophone rock music, with a bias toward classic and progressive rock, the repertoires I know best.(2) In the section that follows, I apply and adapt the model of grouping and displacement dissonances developed by Kaminsky (1989) and Krebs (1999) to rhythmic, metric, and hypermetric structural levels. The second section of the article offers a categorization scheme for metric dissonances in terms of their formal functions, demonstrating that they can serve on a small scale as initiating dissonances, links between sections, or cadential hemiolas, and on a large scale to help demarcate formal sections. The last section presents corpus studies of music by the Beatles, the Rolling Stones, Jimi Hendrix, Led Zeppelin, Tool, Radiohead, and 200 of Rolling Stone Magazine’s “Top 500 Songs of All Time,” and compares their different usages of metric dissonance by category and over time.
Example 1. Temporal organization of pop-rock music
(click to enlarge)
[1.2] The temporal organization of music can be shown as a series of layers moving from subdivisions of the beat at the subtactus level, through the rhythmic or tactus level, the metric or bar level, to the hypermetric level and above, as shown in Example 1. Higher levels of organization are perceived as grouping structures rather than metric structures, although phrase and hypermeter occur at the same level and often coincide. This model subdivides Brower’s (1993) paradigm of rhythmic organization into foreground (subtactus and tactus), middleground (meter and hypermeter) and background (larger units), which are governed by different kinds of memory. London describes metric entrainment at the lowest three levels and possibly at the hypermetric level (2012, 16–18). Because of the high degree of repetition, the short length of repeated units, and clear formal boundaries demarcated by changes in text, texture, and other parameters, structural patterns of larger units such as phrases and sections are generally more perceptually salient in vernacular music than in many forms of art music.
[1.3] As numerous commentators have observed, the layers in this model of temporal organization do not all behave in precisely the same way, nor are they perceived in the same way.(3) Rhythmic dissonances, which do not normally disrupt the meter (Krebs’s “submetrical dissonances”; 1999, 30), occur at the tactus level—in 4/4, the quarter-note beat—and below. Layers below the tactus typically include at least one level of subdivision that might be quadruple, duple, triple, or in-between—for example, straight 16th notes, straight 8th notes, triplet 8ths, or uneven pairs in a swing or shuffle rhythm (Krebs’s “low-level dissonances”; 1999, 53).(4) Metric dissonances disrupt the bar and the conducting pattern, which is normally quadruple, sometimes duple or triple, or less commonly an additive combination of these. Metric dissonances in rock music typically play a syntactic role in articulating formal function, discussed in greater detail below, as well as an expressive role in heightening tension.(5) In maintaining a distinction between the rhythmic and metric layers, I am following Huron (2006), London (2012), and other cognitive theorists.(6) A similar distinction between rhythmic dissonances that fit within a comparatively regular metric grid and metric dissonances that do not is made by Hatten (2002, 276–77) and Love (2013, 48), as well as Sykes (1992), Temperley (1999, 26), Pressing (2002, 301), and Everett (2009a, 8 and 311–15), in discussions specific to popular music. Hypermetric dissonances disrupt the well-established pop-rock norm of 4-bar units.(7) Schachter (1987, 88–89) and Huron (2006, 195–196) have observed the increased preference for duple-based groupings at higher levels of organization, which Huron calls the “binary default.” In rock music, displacements and groupings other than quadruple are more common at lower levels and increasingly less common at the hypermetric level and above. Dissonances at any level may be weak or strong and small-scale or large-scale; weak and small-scale dissonances are likely to function on a single level, while strong and large-scale dissonances have the potential to disrupt the next higher level as well.
[1.4] Rock music developed from a combination of other genres, including rhythm & blues and country, but from its beginnings it was strongly associated with dance. Thus many rock songs are indeed in a regular 4/4 meter, which is often overtly iterated in the accompaniment pattern. Interest and tension are created through rhythmic dissonance at the tactus level, which is an essential style feature of the genre (Hesselink 2014). Rhythmic dissonance is typically most prominent in the main melodic layer, normally voice or lead guitar, figured against the ground of a generally regular pattern in the drum part, which is most often ½ or 1 bar long. Due to the ubiquity of these short repeated patterns in the drum parts and the explicit metric framework provided by the timekeeping layer(s) of the texture such as the drum part and rhythm guitar, the metric unit of the bar and the background grid of the meter have greater salience in rock and other vernacular musics than in art music.(8) Thus I have adopted a paradigm that separates rhythm and meter, in contrast to the model of meter as the sum total of interacting rhythmic layers in a work used by Krebs and others. As Gracyk has observed, “Rock bears constant witness to the distinction between meter and rhythm” (1996, 134).
Theoretical Model
Example 2a. Krebs’s types of dissonance
(click to enlarge)
[2.1] Krebs (1999) identifies two basic types of metric dissonance: displacement dissonance, in which the grouping of units remains the same but the position of the first unit is shifted either forward or backward in time, and grouping dissonance, in which the grouping of units changes, as in a hemiola (Example 2a).(9) Either type of dissonance can be direct, occurring simultaneously within the musical texture, or indirect, occurring successively between phrases or sections. Direct displacement dissonances remain out of phase until one or the other pattern is adjusted, but direct grouping dissonances cyclically realign at a period equal to the product of their groupings (duple and triple groupings align every six units, triple and quadruple groupings align every twelve units, etc.). Mirka (2009, 143) further categorizes metric dissonances as split, belonging to different auditory streams, or merged, belonging to the same stream. This study will consider both displacement and grouping dissonances as they most commonly occur in rock-compositional practice: indirect and split.
Example 2b. Waters’s types of grouping dissonance
(click to enlarge)
[2.2] Butler (2006) groups rhythmic patterns in electronic dance music into categories that are similar to those of displacement and grouping dissonance: syncopated rhythms, comprising accents on weak beats that (unlike in Krebs’s model) may or may not form a regular pattern and may or may not periodically realign, and diatonic rhythms, comprising an odd number of attacks distributed across an even number of beats, which are maximally even and maximally individuated—each note has a unique set of relationships to the other notes (81–89).(10) Waters (1996) further subdivides grouping dissonance into two types: measure-preserving, in which the barlines line up but the beats do not, and tactus-preserving, in which the beats line up but the barlines do not (Example 2b). This distinction is essentially the same relationship envisioned on different structural levels, but it is worth making because of the salience of the bar as an organizing unit in popular music.
[2.3] Krebs does not include a model for asymmetrical or odd-cardinality meters with, for example, 5 or 7 beats to a bar, or for changing meters without a larger periodicity. (11) Asymmetrical meters are typically perceived, and are often explicitly marked in the musical texture, as combinations of duple and triple groupings: 5 is 3+2 or 2+3; 7 is 3+2+2, 2+2+3, or less commonly, 2+3+2. London (2012) refers to these as non-isochronous (NI) meters, which are maximally even and have groupings of roughly but not precisely equal size that participate in a larger isochronous cycle.(12) Because of these larger periodic cycles, asymmetrical meters are considered consonant, but because of their unequal groupings they are inherently less stable than symmetrical meters such as 4/4. Changing or asymmetrical meters in one section often create an indirect grouping dissonance with regular 4/4 meter in an adjacent section, most commonly between the introduction and verse or between the verse and chorus.
[2.4] The following section offers examples of displacement and grouping dissonances at rhythmic (tactus), metric, and hypermetric levels. Although the primary concern of this study is the metric or bar level, I have provided examples at the levels immediately above and below for comparison, as well as a few examples of dissonances that participate in more than one level.
Rhythmic Dissonance
Example 3a. Kansas, “Carry On Wayward Son” (1976), rhythmic displacement dissonance in first phrase of chorus melody
(click to enlarge and listen)
Example 3b. Black Sabbath, “Paranoid” (1970), rhythmic displacement dissonance in first phrase of verse melody
(click to enlarge and listen)
[3.1] An instance of direct rhythmic displacement at the tactus level occurs in the chorus melody of Kansas’s “Carry On Wayward Son” (1976). The first line of the chorus is shown in Example 3a; the next two lines are very similar and are set in the same trochaic tetrameter (four strong-weak syllable pairs).(13) At its registral high point, the melody is displaced backward by an eighth note and it remains out of phase with the meter until the fourth beat of the second bar. In this and the following examples, points of consonant alignment are shown with arrows and out-of-phase notes are bracketed, with the grouping structure shown inside the bracket. This kind of medial rhythmic dissonance, which increases tension and momentum within the body of the phrase without challenging the meter, resolves to consonance at the end of the phrase.
[3.2] A more extended rhythmic displacement dissonance is found in the verse of Black Sabbath’s “Paranoid” (1970), shown in Example 3b, with the microtiming anticipations in the vocal melody quantized to the nearest sixteenth-note pulse.(14) The lyric lines are twice as long as in the previous example (trochaic octometer), and the rhythmic displacement is almost immediate, so that after the first attack, none of the notes in the first two bars are on the beat. The backward eighth-note displacement chain in the melody is increasingly fragmented from the beginning to the end of the phrase. The first note is on the downbeat, and then the melody is displaced for the remainder of the first two bars. The third bar has a consonant downbeat followed by one bar of displacement, and the fourth bar has consonant attacks on beats 1 and 3, with a single displaced note in between, taking up just under half a bar, so that the points of consonant alignment accelerate to the end of the phrase, in conjunction with the accelerating harmonic rhythm and the increased dissonance between the guitar and vocal parts.
Example 3c. AC/DC, “For Those About to Rock” (1981), rhythmic grouping dissonance in guitar introduction
(click to enlarge and listen)
Example 3d. Van Halen, “Jump” (1983), rhythmic displacement and grouping dissonances in synthesizer introduction
(click to enlarge and listen)
[3.3] Rhythmic grouping dissonance at the tactus level is demonstrated by the introduction to AC/DC’s “For Those About to Rock (We Salute You)” (1981), shown in Example 3c. Through its accent pattern, the guitar groups 16 eighth notes in 4/4 meter into four groups of 3 and two groups of 2 (333322), a rhythm I call the “double tresillo” since it represents a doubling of the 332 grouping structure of the tresillo, or “three-side” of the clave pattern. The double-tresillo rhythm is common in jazz from the mid-twentieth century onwards and in rock and related genres from the 1970s onwards; other clave-based rhythms are discussed briefly below in paragraph 6.4. Like the examples of rhythmic displacement shown above, the pattern begins and ends in alignment with the 4/4 meter but is out of phase in the middle, creating tension within the body of the phrase. The first two statements of the pattern are unaccompanied and could be heard as metrically ambiguous, but when the drums enter at the beginning of the third statement the 4/4 meter is clear.
[3.4] My final example of rhythmic dissonance at the tactus level is the opening of Van Halen’s “Jump” (1983), shown in Example 3d, which uses both displacement and grouping dissonance.(15) The synthesizer rhythm can be heard as a double tresillo pattern displaced backward by an eighth note with a silent initial triple grouping, followed by a truncated version of the pattern that shifts to duple groupings after only two triple groupings. The rhythm aligns with the meter only on the weak beat 2 of the first and third bars, and on the downbeat of the hypermetrically weak second bar; thus the pattern is significantly more unstable than the AC/DC example, but still functions within the 4/4 metric frame.
Metric Dissonance
Example 4a. Rufus featuring Chaka Khan, “Tell Me Something Good” (1974), perceptual strong beats in bass and vocals at end of verse (audio begins four bars before this transcription and extends two bars after, leading into the chorus)
(click to enlarge and listen)
[4.1] Indirect displacement dissonance at both the rhythmic and metric levels is exemplified in “Tell Me Something Good” by Rufus with Chaka Khan (1974). In the verse, the bass and vocals are aligned, and the guitar answers with a mid-range chord on alternating beats, which sound like off-beats but which align with the drum part. The prominence of the vocals and bass in combination with the accented words in the text (“got,” “knock,” “pride,” “-side”) create perceptual strong beats, as shown in Example 4a, but this puts the hi-hat on the beat and the bass and snare off the beat, in sharp contradiction to the normative pattern. In this hearing there is an extra half-beat at the end of the verse, which reassigns the downbeat when all the parts line up at the beginning of the chorus. The chorus begins on a downbeat 8½ quarter notes after the last barline of the example, and ends with a “missing” half-beat when it moves back to the verse. An alternative but more counterintuitive hearing puts the bass drum, snare drum and guitar on the beat and the bass guitar and accented vocals off the beat, requiring no metric adjustment between sections. In either interpretation, this is an instance of the “loose verse/tight chorus” (LVTC) form described in Temperley 2007, in which choruses are rhythmically, texturally, and tonally more unified than verses. The displacement in Example 4a is rhythmic because the shift by an eighth note occurs below the tactus level, but it is also metric because the downbeat is reassigned and the 4/4 pattern cannot be maintained uninterrupted.
Example 4b. Steve Winwood, “Slowdown Sundown” (1981), end of chorus
(click to enlarge and listen)
Example 4c. Rush, “Free Will” (1980), metric grouping dissonance in verse melody
(click to enlarge and listen)
[4.2] A smaller-scale instance of an eighth-note displacement occurs within the chorus of Steve Winwood’s “Slowdown Sundown,” as shown in Example 4b. My transcription follows the drum part and harmonic rhythm, assigning the bass drum, cymbal hits, and chord changes to downbeats. In this interpretation, the second bar of the example is missing a half-beat and the third bar has an extra half-beat. Because this disruption is comparatively brief, however, it is also possible to maintain a 4/4 hearing; thus this dissonance is rhythmic but only weakly metric.
[4.3] Indirect grouping dissonance at the metric level is created between the changing meter in the verse of Rush’s “Free Will” (1980) and the regular 4/4 of the chorus. The first phrase of the verse is shown in Example 4c. Some rock songs use changing meters in regular pairs, so that alternating bars of 3/4 and 4/4 can be heard as a larger cycle of 7 beats. In “Free Will” the pattern is still larger and less regular: once the full band has entered after the 4-bar introduction, the metric groupings are |6|7|6|7|6|8|. The repetition of this pattern occurs at the midpoint of the verse, so the meter and hypermeter are not only asymmetrical but also out of alignment with the form. The additive structure of the meter is clear, however, because the beginning of each bar is marked by the ascending-fifth motive and anticipation of beat 2 in the melody, and the end of each bar is marked in the drum part by a shift from the backbeat pattern to extra hits or fills that adjust to the varying bar lengths. In addition to the changing groupings, there is also a subtle rhythmic dissonance created by the anticipations, which form two triple groupings at the beginning of each bar, in conflict with the backbeat and highlighted by the disjunct motion and change of contour. This song is another instance of LVTC form: the changing meter, unison texture, and Lydian mode of the verse resolve in the chorus to a regular 4/4 and chordal texture in D major (not shown).
Hypermetric Dissonance
Example 5a. The Beatles, “I Want to Hold Your Hand” (1963), hypermetric displacement dissonance at end of bridge
(click to enlarge and listen)
Example 5b. The Beatles, “I am the Walrus” (1967), hypermetric grouping dissonance in verse
(click to enlarge and listen)
[5.1] An instance of indirect hypermetric displacement occurs at the end of the bridge in The Beatles’ “I Want to Hold Your Hand” (1963), shown as a chord chart in Example 5a.(16) In this song, the 4-bar units of the introduction, verse, and refrain establish a quadruple hypermeter. The verse plus refrain form a larger unit, a modified 12-bar blues in G major. The first phrase of the bridge, which tonicizes the subdominant, conforms to this 4-bar hypermeter, but the second phrase, which we expect to end on the dominant (D), elides into a repetition of the introduction (now with vocals), which also ends on the dominant (D). Because of this elision, the third phrase of the bridge arrives one bar earlier than expected, an effect enhanced by the faster harmonic rhythm, and the bridge section is eleven bars long rather than twelve, disrupting the 4-bar hypermeter.
[5.2] Hypermetric grouping dissonance is exemplified in another Beatles song, “I Am the Walrus” (1967), diagrammed in Example 5b. The 3-bar vocal phrases are out of alignment with the harmonic pattern. The harmony in the first bar is an A major chord over a bass A that moves down a step to G. The repetition of this progression in the third bar sounds like a new beginning, grouping the chord pattern as 2+4 or perhaps 2+2+2. The drums, however, follow the vocal phrases, shifting after three bars from a bass-drum hit on beats 1 and 3 to a bass hit on each beat. Although the Beatles are known for their irregular phrase structures (Everett 2009b), in the broader context of rock music in general, these regular 3-bar phrases diverge from the 4-bar norm. Within the context of this song, they represent an increase in stability over the ambiguous groupings of the 7½-bar introduction and 5-bar bridge, and create an indirect grouping dissonance against the regular 4-bar phrases of the outro.
Backbeat Accompaniment Patterns
Example 6. Standard rock beat
(click to enlarge and listen)
[6.1] Before moving on to the formal functions of metric dissonance, I will address the status of an important foundational metric unit, the backbeat. The most common drum pattern throughout rock and related genres is a backbeat pattern known as the “standard rock beat” (Example 6),(17) a quarter-note pattern in 4/4 consisting of a bass (or kick) drum on beats 1 and 3 and a snare drum on beats 2 and 4, with the hi-hat cymbals or sometimes the ride cymbal iterating a regular 8th-note subdivision.(18) The snare drum is higher in pitch, has a sharper timbre, and as the sound waveform below the notation shows, is louder than the bass drum—thus it is registrally, timbrally, and dynamically more prominent. This creates a clear distinction within the pattern between odd-numbered and even-numbered beats, and places several types of phenomenal accent on what are traditionally the weak beats in a 4/4 pattern. Butterfield (2006) interprets the role of the snare in this pattern as fundamentally anacrustic because of its timbre, frequency, and durational brevity compared to the bass drum. I interpret this last reason as support for the opposite interpretation: I hear the snare hits primarily as reactive rebounds, functionally more continuational than anacrustic.(19) Because the bass drum is more resonant than the snare, it is more strongly connected to the snare than the snare drum is to the bass. Subdivisions of the snare hits into 8th or 16th notes on beats 2 and/or 4 make the backbeats more anacrustic, because they are followed by a longer duration, and subdivisions of the bass drum into 8th notes on beat 1 and/or 3 make the backbeats more continuational, because they are preceded by shorter durations.(20)
[6.2] Because it is an essential component of the meter, functioning as a timeline—a rhythmic ostinato around which the other parts are organized—I consider the backbeat in rock music to be an instance of displacement consonance rather than dissonance. I hold this view in part because there is still an accent on beats 1 and 3, as demonstrated by the propensity of musically untrained listeners to clap on beats 1 and 3 of a backbeat rather than 2 and 4 (see Hein 2013). More importantly, the backbeat is contextually consonant because it is a basic rhythmic unit that typically continues throughout the song, with no expectation of a resolution to a consonant pattern. A pitch-based analogy is the consonant status of the dominant 7th chord in the context of the blues: it is the basic harmonic unit, which does not resolve. Just as the tension of the dominant function in blues is often expressed through alterations or extensions of a dominant 7th chord such as raised or lowered chord fifths or ninths, temporal dissonance in rock music is typically expressed by patterns that create tensions against the underlying backbeat. Butler expresses a similar view of the backbeat as consonant: “In rock, funk, and other traditions with roots in African-American musical practice, strong phenomenal accents on the second and fourth beats of the measure are so pervasive that this trait can be regarded as normative . . . there is little reason to regard the attacks on beats 2 and 4 as belonging elsewhere” (2006, 87). In a recent paper, Wilson (2014) makes the same argument for regarding triple meter in the Sarabande as a “dual-aspect meter” which establishes a beat hierarchy and a separate accent pattern, creating a “complex metrical consonance” that treats the emphasis on beat 2 as expected and referential and thus not in need of resolution. Similarly, Zbikowski (2004, 289) puts forth the proposition that meter in pop and rock is typically quadruple with two levels that distinguish beats 1 and 3 from beats 2 and 4. In contrast, the conception of “shadow meter” explored in Rothstein (1995) and Samarotto (1999) interprets regularly recurring accent patterns as challenging, rather than enriching, the primary meter.
Example 7a. Queen, “We Will Rock You” (1977), body percussion backbeat
(click to enlarge and listen)
Example 7b. Jimi Hendrix, “Foxy Lady” (1970), guitar mimicking backbeat
(click to enlarge and listen)
Example 8. Common clave-based rhythms in rock music
(click to enlarge)
[6.3] An essential characteristic of the backbeat pattern is that beats 1 and 3 are in a lower register than beats 2 and 4, even in instrumentations other than drums. In Queen’s “We Will Rock You,” the standard rock backbeat is expressed with foot stomps and hand claps rather than bass and snare hits (Example 7a). In Jimi Hendrix’s “Foxy Lady,” the guitar riff rhythmically and registrally doubles the backbeat (Example 7b). In both of these examples, beats 1 and 3 are subdivided, enhancing the continuational function of beats 2 and 4. In “Foxy Lady,” the anacrustic function is taken over by the 16th notes at the end of these beats. The backbeat was a stock accompaniment pattern in music from the late-eighteenth and nineteenth centuries and later in ragtime, typically in the form of a bass note followed by a mid-range chord.(21) Both the bass-chord accompaniment pattern and the backbeat are strongly associated with dance, perhaps because their repeated traversals of register suggest or impel motion.(22)
[6.4] Backbeat patterns are accompanimental and are typically iterated in one layer of the texture. Another very common family of patterns is based on the clave rhythm, which can be found in both melody and accompaniment layers. Many common syncopations in rock music are based on the son clave, a 33424 grouping. Part of this rhythm’s appeal may be its progression from dissonance to consonance on two levels, within both 8-pulse and 16-pulse cycles, or 1- and 2-bar units in 4/4 with an 8th-note subdivision. I interpret the first bar as a grouping dissonance that resembles an uneven triplet with a short final beat adjusted to conform to a 4/4 background, but it could also be considered a forward displacement of beat 2, or a backward displacement of beat 3. Osborn describes this as an “idiomatic subdivision” in rock music (2010, 46); Chor (2010a, 2010b) differentiates between clave patterns as surface rhythms, which is their most common role in rock music, and as rhythmic frameworks at a background level, as in many Latin and Afro-Cuban musics. Rhythms in this family, including the clave, tresillo, double tresillo, and related patterns (Example 8) are very common in rock and related genres.(23) They are more likely to be iterated by multiple layers of the texture than displacement syncopations, perhaps because displacement in multiple layers challenges the downbeat, while clave-based rhythms realign with it every one or two bars.
Formal Functions of Metric Dissonance
Example 9. Formal functions of metric dissonance
(click to enlarge)
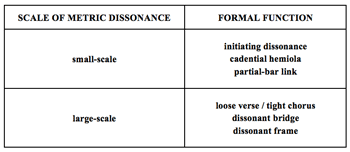
[7.1] Metric dissonances in rock typically contribute to formal articulation at the phrase or section level.(24) Like rhythmic dissonances (see note 19), metric dissonances can be interpreted as expressing the Caplinian formal functions of introduction, initiating, medial, cadential, and postcadential, on one or more levels (see Caplin 1998). Small-scale metric dissonances that disrupt only a few bars or even a single bar typically function in one of three ways: as an initial ambiguity or irregularity that draws attention to the beginning of a phrase or section, as a cadential hemiola that creates a sense of accelerating motion toward the end of a phrase, or as a truncated link at the end of a formal section that provides momentum into the following section; the functions of these techniques are initiating, concluding, and transitional, respectively. Larger-scale metric shifts frequently emphasize sectional contrasts between verses, choruses, bridges, and framing sections such as introductions and codas. More specifically, indirect metric dissonances between sections often mark some sections as more dissonant and unstable than others. These functions are shown in Example 9.
Example 10a. The Beatles, “Martha My Dear” (1968), opening of introduction and verse
(click to enlarge and listen)
[7.2] Initiating dissonances are metrically irregular or ambiguous openings, attention-getting devices that serve to mark the beginning of a phrase or section. There are two basic types: anomalous bars within a prevailing meter, which are usually tactus-preserving grouping dissonances, and initial downbeat or grouping structures that differ from the ones that ultimately prevail, which London calls “metric fake-outs.”(25) Typically the metric dissonance is resolved later in the phrase. The first technique, of initial irregularity, is demonstrated in the introduction and verse of The Beatles’ “Martha My Dear.” The top two staves of Example 10a show the beginning of the piano introduction, which is repeated (in full) with the addition of vocals and strings as the first verse. An extra beat in the opening phrase creates a metric ambiguity, which then resolves into a regular 4/4 for the rest of the section. Everett (1999, 197) describes this as an initial bar of 5/4 moving to 4/4. In The Beatles: Complete Scores, the initial grouping of 5 beats is subdivided into a bar of 3/4 followed by a bar of 2/4, but because of the motivic repetition of G–
[7.3] The second type of initating dissonance, the “fake-out,” is exemplified by the beginning of The Cars’ “Just What I Needed” (Example 10b), a metrically displaced opening. The loud chords spaced four beats apart suggest downbeats, but when the vocals come in and the harmony changes on what turns out to be the real downbeat, we retrospectively reinterpret the chords in the introduction as displaced backward by a quarter note. The palm-muted guitar strumming does begin on beat 1 of the real meter, but in the absence of any other metric cues this could also be heard as beginning on beat 2 following an empty downbeat. Additional examples of initiating dissonances are shown in Example 10c, correlated with London’s categories of metric fake-out (2006).
Example 10b. The Cars, “Just What I Needed” (1978), opening (click to enlarge and listen) | Example 10c. Other initiating dissonances (click to enlarge) |
[7.4] Cadential hemiolas are a familiar form of grouping dissonance, in which the perceived value of the beat or the bar is changed leading into a cadence.(26) In art music, most commonly a triple meter temporarily shifts to a duple grouping, while conversely, in rock music, typically a quadruple meter becomes triple.(27) Either of these formulations could create a sense of acceleration because of the shorter groupings or a sense of deceleration because of the expanded tactus; Willner (1991) refers to these as contraction and expansion hemiolas respectively. Cadential hemiolas are usually of short duration and are only minimally disruptive, realigning with the meter after two or four bars; hence in many cases they can be interpreted as rhythmic rather than metric dissonances.
Example 11a. David Bowie, “Changes” (1971), end of chorus melody
(click to enlarge and listen)
Example 11b. Led Zeppelin, “Rock and Roll” (1971), refrain melody
(click to enlarge and listen)
[7.5] In the chorus of David Bowie’s “Changes” (Example 11a), the prevailing 4/4 meter is first destabilized by a half bar, and then becomes triple meter for four bars. The shorter bar lengths and faster harmonic rhythm—now changing every quarter note, twice as fast as the half-note changes in the verse and the first part of the chorus—intensify the motion leading into the cadence at the end of the section. The refrain of Led Zeppelin’s “Rock and Roll” (Example 11b) features two different types of cadential hemiola, at the quarter-note level and the 8th-note level.(28) The example shows the final phrase of the verse, a 24-bar blues. The initial 3-beat motive, “It’s been a long time,” is repeated twice, displaced backward by a quarter note each time relative to the 4/4 meter.(29) Since the last statement of Led Zeppelin’s motive is interrupted, a 332 tresillo pattern is formed. In the second part of the phrase, the grouping shifts down to the 8th-note level and the word “lonely” is repeated in a double tresillo rhythm (333322). In the Beatles’ “The End” (Example 11c), the uneven triple divisions of the tresillo rhythm used for “And in the end” and “love you take” pave the way for a cadential hemiola that uses an even triple rhythm to accomplish one of the few true metric modulations in rock music. The change from a quarter-note tactus to dotted quarters functions as a built-in ritard leading to a slower 4/4 than the medium-tempo 4/4 used earlier in the song. The metric modulation coincides with a tonal modulation from A major to C major (two keys motivic to the Abbey Road medley).(30) Example 11d offers a few additional examples of cadential hemiolas in rock music.
Example 11c. Beatles, “The End” (1969), ending (click to enlarge and listen) | Example 11d. Other cadential hemiolas (click to enlarge) |
Example 12a. Prince, “Purple Rain” (1984), verse into chorus (audio begins one phrase before notated example)
(click to enlarge and listen)
Example 12b. Derek and the Dominos, “Layla” (1971), chorus into verse
(click to enlarge and listen)
Example 12c. Other partial-bar links
(click to enlarge)
[7.6] Partial-bar links are small-scale grouping dissonances at the ends of formal sections. They function as sectional boundary markers and connecting turnarounds into the next section. Anomalous measures in rock songs are usually truncations—most often, a 2/4 bar in the context of a regular 4/4—which minimally disrupt the meter and hypermeter and also create momentum leading into the next formal section. Often, a melodic arrival on beat 3 is reinterpreted as the downbeat of a new unit to create the 2/4 bar, a technique dubbed “metric reinterpretation” by Rothstein (1989, 52) and others, and “metric deletion” by Lerdahl and Jackendoff (1983, 101). One such example occurs in Prince’s “Purple Rain,” when the arrival on the title text at the end of the verse, on beat 3 of the eighth bar, is reinterpreted as the downbeat of the first bar of the chorus (Example 12a), eliding the end of the verse into the beginning of the chorus. Other cues for this structural shift are the sharp increase in texture at this point and the change in harmonic rhythm, breaking the regular pattern of one chord per bar maintained in the rest of the verse. Derek and the Dominos’ “Layla” (Example 12b) exemplifies a contraction rather than an elision: the cadential arrival in the chorus is on the downbeat of the seventh bar, and the eighth “turnaround” bar is truncated. The metric slippage in this song happens in tandem with tonal slippage since the verse begins in
[7.7] One of the most common large-scale uses of metric dissonance follows the formal model that Temperley (2007) calls “loose verse/tight chorus” or LVTC. Songs with this structure have choruses that are more regular than the verses in several ways: more rhythmically consonant, harmonically stable, texturally unified, and lyrically regular and repetitive (as well as being louder and texturally thicker). The contrast between “loose” and “tight” recalls Caplin’s (1998) formal model of tight-knit and loose-knit themes, and development sections of sonata forms and bridge sections of verse-chorus forms also share some structural characteristics: both are typically located in the middle of the work, end with a dominant prolongation, and feature destabilizing techniques such as sequence, modulation, and fragmentation. Thus, broadly speaking, sonata form and verse-chorus form feature the same kinds of sectional contrasts, although the sections do not occur in the same order: in sonata form, tight-knit main theme, loose-knit subordinate theme, and unstable development; in verse-chorus form, loose-knit verse, tight-knit chorus, and unstable bridge. In the LVTC model the chorus functions as both a contrast to the verse and a resolution of it, and is often repeated multiple times at the end of the song to create a de facto coda. A shift from changing or asymmetrical meter to regular meter between the verse and chorus can serve as an additional parameter reinforcing the role of the chorus as culmination and resolution (these roles are perhaps analogous to that of the main theme in a sonata recapitulation).(31) While irregular changing meters are metrically unstable and cannot be entrained, asymmetrical meters—including regular changing meters such as a consistent alternation of 3/4 and 4/4, equivalent to a larger 7/4 grouping—are consonant, and often participate in a larger cycle. However, because they are less regular than 4/4 they may be perceived as more dissonant in comparison.(32) Formal sections in changing or asymmetrical meters can create indirect grouping dissonances when juxtaposed against sections in 4/4 or other more regular meters.
Example 13a. Alice in Chains, “Them Bones” (1992)
(click to enlarge and listen)
Example 13b. Rush, “Limelight” (1981)
(click to enlarge and listen)
Example 13c. Other metric LVTC structures
(click to enlarge)
Example 14c. Other metrically dissonant middle sections
(click to enlarge)
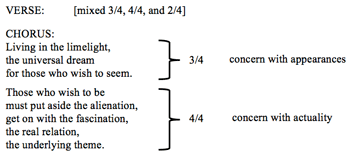
[7.8] One instance of LVTC is Alice in Chains’s “Them Bones” (Example 13a). The verses are in 7/4 and the refrains in 4/4; the refrains also use simpler rhythms and more diatonic harmonies. I have shown the verses as eight bars long followed by 4-bar refrains, following the proportions of the 12-bar blues, but it is also possible to hear each verse section as two 4-bar verses, an interpretation that better reflects the aabb rhyme scheme. In the formal diagram below and those that follow, sections in asymmetrical meter are shaded in light gray. The verse of Rush’s “Limelight” (Example 13b) features a frequently changing meter, while the single metric shift in the chorus has a programmatic function related to the text: a less normative 3/4 meter underlies the first half of the chorus, which describes a concern with appearances, while the more normative 4/4 underlies the second half, which describes the importance of recognizing an underlying reality. The beginning of the last chorus is intensified by a direct metric dissonance: the singer and guitarist are in triple meter as before, but the drummer suggests a conflicting duple meter (second audio example). Other examples of metric LVTC structures are shown in Example 13c.
[7.9] As noted above, the formal organization of LVTC structures stands in contrast to the traditional model of sonata form, in which the tight-knit main theme is presented first, followed by the loose-knit second theme, but both often feature an unstable middle section—the development or bridge—that heightens tension. While developmental techniques in rock music are far more constrained than those used in art music, bridge sections and sonata developments have a variety of features in common: medial temporal position, maximal contrast with other sections, departure from the tonic (in rock music this often occurs through tonicization of IV rather than successive modulations), increased harmonic dissonance and chromaticism, wider or higher register, use of sequence and fragmentation, a less unified texture, and a tonally open ending on the home dominant that is resolved by the return of the A section.(33) Irregular, changing or conflicting meters can also serve to heighten the instability and dissonance of a middle section. In the form chart of Yes’s “Roundabout” (Example 14a), the middle section, shaded in dark gray, features a measure-preserving direct grouping dissonance between the drums and guitars, in 4/4 and 6/4 respectively.(34) Because the bar lengths are preserved, this could also be interpreted as a rhythmic dissonance rather than a metric conflict. This section is texturally and rhythmically as well as metrically climactic. The following section recapitulates the opening material, in a familiar ABA paradigm. Radiohead’s “Paranoid Android” (Example 14b), which began as 3 different songs, has a dissonant middle section that features changing and asymmetrical meters, in contrast to the verse and refrain of the A section and the passacaglia of the C section, both of which are in a regular 4/4. The B section also becomes increasingly dissonant, both harmonically and timbrally. Since it returns as the coda, the B section acts as both a climactic midpoint and a climactic ending.(35) Example 14c offers additional examples of metrically dissonant middle sections.
Example 14a. Yes, “Roundabout” (1971) (click to enlarge and listen) | Example 14b. Radiohead, “Paranoid Android” (1997) (click to enlarge and listen) |
Example 15a. Rush, “YYZ” (1981)
(click to enlarge and listen)
Example 15b. Led Zeppelin, “Kashmir” (1975)
(click to enlarge and listen)
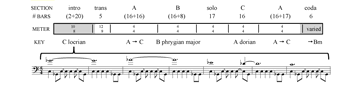
[7.10] In a metrically dissonant framing structure, unstable outer A sections or an introduction and coda surround a more stable central section or sections. This central section often includes or consists of an improvised solo, which may be the source of the preference for a regular and consonant meter. The decreased metric interest in such middle sections is often compensated for by heightening in other musical parameters such as harmony, texture, or rhythmic density. Rush’s “YYZ” (Example 15a) has an introduction that is both metrically irregular, in 5/4 or 10/8, and tonally unstable, in the Locrian mode with a tritone ostinato in the bass and a C locrian melody featuring
[7.11] The small-scale types of metric dissonances listed in Example 9 and demonstrated above—initiating dissonances, cadential hemiolas, and fragmentary links between sections—are familiar concepts from western art music, but as I have demonstrated, they are prevalent in rock music as well. Among the large-scale types of metric dissonance, dissonant middle sections are most clearly analogous to classical models, but the interplay between tight-knit and loose-knit structures more generally is common to both art music and rock music, although the sections may be differently deployed. While metric dissonance is the focus of this study, the functions described here are also expressed at the rhythmic level and in other domains such as pitch, texture, and timbre.
Corpus Studies
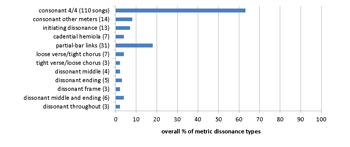
[8.1] In the last section of this paper, I provide a more empirically oriented survey of the ways in which these types of dissonance play out in the repertoire, through a series of corpus studies. I have analyzed the metric structures of large collections of songs by The Beatles, The Rolling Stones, Jimi Hendrix, Led Zeppelin, Radiohead, Tool, and a multi-artist corpus of 200 songs extracted by De Clercq and Temperley (2011) from Rolling Stone magazine’s list of “The 500 Greatest Songs of All Time.” The Beatles are arguably the greatest and most important rock band of all time, while The Rolling Stones were their contemporaneous rivals and the two groups are still frequently compared (see, for example, DeRogatis and Kot 2010; McMillian 2013). The Beatles were more compositionally inventive and drew from a wider range of stylistic influences, whereas the Stones were more firmly rooted in blues and rock. Hendrix and Led Zeppelin, like the Beatles, were seminal innovators, influential on the later development of both rock and metal. Of the two more recent bands, Tool is a progressive metal band participating in and extending many of the same stylistic elements as Led Zeppelin, while Radiohead is perhaps best classified as experimental alternative rock. The Rolling Stone corpus functions as a control, averaging the metric profile of a wide variety of artists and styles. For the analyses, I tabulated instances of each separate type of metric dissonance within a song, not counting repeats.(38) Unmetered songs were excluded from the study. Numerous songs use more than one type of dissonance, which is why the numbers in the graphs add up to more than the song totals in some cases. For each corpus, a typological bar graph shows the relative proportions of metric consonance and the different types of metric dissonance, and a chronological bar graph shows the proportions of consonance and small- and large-scale metric dissonances by year. These statistics can be used as a comparative tool to examine the metric profile of each band’s oeuvre. The data show a general trend of increasing metric dissonance over time within the work of each band, as well as a generally increasing trend throughout the latter half of the twentieth century.(39)
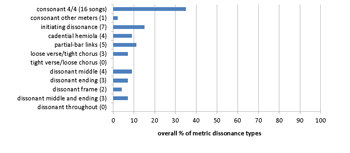
Example 16. Beatles corpus: 176 songs (all songs excluding covers)
(click to enlarge and see the rest)
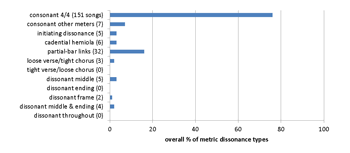
[8.2] The Beatles corpus consists of the original songs from their studio albums, Please Please Me (1963), With the Beatles (1963), A Hard Day’s Night (1964), Beatles For Sale (1964), Help! (1965), Rubber Soul (1965), Yesterday and Today (1966), Revolver (1966), Sgt. Pepper’s Lonely Hearts Club Band (1967), Magical Mystery Tour (1967), The Beatles/The White Album (1968), Yellow Submarine (1969), Abbey Road (1969), Let It Be (1970), and the original singles released during the same time period. The typological and chronological distributions of metric dissonance in their music are shown in Examples 16a and 16b. About two-thirds of their songs are in consonant 4/4 meter; their most common type of metric dissonance is the partial-bar link. The Beatles’ use of metric dissonance becomes significant beginning with Sgt. Pepper, which is generally considered to be the peak of their experimental middle period (Eerola 1998), and continues throughout their late period. The spike in 1968 represents the White Album, a double album that contains many partial-bar links; apart from this, both types of metric dissonance increase until 1970, the release of Let It Be, which contains no small-scale dissonances.
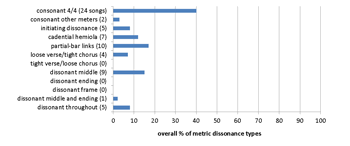
Example 17. Rolling Stones corpus: 118 songs (all songs through 1972 excluding covers)
(click to enlarge and see the rest)
[8.3] The Rolling Stones corpus comprises the original songs from their first thirteen studio albums, up to Exile on Main Street (1972), along with the singles released during the same period; the data are shown in Examples 17a and 17b. I have chosen this endpoint for a number of reasons: their “golden age” is generally considered to comprise the four albums from Beggar’s Banquet (1968) to Exile on Main Street; critical reception of later albums was more negative; the following album, Goat’s Head Soup (1973), represented a significant style shift toward soul and funk; and later albums used a different producer and more importantly, a different guitarist, Mick Taylor, following the departure and subsequent death of Brian Jones. The music of the Rolling Stones is far more metrically consonant than that of the Beatles, which is unsurprising in light of their strong blues-rock influence and comparatively mild stylistic and compositional experimentation.
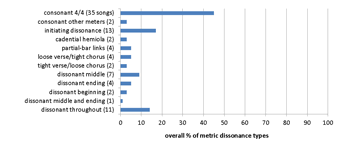
Example 18. Hendrix corpus: 45 songs (studio albums and singles released during lifetime)
(click to enlarge and see the rest)
[8.4] The Hendrix corpus is comparatively small, comprising Are You Experienced (1967), Axis: Bold as Love (1967), Electric Ladyland (1968), and Band of Gypsys (1970), plus the two singles “Stone Free” (1966) and “Stepping Stone” (1970). Although Hendrix’s bands were trios rather than quartets and thus have a simpler basic texture, his corpus (Examples 18a and 18b) is more dissonant overall than the previous two, with two-thirds of the songs incorporating some form of metric dissonance. Rhythmic, metric, harmonic and timbral dissonance are all characteristic features of his style. His use of rhythmic and metric dissonance may also be related to the lack of a separate rhythm guitarist in the band; like other rock-trio guitarists such as Eric Clapton in Cream and Alex Lifeson of Rush, Hendrix’s playing combined the typical roles of lead and rhythm guitar. The data show a mild increase of dissonance until the 1970 release of Band of Gypsys, which featured a different drummer and bass player from the earlier albums (Buddy Miles and Billy Cox rather than Mitch Mitchell and Noel Redding). The overall style on this album has strong funk and jazz-fusion influences, but Miles’s drumming style is more straight-ahead rock than Mitchell’s freer and more variegated drumming, which may be a reason for the decrease in large-scale metric dissonance.
Example 19. Led Zeppelin corpus: 59 songs (first six albums)
(click to enlarge and see the rest)
[8.5] Rhythmic and metric playfulness is a noted style feature of Led Zeppelin’s music; see, for example, Fast 2001 and Brackett 2008. Ann Wilson of Heart has commented: “When you do a Led Zeppelin song, you’re really taking on a lot in terms of meter” (Bream 2010, 182). Their corpus (Examples 19a and 19b) consists of the canonical albums Led Zeppelin I through IV (1969, 1969, 1970, 1971), Houses of the Holy (1973), and Physical Graffiti (1975). Led Zeppelin’s metric profile is fairly similar to Hendrix’s, with slightly higher proportions of consonance but also of large-scale metric dissonance. Led Zeppelin IV, released in 1971, represented a shift away from blues borrowings and a greater proportion of original compositions; the decreased metric dissonance on this album may reflect the move away from the metric freedom typical of the Delta blues that was their strongest early influence.
Example 20. Radiohead corpus: 77 songs (first seven albums)
(click to enlarge and see the rest)
[8.6] All of Radiohead’s studio albums but the most recent (King of Limbs, 2011) were analyzed: Pablo Honey (1993), The Bends (1995), OK Computer (1997), Kid A (2000), Amnesiac (2001), Hail to the Thief (2003), and In Rainbows (2007). Their corpus, shown in Examples 20a and 20b, has a surprisingly consonant overall profile, largely because the band uses rhythmic dissonance much more pervasively than metric dissonance. Their 1995 album The Bends is especially consonant, which may reflect its strong grunge influence, the band’s preoccupation with world touring just before the album was recorded, or simply the faster rate of composition required for a second album, when within the space of a year or two a band is pressured to equal or surpass a successful first album that represented the compositional culmination of their lives up to that point.
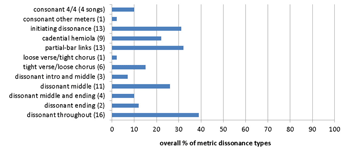
Example 21. Tool corpus: 39 songs (four studio albums)
(click to enlarge and see the rest)
[8.7] The Tool oeuvre analyzed consists of their four studio albums, Undertow (1993), Aenima (1996), Lateralus (2001), and 10,000 Days (2006). The data are presented in Examples 21a and 21b. Unsurprisingly, it is the most metrically dissonant corpus, since the band’s style is the most progressive among those considered here, and they are well known for their use of asymmetrical and changing meters. In some cases their metric and syllabic patterns are organized according to mathematical patterns such as the Fibonacci sequence, most famously in the title track to “Lateralus” (DiCarlo 2001), although the album as a whole is more metrically consonant that the rest of their oeuvre. The band’s focus on metric dissonance is reflected by the comparative preponderance of tight verse/loose chorus forms; uniquely among these corpora, in Tool’s oeuvre it is more common for the chorus to be less consonant than the verse, rather than vice versa.
Example 22. Rolling Stone 200 corpus: 200 songs (extracted from Rolling Stone Magazine’s “500 Greatest Songs of All Time” in DeClercq and Temperley 2011)
(click to enlarge and see the rest)
[8.8] The most consonant corpus overall, also unsurprisingly, is the Rolling Stone 200 corpus used in DeClercq and Temperley’s study of rock harmony (2011). This set of songs was distilled from Rolling Stone’s list of the “500 Greatest Songs of All Time” (#963, Dec. 9, 2004) by taking the top 20 songs from each decade from the 1950s through the 1990s, plus the next 101 top-ranked songs not already in the list (among the first 100 songs, Public Enemy’s “Bring Da Noise” was determined not to contain any harmony, and was replaced with an additional song). Most of the songs were released between 1963 and 1969, with others from the late 1950s and mid 1970s; there are very few songs from the 1980s and 1990s. One interesting aspect of the corpus, graphed in Examples 22a and 22b, is that it includes songs from genres outside of rock, such as country, gospel, disco, and rap, in addition to rock-related genres such as rhythm & blues, funk, and heavy metal. I have not done a large-scale study of genre correlations and metric dissonance, but on the basis of these data I can make a few generalizations: country music is very metrically regular, as is 1950s pop music and any other songs that use tambourine. In genres such as funk, rap, and dance music, which incorporate a lot of displacement dissonance, it seems to be inversely correlated with grouping dissonance, which is significantly less common in these genres. Outside of these genres, displacement dissonance tends to be more often rhythmic rather than metric, and in either case is usually confined to the main melody layer (guitar or voice), perhaps in order to avoid challenging the downbeat. Grouping dissonances also occur in the melody layer alone, but unlike displacement dissonances they are more often expressed by multiple layers of the texture, perhaps because they do not challenge the downbeat in the same way, but rather periodically realign. The most pervasive use of grouping dissonance is found in progressive rock, a genre in which metric play is a stylistic hallmark.(40) Finally, in terms of recording techniques, often when metric dissonance occurs in a song the metrically consonant bass and drums are adjusted to be more prominent in the mix.
[8.9] In summary, in this paper I have offered a model of structural temporal levels of rhythmic, metric, and hypermetric dissonance, proposed an interpretive model for the backbeat, demonstrated the common functions of small-scale metric dissonances in rock to begin and end phrases and sections, demonstrated the common functions of large-scale metric dissonances in rock to enhance contrast between sections and create a large-scale interplay between tension and stability, and surveyed the prevalence of these types in rock-compositional practice through a series of selected corpus studies. I hope this work can serve as a useful basis for future research, as the interactions of rhythm, meter, form, and texture in rock music are rich and varied, offering fertile ground for future theoretical and analytical work in this domain. I hope, also, to have suggested some ways of understanding the ways in which we hear, perform, and engage bodily with rock music.
Nicole Biamonte
McGill University
Department of Music Research, Music Theory Area
555 rue Sherbrooke O.
Montreal, QC H3A 1E3
Canada
nicole.biamonte@mcgill.ca
Works Cited
Adam, Nathan. 2011. “Coding OK Computer. Categorization and Characterization of Disruptive Harmonic and Rhythmic Events in Rock Music.” PhD diss., University of Michigan.
Attas, Robin. 2011. “Meter as Process in Groove-Based Popular Musics.” PhD diss., University of British Columbia.
Banfield, Stephen. 1993. Sondheim's Broadway Musicals. University of Michigan Press.
Baur, Stephen. 2012. “Backbeat.” Grove Dictionary of American Music, 2nd ed. Oxford University Press.
The Beatles. 1993. Complete Scores: Full Transcriptions from the Original Recordings. Hal Leonard.
Benadon, Fernando, and Ted Gioia. 2009. “How Hooker Found His Boogie: A Rhythmic Analysis of a Classic Groove.” Popular Music 28 no. 1: 19–32.
Benjamin, William. 2011. “Hypermetric Dissonance in the Later Works of Robert Schumann.” In Rethinking Schumann, ed. Roe-Min Kok and Laura Tunbridge, 206–34. Oxford University Press.
Berry, Wallace. 1976. Structural Functions in Music. Prentice-Hall.
Bourque, Matthew. 2004. “Approaching the Edge: Yes’s Techniques that Lead to ‘Close to the Edge.’” MA thesis, Arizona State University.
Brackett, John. 2008. “Examining Rhythmic and Metric Practices in Led Zeppelin’s Musical Style.” Popular Music 27, no. 1: 53–76.
Bream, Jon. 2010. Whole Lotta Led Zeppelin: The Illustrated History of the Heaviest Band of All Time. Voyageur Press.
Brewer, Roy. 1999. “The Use of Habanera Rhythm in Rockabilly Music.” American Music 17, no. 3: 300–317.
Brower, Candace. 1993. “Memory and the Perception of Rhythm.” Music Theory Spectrum 15, no. 1: 19–35.
Butler, Mark J. 2001. “Turning the Beat Around: Reinterpretation, Metrical Dissonance, and Asymmetry in Electronic Dance Music.” Music Theory Online 7, no. 6.
—————. 2006. Unlocking the Groove: Rhythm, Meter, and Musical Design in Electronic Dance Music. Indiana University Press.
Butterfield, Matthew. 2006. “The Power of Anacrusis: Engendered Feeling in Groove-Based Musics.” Music Theory Online 12, no. 4.
Caplin, William. 1998. Classical Form. Oxford University Press.
Chor, Ives. 2010a. “Cognitive Frameworks for the Production of Musical Rhythm.” Ph.D. diss., Northwestern University.
—————. 2010b. “Microtiming and Rhythmic Structure in Clave-Based Music: A Quantitative Study.” In Musical Rhythm in the Age of Digital Reproduction, ed. Anne Danielsen, 37–50. Ashgate Publishing.
Clarke, Eric. 1987. “Levels of Structure in the Organization of Musical Time.” Contemporary Music Review 2, no. 1: 211–38.
Cohn, Richard. 1992a. “The Dramatization of Hypermetric Conflicts in the Scherzo of Beethoven's Ninth Symphony.” 19th-Century Music 15, no. 3: 188–206.
—————. 1992b. “Metric and Hypermetric Dissonance in the Menuetto of Mozart’s Symphony in G minor, K. 550.” Intégral 6: 1–33.
—————. 2001. “Complex Hemiolas, Ski-Hill Graphs and Metric Spaces.” Music Analysis 20, no. 3: 295–326.
Covach, John. 1997. “Progressive Rock, ‘Close to the Edge,’ and the Boundaries of Style.” In Understanding Rock, ed. John Covach and Graeme M. Boone, 3–31. Oxford University Press.
Danielsen, Anne. 2006. Presence and Pleasure: The Funk Grooves of James Brown and Parliament. Wesleyan University Press.
De Clercq, Trevor and David Temperley. 2011. “A Corpus Analysis of Rock Harmony.” Popular Music 30, no. 1: 47–70.
De Clercq, Trevor. 2012. “Sections and Successions in Successful Songs: A Prototype Approch to Form in Rock Music.” PhD diss., University of Rochester.
DeRogatis, Jim, and Greg Kot. 2010. The Beatles vs. The Rolling Stones: Sound Opinions on the Great Rock’n’Roll Rivalry. Voyageur.
DiCarlo, Christopher. 2001. “Interview with Maynard James Keenan.” http://www.cdicarlo.com/paper_04maynard.htm
Downs, Clive. 2000/1. “Metric Displacement in the Improvisation of Charlie Christian.” Annual Review of Jazz Studies 11: 39–68.
Eerola, Tuomas. 1998. “The Rise and Fall of the Experimental Style of the Beatles.” Beatlestudies 1: 33–60. Reprinted in Soundscapes 3 (2000), http://www.icce.rug.nl/~soundscapes/VOLUME03/Rise_and_fall0.shtml
Eggertson, Kristine. 2003. “‘Where is the Meter?’ An Investigation of Rhythmic Process in Bjork’s Music.” PhD diss., University of Saskatchewan.
Everett, Walter. 1995. “The Beatles as Composers: The Genesis of Abbey Road, Side Two.” In Concert Music, Rock and Jazz since 1945, ed. Elizabeth Marvin and Richard Hermann, 172–227. University of Rochester Press.
—————. 1999. The Beatles as Musicians: Revolver through the Anthology. Oxford University Press.
—————. 2001. The Beatles as Musicians: The Quarry Men through Rubber Soul. Oxford University Press.
—————. 2009a. The Foundations of Rock: from “Blue Suede Shoes” to “Suite: Judy Blue Eyes.” Oxford University Press.
—————. 2009b. “Any Time at All: The Beatles’ Free Phrase Rhythms.” In Cambridge Companion to the Beatles, ed. Kenneth Womack, 183–99. Cambridge University Press.
Fast, Susan. 2001. In the Houses of the Holy: Led Zeppelin and the Power of Rock Music. Oxford University Press.
Fitch, W. Tecumseh. 2013. “Rhythmic Cognition in Humans and Animals: Distinguishing Meter and Pulse Perception.” Frontiers in Systems Neuroscience 7. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3813894/
Fleet, Paul, and Jonathon Winter. 2014. “Investigating the Origins of Contemporary Basics on the Drum Kit: An Exploration of the Role of the Hi-hat in Anglo-American Popular Musics from 1960 until 1974.” Popular Music 33, no. 2: 293–314.
Folio, Cynthia. 1995. “An Analysis of Polyrhythm in Selected Improvised Jazz Solos.’’ In Concert Music, Rock, and Jazz Since 1945: Essays and Analytical Studies, ed. Elizabeth West Marvin and Richard Hermann, 103–34. University of Rochester Press.
Frisch, Walter. 1990. “The Shifting Bar Line: Metrical Displacement in Brahms.” In Brahms Studies: Analytical and Historical Studies, ed. George S. Bozarth, 139–63. Clarendon Press.
Gracyk, Theodor. 1996. Rhythm and Noise: An Aesthetics of Rock. Duke University Press.
Graham, James D. 2008. “Rhythms in Rock Music.” Popular Music and Society 1, no. 1: 33–43.
Handel, Stephen. 1998. “The Interplay between Metric and Figural Organization.” Journal of Experimental Psychology: Human Perception and Performance 24, no. 5: 1546–61.
Hasty,Christopher. 1997. Meter as Rhythm. Oxford University Press.
Hatten, Robert. 2002. Review of Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann by Harald Krebs. Music Theory Spectrum 24, no. 2: 273–82.
Hein, Ethan. 2013. Unpublished paper, “Friends Don’t Let Friends Clap on One and Three: A Study of Clapping on the Backbeat.”
Hernandez, Horacio. 2000. Conversations in Clave. Alfred Music Publishing.
Hesselink, Nathan. 2014. “Rhythmic Play, Compositional Intent and Communication in Rock Music.” Popular Music 33, no. 1: 69–90.
Hoffman, Alan. 1983. “On the Nature of Rock and Roll: An Enquiry into the Aesthetic of a Musical Vernacular.” PhD diss., Yale University.
Holm-Hudson, Kevin. 2013. Progressive Rock Reconsidered, 2nd. ed. Routledge.
Honing, Henkjan. 2012. “Without It No Music: Beat Induction as a Fundamental Musical Trait.” Annals of the New York Academy of Sciences 1252: 85–91.
Horlacher, Gretchen. 1992. “The Rhythms of Reiteration: Formal Development in Stravinsky's Ostinati.” Music Theory Spectrum 14, no. 2: 171–87.
Hughes, Timothy. 2003. “Groove and Flow: Six Analytical Essays on the Music of Stevie Wonder.” PhD diss., University of Washington.
Huron, David. 2006. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press.
Huron, David, and Ann Ommen. 2006. “An Empirical Study of Syncopation in American Popular Music, 1890–1939.” Music Theory Spectrum 28, no. 2: 211–32.
Iyer, Vijay. 1998. “Microstructures of Feel, Macrostructures of Sound: Embodied Cognition in West African and African-American Musics.” PhD diss., University of California at Berkeley.
—————. 2002. “Embodied Mind, Situated Cognition, and Expressive Microtiming in African-American Music.” Music Perception 19, no. 3: 387–414.
Josephson, Nors. 1992. “Bach Meets Liszt: Traditional Formal Structures and Performance Practices in Progressive Rock.” Musical Quarterly 76, no. 1: 67–92.
Kaminsky, Peter. 1989. “Aspects of Harmony, Rhythm and Form in Schumann's Papillons, Carnaval and Davidsbündlertanze.” Ph.D. diss., University of Rochester.
Keller, Peter, and Denis Burnham. 2005. “Musical Meter in Attention to Multipart Rhythm.” Music Perception 22 no. 4: 629–61.
Krebs, Harald. 1987. “Some Extensions of the Concept of Metrical Consonance and Dissonance.” Journal of Music Theory 31, no. 1: 99–120.
—————. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press.
—————. 2005. “Hypermeter and Hypermetric Irregularity in the Songs of Josephine Lang.” In Engaging Music: Essays in Music Analysis, ed. Deborah Stein, 13–29. Oxford University Press.
—————. 2009. “The Expressive Role of Rhythm and Meter in Schumann’s Late Lieder.” Gamut 2 no. 1: 267–98.
—————. 2011. “Meter and Expression in Robert Schumann’s Op. 90.” In Rethinking Schumann, ed. Roe-Min Kok and Laura Tunbridge, 183–205. Oxford University Press.
Ladinig, Olivia, Henkjan Honing, Gábor Háden and István Winkler. 2009. “Probing Attentive and Preattentive Emergent Meter in Adult Listeners without Extensive Music Training.” Music Perception 26, no. 4: 377–86.
Leong, Daphne. 2007. “Humperdinck and Wagner: Metric States, Symmetries and Systems.” Journal of Music Theory 51 no. 2: 211–43.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.
Lester, Joel. 1986. The Rhythms of Tonal Music. Southern Illinois University Press.
Lewin, David. 1981. “On Harmony and Meter in Brahms’s Opus 76 #8.” 19th-Century Music 4, no. 3: 261–65.
—————. 1987. Generalized Musical Intervals and Transformations. Yale University Press.
London, Justin. 2002. “Some Non-Isomorphisms Between Pitch and Time.” Journal of Music Theory 46, no. 1–2: 127–51.
—————. 2006. “Metric Fake Outs.” Excel spreadsheet posted at http://people.carleton.edu/~jlondon/.
—————. 2012. Hearing in Time: Psychological Aspects of Musical Meter. 2nd ed. Oxford University Press.
Love, Stefan. 2013. “Subliminal Dissonance or ‘Consonance’? Two Views of Jazz Meter.” Music Theory Spectrum 35, no. 1: 48–61.
Malin, Yonatan. 2006. “Metric Displacement Dissonance and Romantic Longing in the German Lied.” Music Analysis 25, no. 3: 251–288.
—————. 2010. Songs in Motion: Rhythm and Meter in the German Lied. Oxford University Press.
Mauch, Matthias, and Simon Dixon. 2012. “A Corpus-Based Study of Rhythm Patterns.” 13th International Society for Music Information Retrieval Conference (ISMIR), 163–68.
Mauleón, Rebecca. 1993. Salsa Guidebook. Sher Music.
McCandless, Gregory. 2010. “Rhythm and Meter in the Music of Dream Theater.” PhD diss., Florida State University.
—————. 2013. “Metal as a Gradual Process: Additive Rhythmic Structures in the Music of Dream Theater.” Music Theory Online 19 no. 2.
McMillian, John. 2013. Beatles vs. Stones. Simon & Schuster.
Mehldau, Brad. 2012. “Rock Hemiolas.” In Arcana VI: Musicians on Music, ed. John Zorn. Available at http://www.bradmehldau.com/rock-hemiolas/.
Mirka, Danuta. 2009. Metric Manipulations in Haydn and Mozart: Chamber Music for Strings, 1787–1791. Oxford University Press.
Moore, Allan F. 2001. Rock: The Primary Text, 2nd ed. Ashgate Publishing.
—————. 2012. Song Means: Analysing and Interpreting Recorded Popular Song. Ashgate Publishing.
Murphy, Scott. 2009. “Metric Cubes in Some Music of Brahms.” Journal of Music Theory 53, no. 1: 1–56.
Neal, Jocelyn. 1998. “The Metric Makings of a Country Hit.” In Reading Country Music: Steel Guitars, Opry Stars, and Honky-Tonk Bars, ed. Cecelia Tichi, 322–37. Duke University Press.
Ng, Samuel. 2005. “A Grundgestalt Interpretation of Metric Dissonance in the Music of Johannes Brahms.” PhD diss., University of Rochester.
Osborn, Brad. 2010. “Beats that Commute: Algebraic and Kinesthetic Models for Math-Rock Grooves.” Gamut 3, no. 1: 43–68.
—————. 2013. “Subverting the Verse-Chorus Paradigm: Terminally Climactic Forms in Recent Rock Music.” Music Theory Spectrum 35, no. 1: 23–47.
—————. 2014. “Kid Algebra: Radiohead’s Euclidian and Maximally Even Rhythms.” Perspectives of New Music 52: 1–25.
Phillips-Silver, Jessica, C. Athena Aktipis, and Gregory Bryant. 2010. “The Ecology of Entrainment: Foundations of Coordinated Rhythmic Movement.” Music Perception 28, no. 1: 3–14.
Pieslak, Jonathan. 2007. “Re-casting Metal: Rhythm and Meter in the Music of Meshuggah.” Music Theory Spectrum 29, no. 2: 219–45.
Pressing, Jeff. 2002. “Black Atlantic Rhythm: Its Computational and Transcultural Foundations.” Music Perception 19, no. 3: 285–310.
Prögler, Joseph. 1995. “Searching for Swing: Participatory Discrepancies in the Rhythm Section.” Ethnomusicology 39 no. 1: 21–54.
Rahn, John. 1996. “Turning the Analysis Around: Africa-Derived Rhythms and Europe-Derived Music Theory.” Black Music Research Journal 16, no. 1: 71–89.
Rockwell, Joti. 2009. “Banjo Transformations in Bluegrass Rhythm.” Journal of Music Theory 53, no. 1: 137–62.
Rohr, Deborah. 1997. “Brahms’s Metrical Dramas: Rhythm, Text Expression, and Form in the Solo Lieder.” PhD diss., University of Rochester.
Rosenberg, Nancy. 2010. “Popular Music in the College Music Theory Class: Rhythm and Meter.” In Pop-Culture Pedagogy in the Music Classroom, ed. Nicole Biamonte, 47–71. Scarecrow Press.
Rothstein, William. 1989. Phrase Rhythm in Tonal Music. Schirmer Books.
—————. 1995. “Beethoven With and Without ‘Kunstgepräng’ : Metrical Ambiguity Reconsidered.” Beethoven Forum 4: 165–93.
Rusch, René. 2013. “Crossing Over with Brad Mehldau’s Cover of Radiohead’s ‘Paranoid Android’: The Role of Jazz Improvisation in the Transformation of an Intertext.” Music Theory Online 19.4.
Samarotto, Frank. 1999. “Strange Dimensions: Regularity and Irregularity in Deep Levels of Rhythmic Reduction.” In Schenker Studies 2, ed. Carl Schachter and Hedi Siegel, 222–38. Cambridge University Press.
—————. 2005. “Multiple Voices and Metrical Dramas in Beethoven’s Goethe-Songs, Op. 83.” Beethoven Forum 12, no. 2: 151–75.
Savage, Steve. 1989. The Billboard Book of Rhythm. Billboard Books.
Schachter, Carl. 1987. “Rhythm and Linear Analysis: Aspects of Meter.” Music Forum 6: 1–59.
Schlueter, Brad. 2005. “How to Survive a Train Wreck: Analysis of the Trickiest Drum Intros on Record.” DRUM! Magazine, December 2005. http://www.drummagazine.com/lessons/post/analysis-of-the-trickiest-drum-intros-on-record/
Sheinbaum, John. 2013. “Progressive Rock and the Inversion of Musical Values.” In Progressive Rock Reconsidered, 2nd ed., ed. Kevin Holm-Hudson, 30–52. Routledge.
Smith, Peter. 2001. “Brahms and the Shifting Barline: Metric Displacement and Formal Process in the Trios with Wind Instruments.” In Brahms Studies, ed. David Brodbeck, 191–229. University of Nebraska Press.
Stephens, Betsey (BetZe13). 2013. “Odd Time Obsessed.” Website at http://www.oddtimeobsessed.com/.
Stewart, Alexander. 2000. “‘Funky Drummer’: New Orleans, James Brown and the Rhythmic Transformation of American Popular Music.” Popular Music 19, no. 3: 293–318.
Stewart, Michael. 1987. “The Feel Factor: Music with Soul.” Electronic Musician, October 1987: 57–65.
Stover, Christopher. 2009. “A Theory of Flexible Rhythmic Spaces for Diasporic African Music.” PhD diss., University of Washington.
Sykes, Charles. 1992. “A Conceptual Model for Analyzing Rhythmic Structure in African-American Popular Music.” D.Mus.Ed diss., Indiana University.
Tamlyn, Garry. 1998. “The Big Beat: Origins and Development of Snare Backbeat and other Accompanimental Rhythms in Rock’n’Roll.” PhD diss., University of Liverpool.
Temperley, David. 1999. “Syncopation in Rock: A Perceptual Perspective.” Popular Music 18, no. 1: 19–40.
—————. 2007. “The Melodic-Harmonic ‘Divorce’ in Rock.” Popular Music 26, no. 2: 323–42.
Toiviainen, Petri, Geoff Luck, and Marc R. Thompson. 2010. “Embodied Meter: Hierarchical Eigenmodes in Music-Induced Movement.” Music Perception 28, no. 1: 59–70.
Toussaint, Godfried. 2013. The Geometry of Musical Rhythm: What Makes a “Good” Rhythm Good? CRC Press.
Traut, Don. 2005. “‘Simply Irresistible’: Recurring Accent Patterns as Hooks in Mainstream 1980s Music.” Popular Music 24, no. 1: 57–77.
Trucks, Amanda. 1992. “The Metric Complex in Johannes Brahms’s Klavierstücke, Op. 76.” PhD diss., University of Rochester.
Vurkaç, Mehmet. 2012. “A Cross-Cultural Grammar for Temporal Harmony in Afro-Latin Musics: Clave, Partido-Alto and Other Timelines.” Current Musicology 94: 7–35.
Washburne, Christopher. 1997. “The Clave of Jazz: A Caribbean Contribution to the Rhythmic Foundation of an African-American Music.” Black Music Research Journal 17, no. 1: 59–80.
Waters, Keith. 1996. “Blurring the Barline: Metric Displacement in the Piano Solos of Herbie Hancock.” Annual Review of Jazz Studies 8: 19–37.
Willner, Channan. 1991. “The Two-Length Bar Revisited: Handel and the Hemiola.” Göttinger Händel-Beiträge 4: 208–31.
—————. 1996. “More on Handel and the Hemiola: Overlapping Hemiolas.” Music Theory Online 2, no. 3.
—————. 2013. “Metrical Displacement and Metrically Dissonant Hemiolas.” Journal of Music Theory 57, no. 1: 87–118.
Wilson, Andrew. 2014. “Metrical Normativity in the Sarabande: A Call for Contextual Analysis.” Paper presented at Music Theory Midwest, Appleton, WI.
Witek, Maria, Eric Clarke, Mikkel Wallentin, Morten Kringelbach, and Peter Vuust. 2014. “Syncopation, Body-Movement and Pleasure in Groove Music.” PLoS (Public Library of Science) One 9, no. 4: 1–12.
Yeston, Maury. 1976. The Stratification of Musical Rhythm. Yale University Press.
Zbikowski, Lawrence. 2004. “Modelling the Groove: Conceptual Structure and Popular Music.” Journal of the Royal Musical Association 129, no. 2: 272–97.
Zeiner-Henriksen, Hans. 2010. “The ‘PoumTchak’ Pattern: Correspondences Between Rhythm, Sound, and Movement in Electronic Dance Music.” PhD diss., University of Oslo.
Transcription Sources
Ex. 3a. Transcription by the author, in consultation with Kerry Livgren, “Carry On Wayward Son” in The Best of Kansas, Guitar Recorded Versions, transcribed by Jesse Gress and Bill LaFleur (Hal Leonard, 1999).
Ex. 3b. Transcription adapted from Anthony Iommi, John Osbourne, William Ward and Terence Butler, “Paranoid” in Black Sabbath: Paranoid, Guitar Recorded Versions (Hal Leonard, 1997).
Ex. 3c. Transcription adapted from Angus Young, Malcolm Young, and Brian Johnson, “For Those About to Rock (We Salute You)” in AC/DC Anthology, Guitar Tablature Edition (AMSCO, 1992).
Ex. 3d. Transcription by the author, in consultation with Edward Van Halen, Alex Van Halen, Michael Anthony and David Lee Roth, “Jump” in Van Halen: 1984, Guitar Authorized Edition, transcribed by Brad McPhail (Cherry Hill Music, 1991).
Ex. 4a. Transcription by the author, in consultation with Stevie Wonder, “Tell Me Something Good” (Jobete Music, 1974).
Ex. 4b. Transcription by the author.
Ex. 4c. Transcription adapted from Geddy Lee, Alex Lifeson, and Neil Peart, “Free Will” in Rush: Complete, vol. 2 (Alfred Publishing, 1983).
Ex. 5a. Chord chart by the author, in consultation with John Lennon and Paul McCartney, “I Want to Hold Your Hand” in The Beatles: Complete Scores (Hal Leonard, 1993).
Ex. 5b. Chord chart by the author, in consultation with John Lennon and Paul McCartney, “I Am the Walrus” in The Beatles: Complete Scores (Hal Leonard, 1993).
Ex. 6. Transcription adapted from Wikipedia, “Drum beat.”
Ex. 7a. Transcription by the author.
Ex. 7b. Transcription adapted from Jimi Hendrix, “Foxy Lady” in The Jimi Hendrix Experience: Are You Experienced, Guitar Recorded Versions (Bella Godiva Music, 1989).
Ex. 10a. Transcription adapted from John Lennon and Paul McCartney, “Martha My Dear” in The Beatles: Complete Scores (Hal Leonard, 1993).
Ex. 10b. Transcription adapted from Ric Ocasek, “Just What I Needed” (Alfred Publishing, 1983).
Ex. 11a. Transcription by the author, in consultation with David Bowie, “Changes,” in The Songs of David Bowie (Music Sales Ltd, 1973).
Ex. 11b. Transcription by the author, in consultation with Jimmy Page, Robert Plant, John Paul Jones, and John Bonham, “Rock and Roll” in Led Zeppelin: 4th Album, Off the Record (International Music Publications, 1998).
Ex. 11c. Transcription by the author, in consultation with John Lennon and Paul McCartney, “The End” in The Beatles: Complete Scores (Hal Leonard, 1993) and Walter Everett, “The Beatles as Composers: The Genesis of Abbey Road, Side Two” in Concert Music, Rock and Jazz since 1945, ed. Elizabeth Marvin and Richard Hermann, 226 (University of Rochester Press, 1995).
Ex. 12a. Transcription by the author, in consultation with Prince, “Purple Rain” in Prince and the Revolution, Purple Rain, Off the Record (Rittor Music, 1991)
Ex. 12b. Transcription by the author, in consultation with Eric Clapton and Jim Gordon, “Layla” (Throat Music Ltd., 1971).
Ex. 14a. Transcription from Steve Howe and Jon Anderson, “Roundabout” (Topographic Music, 1972).
Ex. 14b. Transcription from Thomas Yorke, Jonathan Greenwood, Philip Selway, Colin Greenwood and Edward O’Brien, “Paranoid Android” in Radiohead: OK Computer, Guitar Tablature (Warner/Chappell, 1997)
Ex. 15a. Transcription by the author, in consultation with Geddy Lee, Alex Lifeson, and Neil Peart, “YYZ” in Rush: Complete, vol. 2 (Alfred Publishing, 1983).
Ex. 15b. Transcription from Jimmy Page, Robert Plant, and John Bonham, “Kashmir,” arr. Terry Davison (Vulcan, 2010).
Footnotes
* Thanks to Yonatan Malin and the anonymous readers for helpful comments on this article.
Return to text
1. See, for example, Eggertson 2003, 3; Graham 2008, 35; and Pressing 2002, 291.
Return to text
2. The concept of metric dissonance as analogous to pitch dissonance has been explored in Yeston 1976, Lewin 1981 and 1987, Lester 1986, Kaminsky 1989, Krebs 1987 and 1999, Cohn 1992b and 2001, Murphy 2009, Malin 2010, and other sources; many of these note the common coincidence of dissonance in both domains in compositional practice (for an argument against the view of metric space and pitch space as isomorphic, see London 2002). For analyses of metric dissonances in electronic dance music, see Butler 2001 and 2006; in funk, see Hughes 2003 and Danielsen 2006; in math-rock, see Osborn 2010; in country, see Neal 1998, and in bluegrass, see Rockwell 2009.
Return to text
3. See, for example, Clarke 1987; Brower 1993; Iyer 1998, 72–73; and Malin 2010, 45–46.
Return to text
4. See Stewart 2000 and Benadon and Gioia 2009 for discussions of the shift from swung to straight subdivisions in American popular music from the later twentieth century.
Return to text
5. The role of metric dissonance in articulating form is considered in Rothstein 1989, Frisch 1990, Horlacher 1992, Trucks 1992, Krebs 1999, Smith 2001, Ng 2005, and others. The expressive roles of rhythmic and metric dissonance in Lieder are explored in Rohr 1997; Krebs 1999, 2009, and 2011; Samarotto 2005; and Malin 2006 and 2010.
Return to text
6. See, for example, Clarke 1987, Handel 1998, Iyer 1998, and Keller and Burnham 2005. The model of rhythm and meter as separate, although interrelated, domains stands in contrast to those presented in Krebs (1999), Cohn (2001), Leong (2007) and Murphy (2009), which include different durational levels under the rubric of meter, or Hasty (1997), in which meter is a form of rhythm.
Return to text
7. Hypermetric displacement is analyzed in the music of Beethoven in Cohn 1992a and Rothstein 1989 and 1995; Herbie Hancock in Waters 1996; Josephine Lang in Krebs 2005; and Schumann in Benjamin 2011 and Krebs 2011.
Return to text
8. See De Clercq 2012, 37–38 for a discussion of potential problems in determining the bar in rock music.
Return to text
9. These categories are called Type B and Type A respectively in Krebs 1987 and Folio 1995.
Return to text
10. See Rahn (1996) for a discussion of diatonic rhythms, and Toussaint (2013, chs. 19 and 21) for a discussion of maximally even and near-maximally even rhythms in popular musics throughout the world.
Return to text
11. Osborn prefers the term ‘odd-cardinality meter’ to ‘asymmetric meter’ on the grounds that “an odd number of pulses is every bit as symmetrical as an even number—perhaps more so, as the symmetrical division of an odd number of pulses falls on a beat instead of between two beats” (2010, 43); however, the unequal groupings of beats within these meters are likely to be perceived by listeners as asymmetric.
Return to text
12. London identifies the property of maximal evenness as a required criterion for metric well-formedness, noting that it ensures that different groupings occupy the same approximate temporal range and also allows listeners to optimize their allocations of attentional energy (2012, 125–29).
Return to text
13. Sources for the transcriptions in this example and those that follow are given at the end of the article, after the Works Cited.
Return to text
14. The notation ‘5’ in the chord chart refers to a power chord with no third.
Return to text
15. Thanks to Andrew Wilson for pointing out the pattern in this example.
Return to text
16. See Everett (2001, 197–204) for a detailed discussion of this song; he refers to the elision as a phrase-level metric reinterpretation.
Return to text
17. The notation is reproduced from Wikipedia, “Drum beat” (I have added the instrument labels). The audio file is “Basic Rock Beat” from Studio Rock Drum Loops, Beats & Drum Patterns, “99 Drum Loops for Creating Songs” at http://www.cdbaby.com/cd/99rockloops/from/greatindiemusic. The spectrogram was created from this audio file using the audio-editing program Audacity.
Return to text
18. Savage 1989 observes that “contemporary drum beats reflect a wide diversity of influences in Western popular music. But what ties all these different threads together is the overriding force of the ever-present backbeat” (100; quoted in Tamlyn 1998, 15). Iyer 2002 describes the backbeat as “indigenous to the modern drum kit” (405). Baur 2012 identifies it as “one of the most common and distinctive features of post-1950s popular music.” Tamlyn estimates that an hour of rock or related music comprises three thousand snare backbeats (1998, 1). These assertions are supported by the prevalence of backbeat-based rhythms demonstrated in Mauch and Dixon 2012; see also Fleet and Winter 2014.
The pattern shown in Example 6 is often described as the “standard” or “basic” rock beat or groove: see, for example, Hoffman 1983, 170; Butterfield 2006, ¶40; Attas 2011, 46–56; Moore 2001, 42; and Moore 2012, 51–52. See Tamlyn 1998 for a historical and analytical study of the backbeat and other accompanimental rhythms in early rock and roll and other genres.
Return to text
19. Berry (1976) categorizes the directionality of rhythmic events as anticipative, initiative, reactive, and conclusive, which are similar to Hasty’s (1997) categories of anacrusis, beginning, and continuation, although Hasty has no concluding impulse. Both of these models align, albeit at a much more local level, with Caplin’s (1998) formal functions of introductory or before-the-beginning (anticipative/anacrustic), initiating or beginning, medial (reactive/continuational), and concluding.
Return to text
20. Butterfield’s main point is that microtiming variations in the placement of the backbeat snare can render it more anacrustic or more continuational. Early backbeats are perceived as more anacrustic, even though they are further away from the goal attack, because the early attack (being “on top of the beat”) creates additional forward drive and nervous energy. Late backbeats (“behind the beat”) are perceived as more relaxed and thus more continuational by comparison. See Butterfield 2006, ¶41–42. Stewart offers a “feel spectrum” of early and late microtiming deviations from the beat at a tempo of 130 bpm (Stewart 1987, 64, reproduced in Prögler 1995, 23–24). Iyer 2002 asserts that the late backbeat is the norm, which supports a continuational interpretation.
Return to text
21. Examples include Chopin’s Nocturnes op. 48 no. 1, A section, and op. 55 no. 1. Because they are two-steps, most of Joplin’s rags are in 2/4 with the bass on the beats and chords on the off-beats, but “Magnetic Rag” more closely resembles the standard backbeat in 4/4, with bass notes on beats 1 and 3 and chords on 2 and 4. The triple-meter version of this pattern is extremely common as a waltz accompaniment.
Return to text
22. See, for example, Zeiner-Henriksen 2010, Phillips-Silver et al. 2010, and Toiviainen et al. 2010 for studies on the relationship between backbeats and dance, and Witek et al. 2014 on syncopation and dance. (Although Toiviainen et al. 2010 does not describe the rhythmic features of the musical excerpt used as the basis of the study, Toiviainen was kind enough to send me the audio file, which features a prominent backbeat in 4/4.)
Return to text
23. Clave-based patterns are surveyed in Mauleón 1993 in salsa, Washburne 1997 in jazz, Brewer 1999 in rockabilly, Hernandez 2000 in Afro-Cuban music, Traut 2005 in rock music from the 1980s, Chor 2010a in African-American and Afro-Cuban musics, and Stover 2009 and Vurkaç 2012 in Afro-Latin musics.
Return to text
24. See De Clercq 2012 for a detailed consideration of various typical characteristics of formal sections in rock music.
Return to text
25. See London 2006 and also Schlueter 2005.
Return to text
26. Hemiolas in art music are discussed in Murphy 2009; Mirka 2009, chapter 4; Malin 2010, chapter 2; and Willner 1991, 1996, and 2013. Hemiolas in rock music are discussed in Mehldau 2012.
Return to text
27. A temporary shift from duple to triple groupings has been described as “reverse hemiola” by Banfield (1993, 229), Rohr (1997, 178), Malin (2010, 55), and others.
Return to text
28. See Brackett 2008 for a discussion of other rhythmic and metric dissonances in the music of Led Zeppelin.
Return to text
29. This kind of motivic displacement is the basis of numerous jazz standards, such as Gershwin’s “Fascinating Rhythm,” Horace Silver’s “Doodlin,’ ” and Thelonious Monk’s “Epistrophy.” Waters 1996 discusses it in the music of Herbie Hancock, and Downs 2000 in the music of Charlie Christian.
Return to text
30. “The End,” along with the rest of Abbey Road side two, is analyzed in more depth in Everett 1995 and also discussed in Everett 1999, 268–71.
Return to text
31. The metric instability of the verse in LVTC forms usually involves a grouping dissonance.
Return to text
32. Caplin (1998, 85) identifies grouping asymmetry as typical of loose-knit organization.
Return to text
33. See De Clercq 2012 for a more detailed discussion of typical characteristics of bridges and other rock song sections.
Return to text
34. “Roundabout” is analyzed in Sheinbaum 2013 and Bourque 2004, 15–46; see also Covach 1997 on “Close to the Edge.”
Return to text
35. See Osborn 2013 for a discussion of “terminally climactic” song structures, and Osborn 2014 for a consideration of maximally even rhythms in the music of Radiohead. “Paranoid Android” is analyzed in Adam 2011, 35–51, 35–51, and Rusch 2013.
Return to text
36. This example is discussed in Brackett 2008 and Mehldau 2012.
Return to text
37. In a similar vein, Butler observes that the complex layering of electronic dance music allows for interpretive multiplicity and “diverse experiences of time” (2006, 166).
Return to text
38. For the purposes of this study, two song pairs have been treated as single songs because they have the substantially the same content and the same metric profile: “Sgt. Pepper’s Lonely Hearts Club Band” and its reprise (both from Sgt. Pepper’s Lonely Hearts Club Band), and “Revolution” (1968 single, B-side of “Hey Jude”) and “Revolution 1” (The Beatles/The White Album).
Return to text
39. Huron and Ommen (2006) have documented a similar historical tendency, of increasing rhythmic syncopations in early American popular song.
Return to text
40. On progressive rock, see Josephson 1992 and Holm-Hudson 2013; on rhythm and meter in progressive metal, see Pieslak 2007 and McCandless 2010 and 2013.
Return to text
The pattern shown in Example 6 is often described as the “standard” or “basic” rock beat or groove: see, for example, Hoffman 1983, 170; Butterfield 2006, ¶40; Attas 2011, 46–56; Moore 2001, 42; and Moore 2012, 51–52. See Tamlyn 1998 for a historical and analytical study of the backbeat and other accompanimental rhythms in early rock and roll and other genres.
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial assistant
Number of visits:
64326