Challenging Some Misconceptions about the Règle de l’octave*
Patrice Nicolas
KEYWORDS: Jean-Philippe Rameau, François Campion, François Couperin, accompaniment, thoroughbass, basso continuo, partimento, rule of the octave, counterpoint, harmony, composition, improvisation, prelude, modulation, Baroque, music theory, pedagogy
ABSTRACT: In this paper, I use Rameau’s contradictions as a basis for my defense of the règle de l’octave. I also challenge certain misconceptions about the règle in current scholarly literature, notably its alleged harmonic incompleteness and stepwise motion requirement, while asserting some of its rarely discussed uses and properties.
DOI: 10.30535/mto.25.4.5
Copyright © 2019 Society for Music Theory
1. Rameau’s repudiation
[1.1] In the preface to his Nouveau système de musique théorique, Jean-Philippe Rameau (1726) boldly states that the great musicians of the past and present lacked sufficient theoretical knowledge in order to inform their compositions, and were instead led purely by their musical tastes and instincts. By that he meant, of course, that they were unaware of his own concept of the basse fondamentale and its regularized succession of chord roots. He encouraged any musician to defend the reputations of their masters in the public arena, proclaiming that “a dispute on such a subject could only be very instructive, and it is in the interest of all musicians to make it public” (viii).(1) One composer, Michel Pignolet de Montéclair, took Rameau up on his offer and lost the argument with him. In the midst of their quarrel that went on publicly in the Mercure de France from June 1729 to September 1731, Rameau offered the following criticism of the règle de l’octave:
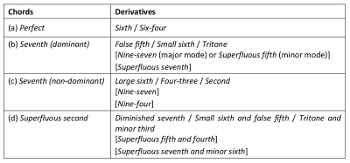
Example 1. Rameau’s (1722, 1760) nomenclature of chords
(click to enlarge)
Example 2. Chords and their figures (after Rameau 1722, 1760)
(click to enlarge)
Example 3. Règle de l’octave (Rameau 1722)
(click to enlarge and see the rest)
The primary purpose of the règle de l’octave is to accustom the fingers to the chords it prescribes on consecutive scale steps of the key. This règle contains something useful, but it is so limited that it must admit an infinite number of exceptions, which the masters reserve to teach as cases arise. [. . . ] For example, instead of the perfect chord on the first scale step, that is the tonic note, there may be those of the large sixth, of the five-four, of the four-three, of the second, or of the superfluous seventh with or without the minor 6th. Likewise, instead of the chord of the small sixth on the second scale step, there may be those of the seventh or of the nine-four, as on all the other scale steps but the seventh, called leading tone.(2) (Rameau 1730a, 253, 256–57)
As a reminder, a summary of Rameau’s chord nomenclature is provided in Example 1. The “chords by supposition” enclosed within brackets, as well as the “chords by borrowing” of section d, will be rationalized later on.(3) Example 2 represents these chords in musical notation.(4) Example 3 shows the règle de l’octave for both major and minor keys, as printed in book IV of Rameau’s Traité de l’harmonie (Rameau 1722, 382–83), and the other above-mentioned chord possibilities.(5) Rameau was to put another nail in the règle’s proverbial coffin two years later, in his Dissertation (1732), when he decried the fact that its chords are “generally only determined in a diatonic [i.e., stepwise] order” (8),(6) therefore supposedly keeping silent about how to manage leaping bass lines (ordre consonant). By the same token, he emphasized once more the règle’s limited harmonic content (8).
[1.2] This denigration, to be sure, is as unexpected as it is unfavorable, for the règle de l’octave, which Rameau had apparently learned around 1703 (1730c, 1337–38), played a central role in his seminal Traité of 1722. Indeed, as Holtmeier pointed out, “Rameau’s theory of the basse fondamentale arose from the attempt to theoretically pinpoint the Rule of the Octave. [
[1.3] Rameau, without a doubt, had a deep conviction in the power of his system to lead to the true knowledge of harmony. Towards the end of his life, he would still affirm that “this method seems to have been imagined for the blind, as it also seems that nature intended the most natural movement of the fingers on the keyboard to follow exactly the most regular order of harmony” (1760, xii).(10) So much for the règle, which paradoxically became “first a counterproposal to the basse fondamentale, and finally the epitome of a spiritless, atheoretical practice pitted against the lone scientific theory in the form of the basse fondamentale” (Holtmeier 2007, 12). Here one is tempted to agree with Montéclair when he reproaches Rameau, saying:
I do not understand how one can speak so boldly against one’s conscience. The lessons of your master who is still alive, the books of our schoolgirls that you have examined, and the conversations you have had with many of us, does all this not upbraid you with your ingratitude? Without all this, you would not know how to reason about the fundamental tone of a chord, its inversions, and its most natural progressions; you would not be able to explain the various motions of dissonances, [nor] the scale steps on which certain chords are principally suited [. . . ]. It is through all this that you know the mécanique des doigts, that you easily find your chords and all that is good in your method.(11) (Montéclair 1730, 1080–81)
2. The alleged incompleteness of the règle de l’octave
[2.1] The règle de l’octave, according to Rameau, was first unveiled publicly by François Campion, theorbist at the Académie Royale de Musique, in 1716.(12) Campion himself confirms it proudly at the very opening of his Addition, stating: “The règle de l’octave has been so well received by the public that I am grateful for having brought it to light. Indeed, there are few masters who have not adopted this sensible, abridged way of teaching accompaniment” (1730, [3]).(13) This original règle differs in form from that of Example 3 in being a simple ascending and descending scale harmonization, without the bracketed interpolated cadential gestures. Rameau’s version is not unusual, however, as other musicians are also known to have inserted such cadential progressions. To name but two, Alessandro Scarlatti’s ascending scale model exhibits the same –– motion (see Sanguinetti 2012, 119), and Jean-François Dandrieu rounds off his descending octave with a – cadence (1718, sss–zzz). Be that as it may, the règle as it appears in Campion’s Traité is the basic form most frequently found in accompaniment and composition treatises of the eighteenth-century, and we will have occasion to come back to Campion throughout this article. Let us just say for now that there is more to it than meets the eye.
[2.2] Although Rameau is not the only musician to have belittled the règle de l’octave, he is certainly the first to have done so with such vehemence and effectiveness. In fact, his criticism probably had the most profound and lasting impact, given his prestige and the quality and influence of his theoretical writings. To be sure, Rameau’s basse fondamentale was, “by the end of the 18th century, the dominant pedagogical paradigm throughout Europe,” and his writings have “furnished the basic agenda for tonal harmonic theory over the last two centuries” (Sadler and Christensen 2001). In any event, and in light of this, it is hardly surprising that the alleged incompleteness of the règle should find its way into nearly every musicological publication that concerned it. This incompleteness encompasses two main points, which we will examine in turn.
A. The stepwise motion prerequisite
[2.3] While underlining the règle’s essential role in the formation of eighteenth-century musicians, and the fact that it is invariably the object of negative critique in modern thoroughbass tutors and music history textbooks, Christensen describes it as “a handy rule-of-thumb for harmonizing most any bass progression that move[s] by step” (1992, 92). In much the same vein, Sanguinetti acknowledges that the règle “is more than an ingenious tool for accompaniment of a scale, it is a powerful means of tonal coherence” (2012, 113); but he argues that “the structural notes of the bass must move stepwise” (99), and stresses that moti del basso (i.e., a system of sequential bass motions) are a necessary complement to help “the performer of an unfigured bass decide which chord to give to a disjunct bass line, where the R[ule of the] O[ctave] has no use” (135). This supposed reliance on stepwise motion is also hinted at by Gjerdingen, who says: “If the Rule of the Octave described, by analogy to the game of chess, the simple, straightforward moves of pawns, movimenti [i.e., Sanguinetti’s moti del basso] described all the sequences of leaps and/or steps available to a Knight or Queen” (2007, 472). Even more recently, Ijzerman issued an unequivocal statement to the effect that the règle “does not address bass leaps at all” (2018, 78).
[2.4] It would be easy to multiply testimonies of this kind, but those mentioned above are sufficient to show general consensus. It should nevertheless be said that the latter three authors’ writings concern the Italian partimento tradition, and though it shares many similarities with the contemporary practice of French accompagnement, it also differs in distinct ways. A partimento, Sanguinetti says, “is a sketch, written on a single staff, whose main purpose is to be a guide for improvisation of a composition at the keyboard” (2012, 14), and for the realization of which five classes of rules need to be applied, “class II” being the regola dell’ottava (100).(14) Whereas, according to Rameau, accompagnement is “the art of successively performing a complete and perfect harmony on a given melody called basse continue” (1730b, 490),(15) also with the help of the règle. Another distinctive difference is that a lute or keyboard accompagnement usually supports a vocal-instrumental ensemble, while a keyboard partimento “does not accompany anything except itself” (Sanguinetti 2007, 51). To be sure, an accompanist may also prelude by himself, improvising the bass line and its accompanying chords as he goes along. So, perhaps Italian partimentists are really explicitly stressing the stepwise motion of the bass as a prerequisite if the règle is to be implemented, but the same could hardly be said of the French accompanists.
[2.5] Like the notes of a scale, the chords prescribed by the règle de l’octave can occur in order or in disorder and be approached or left by leap;(16) that is true even for the chords of the large sixth and of the tritone on , or that of the false fifth on (more on that in section 3). The fact that Campion presented his règle in the most logical and concise way possible, in the form of a mere ascending and descending scale harmonization, in no way entails that the bass should move exclusively by step. One would look in vain for this prescription in Campion’s Traité (1716) or in Rameau’s Traité (1722), and the latter’s version of the règle, which was to be reused by Michel Corrette (1753), does indeed exhibit disjunct motion of the bass. The alleged requirement for conjunct motion was only loosely implied by Rameau in his Dissertation (1732; see again, [1.1]), following a lengthy discussion of the merits and (mostly) demerits of Étienne-Denis Delair’s (1690) accompaniment method that had been reissued and augmented in 1724. Of particular interest is the fact that eight years after the publication of Campion’s book and two years after Rameau’s, Delair added the règle to his Nouveau traité (1724), but, as if to diminish its importance, with the remark that “the règle de l’octave is of no use when the bass proceeds by skips and the key is not established” (M).(17) It thus seems like Rameau’s criticism, even if not categorical, was modeled directly on that of Delair, seeing that it could serve his new-found agenda. Yet, the fact that he had not utilized this argument in his Traité (1722) can constitute proof of its illegitimacy, if not of its invalidity.
Example 4. Delair’s (1724) leaping bass
(click to enlarge)
[2.6] As to be expected, Delair supported his statement by presenting his readers with a well-thought-out leaping basse continue, purposely composed so as to avoid any sense of key center (Example 4a). While it is true that applying the règle at face value would, in that particular situation, give results that are musically unconvincing (supposing an initial key of C major), I consider it to be a false problem for two reasons. First, no musician of the late seventeenth and early eighteenth centuries would probably have improvised or composed such a tonally ambiguous and directionless basse continue. Second, even if one had ventured to do so, he would have known very well how to tackle it. Delair himself (1690, H–I; 1724, H–I), like many other pedagogues,(18) provides generally accepted règles pour les intervalles (i.e., rules based on characteristic bass motions regardless of the key) of which the following may serve as example: (i) when the bass rises a 4th or falls a 5th, the first note has a major 3rd and a passing minor 7th; (ii) when the bass falls a minor 3rd or rises a major 6th, the second note has a minor 3rd; (iii) when the bass rises a 5th or falls a 4th, the first note has a 5th and a passing 6th (accompanied or not by a passing 4th or augmented 4th); (iv) when the bass falls a major 3rd or rises a minor 6th, the second note has a major 3rd. Taken together, these four règles pour les intervalles allow for a good realization of Delair’s leaping bass line (Example 4b).
[2.7] Furthermore, it goes without saying that adding the règle de l’octave to one’s stock of improvisatory reflexes in no way requires the abandonment of those previously acquired, nor does it demand rejection of commonly known music theory. Both the règle de l’octave and the older règles pour les intervalles were used concurrently. As a matter of fact, these commonly known règles were also summarized by Rameau, as part of his new theory, under two principles: (i) “the perfect chord may be given to all notes proceeding by consonant intervals [of a 3rd, a 4th, a 5th, or a 6th]”; (ii) “the seventh may be added to the perfect chord of every note followed by an ascending fourth or a descending fifth[, and] [t]he sixth may also be added to the perfect chord of every note followed by an ascending fifth or a descending fourth” (1722, 393).(19) As we will see, the added 6th and 7th, also integral to Nicolas Fleury’s prototypical cadential progression of 1660, will play a crucial role in Rameau’s own cadential paradigm.
Example 5. Older scale harmonization models
(click to enlarge and see the rest)
[2.8] Though they are somewhat similar, the règles pour les intervalles are to be distinguished from the moti del basso, as they do not concern or are not limited to harmonic sequences where a model, generally composed of two bass notes, is then transposed stepwise or by any other interval. They also fundamentally tackle the problem of whole- and half-step intervals, for what proved more challenging to seventeenth-century musicians was not the chordal harmonization of leaping basses, but that of diatonic scales. This difficulty is demonstrated by the number of different harmonic formulas encountered in practice, before the general acceptance of that which, through Campion, became known as the règle de l’octave. Scale harmonization models proposed by Fleury (1660, 11, 17), the anonymous author of the Petites reigles ([1680?], 8r), and Guillaume-Gabriel Nivers (1689, 160), are provided for comparison in Example 5.(20) Christensen sums up the problem perfectly, when he says: “As elementary as [these] harmonization[s] may strike us today, it was anything but that to [
[2.9] Consequently, the règle de l’octave’s main purpose is to help the improviser-composer “modulate harmonically when the bass is given a diatonic progression” (Rameau 1722, 200),(21) hence its chords being “generally only determined in a diatonic order” (Rameau 1732, 8; see again, [1.1]). But “generally” does not mean “always,” and as a “theory of harmonic functionality” (Holtmeier 2007, 11) and “a powerful means of tonal coherence” (Sanguinetti 2012, 113), the règle de l’octave can still be applied in almost all situations where a leaping bass is involved, as long as it is tonally directed. Rameau himself certainly said this much in his Traité, before his repudiation of the règle: “knowing that certain notes should bear certain chords, according to the different progressions of these notes, we can never go wrong by giving to these notes the chords suitable for each situation. As our experience grows with practice, we become master of the choice between two different chords that may be placed on the same note” (1722, 223–24; my italics).(22) These “extraordinary” chords will be addressed more fully in sections 2.B and 3.B.
Example 6. Realization of Campion’s (1730) basse continue
(click to enlarge and see the rest)
Example 7. Chord inversions, delayed resolutions, and disjunct resolutions (Rameau 1722)
(click to enlarge and see the rest)
[2.10] Besides, how else could we explain the fact that when Campion decided to include in his Addition a basse continue for the real-life practice of accompaniment according to his règle de l’octave, he selected an excerpt from Lully’s Atys that he thought was easy enough to be “within reach of beginners” (1730, 31), which nonetheless contains many leaps and requires the knowledge of four octaves, that is, the ability to transpose the règle in four different keys? A realization is given in Example 6. Campion advises beginners to harmonize only the first and third quarter notes of the measure, except where otherwise indicated by figures or verbal instructions. These figures are few and only specify “extraordinary” chords previously introduced in his Traité’s minor key progression (1716, [plate 3]). Note in passing that Christensen, in claiming to have “realized Lully’s bass following Campion’s guidelines,” qualifies the result as “admittedly clumsy in places (particularly in the thick voicing and occasional dissonant clashes with the melody)” (1992, 94). These glitches, however, arise from his harmonizing almost every unaccented quarter note, contrary to Campion’s clear directive. He also misinterpreted the original figure 6 on as meaning a sixth chord, whereas Campion’s règle and minor key progression make clear that whenever descends to , it calls for a four-three chord. Be that as it may, I am of the opinion that no matter how the règle was displayed in accompaniment treatises, it was clear to eighteenth-century musicians how it could be used. The implicit fact that it could be put to good use doing more than simply following the diatonic scale in its clear path and straight course certainly did not need to be specified. In fact, the applicability of the règle, even in such situations where the bass skips and modulates, is the only way to make sense of Corrette’s claim, who went so far as to say that the règle is the “compass of the accompanist, who must always know in what key and on which scale degree of the key he is on, and the chord proper to it, or else he will fail” (1753, 22).(23) As additional proof, we need simply refer back to Rameau’s version of the règle de l’octave and to the following excerpts (Example 7), on which I will comment in turn, also drawn from his Traité.
[2.11] Right after having introduced Campion’s règle in book III (1722, 212), Rameau goes on to discuss chord inversion, explaining that “we may pass from one note to another when the chords they bear differ only in name [e.g. perfect on , sixth on , and six-four on
Example 8. –– cadences
(click to enlarge and see the rest)
Example 9. Campion’s cadential formulas
(click to enlarge and see the rest)
Example 10. The règle with its –– cadential formula
(click to enlarge and see the rest)
[2.12] Consequently, despite the numerous skips, the bass notes in Examples 7a–d bear, for the most part, their regular chords. Those that exceptionally do not are in accordance with another of Rameau’s principles, stipulating that both the tonic and dominant should be preceded by a seventh chord whenever the bass rises a 4th or falls a 5th (1722, 388; cf. 227–28).(29) This accounts for the 7th that is added to the perfect chord on (7a, mm. 4 and 8; 7b, m. 3; 7d, mm. 2 and 8), and the substitution of the chord of the small sixth on for that of the seventh (7a, m. 3; 7b, m. 6; 7d, mm. 2 and 7)—the rationale behind this latter case being that should bear the same harmony as does when it precedes . In any event, given disjunct cadential gestures such as those of Examples 7a–b, d (where goes to instead of , and to instead of or ), it was standard practice for accompanists to give perfect or seventh chords to and long before it was theorized by Rameau. Excerpts illustrating this point—by Jacques Boyvin (1700, 14), Monsieur de Saint-Lambert (1707, 24), and Jean-François Dandrieu (1718, ee)—are shown in Example 8. Referring back once again to Example 7b (mm. 5–6), it was also common knowledge that, in a major key, should not bear the chord of the small sixth when preceded or followed by that of the large sixth on , but that of the four-three. In other words, the 6th on should not be raised chromatically.(30)
[2.13] Now, as regards the (––)– cadence that caps off both Dandrieu’s and Rameau’s versions of the règle de l’octave (see again, [2.1] above), it cannot be emphasized too strongly that, far from being a mere addition to the règle, it actually is a part of it. In that respect, Campion’s musical plates of 1716 must not be taken at face value, as proved by the verbal instructions of his Addition: “When you have studied each octave individually, you must not fail to end it with its cadence, as this habit is very profitable. When you have descended to the last note [of the scale], you will play the 4th note of the ascending octave, then you will prepare the cadence on the 5th note of the key with a [five-four or a six-four chord]. [
Example 11. Chords of the dominant seventh and of the superfluous second
(click to enlarge)
Example 12. Campion, Apollon! C’est toi que j’implore and Enseigne-moi le beau mélange
(click to enlarge and see the rest)
Example 13. Saint-Georges ([1724?]), Leçon sur le ton de ré mode mineur
(click to enlarge)
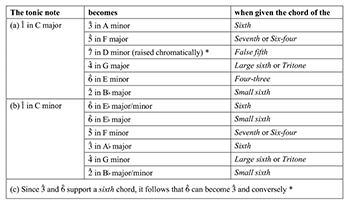
[2.14] The full understanding of Example 9b requires a little digression. Eighteen-century musicians knew that, in minor keys, the dominant could lend its fundamental to the sixth note. Thus, by substituting for , the dominant seventh chord and its derivatives (false fifth on , small sixth on , and tritone on ) become “chords by borrowing” of the superfluous second on , of the diminished seventh on , of the small sixth and false fifth on , and of the tritone and minor third on (Example 11; cf. Example 2d). This explains how Campion could give the chord of the superfluous second instead of its regular four-three chord. And since
B. Limited harmonic content
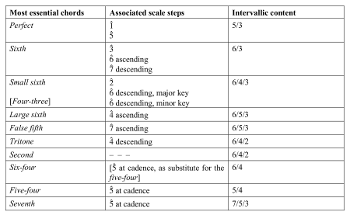
Example 14. A comparison of Rameau’s (1722) “most essential chords” with those present in his régle
(click to enlarge)
[2.15] As discussed earlier, the main point of Rameau’s criticism lies in the fact that the règle de l’octave “is so limited that it must admit an infinite number of exceptions, which the masters reserve to teach as cases arise” (Rameau 1730a, 253). But this was nothing new. Campion himself had already implied the same, though in a less negative way, when he said: “It would have been easy for me to expand this little treatise, but I am convinced that it suffices [if used] with the help of a master versed in the règle des octaves, for it is a mistake to think that one can succeed on his own with a book” (1716, 22).(35) The general idea emerging from Campion’s statement is that there is more to the règle than what he has given in his Traité—the above mentioned cadence being a case in point—and that a good teacher will know how to supplement these basics once they have been mastered by the student. That is precisely what Montéclair said, in one of his responses to Rameau: “Each teacher arranges his lessons as he sees fit, and gives explanations more or less according to the pupil’s capability” (1730, 1081).(36) Be that as it may, it is interesting to note that out of the ten chords listed by Rameau as the “most essential” ones (1722, 373),(37) only that of the second is not at play in his own version of the règle de l’octave (Example 14; cf. Example 3).
[2.16] In light of this, one can ask: Is the règle really so limited? To which one can reply that it is missing the chord of the second, as well as all of the other ones shown in Example 3c. Or is it? At this point, we should ask ourselves what would a teacher well versed in the règle de l’octave have taught an apprentice, once its most basic and preliminary form had been mastered? Again, Campion offers a glimpse of his private teaching when he stipulates, toward the end of his Traité, that “after the master will have taught the règles des octaves as it is presented here, he must teach it ascending and descending by 6th, 7th, etc., in order to make a consummate pupil” (1716, 19; my italics).(38) Earlier in his book, he had also mentioned that even though his musical examples are presented in simple (i.e., note-against-note) counterpoint, “one can ascend or descend the octaves with other figurated chords; nonetheless, one must always find the true framework therein” (1716, 9, 18; my italics).(39) Campion is very clearly telling us that the règle can take other forms, of which only the first and simplest is shown in his Traité.
Example 15. Corrette’s (1753) règle de l’octave with its “extraordinary” chords
(click to enlarge)
Example 16. Chords “by supposition”
(click to enlarge)
[2.17] So, Campion did not include an example of such a figurated règle de l’octave in his Traité, nor in his Addition. Fortunately, others like Michel Corrette did (Example 15).(40) To understand the idea behind this expanded règle, it is necessary to recall two things. First, as can be inferred from Example 14, only and support perfect chords, while , , , , and bear some kind of sixth chord. Second, according to the rules of figurated or florid counterpoint, a 7th suspension is allowed as long as it resolves naturally to the 6th that it delays. Looking at Corrette’s ascending octave (mm. 1–11), it appears that the regular prescribed chords on , , , , and (i.e., Campion’s “true framework”) now fall on the second part of the bass notes, preceded by a seventh or a nine-seven chord. All of a sudden, Campion’s words take on their full meaning (see again, [2.16]); and we also know from his writings that the nine-seven chord, though more commonly found on the ascending fourth scale step, can be given to several notes in a row (1716, 14).(41) Corrette places it on , ,and , and Rameau has it on as well. As regards the tonic and dominant, they too have their own “extraordinary” chords: supports those of the superfluous seventh (m. 1), of the sixth (m. 2), of the ninth (m. 9), of the second (m. 10), and of the nine-four (m. 11); and the chords of the six-four (m. 6) and of the sixth (m. 14). Again, a digression is needed here to briefly explain the chord of the nine-seven and other cognate “chords by supposition,” which all consist of a seventh chord with a fifth note added below. The nine-seven chord occurs when a seventh chord is played over a bass note that is a 3rd below its fundamental note; when it appears on in a minor key, it produces an augmented 5th and thus becomes the chord of the superfluous fifth (Examples 16a–b). The nine-four chord differs only in that the seventh chord is played over a bass note that is a 5th below its fundamental note; and when it occurs on the tonic note, it becomes the chord of the superfluous seventh, which should always be preceded and followed by the perfect chord on (Examples 16c–d; cf. Example 2). Note in passing that Corrette ends his expanded règle with a
Example 17. Alternative descending octave according to Gervais (1733)
(click to enlarge)
Example 18. Rameau’s (1731) standardized règle de l’octave with its “extraordinary” chords
(click to enlarge)
[2.18] In teaching the ascending octave, Campion and Corrette, like Rameau, no doubt stressed to pupils that when the bass ascends stepwise (diatoniquement), one can tell “which sixth chord should be given to the same note that bore the seventh chord, not only because of the position of this note in the key, but also because of the position of the note which follows it and the chord which this following note should bear” (1722, 399; my italics).(42) In the descending octave, however, Corrette gives a sixth chord to and , obviously disagreeing with Rameau’s opinion that “the chord which should precede the seventh chord, when the bass descends diatonically, is always the chord of the small sixth [or of the four-three]” (1722, 399; my italics).(43) Here again, it comes as no surprise to find Rameau conforming everything to his doctrine of the basse fondamentale: while the sixth and six-four chords are suitable on and , having both the tonic and dominant bear the four-three chord has the advantage of making the harmony go twice through the circle of fifths. But by the time of his Prototipes (1754, 7), Corrette seems to have changed his mind and preferred a four-three chord on (and probably on too, as implied by his verbal instructions). In any case, Campion may have told his écoliers to stay true to the “true framework,” as did Gervais: “when there is a string of seventh [chords, they should each be followed by] the sixth chord proper to the scale step we are on. The same observation must be made with regards to all the other dissonant chords; that is, the one that follows them, when the progression does not cease to be diatonic, is always the chord that is in the ordinary rule of the octave” (1733, 10).(44) This would result in something very close to Example 17. Almost a decade after the publication of his Traité, in what was to be the last of his public letters to Montéclair, Rameau (1731, 2) gave an even more uniform version of the figurated règle, in which the seventh chords of the ascending octave are invariably preceded by the chord of the large sixth (Example 18). Montéclair, deflated by the perfection of Rameau’s last demonstration, was unable to continue their public discourse. More generally, that these “extraordinary” chords were considered an integral part of the règle is confirmed also by Montéclair (1730) and Rameau (1730a), who refer to the “règle de l’octave with its exceptions.”(45)
Example 19. Couperin’s (1698?) expanded scale harmonization model
(click to enlarge and see the rest)
[2.19] Also of interest, and related to Rameau’s and Corrette’s expanded règles, is François Couperin’s Progrez des dissonances harmoniques et chromatiques ([1698?]) (Examples 19a–b). Worthy of mention is the harmonic boldness of mm. 5, 19, and 25, where the major 3rd is combined with the minor 6th, and the major 6th with the minor 2nd, as substitutes for the perfect chord on and that of the small sixth on (the A of m. 19 acting as in G minor).(46) Interestingly enough, removing all the “extraordinary” chords reveals a scale harmonization model that is almost identical to Campion’s (Example 19c): in the ascending octave, bears the chord of the false fifth instead of that of the sixth;(47) while in the descending octave, the chord of the major sixth and minor second on replaces that of the small sixth. Like “Monsieur de Maltot” who revealed the règle to Campion (1716, 7), and “Monsieur Lacroix” who taught it to Rameau (1730c, 1337–38), Couperin was part of a closed circle of initiated masters and apprentices in France at the turn of the century, who knew about the “secret” règle de l’octave long before Campion made it known to the public.
[2.20] In sum, we have seen that the alleged stepwise motion requirement is too strong a claim, and that the règle de l’octave, with its “extraordinary” chords and implicit cadential formulas, not only is not as limited as Rameau would have us believe, but also contains in its more advanced form all the other chord possibilities he was alluding to. It is no wonder, then, that Rameau should have made the règle the main subject of his first and most influential treatise, developing theoretically in the first two books of the Traité de l’harmonie “what in the central, third book he achieves by practical application in the example of the Rule of the Octave” (Holtmeier 2007, 12).
3. Rarely discussed uses and properties of the règle de l’octave
[3.1] As a complement to what was argued above, I should now like to provide a brief overview of some rarely discussed uses and properties of the règle de l’octave. On the one hand, I want to point out another generally disregarded manner of resolving the diminished 5th and augmented 4th, and, on the other hand, stress how easy the practice of modulation (in its meaning of passing from one key to another) becomes by means of the règle.
A. Resolution of the diminished fifth and augmented fourth
[3.2] It is a well-known, if unfortunate, belief that “harmony courses were designed in the nineteenth century for middle-class amateurs who wanted a course ‘about’ music, but who did not want to spend the years of apprenticeship required to become a professional musician” (Gjerdingen 2009, [1]). In this “simplified harmony” with its “theory of the tonal functions of chords” (cf. Riemann’s Vereinfachte Harmonielehre, oder die Lehre von den tonalen Funktionen der Akkorde, 1893), there occurs “a shift from a ‘ritual’ mode, with its required years of inculcation in the rites [
Example 20. Fleury’s (1660) cadential model
(click to enlarge)
[3.3] Early in the eighteenth century, “cadential classifications became based primarily on harmony rather than on melodic or contrapuntal interval” (Caplin 2004, 54). Still, the weight of tradition ensured a certain continuity that can still be felt, as we will see, in Rameau’s cadential paradigm. But first, let us look at how his predecessor, Fleury (1660, 37), conceived and taught the cadence (Example 20). Easily recognizable here are conditioned reflexes any accompanist would have developed through years of practicing the many règles pour les intervalles. Since the first bass note leaps down a 4th from to , Fleury gives it a 5th and a passing 6th, a practice Delair was still recommending in 1724. Then, falling a 5th from to , the second note is harmonized with a major 3rd and a passing minor 7th, according to tradition.
Example 21. Rameau’s (1722) cadential models
(click to enlarge)
[3.4] Rameau’s entire harmonic system lies on two main types of cadence, which he termed “perfect” (parfaite) and “irregular” (irrégulière). Both cadences end with a perfect chord on , preceded by the seventh chord on in the perfect cadence, and by that of the large sixth on in the irregular cadence—the irregular (or plagal) cadence may also begin on and end on , resulting in what is now called a half cadence. The perfect cadence is rendered “imperfect” (imparfaite) by chord inversion, that is, by giving the bass any motion from the upper parts (Example 21).(48) Now, comparing Examples 21a–b with Example 20, it is plain to see that the old passing 6th and 7th of the règles pour les intervalles became integral to Rameau’s cadential process, acquiring an important role in defining the identity of the dissonant chords involved. And, as he was to specify in his Nouveau système (1726, 61–62), in order to show their similarities, both of these dissonances are added between the perfect chord fifth and doubled root (at the 8ve), and both resolve on the following perfect chord third, the 7th downward and the 6th upward.
[3.5] It should now also appear from Example 21c that the règle is an almost continuous succession of Rameauian imperfect cadences whose intermingling of dissonant and consonant chords, Rameau had no choice but to concede, “is the essence of what is best in the règle de l’octave” (1732, 22).(49) As seen earlier in Example 7c, the règle’s property to be operative still in most cases of a leaping bass allows the chord of the false fifth on to resolve to the sixth chord on instead of the perfect chord on , thus permitting the resolution of the diminished 5th (B–F) on the 8ve (E–E) rather than on the conventional 3rd (C–E). The same is of course possible with other derivatives of the dominant seventh chord, by this capacity of the bass to move on to any constituent note of the following resolution chord (see again, [2.11]). Applying likewise to the irregular cadence, this principle is explained by Rameau as follows:
If we may descend diatonically to [the sixth chord on ] after the chord of the large sixth or of the tritone [on ], then we may therefore descend a fourth to [the perfect chord on ] or ascend diatonically to [that of the six-four on ] after the chord of the large sixth or of the tritone; for the perfect chord of the tonic note is the origin of the sixth chord of its mediant and of the six-four chord of its dominant, even though we seldom ascend to the dominant after the chord of the tritone. [. . . ] Observe that the fourth note [. . . ], when descending to the mediant [. . . ] or to the tonic note [. . . ], may bear the chord of the large sixth or the chord of the tritone, or even both of them one after another, as long as the chord of the large sixth comes first.(50) (Rameau 1722, 393, 403; my italics)
Example 22. “Extraordinary” bass motions drawn from the perfect cadence and the irregular cadence
(click to enlarge and see the rest)
The resulting “extraordinary” bass motions, as drawn from the perfect and irregular cadences, are shown in Example 22. Like the added 6th and 7th, the resolution of the augmented 4th on the 8ve, by having the bass fall a 4th from the chord of the tritone on to the perfect chord on , was standard practice before Rameau’s Traité: it is described notably by Monsieur de Saint-Lambert (1707, 51), and Campion (1716, [plate 3]) uses it to modulate to the dominant key (see also Examples 4b, mm. 3–4 and 22a, m. 3).
[3.6] The irregular cadence with its added 6th, and these “extraordinary” bass motions (whether producing unorthodox resolutions or not), are passed on silently in most French harmony textbooks.(51) Yet, it is probably safe to assume they were of invaluable aid to musicians when improvising or composing with the help of the règle de l’octave. Not only do they greatly enrich the range of harmonic possibilities, but they also provide surprise and a welcomed variety, by deviating from the normal stepwise progression. As with the règle, it would certainly be profitable to reintegrate these alternative resolutions into the classroom and from there into the modern improviser-composer’s toolkit.
B. Modulation
Example 23. Harmonic content of the règle de l’octave
(click to enlarge)
Example 24. “Of all the chords possible on the same note” (Corrette 1753, 66)
(click to enlarge)
Example 25. Modulations
(click to enlarge and see the rest)
Example 26. Reinterpretations of cadential
(click to enlarge and see the rest)
[3.7] Eighteenth century musicians understood the term modulation in two main ways. On the one hand, it was “properly the method of establishing and treating the mode” (Rousseau 1768, 298). In that sense, the règle de l’octave is the very paradigm of good modulation (see again, [2.9]). On the other hand, still according to Rousseau, it was also “the art of conducting the harmony and the air successively in several modes” (1768, 298).(52) And here again, the règle is a most effective tool for achieving easy and musically convincing modulations.
[3.8] In the basic règle, as could be inferred from Examples 3 and 14, and as is apparent from Example 23, scale steps , , , and are harmonized the same way, whether ascending or descending; whereas scale steps , , and bear two different chords according to context—as shown by the arrows, the only harmonic difference between major and minor keys is to be found on when it descends to . Since these chords are determined relative to the scale steps in the key, it follows that if one knows the chords proper to each scale step, one can also distinguish scale steps by the chords they support. This is where the power of the règle de l’octave lies, as modulation occurs when a scale step is turned into another one by supporting its proper chord relative to the new key. Although this can be achieved in many ways, Rameau tells us that “we learn to change the key primarily by means of cadences [
4. A concluding fantasia
[4.1] It is at this point, perhaps, that we can most fruitfully exercise our historical imagination. Inspired by the “Epilogue” of Sanguinetti’s magisterial book on The Art of Partimento, I should like to conclude by retracing the hypothetical generative process behind most notated, but improvisation-based, high Baroque compositions. In the above last quotation, Corrette alluded to the art of preluding, that is, “to compose and play extempore pieces, filled with all that composition has most ingenious, in design, in fugue, in imitation, [in] modulation, and [in] harmony” (Rousseau 1768, 389).(56) Indeed, court and church musicians were master improvisers, thanks to a most efficient practical training system. For though the principles of accompaniment are the quickest and surest way to mastery of harmony, Rameau cautions that “it is not simply about acquiring the practice of accompaniment[;] this practice must also lead to that of preluding” (1726, 91).(57)
Example 27. Improvised, unmeasured harmonic framework
(click to enlarge and see the rest)
[4.2] Let us thus imagine such a court musician improvising on a keyboard or lute-family instrument. Years of apprenticeship spent mastering the règle de l’octave—with its cadences, its “extraordinary” chords and bass motions, its modulatory possibilities in all the major and minor keys—allow him to easily improvise a bass line, while at the same time harmonizing it in simple counterpoint. Preluding, for him, is second nature, and every time he does it, we might even say that he is reusing old material but is adapting it or polishing it as he goes along. Within thirty minutes or so, he arrives at the following unmeasured harmonic framework, made up of three phrases, each conveniently beginning with the same musical idea (Example 27).
Phrase 1: The first clause starts off with a six-four chord on , the only “extraordinary” chord of the whole phrase. A brief modulation occurs at the beginning of the second clause, when scale steps –– are reinterpreted as –– in C minor. From the beginning of the short third clause to the beginning of the fourth, our musician bypasses the règle de l’octave in favor of the règles pour les intervalles, but he comes back to it after the – bass motion that takes the fourth clause to a conclusion in the relative major.
Phrase 2: After the return of the opening idea, the second clause has the music shift to D minor. An “extraordinary” seventh chord on leads to a –– cadence, as described by Campion, that unpredictably ends with a major chord. Since “the perfect chord may be given to all notes proceeding by consonant intervals,” the following third clause opens in the relative key (F major), but quickly moves to its dominant key (C major) by way of the interchangeability of scale steps and . Concluded by means of a half-cadence, the fourth clause brings the music back to the initial key of G minor.
Phrase 3: This third and last improvised phrase is but an extended iteration of the opening musical idea. Reinterpreting as , our musician initiates a subtle modulation to C major, followed by another to F major through the chord of the tritone. This last chord, which should naturally resolve to a sixth chord (A = in F major), instead goes to a perfect chord (A = in G minor), as in the –– cadence. By this harmonic twist, our musician has the music quickly shift to G minor; and this perfect chord on is followed by a diminished seventh chord on —a derivative “by borrowing” of the dominant seventh chord on —that, in turn, morphs into the regular chord of the small sixth on before resolving to the sixth chord on .(58)
Example 28. Refinement of the bass line
(click to enlarge and see the rest)
[4.3] Then, remembering the old saying that “a tuneful bass promises a beautiful piece of music” (Rameau 1722, 329), our court musician focuses his preluding on refining the bass line: he gives it rhythm as well as diminutions, knowing that in selecting the structural notes of his bass he is “free to choose among the sounds of a chord [those he wants]” (323).(59) Comparing the many possibilities, and guided by reflexes acquired by the practice of diminutions, he shortly arrives at this basse continue that exhibits the typical motor rhythm of high Baroque compositions (Example 28). It is now time for him to refine the melody by following the same process, for “once we know the chords each bass note should bear, we may choose any of the sounds in each chord so as to form a melody to our liking” (Rameau 1722, 303).(60) We should bear in mind, here, that once our musician has imagined his harmonic framework, he may even devise both the florid bass and melody at the same time. Indeed, according to Rameau, “it is difficult to compose successfully pieces in two and three parts unless we compose all the parts together, for each part should have a flowing and graceful melody. The skillful man hardly ever composes one part without simultaneously feeling the effect of the other parts which should accompany it” (1722, 329; my italics).(61) Be that as it may, after an hour or two our court musician’s improvisation-based composition is finished, and he may write it down if he so desires.
Example 29. C.P.E. Bach (1762, 340–[43]), Fantasia in D major with its framework
(click to enlarge and see the rest)
[4.4] Before looking at his final version, however, I should like to stress once more the hypothetical nature of the above described generative process. Nonetheless, it decidedly has a basis in the actual practice of the time. As Sanguinetti rightly pointed out, “the idea that a piece of music may grow out of gradual refinement of a handful of partimento schemata is comparable to the way in which, according to classical rhetoric, an orator should work out his speech” (2012, 344). This, of course, also applies to an improvised basse continue harmonized according to the règle de l’octave. Interestingly, C. P. E. Bach ends his Versuch (1762, 340–[43]) with an example of the reverse analytical process, by providing his readers with an improvised “free fantasia” and its framework in the form of a figured bass (Example 29). Saint-Lambert even goes so far as to claim that “it is rhetoric that resembles the music, since harmony, number, measure, and the like, which a skillful orator uses in composing his work[s], belong more naturally to music than to rhetoric,” before adding that
just as a piece of rhetoric is a whole unit that is usually made up of several parts, each of which is composed of sentences that each have a complete meaning, these sentences being composed of clauses, the phrases of words, and the words of letters, so a melody in a piece of music is a whole that is composed of several sections. Each section is composed of phrases that have a complete meaning and are the sentences of the melody. The phrases are often composed of clauses, the clauses of measures, and the measures of notes. Thus the notes correspond to letters, the measures to words, the phrases to sentences, the sections to parts, and the whole to the whole.(62) (Saint-Lambert 1702, 14)
Example 30. Fançois Couperin, Septiéme Concert “Prelude” (1724)
(click to enlarge and see the rest)
With that said, it is now time to reveal the identity of our court musician, who is none other than François Couperin, “Organiste de la Chapelle du Roy, Ordinaire de la musique de la chambre de sa Majesté, [et] Professeur-maître de composition et d’accompagnement,” as stated on the title page of his Les Goûts-réünis of 1724. Example 30 shows his finished, improvisation-based “Prélude” from the Septiéme Concert, composed according to the règle de l’octave and, occasionally, to concomitant principles inherited from the old règles pour les intervalles. Note, in the right-hand staff, the comma-like symbol that, from his Troisiéme livre de pieces de clavecin (1722), Couperin started using to mark the end of harmonic phrases. It thus seems fitting to give him the last word on the improvised nature of preludes and music as rhetorical discourse:
Although these preludes are notated [and] measured, there is nevertheless a customary esthetic that must be followed. Let me explain. A prelude is a free composition, where the imagination devotes itself to everything that comes to it. [. . . ] It is necessary that those who have recourse to these measured preludes play them in an easy way, without attaching themselves too much to the precision of the movements, unless I have marked it expressly by the word “measured.” Thus, one can hazard to say that, in many things, music (as compared to poetry) has its prose and its verses. One of the reasons I have measured these preludes was the greater facility for teaching or learning them.”(63) (Couperin 1716, 60)
Patrice Nicolas
Université de Moncton
Campus de Moncton
Pavillon Léopold-Taillon
18, avenue Antonine-Maillet
Moncton, NB
Canada E1A 3E9
patrice.nicolas@umoncton.ca
Works Cited
Primary Sources
Primary Sources
Bach, Carl Philipp Emanuel. 1762. Versuch über die wahre Art das Clavier zu spielen. Zweiter Teil. George Ludewig Winter.
—————. 1951. Essay on the True Art of Playing Keyboard Instruments. 2nd ed. Translated by William J. Mitchell. Cassel.
Bartolotti, Angelo Michele. 1669. Table pour apprendre facilement a toucher le theorbe sur la basse-continuë. Robert Ballard.
Boismortier, Joseph Bodin de. 1734. Quinque sur l’octave ou espece de dictionaire harmonique. Chez l’auteur, veuve Boivin, Le Clerc.
Boyvin, Jacques. 1700. Traité abregé de l’accompagnement pour l’orgue & pour le clavessin. Christophe Ballard.
Campion, François. 1716. Traité d’accompagnement et de composition, selon la règle des octaves de musique. Chez l’auteur, veuve G. Adam.
—————. 1730. Addition au traité d’accompagnement et de composition par la régle de l’octave. Chez l’auteur, veuve Ribou, Boivin, Le Clerc.
—————. 1734. Second recueil d’airs. Chez l’auteur, veuve Boivin, Le Clerc.
Chaumont, Lambert. 1695. Petit traité de l’accompagnement. Chez Danielis.
Clément, Charles-François. 1758. Essai sur l’accompagnement du clavecin. Christophe Ballard.
Corrette, Michel. 1753. Le Maitre de clavecin pour l’accompagnement. Chez l’auteur, Bayard, Le Clerc, Castagnere.
—————. 1754. Prototipes, contenant des leçons d’accompagnement. Chez l’auteur.
Couperin, François. [1698?]. Regles pour l’acompagnement. F-Pn, N. a. f. 4673.
—————. 1716. L’Art de toucher le clavecin. Chez l’auteur, Foucaut.
—————. 1724. Les Goûts-réünis ou Nouveaux concerts. Chez l’auteur, Boivin.
Dandrieu, Jean-François. 1718. Principes de l’acompagnement du clavecin. Chez Bayard, Vernadé, Castagneri, Corrette.
D’Anglebert, Jean-Henry. 1689. Principes de l’accompagnement. Chez l’auteur.
Delair, Étienne-Denis. 1690. Traité d’accompagnement pour le théorbe, et le clavessin. Chez l’auteur.
—————. 1724. Nouveau traité d’accompagnement pour le théorbe, et le clavessin. Chez l’auteur, Boivin.
Dubugrarre, François. 1754. Methode plus courte et plus facile que l’ancienne pour l’accompagnement du clavecin. Chez l’auteur, Le Clere, Mangean, Bayard, Castagnery.
Duphly, Jacques. 1765. [Méthode d’accompagnement]. GB-Cfm, Mu.Ms.100.
Fleury, Nicolas. 1660. Methode pour apprendre facilement a toucher le theorbe sur la basse-continuë. Robert Ballard.
Gervais, Laurent. 1733. Methode pour l’accompagnement du clavecin. Chez la veuve Boivin, Le Clerc.
Grenerin, Henry. [1680?]. Livre de theorbe contenant plusieurs pieces sur différens tons, avec une nouvelle methode très facile pour aprendre a joüer sur la partie les basses continues. Chez l’auteur, Bonneuïl.
La Porte, Claude de. 1753. Traité théorique et pratique de l’accompagnement du clavecin. Chez l’auteur, Vernadé, Bayard.
Montéclair, Michel Pignolet de. 1729. “Conférence sur la musique.” Mercure de France, June 1729, 1281–89.
—————. 1730. “Réponse du second musicien au premier musicien, sur les deux écrits qui concernent l’accompagnement du clavecin insérés dans les Mercures de février & mars de la présente année.” Mercure de France, June 1730, 1079–85.
Nivers, Guillaume-Gabriel. 1689. L’Art d’accompagner sur la basse continue, pour l’orgue et le clavecin. Chez l’auteur.
Perrine. 1679. Livre de musique pour le lut. Contenant une metode nouvelle et facile pour aprendre à toucher le lut sur les notes de la musique. N.p.
—————. 1682. Livre de musique pour le lut. [
Anonymous. [1680?]. Petites reigles generalles qui peuvent servir de methode pour l’acompagnement. [1680]. F-Psg, 2352.
Saizenay, Vaudry de. Pieces de lut et de theorbe. 1699–. F-B, 279152.
Rameau, Jean-Philippe. 1722. Traité de l’harmonie réduite à ses principes naturels. Jean-Baptiste-Christophe Ballard.
—————. 1726. Nouveau systême de musique theorique. Jean-Baptiste-Christophe Ballard.
—————. 1730a. “Observations sur la méthode d’accompagnement pour le clavecin qui est en usage, & qu’on appelle echelle ou regle de l’octave.” Mercure de France, February 1730, 253–63.
—————. 1730b. “Plan abregé d’une Méthode nouvelle d’accompagnement pour le Clavecin.” Mercure de France, March 1730, 489–501.
—————. 1730c. “Replique du premier musicien à la réponse du second, insérée dans le Mercure du mois de may dernier.” Mercure de France, June 1730, 1337–44.
—————. 1730d. “Replique du premier musicien à l’ecrit du second, inseré au Mercure de juin 1730.” Mercure de France, September 1730, 1945–50.
—————. 1731. “Lettre de M. à M. sur la musique [avec une Carte générale de la Basse fondamentale].” Mercure de France, September 1731, 2126–45 + 1–2.
—————. 1732. Dissertation sur les différentes métodes d’accompagnement pour le clavecin, ou pour l’orgue. Chez Boivin, Le Clair.
—————. 1760. Code de musique pratique. Imprimerie royale.
—————. 1971. Treatise on Harmony. Translated by Philip Gossett. Dover Publications.
Saint-Arroman, Jean, ed. 2006–12. Basse continue : France 1600–1800. 6 vols. Anne Fuzeau Classique.
Saint-Georges, Monsieur de. [1724?]. Regles pour l’acompagnement. F-Pn, Vm8 1139.
Saint-Lambert, Monsieur de. 1702. Les principes du clavecin. Christophe Ballard.
—————. 1707. Nouveau traité de l’accompagnement du clavecin, de l’orgue, et des autres instruments. Christophe Ballard.
Studies
Studies
Canguilhem, Philippe. 2015. L’Improvisation polyphonique à la Renaissance. Classiques Garnier.
Caplin, William E. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–117.
Christensen, Thomas. 1992. “The ’Règle de l’Octave’ in Thorough-Bass Theory and Practice.” Acta Musicologica 64 (2): 91–117.
—————. 2010. “Thorough bass as music theory.” In Partimento and Continuo Playing in Theory and Practice, edited by Dirk Moelants, 9–41. Leuven University Press.
Dragone, Luann R. 1992. “François Campion’s Treatise on Accompaniment: A Translation and Commentary.” Theoria 6: 135–62.
Gjerdingen, Robert O. 2007. Music in the Galant Style. Oxford University Press.
—————. 2009. “The Basics of Figures.” Traditional Skills in Classical Music. https://sites.google.com/site/partimenti/courses.
Grazzini, Stephen C. 2014. “Reconstructing the Improvised Keyboard Prelude of the French Baroque.” PhD diss., Indiana University.
Haynes, Bruce, and Geoffrey Burgess. 2016. The Pathetick Musician: Moving and Audience in the Age of Eloquence. Oxford University Press.
Holtmeier, Ludwig. 2007. “Heinichen, Rameau, and the Italian Thoroughbass Tradition: Concepts of Tonality and Chord in the Rule of the Octave.” Journal of Music Theory 51 (1): 5–49.
Ijzerman, Job. 2018. Harmony, Counterpoint, Partimento: A New Method Inspired by Old Masters. Oxford University Press.
Lester, Joel. 1994. Compositional Theory in the Eighteenth Century. Revised ed. Harvard University Press.
Sadler, Graham and Thomas Christensen. 2001. “Rameau, Jean-Philippe.” Grove Music Online. https://www-oxfordmusiconline-com.
Sanguinetti, Giorgio. 2007. “The Realization of Partimenti: An Introduction.” Journal of Music Theory 51 (1): 51–83.
—————. 2012. The Art of Partimento: History, Theory, and Practice. Oxford University Press.
Secondary Sources
Secondary Sources
Bazin, François-Emmanuel-Victor. 1857. Cours d’harmonie théorique et pratique. Léon Escudier.
Bitsch, Marcel. 1957. Précis d’harmonie tonale. A. Leduc.
Catel, Charles-Simon. 1802. Traité d’harmonie. Imprimerie du Conservatoire.
Choron, Alexandre-Étienne. 1808. Principes de composition des écoles d’Italie. Vol. 1. Auguste Le Duc.
Cohen, Henry. (1841) 1875. Traité d’harmonie pratique et facile. 2nd ed. Léon Escudier.
D’Indy, Vincent. (1902) 1912. Cours de composition musicale. A. Durand.
Dourlen, Victor. 1834. Traité d’harmonie. Prilipp.
—————. 1840. Traité d’accompagnement. Cendrier.
Dubois, Théodore. 1921. Traité d’harmonie théorique et pratique. Heugel.
Fétis, François-Joseph. (1844) 1849. Traité complet de la théorie et de la pratique de l’harmonie. 4th ed. Brandus.
Gevaert, François-Auguste. 1905–7. Traité d’harmonie théorique et pratique. H. Lemoine.
Koechlin, Charles. 1927. Traité de l’harmonie. Vol. 1. M. Eschig.
Lemoine, Henry. [1833?]. Traité d’harmonie pratique et théorique. Henry Lemoine.
Reber, Henri. 1862. Traité d’harmonie. Colombier.
Rousseau, Jean-Jacques. 1768. Dictionnaire de musique. Chez la veuve Duchesne.
—————. 1779. A Complete Dictionary of Music. Translated by William Waring. 2nd ed. Printed for J. Murray and Luke White.
Riemann, Hugo. 1893. Vereinfachte Harmonielehre, oder die Lehre von den tonalen Funktionen der Akkorde. Augener.
Footnotes
* I am grateful to the anonymous reviewers who offered both encouragement and constructive criticism, helping to sharpen and focus this article with their insightful comments.
Return to text
1. “Une dispute sur un pareil sujet ne peut être que tres-instructive, & il est de l’interest de tous les Musiciens qu’on la rende publique.” Unless otherwise noted, translations are my own. In places where I have included the citations for the English translations, my discussion nonetheless primarily draws from the original source materials.
Return to text
2. “Les premiers élemens de la regle de l’Octave consistent à donner aux doigts des habitudes conformes aux accords qu’elle prescrit sur les dégrés consécutifs d’un Mode. Cette regle renferme quelque chose de bon; mais elle est tellement bornée, qu’il faut dans la suite y faire un nombre infini d’exceptions, que les Maîtres se reservent d’enseigner, à mesure que les cas s’en présentent. [
Return to text
3. Parenthesized letters in Example 1 refer to Example 2.
Return to text
4. Throughout this article, I have adopted the simplified bass figures proposed by Rameau in his Code de musique pratique (1760, 74–78). The “+” sign always points to the leading tone, and the slash “\” means a diminished interval. All other accidentals are marked by the sharp, flat and natural symbols.
Return to text
5. Brackets are mine and indicate chords that are not part of Campion’s original règle (to be discussed shortly), which Rameau had previously introduced in book III (1722, 212).
Return to text
6. “Outre que ces Accords n’y sont généralement déterminez que dans un ordre Diatonique, attendu qu’il y a d’autres ordres sur lesquels cette Regle garde presque par tout le silence, sçavoir, le Consonant, le Chromatique, & l’Enharmonique; c’est que tous les Accords possibles dans cet ordre Diatonique n’y sont pas spécifiez.”
Return to text
7. “La Méthode nouvelle est appuyée sur la Basse fondamentale, seul & premier principe, où tout se rapporte en Musique, & d’où émanent des regles aussi certaines que simples.”
Return to text
8. “Même avec cette connoissance [de la Basse-Fondamentale], il faut avoir encore celle du Doigter, proportionnellement à l’ordre & au progrès des Accords.”
Return to text
9. “Comme la dissonance est le guide le plus assuré des successions, on commence par celle des Accords dissonans entr’eux, où il ne s’agit que de faire descendre alternativement deux doigts contigus sur les touches voisines de celles qu’ils occupent, & cela d’un Accord à un autre; de sorte que les dissonances y sont toujours préparees & sauvées dans la derniere rigueur. [
Return to text
10. “Cette méthode semble être imaginée pour les Aveugles, comme il semble aussi que la Nature ait prévû que la marche la plus naturelle aux doigts sur le Clavier suivroit exactement l’ordre le plus régulier de l’harmonie.” As a matter of fact, Rameau (1760, 7) claims to have taught the principles of accompaniment in less than six months, by means of this mécanique des doigts, to a blind keyboard player of about twenty-five.
Return to text
11. “Je ne comprens pas comment on peut parler si hardiment contre sa conscience; les leçons de votre Maître, qui vit encore, les livres de nos Ecolieres que vous avez examinés, & les conversations que vous avez euës avec plusieurs de nous, tout ne vous reproche-t’il pas votre ingratitude? Sans eux vous ne sçauriez pas raisonner du son fondamental d’un Accord, de ses renversemens & de ses successions les plus naturelles. Vous ne pourriez pas expliquer les divers mouvemens des dissonances, les degrés du mode où certains Accords conviennent principalement, [
Return to text
12. “M. Campion est le premier qui en ait favorisé le Public” (Rameau 1732, 7).
Return to text
13. “La régle de l’Octave a été si bien reçûë du Public, que je me sçai gré de l’avoir mise au jour. Effectivement, il y a peu de Maîtres qui n’ayent adopté cette maniére sensible, & abbregée d’enseigner l’accompagnement.” The text of one of his songs also goes like this: Je m’appelle Campion, Disciple d’Apollon, Philosophe joyeux et grave, Qui mit au jour la Régle de l’Octave (My name is Campion, disciple of Apollo, joyful and serious philosopher, who brought to light the règle de l’octave) (Campion 1734, 11).
Return to text
14. This regola dell’ottava, as given by Sanguinetti (2012, 115), is identical with Campion’s règle.
Return to text
15. “L’accompagnement du Clavecin est l’Art d’executer successivement une harmonie complete & parfaite sur un Chant donné qu’on appelle Basse continue.”
Return to text
16. In presenting various scale harmonizations as the “most natural means of which a keyboardist [
Return to text
17. “La regle de l’octave ne sert point lors que la basse procede par degrez disjoints, et que le ton n’est point fixé.”
Return to text
18. Cf. amongst others, Fleury (1660), Bartolotti (1669), Perrine (1679), Grenerin ([1680?]), Nivers (1689), D’Anglebert (1689), and Saint-Lambert (1707).
Return to text
19. “L’on peut donner l’Accord parfait à toutes les Nottes qui procedent par des intervales consonans ; [
Return to text
20. Example 5a combines both examples lettered O given by Fleury. For convenience of comparison with Example 3, I have transcribed the theorbo tablature in standard notation (assuming a re-entrant tuning only for the first string, as it offers the best voice-leading) and transposed it up a fifth from F major to C major. Example 5c presents only the first of three “destroit pour monter par plusieurs dégrez conjoints avec notes longues” given by Nivers. For scale harmonizations similar to that of Nivers, see Anonymous, Petite reigles ([1680?]) and Chaumont (1695). See also the other scale triads discussed by Christensen (1992, 97–99).
Return to text
21. “De la manière de Moduler harmoniquement, lorsqu’on donne à la Basse une progression diatonique”. English translation from Gossett (1971).
Return to text
22. “Sçachant que telles & telles Notes doivent porter un tel Accord, selon leur differente progression, on ne peut jamais manquer, en donnant à ces Nottes l’Accord qui leur convient en pareil cas ; & l’experience s’augmentant par la pratique, l’on devient l’arbitre du choix que l’on peut faire de deux differens Accords, qui peuvent être entendus sur une même Notte”. English translation from Gossett (1971).
Return to text
23. “C’est la Boussole de l’accompagnateur, qui doit toûjours sçavoir dans quel ton et sur quel degré du ton ou il est et l’accord qui luy convient, sans quoy il a bien-tôt fait naufrage.”
Return to text
24. “L’on peut encore passer d’une Notte à une autre, dont l’Accord ne differe que par le nom, [
Return to text
25. “Il faut remarquer que l’Accord de la Septiéme est composé de quatre Nottes differentes, qui peuvent précéder la même Notte, & que ces Nottes peuvent être arrangées consécutivement dans la Basse”. English translation from Gossett (1971).
Return to text
26. “De l’ordre qu’il faut se prescrire pour la suite des Accords qui se rencontrent dans l’étenduë de l’Octave de chaque Ton”. English translation from Gossett (1971).
Return to text
27. “Toute Notte ne prêtant son Accord parfait ou de Septiéme qu’à sa Tierce, à sa Quinte ou à sa Septiéme, les Accords de Sixte & de Sixte-quarte, qui proviennent du Parfait, doivent être précédez du même Accord qui précéde naturellement ce Parfait”. English translation from Gossett (1971).
Return to text
28. “L’Harmonie renversée de la Cadence irreguliere convient à merveille.” Section 3.A will further address the perfect and irregular cadences, and their “extraordinary” bass motions.
Return to text
29. “Si la Notte tonique doit être précédée d’un Accord de Septiéme, lorsque la Basse monte de Quarte ou descend de Quinte (ce qui est la même chose) sa Dominante doit l’être également en pareille progression.” This is, of course, in agreement with his other principle mentioned earlier in [2.7].
Return to text
30. Cf. Example 2a, mm. 12 and 18. Jean-François Dandrieu also taught this by examples (1718, q–v). Others stated it plainly, including Monsieur de Saint-Georges ([1724?], 12: “quand la sixte du ton ne descand pas directement sur le cinquieme degré pour y faire l’Accord parfait; il n’y faut pas faire la sixte majeure; mais il la faut faire mineure”), and Michel Corrette (1753, 24: “En mode majeur sur la sixieme note du ton [
Return to text
31. “Lorsque vous aurez étudié chaque octave en particulier, vous ne devez pas manquer de la terminer par sa finale. Cette habitude est très profitable. Quand vous serez descendu à la derniére note, vous ferez la quatriéme de l’octave en montant; puis vous préparerez la finale sur la cinquiéme du ton par 4te 5te & 8ve, ou par 4te 6te [
Return to text
32. “Cependant à la seconde du ton mineur en montant, j’aime beaucoup mieux la fausse quinte, au lieu de la 4te, je trouve cet accord plus sensible, quand on procede par degres conjoints.”
Return to text
33. “Les trois premiers airs de ce livre doivent servir de modèles, où pour mieux dire, de catégories a ceux qui se destinent à l’accompagnement” (Avis aux disciples de l’Accompagnement). Such songs are also to be found in Dandrieu (1718) and Dubugrarre (1754), to name but two.
Return to text
34. For similar lessons on the real-life use of the règle de l’octave, see especially Dandrieu (1718), Campion (1734), Corrette (1753; 1754), and Duphly (1765).
Return to text
35. “Il m’auroit esté facille d’amplifier ce petit Traité; mais je me persuade qu’il suffit, aidé d’un Maistre versé dans la Regle des octaves; car c’est une erreur de croire parvenir seul avec un Livre.”
Return to text
36. “Chaque Maître arrange [ses leçons] comme il lui paroît le plus convenable, & donne des explications plus ou moins selon la portée de l’Ecolier.”
Return to text
37. “Dénombrement des Accords les plus necessaires.”
Return to text
38. “Aprés que le Maistre aura enseigné la regle des octaves, comme elle est icy marquée, il doit l’enseigner à monter & à descendre par 6tes, par 7mes, &c. afin de consommer l’Ecolier.” Note that in Campion’s French l’enseigner, the contracted article la refers to the previously mentioned règle and not to the “pupil,” as in Dragone’s English translation (1992, 160).
Return to text
39. “L’exposition de ces deux planches sont de contre-point simple; car on peut monter ou descendre les octaves par d’autres accords figurez [
Return to text
40. Corrette (1753, 31) labeled this example L’Octave avec les accords extraordinaires. Ossia alternatives are taken from Rameau (1722, 276, 396; 1731, 1). Corrette does not furnish us with an example in a minor key, but it is easy enough to transpose the above by following guidelines and similar examples from Rameau’s Traité. A particularly interesting version of the “Règle de l’octave in all the major and minor keys with several other chords” (Regle de l’Octave dans tous les tons Majeurs et Mineurs avec plusieurs autres accords) is given by La Porte (1753). Finally, I should like to add that these versions of the règle (and much more) will be offered in my forthcoming book on the French principes d’accompagnement.
Return to text
41. “L’endroit où l’on place ordinairement la 9e & la 7e, est à la 4e du ton en montant, elle se place aussi sur plusieurs nottes de suite.”
Return to text
42. “Vous connoissez ici l’Accord de Sixte, que vous devez donner à la même Notte qui a porté celui de la Septiéme, non seulement par le rang que cette Notte tient dans le Ton, mais encore par le rang qu’y tient celle qui la suit, & par l’Accord que doit porter cette Notte suivante”. English translation from Gossett (1971).
Return to text
43. “[L]’Accord qui doit précéder celui de la Septiéme en descendant diatoniquement, est toüjours celui de la petite sixte”. English translation from Gossett (1971).
Return to text
44. “Et quand il se rencontre une suite de plusieurs Septiémes, on doit faire l’Accord de Sixte qui convient au degré où on est. La même observation doit se faire pour tous les autres Accords dissonans; c’est-à-dire, que celuy qui les suit, lorsque la progression ne cesse point d’être Diatonique, est toûjours l’Accord qui se trouve dans la Regle ordinaire de l’Octave”.
Return to text
45. “La regle d’Octave & ses exceptions” (Montéclair 1730, 1080), and “La Regle de l’Octave, avec ses exceptions” (Rameau 1730a, 254). For a fascinating example of the règle with its “exceptions,” see Joseph Bodin de Boismortier’s Quinque sur l’octave ou espece de dictionaire harmonique (1734).
Return to text
46. Rameau (1730a, 254) did not approve of the chord of “the minor 6th with the major 3rd, which some have introduced rather amiss” (“la 6e mineure avec la 3e majeure, que quelques-uns ont introduit assez mal à propos”).
Return to text
47. Corrette (1753, 46) condemns the chord of the false fifth on (in minor) instead of that of the sixth, but approves the chord of the large sixth (in major) when the bass goes from to to . Rameau (1722, 95) does not see any inconvenience in it.
Return to text
48. All cadences are in C major with minor-key accidentals displayed in parentheses. Blackened notes indicate alternative bass motions, and their figures (if any) appear parenthesized above the staff.
Return to text
49. “C’est le fond de ce qu’il y a de meilleur dans la Régle de l’Octave.”
Return to text
50. “Si l’on peut descendre diatoniquement sur la Mediante après un Accord de grande Sixte ou de Triton, donc on peut descendre aussi de Quarte sur la Notte tonique, ou monter diatoniquement sur la Dominante, portant l’Accord de Sixte-quarte après les Accords de grande Sixte ou de Triton, puisque l’Accord parfait de la Notte tonique compose celui de la Sixte de sa Mediante, & celui de la Sixte-quarte de sa Dominante, bien que l’on monte rarement sur la Dominante après l’Accord du Triton. [
Return to text
51. Choron’s Principes de composition des écoles d’Italie (1808) is a notable exception, approving most of these resolutions. But as implied by its title, it is not a harmony textbook per se, but a partimento treatise. In his Traité complet de la théorie et de la pratique de l’harmonie (1849), Fétis remarks that alternative resolutions of the chord of the tritone, where descends to or ascends to , though they are found in many reputable works by famous composers, are nonetheless vitiated. As regards the plagal cadence, Koechlin (1927) stands out by listing the chord of the large sixth as one of many possibilities. Catel (1802), Reber (1862), Lemoine ([1833?]), Dubois (1921), and Bitsch (1957) give the option of approaching the final perfect chord either by a perfect or a sixth chord (or both, one after the other), but not that of the large sixth. D’Indy (1912) gives examples of the passing 6th, as in the old règles pour les intervalles, while Choron (1808), Dourlen (1834), Cohen (1875), Bazin (1857), and Gevaert (1905–7) limit the whole process to a succession of perfect chords. In this sample of authors, Choron (1808) is the only one that groups under the term “plagal” both forms of Rameau’s irregular cadence.
Return to text
52. “C’est proprement la manière d’établir & traiter le Mode ; mais ce mot se prend plus communément aujourd’hui pour l’art de conduire l’Harmonie & le Chant successivement dans plusieurs Modes”. English translation from Waring (1779).
Return to text
53. “C’est d’abord par le moyen des Cadences que l’on apprend à changer de Ton ; [
Return to text
54. “De tous les accords que l’on peut faire sur la même note.” Parenthesized letters in Example 24 refer to Example 25 and asterisks indicate complementary information drawn from Rameau (1722, 251–54). Blackened “x” indicate alternative bass motions, and their figures (if any) appear parenthesized above the staff. The “chords by borrowing” of the superfluous second and its derivatives are, of course, possible substitutes.
Return to text
55. “Donnera une grande facilité en Préludant de passer d’un ton à un autre sans que l’oreille s’en apperçoive.”
Return to text
56. “PRÉLUDER. [
Return to text
57. “Le plus court & le plus seur moyen de se render promptement sensible à l’Harmonie, consiste dans l’Accompagnement [
Return to text
58. The perfect and seventh chords of the –^5– cadence are also practicable in all their inversions. This explains notably why , when descending to or , may bear the chords of the large sixth and of the tritone, one after another, “as long as the chord of the large sixth comes first” (see again, [3.5] and Example 22b). See Rameau 1722, 227‒28, 392.
Return to text
59. “Une Basse bien chantante, nous annonce une belle Musique”; “La liberté que l’on a de choisir parmi les Sons d’un Accord, ceux que l’on veut, pour en former une Basse”. English translation from Gossett (1971).
Return to text
60. “Lorsque l’on sçait les Accords que chaque Notte d’une Basse doit porter, l’on peut choisir dans chaque Accord l’un des Sons dont il est composé, pour en former un Chant à son gré”. English translation from Gossett (1971).
Return to text
61. “Il est difficile de réüssir parfaitement dans les Pièces à deux & à trois Parties, si l’on ne compose toutes les parties ensemble ; parce que chaque partie doit avoir un Chant coulant & gratieux ; & l’habile homme ne compose guéres une partie, qu’il ne sente en même temps l’effet des autres parties qui doivent l’accompagner”. English translation from Gossett (1971).
Return to text
62. “C’est la Piéce d’Eloquence qui ressemble à la Piéce de Musique : car l’harmonie, le nombre, la mesure, & les autres choses semblables qu’un habile Orateur observe en la composition de ses Ouvrages, appartiennent bien plus naturellement à la Musique qu’à la Rhétorique. Quoi qu’il en soit, tout ainsi qu’une Piéce d’Eloquence a son tout, qui est le plus souvent composé de plusieurs parties ; Que chaque partie est composée de périodes, qui ont chacune un sens complet ; Que ses périodes sont composées de membres, les membres de mots, & les mots de lettres ; De même le chant d’une Piéce de Musique a son tout, qui est toûjours composé de plusieurs reprises. Chaque reprise est composée de cadences, qui ont chacune leur sens complet, & qui sont les périodes du chant. Les cadences sont souvent composées de membres ; les membres de mesures, & les mesures de notes. Ainsi, les notes répondent aux lettres, les mesures aux mots, les cadences aux périodes, les reprises aux parties, & le tout au tout.” English translation from Rebecca Harris-Warrick, Principles of the Harpsichord by Monsieur de Saint Lambert (Cambridge: Cambridge University Press, 1984), quoted in Haynes and Burgess (2016). On spontaneous creation, poetic and musical, see Canguilhem (2015), esp. pp. 19–29.
Return to text
63. “Quoy que ces Preludes soient ècrits mesurés, il y à cependant un goût d’usage qu’il faut suivre. Je m’explique. Prelude, est une composition libre, ou l’imagination se livre à tout ce qui se prèsente à elle. [
Return to text
Copyright Statement
Copyright © 2019 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sam Reenan, Editorial Assistant
Number of visits:
16304