Cadential Melodies: Form-Functional Taxonomy and the Role of the Upper Voice

0. Introduction

[0.1] Cadences—how they are understood, are categorized, and function—have been central in the emergence of the “new Formenlehre” (Marston 2001) over the past two decades. Much of the discussion either revolves around, or builds on, William Caplin’s (1998) theory of formal functions, a theory whose “outstanding achievement” is the definition of formal functions in intrinsic terms, and whose taxonomy, in part, is characterized by the presence (or absence) of various cadences.⁽¹⁾ Caplin himself describes cadences as events that bring about closure by “essentially represent[ing] the structural end of broader harmonic, melodic, and phrase-structural processes” (1998, 43); while this is certainly not the only possible definition of a cadence, this is the one we will adopt for the purposes of this paper.⁽²⁾ In practice, however, form-functional theory and analysis typically accentuates only harmonic and phrase-structural elements, rarely giving the same weight to melodic considerations.⁽³⁾ This selective focus is something for which Caplin advocates in his early treatise, where he argues that local harmonic progression should be “the most important factor in expressing formal functions” (1998, 5). Steven Vande Moortele refers to this focus on harmony as a “self-imposed methodological restriction,” observing that melodic considerations are often “conspicuously absent from [form-functional theory]” (2013, 407).⁽⁴⁾

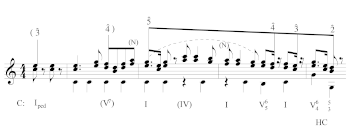
[0.2] Consider, for instance, Caplin’s analysis of the opening of the second movement of W.A. Mozart’s Eine kleine Nachtmusik, shown in Example 1. Caplin describes the phrase as an antecedent consisting of a two-measure basic idea (BI) followed by a two-measure contrasting idea (CI) that closes with a half cadence in m. 4. Harmonically, there is minimal movement: the first three measures feature a tonic pedal, with a six-four motion above the pedal in m. 2 and a neighbouring V in m. 3. There is no predominant, and the opening tonic prolongation moves straight to the cadential dominant in m. 4. Caplin’s analysis highlights both the taxonomic nature of form-functional theory and its predisposition towards harmony and grouping structure, but it is unclear how (or even if) melody figures into these considerations.

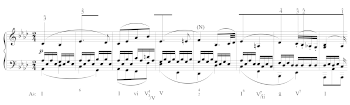
[0.3] The opening measures of Ludwig van Beethoven’s Piano Concerto No. 1, Op. 15, shown in Example 2, produces a structure similar to the opening of the second movement of Eine kleine Nachtmusik when analyzed under the same parameters. This four-measure unit can also be described as a two-measure BI followed by a two-measure CI. The phrase’s harmonic structure similarly consists of an initial tonic prolonged via a neighboring dominant, which then concludes on the dominant with no intervening predominant. In other words, an analysis relying on grouping structure and harmonic progression (or even surface rhythm or hypermeter) is unlikely to find much by way of difference in the construction of these two four-measure phrases.⁽⁵⁾

[0.4] There is, however, a crucial difference between the two phrases: Example 1 is an antecedent, while the first four measures of Example 2 are a compound basic idea (CBI). This differentiation arises owing to questions of cadential closure. In Example 1, the concluding dominant is determined to support a half cadence, while it is unlikely that a similar rhetorical pause would be assigned to the dominant in m. 4 of Example 2. Indeed, having used both examples in pedagogical contexts, the lack of a cadence in the Beethoven concerto is often a point of confusion: the grouping structure, the harmonic progression, and the repose generated by the subsequent silence frequently prompt students to interpret this moment as a half cadence (which consequently complicates analyzing the rest of this theme). Consideration of what follows immediately after Example 2’s m. 4 does not alleviate these challenges: mm. 5–8 are a repetition of mm. 1–4 but ending with a V–I motion, which in conjunction with the pause on V in m. 4 gives the impression of an antecedent-consequent relationship within the first eight measures.⁽⁶⁾ It requires an even further step back to determine that, at the sixteen-measure level, the theme resembles a compound sentence, and it is typically this criteria that is used to rationalize why no cadence coalesces in m. 4.⁽⁷⁾ In other words, distinguishing why there is no cadence (especially when put into relief against a comparable passage such as Example 1) relies on navigating multiple levels of conflicting intrinsic and contextual information: based on the antecedent characteristics at the four-measure level there should be a cadence in m. 4; based on the periodic characteristics at the eight-measure level we might equally say that there must be cadences in m. 4 and m. 8; but these two levels conflict with the sixteen-measure level, whose sentential features suggest there must not be cadences at these points.

[0.5] The underlying issue is that accentuating only harmonic and phrase-structural features does not, in this case, permit a clear explanation as to why a cadence does not coalesce in a place where both of these parameters seem to indicate one could reasonably be said to exist. While seasoned analysts might point out the role of surrounding contexts and the effects of retrospective reinterpretation,⁽⁸⁾ the question we would like to raise, at this juncture, is whether there are other intrinsic parameters at play that might help explain, or at least reinforce, why there is a cadence in one passage, but not the other. Notably, nothing has hitherto been said about the melodic dimension of these passages, and as we previously noted, it is an element that is rarely given the same systematic consideration as harmony and grouping structure in form-functional theory and analysis. Caplin does acknowledge that presentation phrases typically “project an ‘opening up’ of melodic space through ascending gestures” (2013, 38), and likewise describes that “the general melodic contour of a cadence is descending” (2013, 56); however these observations, and implications derived from them, rarely feature prominently in either his analyses or theoretic models.⁽⁹⁾ Thus, while Vande Moortele’s claim of melody being “conspicuously absent” from Caplin’s approaches may perhaps be overstated, melody is certainly not accorded the same level of importance as harmony and grouping structure. When questions of melodic function are considered, most often it is as a means of differentiating between Perfect and Imperfect Authentic Cadences.⁽¹⁰⁾

[0.6] What this article proposes is that the disposition of the melodic line—specifically a more middleground-level structural melody—is as integral to cadential articulation as the harmonic progressions that support it.⁽¹¹⁾ Thus, our aim is to neither diminish nor exclude the roles of harmony or phrase structure, but rather to highlight their symbiotic relationship with structural melody, and to demonstrate how considerations of the structural melodic line contribute an additional level of nuance into Caplin’s more harmonically driven approach to formal analysis. Drawing on discussions by theorists whose work has influenced the new Formenlehre tradition, such as Heinrich Schenker, Adolf Bernhard Marx, and Arnold Schoenberg, the first section of the paper proposes a distinction between structural melodic lines and the melodic surface.⁽¹²⁾ Specifically, we engage with Marx’s observations that melodies can be viewed in the abstract to project a more directed ascent or descent, despite the various changes in direction that occur on the musical surface, and integrate Marx’s perspective with Schenker’s more interpretive Urlinie in order to provide a means of discussing melody in a more structural way. In the second section, we then extrapolate several melodic processes that can be interpreted more taxonomically through form-functional terminology: ascending and static lines are often associated with initiating or medial functions, while descending lines, especially to $\hat{1}$ (or an interrupted $\hat{2}$ in the case of half cadences), are almost always associated with concluding, and thus cadential, functions.⁽¹³⁾ The third and fourth sections then apply these melodic considerations to formal functions, and discuss instances where harmonic and phrase-structural considerations alone are insufficient in understanding closure. Ultimately, we advocate that a renewed focus on melodic considerations allows for further levels of nuance in interpreting cadences, and that such a focus will provide another parameter to consider in discussing more idiosyncratic cases of formal ambiguity.

1. The Fundamental Line – Concepts and Precedents

[1.1] In many ways, melody is more difficult to discuss in the abstract than harmony; Classical-style harmonic progressions, especially those that lead to a cadence, are typically limited to a small number of specific patterns that can be quickly abstracted via the T–PD–D(–T) model. Melody, however, is far more open-ended, with the possibilities for successions of notes being virtually limitless and restricted by fewer constraints than harmonic successions. One well-recognized means of abstracting melody comes in the form of the Schenkerian Urlinie, or fundamental line. As Schenker describes it, the fundamental line is “a melodic succession of definite steps of a second [which] signifies motion, striving toward a goal, and ultimately the completion of this course” ([1935] 1979, 4–5).⁽¹⁴⁾ Elaborating further, he suggests that “this is the fundamental, determinate melodic succession, the primal design of melodic content.” Schenker’s treatment of the Urlinie, however, is most often applied to deep levels of structure, and as such is often highly abstracted from the successions of pitches as they are heard on the melodic surface, or even at a more middleground level.⁽¹⁵⁾ But rather than using the concept of a fundamental line as a procrustean bed for deep-level musical structure, we propose to adapt the model as means of describing the overarching melodic proclivities at the level of the phrase.⁽¹⁶⁾

[1.2] In Der freie Satz ([1935] 1979, 13), Schenker’s rationale for the Urlinie is described as follows:

To [humankind] is given the experience of ending, the cessation of all tensions and efforts. In this sense, we feel by nature that the fundamental line must lead downward until it reaches $\hat{1}$, and that the bass must fall back to the fundamental. With $\hat{1}$/I all tensions in a musical work cease.

In short, what Schenker is noting on a technical level is a tendency in eighteenth- and early nineteenth-century European tonal music for the melodic line to gravitate in a descending direction toward the tonic pitch at the conclusion of a musical unit, which creates, as Schenker describes, a feeling of conclusion and release of tension.

[1.3] A. B. Marx ([1868] 1997, 38) describes melody in a similar manner:

One can easily observe that ascending successions awaken the feeling of intensification, elevation, and tension, while falling successions awaken the contrasting feelings of slackening, depression and the return to rest.

Marx thus ascribes different sensations to melodies that ascend—which he describes as a process of “elevation from repose, and intensification. . .up to a natural high point”—from those that descend, which by contrast lead “to the tone of true repose [the tonic]” ([1868] 1997, 43). Marx’s description here is useful in providing further context to Schenker’s claims: since an increase in tension cannot, by definition, create a sense of repose, this in turn implies that the articulation of a cadence—defined in Caplinian terms as a concluding function and a point wherein the processes of a musical unit come to a cessation and conclusion—typically achieves a state of repose and conclusion through a melodic descent.

[1.4] Both Schenker and Marx also describe how structural linear-melodic motion is often obscured on the musical surface. “A sequence of tones,” Schenker ([1935] 1979, 13) writes, “cannot live in the foreground unless the total tension of the fundamental linear progression provides it with breath; no life can be breathed into it from the foreground. How preposterous therefore to try to fashion an organic, living work by assembling various tone series without background!” To interpres his metaphorical prose, Schenker is noting that despite the almost infinite number of possibilities by which a melody might occur at the musical surface, it is possible to trace a more abstract, or structural, underlying motion in tonal melodies. Again, Marx’s prose presents a perspective similar to Schenker’s, but presented in more conventional terms. Marx describes melodic successions that switch between an ascent and descent on the surface as “roving” progressions; they “hold fast to neither side but partake of both. And yet no matter how their individual tones may roam, they can belong in the main to one of the two primary directions” ([1868] 1997, 38). For instance, despite all of the surface-level melodic figuration in Example 3, a more structural melody—that begins on $\hat{3}$ (B), remains static on that pitch (via a neighbouring $\hat{4}$ (C) in mm. 3–5), before descending from $\hat{3}$ through $\hat{2}$, to $\hat{1}$ at the point of cadential articulation in m. 8—can also be traced.

[1.5] Applying a similar perspective to the melody in Examples 1 and 2 shows that it is in the melodic domain, rather than the harmonic or phrase-structural ones, that we find the primary differences between these units. As shown in Example 4, the melody in the second movement of Eine kleine Nachtmusik begins on E ($\hat{3}$) and passes up through F ($\hat{4}$) to land on $\hat{5}$ on the first beat of m. 2. This $\hat{5}$ is then prolonged via a neighboring $\hat{6}$ before the melodic line begins a descent from $\hat{5}$ in m. 3 down to $\hat{2}$ in m. 4, where the line stops in conjunction with the half cadence (the entire structure is then repeated in the consequent phrase, but this time leads instead to $\hat{1}$).⁽¹⁷⁾ Conversely, despite the ascending and descending surface-level scalar motion in the first eight measures of Beethoven’s First Piano Concerto in Example 2, the underlying melodic motion, as shown in Example 5, is as an ascent: from $\hat{1}$ to $\hat{2}$ in mm. 1–4, and from $\hat{2}$ to $\hat{3}$ in mm. 4–8. This $\hat{3}$ is supported by a prolongation of tonic harmony through the next four measures before stepping back down through $\hat{1}$ (itself prolonged first by an upper and lower neighbor (E and C♯), as well as by a surface-level unfolding down to $\hat{7}$) to return to $\hat{1}$ at the end of the phrase in m. 16. In other words, the melodic lines of the two phrases diverge significantly: Example 1 contains an ascent to $\hat{5}$ followed by a descent to $\hat{2}$, while Example 2 contains only an ascent (this characterization likewise holds for the subsequent four-measure units in each case).

2. Melodic Direction and Formal Functions

[2.1] While musing on Schenker’s writings, Caplin offers a brief statement on the interrelationships between various melodic directions and formal functions:

In this respect, Schenker’s own writings on the matter are interesting, but somewhat inconclusive. At one time, he refers to the final $\hat{2}$–$\hat{1}$ (supported by V–I) component of the Ursatz as a “cadential formula,” thus suggesting that the preceding $\hat{3}$ ($\hat{5}$ or $\hat{8}$) represents material of an initiating (as well as possibly medial) formal function. (2004, 64)⁽¹⁸⁾

In effect, Caplin is translating Schenkerian terminology into his form-functional language, a process that can be refined and taxonomized even further. There are, of course, many ways in which even a middleground melody could unfold prior to a cadence. For instance, Example 3 above sees $\hat{3}$ as its initiating element, while a prolongation of $\hat{3}$ via the neighboring $\hat{4}$ serves a medial role prior to the onset of the descent through $\hat{2}$ to $\hat{1}$ which serves as a concluding gesture. Alternately, $\hat{3}$ or $\hat{5}$ might serve as the initiating function, resulting in the medial function having a more protracted descent to the concluding $\hat{1}$. This is precisely the case in the minuet from Joseph Haydn’s Symphony No. 104, which Janet Schmalfeldt (1991, 240–242) analyzes: as shown in Example 6 with stems reproducing Schmalfeldt’s analysis, $\hat{5}$ is prolonged throughout the presentation, while the descent to $\hat{4}$ occurs in conjunction with the onset of the continuation.

[2.2] If, however, $\hat{3}$ or $\hat{5}$ were serving as medial functions—as in Examples 4 and 5—this presupposes that some sort of melodic event precedes them. One such possibility is an initial ascent from $\hat{1}$ to $\hat{3}$ or $\hat{1}$ to $\hat{5}$, which could be achieved either through a stepwise ascent, or an arpeggiation. Schmalfeldt (1991, 254) demonstrates such an ascent in her analysis of Haydn’s Keyboard Sonata in G Major, Hob. XVI: 27, shown in Example 7. According to Schmalfeldt, the ascent occurs over the course of the presentation phrase, with the progression from G up to B serving as the melodic initiating function. The continuation then prolongs $\hat{3}$, before concluding with a descent to $\hat{2}$ to create the half cadence in m. 8.⁽¹⁹⁾

[2.3] To Schmalfeldt’s examples we might add the opening of the third movement of Beethoven’s Piano Sonata Op. 31, no. 2 (“Tempest”), shown in Example 8. While there is nothing particularly controversial about cadences in this example, it provides an excellent comparative opportunity to consider the relationships between melody and formal functions. In m. 8 there is a move from the dominant (that had harmonized the repetition of the basic idea) to the tonic that does not sound particularly cadential. A similar resolution from V to I occurs in m. 15, this time sounding far more conclusive. If we consider the melodic character, first of the presentation, then of the entire theme, it becomes apparent that there is an intrinsic reason for the distinction between the two similar events. As in the Haydn sonata above, mm. 1–8 contain an ascending melodic line, from $\hat{1}$ over the initial basic idea (mm. 1–4), through $\hat{2}$ over its repetition (mm. 5–8), to $\hat{3}$ at the outset of the continuation in m. 8. $\hat{3}$ is then prolonged via a neighboring motion, before stepping down though (the implied) $\hat{2}$, to conclude on $\hat{1}$ at the point of cadential articulation in m. 15. For us, the difference in melodic content provides a means of articulating structural differences between these two V–I motions:⁽²⁰⁾ in m. 8 the melodic tension is still in the process of increasing, as the initiating function of the melody has just reached its apex. Following a medial prolongation of this apex, the melody then descends, leading to its concluding $\hat{2}$–$\hat{1}$ motion over the V–I harmony as the tension dissipates.⁽²¹⁾

[2.4] Caplin (2004, 82) further clarifies that

most cadential melodies of the classical style remain conventional (if not formulaic) by projecting a consistent descending stepwise motion within a series of uniform durational values. On the contrary, the characteristic melodies of opening gestures tend to feature a diversity of intervallic content (combinations of leaps, steps, and directional changes) and a variety of durational patterning.

One might therefore generalize that the directional proclivity of a melodic line associates it with certain formal functions. Ascending melodic lines (e.g., in Examples 1, 2, 7, and 8) are generally more characteristic of initiating functions, while static ones (e.g., in Examples 3 and 6) are equally characteristic of both initiating and medial functions.⁽²²⁾ Ascending and static lines, however, rarely correlate to concluding functions, whose first-level default (used conceptually after Hepokoski and Darcy 2006) is characterized by a descending melodic line (see Caplin 2013, 56–57, especially Example 2.22). Schoenberg discusses cadential melodic contours in just such terms, describing how “in order to exercise the function of a cadence, the melody must assume certain characteristics, producing a special cadence contour, which usually contrasts with what precedes it” (1967, 29–30, italics original).⁽²³⁾ He goes on to describe how the melody will often recede from a climax, a “decline in contour, [which] combined with concentration of the harmony and liquidation of motivic obligations, can be depended on to provide effective delimitation of the structure.”⁽²⁴⁾

[2.5] How might the above taxonomy of melodic structure and formal functions inform analysis? As noted previously, the first four measures in Example 1 and Example 2 share similar underlying harmonic and phrase-structural content; using only these parameters, it becomes difficult to articulate why the two four-measure units have differing classifications based on intrinsic features alone. Applying criteria from a structural-melodic parameter offers a means of distinguishing between these two phrases. As shown in Example 4, the melodic structure in the second movement of Eine Kleine Nachtmusik begins with an ascent characteristic of initiating function (from $\hat{3}$ to $\hat{5}$), which is then followed by a medial function where $\hat{5}$ is prolonged, and finally a concluding descent to $\hat{2}$. By contrast, the melody in the first four measures of the Beethoven concerto consists only of a melodic initiating function, as the melody ascends from $\hat{1}$ to $\hat{2}$ (and then $\hat{2}$ to $\hat{3}$ in mm. 5–8), a behavior that would be highly atypical of the concluding function associated with cadential articulation.⁽²⁵⁾

[2.6] In sum, while the melodic content of the four-measure unit in Example 1 cycles through a complete beginning-middle-end paradigm, the melodic structure of the first four measures in Example 2 consists only of an initiating function in the form of a melodic ascent. Regardless of whether we couch this melodic ascent in form-functional terms or filter it through the metaphorical language of Schenker (or even Marx), if a cadence is by definition a function of repose that effects closure of harmonic, melodic, and phrase-structural processes, then the melodic activity in the initial four measures of Example 2 does not correspond with that definition.⁽²⁶⁾ It is not until m. 16 that the melodic processes of the theme come to a conclusion, when the melody undergoes a descent from $\hat{3}$, through $\hat{2}$, to $\hat{1}$, while the harmonies that support this descent present a conventional cadential progression of ii⁶–V⁷–I.

[2.7] This is not to say that melodic content alone definitively confirms or refutes cadential articulation; rather, various elements work symbiotically to contribute to the sense of closure we associate with cadences. Again, our aim is not to minimalize or exclude the role of harmony, phrase structure, context, or any other parameter, but rather to highlight how they can be complemented by structural melody. A perfectly smooth melodic descent to $\hat{1}$ or $\hat{2}$ will not generate a cadence if the harmonic progression does not support it; conversely, harmonic progressions that might appear cadential can be overridden by melodic configurations that project non-concluding functions.⁽²⁷⁾ Simply put, melody is another parameter through which we can systematically engage, refine, and in some cases, enhance our understanding of what processes contribute to musical-syntactic closure. Such considerations also give an additional intrinsic functional explanation to specific cases where Caplinian theory currently resorts to contextual relationships, despite—as we cited at the beginning of the article—its outstanding achievement being the articulation of intrinsic functionality. The following section explores applications of this theory to cases in the Classical repertoire with further issues of cadential ambiguity.

3. Ambiguous Cases in the Classical Repertoire

[3.1] In many cases, especially in the Classical repertoire, melodic and harmonic factors align neatly, and it is not necessary to engage in a detailed study of both in order to demonstrate that a phrase concludes (or does not conclude) with a cadence. Poundie Burstein (2014 and 2015), however, has also suggested that cadential articulations are not always as cut-and-dry as a taxonomic theory of formal functions might suggest: “In many specific instances determining a phrase’s cadential status can be quite tricky. At times even seasoned scholars disagree on matters such as where a phrase ends or whether its ending should be regarded as a half or full cadence” (2014, 203). Burstein’s observations are mostly directed toward cases wherein it is difficult to discern whether a phrase’s endpoint is a HC or whether the dominant continues through and resolves to the subsequent tonic. More broadly, however, he points out that analytic interpretation of cadential events both influences and is influenced by analytic readings of voice-leading structures within a musical phrase. Sometimes we find cadential harmonic progressions in places where we intuit there should not be a cadence, and it is in these cases where we could look beyond harmony to describe why we do not interpret a cadence.⁽²⁸⁾

[3.2] The opening of the second movement of Beethoven’s Piano Sonata Op. 10, shown in Example 9 is one such instance. In his analysis of this theme, Caplin (1998, 64–65) refers to the first four measures as a “regular presentation phrase,” and thus does not analyze a half cadence in m. 4. Burstein, on the other hand, offers a more detailed description, writing that the “V of m. 4 marks the end of melodic, rhythmic, and phrase-structural process[es], but as the end of a presentation phrase, it is not classified as a cadence” (2015, 86–87). Burstein’s assessment is enlightening: if a cadence is an event that closes melodic, harmonic, and phrase-structural processes, what prevents the arrival on V in the fourth measure from articulating such an event? In this case, consideration of the structural melodic line reinforces Caplin’s analysis: as depicted by the stems in Example 9, the melody rises from $\hat{1}$ (A♭) in mm. 1–2, to $\hat{2}$ (B♭) in mm. 3–4, before reaching $\hat{3}$ (C) in m. 5; it only falls at m. 8. In other words, while the phrase-structural and harmonic processes may signal a conclusion in m. 4, the melodic line is still in its initiating phase; its processes do not end in m. 4 and start again in m. 5, but rather continue through m. 4 only to conclude at the end of the eight-measure unit. Considering this middleground melody thus helps explain why m. 4 should not be interpreted as cadential despite cues to the contrary.⁽²⁹⁾

[3.3] The opening phrase of the second movement of Beethoven’s Piano Sonata Op. 13 (“Pathétique”), shown in Example 10, is another example Burstein considers. In this case, the initial four-measure unit could ostensibly be an antecedent (thus creating an ANT+CONT hybrid) or a CBI (thus creating a CBI+CONT hybrid), depending on how one interprets the dominant arrival in m. 4. As Burstein describes, interpreting a HC “is supported by the hypermeter, the momentary melodic pause in m. 4, and the rhythmic drive in m. 3 that leads to the root-position V in the next measure” (2014, 208). Burstein contrasts these features with those that speak against a cadence, specifically:

the sense of closure here is undercut by the slurs and descent in the bass that span mm. 4–5, as well as by the highly continuational nature of what follows in mm. 5–8. In other words, since it is so strongly linked to an ensuing passage that seems much like what typically is found midphrase, this in turn suggests that the V in m. 4 might likewise be best interpreted as lying midphrase. It thus is not surprising that some have suggested that the V of m. 4 should be understood not as part of a half cadence but instead as part of an unbroken tonal motion that embraces mm. 1–8. (2014, 208)⁽³⁰⁾

The status of the dominant chord in m. 4 is further complicated by the fact that it occurs after a two-measure BI followed by a two-measure CI whose harmonic underpinning is a complete cadential progression: the tonic in m. 3 progresses through vi to the applied predominant V of V, and then to the dominant in m. 4. In addition to the cues Burstein cites, the presence of a complete T–PD–D harmonic progression gives further weight to understanding the dominant in m. 4 as a half cadence. However, as Burstein describes, what follows is continuational, and the melodic and harmonic processes do not restart, as would often be the case following a half cadence.⁽³¹⁾

[3.4] Burstein’s argument might be further strengthened through considerations of the melodic structure. As shown in the analysis, the opening four measures of the phrase consist of a melodic arpeggiation from $\hat{3}$ to $\hat{5}$, which remains prolonged as the active tone through m. 4: it is neighbored by the F in m. 5, and only begins its descent in m. 7, through D down to B♭ (the A♭ and G are motions to an inner voice) and finally to the tonic A♭ in m. 8. The melodic structure in mm. 1–4 thus suggests only initiating (the initial arpeggiation) and medial (the prolongation of $\hat{5}$) functions, with the concluding descent being absent until mm. 7 and 8.⁽³²⁾ Combined with the elements Burstein discusses, such as the continuation of dominant function through the vii^o in the subsequent measure and the lack of harmonic or melodic return in m. 5, our reading argues against a HC in m. 4 despite the admittedly strong predominant function afforded by the applied V of V.⁽³³⁾

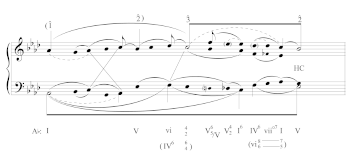
[3.5] Like the opening of the second movement of the “Pathétique” sonata, the opening of the third movement of Beethoven’s Piano Sonata, Op. 79 (Example 11) illustrates how melody can affect how we interpret form. This theme comes across as being peculiar, owing to a high degree of repetition at the musical surface, ambiguity regarding how the theme’s two halves relate to each other, and whether the V–I progression in m. 4 constitutes a cadence. At first glance, mm. 1–4 appears presentational: a two-measure basic idea is followed by another two measures that closely resemble it in terms of rhythmic profile. However, the two units are quite different: melodically, mm. 1–2 arpeggiate the tonic (from $\hat{3}$ to $\hat{5}$ to $\hat{1}$, then back to $\hat{3}$) while mm. 3–4 contain $\hat{6}$–$\hat{1}$–$\hat{2}$–$\hat{3}$; harmonically, mm. 1–2 are tonic prolongational through the descending thirds sequence, whereas mm. 3–4 concludes the sequence before moving to what could be the initial I⁶ of a cadential progression. This suggests that we are dealing with a BI+CI complex, though whether mm. 1–4 are an antecedent or CBI remains ambiguous.

[3.6] As the analysis of Example 11 shows, while the harmonic content in m. 4 is indeed cadential in nature, there is little in terms of melody that supports the interpretation of a cadence at this juncture: using a localized ascent from $\hat{1}$ to $\hat{3}$, mm. 3–4 continue to prolong the $\hat{3}$ that mm. 1–2 had established. Indeed, concluding function does not materialize until m. 7: after the BI returns in m. 5, the D ($\hat{5}$) in m. 5 pivots to become $\hat{1}$ in the dominant, which then arpeggiates up to F♯ via the neighboring G. From here, the F♯ then descends through E to reach the local $\hat{1}$, D, at the articulation of a V: PAC in m. 8.⁽³⁴⁾ In this case, consideration of melody does indeed have a demonstrable bearing on how we interpret the form of the phrase in question—if interpreted as an antecedent, this suggests that the melodic processes close at m. 4 and start again in m. 5, whereas if interpreted as a CBI, the melodic processes are left open after m. 4, and close only in m. 8.⁽³⁵⁾

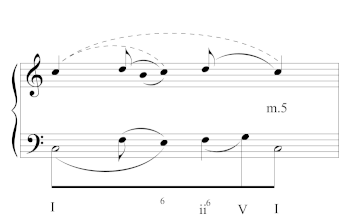
[3.7] A situation similar to the two preceding passages emerges in the opening of the first movement of Beethoven’s Piano Sonata Op. 26, shown in Example 12. Here, however, the question of whether there is a cadence in m. 4 has important implications beyond simply determining whether the first four measures are an antecedent or a CBI. Caplin’s analysis of the theme suggests that it is a compound period made up of two parallel eight-measure ANT+CONT hybrids. As such, he analyzes a half cadence in both m. 4 and m. 12. Despite being recognized within form-functional theory, however, the compound antecedent = ANT+CONT construction is problematic against Caplin’s contention that an antecedent, by definition, must contain a cadence that is weaker than the one that closes the theme. This means that in Op. 26, not only does the cadence at m. 16 have to be stronger than the one at m. 8—an unproblematic assertion—the one in m. 4 should also be weaker than the one at m. 8. Since the HC at m. 8 already represents the weakest cadence, the cadence in m. 4 cannot be comparatively weaker unless one wants to further subdivide half-cadential strengths.⁽³⁶⁾

[3.8] It is, however, worthwhile to consider whether the dominant in m. 4 is cadential at all. Indeed, analyses put forth by Schenker ([1935] 1979, Fig. 85), as well as David Beach, make a point of accentuating that m. 4 is not a cadence, but merely a phrase-dividing dominant. Beach, for instance, writes that it is necessary to determine “a distinction between the dominant in m. 4 (or m. 12), which is the division of the phrase, and the dominant in m. 8, which in the hierarchy is the more important of the two. That is, the dominant in m. 8 is the goal of the phrase (as the tonic in m. 16 is the goal of the consequent phrase), while the dominant in m. 4/12 marks a division of the phrase” (1989, 13). Beach’s prose clarifies his reasoning:

[The V in m. 4] cannot be considered equivalent to the dominant in m. 8. Rather. . .it divides the phrase while prolonging the tonic. The harmony moves beyond this point to the subdominant, which is subsequently prolonged, and then on to the dominant in m. 8. Thus, the controlling harmonic progression for this eight-bar antecedent phrase is I-IV⁶-V, with the dominant in m. 4 functioning. . .as a means of dividing the phrase. (1989, 39)

In other words, Beach’s reading (which closely resembles Schenker’s), sees the V in m. 4 not as a cessation of tonal processes, but one that continues those processes. While Beach accentuates harmonic continuity, our reading of mm. 1–8 in Example 13 suggests that melodic continuity is also a factor in this theme.

[3.9] Both Schenker and Beach interpret the fleeting C in m. 4—part of the D♭–C–B♭ motive—as the onset of the structural melodic line. As Beach describes it, the C is the consonant chord tone, even if fleeting, while the accented tone D♭ is merely an appoggiatura.⁽³⁷⁾ While we agree with Beach’s latter observation, we find his and Schenker’s use of this specific C as the onset of the melodic line problematic. First, because it arises from a voice exchange with the bass, we read it as a neighbor tone embellishing the B♭ that arises from the more structural A♭. Second, if this C is indeed the structural upper voice, it cannot both immediately step back down to B♭ and not be a cadence. Both Schenker and Beach acknowledge this second problem, but interpret the descent from $\hat{3}$ to $\hat{2}$ in m. 4 as an inner-voice process, despite B♭ being clearly articulated in the upper voice.

[3.10] Our reading in Example 13 suggests instead that the opening four measures project a melodic ascent from A♭ ($\hat{1}$) in mm. 1–3 to B♭ ($\hat{2}$) in m. 4; the structural $\hat{3}$ thus does not appear until m. 5. One potential criticism we want to address is that in taking the C in m. 5 as the structural note, we are choosing what appears to be a note supported by an unstable six-four sonority. On the surface this is true, but our reading suggests that that C has been displaced from sounding over the F on the downbeat of m. 5. In other words, the V of m. 4 progresses deceptively to vi, but the consonant fifth above F is displaced by the sixth, D♭—which we hear as a remnant of the preceding V (its seventh) whose delayed appearance over F creates the impression of IV⁶ but which is ultimately a neighboring note to $\hat{3}$, a reading which correlates to Beach’s assessment that the V in m. 4 prolongs tonic.⁽³⁸⁾ From here, F in the bass passes down through its seventh (E♭) to V of V, followed by V, which resolves to I⁶ at the end of m. 6. The submediant then returns in the bass—once again with a D♭ displacing the fifth such that it resembles a IV⁶ on the surface—before resolving to the cadential dominant in m. 8.⁽³⁹⁾

[3.11] Based on the readings by Beach and Schenker, the idea that m. 4 is not a cadence is certainly not novel; rather, we believe that considering the role of melody helps to articulate precisely why is it not a moment of cadential repose, especially when compared to the HC in m. 8. In addition to the continuation of harmonic processes via the move from V to IV⁶ (vi), the melodic processes likewise remain open: the ascent from $\hat{1}$ to $\hat{3}$ in mm. 1–5 is endemic of initiating function, while the prolongation of $\hat{3}$ through mm. 5–7 reflect medial function, and the descent from $\hat{3}$ to $\hat{2}$ in m. 8 is characteristic of concluding function, which coordinates with the harmony to articulate a half cadence.⁽⁴⁰⁾

[3.12] While the previous examples have engaged with passages where the question of a half cadence (or lack thereof) was critical in determining the form of the theme in question, the final two examples in this section—the opening of the third movement of Mozart’s Sonata in D major, K. 311 in Example 14, and the opening of the aria “Dove Sono” from his Le nozze di Figaro in Example 16—consider themes whose basic ideas contain unequivocally cadential harmonic progressions. In Example 14, the underlying harmonic progression of mm. 1–2 suggests a half-cadential gesture: I–vii^o6/V–V. Of course, these measures contain only what Caplin (2004, 81–85) calls cadential content and not cadential function: not only is cadential function denied on the basis of grouping structure, we can see that the melodic structure conflicts with the harmonic one. As shown in Example 15, the upper line begins on $\hat{1}$ (having arpeggiated down from $\hat{5}$ in the pickup), which remains the active tone throughout m. 1. When the harmony changes to the dominant in m. 2, $\hat{1}$ steps up to $\hat{2}$, increasing the melodic tension. Measures 3–4 function in a similar manner but support a further ascent to $\hat{3}$ over the V–I progression, which given the inverted dominant is clearly non-cadential. As in several of the previous examples, the presentation in its entirety supports an initiating melodic function in the form of an ascent from $\hat{1}$ to $\hat{3}$. Thus, while the harmonic content of mm. 1–2 could be described as a cadential progression, its melodic content is more typical of initiating function.⁽⁴¹⁾

[3.13] Example 16, the opening phrase of “Dove Sono,” presents a case where the initial basic idea in mm. 1–2 contains a complete cadential progression (I–ii⁶–V^{${}_{\mathrm{4–3}}^{\mathrm{6–5}}$}–I); this progression is then repeated in mm. 3–4 but with the melody a third higher. We can once again see how the melody signals that mm. 1–4 are only in their initiating stages: mm. 1–2 exhibit a melodic structure typical of initiating functions as $\hat{1}$ (C) is prolonged via a neighbor motion before arpeggiating up to $\hat{3}$, which is prolonged via the same upper-neighbor figure in mm. 3–4.⁽⁴²⁾ The melody then enters its medial phase at m. 5 with a repetition of the upper-neighbor motion above $\hat{3}$ in m. 6, before descending in mm. 7–8 to $\hat{2}$ at the conclusion of the antecedent phrase (the melody descends to $\hat{1}$ in the consequent phrase).⁽⁴³⁾ Despite containing cadential content, therefore, mm. 1–4 does not have cadential function, and sensitivity to the melodic domain gives an additional reason as to why m. 2 and m. 4 are not cadential: beyond being basic ideas, their melodic content conflicts with the conventions of Classical cadential closure by projecting processes of melodic initiation.⁽⁴⁴⁾

4. Limited-Scope Cadences, Mozartean Loops, and their Derivatives

[4.1] The structure of “Dove Sono” is not entirely unique: the opening of the first movement of Mozart’s Piano Sonata K. 279 shown in Example 17 is also, as Caplin (2004, 86) describes, a sentence whose basic ideas contain cadential content. In his commentary on this theme, Caplin notes that Lerdahl and Jackendoff (1983, 62) refer to the tonic arrivals in m. 3 and m. 5 as cadences, but counters by adding that

If we identify cadences at the downbeats of measures 3 and 5, as do Lerdahl and Jackendoff, then we must ask exactly what formal units these cadences are closing. Clearly, it is too early to speak of closing the main theme itself, for when we consider the broader context, we can identify a sentence structure for that theme as a whole, one whose promised cadential close is initially denied by the deceptive cadence in measure 10, but then realized by the perfect authentic cadence in measure 12. To the extent that we want to identify cadences at the downbeats of measures 3 and 5, it is best to see them functioning to provide closure to the basic idea itself, but having no further effect on the theme. For at the level of the theme, a basic idea is exclusively an opening idea; that idea itself cannot bring a formal cadence. (2004, 86)

[4.2] James Hepokoski and Warren Darcy refer to this theme as a “Mozartean Loop,” which they describe as a theme that “begins with a short module (two to six measures)—usually closing with a cadential progression—that is either elided or flush-juxtaposed with a repetition of itself before moving forward into differing material” (2006, 81–84). Hepokoski and Darcy compare the Mozartean Loop with the Caplinian sentence, with one difference, “the unmistakable cadence (PAC) at the end of each loop,” which they acknowledge “would appear to contradict the general principle that the presentation portion of a sentence (or compound sentence) does not end with a cadence” (2006, 84). Like Caplin, Hepokoski and Darcy cite the larger context as reasons for a sort of cadential hierarchy:

Here the crucial observation is that although the two cadences are obvious enough—perfectly recognizable as enacting the final elements of cadential-progression formulas—both within their larger sentential format and within their own context of appearing at the ends of reiterated loops, they are incapable of serving as structural goals that conclude the broader musical idea. Their local cadences are subsumed under their larger presentational function, that of opening a larger sentential idea. (2006, 84)

[4.3] The explanations above reinforce the issue that in more complex instances, harmony and grouping structure are unable to arbitrate questions of cadential content. The problem here arises from what Felix Diergarten describes as a “dilemma” within Caplin’s methodology—and more broadly within modern conceptions of cadences—which Caplin “resolves by introducing the concept of a ‘limited cadential scope,’ a kind of hierarchy of cadences that measures the ‘weight’ of cadence not according to their intrinsic features, but by their temporal position and context” (2015, 71). This dilemma, however, is not quite as problematic when the melodic parameter is considered: the melodic content of these “limited scope” cadences—and indeed, the melodic processes of the theme writ large—provide intrinsic perspectives into why these two measures are less endemic of cadential articulation.

[4.4] Consider the voice-leading analysis of from the opening passage of Mozart's Piano Sonata in C Major, K. 279, I, given in Example 18. This graph covers the first five measures of the theme, which constitute the basic idea and its repetition. Here, our analysis shows that the melodic structure of the basic idea and its repetition serves to prolong the tonic scale degree, despite the surface-level scalar ascent from C up to A and back down again in each two-measure unit. There are several reasons for this interpretation. Firstly, neither the melodic D nor F in m. 1 are supported, suggesting that this first measure is merely a decorated arpeggiation of the tonic triad—an opening flourish of sorts. As such, we interpret the F and the A on the downbeat in m. 2 as covering tones that arise from motion from an inner voice: if we reduce the voice leading in this passage to a four-part harmonic context, as shown in Example 19, under the auspices of idealized voice-leading employing the path of least motion, we see that the F and A are neighbors to the inner-voice E and G in the tonic chord, and the D and B serve as a double neighbor around the tonic pitch.⁽⁴⁵⁾

[4.5] This suggests that while the two BIs that form the theme’s presentation contain cadential harmonic content, the melodic domain conflicts with the harmonic one: the opening flourishes, and the way in which they prolong the tonic scale degree, are more endemic of an initiating melodic function, especially when put into relief against the melodic processes that begin to unfold in m. 5. As shown in Example 20, it is only once the presentation portion of the theme concludes that the melody begins to exhibit activity, launching into an ascent to $\hat{5}$ in m. 8. This ascent is then followed by a descent—first interrupted by the deceptive resolution in m. 10, but rectified by the reprise in mm. 11–12—to the structural tonic over a conventional cadential harmonic progression. These observations in some ways reinforce Caplin’s notion of limited-scope cadences, but suggest that it is not so much that the cadences are limited in scope, but rather that there is a conflict between the harmonic domain (which contains cadential content) and the melodic one (which does not). Focusing on only one or the other of these parameters does not deliver the full story in this passage, and highlights the need to treat the two parameters as symbiotic.

[4.6] Related to the looping structure, Vande Moortele (2013, 412–13) describes something he terms a “large-scale sentence with periodic presentation,” as illustrated by the main theme of Beethoven’s “Bridgetower [Kreutzer]” sonata, shown in Example 21. Citing Schmalfeldt’s (2011, 93–97) analysis of this passage, Vande Moortele notes that it can be viewed as a large sentence, in which mm. 19–27 and their subsequent repetition form two large-scale BIs (made up of a two-measure BI followed by fragmentation), which then group with the continuational mm. 37–45 to create a sentence. The challenge, as Vande Moortele (2013, 413) points out, is that in contrast to the more typical Mozartean Loops,

in Beethoven’s theme, the cadences at the end of the initiating nine-bar unit and its repetition are not elided and therefore cannot be considered to be undone. As the conclusion of nine-bar chunks, moreover, they can hardly be said to be of limited scope. Rather, they appear as a correlate of this music’s expanded scale, which gives rise to the presence of an additional formal level.

Here we have a case where the apparent cadences are even more pronounced, and thus present what Vande Moortele refers to as a risk in terms of conflation of levels: “because the large-scale basic idea and its repetition stand in an antecedent-consequent relationship which is articulated by cadences, the cadence at the end of the consequent might be mistaken for the end of the theme” (2013, 413).

[4.7] Schmalfeldt, however, describes an important feature of both large-scale basic ideas. Her reading of mm. 19–27 (and its repetition), shown by the beamed notes in Example 21, “proposes that a stepwise ascent through the interval of a seventh—<F–G♯–A–B–C–D–E>—fundamentally carries the violinist’s line to the primary tone of the movement, the mediant-supported E♮ as $\hat{5}$ at the fermata” (2011, 94). Schmalfeldt thus explains why one might not interpret a cadence at m. 27 despite other cues suggesting one: the melodic domain is still in its initiating phase, ascending from $\hat{6}$ below the tonic up to the dominant tone. It is only in the continuation at m. 37ff. that the melody projects medial and concluding function, as $\hat{5}$ is first prolonged before making its way back down to $\hat{1}$ in m. 45; the arrival on the tonic coincides with what Schmalfeldt describes as “the first and only genuine authentic cadence thus far” (2011, 96).⁽⁴⁶⁾

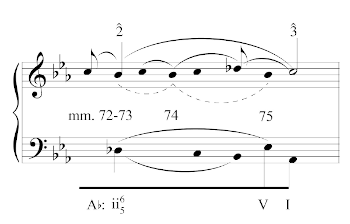
[4.8] Another “large-scale sentence” can be found in the subordinate theme of the final movement of Schumann’s “Rhenish” Symphony, shown in Example 22.⁽⁴⁷⁾ Since Vande Moortele describes the “large-scale sentence” as being more closely tied to nineteenth-century style, the category provides a way for us to apply considerations of melodic structure beyond the Classical style. Rather than having a periodic presentation, however, this large-scale sentence has CBIs that end in apparent IACs in the local tonic of A♭ major (m. 75 and m. 79). Unlike the “Bridgetower” sonata, both cadences remain in the tonic; nevertheless, they also have less-apparent looping structures. As shown in Example 23, the structural melody of both CBIs ascends from $\hat{2}$ (B♭) to $\hat{3}$ (C), with surface-level embellishments prolonging both scale degrees over the course of the presentation. C remains the active tone, prolonged now by an upper-neighbor D♭, and only begins its descent at the end of the continuation phrase. Ultimately, the theme does not create a conclusive cadence in A♭, but rather reopens both the melodic and harmonic structure through a deceptive resolution to V⁷/IV, after which the music moves away from A♭.

5. Conclusion

[5.1] One trend that became apparent over the course this paper is that cadences are, generally speaking, conceived as a type of formula, whose local ingredients we can tabulate in order to come up with a sort of recipe for the ways in which a cadence is made. In particular, the urge to generalize leads to the idea that cadential formulae can be cordoned off from the music that precedes, and leads to, the cadence. However, Rohrmeir and Neuwirth state that attempts at articulating specific cadential features “may not be capable of providing the differentia specifica to other (non-cadential) types of progressions” (2015, 288). This is true not only in the harmonic domain, but also in attempts to relegate the cadence to a specifically local set of voice-leading configurations. While a cadence thus has certain formulaic features, it is also highly dependent on what precedes it. Caplin (2004, 56) acknowledges this fact almost axiomatically (“a cadence must end something”—italics Caplin’s). Here, we show that this “something” can, and should, include melodic processes, in addition to harmonic and phrase-structural ones.

[5.2] This is not to say that there are not recognizable and generalizable features of a cadence, but rather that generalized features do not always give a clear result. In more ambiguous cases, the melodic structure provides an additional means of articulating the distinction between “cadential content” and “cadential function.” Conversely, however, considerations of melodic structure could also inform cases where melodic factors, rather than harmonic ones, contribute to ambiguity. The conclusion of Frédéric Chopin’s Prelude Op. 28, no. 9 shown in Example 24, for instance, closes with a V⁷–I cadence, but this ending still somehow feels incomplete. One reason for this sense of inconclusiveness could be found in the atypical melodic structure, which rises from $\hat{5}$, through ♭$\hat{6}$, ♭$\hat{7}$, $\hat{7}$, to $\hat{1}$. Despite this moment appearing resoundingly cadential in terms of harmonic and contextual considerations, the ascending melodic line gives the sense of an increasing tension, rather than the decrease in tension usually associated with cadences.⁽⁴⁸⁾ This is not to say that this is not a cadence, but rather that sensitivity to the melody allows one to articulate that this ascending line is not of the default type typically associated with Classical-style cadential articulation. This in turn allows for a greater dialogic engagement—not only with this specific piece, but with other works whose melodic content is atypical.⁽⁴⁹⁾

[5.3] In Daniel Harrison’s opinion, the “success of [Caplin’s] project and the intensive activity taking place around it have certainly fostered innovative thinking about cadence, which had not enjoyed serious theorizing for some time, and had become a commonplace of the harmony textbook” (email correspondence, April 25–26, 2022). However, Harrison also cautions that “the project also has shown signs of making cadence a creature of formal function in a particular repertory and stylistic practice. That is, a broadly general theory of cadence as a musical effect, convention, and structure seems in danger of losing out to a particularistic theory of cadential function in the galant style.” This leads Harrison to conclude that “putting the cadence into a dependent relationship with classical formal functions leads to an impoverishment of recognized cadence types.”

[5.4] Rather than being an event that can be discussed in a generalized manner, the answer to “what is a cadence?” lies in the cadence’s function as a terminus of both harmonic and melodic musical processes. If a cadence closes something, it stands to reason that understanding what it closes is as important as understanding the mechanics of that closure in more generalized terms. As such, attempts to cordon off generalized “cadential formulae” can only get us so far. In that sense, we share a common cause with Harrison’s concerns regarding Caplin’s somewhat restrictive definition of cadence. Our view of the melodic role of the cadence, however, also positions us to see certain types of initiating, medial, and closing structural melodic motions as synchronizing well with Caplin’s broader theoretic claims. As we noted, structural melodic ascents, or structural melodic stasis, appears to be relatively consistent in their association with initiating function, while a structural descent is the default associated with concluding function. These melodic functions exist in a symbiotic relationship with harmony: either dimension has the ability to undermine the other, and musical drama plays out when considering the ways in which the structural melody and the structural harmony reinforce, diverge from, or contradict each other.

[5.5] While Caplin’s definition of a cadence may give the impression that his approach is overly restricted to the late eighteenth century, once the taxonomy of the cadence is refined to include more than merely harmonic or grouping signposts, we see an increased ability to temper our discussion of phrase endings—whether they result in cadential articulations or not—with greater nuance and musical sensitivity. We can, for instance, describe in greater detail the disjunction of melodic and harmonic conclusions, and the ways in which they work in tandem to delay, defer, or obscure the conclusion of the melodic and harmonic processes of a phrase. Taking the step to accord the structural melodic features a place at the table in discussions of formal functions serves to open the theory to greater and more varied applications. For instance, while nineteenth-century harmonic innovations have long held a prominent place in music-theoretic discourse, melodic innovations have been considered far less often. Indeed, we might go as far as to note that a greater sensitivity to the role of melody could allow for future research to generate an increasingly nuanced dialogue between nineteenth-century processes and their predecessors in the late eighteenth century that is not as readily apparent when formal considerations are restricted to, or even prioritize, harmony.

Kyle Hutchinson
University of Toronto
80 Queen's Park
Toronto, ON, Canada
M5S 2C5
kyle.hutchinson@mail.utoronto.ca

Matthew Poon
University of Toronto
80 Queen's Park
Toronto, ON, Canada
M5S 2C5
matthew.poon@mail.utoronto.ca

Works Cited

Aldwell, Edward, Carl Schachter, and Allen Cadwallader. 2010. Harmony and Voice Leading. 4th ed. Schirmer.

Beach, David. 1989. “The Analytic Process: A Practical Demonstration. The Opening Theme from Beethoven’s Op. 26. Journal of Music Theory Pedagogy 3 (1): 25–46. https://jmtp.appstate.edu/analytic-process-practical-demonstration-opening-theme-beethovens-op-26.

Burstein, L. Poundie. 2014. “The Half Cadence and Other Such Slippery Events.” Music Theory Spectrum 36 (2): 203–27. https://doi.org/10.1093/mts/mtu010.

—————. 2015. “The Half Cadence and Related Analytic Fictions.” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Markus Neuwirth and Pieter Bergé, 85–116. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.6.

—————. 2019. “The Joy of Sextabsätze: The Deceptive Cadence and Other Such Slippery Events.” Paper presented at the Annual Meeting of the Society for Music Theory, Columbus Ohio.

Byros, Vasili. 2013. “Trazom’s Wit: Communicative Strategies in a ‘Popular’ Yet ‘Difficult’ Sonata.” Eighteenth-Century Music 10 (2): 213–52. https://doi.org/10.1017/S1478570613000055.

Caplin, William. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.

—————. 2004. “The Classical Cadence: Conceptions and Misconceptions.” Journal of the American Musicological Society 57 (1): 51–118. https://doi.org/10.1525/jams.2004.57.1.51.

—————. 2009. “What are Formal Functions?” In Musical Form, Forms, and Formenlehre: Three Methodological Reflections, ed. Pieter Bergé, 21–40. Leuven University Press. https://doi.org/10.2307/j.ctt9qf01v.5.

—————. 2013. Analyzing Classical Form: An Approach for the Classroom. Oxford University Press.

—————. 2014. “Topics and Formal Functions: The Case of the Lament.” In The Oxford Handbook of Topic Theory, ed. Danuta Mirka, 415–52. Oxford University Press. https://doi.org/10.1093/oxfordhb/9780199841578.013.0016.

—————. 2018. “Beyond the Classical Cadence: Thematic Closure in Early Romantic Music. Music Theory Spectrum 40 (1): 1–26. https://doi.org/10.1093/mts/mty002.

Diergarten, Felix. 2015. “Beyond Harmony: Cadence in the Partitura Tradition.” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Markus Neuwirth and Pieter Bergé, 59–84. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.5.

Drabkin, William. 1996. “Schenker, the Consonant Passing Note, and the First-Movement Theme of Beethoven’s Sonata Op. 26.” Music Analysis 15 (2–3): 149–89. https://doi.org/10.2307/854064.

Ewell, Philip. 2020. “Music Theory and the White Racial Frame.” Music Theory Online 26 (3). https://doi.org/10.30535/mto.26.2.4.

Gjerdingen, Robert O. 2007. Music in the Galant Style. Oxford University Press.

Goldenberg, Yosef. 2020. “Continuous Question-Answer Pairs.” Music Theory Online 26 (3). https://doi.org/10.30535/mto.26.3.2.

Harrison, Daniel. 2019. “Cadence.” In The Oxford Handbook of Critical Concepts in Music Theory, ed. Alexander Rehding and Steven Rings, 535–76. Oxford University Press.

Heneghan, Áine. 2018. “Schoenberg’s Sentence.” Music Theory Spectrum 40 (2): 179–207. https://doi.org/10.1093/mts/mty014.

Hepokoski, James. 2009. “Comments on William E. Caplin’s Essay ‘What Are Formal Functions?’” In Musical Form, Forms, and Formenlehre: Three Methodological Reflections, ed. Pieter Bergé, 41–45. Leuven University Press. https://doi.org/10.2307/j.ctt9qf01v.6.

Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late Eighteenth-Century Sonata. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001.

Hutchinson, Kyle. Forthcoming. “The Predominant Six-Four in the Late Music of Richard Strauss.” Music Theory Spectrum.

Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. MIT Press.

Marston. 2001. Review of Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven, by William E. Caplin. Music Analysis 20 (1): 143–9. https://doi.org/10.1111/1468-2249.00131.

Martin, Nathan John. 2011. Review of Musical Form, Forms, and Formenlehre: Three Methodological Reflections, by William E Caplin, James Hepokoski, and James Webster, ed. Pieter Bergé. Notes 67 (3): 559–63. https://doi.org/10.1353/not.2011.0025.

Martin, Nathan John, and Julie Pedneault-Deslauriers. 2015. “The Mozartean Half Cadence.” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Markus Neuwirth and Pieter Bergé, 185–214. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.9.

Marx, A. B.. [1868] 1997. Musical Form in the Age of Beethoven: Selected Writings on Theory and Method. Edited and Translated by Scott Burnham. Cambridge University Press.

Neuwirth, Markus, and Pieter Bergé. 2015. “Introduction: What is a Cadence?” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Markus Neuwirth and Pieter Bergé, 7–16. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.3.

Reicha, Anton. 1814. Traité de Mélodie. J.L. Scherff.

Richards, Mark. 2010. “Closure in Classical Themes: The Role of Melody and Texture in Cadences, Closural Function, and the Separated Cadence.” Intersections 31 (1): 25–45. https://doi.org/10.7202/1009283ar.

Rohrmeir, Martin, and Markus Neuwirth. 2015. “Towards a Syntax of the Classical Cadence.” In What is a Cadence? Theoretical and Analytical Perspectives on Cadences in the Classical Repertoire, ed. Markus Neuwirth and Pieter Bergé, 287–338. Leuven University Press. https://doi.org/10.2307/j.ctt14jxt45.12.

Schenker, Heinrich. [1935] 1979. Free Composition. Edited and translated by Ernst Oster. Longman.

Schmalfeldt, Janet. 1991. “Towards a Reconciliation of Schenkerian Concepts with Traditional and Recent Theories of Form.” Music Analysis 10 (3): 233–287. https://doi.org/10.2307/853969.

—————. 1992. “Cadential processes: The Evaded Cadence and the “One More Time” Technique.” Journal of Musicological Research 12 (1–2): 1–52. https://doi.org/10.1080/01411899208574658.

—————. 2011. In the Process of Becoming: Analytical and Philosophical Perspectives on Form in the Early Nineteenth Century. Oxford University Press.

Schoenberg, Arnold. 1967. Fundamentals of Music Composition. Edited by Gerald Strang and Leonard Stein. Faber and Faber.

Vande Moortele, Steven. 2013. “In Search of Romantic Form.” Music Analysis 32 (3): 404–31. https://doi.org/10.1111/musa.12015.

—————. 2017. The Romantic Overture and Musical Form from Rossini to Wagner. Cambridge University Press. https://doi.org/10.1017/9781316678701.

—————. 2020. “Expansion and Recomposition in Mendelssohn's Symphonic Sonata Forms.” In Rethinking Mendelssohn, ed. Benedict Taylor, 210–35. Oxford University Press. https://doi.org/10.1093/oso/9780190611781.003.0010.

Vande Moortele, Steven, Julie Pedneault-Deslauriers, and Nathan John Martin, eds. 2015. Formal Functions in Perspective: Essays on Musical Form from Haydn to Adorno. University of Rochester Press.

Waltham-Smith, Naomi. 2011. Review of Musical Form, Forms, and Formenlehre: Three Methodological Reflections, by William E Caplin, James Hepokoski, and James Webster, ed. Pieter Bergé. Eighteenth-Century Music 8 (1): 105–7. https://doi.org/10.1017/S1478570610000448.

Footnotes

1. “Intrinsic function . . . depends on markers internal to the unit in question . . . The outstanding achievement of Caplin’s thinking is to have clearly articulated the idea of intrinsic formal function, and to have fleshed out that notion through a careful delineation of the musical features that define such functions” (Vande Moortele, Pedneault-Deslauriers, and Martin, 2–3).
Return to text

2. For discussion on other definitions of cadence and their historical backgrounds, see Caplin 2004, 51–56, and Harrison 2019.
Return to text

3. Other parameters that could also play a role include texture, meter, and hypermeter, but Caplin considers them to have little bearing on a cadence’s syntactic function: “For the specific purpose of analyzing form, all cadences of the same type are considered to have the same syntactical strength. Other factors, such as the cadence’s metrical position and its dynamic intensity and texture, do not alter the syntactical strength. These factors do, however, determine the rhetorical strength that a particular cadence may make” (2013, 80).
Return to text

4. The shortcomings of accentuating harmonic features in particular have been challenged in several essays from the 2015 collection What is a Cadence?. Felix Diergarten, for instance, writes that “harmonic analyses based on progressions of a basse fondamentale and voice-leading analyses abstracting from dissonances risk neglecting contrapuntal details that were highly important for eighteenth-century musicians,” and suggests that we “rethink the generally accepted notion that in the eighteenth century, ‘cadential classifications become primarily based on harmony rather than on melodic or contrapuntal interval’” (cited in Caplin 2004, 54; original quotation from Diergarten 2015, 79). Similarly, Julie Pedneault-Deslauriers and Nathan Martin’s (2015) survey of half cadences in Mozart invites “further reflection on the relationship between Caplin’s definition of intrathematic functions, couched largely in harmonic and rhythmic/metrical terms, and the various voice-leading patterns that might be correlated with these functions, whether those patterns might be described in terms taken over from Schenker or from Gjerdingen” (Martin and Pedneault-Deslauriers 2015, 205). Martin Rohrmeir and Markus Neuwirth attack the issue more directly, concluding that “the bare harmonic essence may not be capable of providing the differentia specifica to other (non-cadential) types of progressions” (2015, 288).
Return to text

5. While these four measures conclude on a weak beat (which might have implications for cadential articulation), the silence that follows also gives the impression that the V chord is indeed meant to be understood as a concluding gesture.
Return to text

6. Yosef Goldenberg (2020) might call mm. 1–8 a “question-answer pair” (or “QAP”), a “deliberately general” category he uses to account for designs that are period-like but not strictly periodic from a form-functional point of a view.
Return to text

7. Contextual functionality is not problematic in itself, but it poses a challenge for a theory built on defining formal functions bottom-up using intrinsic characteristics.
Return to text

8. It is also worth pointing out that the continuational characteristics in the Beethoven Concerto are extremely weak: there is neither fragmentation nor faster surface rhythm, and the harmonic rhythm even slows down in mm. 11–12. The sense of a compound sentence only coalesces at m. 13, at the onset of the cadential idea.
Return to text

9. One might also recall Anton Reicha’s complaint—made more than 200 years ago—that melody is too often given the short shrift compared to harmony (1814, i–iv). In particular, Reicha laments that melody is typically only described in general terms, describing how “melody is the most positive of all the arts, however, it is the one that has been regarded so far as the most vague, for lack of contemplations, research and analysis” (1814, 4 [our translation]). (“Ainsi, la melodie est le plus positif de tous les arts, et c’est pourtant celui qu’on a regarde jusq’au present comme le plus vague, faute des meditations, des recherches et des analyzes.”)
Return to text

10. For instance, Caplin writes that “Determining which specific musical processes are closed by cadences can be somewhat complicated and will sometimes vary from case to case. At all times, however, a definite harmonic process is closed, since the harmonies associated with the cadence always bring to some degree of completion a broader harmonic progression beginning prior to the onset of the cadence. Often, we can identify a distinctly melodic process closed by cadences, such as when, in the case of a perfect authentic cadence (PAC), the melodic line descends to the tonic scale degree” (Caplin 2004, 56–57). Mark Richards (2010) likewise notes that there are cases even in the Classical repertoire wherein the final melodic note is ambiguous, and the question of whether a PAC or IAC occurs remains contentious.
Return to text

11. Because this paper specifically aims to refine Caplin’s work, we generally limit our repertoire to the same composers Caplin considers, namely Haydn, Mozart, and Beethoven (with some augmentation near the end).
Return to text

12. The marriage of Schenkerian and Schoenbergian concepts have roots in the work of Janet Schmalfeldt (1991), though Schmalfeldt’s focus is directed toward initiating and medial functions.
Return to text

13. Caplin (2009) provides a detailed discussion of the relationship between initiating, medial, and concluding functions and phrase structure.
Return to text

14. While Caplin excludes theorists such as A. B. Marx when crafting his own theory (1998, 5), subsequent scholars such as Áine Heneghan (2018) trace certain form-functional categories to the nineteenth century. Moreover, although Schenker and Schenkerian theory are not without their problems (many of which are discussed in Ewell 2020), we invoke Schenker here because his theories, as well as those of Marx, were developed with respect to the same repertoire that Caplin uses.
Return to text

15. Schenker’s conception of a fundamental line is often treated as axiomatic, in that he positions it as an a priori feature of tonal music with an immutable form: the Urlinie must begin on a non-tonic pitch—either $\hat{3}$ or $\hat{5}$ (and rarely $\hat{8}$)—and descend linearly to $\hat{1}$, or, in cases of the half cadence, to $\hat{2}$. As such, we adopt Schenker’s concept with the acknowledgement that many of his views do not reflect our own.
Return to text

16. While we are using a quasi-Schenkerian conception of the fundamental line, for the most part, we have opted to demonstrate our claims by beaming notes on the musical examples themselves. This decision was made for two reasons: first, it visually provides a degree of separation from orthodox Schenkerian readings, to which our concept of middleground descent might seem somewhat loose. Second, we want to avoid having our larger claims possibly getting lost amidst the orthographies surrounding traditional Schenkerian graphs. In a few cases, we use minimal graphic notation to clarify particularly complex examples.
Return to text

17. A deeper-level reduction of the melody might suggest that $\hat{3}$ (E) remains the active Kopfton, but it does not fundamentally alter the reading of a descent accompanying the cadential articulation.
Return to text

18. Naomi Waltham-Smith (2011, 106) notes that “since the publication of Classical Form, Caplin has sought consistently to isolate function from other formal dimensions, [including] thematic content.” Conversely, Nathan Martin (2011, 560) finds interest in the way Caplin (2009) engages more with the relationship between formal functions and their ability to express temporality.
Return to text

19. Schmalfeldt analyses the B–A–G in mm. 5–7 as a descent into an inner voice, with $\hat{2}$ implied over the terminal dominant. This means that Schmalfeldt considers the phrase to conclude with a HC in the home key rather than a PAC in V; indeed, the cadence turns out to be a reinterpreted half cadence (RHC) within the context of the overall small ternary. Interpreting the conclusion as a PAC would require a minor reconfiguration of which voices are interpreted as structural, but would not contradict Schmalfeldt’s analysis at the level she depicts.
Return to text

20. Hypermetric considerations in this passage might also mitigate the hearing of m. 8 as a cadence, since the tonic returns on a weak beat.
Return to text

21. Given that Examples 2, 7, and 8 are sentential and see each two-measure BI as supporting a single scale degree in an ascent to 3, it may be tempting to take this taxonomizing further by attempting to categorize typical melodic contours for each phrase or even sub-phrase type. We feel, however, that this goes beyond the scope of this paper, and may ultimately be untenable, given that the passages in Examples 3 and 6 are also sentential, but with melodic structures different from those in Examples 2, 7 and 8.
Return to text

22. Associations between ascending and static melodic lines, and their relationship to initiating and medial formal functions, are features of the analyses in Schmalfeldt 1991.
Return to text

23. A further point of interest regarding melodic contour can be found in Schoenberg’s Fundamentals of Musical Composition (1967, 113–15), wherein he presents several abstract graphs outlining the contour of various melodies. In almost every case, the melody begins on, or reaches, a peak before descending.
Return to text

24. This is, of course, not to say that these melodic and form-functional parallelisms should be interpreted as axiomatic—we invoke Hepokoski and Darcy’s notion of defaults because there are always cases in which the default situation will be eschewed.
Return to text

25. This ascent from $\hat{1}$ to $\hat{3}$ is nearly identical to the one Schmalfeldt describes in her analysis of the Haydn sonata shown in Example 7. Of course, in Example 7, there was no question of a cadence materializing because the harmony is not cadential in nature. This suggests that the ascent is indeed an initiating function: it is especially clear supported non-cadential harmony, but can be seen even when combined with apparently cadential harmony.
Return to text

26. Indeed, one might draw a connection between how Schenker and Caplin each discuss cadences. Schenker views the half cadence as an interruption, after which the melodic and harmonic processes restart. This suggests that some process has come to an end, a view that is synergetic with how Caplin describes cadences as a formal function of closure. Burstein (2015, 86) articulates a similar point, noting that “to label a V as part of a half cadence necessarily implies that its voice-leading is to be regarded as essentially disconnected from the harmony that follows it on its own structural level.”
Return to text

27. See, for instance, Schmalfeldt’s (1992) discussion of cadential evasion. Burstein (2019) engages with the notion of the deceptive cadence with more nuance, arguing that it can serve more structural functions than we normally accept.
Return to text

28. The opposite case, wherein the melodic factors suggest a cadence but harmonic ones do not align, are more commonly understood as the deceptive or evaded cadences.
Return to text

29. Caplin cites other parameters, such as the hypermetric placement of V relative to I in m. 3, as factors contributing to the lack of a cadence in m. 4.
Return to text

30. Caplin (2013, 105), for instance, refers to this theme as a hybrid, consisting of an antecedent (ending with a HC) followed by a continuation.
Return to text

31. Schenker’s ([1935] 1979, Fig. 155) own analysis of this movement likewise suggests an uninterrupted structure, though the analysis itself is only of the deep middleground level, and takes C as the main pitch.
Return to text

32. The status of C in this passage is contentious: we are inclined to interpret the descending line C–B♭–A♭–G as a composed-out version of a 6-5 and 4-3 over the bass. The issue that arises is that the chordal 7^th, D♭, is sounded simultaneously, which complicates whether or not C is supported. Fundamentally, while analysts may disagree on this technical point, it is impossible to not hear the C as part of a descent from E♭ (m. 6) down to A♭. Additionally, Schenker ([1935] 1979, Fig. 155, no. 1) takes $\hat{3}$ as the Kopfton in this movement, which diverges from our analysis, but does not affect the melodic structure with respect to cadences.
Return to text

33. A comparison of Beethoven’s theme might be made with, for example, the slow movement of Mozart’s Sonata K. 283: both pieces feature a filling-in of the dominant arrival that results in a V. However, while the structural melody in the “Pathétique” example remains static in mm. 1–4, the Mozart sonata descends from $\hat{3}$ to $\hat{2}$ in m. 2 (under R=2N).
Return to text

34. One might say that at an even deeper level, this theme moves from B up to D, setting up the latter as the movement’s primary tone.
Return to text

35. Indeed, this melodic distinction between an Antecedent and a CBI—the former closes and then reopens melodic activity while the other engages a continuous melodic process—has received little consideration in scholarly literature.
Return to text

36. Caplin specifies that “the half cadence is the weakest [cadence],” and that “all cadences of the same type are considered to have the same syntactical strength” (2013, 80).
Return to text

37. “But remember that the D♭ is an appoggiatura, a displacement of the C. So we have a real dichotomy here between surface design and structural weight. What, in fact, is stated as a passing surface event is the displaced goal of the deeper-level ascending third A♭/B♭/C, and, as it turns out, this goal pitch is the primary tone (scale degree 3) of the piece and thus a member of the deepest structural level. I do not want to belabor the point, but it is crucial to understand that there is no correspondence between duration and structural significance in tonal music. . .” (Beach 1989, 37).
Return to text

38. Hutchinson (forthcoming) describes how the sixth above a bass note, often retained as a suspension from the preceding chord, can give the impression of an inverted triad, especially when the resolution of the sixth is displaced such that it occurs over what appears to be a subsequent harmony, as the C does in this case. Note also that this reading suggests that these two measures are in effect a sequence of roots descending by fifths: F–B♭–E♭–A♭.
Return to text

39. Beach, Schenker, and William Drabkin (1996, 156–171) all agree that the F–G–A♭ bass progression in m. 7 should be treated as an unfolding of the F: vii^o7 and I are used to avoid undesirable parallels between the bass (F–E♭) and the soprano (C–B♭). While the aforementioned scholars take the IV⁶ at face value, we feel our interpretation of the D♭ as a recurring motif that displaces C to be of interest: namely, what begins as a surface-level displacement in m. 4 grows to become more salient in the continuation phrase.
Return to text

40. As to why we, like both Schenker and Beach, have chosen $\hat{3}$ instead of $\hat{5}$ as the onset of the structural melody, this consideration is mostly a result of the consequent phrase in the sixteen-measure period; therein, there is no D♭ in the melody that could support a reading from $\hat{5}$. Drabkin (1996, 158–171) summarizes Schenker’s rationale via a study of Schenker’s correspondences with his pupil Felix-Eberhard von Cube, who had taken $\hat{5}$ as the Kopfton in an analysis he sent to Schenker.
Return to text

41. As our analysis shows, the line then descends to $\hat{2}$ above the half cadence in m. 8. The line is covered by the B–A motion used to avoid the parallel fifths that would otherwise accrue between B–F♯ and A–E in the penultimate and final chords of the phrase. This is further clarified in the consequent phrase, where the sixteenth-note runs more clearly make their way to $\hat{1}$ without the covering tone.
Return to text

42. Our analysis here reflects the same melodic configuration analyzed in Schmalfeldt 1991, 259.
Return to text

43. Schmalfeldt links the use of $\hat{3}$ as the Kopfton to the dramatic contexts of the aria. Specifically, she writes that “here is an Anstieg that promises a complete arpeggiation to $\hat{5}$ but settles instead for $\hat{3}$. A broad turn around $\hat{1}$ informs the melody of the Countess’s tonic-prolonging 2-bar basic idea. With the first oboe providing the passing $\hat{2}$ as the link upwards at b.2, a harmonically exact repetition at bs. 3–4 permits the Countess to present the turn around $\hat{3}$. Again, the oboe moves upward, now to the high g² ($\hat{5}$), and we are fully prepared to hear the Countess do the same. But, deeply troubled over her husband’s infidelity, and uncertain how to handle her situation, the Countess is not ready to achieve what might have become the primary note of the aria. The oboe having prompted her to try, she reaches only the f² within the continuation at b.6, and then the sentence ends with a half cadence, effecting an interruption within the descent and bringing the continuation to a close on unstable $\hat{2}$” (1991, 256–58).
Return to text

44. If one were to transplant mm. 1–2 to mm. 7–8, the resulting cadence would be extraordinarily weak.
Return to text

45. Vasili Byros employs Gjerdingen’s terminology to describe the basic ideas of this theme as “Passo Indietro. . .Cadenza Semplice” (2013, 221). According to Gjerdingen, a Passo Indietro is a “descent in the bass from $\hat{4}$ to $\hat{3}$. . .most strongly characterized [by] the pair of thoroughbass figures 6/4/2 and 6/3, usually shortened to 4/2 and 6” (2007, 167). In other words, it characterizes V proceeding to I⁶, for which the vii^o in parentheses in our Figure 5b could be seen as a substitute. A Cadenza Semplice, on the other hand, refers simply to the $\hat{5}$–$\hat{1}$ bass progression (Gjerdingen 2007, 141).
Return to text

46. Schmalfeldt also attributes these cadences’ mediant key of C major—and the sudden way C major emerges—as contributing to their unsuitability to close the theme. By contrast, Vande Moortele gives them more weight, citing that as the conclusion of nine-bar chunks they “can hardly be of limited scope” (2013, 413).
Return to text

47. To be sure, the status of this theme (and indeed, the form of this movement) is quite opaque. We identify it as a subordinate theme because it follows a clearly articulated cadence (a V: PAC in m. 65) and a six-measure introductory fanfare. In the recapitulation, everything up to the V: PAC remains the same as in the exposition, and only the fanfare and ensuing music is transposed into the home key. Ultimately, however, whether this theme is a subordinate theme or not does not change its status as a sentential theme type.
Return to text

48. Another case with a locally ascending melodic line involves the Phrygian half cadence, which, as Aldwell and Schachter describe, typically has a top-voice $\hat{4}$–$\hat{5}$ motion (2010, 200).
Return to text

49. Nineteenth-century music, in particular, is more susceptible to divergences between upper-voice processes and harmonic ones; though beyond the scope of this paper, we intend to discuss it in future work.
Return to text

Caplin cites other parameters, such as the hypermetric placement of V relative to I in m. 3, as factors contributing to the lack of a cadence in m. 4.

A comparison of Beethoven’s theme might be made with, for example, the slow movement of Mozart’s Sonata K. 283: both pieces feature a filling-in of the dominant arrival that results in a V. However, while the structural melody in the “Pathétique” example remains static in mm. 1–4, the Mozart sonata descends from $\hat{3}$ to $\hat{2}$ in m. 2 (under R=2N).

Vasili Byros employs Gjerdingen’s terminology to describe the basic ideas of this theme as “Passo Indietro. . .Cadenza Semplice” (2013, 221). According to Gjerdingen, a Passo Indietro is a “descent in the bass from $\hat{4}$ to $\hat{3}$. . .most strongly characterized [by] the pair of thoroughbass figures 6/4/2 and 6/3, usually shortened to 4/2 and 6” (2007, 167). In other words, it characterizes V proceeding to I⁶, for which the vii^o in parentheses in our Figure 5b could be seen as a substitute. A Cadenza Semplice, on the other hand, refers simply to the $\hat{5}$–$\hat{1}$ bass progression (Gjerdingen 2007, 141).

Copyright Statement

Copyright © 2022 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.