An Idiom of Melodic-Harmonic Divorce: Sub-Circle Motion in Popular Music*
S. Alexander Reed
KEYWORDS: popular music, rock, melodic-harmonic divorce, deceptive cadence, chromatic mediant, sub-circle motion
ABSTRACT: Within the stratified harmonic behavior known as melodic-harmonic divorce, this paper identifies a gesture repeated idiomatically across rock repertory. Dubbed “sub-circle” motion, this idiom is specifically a form of syntax divorce wherein a melodic layer unfolds in a way consonant with and suggestive of circle-of-fifths root motion (+P4) between two accompanying major chords; however, the harmonic layer’s root instead moves up by a minor third (+m3), creating a stratified dissonance, or divorce. The paper then identifies a standard set of paradigms—specific transpositional instances of the idiom—and catalogues numerous examples of their use in rock music. One paradigm, V-
DOI: 10.30535/mto.28.2.6
Copyright © 2022 Society for Music Theory
1.1 An Idiom of Melodic-Harmonic Divorce
[1.1.1] David Temperley (2007, 328) shows that in rock, “pitch organization is stratified: there are different frameworks for the melody and accompaniment.” In moments of so-called melodic-harmonic divorce (MHD), “the listener senses
[1.1.2] Drew Nobile (2015) lends further granularity to the discussion by indicating three ways that musical strata operate with harmonic independence. The first of these is hierarchy divorce, in which a melody articulates a stable harmonic orientation (typically around the tonic triad) while the accompaniment chords change at a comparatively shallow stratification: these superficial chords are “analogous to melodic non-chord tones and are either prepared by or resolve into structural harmonies” (193). The second, loop divorce, arises when, in a song marked by a recurring accompanimental chord loop, a melody maps its own apparent progression in order to attain a more dramatic shape than the nominal harmony provides. The third is syntax divorce, in which both melody and harmony converge upon “a cadence or other structural motion but in incompatible ways” (189).
[1.1.3] I seek to deepen our understanding of these phenomena by describing and itemizing a common but previously unrecognized idiom of MHD, and specifically of syntax divorce. Within rock practice primarily of the late twentieth century, I identify a family of progressions wherein the melodic layer is consonant with (and suggests) circle-of-fifths root motion (+P4) from one accompanying major triad to the next, but the harmonic layer’s root moves up instead by a minor third (+m3). Because the new chord has a local subtonic relationship to the expected root, I refer to this behavior with the portmanteau sub-circle motion.(2) This necessarily creates a stratification or divorce between the melodic layer and the harmonic and bass layers. I theorize sub-circle motion in both its general archetype and its individual paradigms.
[1.1.4] Beyond detailing MHD phenomena, this article considers the wider narrative of rock. I give special attention to the most significant paradigm of sub-circle motion, a deceptive cadence (DC) resolving from V to
1.2 Describing Sub-Circle Motion
Example 1. Archetype of voices in sub-circle motion
(click to enlarge)
[1.2.1] Example 1 offers an archetype of sub-circle motion. Its top voice indicates the melodic stratum, and its bottom voice indicates the root motion of the harmonic stratum, from which inner voices derive.
[1.2.2] As a grammatical behavior in popular music harmony, sub-circle motion contains the following required features:
- The motion of one melody note to the next (allowing for intervening embellishment) is consonant with circle-of-fifths root motion.
- The harmonic layer’s first chord is built on a major triad.
- Its second chord, also major, arrives not by +P4 root motion but by +m3, thus creating a stratified dissonance between the new chord root and the melodic resolution.
[1.2.3] Additional factors strengthen the unique function of this idiom. Given a pair of successive simultaneities that fulfills all required features, the more of the following optional features the pair exhibits, the more audible and unambiguous its sub-circle motion.
- Both chords in the harmonic layer are in root position.
- The melody moves, by step, to a major ninth above the new chord root (that is, it moves to the root of the expected circle-of-fifths chord).
- In unembellished rhythmic unison between melodic and harmonic strata, the second simultaneity arrives on a hypermetric accent, with a cadence being the strongest emphasis.
[1.2.4] Before this article explores particular uses of sub-circle motion, a few qualifying statements are needed. Musical examples are chiefly selected for their clarity of sub-circle motion. But, as with MHD itself and its subcategories, ambiguous cases and weak instances exist—and I shall occasionally cite them when they illustrate the idiom in nascent forms, as with Example 7. Furthermore, it is important to acknowledge that our expectations of rock and pop harmony are by no means bound to circle-of-fifths motion. Nonetheless, de Clercq and Temperley (2011, 63) reveal +P4 root motion as the single most common succession in their “RS 5 x 20” corpus of historical popular music. Its 2,266 occurrences in their 1955–1997 repertory far outweigh the 410 occurrences of +m3. From this I assert, borrowing a phrase from de Clercq (2019, 278), that the harmonic layer (with attached bass) is usually the “renegade element” in a sub-circle motion’s stratification, breaking away from the melody’s lead.
[1.2.5] Understanding the importance of melody among these strata refines our approach to labeling the phenomenon. To classify a sub-circle melodic arrival as a mere non-harmonic tone is to misapprehend the comparative structural depths of melody and harmony—to get the identity of the renegade element wrong. Nobile (2015, 198) writes of situations where structural formulas for melodic and harmonic progression are “conceptually prior” to the simultaneities they produce. Sub-circle motion is such a situation. But when he asserts that a syntax divorce’s resulting “‘chord’ is simply the by-product of two coincident but separately unfolding processes,” he continues, “It ultimately does not matter whether we call” the melodic note a non-chord tone or specify it with “add” notation (198). I think in this case it does matter. As examples will demonstrate, the stylized sound of sub-circle motion is so widespread and repeated in rock that listeners can learn to hear it with a kind of oneness.
[1.2.6] For these reasons of strata relations and idiomatic pervasiveness, I opt to use “add” notation in labeling the second simultaneity of a sub-circle gesture. This acknowledges that the stratification (e.g., of the ninth in the melody) does not rely upon tertian extensions of the underlying chord (e.g., the seventh), and is in fact clearest in their absence. It also situates the move expressly in a popular music context, where “add” is standard label. The notation admittedly falls short of fully indicating the melody’s situational primacy; where I write V–
[1.2.7] Sub-circle motion is necessarily a type of chromatic mediant progression, yet the harmonic function of its +m3 arrival nonetheless can situationally resemble that of the expected +P4 root motion.(3) This is an instance of “functional multivalency,” a quality whose presence in popular music Christopher Doll (2017, 64) convincingly theorizes (wherein for example, “V can function in more than one way: it is not necessarily a dominant, and not necessarily just a dominant”). Nobile (2016) reinforces Doll’s findings.
1.3 Standard Paradigms of Sub-Circle Motion
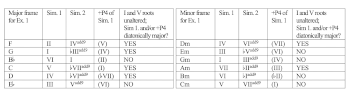
[1.3.1] Having described the general archetype and criteria for sub-circle motion, I now set the stage for a case-by-case consideration of the idiom’s standard paradigms. In rock music, what modal transpositions of successive +m3 major chords are grammatical? The most abundant and most convincing sub-circle paradigms derive from frames where the first simultaneity of the pair and/or its expected +P4 resolution are diatonically major within a song’s tonality, as represented by its nominal key signature. An additional factor delimiting standard uses of sub-circle motion is that in rock, the tonic and dominant as chord roots are chromatically inflexible, and so minor-mode gestures of VI–
[1.3.2] Transpositional paradigms of sub-circle motion contravening these tendencies are possible but nonstandard in popular music, growing less common and less idiomatic as they rely more on chromatic alterations. For instance, in major-mode gestures of VI–Iadd9 and III–V add9, neither of their first simultaneities nor their +P4 cousins are diatonically major, which makes them very difficult for a melodic stratum to suggest. Minor-mode gestures of I–
Example 2. Sub-circle paradigms derived from tonal framings of Example 1
(click to enlarge)
[1.3.3] Recall that in the sub-circle archetype of Example 1, a melody resolves from B to C atop root-position major chords moving from G to
2.1 II–IVadd9
Example 3. Foo Fighters: “Long Road to Ruin” (2007) [@0:52]
(click to enlarge and listen)
[2.1.1] Although not the most common sub-circle paradigm, II–IVadd9 appears across popular music. Exemplary is the chorus of Foo Fighters’ 2007 single “Long Road to Ruin” (#1, Billboard Modern Rock). As shown in Example 3, the C-major melody on the lyric “no tomorrow, no dead end in sight” appropriately suggests an open cadence, complete with its secondary leading tone of
Example 4. Pink Floyd: “One Slip” (1987) [@1:29]
(click to enlarge and listen)
[2.1.2] Similarly voicing a II–IVadd9 gesture is Example 4, Pink Floyd’s 1987 single “One Slip” (#5, Billboard Mainstream Rock Tracks). In the key of
[2.1.3] These examples underscore the reliance of II–IVadd9 on cadential coordination.(7) Not all paradigms, as I will show, are so entwined with hypermetric accent, but it is instructive to compare Examples 3 and 4 with other instances of II–IV motion in popular music. By far, the gesture’s most common appearance is within a looping I–II–IV–I progression (per Donovan’s “Atlantis”), in which the third chord is unlikely to offer even a local melodic arrival, much less a stratified one. In these cases, rhythm and phrasing offer little support to the upward tendency of a melodic
[2.1.4] More to the point, the heart (and perhaps the historical origin) of I–II–IV–I is the chromatic descent –
[2.1.5] Naphtali Wagner (2003, 354) gives theoretical context to similar behavior in the Beatles’ music. Much of pop’s harmonic innovation began with the characteristic “blue notes” of blues practice. Over time, musicians inventively reharmonized such blue notes, making chord tones out of what previously had been local dissonances: “these notes may achieve their own independent harmonization, thereby being domesticated and turning into ‘environment-friendly’ consonant notes,” writes Wagner. He continues, “This domesticating, consonantizing process led the Beatles to invent original chord combinations that seem more acts of harmonic daring than attempts to sterilize basic rhythm & blues.” Vitally, the sub-circle uses of II–IVadd9 reflect an inversion of what Wagner describes. Where the Beatles sang blue notes and contextualized them as newly consonant, the melodies of Examples 3 and 4 follow traditional, un-blue formulas, but are contextualized—stratified—with newly dissonant chords.
2.2 IV–♭ VIadd9
Example 5. Nirvana: “On a Plain” (1991)
(click to enlarge and listen)
[2.2.1] The relative-minor reframing of II–IVadd9 is IV–
Example 6. The Chameleons: “Soul in Isolation” (1986) [@0:26]
(click to enlarge and listen)
[2.2.2] Because IV–
[2.2.3] Both Examples 5 and 6 at times buck against their ostensible mode. But I still hear the former as broadly major and the latter as broadly minor—even as both employ a similar IV–
2.3 I–♭ IIIadd9
[2.3.1] The next sub-circle paradigm I consider is I–
Example 7. Jimi Hendrix “Wait Until Tomorrow” (1967) [@0:29]
(click to enlarge and listen)
[2.3.2] One such early circumstance arises in Example 7, which transcribes the falsetto backing vocals of Jimi Hendrix’s 1967 “Wait Until Tomorrow.” In an act of remarkable text painting, Hendrix uses a version of the paradigm in the song’s
Example 8. Peter Murphy “Cuts You Up” (1989) [@2:30 & 5:14]
(click to enlarge and listen)
[2.3.3] Skipping ahead several decades we find a somewhat clearer case of the I–
Example 9. Oasis: “Go Let It Out” (2000) [@1:10]
(click to enlarge and listen)
[2.3.4] By 2000, the I–
Example 10. Linkin Park: “Somewhere I Belong” (2003) [@0:23]
(click to enlarge and listen)
[2.3.5] Released three years later is Example 10, Linkin Park’s hit “Somewhere I Belong” (#1, Billboard Mainstream Rock). Its signature guitar riff adheres strictly to the archetypical (major) - voice leading atop (minor-key) motion of I–III, followed by VI7–IV. Again, the effect is a stratified IIIadd9 sound in which the melody searches for a harmony where, per the lyric, it “belongs.”(12)
[2.3.6] The sub-circle arrival in this example is less hypermetrically accented than previous excerpts. But the passage brandishes all other features of sub-circle motion, and its I–IIIadd9 harmony is the clearest of all my examples. Cross relations and melodic ascending motion in this excerpt (and to a lesser extent in Example 6) constitute important ways to raise musical stakes and delimit the territory that phrases may traverse. Melody and harmony each embark, their stratified dissonance marking the incompatibility of their respective roadmaps. Thus the motion is still syntactic, if not cadential. Recall that Nobile (2015, 189) writes that in syntax divorce, “melody and harmony participate in a cadence or other structural motion
2.4 VII–♭ IIadd9
[2.4.1] The next standard paradigm in the order outlined by the chart in Example 2 is V–
Example 11. a-ha: “The Living Daylights” (1987) [@2:29]
(click to enlarge and listen)
[2.4.2] Example 11 is from a-ha’s 1987 James Bond theme song “The Living Daylights” (#5, UK singles). Here the second chorus proceeds to the bridge. Excepting the eighth-note retardation in the melodic resolution, this is a textbook VII–
Example 12. Fury in the Slaughterhouse: “Radio Orchid” (1993) [@1:14]
(click to enlarge and listen)
[2.4.3] Example 12 shows the prechorus approaching the chorus of “Radio Orchid,” a 1993 cut by Fury in the Slaughterhouse (#49, German singles). Its verse and chorus are in A minor, though the comparatively unstable prechorus hints momentarily at D minor and C major. The prechorus melody reaches a cadence by leading down from D to C while the bass moves from B to
Example 13. Snow Patrol: “Set the Fire to the Third Bar (ft. Martha Wainwright)” (2006) [@1:40]
(click to enlarge and listen)
[2.4.4] In Example 13, a similar action concludes the dolorous chorus of Snow Patrol’s “Set the Fire to the Third Bar (ft. Martha Wainwright)” from 2006 (#54, Billboard Hot 100). In B minor, the harmony moves at this cadence from VII to
[2.4.5] The locus of this paradigm implies much of its impact: being the minor-mode relative transposition of V–
2.5 V–♭ VIIadd9
[2.5.1] Within sub-circle motion, V–
Example 14. Starship: “Nothing’s Gonna Stop Us Now” (1987) [@1:13]
(click to enlarge and listen)
[2.5.2] Consider Example 14, from the first chorus of Starship’s hit of 1987, “Nothing’s Gonna Stop Us Now” (#1, Billboard Hot 100). The song uncorks a familiar I–vi–IV–V 1950s progression in
[2.5.3] In the song, later occurrences of the chorus resolve the final dominant chord to the tonic—in each case with an elision: first to the bridge, and thereafter to chorus repetitions that eventually fade out. This structure reinforces the role of
Example 15. Midnight Oil: “Warakurna” (1987) [@1:59]
(click to enlarge and listen)
[2.5.4] The deceptive
Example 16. U2: “Where the Streets Have No Name” (1987) [@1:54]
(click to enlarge and listen)
[2.5.5] In Example 16, U2 also employs the chord to conclude a verse in 1987’s “Where the Streets Have No Name” (#4, UK singles). Again coming out of dominant harmony,
3.1 The Deceptive ♭ VIIadd9
[3.1.1] A new kind of DC is at work in these examples, and this warrants clarification. Cadence is a less precise idea in popular music than in common-practice musical forms. Indeed Ken Stephenson (2002, 56) notes that rock style enforces no “necessity for all aspects of a piece to lead to simultaneous resolution.” Songs without melody or those based on chord loops and static grooves are especially likely to avoid such coordinated arrival. Stephenson’s language here (“all aspects”) is mindful of the stratification that allows for the divorce of melody and harmony—and for that matter, of bass, rhythm, lyrical rhyme and meter, and more. (The coda to David Bowie’s “Ashes to Ashes” offers a quick case study in such bewildering stratification.) Thus, in popular styles we should differentiate not merely between cadences’ harmonic paradigms, but also between single-stratum versus coordinated action. For my purposes (and per Nobile’s definition of syntax divorce), some metric alignment between melodic and harmonic arrival is a minimum requirement for a cadence.
[3.1.2] The DC creates surprise by presenting an alternative to an expected tonic chord. Writing of classical style, Caplin (1998, 101) stipulates that in a deceptive cadence, the expected “final tonic is replaced by a related harmony, one usually built over the sixth scale-degree in the bass.” In their undergraduate textbook, Stefan Kostka and Dorothy Payne (1995, 157) describe the DC in looser and more rock-compatible terms: the cadence’s first chord “contains [the] leading tone” and its second chord is simply “not tonic.”
[3.1.3] Harmonically, popular music allows for cadential motion (at least hypothetically) between any two chords. But melodically, cadence formulas are more limited: “If any standard patterns of melodic cadence exist,” Stephenson writes (2002, 64), they ultimately derive from “certain frequent harmonic combinations ending on the tonic chord.” (He specifies approaches from IV and extensions of V.) In practice this most often means stepping or holding to , , or . To reconcile these standard melodic tendencies with rock’s “common avoidance of [harmonic] cadential closure” is therefore to glimpse why “not tonic” resolutions are stylistically important. (69)
[3.1.4] The
[3.1.5] For all that Moore discusses
[3.1.6] The deceptive
[3.1.7] Theorists wishing to explore individual cases of the deceptive
[3.1.8] Stephenson (2002, 70) notes that in rock, “totally coordinated resolution” is strikingly rare, and often “leaves the listener no room to doubt the sincerity” of its musical moment. We expect authentic cadences more in heartfelt power ballads than dance tracks—regardless of whether those expectations are fulfilled or subverted. It is safe to say that as a pop cadence with power to substitute for V–I motion, V–
3.2 Historical Readings of the Deceptive ♭ VIIadd9
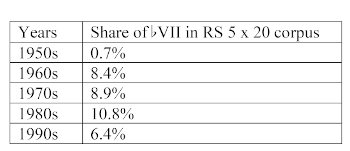
Example 17. Percentage of
(click to enlarge)
[3.2.1] At a glance, the examples I offer suggest (even above and beyond my undeniable selection bias) that this cadence was most popular during the 1980s. In Example 17, de Clercq and Temperley (2011, 64) trace the
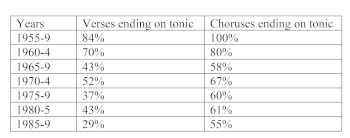
Example 18. Percentage of song sections ending on tonic harmonies in Summach’s corpus over time
(click to enlarge)
[3.2.2] This timeline is consonant with a narrative in which the apparently sudden emergence of
[3.2.3] These findings duly support the idea, which Stephenson (2002) hints at, that as rock has become a style over time separate from its ancestors, it has grown less concerned with cadences at all. (Looking ahead, the decline of the subtonic’s share in rock harmony during the 1990s accords with a decline in popularity of the cadence-reliant ballads discussed in [3.1.7–3.1.8]. After all, 1990s pop boomed with groove- and loop-based practices that avoided chromaticism and are thus incompatible with sub-circle motion. And ascendant in them we can hear popular music’s modern era, comparatively detached from the legacies of both the Great American Songbook and classic blues.)
[3.2.4] I propose that popular music’s adoption of
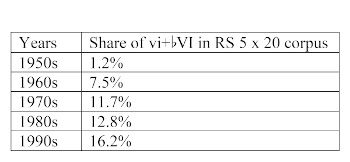
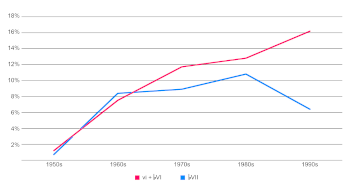
Example 19. Percentage of vi+
(click to enlarge)
Example 20. Total percentage of vi+
(click to enlarge)
[3.2.5] More convincingly, as we dive deeper into the timeline of popular music, we see the submediant’s use correlating closely with that of the subtonic. Example 19 shows the percentage shares of vi+
[3.2.6] From the 1950s through the 1980s, as Example 20 shows,
4.1 Future Avenues and Conclusion
[4.1.1] In 2000, ethnomusicologist Chris McDonald (356) asked, “Are there any techniques of rock harmony that, perhaps as a result of cross-pollination or synthesis, have emerged as distinctive or unique?” By now there is no doubt that the answer is yes. Discussions of popular music’s MHD have productively introduced categories of stratification, such as Nobile’s three aforementioned types and de Clercq’s bass-harmonic divorce. This paper’s contribution is in recognizing idioms of stratification. Many potentially exist; for now I call attention to sub-circle motion, an idiom of syntax divorce that has recurred with consistency, flexibility, and durability across decades of repertory. Within sub-circle motion, the deceptive
[4.1.2] This article is foremost concerned with laying a groundwork, and our understanding of sub-circle motion may yet be refined or expanded. Paradigms exist beyond the standard set I explore, such as those marked NO in Example 2, or chromatic transpositions. Some of these rare gestures appear in rock repertories, but most await intrepid songwriters of the future.(22) I have also not explored the degree to which the second chord’s status as a substitute for a circle-of-fifths progression is affected by particular melodic outlines, or by precedents either in a given song or a wider corpus (e.g., that of an artist or a genre). Toward expansion, effects similar to sub-circle motion are possible in other chord progressions—especially bearing in mind the aforementioned concept of functional multivalency.(23)
[4.1.3] Worthy too of immediate attention is the idiom’s appearance in broader repertories. Nearly all examples above are from rock music made between 1980 and 2010, and while they serve to situate this paper’s argument tightly within history and genre, the demographics of musicians represented testify troublingly to rock’s overwhelmingly white and male frame. Venturing into other popular styles, one finds sub-circle motion in the works of Earth, Wind, & Fire (V–
[4.1.4] Finally, the historical hypotheses regarding the deceptive
S. Alexander Reed (he/him)
Whalen Center for Music
Ithaca College
953 Danby Rd
Ithaca, NY 14850
sreed@ithaca.edu
Works Cited
Biamonte, Nicole. 2010. “Triadic Modal and Pentatonic Patterns in Rock Music.” Music Theory Spectrum 32 (2): 95–110. https://doi.org/10.1525/mts.2010.32.2.95.
Caplin, William E. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. Oxford University Press.
—————. 2013. Analyzing Classical Form: An Approach for the Classroom. Oxford University Press.
Capuzzo, Guy. 2004. “Neo-Riemannian Theory and the Analysis of Pop-Rock Music.” Music Theory Spectrum 26 (2): 177–99. https://doi.org/10.1525/mts.2004.26.2.177.
Chenette, Timothy. 2014. “Secondary Dominants in Rock and Pop.” Music Theory Bridges (blog), November 3, 2014. Accessed October 12, 2019. https://musictheorybridges.wordpress.com/2014/11/03/secondary-dominants-in-rock-and-pop/'.
de Clercq, Trevor. 2019. “The Harmonic-Bass Divorce in Rock.” Music Theory Spectrum 41 (2): 271–84. https://doi.org/10.1093/mts/mtz006.
—————. 2021. “The Logic of Six-Based Minor for Harmonic Analyses of Popular Music.” Music Theory Online 27 (4). https://doi.org/10.30535/mto.27.4.4.
de Clercq, Trevor, and David Temperley. 2011. “A Corpus Analysis of Rock Harmony.” Popular Music 30 (1): 47–70.
Doll, Christopher. 2013. “Definitions of ‘Chord’ in the Teaching of Tonal Harmony.” Tijdschrift voor Muziektheorie (Dutch Journal of Music Theory) 18 (2): 91–106.
—————. 2017. Hearing Harmony: Toward a Tonal Theory for the Rock Era. University of Michigan Press. https://doi.org/10.3998/mpub.3079295.
Everett, Walter. 2004. “Making Sense of Rock’s Tonal Systems.” Music Theory Online 10 (4). https://www.mtosmt.org/issues/mto.04.10.4/mto.04.10.4.w_everett.html.
—————. 2009. The Foundations of Rock: From “Blue Suede Shoes” to “Suite: Judy Blue Eyes.” Oxford University Press.
Forrest, David L. 2017. “PL Voice Leading and the Uncanny in Pop Music.” Music Theory Online 23 (4). https://doi.org/10.30535/mto.23.4.6.
Kostka, Stefan, and Dorothy Payne. 1995. Tonal Harmony with an Introduction to Twentieth-Century Music. 3rd ed. McGraw-Hill.
Lehman, Frank. 2014. “Film Music and Neo-Riemannian Theory.” Oxford Handbooks Online. Accessed November 2, 2019. https://doi.org/10.1093/oxfordhb/9780199935321.013.002.
McDonald, Chris 2000. “Exploring Modal Subversions in Alternative Music.” Popular Music 19 (3): 355–63. https://doi.org/10.1017/S0261143000000210.
Moore, Allan F. 1992. “Patterns of Harmony.” Popular Music 11 (1): 73–106. https://doi.org/10.1017/S0261143000004852.
—————. 1995. “The So-Called ‘Flattened Seventh’ in Rock.” Popular Music 14 (2): 185–201. https://doi.org/10.1017/S0261143000007431.
—————. 2012. Song Means: Analysing and Interpreting Recorded Popular Song. Ashgate.
Nobile, Drew. 2015. “Counterpoint in Rock Music: Unpacking the ‘Melodic-Harmonic Divorce.’” Music Theory Spectrum 37 (2): 189–203. https://doi.org/10.1093/mts/mtv019.
—————. 2016. “Harmonic Function in Rock Music: A Syntactical Approach.” Journal of Music Theory 60 (2): 149–80. https://doi.org/10.1215/00222909-3651838.
Peres, Asaf. 2016. The Sonic Dimension as Dramatic Driver in 21st-Century Pop Music. PhD diss., University of Michigan.
Schmalfeldt, Janet. 1992. “Cadential Processes: The Evaded Cadence and the ‘One More Time’ Technique.” Journal of Musicological Research 12: 1–51. https://doi.org/10.1080/01411899208574658.
SMT-Talk Archives. 2009a. Threads from August 16–31. Accessed Oct. 12, 2019. http://lists.societymusictheory.org/pipermail/smt-talk-societymusictheory.org/2009-August/thread.html#3026.
SMT-Talk Archives. 2009b. Threads from September 1–28. Accessed Oct. 12, 2019. http://lists.societymusictheory.org/pipermail/smt-talk-societymusictheory.org/2009-September/thread.html#3053.
Stephenson, Ken. 2002. What to Listen for in Rock: A Stylistic Analysis. Yale University Press. https://doi.org/10.12987/yale/9780300092394.001.0001.
Summach, Jason. 2012. Form in Top-20 Rock Music, 1955–89. PhD diss., Yale University.
Temperley, David. 2007. “The Melodic-Harmonic ‘Divorce’ in Rock.” Popular Music 25 (2): 323–42. .
Tymoczko Dmitri. 2003. “Root Motion, Function, Scale-degree: A Grammar for Elementary Tonal Harmony.” Musurgia. X (3–4): 35–64.
Wagner, Naphtali. 2003. “‘Domestication’ of Blue Notes in the Beatles’ Songs.” Music Theory Spectrum 25 (2): 353–65. https://doi.org/10.1525/mts.2003.25.2.353.
Footnotes
* I am grateful to Trevor de Clercq, Jeffrey Perry, Drew Nobile, and an anonymous reviewer for their comments and suggestions on this research.
Return to text
1. In a 2019 article, Trevor de Clercq amends the melodic-harmonic dualism to include bass as a third stratum, able to move independently of the harmonic layer. And one can suppose that even more than three strata are theoretically possible. With just one exception (Example 7), the song excerpts I discuss in this article make no meaningful use of bass-harmonic divorce, given that their bass and harmonic layers are “married.”
Return to text
2. The neo-Riemannian expression of this move is PR (parallel, e.g., C to C minor, then relative, e.g., C minor to
Return to text
3. As stated in the previous note, this is neo-Riemannian operation PR.
Return to text
4. These paradigms especially overlap with rock’s use of modal subversion as described by McDonald (2000).
Return to text
5. In this article, capitalized Roman numerals always indicate major harmonies. I do not notate secondary dominants because sub-circle motion specifically resists their fulfillment and arguably their function.
Return to text
6. “One Slip” hints variously at
Return to text
7. In 2009, the email discussion list of the Society for Music Theory exchanged over a hundred messages in a thread about this chord succession, beginning with a citation of Donovan’s 1968 “Atlantis” and ultimately finding related motion in (among others) ABBA, Snoop Dogg, William Byrd’s setting of “The Hunt’s Up,” and Antonín Dvořák’s Symphonic Variations op. 78, var. 5. See SMT-Talk Archives (2009a; 2009b).
Return to text
8. Cee-Lo Green’s 2010 “Forget You” employs the I–II–IV–I chord loop, and its title hook emphatically voices the fifth scale degree over IV, but this behaves as much like a hierarchy divorce as it does a syntax divorce—owing to the note’s lack of stepwise approach, its weak-beat, mid-phrase arrival, and the melody’s greater implication of the tonic triad than the dominant.
Return to text
9. Nirvana’s music is infamous for precisely this sort of dissonance. See McDonald (2000) for more.
Return to text
10. It is initially possible to hear the chorus in
Return to text
11. This excerpt is framed on both sides by A major, but if one hears it in D, then the active paradigm is V–
Return to text
12. This is the single minor-mode example of I–
Return to text
13. As tests of alternative classifications: we should not simply call the melodic atop III a non-chord tone, as it occupies the entire measure without deferring; nor is it a clear case of hierarchy divorce, given that the dissonance doesn’t derive from the melody’s prolonged tonic harmony but instead from linear motion; nor is it a loop divorce, given that no harmonic loop is established as separate from the melody.
Return to text
14. Because the present article introduces a generalized phenomenon of sub-circle motion, I choose to acknowledge each standard paradigm of general possibility without attempts to collapse them. I am sympathetic to de Clercq’s recommendations such as his advocacy of “six-based minor” and the Nashville number system. At this early stage, however, I wish to retain two important considerations regarding sub-circle phenomena. First, Roman numeral notation (including its affordance of the minor tonic i) underscores the way these gestures reinscribe functional tonality—even to a degree that appropriately marks them as old fashioned, per [3.1.6], [3.1.8], and their footnotes. Second, I do not want to flatten certain distinctions between relative reframings, such as the strong hypermetric tendency of II–IVadd9 that IV–
Return to text
15. It is true that in Example 14, Starship uses a synthesizer to arpeggiate through the
Return to text
16. In the corpus of de Clercq and Temperley, +M2 chord motion occurs 1,384 times to +m3’s 410, and more specifically (61),
Return to text
17. As ever, there are idiosyncrasies: Bono’s subtonic neighbor tone at the end of the chorus over V (“all I can do” at 3:11) is particularly intriguing. In a cover version, the Pet Shop Boys use an unflattened leading tone briefly over the subtonic chord.
Return to text
18. Historicizing rock’s largely premillennial harmonic language is important, especially because post-2000 popular music offers new and alternative sonic strategies for navigating form. Asaf Peres (2016, 39) boldly asserts that pop since 2011 “has largely abandoned harmonic function as a means of achieving tension and release.”
Return to text
19. Less straightforwardly cadential V–
Return to text
20. de Clercq and Temperley do not indicate how many of these uses occur within major- versus minor-mode songs, though some of this blues-based corpus vexes that binary anyway.
Return to text
21. To this effect,
Return to text
22. For example, in “Radio Free Europe,” REM’s 1981 debut single for Hib-Tone Records, the first utterance of the lyric “radio station” at 0:18 may potentially be heard as VI–Iadd9, though it is also locally analyzable as II–IVadd9.
Return to text
23. For instance, the final moments of Nine Inch Nails’ 1989 “Something I Can Never Have” prepare a plagal cadence, but instead of a conclusive tonic, the harmonic layer stratifies to
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
11337