The Poetics and Politics of Ambiguity: Overtone Structures and Equal Temperament in Works by Julian Anderson and Rand Steiger*
Alex Stephenson
KEYWORDS: harmonic series, overtonality, just intonation, equal temperament, microtonality, macrotonality, political music, Julian Anderson, Rand Steiger
ABSTRACT: The use of the harmonic series as a pitch-generating resource is a significant trend in twentieth- and twenty-first-century composition. While the principle of equal temperament prioritizes an additive understanding of intervals, the harmonic series implies a ratio-based approach to pitch relationships. Despite these philosophical differences and the sometimes polemical debates that have attended to them, the works of Julian Anderson (1967–) and Rand Steiger (1957–) draw simultaneously on overtone-based and equal-tempered harmonic thinking. These two composers are part of a group of musicians who have proposed various hybrid approaches to harmonic construction, and their works are also notable for playing out interactions between these influences in ways that reflect the composers’ political concerns. In this paper, I combine examinations of Anderson’s and Steiger’s characteristic harmonic strategies with close analyses of two quartertone-based works: Anderson’s Eden (2005) and Steiger’s Post-truth Lament (2017). I use these discussions to consider the pieces’ diverse political resonances. Ultimately, I argue that their hybrid harmonic approaches serve to highlight the multifaceted implications of ambiguity—not only its musically generative potential, but also its capacity to transform contemporary political life in ways both corrosive and constructive.
DOI: 10.30535/mto.28.2.8
Copyright © 2022 Society for Music Theory
[1] This essay examines the harmonic constructions and political engagements of two recent works: Eden (2005) by Julian Anderson (1967–) and Post-truth Lament (2017) by Rand Steiger (1957–). Both Anderson and Steiger draw on the harmonic series as a resource for generating pitch materials, yet their works also show significant influence from other conceptions of pitch rooted in equal temperament. At first glance, these compositional interests might seem to exist in a state of uneasy tension. The harmonic series, which underlies many pitched instruments’ basic acoustical properties, is a theoretically infinite collection of frequencies (overtones or partials) that are whole-number multiples of some base frequency (fundamental). By contrast, equal temperament (ET) understands pitches to be related not by integer frequency ratios but instead by an additive grid of distance intervals. Twelve-tone equal temperament (12-TET), a type of ET that divides the distance between pitches whose frequencies are in a 2:1 ratio (i.e., an octave) into twelve equal steps, has been a particularly dominant pitch-organizing force in Western music-making for several centuries. I suggest that in Anderson’s and Steiger’s works, these different conceptual structures interact in musically generative and politically suggestive ways.
[2] Anderson was born and primarily trained in the United Kingdom, where he also currently lives and teaches. In addition to a longstanding interest in Eastern European folk music, Anderson cultivated an affinity for overtone-based concepts early in his career through encounters with spectral composers such as Tristan Murail, with whom he studied, and Horațiu Rădulescu (Julian Anderson, interview via Zoom, June 2, 2021). Steiger, meanwhile, had his earliest musical encounters in New York but has spent much of his career in Southern California, where he has explored both 12-TET and microtonal conceptions of harmony. In addition to significant training in 12-TET set-theoretic techniques, he developed an early interest in the harmonic series through the work of Morton Subotnick, who was among his teachers (Rand Steiger, interview via Zoom, May 17, 2021).
[3] A composer myself, I count these two musicians among my most significant mentors, and I initially sought to study their works in order to understand how my approaches to harmony are both influenced by and distinct from two composers with whom I have shared working relationships over several years. As I embarked on this research, however, I came to sense that Anderson’s and Steiger’s pluralistic harmonic strategies suggest striking alternatives to the binary-infused divides that have historically characterized debates about tuning and harmony. So, too, did I become increasingly interested in how these composers’ hybrid approaches reflect their political concerns and express in sound their understandings of the world. Anderson’s and Steiger’s harmonic strategies embody notions of ambiguity, a notable act in a musical landscape often dominated by clear-cut extremes and one which, moreover, has various resonances with contemporary political life.
Theoretical and Historical Contexts
[4] Music-theoretical thought has a long history of engagement with the harmonic series; for instance, theorists from Rameau to Schoenberg have claimed that its low partials generate the major triad. More recent harmonic series-interested composers, including Anderson and Steiger, have also worked with higher partials of the series beyond those arguably utilized in historical tonal styles. Picking up on the variety of musical results toward which the series can seemingly be put, Daniel Harrison defines the term “overtonality” as a property of “any tonal hierarchy that relies on spectral overlap for its stability conditions” and thus “freely imitates the tonal hierarchy modeled in the overtone series” (Harrison 2016, 17). For Harrison, however, works that focus on upper overtones of the series sometimes lead to complex relationships between overtonality as a compositional device and overtonality in perceptual reality; at times, Harrison says, the listener might be able to experience representations of high partials as elements within a palpable hierarchy centered on some fundamental frequency, while at others it might be far more challenging to perceive such a relationship.(1) Much of this article is concerned with the fluctuating degrees to which Anderson’s and Steiger’s harmonic languages invite “overtonal” hearings—whether, to what extent, and in what ways we might perceive these composers’ pitch choices in relation to a harmonic series-based framework.
[5] Pushed to its furthest logical extent, overtonal thinking leads to a subset within the broader field of just intonation (JI), which holds that pitches should be tuned precisely in accordance with whole-number frequency ratios. Many recent JI advocates have explored ratios involving prime numbers higher than those useful for tuning earlier tonal repertoires in order to generate novel pitch resources. Building on work by Harry Partch, the composer and theorist Ben Johnston refers to this expansion of the useable ratio palette as “extended just intonation” ([2003] 2006). Johnston invokes matters of listener perception and comprehensibility to explain his interest in relating pitches by ratios rather than tempered distance intervals:
Interval-scale thinking emphasizes symmetry of design. The harmonic and tonal meaning of symmetrical pitch structures is ambiguity. Chordally they produce either a sense of multiple root possibilities or of no satisfactory root possibility. Tonally they cause either a sense of several possible tonics or of no adequate tonic.
Ratio-scale thinking, on the contrary, emphasizes a hierarchical subordination of details to the whole or to common reference points. The harmonic and tonal meaning of proportional pitch structures is clarity and a sense of direction. (Johnston 1964, 74; italics original)
Johnston thus seems focused on the “senses” that these opposing methods of pitch organization might arouse: while two pitches related by integer frequency ratios share a “common reference point”—i.e., a governing fundamental frequency—and thus engender “clarity,” pitches separated by a tempered interval do not have this property and therefore promote “ambiguity.” Johnston also brought these ideas into his own compositions; he designed an elaborate notation system in which every pitch’s meaning is fixed according to a particular ratio-based derivation and sought to establish a performance practice for achieving such just-tuned intervals in acoustical reality.
[6] Johnston set forth these proposals in the mid-1960s, when totalizing ideologies of harmony frequently characterized the musical discourse around him. In particular, methods of constructing atonal harmonic languages via 12-TET pitch-class serialization wielded considerable influence, especially in the United States. As Anne Shreffler notes, American discussions around serial techniques were shaped early on by the ideological zeal of post-Schoenberg European writers such as René Leibowitz, and their increasing adoption was then widely inflected with the language of objective scientific progress and academic prestige (Shreffler 2000). In a 1963 article, meanwhile, Charles Wuorinen attempts to position dodecaphony as an unquestioned lingua franca for composers of his generation—one “so familiar that there is today hardly a conscious decision on their part in employing it” (Wuorinen 1963, 57). As Wuorinen himself acknowledges, this attitude toward composition assumes the 12-TET conception of pitch class to be axiomatic (Wuorinen 1979, 5).(2) Around this time, other leading composers and theorists associated with atonal pitch-class-based techniques, such as Milton Babbitt ([1965] 1972) and Allen Forte (1955), also broke with earlier generations of writers and launched broad challenges to the harmonic series’ relevance in music-making. For these reasons, composers whose interest in overtone-based relationships led them to conceive of pitches between the cracks of the modern Western keyboard felt excluded from the mainstream discourse; Joel Mandelbaum, for instance, gave a talk at the 1967 meeting of the American Society of University Composers entitled “The Isolation of the Microtonal Composer” (Mandelbaum 1967). Mandelbaum argues that, despite the rich theoretical promise of working beyond the boundaries of 12-TET, the then-mainstream avant-garde outlook had all but dismissed microtonal composition as a mere historical curiosity.
[7] In the face of this perceived hegemony, many JI proponents in turn couched their embrace of just intervals—and, equally, their rejection of ET—in polemical terms. For instance, Partch describes the piano keyboard’s octave divisions as “twelve black and white bars in front of musical freedom” (Partch 1991, 12), and Johnston speaks in two essays of his desire to “purify” Western music of the “adulterations” introduced by temperament (Johnston [2003] 2006, 63; 1987, 519) and calls ET an “acoustical lie” (Johnston [2003] 2006, 62). The inaugural issue of the JI journal 1/1 features an article in which its founding editor, David B. Doty, mirrors Wuorninen’s rhetorical strategy and claims that “the simple-ratio intervals of Just Intonation are the only musically meaningful entities from which melody or harmony are to be constructed” (Doty 1985, 15). Running throughout these comments is an apparent feeling that the gradual encroachment of ET-based thinking into Western music—one which, in Johnston’s telling, began with the fourteenth-century’s notational response to a burgeoning use of thirds and sixths as consonances and intensified with the widespread adoption of temperaments for keyboard instruments in the sixteenth and seventeenth centuries (Johnston [2003] 2006, 65)—has amounted to something of a slow-motion, centuries-long fall from grace. Indeed, surveying the language used by several generations of JI-oriented writers, Marc Perlman identifies a tendency to equate the practice of just intonation with “nature” and equal temperament with the “corruptions of civilization” (Perlman 1994, 516).(3)
[8] Anderson and Steiger are part of a group of composers who, rather than choosing clear sides in these opposing polemics of harmony, have experimented with more inclusive methods of pitch construction. Hybrid compositional strategies that allow overtonality to enter into dialogue with equal-tempered pitch structures can take at least two forms. The first form simply involves using equal-tempered grids to realize musical ideas that are derived from overtones or related acoustical phenomena. This is a notion with longstanding precedence. For instance, Ivan Wyschnegradsky’s Manual of Quarter-Tone Harmony, though primarily focused on deriving microtonal pitch resources from symmetrical distance intervals rather than frequency ratios, includes a discussion of how equal-tempered quartertones (24-TET) can be used to approximate a range of overtones, particularly the 11th partial and its octave transpositions (Wyschnegradsky [1932] 2017, 27–28). More recently, Ezra Sims has suggested dividing the octave into seventy-two equal parts (72-TET) as a means of even more accurately representing the harmonic series (Sims 1988); this tuning system appears not only in Sims’ music but also in works by James Tenney (Changes, 1985), Hans Zender (Bardo, 2000), and Georg Friedrich Haas (limited approximations, 2010), among others. Several strategies of dividing of the octave into numbers of pitches that are not multiples of twelve, such as nineteen (Yasser 1932) and thirty-one (Fokker 1955), have also been proposed on similar acoustical grounds. In other cases still, a composer might use none other than 12-TET itself as a grid for realizing overtonal harmonies, as in several of Unsuk Chin’s piano etudes (In C, 2003; Toccata, 2003) as well as certain early twentieth-century works, such as the piano preludes of Claude Debussy.(4) Lastly, many works of French spectralism, including those by Gérard Grisey and Tristan Murail, round the tunings of overtone harmonies and other frequency-based pitch structures to several of these equal-tempered grids, including 12-TET, 24-TET, and others.(5),(6)
[9] A second, sometimes overlapping sense in which a composer might hybridize influences from both the harmonic series and ET involves treating these structures’ theoretical differences as a prompt for generating a variety of harmonic configurations on the surface of their music. These might range between confirming, challenging, and even contradicting the listener’s ability to hear overtonally. One could include in this category works such as Magnus Lindberg’s Joy (1990), which invites the listener to hear 12-TET pitch sets both as isolated, atonal entities and as subsets of larger overtonal harmonies; Haas’ in vain (2000), which creates aurally frictious sonorities by transposing various just-tuned harmonic series through a 12-TET grid; György Ligeti’s Hamburg Concerto (2003), which similarly manipulates the harmonic series of natural horns; and Chin’s Double Concerto (2002) and Rocanā (2008), in which overtone-based chords interact with more atonal-sounding and often noise-colored materials. Beyond the boundaries of traditionally notated concert music, Pauline Oliveros explored a related interest in creating dialogues between different conceptions of pitch through the performing group The Space Between, which combined Oliveros’s custom just-tuned accordion with a shakuhachi and a 12-TET piano (Oteri 2000).(7)
[10] As I demonstrate below, Anderson and Steiger draw on both types of hybridity in their works. I suggest, furthermore, that these two composers utilize hybrid harmonic strategies in ways that connect to their views of the broader political landscapes around them, from Anderson’s celebration of multiplicity as an antidote to one-sided ideological dogmatism to Steiger’s alarm at the blurring of lines between truth and fiction in the United States’ political discourse.(8) This essay seeks to unpack the complex—indeed, to borrow a word from Johnston, ambiguous—manners in which these things happen in Anderson’s and Steiger’s works. To do so, I engage in analyses of two recent quartertone-based compositions: Julian Anderson’s Eden and Rand Steiger’s Post-truth Lament.
Julian Anderson: Eden
[11] In this section, I explore broad connections between Anderson’s political concerns, musical aesthetics, and technical approaches to tuning and harmony before turning to a more detailed discussion of his orchestral work Eden (2005). I consider how Eden evokes a constellation of ambiguities—both contrasts and overlaps, divergences and convergences—between the multiple conceptions of harmony that animate this composer’s practice.
[12] In a 2012 interview, Anderson identifies a spirit of “anti-fundamentalism” as one of his guiding musical and political principles:
I admit very happily into my music all the contradictions of the world I see and experience, which basically means I’m not a fundamentalist. In fact, everything I compose is anti-fundamentalist, and the regrowth of fundamentalism that we’ve seen in so many areas of life in the past thirty-five years is frankly repugnant to me. There’s no doubt that new music, too, has its fundamentalists: people who believe that all problems in composition can be solved by subscribing blindly to a single overriding aesthetic, for life. Such people admit no contradictions and are perhaps the greatest single danger to creativity (some of them teach composition, alas). Clearly, some people are very frightened by danger and ambiguity. I grew up in the 1980s, and the hideous political climate of that time—social and sexual intolerance, dogma against dogma, while society went to the bad—gave me a permanent allergy to all extremism and really left me wondering what to expect from politics. (Palmer 2015, 12)
Given his identity as an out gay man and decades-long involvement in LGBTQIA+ activism (Anderson 2020), Anderson’s stance of revulsion toward the intolerant climate of the eighties is surely one that is deeply and personally felt. Anderson also carries this position into an equally strong rejection of fundamentalism in the musical sphere, and it is notable how freely he seems to drift between music and politics in the comment above: these two spaces are, for him, evidently isomorphic and deeply interrelated. Placed side-by-side with Johnston’s advocacy for just tunings, moreover, Anderson’s evocation of “ambiguity” is particularly striking. That sensation, of which Johnston was suspicious and sought to replace with “clarity” through his eschewal of equal-tempered systems, is for Anderson something of a rallying cry—an antidote to the unflinching dogmas he sees around him.
[13] Anderson’s distaste for the easy answers of fundamentalism, and his preference instead for dialectical thinking, are at play in his approaches to pitch construction. In an email to the author, Anderson summarized his harmonic strategies as the result of an intricate dance between the inherent acoustical properties of instruments and culturally evolved tuning systems:
In any music, two contradictory factors are at play: 1) the tuning of pitch; this may well be but (as we know from many different cultures) does not necessarily have to be related to the lower partials of the harmonic series
. . . . Either way, in most cultures the question of tuning, whether extrapolated from resonance spectra or not, is usually expressed as a viable practical system which has to be playable at any speed in any register. This involves solving certain problems, and equal temperament solves them one way, whilst other systems solve them differently. But it is almost unheard of for a musical culture not to have any tuning system for its pitches. I never heard of one that didn’t. Once evolved, such systems take on a life of their own.2) The other factor is sound itself, and here we enter the realm of resonances pure and simple, regardless of tuning considerations. It is obvious that resonances are simply a property of the materials being used to make instruments, plus the shaping and treatment of those materials to construct the instruments concerned, and the manner in which they are played
. . . . These resonance considerations may well—and usually do—contradict any tuning system human cultures set up.These two factors seem to me to be central and in constant, if often unconscious, changing dialogue with each other
. . . . Any composer is taking a decision as to where they or their music stands in relation to the above issues, however unconsciously. And my music expresses my varying positions on these matters, sometimes. . . very explicitly. (Julian Anderson, email to the author, August 19, 2020)
Anderson is commenting here on a state of affairs that some JI proponents lament in their writings: that tuning systems such as 12-TET, once introduced, take on “a life of their own” and become culturally ossified. But for Anderson, this is not necessarily problematic; to the contrary, he seems to feel that it makes for a dialogue between different pitch structures ripe with opportunities for musical exploration. Anderson appears unbothered by the fact that such a rich network of influences might come to bear on one’s work, even if those influences are in conflict with one another. Even more notably, he acknowledges unapologetically that his own viewpoints on their interactions are multiple in nature and subject to change.
[14] Anderson uses his own harmonic system, which he calls “macrotonality,” for exploring interactions between overtone-based and equal-tempered frameworks.(9) Generally speaking, Anderson draws only from the set of 12-TET pitches to determine the fundamental for a given harmonic series, and within a series he focuses on partials no higher than the 13th, with octave transpositions of the first thirteen partials also allowed (Anderson and Dingle 2020, 422). Given these constraints, Anderson rounds a series’ 7th, 11th, and 13th partials to 12-TET pitches altered by equal-tempered quartertones, while the remaining partials are represented as unmodified 12-TET pitches (Anderson 2019). Anderson’s system thus takes as a starting point the first type of hybridity between overtonal and ET-based thinking introduced above—i.e., the incorporation of pitch relationships inspired by overtones into an equal-tempered (in this case quartertone-based) landscape.(10)
Example 1. The first thirteen partials of a C1 fundamental rounded to the nearest cent
(click to enlarge and listen)
Example 2. The first thirteen partials of a C1 fundamental rounded to the nearest equal-tempered quartertone
(click to enlarge and listen)
[15] Example 1 and Example 2 illustrate these principles by realizing a fragment of a harmonic series in two ways. Example 1 gives the first thirteen just-tuned partials of a C1 fundamental to the nearest cent, or hundredth of a 12-TET semitone. Example 2, meanwhile, realizes these same partials in a manner consistent with the macrotonal system, with all partials rounded to the nearest equal-tempered quartertone (50 cents). Note the varying degrees of tuning discrepancy that exist between the two versions. For instance, the quartertone-rounded 11th partial of Example 2 is within just one cent of its counterpart in Example 1. By contrast, rounding the 7th partial to the nearest quartertone results in a pitch nineteen cents “too flat” relative to a cent-precise realization.
[16] Eden, which was commissioned by the City of Birmingham Symphony Orchestra as part of a multi-year residency that Anderson held with that ensemble, is one of several compositions by Anderson to feature prominent applications of the macrotonal system. The title of the work is highly suggestive, conjuring images of an undefiled, paradisal terrain with which just-tuned sonorities have so often been associated. In its deployment of the macrotonal framework, however, Eden declines to stage the specific type of return to innocence—a full embrace of just intervals and an equally strong rejection of ET—that JI proponents have urged. Alternatively, picking up on a question posed of the work by Arnold Whittall, one might wonder if Eden attempts to portray through its mixing of overtonal and equal-tempered principles a fall from grace, a departure from purely just-tuned innocence instead of a reclaiming of it: “can Eden,” Whittall asks, “possibly have a happy ending?” (Whittall 2015, 15).
[17] Whittall ultimately seems to conclude that his question has no simple answer, and indeed, attempting to project clear-cut valences onto the harmonic language of Eden would be to run counter to the values of ambiguity at the heart of Anderson’s anti-fundamentalist stance. Instead of thinking in such binary-based terms, I suggest that to experience Eden is to notice how the macrotonal system’s theoretical intermingling of different conceptions of pitch engenders an ever-transforming network of sonic identities and possibilities on the surface of the music. Musics in Eden, as we will see, become locked in a teasing, intimate dance, constantly fusing and splitting, converging and diverging. In so doing, they give rise to the second type of hybridity—the overt musical reference to interactions between overtonal and equal-tempered musical constructs—discussed in the introduction to this essay.(11) In short, I suggest that diverse harmonic structures are invited to stage through sound their interactions, coexistence, and even symbiosis in Anderson’s variegated garden of Eden.
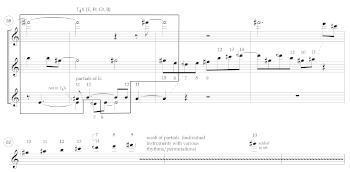
Example 3. Anderson, Eden, mm. 1–20
(click to enlarge, see the rest, and listen)
[18] Eden’s seven-minute duration is divisible into several short sections. The work begins with an introductory dialogue between unaccompanied viola and cello soloists, before much of the rest of the orchestra enters and joins in the exchange of melodic material. The viola and cello soli return in a central section, this time with orchestral accompaniment. Finally, a climactic passage gives way to a slow coda in which the viola and cello soli are again revisited. Example 3 shows the work’s opening passage.(12) The string soloists are asked to play slightly sul ponticello and without vibrato; according to Anderson, these playing techniques are intended to transform the standard timbres of these modern orchestral instruments into ones more reminiscent of Renaissance viols (Julian Anderson, interview via Zoom, June 2, 2021). Note also that Anderson’s pitch language in mm. 1–10 is confined entirely to a white-note diatonic set; this, too, seems as if it might evoke an imaginary, centuries-old, pre-chromatic music. Furthermore, and as if to drive these layered semiotic conjurings even further home, the solo lines are given an expressive marking of “innocente” (innocent), and the score’s tempo specification of half note = 66 comes with the instruction “come una musica virginale” (“like a virginal music”).(13)
[19] Given this context, the arrival of F(+¼)—i.e., F raised by a quartertone(14)—on the downbeat of m. 11 generates considerable surprise. An analyst familiar with Anderson’s praxis might recognize this as a telltale sign of the macrotonal system’s influence and conclude that this music was likely written with some harmonic series in mind. To hear this move to 24-TET through an overtonal lens in the moment, however, is a wholly different matter. To this listener’s ears, the totality of pitches heard up to this point do not cohere into an obvious overtonal picture; to the contrary, the F(+¼) feels jarring and disruptive relative to the exclusively 12-TET music that precedes it. I suspect my perception of rupture here is informed by the fact that the F(+¼) is approached from below by a D, forming what Wyschnegradsky terms a “neutral 3rd”—i.e., a minor 3rd widened by a quartertone or, conceived differently, a major 3rd narrowed by a quartertone (Wyschnegradsky [1932] 2017, 2). Absent any additional clarifying harmonic information, as is the case here, I tend to find it challenging to perceive pitches separated by this interval within some broader overtonal context. Indeed, Anderson appears to feel the same: he typically avoids melodic instances of the neutral 3rd (Anderson and Dingle 2020, 422) because he feels that it tends to present as a distracting “out-of-tune” version of nearby 12-TET intervals (Anderson 2019). It is striking, then, that he selects this as the interval by which to approach Eden’s first quartertone-altered pitch; within the context of Anderson’s harmonic idiolect, it seems to maximize the extent to which we might perceive it as a stark outsider to the preceding, more culturally familiar 12-TET set.(15)
[20] Yet this feeling of disorientation rapidly wanes as a more unifying overtonal hearing for the passage comes into focus in subsequent measures. Beginning in m. 14, 12-TET and quartertone-altered pitches intermingle in every measure of Example 3, with the neutral 3rd also notably being replaced by a proliferation of stepwise intervals; in m. 17, another non-12-TET pitch class,
Example 4. Reduction and analysis of Anderson, Eden, mm. 40–48.1
(click to enlarge and listen)
[21] What are we to make of these mercurial shifts? Eden’s next section (mm. 40–64), in which melodic material is now passed between many orchestral instruments, begins with an even more compressed survey of these same tendencies. At the same time, the passage further elucidates the harmonic paradigms that give rise to them. In mm. 40–48.1, which are reduced and analyzed in Example 4, F(+¼) is once again the focus of much of our attention, with its relationships to surrounding 12-TET pitches now negotiated along the axis of timbre. The example opens with a timbrally blended group of bassoons, horns, and harp articulating only a tetrachordal subset of the white-note 12-TET material first heard in mm. 1–10. This tetrachord, {C, D, E, G}, is boxed and labeled as X on Example 4 and will prove salient in much of the music that follows. Note in particular how the musical surface prominently draws our attention to the pair of 12-TET interval-class 5s, {G, D} and {C, G}, contained within the tetrachord.
[22] In a move reminiscent of m. 11, a retuned clarinet and keyboard suddenly cut in with an accented statement of F(+¼) in m. 42. This time, the note’s contrasts in timbre and articulation, in addition to its tuning, mark it as starkly distinct from the presentation of X that came immediately before, again making it perceptually challenging to posit overtonal hearings that encompass both the F(+¼) and the white-note pitches that immediately precede it. Yet, just as we saw in subsequent measures of Example 3, the boundaries between these seemingly competing identities start to blur almost as soon as they are staked out. In mm. 44–45, for instance, the harp temporarily leaves the bassoons and horns and instead joins the clarinet–keyboard group, which now articulates not only F(+¼) but also E within the X tetrachord. Such maneuvers render overtonal interpretations for the music increasingly plausible to the ear, and indeed, in the remainder of the music shown in Example 4, the two instrumental groups (now further enriched by flutes and a vibraphone) seem to unite in presenting both downward and upward melodic sweeps through various partials of a harmonic series on C.
Example 5. Reduction and analysis of Anderson, Eden, mm. 48.2–58.1
(click to enlarge, see the rest, and listen)
Example 6. Mode for Anderson, Eden, mm. 1–20 and mm. 40–58.1
(click to enlarge)
[23] Measures 48.2–58.1 further develop the interactions between these harmonic paradigms. As Example 5 shows, two registrally differentiated lines collectively articulate T7X—i.e., the X tetrachord transposed up a perfect fifth in 12-TET pitch-class space, yielding {G, A, B, D}—in both mm. 48.2–50.1 and mm. 52–54, with leaping motion by ic5 again prominently characterizing the material. In between and overlapped with these fragments based on 12-TET pitch-class operations, the upper line presents a rhythmically augmented, stepwise sweep of the 9th through 12th partials of a C harmonic series. In mm. 54.2–56, meanwhile, macrotonal realizations of harmonic series partials are repeatedly mixed with an A-natural carried over from T7X. This later portion of the passage thus serves to confirm the pluralistic manner in which we might listen to Eden: rather than enforcing a singular harmonic interpretation on the music, Anderson’s compositional approach invites 12-TET pitch-class-derived fragments to give way toward sensations of overtonality while simultaneously continuing to assert their independence.(16) Example 6 summarizes these interactions by tracing the derivation of a hybrid mode whose pitch classes are formed by the union of X, T7X, and a macrotonal realization of a fragment from a C harmonic series. This collection, we might note, accounts for not only the music in Examples 4 and 5 but also the viola and cello soli heard at the work’s opening (Example 3).
[24] In mm. 58.2–64, Anderson closes out the passage under discussion with a pivot to a new pitch collection in which the underlying harmonic series is no longer based on C but rather on E. Example 7 reduces and analyzes this final portion of the passage, and Example 8 summarizes its underlying pitch-class material. As both examples show, the now-familiar 12-TET tetrachords remain in the picture, this time in the form of T4Xs—i.e., X transposed up a major third in 12-TET pitch-class space, which yields {E,
Example 7. Reduction and analysis of Anderson, Eden, mm. 58.2–64 (click to enlarge and listen) | Example 8. Mode for Anderson, Eden, mm. 58.2–64 (click to enlarge) |
Example 9. Analysis of the modulation between collections in Anderson, Eden, mm. 40–64
(click to enlarge)
[25] This pivot from a C-based collection to an E-based one also highlights a compositional advantage of snapping overtonally-derived materials to the 24-TET grid: namely, it introduces the possibility of asserting multiple common tones between collections. Because Anderson rounds the tunings of partials to the nearest quartertone, the modes shown in Example 6 and Example 8 share two common tones, E and
Example 10. Two possibilities for realizing the modulation shown in Example 9 in just intonation
(click to enlarge)
[26] By contrast, attempting this modulation in just intonation (i.e., with precise, overtonally-derived frequency ratios devoid of any quartertone rounding) could preserve one, but not both, of these common tones. Example 10 shows two possibilities for handling the pivot in JI, with the tunings of all pitch classes represented in cents. Note how maintaining the tuning of the E between the collections would necessitate an adjustment to the tuning of the
Example 11. Reduction and analysis of Anderson, Eden, mm. 80–106
(click to enlarge, see the rest, and listen)
[27] With Eden now having twice played out a process of disrupting but then encouraging overtonal hearings—once in the opening viola and cello soli of Example 3 and again in the passage divided between Examples 4, 5, and 7—sensations of overtonality remain more consistently in focus in much of the remainder of the work. Example 11 reduces and analyzes mm. 80–106, a portion of Eden’s central section in which the viol-like string soli return. Rather than conspicuously intruding upon several measures’ worth of entirely 12-TET music, as they did at the beginning of the piece, quartertones now feature prominently in the viola’s and cello’s pitch languages from the outset, yielding a series of overtly overtonal melodic sweeps spanning fundamentals of G, D, C,
[28] Consider also the large-scale harmonic progression that this passage traverses. In mm. 80–91, there is a toggling of attention between fundamentals of D (winds, harp, keyboard, and violins) and G (solo viola, horns, and trumpet); in m. 92, the viola briefly entertains the upper layer’s D fundamental before switching to a C fundamental in m. 93. The pitch classes of these three fundamentals, {C, D, G}, are subsets of X {C, D, E, G} introduced in Example 4; indeed, they are related by precisely the interval class, ic5, that the music of Example 4 repeatedly highlighted when presenting that tetrachord. Throughout Examples 4, 5, and 7, we saw how X and its transformations moved from impeding overtonality to coinciding with it on the surface of the music; with that process now complete, X’s characteristic interval classes here play a more structural role, providing the underlying fundamentals for a series of unambiguously overtonal lines and chords. After a sudden downward-major-3rd shift in fundamental, from C to
Example 12. Pitch content of Anderson, Eden, mm. 103–6, compared with quartertone-approximated partials of A1
(click to enlarge)
[29] The moment at which this last fundamental arrives deserves particular attention. Note that when the cellos, basses, and harp enter on the downbeat of m. 103—an aurally notable event in itself, given the piece’s limited use of the bass register thus far—chords representing the previous two fundamentals,
[30] This moment therefore unites—within a single harmonic series—pitches that we had previously understood to originate from separate fundamentals. In this sense, we might think of the passage as an illustration of the harmonic series’ recursive nature—the fact, in other words, that within a given harmonic series there are embedded infinitely many more series, with the fundamental of each of these “child” series being a partial in the original “parent” series. Indeed, Anderson has identified this as among the harmonic series’ properties most salient in his compositional thinking (Anderson 2019). Its instantiation on the surface of Eden is especially suggestive: by positing several musical layers as contextually distinct yet partially acoustically unified, it seems to encapsulate in one fleeting moment the dialectical nature of the work’s approach to harmonic construction.
Example 13. Reduction and analysis of Anderson, Eden, mm. 174–82
(click to enlarge and listen)
[31] I suggest, then, that later passages of Eden engender more stable sensations of overtonality compared to the relative instability of the work’s earlier sections. Yet we should resist pushing this linear narrative too far, for divergences between equal-tempered pitch structures and overtonality nonetheless remain in play until the end. Example 13 reduces the final nine measures of Eden’s coda, which are especially instructive in this regard. The seven-note chord that begins the fragment has, compared to many of Eden’s other harmonies, a strikingly opaque and inharmonic sound, and I similarly find it challenging to hear the almost brooding melody—initiated heterophonically by horns and violins then continued by the viola soloist from m. 179—as the sort of overtonal melodic sweep that Eden has gradually conditioned me to expect.(19) A stronger sense of overtonality is, however, reinstated in the music’s chordal layer from m. 176.4 until the end: as shown on Example 13, the fundamentals in this layer form a complete cycle of major 3rds, <C, E,
Example 14. Pitch content of Anderson, Eden, mm. 179–82 (viola only), compared with quartertone-approximated partials of C1
(click to enlarge)
[32] These considerations result in a particularly enigmatic situation in the work’s last three measures, mm. 180–82: above an overtonal chord on C, the viola soloist—now, notably, playing with vibrato and in ordinary bow position—presents an expressive melodic fragment composed of {B,
[33] But as Whittall suggests, the emotional valence of this is far from obvious. Is the viola positively asserting a degree of independence from overtonality and venturing off into a new region of paradise as yet unexplored? Or are we hearing the soloist straining to participate in one last overtonal complex but, now deprived of its viol-like innocence, ultimately being forced to chart out a different path? One might well think here of feelings of nostalgia running through many twentieth-century modernist works. For Jonathan Cross, modernism is characterized in part by the “impossibility of a longed-for return to the past” (Cross 2006, 40); this quality, he argues, permeates music by composers from Schoenberg and Stravinsky (Cross 2008) to Anderson’s elder compatriot Harrison Birtwistle (Cross 2006). Perhaps we can hear the ending of Eden as joining this long tradition, with Anderson’s viola longing for an overtonality that has, before our ears, suddenly slipped from the present into the past. In the end, however, it is unclear whether the soloist’s divergences from the chord beneath it are in fact being lamented or if, on the contrary, they are meant to be celebrated.
[34] Whatever the precise charge of Eden’s final measures, they encapsulate how the work undercuts single-minded harmonic narratives and instead foregrounds the polysemic potentials of its pitch resources. At the same time, we should note that Anderson’s compositional techniques ultimately place bounds on his music’s pluralism. Perhaps most notably, Anderson excludes a number of 24-TET intervals from the surface of his music; of intervals smaller than the 12-TET semitone, for instance, he says that to his ears “they generally sound like slides, or fuzzy, soured, out of tune tempered intervals” (quoted in Small 2017, 31), and for this reason he fully avoids composing with them. This decision is striking given that one can find such intervals within higher regions of the harmonic series, and it would thus seem to limit the extent to which Anderson’s music can engage with the sorts of ambiguities—the swings in 24-TET intervals’ status between sonorous, overtonality-engendering structures and disruptive, markedly non-12-TET outsiders—that I have explored in the above analysis.
[35] These caveats aside, I hope to have shown how Eden brings notions of anti-fundamentalism to often binary-infused debates in the area of tuning and temperament—and, indeed, to the contemporary political sphere at large. Returning to his remarks that opened this section, Anderson evidently feels that sweeping claims of ideological purity, whether in music or in politics, are to be regarded with suspicion: in both domains, he appears wary of their potential to ultimately engender dangerous states of exclusion. In voicing these concerns through his work, Anderson advocates for the critique of ideological certainty as an ingredient of positive political change.
[36] Turning a skeptical eye toward totalizing viewpoints and dogmatic surety is no doubt a vitally important, even irreplaceable, tool for achieving equity in a pluralistic society. At the same time, we might question whether pushing values of ambiguity to their logical extremes could pose unique perils for our current political moment. As Bruno Latour suggests, necessary and well-meaning attempts to “detect the real prejudices hidden behind the appearance of objective statements” may have unwittingly lent credence to those who would nefariously sow “excessive distrust of good matters of fact” and seek to “destroy hard-won evidence that could save our lives” (Latour 2004, 227). Writing in 2004, Latour cites as an example of this trend the still-pervasive right-wing tendency to undermine scientific evidence for climate change (Latour 2004, 226); thinking even more recently, we might reflect on former President Donald Trump’s attempts to blur distinctions and create false equivalences between anti-racism activists and white supremacists. Does the political climate of the twenty-first century highlight how values of “healthy pluralism,” as Matthew D’Ancona puts it, can be perverted into “unhealthy relativism” (D’Ancona 2017, 84)? Rand Steiger’s work Post-truth Lament engages explicitly with the treacherous waters of the latter, and it is therefore to this piece which I now turn.
Rand Steiger: Post-truth Lament
“Truth isn’t truth.”
—Rudy Giuliani, personal lawyer to Donald Trump
Meet the Press, August 19, 2018
“Don’t be so overly dramatic about it, Chuck. You’re saying it’s a falsehood
and Sean Spicer, our press secretary, gave alternative facts to that.”
—Kellyanne Conway, Counselor to the President
Meet the Press, January 22, 2017
[37] In spring 2017, amid the opening months of the Trump administration, Rand Steiger wrote that “while there is much to lament in our current political moment, I have been particularly unsettled by the diminished respect for objective truth shown by leading public figures.” This “ominous development,” Steiger says, prompted the title of his work Post-truth Lament for two pianos tuned a quartertone apart, which was commissioned by Stephen Drury, the Callithumpian Consort, and the Tanglewood Music Center to accompany Charles Ives’ Three Quartertone Pieces for the same instrumentation (Steiger 2017). Here, I consider how Steiger’s use of harmony in Post-truth Lament explores through sound the manifold interactions between truth and lies, justice and injustice, in the United States’ political environment at large. I argue that in the opening passages of the work, Steiger draws on the multiplicity of harmonic influences that have characterized his music for decades to illustrate troubling slippages between true facts and “alternative” ones. Later passages, on the other hand, gesture fleetingly and tentatively toward something of a reconciliation between different harmonic principles; by extension, they perhaps offer a vision—one which is simultaneously hopeful and remote—of a more just future. Like Anderson’s Eden, then, Steiger’s work features a range of interactions between different conceptions of harmony. I sense in Post-truth Lament’s hybrid approaches a meditation on the fragile dialectics of our present political moment and a sense of uncertain, open-ended questioning of the ways they might be resolved.
[38] Since 2001, Steiger’s work has combined overtonal considerations with atonal aggregate-based concepts grounded in 12-TET; he attributes the former interest to his mentor Subotnick, whose influence was mentioned above, while the latter stems in part from the work of Mel Powell, who was also among his teachers (Rand Steiger, interview via Zoom, May 17, 2021). I suggest that these two streams of influence play vitally important roles in the harmonic language of Post-truth Lament. At the same time, this work is unusual in the context of the rest of Steiger’s catalogue by virtue of its instrumentation and the compositional strategies it does, and does not, enable. In many of his works, Steiger specifies that pitches should be tuned quite precisely relative to their harmonic series counterparts (in many cases to the nearest cent), enabling him to explore liminal perceptual spaces between chords and timbres that emerge when overtonal sonorities are very accurately tuned. In Post-truth Lament, however, Steiger has only two options for realizing a partial of a given harmonic series: namely, with a 12-TET pitch, available on the first piano, or with a 12-TET pitch flattened by one quartertone, available on the second piano. Atypically for Steiger, then, he uses a 24-TET grid similar to that of Anderson’s macrotonal system for realizing overtonal sonorities in the work.
[39] Apparently referencing the potential of this grid to approximate the just tunings of the harmonic series, Steiger writes in his program note for Post-truth Lament that he was “particularly interested in how the quartertone tuning enabled me to voice chords that sounded more in tune than out of tune, attaining ‘justness’ at a time of injustice” (Steiger 2017). But although Steiger asserts that he was generally not interested in the two pianos sounding “out of tune” with one another, in an interview with the author he also observed that there are indeed passages in Post-truth Lament that seem to stray away from overtonal thinking. Such passages, he says, were intended as nods toward the feeling of harmonic “sourness” that seems to permeate some other quartertone piano repertoire (Rand Steiger, email to the author, May 4, 2020). In such scenarios, 24-TET is arguably treated less as a grid for realizing “in tune,” overtonal harmonies and more as an “out of tune” version of 12-TET containing additional, “wrong note”-feeling pitches. This creates a point of connection between Steiger’s harmonic devices and the sometimes ambiguous status of non-12-TET pitches in Anderson’s Eden: as we saw above, at times they might feel like outsiders to the more culturally familiar 12-TET set, while at others they can fuse with standard 12-TET pitches to create a single, harmonically unified overtonal complex.
[40] Extending the analogy between harmony and politics implied by Steiger’s program note, if overtonal uses of the 24-TET grid are “just,” “sour” quartertone harmonies that are otherwise derived are presumably “unjust.” In Post-truth Lament, however, the question of “justice” versus “injustice” seems not to be a simple binary choice; instead, a continuum exists between these poles. While some of Post-truth Lament’s passages seem intended to realize overtonal harmonies as faithfully as possible, other passages contain sonorities that evoke the harmonic series to a more qualified degree, and others still indulge in sounds with little to no apparent resemblance to overtonal principles. Adding further still to the complexity, Steiger’s piece seems to invite us to notice how the same techniques associated with “injustice” at one moment might contribute to a sensation of relative “justice” at another. I suggest, then, that Post-truth Lament amounts to a multifaceted exploration of the intermediate states and rich interactions that can obtain between “just” (“in tune,” overtonal) and “unjust” (“out of tune,” non-overtonal) harmony when composing with equal-tempered quartertones.
Example 15. Steiger, Post-truth Lament, mm. 1–11. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
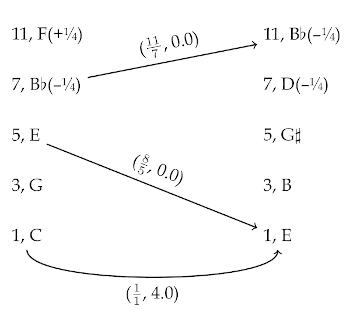
[41] Roughly seven minutes in duration, Post-truth Lament begins with fast, aggressive music shared by the two pianos; after becoming increasingly tense, this music eventually yields to a brief slow section at the center of the work. In the second half of the piece, the opening material returns in varied form, driving the music to a climax that is followed by a slow, contemplative coda. The opening passage provides a particularly clear window into how Steiger uses 24-TET to realize overtonal harmonies. By way of illustration, Example 15 reproduces the first eleven measures of Steiger’s score along with audio of the same passage.(21) In mm. 1–10, the two pianos gradually unfurl several tightly-spaced realizations of partials from a harmonic series whose fundamental is
[42] The polyrhythmic unfurling procedure continues after the outburst of m. 11 until m. 35. Example 16 summarizes the complete set of
Example 16. Pitch content for the polyrhythmic unfurling of partials of (click to enlarge) | Example 17. Pitch content of Steiger, Post-truth Lament, m. 11 (click to enlarge) |
Example 18. Steiger, Post-truth Lament, m. 20. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
[43] It is notable that Steiger packages this revelation of the overtonal paradigm within such an outwardly explosive gesture, and its character perhaps serves as a warning of further interruptions to come—ones that will prove not only aggressive in presentation but also “unjust” at their harmonic core. Indeed, a series of subsequent interjections initiate a drifting away from overtonal sonorities, creating moments of relative “injustice” that interrupt—and eventually, completely overtake—appearances of “just” pitch content. Example 18 reproduces the score for m. 20, which is the piece’s first glimpse into this comparatively “unjust” harmonic world. Like m. 11, this new material is distinguished from the polyrhythmic unfurling it interrupts by virtue of its rhythm (rhythmic unison instead of polyrhythm) and register (relatively expansive use of the pianos’ range). But in contrast to our experience of m. 11, an overtonal manner in which we might hear this new material does not readily present itself. Here, the first piano articulates a pitch-class set {
[44] Steiger’s choice of the “major 4th” as the interval by which to create this doppelgänger effect is especially interesting. In the context of an overtonal sonority, this 24-TET interval can be made to sound particularly “just,” for it very closely approximates the JI interval between the 8th and 11th partials of a given harmonic series. In symmetrical intervallic landscapes such as Wyschnegradsky’s, however, this same interval can take on a far more atonal, alien-sounding quality. To my ears, m. 20 of Post-truth Lament shows off this latter side of the Janus-faced major 4th. While this interval between the first and second pianos could have been derived through recourse to overtonal principles, its deployment on the musical surface challenges the listener’s ability to perceive it in a meaningfully overtonal way. Steiger thus disassociates a potentially “just” interval from a musical context that would reveal its overtonal origins, transforming it into a static and uncanny doubling. I suggest that this moment marks a swing from a “just” (“in tune”) to an “unjust” (“out of tune”) use of the 24-TET grid: rather than perceiving the contents of the measure overtonally, I hear two superimposed versions of a 12-TET set that are “othered” relative to one another due to the contextually unusual-sounding interval separating them. Referring back to the specific political context in which Steiger composed Post-truth Lament, we might even think of this moment as gesturing toward a set of dystopian “alternative facts” about 24-TET, which gradually overtake the music in subsequent passages.
Example 19. Steiger, Post-truth Lament, mm. 44–45. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
[45] Measure 20 is also aurally notable for another of its features—namely, the sheer proliferation of both pitches and pitch classes it quickly introduces. At its densest state, the polyrhythmic unfurling of
Example 20. Steiger, Post-truth Lament, mm. 47–51. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
Example 21. Analysis of Steiger, Post-truth Lament, m. 50
(click to enlarge)
[46] Ultimately, the major 4th doppelgänger idea serves as a transition to another “unjust” passage that again centers around a 12-TET aggregate. In this new type of material, which Steiger begins to introduce as early as m. 39, a polyrhythmic ostinato serves as a backdrop against which the pianos gradually build up a collection of strident perfect 5ths and octaves. Measures 47–51, which are reproduced in Example 20, exemplify this material. The louder, foregrounded 5ths and octaves articulate the pitch-class set {
[47] As we have seen, the opening passages of Post-truth Lament largely cast principles of aggregate formation in an antagonistic relationship with overtonal thinking, with the former ultimately overtaking the latter and perpetrating two types of harmonic “injustice.” However, starting in m. 55—amidst a transition into Post-truth Lament’s central slow section—the music begins to gesture more overtly toward one of Steiger's most characteristic compositional strategies: creating registrally expansive pitch fields that intertwine overtonality with traditionally atonal, 12-TET aggregate-building techniques. The appearance of these hybrid “overtonal aggregate” fields, as I will call them, serves an almost narrative function in Post-truth Lament; over the course of later passages of the work, Steiger introduces the technique with varying degrees of clarity and imperfection, thereby gently and gradually hinting at a reconciliation between harmonic principles that had earlier resulted in divergent sonic results.
[48] In an interview, Steiger explained that he often composes music using a succession of pitch fields, each of which is a collection of pitch classes that are fixed in register and that constitute the core harmonic repertoire of the instruments playing at a given moment (Rand Steiger, interview via Zoom, August 6, 2020). This technique—which has been utilized by such composers as Webern, Carter, Lutosławski, and Powell—is in its traditional conception deeply rooted in 12-TET. Specifically, it generally involves utilizing many, and often all, of the 12-TET pitch classes; and it further involves assigning each of those pitch classes to a register, and often exactly one register, in pitch space. Thus, while there is some degree of flexibility built into the definition, the most prototypical pitch field of this sort contains exactly twelve pitches, all in 12-TET, with no octave duplications. It is also characteristic for such fields to occupy a fairly wide range of pitch space.(23)
[49] Steiger’s use of this technique in his harmonic series-based music variously alters and maintains its core tenets. On the one hand, in many of his works Steiger uses a given pitch field to closely evoke the just tunings of the harmonic series, which prompts him to introduce non-12-TET intervals into the field and pull it out of the tuning universe within which the technique was founded. On the other, Steiger usually accommodates the original technique’s avoidance of pitch-class duplication across octaves; he does this by regarding each just-tuned pitch as a representative of the nearest 12-TET pitch class, with other representatives of the same pitch class (even differently tuned ones) typically not permitted within the same field.(24) In the abstract, the resulting “overtonal aggregate” field is therefore a hybrid of two philosophically distinct structures—i.e., the harmonic series’ theoretically infinite set of ratio-related frequencies and the closed world of an equal-tempered pitch-class space. In what follows, I examine two fields from later passages of Post-truth Lament, considering how they gesture toward, but decline to completely realize, a reconciliation between ideas previously cast in an antagonistic relationship.
[50] Example 22 reproduces the score for mm. 55–64, the work’s first prolonged yet decidedly provisional evocation of Steiger’s overtonal aggregate technique. In this passage, the two pianos arpeggiate a pitch field based on an apparent fundamental of F1; the field is analyzed in Example 23. As is evident from the figure, there are more than twelve pitches in the field; contrary to Steiger’s normative tendency to include only one representative of each 12-TET pitch class, Example 23 contains multiple representatives of several such pitch classes, no matter how the quartertone-altered pitches are parsed.(25) To my ears, the field also contains a more perceptible sort of outlier: the pitch
Example 22. Steiger, Post-truth Lament, mm. 55–64. Piano 2 sounds one quartertone lower than written (click to enlarge, see the rest, and listen) | Example 23. Pitch content of Steiger, Post-truth Lament, mm. 55–64 (click to enlarge) |
Example 24. Steiger, Post-truth Lament, mm. 89–96. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
Example 25. Pitch content of Steiger, Post-truth Lament, mm. 93–101
(click to enlarge)
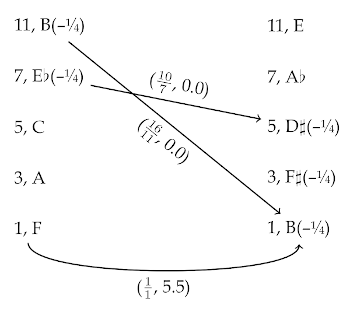
[51] Example 24 reproduces the score for mm. 89–96, an excerpt of one of Post-truth Lament’s most sonically striking passages. Measures 89–92 come from the start of the second half of the work, recalling the gradual polyrhythmic unfurling of
[52] We should also note that the field contains representatives of all twelve 12-TET pitch classes: a plausible option for the 12-TET pitch class instantiated by each pitch in the field is printed at the top of Example 25, with pitch classes altered by a quartertone in their realization placed in quotation marks. Furthermore, if the octave doubling of the fundamental in the bass register (likely for timbral reinforcement) is excepted, each 12-TET pitch class is realized without octave duplication. This harmony would therefore contain the trappings of a prototypical overtonal aggregate field were it not for the fact that it seems to be generated not from a single fundamental but rather from two at the same time. Just as the music satisfies the overtonal aggregate technique’s requirements in terms of 12-TET pitch-class representation, then, it undermines the listener’s sensation of overtonality by creating a complex inharmonic spectrum from the superimposition of what would in isolation be two purely overtonal chords. In this way, the piece continues to gradually move toward, but coyly avoid full realization of, a reconciliation between principles of overtonality and ET pitch-class aggregate formation.
[53] Additionally, Steiger’s use of seemingly anomalously voiced partials—i.e., pitches that seem to be voiced one octave “too low” given the apparent location of the fundamental—occasionally add, at least to my ears, even further nuance and complexity to the fields’ attempt at this sort of harmonic reconciliation. In an interview with the author, Steiger shared that he typically does not think of such pitches as being anomalously voiced when he is composing them. Instead, he imagines the fundamental of the governing harmonic series to be one octave lower than the surface of the music would suggest—thus transforming, for example, an apparent “3.5th” partial into the 7th partial of an implied virtual fundamental, with all other partial numbers similarly being doubled (for instance, an apparent 5th partial would become the 10th partial of such a virtual fundamental). Steiger suggested that he occasionally deploys this maneuver in order to very slightly counteract the harmonic series’ naturally lopsided spacing and instead distribute notes more evenly in pitch space, speculating that he may have inherited this preference from twentieth-century 12-TET composers, such as Webern and Powell (Rand Steiger, interview via Zoom, August 6, 2020).
[54] Perceptually, however, a remarkably dissonant-sounding—and thus musically potent—effect can sometimes occur when pitches not conforming to a fundamental otherwise strongly implied on the surface of the music are introduced.(27) Such a scenario occurs in mm. 55–64; recall Example 23’s summary of that passage’s pitch repertoire, where
Example 26. Steiger, Post-truth Lament, mm. 65–69. Piano 2 sounds one quartertone lower than written
(click to enlarge and listen)
Example 27. Analysis of the modulation between harmonies in Steiger, Post-truth Lament, mm. 55–64 and mm. 65–69
(click to enlarge)
[55] In mm. 65–69, which mark the start of Post-truth Lament’s central slow section and are reproduced in Example 26, the introduction of a new overtonal aggregate field “resolves” the dissonance arguably engendered by this pitch via a common-tone modulation. Specifically, Steiger turns this same pitch,
[56] In the foregoing analysis, I have explored how Post-truth Lament contains a wide variety of sonorities and discussed how those sonorities point to an ever-changing relationship between overtonal and equal-tempered conceptions of harmony. The beginning of Steiger’s work uses these two realms to create sonically divergent results, with equal-tempered aggregate-building techniques used to create harmonic “injustice.” Later sections of the piece, however, inflect this apparent binary with ambiguity and nuance. Specifically, Steiger’s characteristic overtonal aggregate field technique shows how similar aggregate-building ideas can also go hand-in-hand with overtonal principles in contributing to more “just”-sounding sonorities. Even as Steiger introduces this supposed reconciliation, however, he continues to create flickers of harmonic tension, including by not fully realizing the prototypical characteristics of an overtonal aggregate field and by voicing partials anomalously given a field’s apparent fundamental.
[57] Ultimately, then, I read Post-truth Lament as a meditation on an uncertain political future. In its positioning of a fully “just” harmonic landscape as an asymptote toward which the music seems to strive—in sight, yet always tantalizingly out of reach—Steiger’s work arguably shares an even more direct link with the same histories of nostalgia that we pondered at the conclusion of Anderson’s Eden. Writing on Schoenberg’s Piano Piece op. 11/1, for instance, Cross concludes that it seems as if the composer is “straining to reach back” to tonality even though he ultimately “cannot quite touch it” (Cross 2008, 58). I hear Post-truth Lament’s overtonal aggregate fields as doing an analogous sort of labored searching, in that they seem to long for a full restoration not of the tonal but rather of the overtonal. Yet throughout the work’s seven and a half minutes, an unambiguous sense of harmonic “justice” remains elusive; as the music ends, it is almost as if we are hearing Steiger question whether it will ever again be otherwise.
Conclusion
[58] In their primer on just intonation and microtonality, Thomas Nicholson and Marc Sabat echo Johnston’s distinction between the “ambiguity” of tempered intervals and the “clarity” of just-tuned ones:
In [tempered] contexts, the interpretation of intervals no longer depends entirely on their sound alone, but must also be deduced from their context. This alteration of listening focus is perhaps the fundamental difference between conceiving of music in a temperament or in just intonation. The increased interest today in exploring perceptions of sound and time as fundamental materials of music invites a kind of listening, which the appreciation of just intonation also depends upon. (Nicholson and Sabat 2018, 29; italics original)
An interest in listening to sounds “in their own terms” rather than “as part of a system of syntactic relationships,” as Hasegawa puts it (Hasegawa 2008, 197), is indeed an important trend in music of at least the past sixty years. This is not, however, what I sense Anderson’s and Steiger’s works to be inviting us to do. To the contrary, Eden and Post-truth Lament engender teeming networks of relationships that express not only these composers’ pluralistic harmonic influences but also the broader political realities they perceive in the world. I suggest that “context,” to borrow a word from Nicholson and Sabat, is crucial on many levels at once in understanding the work of these composers. Far from producing work that feels tentative or uncommitted, the theoretical blurriness engendered by drawing on both overtonal and equal-tempered pitch structures seems to be musically generative for these two composers and offers them possibilities for thinking in sound about complexities of life in the twenty-first century.
Alex Stephenson
University of California San Diego
Department of Music
9500 Gilman Drive
La Jolla, CA 92093-0099
a7stephe@ucsd.edu
Works Cited
Anderson, Julian. 2005. Program note for Eden. https://www.fabermusic.com/music/eden-4620.
—————. 2019. “Spectral Centrality.” Paper presented at the “Spectralismes” conference, June 2019, Paris, France.
—————. 2020. “Introducing Julian Anderson—A British Composer Inspired by the Beauty of Prague.” Culture and Education, Embassy of the Czech Republic in London (website), November 6, 2020. https://www.mzv.cz/london/en/culture_and_education/what_s_up_in_culture/introducing_julian_anderson_a_british.html.
Anderson, Julian, and Christopher Dingle. 2020. Julian Anderson: Dialogues on Listening, Composing and Culture. Boydell & Brewer. https://doi.org/10.2307/j.ctvt1sjks.
Babbitt, Milton. [1965] 1972. “The Structure and Function of Musical Theory.” In Perspectives on Contemporary Music Theory, ed. Benjamin Boretz and Edward T. Cone, 10–21. W.W. Norton.
Bregman, Albert S. 1990. Auditory Scene Analysis. MIT Press. https://doi.org/10.7551/mitpress/1486.001.0001.
Cheung, Anthony. 2010. “Ligeti’s Magic Horn: Parallel Universes of Tuning and Tradition in the Hamburg Concerto.” DMA diss., Columbia University.
Cowell, Henry. [1930] 1996. New Musical Resources. Edited by David Nicholls. Cambridge University Press. https://doi.org/10.1017/CBO9780511597329.
Cross, Jonathan. 2006. “Modernism versus Tradition, and the Traditions of Modernism.” Muzikologija/Musicology: Journal of the Institute of Musicology of the Serbian Academy of Sciences and Arts 6: 19–42. https://doi.org/10.2298/MUZ0606019K.
Cross, Jonathan. 2008. “Paradise Lost: Neoclassicism and the Melancholia of Modernism.” In Rethinking Musical Modernism, ed. Dejan Despić and Melita Melin, 54–64. Serbian Academy of Sciences and Arts.
D’Ancona, Matthew. 2017. Post Truth: The New War on Truth and How to Fight Back. Ebury Press.
Don, Gary. 2001. “Brilliant Colors Provocatively Mixed: Overtone Structures in the Music of Debussy.” Music Theory Spectrum 23 (1): 61–73. https://doi.org/10.1525/mts.2001.23.1.61.
Doty, David. 1985. “Editorial.” 1/1, The Journal of the Just Intonation Network 1 (1): 2–15.
Fokker, Adriaan. 1955. “Equal Temperament and the Thirty-One-Keyed Organ.” The Scientific Monthly 81 (4): 161–6.
Forte, Allen. 1955. Contemporary Tone-Structures. Columbia University Teachers College.
Gilmore, Bob. 1995. “Changing the Metaphor: Ratio Models of Musical Pitch in the Work of Harry Partch, Ben Johnston, and James Tenney.” Perspectives of New Music 33 (1–2): 458–503. https://doi.org/10.2307/j.ctt21c4sbm.14.
—————. 2017. “Rational Spaces: The String Quartets of Ben Johnston as Experimental Process.” In Experimental Encounters in Music and Beyond, ed. Kathleen Coessens, 101–9. Leuven University Press.
Harrison, Daniel. 2016. Pieces of Tradition: An Analysis of Contemporary Tonal Music. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780190244460.001.0001.
Hasegawa, Robert. 2006. “Tone Representation and Just Intervals in Contemporary Music.” Contemporary Music Review 25 (3): 263–81. https://doi.org/10.1080/07494460600726529.
—————. 2008. “Just Intervals and Tone Representation in Contemporary Music.” PhD diss., Harvard University.
—————. 2015. “Clashing Harmonic Systems in Haas’ Blumenstück and in vain.” Music Theory Spectrum 37 (2): 204–23. https://doi.org/10.1093/mts/mtv014.
Hirs, Rozalie. 2009. “Frequency-based Compositional Techniques in the Music of Tristan Murail.” In Contemporary Compositional Techniques and OpenMusic, ed. Bob Gilmore and Rozalie Hirs, 93–196. IRCAM.
Johnston, Ben. 1964. “Scalar Order as a Compositional Resource.” Perspectives of New Music 2 (2): 56–76. https://doi.org/10.2307/832482.
—————. 1987. “Extended Just Intonation: A Position Paper.” Perspectives of New Music 25 (1–2): 517–19.
—————. (1988). “A.S.U.C. Keynote Address.” Perspectives of New Music 26 (1): 236–42. https://doi.org/10.2307/833326.
—————. [2003] 2006. “A Notation System for Extended Just Intonation.” In Maximum Clarity and Other Writings on Music. Edited by Bob Gilmore, 77–88. University of Illinois Press.
Latour, Bruno. 2004. “Why Has Critique Run out of Steam? From Matters of Fact to Matters of Concern.” Critical Inquiry 30 (2): 225–48. https://doi.org/10.1086/421123.
Mandelbaum, Joel. 1967. “The Isolation of the Microtonal Composer.” In Proceedings of the Second Annual Conference, April 1967, ed. Hubert S. Howe, 107–12. The American Society of University Composers.
Morris, Robert. 1980. “Review of Simple Composition, by Charles Wuorinen.” Theory and Practice 5 (1): 66–72.
Nicholson, Thomas, and Marc Sabat. 2018. “Fundamental Principles of Just Intonation and Microtonal Composition.” Universität der Künste Berlin. https://marsbat.space/pdfs/JI.pdf.
Oteri, Frank. 2000. “Pauline Oliveros: Creating, Performing and Listening.” NewMusicBox, December 1, 2000. https://nmbx.newmusicusa.org/pauline-oliveros-creating-performing-and-listening/11.
Palmer, Andrew. 2015. Encounters with British Composers. Boydell & Brewer.
Partch, Harry. 1991. Bitter Music: Collected Journals, Essays, Introductions, and Librettos.. Edited by Thomas McGeary. University of Illinois Press.
Perlman, Marc. 1994. “American Gamelan in the Garden of Eden: Intonation in a Cross-Cultural Encounter.” The Musical Quarterly 78 (3): 510–55. https://doi.org/10.1093/mq/78.3.510.
Polansky, Larry. 1985. “Guest Editorial.” 1/1, The Journal of the Just Intonation Network 1 (2): 2–13.
—————. 2018. “A Few Words About Tuning.” Sound American 20. http://archive.soundamerican.org/sa_archive/sa20/sa20larrypolanskyafewwords.html.
Rings, Steven. 2011. Tonality and Transformation. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195384277.001.0001.
Shreffler, Anne. 2000. “The Myth of Empirical Historiography: A Response to Joseph N. Straus.” The Musical Quarterly 84 (1): 30–39. https://doi.org/10.1093/mq/84.1.30.
Sims, Ezra. 1988. “Yet Another 72-Noter.” Computer Music Journal 12 (4): 28–45. https://doi.org/10.2307/3680151.
Small, Michael. 2017. “Julian Anderson’s Symphony: Other Worlds Reflected.” DMA diss., Cornell University.
Steiger, Rand. 2017. Program note for Post-truth Lament. http://rand.info/rands/text/lament.html.
Tenney, James. 1983. “John Cage and the Theory of Harmony.” Plainsound Music Edition (website). https://www.plainsound.org/pdfs/JC&ToH.pdf.
Väisäla, Olli. 2002. “Prolongation of Harmonies Related to the Harmonic Series in Early Post-Tonal Music.” Journal of Music Theory 46 (1–2): 207–83. https://doi.org/10.1215/00222909-46-1-2-207.
Whittall, Arnold. 2015. “Measures of Authenticity: The Macrotonal Music of Julian Anderson.” The Musical Times 156 (1930): 7–22. https://www.jstor.org/stable/i24615235.
Wuorinen, Charles. 1963. “The Outlook for Young Composers.” Perspectives of New Music 1 (2): 54–61. https://doi.org/10.2307/832103.
—————. 1979. Simple Composition. Longman.
Wyschnegradsky, Ivan. [1932] 2017. Manual of Quartertone Harmony. Edited by Noah Kaplan. Translated by Rosalie Kaplan. Underwolf Records.
Yasser, Joseph. 1932. A Theory of Evolving Tonality. American Library of Musicology.
Footnotes
* I would like to thank Julian Anderson and Rand Steiger for sharing their time and insights with me. I am also grateful to Robert Hasegawa and an anonymous MTO reviewer for their constructive input on earlier drafts of this article, as well as the many other people—including Landon Bain, Amy Cimini, Daniel Corral, Amelia Glaser, Kevin Green, Nancy Guy, Lei Liang, Alex Taylor, Sora Woo, Shahrokh Yadegari, and Cherrie Yu—who shared important feedback with me at various stages of this project’s development.
Return to text
1. Harrison specifically mentions music in the French spectral tradition, which, in his view, instantiates a “deviant case” of overtonality (Harrison 2016, 23–25).
Return to text
2. In a largely positive review of Wuorinen’s Simple Composition, Robert Morris writes that the book would be improved by greater acknowledgement of the “history of intonation and tuning systems” (Morris 1980, 68).
Return to text
3. Unapologetically polemical advocacy of JI by its practitioners, while hardly uncommon in the literature, is also not universal. For instance, in a 1/1 editorial addressed to his fellow JI-interested colleagues, Larry Polansky warns that there is a difference between “inclusionary fanaticism, or composition, and preclusionary fanaticism, or cultism” and argues that JI “must be viewed as one experiment in many to evolve the musical mind, and not as a socio-political musical act” (Polansky 1985, 2). Writing over thirty years later, Polansky again cautions against exclusionary and moralistic critiques of ET, noting that “even the oft-maligned” 12-TET has produced “an enormous and incredibly varied amount of music” and that “given its legacy, it’s hard to, in good faith, call [12-TET] a limitation” (Polansky 2018). The musicologist Bob Gilmore, meanwhile, speculates that Johnston’s proposals may not have caught on more widely due to feared resemblances to religious or political dogmas (Gilmore 2017, 101–2).
Return to text
4. For a discussion of overtone structures in the music of Debussy as well as other early twentieth-century composers, see Don 2001 and Väisäla 2002. Johnston himself also recognized that Debussy seemed to be composing with upper overtones of the harmonic series, even though the elder composer ultimately notated his harmonies in 12-TET (Johnston 1988, 236).
Return to text
5. For a discussion of these principles in Murail’s work, see Hirs 2009.
Return to text
6. These various methods of using ET to approximate the tunings of overtones are arguably supported by Tenney’s notion of “tolerance,” which holds that the human auditory system accepts intervals that are not perfectly justly tuned as stand-ins for just-tuned ones, assuming that the deviation in tuning is sufficiently small (Tenney 1983, 22). As Robert Hasegawa has shown, Tenney’s hypothesis can be understood as an extension of the “tone representation” (Tonvorstellung) theories of Hugo Riemann (Hasegawa 2006); so, too, does the tolerance concept resonate with the writings of Henry Cowell, who suggests that tempered chords could be analyzed as “approximations” of the harmonic series ([1930] 1996, 21). In correspondence with Bob Gilmore, Johnston expressed skepticism toward the notion of tolerance, saying that “the symbolism of the aim to be perfectly, mathematically accurate in terms of proportionality is more important than the obvious fact that human frailty prevents any performance from attaining to it. I believe that even one’s notation, even one’s performance practices should symbolize what one is trying to communicate” (Gilmore 1995, 502).
Return to text
7. For a discussion of Ligeti’s Hamburg Concerto, see Cheung 2010; for more on Haas’ in vain, see Hasegawa 2015.
Return to text
8. One might also wish to include Haas in this subgroup; Hasegawa 2015 discusses not only in vain’s overt JI-ET harmonic clashes but also the political implications thereof.
Return to text
9. Anderson names his approach in this way because it focuses on intervals at least as large as a 12-TET semitone: he reasons that if “microtonal” refers to the use of intervals smaller than a semitone, an approach that uses only semitones or larger must be “macrotonal” (Anderson and Dingle 2020, 422). The musical implications of this decision will be explored later.
Return to text
10. In many of Anderson’s works, including Eden, he calls for one or more instruments to be tuned an equal-tempered quartertone lower than the rest of the ensemble before the start of the piece. These retuned instruments can then perform quartertone approximations of a given series’ 7th, 11th, and 13th partials with relative ease, including at fast tempi. However, Anderson sometimes also realizes these partials using natural harmonics on various instruments, such as horns. Anderson says that he generally regards the discrepancies arising between a quartertone-approximated partial on a retuned instrument and a natural-harmonic version of the same partial on another instrument to be negligible in the musical contexts within which he works. He notes, for example, a horn’s natural 7th partial can sound relative to 12-TET closer to a quartertone flat than an idealized harmonic series would suggest (Julian Anderson, interview via Zoom, June 2, 2021).
Return to text
11. It is here, moreover, that we might think of the artwork that provided an important inspiration for Eden: Constantin Brancusi’s sculpture The Kiss, which depicts two lovers in an embrace, their bodies pressed impossibly tightly against one another. Although Anderson connects Brancusi’s visual impetus to the piece’s frequent practice of hocketing a single melodic line between different instruments (Anderson 2005), I suggest that overtonal and ET-based modes of thought are, in Eden, also not unlike the simultaneously distinct yet conjoined lovers of Brancusi’s sculpture.
Return to text
12. All audio examples of Eden by Julian Anderson are performed by the City of Birmingham Symphony Orchestra, Martyn Brabbins conducting. NMC Recordings D121, 2012. Courtesy of NMC Recordings Ltd. https://nmc-recordings.myshopify.com/products/julian-anderson-book-of-hours.
Return to text
13. Anderson revealed that the tempo marking doubles as an homage to Brian Ferneyhough’s Funérailles (1969–80), a passage of which is accompanied by the same language in the score (Julian Anderson, interview via Zoom, June 2, 2021).
Return to text
14. I use the shorthand “+¼” and “-¼” throughout to indicate quartertone alterations to 12-TET pitches.
Return to text
15. In an interview, Anderson confirmed that he sees white-note diatonicism as a common signifier for paradise that the opening of Eden simultaneously evokes and, through the introduction of the F(+¼), challenges (Julian Anderson, interview via Zoom, June 2, 2021).
Return to text
16. Though this essay is principally concerned with the domain of harmony, the ways in which the passage shown in Example 5 plays with boundaries between monophony and polyphony arguably constitute another type of ambiguity in Eden. Example 5 suggests that the fragment shown is polyphonic from m. 48.2, though to my ears, mm. 48.2–49 could in fact be heard “both ways”—i.e., as a single line or as two separate lines. (Starting in m. 50, however, there is for this listener an unmistakable sensation of polyphony.) Similarly, I have represented mm. 57– 58.1 as consisting of a single line, though I think a reasonable argument could also be made for multiple lines here. In an interview, Anderson said that he was aware of these questions when he was composing the piece, explaining that he took inspiration from psychoacoustic research on the phenomenon of streaming (Julian Anderson, interview via Zoom, June 2, 2021). For a primer on this and related topics, see Bregman 1990.
Return to text
17. So, too, does Anderson’s practice of melodic splitting and re-fusing continue. To this listener’s ears, and as shown in Example 7, there are as many as four distinct melodic lines at play in m. 59, which by m. 62 collapse into a rich, high-register heterophony articulating a wash of partials from an E harmonic series—a musical texture that, by virtue of being simultaneously variegated and unified, seems to sum up the dialectical character of the entire passage.
Return to text
18. In Example 9, we saw how fundamentals modulated up a major 3rd in pitch-class space via two common tones: the starting fundamental’s 5th partial, E, became the ending fundamental, with the starting fundamental’s 7th partial,
Return to text
19. Indeed, the melody seems if anything to return in its pitch content, if not its expressive character, to the state inhabited by mm. 1–10, given that it is drawn largely from a 12-TET diatonic collection, this time based on
Return to text
20. Along somewhat similar lines, the clarinet—which articulates the very same quartertone-altered pitch, F(+¼), that proved central in Eden’s opening passages—deserves some comment here. On the downbeat of m. 180, I hear the note blending seamlessly with the rest of the overtonal chord by instantiating the 11th partial of C. However, rather than simply fading away like the other partials, the pitch is re-articulated with an accent, thereby gently asserting its independence from the rest of the overtonal sonority and, due to being cast against the viola’s 12-TET melody, highlighting the foreign and uncanny side of its non-12-TET identity. Thus, as Eden comes to a conclusion, there seems to be little in the way of a clear answer on whether ET structures enhance or stand in counterpoint to perceptions of overtonality: indeed, within the final three measures alone, both options seem to hold true.
Return to text
21. All audio examples of Post-truth Lament by Rand Steiger are performed by Stephen Drury and George Xiaoyuan Fu.
Return to text
22. Although this is not shown on Example 17, the fundamental and second partial are presented not only on the first piano but also on the second piano at the end of m. 11. This quartertone doubling is, obviously, not grounded in the
Return to text
23. For examples of such fields, see Carter, String Quartet No. 3; and Powell, Setting for Two Pianos.
Return to text
24. Applying this concept to the 24-TET grid of Post-truth Lament produces some theoretical tensions, since a given quartertone-altered 12-TET pitch is equidistant to two unaltered 12-TET pitches. For that reason, one might object that it is arbitrary to regard such a pitch as being representative of one 12-TET pitch class rather than another. This issue does not arise in many of Steiger’s other works, where he uses cent-specific tunings and where the intonation of a microtonally-altered pitch will therefore almost always be closer to one 12-TET pitch than another. Given how important these ideas have been to Steiger in his compositional process across several decades, I propose referring to them as a potentially useful lens through which we might grapple with some passages of Post-truth Lament, even while acknowledging that they might lose a certain degree of meaning when applied to the particular instrumental resources of this work.
Return to text
25. We might note, for instance, that the field contains multiple instances of E (E5 and E7(-¼)), G (G4 and G6(-¼)), and D (D5(-¼) and D7). The fundamental itself (F) is also doubled at the octave, presumably for timbral reinforcement.
Return to text
26. Note also that Example 25 qualifies its labeling of A4(-¼) as an instantiation of the 14th partial of B0(-¼) with a question mark. This is because the nearest 24-TET pitch to the 14th partial of B0(-¼) is in fact
Return to text
27. The notion that displacing partials into lower octaves can turn otherwise purely overtonal chords into more discordant harmonies has considerable precedence. The technique is perhaps most canonically exemplified by the opening section of Grisey’s Partiels (1975), in which an overtonal chord on a low E fundamental is gradually transformed into a dissonant, inharmonic spectrum through such aberrant voicings.
Return to text
28. As noted in [15], rounding the harmonic series’ just tunings to a 24-TET grid produces a 7th partial that is approximately nineteen cents “too flat.”
Return to text
Copyright Statement
Copyright © 2022 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Fred Hosken, Editorial Assistant
Number of visits:
7116