Mixed Rhythms in Chopin's Ballades and Scherzos*
Soo Kyung Chung
KEYWORDS: phrase rhythm, extension type, mixed rhythm, Chopin’s Ballades and Scherzos, Charm Bracelet Space
ABSTRACT: In this article, I argue that using four different mixed rhythms is one of Chopin’s solutions to what Rothstein (1988, 1989) calls the “Great Nineteenth-Century Rhythm Problem.” In Chopin’s works, sometimes a melodic group does not project a regular four-hyperbeat group, but rather shifts to a five-hyperbeat group while keeping a regular quadruple hypermeter. A five-hyperbeat mixed rhythm is suggested by Ng (2021), which is further expanded in this study. I suggest that these newly proposed phrase-rhythmic types play two crucial roles in Chopin’s form: 1) articulating a formal cadence; and 2) giving rise to irregular melodic groups. The mixed rhythms help us to better understand how Chopin avoids highly symmetrical duple organization in his melodies. In order to demonstrate the interplay between mixed rhythms and familiar phrase-rhythmic groups, I propose a Charm Bracelet Space, which intersperses four mixed rhythms among the four-hyperbeat groups.
DOI: 10.30535/mto.31.4.1
Copyright © 2025 Society for Music Theory
Introduction
[1] The “tyranny of the four-measure phrase”—recognized by Edward T. Cone (1968, 79) and called the “Rhythm Problem” by William Rothstein (1988, 115; 1989, 184)—is a purported characteristic of Western art music in the early nineteenth-century.(1) The frequent organization of phrases into lengths of four, eight, sixteen, and thirty-two measures is seen as a challenge for composers because phrase structure can easily become “too symmetrical, too uniform, and too highly articulated, hence tedious” (Rothstein 1988, 118). Rothstein (1989, 233) finds that “endless melody was Chopin’s ultimate response to the Rhythm Problem”; Chopin uses devices such as slurs against phrase structure, overlaps, lead-in, and avoidance of cadences, often obscuring the boundary between phrases or subphrases. These techniques combine to create an effect of rhythmic continuity that anticipated Wagner’s “endless melody” (Rothstein 1988, 118).
Example 1. Chopin‘s Scherzo no. 2, op. 31 (one hyperbeat = one measure)
(click to enlarge and listen)
[2] In this article, I argue that utilizing four different mixed rhythms is another of Chopin’s solutions to the “Great Nineteenth-Century Rhythm Problem.” In Chopin’s works, a melodic group sometimes does not project a regular four-hyperbeat group, but rather shifts to a five-hyperbeat group while keeping a regular quadruple hypermeter. As shown in Example 1, a melodic group projects a four-hyperbeat 1–2–3–4 group in mm. 1–4.(2) The next melodic group (mm. 5–9) is extended to a five-hyperbeat group. Following Samuel Ng’s (2021, 3) taxonomy, the melodic group in mm. 5–9 can be denoted as the 1–2–3–4–1 group. If the subsequent melodic group had appeared with an overlap in mm. 9–12, the original 1–2–3–4 group could have returned, but instead only an incomplete 2–3–4 group appears. A five-hyperbeat 1–2–3–4–1 group then reappears in both mm. 13–17 and 18–22.(3) This raises the question of how to interpret these consecutive five-hyperbeat groups. In this paper, I illuminate some hitherto unexplored phrase-rhythmic groups and their interaction with more familiar four-hyperbeat groups.
[3] First, I present the analytical notation of phrase-rhythmic types in the recent music-theoretical literature dealing with eighteenth- and nineteenth-century music. Second, I expand the possibilities of mixed phrase-rhythmic types from Ng’s (2021) taxonomy, and offer the Charm Bracelet Space, which expands Ng’s cyclic space by interspersing four mixed rhythms among the four-hyperbeat groups. Lastly, I discuss the four mixed rhythms in Chopin’s music and their roles in formal cadences and irregular melodic groups. The newly proposed mixed groups will help us better understand Chopin’s melodies in a more nuanced way, particularly how they avoid the overuse of equal lengths of melodic groups, such as (2+2) or (4+4), in relation to regular hypermeter.
Phrase-Rhythmic Types
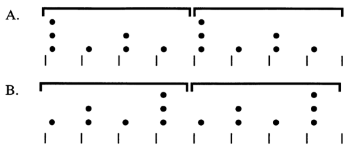
Example 2. Unproblematic cases of beginning- and end-accented structures (from Temperley’s Example 4 [2003])
(click to enlarge)
Example 3. Phrase-rhythmic notation in recent music-theoretical literature
(click to enlarge)
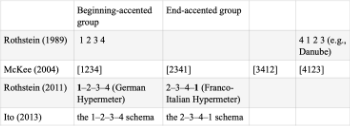
[4] The two most discussed phrase-rhythmic types in the existing literature are beginning- and end-accented groups.(4) David Temperley (2003) adopts a conventional notation introduced by Fred Lerdahl and Ray Jackendoff (1983)—dots and brackets—to show the relationship between metrical structure and grouping. Temperley (2003) explains that beginning-accented groups receive the strongest metric accent at or near the beginning of groups (Example 2; see diagram A), whereas end-accented groups contain the strongest metric accent at or near the end of groups (Example 2; see diagram B). Some scholars, on the other hand, use numeric notation to indicate phrase-rhythmic types. Example 3 provides an overview of phrase-rhythmic notation in recent music-theoretical literature.(5) The beginning-accented group can be denoted as “1–2–3–4,” whereas the end-accented group is as “ 2–3–4–1” (Rothstein 2011, Ito 2013). Besides these two groups, Rothstein (1989) and Eric McKee (2004) discuss the upbeat group 4–1–2–3.(6) McKee also considers a 3–4–1–2 group as one of the four basic rotations.
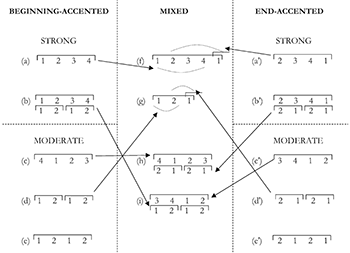
Example 4. Ng’s tripartite taxonomy of phrase-rhythmic types (from Ng’s Example 1 [2021])
(click to enlarge)
[5] Recently, Ng (2021, 3–4) has further expanded beginning-accented and end-accented groups by dividing these two categories into “strong” and “moderate” types (Example 4). He explains that strong types have the most hypermetrically accented beat (1) at the edge of the four-hyperbeat groups, while moderate types have it in the middle of the four-hyperbeat groups. As a result, while the 1–2–3–4 group is strongly beginning-accented and the 2–3–4–1 group is strongly end-accented, 4–1–2–3 is moderately beginning-accented and 3–4–1–2 moderately end-accented.
[6] Ng also adds a third category, “mixed rhythm,” which includes features from both beginning- and end-accented groups. He further divides it into two subtypes: 1) the “extension” type and 2) the “incongruent” type. The first type occurs when the length of a group is extended—for example, when group (f) type starts as group (a), but ends with (a′).(7) The second type projects different schemas between the lower and higher hypermetrical levels. Group (h) is the moderately beginning-accented type at the higher, four-beat level, whereas the subgroups are end-accented at the lower two-beat level. Conversely, group (i) is moderately end-accented at the four-beat level, whereas the subgroups are beginning-accented at the two-beat level.
Expanding Categories of Mixed Rhythm: Charm Bracelet Space
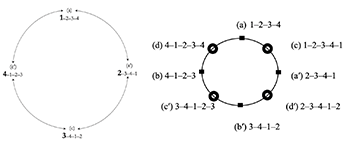
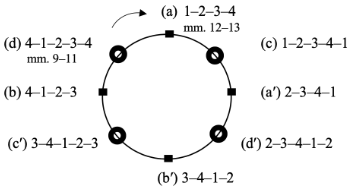
Example 5. Ng’s cyclic space (left side) and my Charm Bracelet Space (right side)
(click to enlarge)
[7] In this article, I expand the possibilities for the extension type of mixed rhythms beyond the 1–2–3–4–1 group to 2–3–4–1–2, 3–4–1–2–3, and 4–1–2–3–4, respectively. In order to show the interaction among four- and five-hyperbeat groups in Chopin’s music, I propose a Charm Bracelet Space. Based on Ng’s (2021) cycle space, which represents the four basic rotations of four-hyperbeat groups (see left side of Example 5), I intersperse four different mixed rhythms among Ng’s four-hyperbeat groups (see the right side of Example 5). I designate the four-hyperbeat groups as fixed points represented by the rectangles, and mixed rhythms as charms, shown by the donut-shaped beads. This new spatial representation allows us to trace phrase-rhythmic progressions, as Ng’s cyclic space promotes.(8) By adding four mixed rhythms, the Charm Bracelet Space helps us to perceive the transitional states between four-hyperbeat groups.
[8] The alphabetical labelling is reorganized because I will focus only on the four-hyperbeat level and omit the two-hyperbeat level. I keep Ng’s (a) 1–2–3–4 and (a′) 2–3–4–1 in which the location of hyperbeat 1 appears at the opposite ends of the group. However, I will assign to 4–1–2–3 and 3–4–1–2 the subsequent letters (b) and (b′) rather than Ng’s (c) and (c′) since I do not use his (b) and (b′) where both the four- and two-hyperbeat levels are considered.(9) Then, I assign (c) to the mixed 1–2–3–4–1 group and (c′) to the mixed 3–4–1–2–3 group. Finally, I assign (d) to the mixed 4–1–2–3–4 group and (d′) to the mixed 2–3–4–1–2 group. As in the previous pairing, hyperbeat 1 occurs in the opposite positions within the group.
Mixed Rhythm Delineating a Formal Cadence
Example 6. Group (c) 1–2–3–4–1 delineating the final structural cadence in Chopin’s Ballade No. 1, op. 23 (one hyperbeat = half measure)
(click to enlarge, see the rest, and listen)
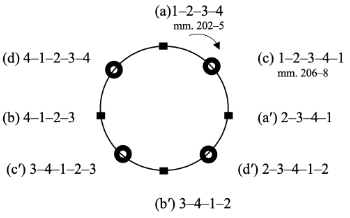
[9] Both the original extension type of mixed rhythm 1–2–3–4–1 and the newly expanded mixed rhythm 4–1–2–3–4 may articulate important formal cadences in Chopin’s works.(10) For instance, the original extension type of mixed rhythm 1–2–3–4–1 often appears at major formal junctures in Classical instrumental music: between the primary theme and the transition, or between the secondary theme and the closing zone (Ng 2012, 55 and 66; Ng 2021, 7).(11) This tendency is found in Chopin’s Ballades as well. For instance, as shown in Example 6, in the First Ballade the original mixed rhythm 1–2–3–4–1 emphasizes the Essential Structural Closure (ESC; see Hepokoski and Darcy 2006), before proceeding to the coda.(12)
Example 7. Phrase-rhythmic progression in Chopin’s Ballade no. 1, mm. 202–8, illustrated with the Charm Bracelet Space
(click to enlarge)
[10] In this passage, the beginning of a cadential melodic group in m. 206 receives the beginning accent supported by a cadential
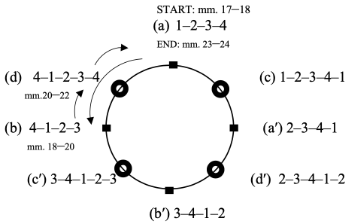
[11] The newly proposed 4–1–2–3–4 may also emerge at formal junctures, specifically at the end of the principal theme in the Fourth Ballade and the first theme in the First Scherzo. In the Fourth Ballade (see Example 8), the 4–1–2–3–4 group occurs in mm. 20–22 at the half cadence of the principal theme. Group 1–2–3–4 proceeds to 4–1–2–3 by overlapping in m. 18. The 4–1–2–3 group seems to punctuate the perfect authentic cadence in the subdominant key,
Example 8. Group (d) 4–1–2–3–4 delineating the HC in Chopin’s Ballade no. 4, op. 52 (one hyperbeat = half measure) (click to enlarge and listen) | Example 9. Phrase-rhythmic progression in mm. 17–24 of Chopin’s Ballade no. 4 illustrated with the Charm Bracelet Space (click to enlarge) |
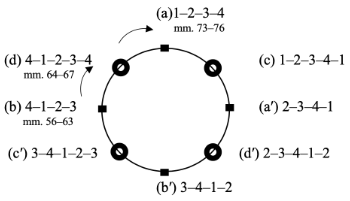
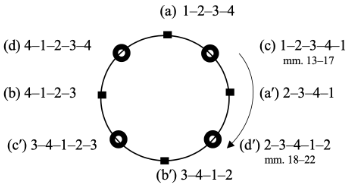
[12] In the First Scherzo, shown in Example 10, the 4–1–2–3–4 group articulates the cadences of the first theme in both endings: first a half cadence and then a perfect authentic cadence. Group 4–1–2–3 momentarily moves to an extension type of mixed rhythm 4–1–2–3–4 at the cadence.(14) The second theme in m. 73 then articulates group 1–2–3–4. The Charm Bracelet Space shows that group (b) 4–1–2–3 gradually shifts counterclockwise to (d) 4–1–2–3–4 at the cadence of the first theme, and then shifts to (a) 1–2–3–4 for the second theme (Example 11).
Example 10. Chopin’s Scherzo no. 1, op. 20; group (d) 4–1–2–3–4 punctuating first HC, then PAC at the end of the first theme (one hyperbeat = one measure) (click to enlarge, listen, and see the rest) | Example 11. Phrase-rhythmic progression in mm. 56–76 of Chopin’s First Scherzo illustrated with the Charm Bracelet Space (click to enlarge) |
Mixed Rhythms Involved in Irregular Melodic Groups
Example 12. Three possible phrase-rhythmic progressions following a mixed rhythm
(click to enlarge)
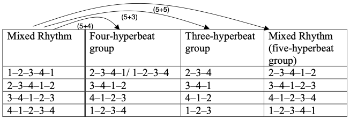
[13] Another function of mixed rhythms is to create irregular melodic groups that consist of five-hyperbeat groups rather than regular four-hyperbeat groups. In Chopin’s works, all mixed rhythms (1–2–3–4–1, 2–3–4–1–2, 3–4–1–2–3 and 4–1–2–3–4) contribute to melodic fluidity while sustaining the quadruple hypermeter. Mixed rhythms interact with regular four-, three-, or even five-hyperbeat groups (see Example 12). I refer to them as (5+4), (5+3), and (5+5) groups, respectively.
[14] The first category, the (5+4) group, can be found in Chopin’s Second Ballade, op. 38. This group appears in a new phrase with groups (d) 4–1–2–3–4 and (a) 1–2–3–4, creating an irregular melodic group (Example 13). A mixed group (d) 4–1–2–3–4, starting a new phrase, emerges when group (a) 1–2–3–4 is left incomplete after only 1–2–3 at the moment of a perfect authentic cadence in mm. 8–9. Then, the original group (a) 1–2–3–4 returns in m. 12ff. A regular four-hyperbeat group (a) is momentarily replaced by the incomplete three-hyperbeat and five-hyperbeat group (d), which contributes to a fluid melody. The Charm Bracelet Space shows that group (d) 4–1–2–3–4 gradually shifts clockwise to (a) 1–2–3–4 (see Example 14).
Example 13. (5+4) group: (d) to (a) in Chopin’s Second Ballade, op. 38 (one hyperbeat = half measure) (click to enlarge and listen) | Example 14. Chopin’s Ballade no. 2 op. 38, phrase-rhythmic progression (d) to (a) illustrated with the Charm Bracelet Space (click to enlarge) |
Example 15. Phrase-rhythmic progression (d) to (a) in Chopin’s Fantaisie-Impromptu, op. 66 (one hyperbeat = half measure)
(click to enlarge)
[15] A similar progression, initiating group (d) 4–1–2–3–4 through the incomplete 1–2–3 and then proceeding to group (a) 1–2–3–4, occurs in the second theme of Chopin’s Fantaisie-Impromptu, op. 66, but group (d) subtly extends to the next hyperdownbeat with an overlap (see Example 15). Group (d) 4–1–2–3–4 launches a new melodic group in m. 46½ after an incomplete 1–2–3 group marking a half cadence at the lower level. However, the melodic group is extended by the tonic arrival of
[16] This particular melody in Fantaisie-Impromptu is discussed by Gerald Abraham (1939) and Edward T. Cone (1994). Both note that deliberately starting a new melodic group a half-measure earlier avoids regular four-measure melodic groups. Abraham (1939, 59–60) marks that the second four-measure melodic group starts a half-measure “too soon” in m. 46, and that this “premature entry” shows how Chopin conceals the squareness of four- or eight-measure phrases and highlights the “rubato of phrase conception.”(16) Cone (1994, 152) describes this passage as “rhythmic dislocation,” which “disguises the hypermeter by shifting the boundaries of an entire phrase.” He explains that the melodic boundary may be shifted by slurs, which conflict with the underlying metrical regularity. For example, in mm. 43–50, using 3½- and 4½-measure melodic segments, Cone illustrates the non-alignment of melodic groups and underlying 4+4 hypermeasures. My early illustration of this passage in Example 15 aims to highlight the phenomenon of a half-measure-early melodic group using phrase-rhythmic group (d) 4–1–2–3–4, and elucidate this irregular pair of 3½- and 4½-measure segments by using both incomplete and mixed groups in relation to hypermeter.
Example 16. (5+3) group in Chopin’s Scherzo no. 4, op. 54 (one hyperbeat = one measure)
(click to enlarge)
[17] The second category (5+3) group emerges in Chopin’s Fourth Scherzo, op. 54, delineating an irregular five-measure melody and three-measure arpeggiations (see Example 16). The 1–2–3–4–1 mixed rhythm immediately proceeds to a 2–3–4 group in mm. 249–56 and 257–64, where it can be regarded as the second idea of the second theme.(17) Instead of a regular four-hyperbeat 1–2–3–4 group, the 1–2–3–4–1 group delineates the five-measure melody, punctuating a perfect authentic cadence in B major. The following incomplete 2–3–4 group outlines an up-and-down three-measure arpeggiation in a playful manner, prolonging the tonic in B major.
Example 17. (5+3) group in Chopin’s Etude op. 10, no. 3 (one hyperbeat= one measure)
(click to enlarge and listen)
[18] Similarly, the opening of Chopin’s Etude op. 10, no. 3 has a progression from 1–2–3–4–1 to 2–3–4 (see Example 17). The mixed group 1–2–3–4–1 outlines the opening five-measure melody, which ends with a perfect authentic cadence in E major.(18) Then, the incomplete group 2–3–4 outlines the contrasting melody, leading to the dominant seventh chord. My phrase-rhythmic analysis reinforces Rothstein’s (1989, 224) observation of how Chopin creates irregular group length (5+3 measures) at the local phrase level but a regular group length (8 measures) at the higher level.
[19] The third category, a successive mixed rhythm (5+5) group, can be found in Chopin’s Scherzo No. 2, op. 31. In the introduction (Example 1), I raised a question about how we could interpret the successive five-hyperbeat groups in mm. 13–17 and mm. 18–22. One may consider the latter to be another 1–2–3–4–1 group in which the hypermetrical downbeat is supported by the harmonic change in m. 18. After that, the 2–3 group occupies a rest in mm. 23–24, and then with a metrical reinterpretation (4=1), group (a) 1–2–3–4 returns (Example 18). On the other hand, my solution is to consider the twelve-measure subphrase as a successive mixed rhythm: the 1–2–3–4–1 group is followed by the newly proposed 2–3–4–1–2 group, with silence taking up the following 3–4 group (Example 19). The advantage of my interpretation is to keep the underlying regular quadruple hypermeter without having the successive hypermetrical downbeats and metrical reinterpretation. In addition, my interpretation highlights the accentuation of a syncopated dominant bass in mm. 20–21 at the hypermetrically weak beat 4 and sustained over the hypermetrical downbeat 1.(19) Furthermore, the consequent 3–4 group naturally leads to the original group 1–2–3–4 in mm. 25–28 without metrical reinterpretation.(20)
Example 18. One possible interpretation in Chopin’s Scherzo no. 2, op. 31 (click to enlarge and listen) | Example 19. (5+5) group: (c) to (d') in Chopin’s Scherzo no. 2, op. 31 (one hyperbeat = one measure) (click to enlarge and listen) |
Example 20. Chopin’s Scherzo no. 2, op. 31, phrase-rhythmic progression (c) to (d') illustrated with the Charm Bracelet Space
(click to enlarge)
[20] The effect of the irregular grouping 5+5+2 against the regular quadruple hypermeter is very dramatic. A mixed rhythm usually plays a transitional role between regular four-hyperbeat groups. However, the successive mixed rhythms in this passage have a prominent effect: they disturb the regularity of the four-hyperbeat groups, while still aligning with the overall quadruple hypermeter. The (c) 1–2–3–4–1 group articulates tonicized III, then the (d′) 2–3–4–1–2 group features the deceptive motion V to VI in the tonic key of
Example 21. A full rotation of mixed rhythms in Chopin’s Ballade no. 1, op. 23 (one hyperbeat = half measure)
(click to enlarge, see the rest, and listen)
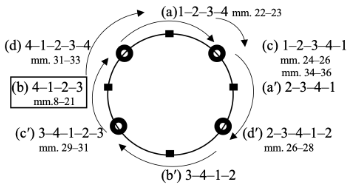
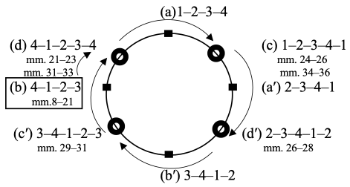
[21] A full rotation of mixed rhythms may be found in the highly irregular and extensive consequent phrase of the primary theme in the Ballade No. 1 in G minor op. 23. These successive mixed rhythms may help us to understand Chopin’s “endless melody,” (Rothstein 1989) or “long long long melodies” (Kasunic 2004).(22) (see Example 21). The initial eight-measure antecedent phrase is responded with an elaborated, twenty-measure consequent phrase.(23) The primary theme emerges with group (b) 4–1–2–3 with an anacrusis gesture. When the consequent phrase is expanded, regularly articulating group (b) traverses all of the rotational mixed rhythms.(24) The beginning moment of phrase expansion in mm. 21–23 can be heard in two ways. In terms used by Andrew Imbrie (1973, 65), one is a “conservative” interpretation, and the other is “radical.”(25) A conservative hearing suggests that phrase expansion starts at mm. 21–23 where group (b) 4–1–2–3 shifts to group (a) 1–2–3–4 through an overlap and metrical reinterpretation in m. 22 (3=1). Because the four-note motive (G–D–C–G) is repeated in mm. 22–23 and mm. 24–25, Lerdahl and Jackendoff’s (1983, 76) “strong beat early” metrical preference rule may influence us to hear G in the first group in m. 22 as the hyperdownbeat. In addition, the G in m. 22 is supported by “bass” and “harmonic rhythm” metrical preference rules (Lerdahl and Jackendoff 1983, 84 and 88).
[22] On the other hand, a radical hearing suggests that an incomplete group (b) 4–1 moves to a mixed rhythm (d) 4–1–2–3–4 because the two dotted-half-notes motive is subsequently expanded to five dotted-half notes in mm. 21–23. Rather than the incomplete 4–1 group proceeding to (d′) 2–3–4–1–2, it shifts to (d) 4–1–2–3–4 because the “strong beat early,” “bass,” and “harmonic rhythm” are still strong factors for hearing the G in m. 22 as the hypermetrical downbeat. Phrase expansion continues through the irregular five-hyperbeat grouping indicated by slurs, implying fully rotated mixed rhythms. Either group (a) from the conservative hearing or group (d) from the radical hearing moves to (c) 1–2–3–4–1 in mm. 24–26. Group (c) delineates the repetition of the four-note motive (G–D–C–G) in mm. 24–25 with one added note, F, in m. 26. The F coincides with the end accent, supported by the cadential
[23] Examples 22 and 23 summarize the phrase-rhythmic progression of the primary theme using the Charm Bracelet Space. Example 22 includes the conservative hearing at the phrase expansion. Group (b) 4–1–2–3 in mm. 8–22 moves clockwise to group (a) 1–2–3–4 in mm. 22–23 through the overlap and metrical interpretation, and then group (a) shifts to group (c) 1–2–3–4–1 in mm. 24–26. Example 23 contains the radical hearing at the phrase expansion. Group (b) 4–1–2–3 moves clockwise to group (d) 4–1–2–3–4 in mm. 22–24 through incomplete group (b) 4–1, and then group (d) shifts to group (c) 1–2–3–4–1 in mm. 24–26. Subsequently, both examples show that the phrase rhythm fully rotates clockwise with mixed rhythms from (d′), (c′), (d), to (c).
Example 22. Chopin’s Ballade no. 1, op. 23, phrase-rhythmic progression in mm. 8–36, illustrated with the Charm Bracelet Space (with a “conservative” interpretation of the phrase expansion) (click to enlarge) | Example 23. Chopin’s Ballade no. 1, op. 23, phrase-rhythmic progression in mm. 8–36 illustrated with the Charm Bracelet Space (with a “radical” interpretation of the phrase expansion) (click to enlarge) |
Conclusion
[24] Expanding the category of mixed rhythms invites us to understand how Chopin skillfully eschews rigid duple organization. As the article demonstrated, sometimes a regular four-hyperbeat group is extended by one hyperbeat, producing a mixed rhythm at the end of a formal area, in conjunction with a cadence. Other times, a regular four-beat group is subtly replaced by a mixed rhythm that combines with four-, three-, and even five-hyperbeat groups, generating irregular melodic groups. The irregular groups delicately conduce to melodic fluidity without changing regular quadruple hypermeter. As this paper has sought to explore, Charm Bracelet Space helps to illustrate Chopin’s melodic fluidity by visually tracing the interplay between mixed rhythms and familiar four-hyperbeat groups. Finally, while in this study I only focused on Chopin’s works, future research could apply this theoretical approach to other composers of the late 19th and 20th century, such as Dvořák, Tchaikovsky, Satie and Ravel.
Soo Kyung Chung
University of Missouri—Kansas City
Volker Campus
4949 Cherry Street
Kansas City, MO 64110
s.chung@umkc.edu
Works Cited
Abraham, Gerald. 1939. Chopin’s Musical Style. Oxford University Press. https://doi.org/10.2307/923708.
Bakulina, Ellen, and Edward Klorman. 2021. “Cadence as a Hypermetrical Focus.” Paper presented at the Annual Meeting of the Society for Music Theory, virtual, November 4–7.
Bielecki, Artur. “Scherzos.” The Fryderyk Chopin Institute. https://chopin.nifc.pl/en/chopin/gatunki/14_scherza.
Burstein, L. Poundie. 2020. Journeys through Galant Expositions. Oxford University Press. https://doi.org/10.1093/oso/9780190083991.001.0001.
Caplin, William. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. New York: Oxford University Press.
Chechlińska, Zofia. 1995. “Scherzo as a Genre—Selected Problems.” In Chopin Studies 5, Warsaw: Towarzystwo im. Fryderyka Chopina, 165–73. Access on October 17, 2025.
Chung, Soo Kyung. 2022. “Large-Scale Form in Chopin’s Four Ballades from Sonata Theory and Phrase-Rhythmic Perspectives.” PhD diss., University of Cincinnati College-Conservatory of Music.
Cone, Edward T. 1968. Musical Form and Musical Performance. W. W. Norton.
—————. 1994. “Ambiguity and Reinterpretation in Chopin.” In Chopin Studies 2, ed. John Rink and Jim Samson, 140–60. Cambridge University Press.
Hepokoski, James, and Warren Darcy. 2006. Elements of Sonata Theory: Norms, Types, and Deformations in the Late-Eighteenth-Century Sonata. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195146400.001.0001.
Imbrie, Andrew. 1973. “‘Extra’ Measures and Metrical Ambiguity in Beethoven.” In Beethoven Studies, ed. Alan Tyson, 45–66. W. W. Norton.
Ito, John Paul. 2013. “Hypermetrical Schemas, Metrical Orientation, and Cognitive-Linguistic Paradigms.” Journal of Music Theory 57 (1): 47–85. https://doi.org/10.1215/00222909-2017106.
—————. 2021. Focal Impulse Theory: Musical Expression, Meter, and the Body. Indiana University Press. https://doi.org/10.2307/j.ctv1c3pdp3.
Kallberg, Jeffrey. 1996. “The Chopin ‘Problem’: Simultaneous Variants and Alternate Version.” In Chopin at the Boundaries: Sex, History, and Musical Genre. Harvard University Press.
Kasunic, David. 2004. “Chopin and the Singing Voice, From the Romantic to the Real.” PhD diss., Princeton University.
Keele, Christy. 2018. “Reconceptualizing Climax in the Four Scherzos of Frédéric Chopin.” PhD diss. Indiana University.
Koch, Heinrich Christoph, and Nancy Kovaleff Baker. 1983. Introductory Essay on Composition: The Mechanical Rules of Melody, Sections 3 and 4. Yale University Press.
Krebs, Harald. 1999. Fantasy Pieces: Metrical Dissonance in the Music of Robert Schumann. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195116236.001.0001.
Leichtentritt, Hugo. 1922. Analyse der Chopin’schen Klavierwerke Bd. 2. Max Hesses Verlag.
Lerdahl, Fred, and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. The MIT Press.
London, Justin. 1993. “Loud Rests and Other Strange Metric Phenomena (or, Meter as Heard).” Music Theory Online 0.2.
Malin, Yonatan. 2010. Songs in Motion: Group and Meter in the German Lied. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780195340051.001.0001.
McKee, Eric. 2004. “Extended Anacruses in Mozart’s Instrumental Music.” Theory and Practice 29: 1–37.
—————. 2010. “Punctuation and Sense in Late-Eighteenth-Century Music.” Journal of Music Theory 54 (2): 235–82. https://doi.org/10.1215/00222909-1214930.
Mirka, Danuta. 2021. Hypermetric Manipulations in Haydn and Mozart: Chamber Music for Strings (1787–1791). Oxford University Press. https://doi.org/10.1093/oso/9780197548905.001.0001.
Niecks, Frederik. 1890. Frederick Chopin, As a Man and Musician. Novello & Co.
Ng, Samuel. 2012. “Phrase Rhythm as Form in Classical Instrumental Music.” Music Theory Spectrum 34 (1): 51–77. https://doi.org/10.1525/mts.2012.34.1.51.
—————. 2021. “End-Accented Sentences: Towards a Theory of Phrase-Rhythmic Progression.” Music Theory Spectrum 43 (1): 1–31. https://doi.org/10.1093/mts/mtaa018.
—————. 2022. “Musical Eschatology in Contemporary Christian Worship Songs.” Music Theory Online 28 (4). https://doi.org/10.30535/mto.28.4.5.
Parakilas, James. 1992. Ballads Without Words: Chopin and the Tradition of the Instrumental Ballade. Amadeus Press.
Rawsthorne, Alan. 1966. “Ballades, Fantasy and Scherzos.” In Frédéric Chopin: Profiles of the Man and the Musician, ed. Alan Walker, 42–72. Barrie & Rockliff.
Rink, John. 1994. “Chopin’s Ballades and the Dialectic: Analysis in Historical Perspective.” Music Analysis 13 (1): 99–115. https://doi.org/10.2307/854282.
Rothstein, William. 1988. “Phrase Rhythm in Chopin's Nocturnes and Mazurkas.” In Chopin Studies, ed. Jim Samson, 115–41. Cambridge University Press.
—————. 1989. Phrase Rhythm in Tonal Music. Schirmer Books.
—————. 1994. “Ambiguity in the Themes of Chopin’s First, Second, and Fourth Ballades.” Intégral 8: 1–50.
—————. 2011. “Metrical Theory and Verdi’s Midcentury Operas.” Dutch Journal of Music Theory 16 (2): 93–111.
—————. 2023. The Musical Language of Italian Opera, 1813–1859. Oxford University Press. https://doi.org/10.1093/oso/9780197609682.001.0001.
Samson, Jim. 1992. Chopin: The Four Ballades. Cambridge University Press. https://doi.org/10.1017/CBO9780511611650.
Santa, Matthew. 2020. Hearing Group and Meter: Analyzing Metrical Consonance and Dissonance in Common-Practice Period Music. Routledge. https://doi.org/10.4324/9781351204316.
Straub, Joshua. 2016. “Hypermeter as an Expressive Determinant in the Four Scherzos of Chopin.” DMA diss., University of Texas at Austin.
Temperley, David. 2003. “End-Accented Phrases: An Analytical Exploration.” Journal of Music Theory 47 (1): 125–54. https://doi.org/10.1215/00222909-47-1-125.
—————. 2008. Hypermetrical Transition.” Music Theory Spectrum 30 (2): 305–25. https://doi.org/10.1525/mts.2008.30.2.305.
Von Lenz, Wilhelm. 1872. “Uebersichtliche Beurteilung der Pianoforte-Compositionen von Chopin, als Prodromus eines kritischen Katalogs seiner sämmtlichen Werke.” Neue Berliner Musikzeitung 26.
Discography
Discography
Pollini, Maurizio. 1972. Chopin Etudes. Deutsche Grammophon 413 794-2. CD.
Rubinstein, Arthur. 1999 [1959/1965]. Chopin: Ballades, Scherzi, Tarantelle. The Rubinstein Collection Vol. 45, RCA Red Seal 09026 63045-2. CD.
—————. 2004 [1964/1965]. Chopin: Waltzes & Impromptus. RCA Red Seal 82876-59422-2. CD.
Zimerman, Krystian. 1988. Chopin: 4 Balladen, Barcarolle, Fantasie. Deutsche Gramophon 423 090-2. CD.
Footnotes
* The majority of this article was presented at the 2021 meeting of the Society for Music Theory. I am deeply indebted to my advisor, Samuel Ng, for sharing his phrase-rhythmic taxonomy and spaces with me before his publication on this topic in 2021. In addition, I am grateful to Steven Cahn, David Carson Berry, Harald Krebs, Andrew Pau, John Paul Ito (signed reviewer), and one anonymous reviewer for reading my article and providing valuable feedback. I also extend my gratitude to my colleagues Adam Shoaff and Carl Burdick for proofreading. Finally, I would like to thank MTO editors, especially, Cecilia Oinas for providing editorial suggestions.
Return to text
1. Rothstein refers to the “Rhythm Problem” in his 1988 article, and he expands the term to the “Great Nineteenth-Century Rhythm Problem” in his 1989 book.
Return to text
2. Throughout the paper, sometimes I perceive one measure as one hyperbeat, and sometimes a half measure as one hyperbeat, depending on the tempo, harmonic rhythm, and grouping. I will notate them as either one hyperbeat = one measure or one hyperbeat = half measure. My notation thus differs from William Caplin (1998, 35) who shows the relationship between the real and notated measures. Caplin (1998, 35, fn5) however acknowledges that “the situation R=2N may seem to resemble the notation of ‘hypermeter’.”
Return to text
3. Usually, after a 1–2–3–4–1 group, a regular four-hyperbeat 1–2–3–4 group returns by melodic overlap, or a 2–3–4–1 group occurs when there is no melodic overlap (see Ng 2021, 4).
Return to text
4. See the discussion of beginning-accented versus end-accented camps in David Temperley (2003, 128). Scholars such as Schachter, Lerdahl and Jackendoff, Kramer, and Rothstein consider beginning-accented phrases more normative. Riemann, Cooper and Meyer, and Komar hold the opposite view (see Samuel Ng’s [2021, 1] review of this issue.
Return to text
5. Ito (2013) uses the fractional notation in his schema. For example, in the 1–2–3–4 schema, 1/4, 2/4, 3/4, and 4/4 represent the first hyperbeat of four, second hyperbeat of four, etc. Each hyperbeat is related to a specific role in the grouping unit. The role of “initiation” in grouping begins with the hyperdownbeat 1; the role of “continuation” in grouping is aligned with the hyperbeats 2 and 3; finally, the function of “conclusion” ends with hyperbeat 4. The advantage of the fractional notation is that it allows the analyst to assign hyperbeats flexibly in relation to the grouping functions when the grouping is not a straightforward four measures in length. See Ito (2013, 50–51; 2021, 37–38). Santa (2020, ch.3) uses a numeric notation with a superscript: 14 2 3 4, 13 2 3, and 12 2 indicate a quadruple, triple, and duple hypermeter, respectively. Malin (2010, 44 and fn 15) uses dots to show the multiple metrical levels but also uses a numeric notation as well. However, his numeric annotation on the score demonstrates the duration of hypermetrical span, adapted from Krebs (1999).
Return to text
6. Rothstein (1989, 9) shows melodic segments of Johann Strauss II’s “Blue Danube” as “4 1 2 3,” and this may refer to Rothstein’s (2023, 97) “melodic four-cycle.” In The Musical Language of Italian Opera, 1813–1859 (2023), he differentiates between a “metric four-cycle” and “melodic four-cycle,” mainly focusing on “melodic four-cycle” unless “metric four-cycle” is specified in the analyses. Rothstein also acknowledges that “the dichotomy is not so tidy, however, because melodic four-cycle can only exist where a robust metrical structure also exists” (2023, 97–98). Throughout my paper, my phrase-rhythmic analysis focuses on “melodic four-cycles” since Chopin’s “metric four-cycle” is so solid.
Return to text
7. This group (f) is equivalent to Ito’s (2013, 71) “hybrid schema” that “combines features both the 1–2–3–4 and the 2–3–4–1 schema.”
Return to text
8. Besides cyclic space, Ng designs a linear space based on his taxonomy of phrase-rhythmic types. His linear space provides a rich palette of phrase-rhythmic types to trace phrase-rhythmic progression along with formal areas. See Ng (2021, 5–7 and 2022, [3.1.6]). Prior to Ng’s 2021 article, scholars who have examined shifts between hypermetrical groups in form include McKee (2004), who traces “metrical rotations” in Mozart’s instrumental music and Temperley (2008), who studies hypermetrical shifts, “hypermetrical transition,” in music by Mozart, Beethoven, Chopin, and Mendelssohn. Furthermore, Temperley (2003) and Ng (2012) have explored tendencies between hypermetrical groups (e.g. end-accented groups) and particular formal areas (e.g. closing zones).
Return to text
9. The labels shown in the figure of Ng’s cyclic space are incorrect. The 4–1–2–3 group should be (c) instead of (c′), and the 3–4–1–2 group should be (c′) instead of (c) based on his tripartite taxonomy.
Return to text
10. The term “formal cadence” (förmliche Cadenz) originates with Heinrich Christoph Koch (1749–1816). See Koch and Baker (1983, 166, 169–70, 178, and 237). Burstein summarizes Koch’s formal cadence as follows: “the cadence that delineates the end of the Periode,” and adds that “the formal cadence at the end of the first Hauptperiode usually equals what Sonata Theory refers to as the ‘EEC’ (Essential Exposition Closure)” (2020, 258). In my paper, a formal cadence is used more loosely. I refer to not only the EEC and ESC (Essential Structural Closure) in Hepokoski and Darcy’s Sonata’s Theory terms but also to the last cadence of the first theme in the First Scherzo, and to the cadence of the principal theme (i.e., the juncture between the principal theme and variation I) in the Fourth Ballade.
Return to text
11. Parallel to Ng’s observation, several scholars have remarked on the relationship between important formal cadences and hypermeter—e.g., “Essential Expositional Closure” (EEC) (Hepokoski and Darcy 2006). Temperley (2003, 139) observes that, before the end-accented closing themes, “an expanded cadential progression ends in a hypermetrically accented I chord.” Malin (2010, 48) describes a hypermetrically strong cadence within vocal music: “Composers frequently extend vocal phrases on the fifth measure” where a hypermetric downbeat coincides with a new beginning melody. “Such extensions tend to occur at the ends of strophes.” Mirka (2021, 280–281) calls formal cadences “augmented cadences” in which the tonic occurs on the strong hyperbeat. Bakulina and Klorman (2021) call structural cadences, such as the EEC, “focal” cadences because structural cadences clarify the hypermetrical ambiguity of a subordinate theme, usually with a hyperdownbeat. Rothstein (2023, 109) uses a 1–2–3–4–1 group for the metrical implication in the cadenza lunga.
Return to text
12. Chopin’s four ballades have been examined with a variety of methodologies such as “literary, descriptive, formal, rhythmic, metrical, tonal, thematic, textural, interpretative, programmatic, semiotic, and hermeneutic” (Rink 1994, 111). Although the second and third ballades are very distant from a traditional sonata form, all four of Chopin’s ballades have been examined from the sonata-form perspective (see Samson 1992). I myself have examined Chopin’s four ballades in dialogue with Hepokoski and Darcy’s Sonata Theory (Chung 2022).
Return to text
13. In the principal theme, analyses of meter and irregular melodic groups (e.g. a half-measure extension) have been explored in the context of a four-measure pattern. Both Leichtentritt (1922, 33) and Rothstein (1994, 30) put the downbeat in m. 17½ when the opening motive reoccurs. In addition, both change the meter from
Return to text
14. Group 4–1–2–3 starts earlier in m. 44 (not shown in the example) by an anacrusis gesture in the left hand. The interpretation of grouping in the passage (mm. 56–68) can be subjective. Keele (2018, 159) analyzes mm. 56–57 as a part of five-measure grouping from m. 53, which delineates the line from E to
Return to text
15. This cadential phenomenon can be described either as Mirka’s “overridden caesuras: the first caesura proves to be false and is canceled by the second” (2010, 243; 2021, 220) or Rothstein’s “cadence-altering suffixes: some suffixes do not extend a cadence already reached; instead, they lead to a different cadence altogether” (1989, 94–95). Interestingly, Chopin uses a perfect authentic cadence in
Return to text
16. Krebs (1999, 55) also observes this kind of half-measure gap between phrases in Schumann’s Waldszenen op. 82 no. 1. He calls the half-measure early entrance in m. 4 “subliminal hypermetrical displacement dissonance.”
Return to text
17. Although Chopin’s manuscript has a single slur both in mm. 249–56 and in mm. 258–64, the second phrase is interesting to observe: his slur descends and marks an arrival on B in m. 261, and his pen immediately curls upward, continuing the slur marking to m. 264. In the French first edition, however, the slurs in the second phrase are more separated between mm. 258–61 and 262–64; there is a slight variation of slur showing the subgroup in the second phrase. In this article, I copied Mikuli’s edition, which follows the first edition. Chopin’s manuscript and the first edition show both an eight-measure group and a subtle subgroup (5+3). Thus, my phrase-rhythmic analysis, with the 1–2–3–4–1 and 2–3–4 groups, attempts not to highlight the clear boundary of groups (5+3), but rather to illustrate how Chopin’s eight-measure group is subtly sub-grouped: a five-measure phrase and a three-measure tonic prolongation. As Kallberg (1996, 226–28) points out, he sees variants “not as a ‘problem’ to be solved but as a reflection of one of the essences of Chopin’s art.”
Return to text
18. In this example, I highlight the upper level of hypermetric analysis (one hyperbeat = one measure). Based on the tempo and harmonic rhythm, I could also incorporate the local level of metric analysis (one hyperbeat = half measure). However, I should then use other phrase-rhythmic types, such as 1–2–3–4–5–6, that are not included in my phrase-rhythmic categories. Exploring other possible phrase-rhythmic types is an area for future research. The (hyper)metrical interpretations in this passage vary considerably: For instance, Ito (2021, 48) views the irregular opening five-measure melody within the “1–2–3–4 schema.” He assigns hyperbeat 1 in m. 1 and hyperbeat 4 in m. 5 based on the functions of the grouping units —“initiation” and “conclusion.” On the other hand, he assigns hyperbeat 2 in both m. 2 and m. 3 because of a “continuing” role. In terms of meter, this passage has raised questions whether its notated odd- or even-numbered quarter-note beats are strong. While Rothstein (1989, 221) favors an odd-strong hearing, Temperley (2008, 316) proposes an even-strong hearing because of a duration accent and harmonic change. Temperley’s even-strong hearing can be equivalent to Ng’s moderate type of end-accented group.
Return to text
19. In addition to the syncopation at the hypermetrical level, the cadential gesture (V–VI in the bass in mm. 18–22) includes a syncopation at the metrical level as well. The bass
Return to text
20. Unlike the opening (mm. 1–4), the returning melodic group (mm. 25–28) is not aligned with hyperdownbeat 1. Adapting Rothstein’s (2011, 101) concept, I consider the melodic group as starting after the “silent hyperdownbeat.” London’s (1993) “loud rest” can be considered as well in m. 25. Since the same melodic group emerges in mm. 25–28, we can retrospectively perceive m. 25 as a hypermetrical downbeat, even though the hypermetrical downbeat was not sounded.
Return to text
21. Bielecki (https://chopin.nifc.pl/en/chopin/gatunki/14_scherza) observes that Chopin’s scherzos are more dramatic than humorous. Chopin’s new approach to writing scherzos represents “Romantic expression—startling, supremely dramatic, creating the impression of extraordinariness, the dimension of tragedy, a shiver of terror. ‘It should be a house of the dead,’ Chopin is supposed to have said of the opening motif of the Scherzo in B flat minor.” This quotation was heard by Wilhelm von Lenz. “Ein Todtenhaus muss es sein, sagte er einmal” (1872; 1890, 257).
Return to text
22. Rothstein has examined Chopin’s mazurkas, nocturnes, and other works after 1840, and finds Chopin’s “seamless style of melodic writing, which in Wagner’s cases has become famous under the name of endless melody” (1989, 233). Rothstein states that “it seems almost as if Chopin wishes us not to know that one phrase is ending and another beginning. This is more than a simple phrase overlap; it is an attempt, within a basically regular phrase structure, to melt away the seams in that very structure” (1989, 220). Kasunic (2004, 189) further mentions that Chopin’s long melodies are influenced by Bellini’s operas of the middle and later 1830s. In addition to a long melody, another operatic influence can be found in m. 33 of the First Ballade, where the melodic style suddenly shifts to a “coloratura mode” (Parakilas 1992, 61).
Return to text
23. Rothstein (1994, 6) intentionally avoids using the term “phrase” mainly because of the unconventional harmonic factor (e.g., ending with a iiø7 chord in m. 16), so he rather uses the terms antecedent and consequent.
Return to text
24. The regularly articulated 4–1–2–3 group in mm. 8–20 may support Parakilas’s (1992, 60) and Rothstein’s (1994, 7–9) prosodic analyses—repetitive stanzaic structure from the perspective of poetic ballad.
Return to text
25. The conservative hearing is to push the interpretation “as far forward as possible in order to see how long one could cling to an established pattern.” On the other hand, the radical hearing is to see “how far back one could push a ‘radical’ interpretation in order to see how soon one could adopt a new pattern” (Imbrie 1973, 65).
Return to text
26. The interpretation of phrase-rhythmic groups in mm. 31–36 can vary because the boundaries of subgroups are not clear. One may suggest that group (d) 4–1–2–3–4 ends in m. 33, relying on the slurs, and group (c) opens in m. 34. One may also suggest that group (d) extends to the hypermetrical downbeat of m. 34 because of the continuous motion of the previous melody and the resolution of the secondary dominant of III. The latter interpretation reflects my current reading. This view finds even more support in Cortot’s edition, where the slur reaches up to the
Return to text
Copyright Statement
Copyright © 2025 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Lauren Irschick, Editorial Assistant
Number of visits:
915