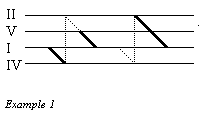Toward a Post-Schoenbergian Grammar of Tonal and Pre-tonal Harmonic Progressions
Nicolas Meeus
KEYWORDS: Schoenberg, Rameau, fundamental bass, progression, substitution
ABSTRACT: Schoenberg appears to have been among the first authors to revive Rameau’s theory of fundamental bass progressions. His categorization of the progressions in three categories (“strong or ascending,” “descending,” and “superstrong”) can be further systematized on the basis of a theory of chord substitutions. A study of the use of the progressions so categorized allows a general description of harmonically well-formed tonal phrases. A comparison with the usage of progressions in pre-tonal music evidences important differences.
Copyright © 2000 Society for Music Theory
[1] Contrary to a common prejudice, Rameau’s theory of the basse fondamentale is not about chord inversion, but about chord progressions. Rameau’s claim is that tonality is ruled by the leading of the fundamental bass line. From considerations of what he calls the resonance (the production of harmonic partials), he deduces not only that progressions by a second must be forbidden (except in special cases), but also that progressions down a fifth or a third are better than those up the same intervals.
[2] This theory has been forcefully rejected in the late 18th and the 19th centuries, especially in France where theorists argued that it does not correspond to the usage of the great masters. The rejection may be linked with a Romantic conception, still vivid today, that views tonality as immanent, precompositional: in both the Viennese (Simon Sechter) and the German (Hugo Riemann) theories, the tonal significance of a chord is seen to derive from its position in a preexisting, abstract system of hierarchies. Rameau, to the contrary, had considered that the function of a chord depends on its relation to the following chord; more specifically, he considered that any chord followed by another rooted a fifth below was the latter’s dominant and that any chord followed by another rooted a fifth above was the latter’s subdominant.
[3] One of the first authors to have returned to a theory of chord progressions is Arnold Schoenberg,(1) followed in this by Yizhak Sadai.(2) Both authors establish three categories of progressions:
- Strong or ascending progressions (Sadai’s dynamic progressions), a fourth up or a third down, which “can be used without restriction” (Schoenberg) and became “standard” (Sadai).
- Descending progressions (Sadai’s static progressions), a
fourth down or a third up, “sometimes appearing as a mere interchange
(I-V-V-I, I-IV-IV-I)”, but “better used in combinations of three
chords which [
. . . ] result in a strong progression” (Schoenberg). - Superstrong progressions (Sadai’s accented progressions), a second up or down, which “often appear as deceptive [i.e. false]” and which “may be considered too strong for continuous use” (Schoenberg).
[4] My aim today is to propose a rereading of these theories, attempting both to systematize them and to make them more descriptive than prescriptive. Prescriptive theories usually consider that progressions and their directions are determined by the preexisting set of tonal hierarchies (the justifications given often are metaphoric: they deal with “attractions,” with “centripetal forces,” etc.). My position is different: I list progressions in common practice tonal works, without any preconception of what they should be, in order to verify whether their usage is random—it soon appears that it is not.
[5] Schoenberg’s commentary about superstrong progressions being “false” probably refers to the teaching of Anton Bruckner (following that of Simon Sechter) according to whom progressions of a second often are but scheinbare Schritte, apparent progressions, to be explained as the result of the elision of an intermediate root. This doctrine is similar to that of Rameau’s double emploi, which states that, in a progression such as I-IV-V-I, IV as seen from the point of view of the following V is a II without fundamental, or that, in a I-II-V-I progression, II seen from the point of view of the preceding I is a IV with added 6th:
I -->> IV -> V -->> I = I -->>
IV(=II) -->> V -->> I
I -> II -->> V -->> I = I -->> (IV=)II -->> V
-->> I
The double emploi, as can be seen, transforms in each case a progression a second up, indicated by the sign ->, into one a fourth up, indicated by -->>.
[6] This reduces to saying that IV, in the first case, is a substitute for II (with respect to the following V) and II, in the second case, a substitute for IV (with respect to the preceding I). Substitution is a recurrent feature of harmonic theories from Rameau’s double emploi to Riemann’s Scheinkonsonanzen. Riemann, however, views the harmonic functions as imbedded in an a priori tonal hierarchy and independent from the context of any particular progression. The substitution, therefore, always is of a secondary degree for a primary one (e.g., the IId degree always is a substitute for the IVth), while ramist conceptions consider the substitutions as reciprocal: IV can stand for II as well as II for IV. In all cases, the substitutions imply chords a third apart—a fact that must be linked, in one way or another, with the parsimony of the transformation; but the many different justifications proposed for the substitutions need not retain us here.
[7] When Schoenberg includes progressions a fourth up and a third down in one category, a fourth down and a third up in another, it obviously is because the two progressions in each category can be considered substitutions for each other—or, in other words, because the two progressions belonging in the same category differ merely by the substitution of one chord for another. Both V -->> I and V -->> III, for instance, are strong progressions because I and III can be considered substitutes for each other. But the same reasoning could be applied to superstrong progressions as well, a second up or down, which also can be considered substitutions for progressions a fourth up or down. As we saw, IV -> V, a “superstrong” progression, is a substitution for II -->> V, a “strong” progression. The same could be said of V -> VI, a substitution for V -->> I, etc. This allows reducing Schoenberg’s and Sadai’s categories to two, each of which including one “principal” and two “substitute” progressions. This view actually returns to Rameau’s conception of the dominant and subdominant functions, so that the categories may be renamed as “dominant” and “subdominant”:
| CATEGORY | MAIN PROGRESSION | SUBSTITUTES |
| Dominant | A fifth down | A third down or a second up |
| Subdominant | A fifth up | A third up or a second down |
[8] Let us return to the paradigmatic tonal phrase I -->> IV -> V -->> I. The first and the third progressions, I -->> IV and V -->> I, are ordinary dominant progressions. The second, IV -> V, now appears as a substitution for a dominant progression. The characteristics of this phrase are the following:
- it is formed of dominant progressions exclusively;
- it includes one substituted progression.
These I take to be normal features of any good tonal progression. I ->
II -->> V -->>
I differs from the previous one only in the position of the substituted
progression. More extended phrases evidence the same features, usually with a
larger number of ordinary dominant progressions, but always with at least one
substituted progression:
I -->> IV -> V -->> I
I -> II -->> V -->> I
I -> VI -->> II -->> V -->> I
I -->> IV -> V -> VI -->> II -->> V -->> I
etc.
(Arrows pointing to the right indicate dominant progressions; subdominant progressions would be indicated by arrows pointing to the left).
[9] The reason why the phrases include at least one substituted progression is that this is the necessary condition for the phrase to return to its starting point, the tonic. A continued series of unsubstituted dominant progressions, following a cycle of fifths, indeed, could only inexorably lead away from the original tonic. A well formed tonal phrase can therefore be defined, from the point of view of harmonic progressions, as a series of dominant progressions of which at least one is substituted.
Example 1
(click to enlarge)
Example 2
(click to enlarge and hear the audio)
Example 3
(click to enlarge and hear the audio)
Example 4
(click to enlarge, see the rest, and hear the audio)
Example 5
(click to enlarge and hear the audio)
[10] A graphic device may help illustrate this. Example 1 shows both a I-IV-V-I and a I-II-V-I progressions. The bass roots are arranged on horizontal lines following the cycle of fifths, and connected either by thick lines (main progressions) or by dotted lines (substituted progressions, with a vertical dotted line linking the implied root to the real one). Dominant progressions appear as lines descending from left to right. The overall Z shape of these figures, which I take to be characteristic of a well formed tonal phrase, differs only in the position of the dotted lines.
[11] Example 2 shows the same graphic presentation applied to a real example, Bach’s choral Gottlob es geht nunmehr zu Ende (BWV 321, Bpf 192). One will note the two subdominant progressions (appearing as ascending thick lines) in the second system, characteristically followed by compensating dominant progressions, in what Schoenberg calls “a mere interchange” or, in Sadai’s terminology, forming a b a patterns, V-II-V in measures 9–10, I-V-I in measures 15–16. This choral counts 25 progressions in all, of which 23 (92%) are dominant progressions according to my definition; 7 of these (about 30%) are substitutions. Although it may be difficult to obtain statistics for the tonal corpus as a whole, I consider these figures to be quite typical of the common tonal practice.
[12] Subdominant progressions in some cases may be more frequent, but they
are normally not found in immediate succession, unless for special effect. Example 3, from Chopin’s Mazurka op. 6 no. 3 (measures 33–39), shows one such instance,
where the successive subdominant progressions contribute to a “modal”
effect, together with the D natural in measure 33 and the descending conjunct line
(with descending
[13] Example 4 applies similar principles to a late-16th-century composition, Lassus’ chanson
Bon jour mon coeur, evidencing drastically different results which
illustrate fundamental differences in the way pre-tonal harmony functions. The
horizontal lines have here been labeled with note names instead of roman
numerals: it is indeed one advantage of this description that it does not
necessarily presuppose the key of the piece. The most obvious difference with
respect to the examples above is that the work makes use of seven different
roots, while the other examples had only four or five. Dominant and subdominant
progressions tend to be more equally distributed: of 72 root progressions, 46
(64%) are dominant, compared to 26 (36%) subdominant. About one third of the
progressions are substitutions. The most striking, however, and probably the
most significant, is the disposition of the progressions, with long chains of
subdominant and of dominant progressions, stretching the diatony to its limits.
See in particular, at the beginning of the second system, the ascent by
subdominant progressions from F to A or E, or, in the third system, the descent
by dominant progressions from E to
[14] Example 5 proposes an alternative presentation of the progressions for the two first systems of the same piece. This presentation is more compact than the preceding one and allows notating additional information, but at the expense of a less easy reading. The fundamental bass is written on an additional staff—which in this case allows one to verify that it is almost identical with the real bass or, in other words, that most of the chords are in root position; this fact can be seen as a justification of a procedure which, otherwise, might seem anachronic. The roots of major chords have been indicated by half-notes, those of minor chords by quarter-notes. One will note the very large number of major chords, again stretching the diatony to its limits. Arrows attached to the note stems indicate the progressions: they point to the right for dominant progressions, to the left for subdominant progressions; substitutions are denoted by dotted arrows. This notation allows identifying leading note movements, which occur whenever a major chord is followed by a full (unsubstituted) progression, or by a substituted dominant progression a tone up with a change of mode from major to minor. In other cases, a sign could be added to indicate harmonic dissonances and their resolution (no such case occurs in this example).
[15] I am aware that it is not possible to draw important conclusions from only two or three examples. I leave it to the reader to examine other pieces with the principles outlined above. Let me briefly outline, as a conclusion, some of the theoretical assumptions of the above:
- Harmonic functions do not reside in chords, nor in the position of chords within an immanent tonal hierarchy. They result from a relation between chords. No chord is a dominant in itself, none is a tonic in itself; they become dominant and tonic with respect to each other when they occur in that relation.
- The same is true of “obbligato” movements in the voice leading. The tendency of leading notes to go to the tonic, or of dissonances to resolve, exists only in retrospect. A note a semitone below another becomes the latter’s leading note only if, and only after it raised to it.
[16] These conceptions are necessary to avoid a circularity in the determination of the tonality, in which one cannot determine harmonic functions without knowing the key of the piece, nor the key of the piece without knowing which chord is its tonic. My graphic representation in Example 2 would not have been different if I had labeled the horizontal lines with note names instead of roman numerals, as in Example 4. I might even argue that it is the shapes of the progressions, in Example 2, that allow deciding the roman numerals—which is another way of saying that the progressions determine the tonality. In this view, the role of obbligato melodic movements is merely to enhance the cadential effect of progressions; it is striking that these obbligato movements appear in some way linked with dominant progressions.
[17] As to the change from pre-tonal to tonal harmony, I view it as the result of a growing awareness both of the particular expressive effect of the flow of dominant progressions (subdominant progressions being perhaps resented as an interruption of the flow) and of the unifying effect of strict diatonicism, resulting both in a diminution of the number of roots and in a restriction to leitereigene chords, to chords belonging to the diatonic scale of the key.
Nicolas Meeus
Universite de Paris Sorbonne (Paris IV)
UFR de Musique et Musicologie
1, rue Victor Cousin F-75230 Paris cedex 05
nicolas.meeus@paris4.sorbonne.fr
Footnotes
1. Arnold Schoenberg, Structural Functions of Harmony (New York: Norton, 1954); rev. ed., ed. Leonard Stein (New York: Norton, 1969).
Return to text
2. Yizhak Sadai, Harmony in its Systemic and Phenomenological Aspects (Jerusalem: Yanetz, 1980).
Return to text
Copyright Statement
Copyright © 2000 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason and Tahirih Motazedian, Editorial Assistants