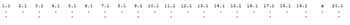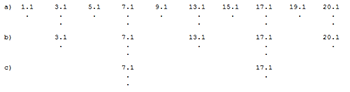Performance and Hypermetric Transformation: An Extension of the Lerdahl-Jackendoff Theory *
Alan Dodson
KEYWORDS: meter, hypermeter, performance, Lerdahl, Jackendoff, ambiguity, Gestalt
ABSTRACT: In the course of the introductory commentary on hypermeter in A
Generative Theory of Tonal Music (GTTM), Lerdahl and Jackendoff discuss
the opening measures of Mozart’s Symphony No. 40 in G Minor, a hypermetrically ambiguous
passage in which “the performer’s choice
Copyright © 2002 Society for Music Theory
[1] Introduction
[1.1] During the past few decades, theorists have been rethinking the concept of musical meter at a fundamental level. In recent literature, meter has been described not as a static pattern of accents intrinsic to the musical object, but rather as a dynamic process whose existence depends on human participation.(1) This shift can be demonstrated through the following contrasting definitions of meter, drawn from the first and second editions of The New Grove, respectively:
1980 ed.: The organization of the notes in a composition, or a section thereof, with respect to time, in such a way that a regular pulse made up of beats can be perceived and the time span occupied by each note can be measured in terms of these beats; in addition, the beats are grouped into larger units called bars, within which the number of beats is always the same.(2)
2001 ed.: [T]he temporal hierarchy of subdivisions, beats and bars that is maintained by performers and inferred by listeners which functions as a dynamic temporal framework for the production and comprehension of musical durations. In this sense, meter is more an aspect of the behaviour of performers and listeners than an aspect of the music itself.(3)
Both of these definitions allude to music perception, and the distinction between them might be understood to reflect a shift in the orientation of music perception research that occurred in the 1980s. Traditionally, perception was understood as the relatively passive mental reproduction of a given physical stimulus, but it is now generally considered to be an active, constructive (as opposed to reconstructive) process.(4) The revised definition of meter might also be understood against the backdrop of a similar, though perhaps more gradual, paradigm shift in music theory and in music scholarship generally. Largely in response to far-reaching methodological and ideological critiques, notably Joseph Kerman’s Contemplating Music and subsequent work by postmodernists and gender theorists, we seem to have become increasingly skeptical of the objectification of musical works and the quasi-taxonomic interpretation of their elements.(5) In this light, it seems especially appropriate that today’s theorists should emphasize the subjective contingency, as opposed to the autonomy, of meter.
[1.2] In the present article, I will explore some of the theoretical and analytical ramifications of the recent reconceptualization of meter, especially the effects of performing nuance on meter perception. I will take as my point of departure the discussion of the interaction of meter and performance in Fred Lerdahl and Ray Jackendoff’s A Generative Theory of Tonal Music (GTTM).(6) I have chosen this text for several reasons. First, GTTM has proven to be among the most convincing sustained exercises in psychologically informed music theory.(7) Second, it has been highly influential among theorists interested in meter and among music psychologists interested in performance, so it can be seen as a well-established link between the literatures on which I will draw.(8) Third, the language of GTTM is extremely clear, and the theory’s methodological foundations and orientation have been explained thoroughly.(9) For example, the authors introduce the theory as an attempt to capture in formal language “the musical intuitions of a listener who is experienced in a musical idiom,” rather than aspects of the composer’s intentions or intrinsic properties of musical works.(10) Furthermore, the authors are frank about the theory’s shortcomings, thus reminding the reader that GTTM is incomplete and suggesting that it has room for expansion and refinement.(11) Fourth, the passage from GTTM that I will take as my point of departure is related to three topics that have remained controversial during the nearly two decades since the publication of GTTM. These include discussions on the interrelationship between musical structure and performance, on the epistemological foundations for comparing different performances of the same piece, and on the degree to which hypermeter can be irregular. (By “hypermeter,” I mean the projection of a pattern of strong and weak beats across units larger than one measure.(12)) Of these three controversial topics, I will say most about the third, but I would like to offer a few remarks on the first two issues at the outset.
[1.3] Commentaries on the relationships between musical structure and performance form an increasingly prominent genre in the literature of music theory.(13) In a recent critique of the rhetoric most often employed in this genre, and in music analysis generally, Nicholas Cook draws attention to the dogmatic, prescriptive tone that is typical of analysts’ suggestions to performers.(14) As an alternative, Cook recommends that we strive for a more balanced dialogue in which neither the analyst nor the performer is considered to have the upper hand. By invoking J. L. Austin’s theory of speech-acts, Cook proposes that we might begin to read analyses not only as truth-claims (which Austin terms “constative utterances”) but also as acts of persuasion (“performative utterances”), thus highlighting a deep similarity between musical performance and analytical writing.(15) Building on earlier polemics by Tim Howell and Lawrence Rosenwald, Cook also encourages analysts to listen to performances and recordings and to make descriptive, as opposed to prescriptive, remarks on the relationships between structure and performance.(16) In another recent essay, Joel Lester demonstrates this strategy convincingly by showing parallels between various recordings and analyses in the case of structurally ambiguous passages. For example, Lester shows how two different analytic perspectives on a Mozart minuet correspond to details in recordings of the piece by Lili Kraus and Vladimir Horowitz.(17) I will adopt a similar discursive strategy in my readings of hypermeter in the opening of a Mozart symphony by showing structural models that seem to fit best with the nuances of four different recordings, but I will also go further and explore in purely theoretical terms how we might begin to account for the diversity encountered in a comparison of diverse performances.
[1.4] An important methodological question faces those of us who would like to theorize the interrelationships of performance and structure, and in particular the effects of different performances on the listener’s perception of structure: what is the conceptual framework within which comparisons between performances can be made at all, that is, how can we account (in theoretical, as opposed to historical or stylistic, terms) for the differences that we encounter in comparative listening? At one extreme, scholars who aspire to positive knowledge, who contend that we should aim for a single, comprehensive analysis of any work, might be expected to evaluate the quality of a performance on the basis of the convincingness of the analysis that it seems to reflect and to consider the differences between performances to be a result of differences between performers’ levels of insight.(18) At the other extreme, those who have embraced pluralism and liberalism would, on principle, question the validity of any theory that encourages positivistic thinking, and might instead attribute differences between interpretations to the diverse and unpredictable personal and cultural contexts of each performance.(19) My own approach lies somewhere between these two extreme positions, because I would like to bypass certain methodological obstacles latent in each: the former paradigm (which we might call the positivist “competition” model) is inconsistent with our ability to recognize two very different performances of the same work to be more-or-less equally convincing, and the latter (which we might call the pluralist “free-for-all” model) seems too broad to be commensurate with the project of discussing differences between performances primarily in terms of the perception of structure.
[1.5] My approach is based on a third paradigm, which I call the “alternative stabilization” model of performance comparison. This paradigm will allow me to theorize the differences between performances in structural terms, but to do so without privileging one performance over the others. At this point, I will describe its premises in only the most general and practical terms. When analyzing a work through reading it from the score, one sometimes encounters genuine ambiguities, passages in which some aspect of the structure perplexingly eludes a single preferred interpretation.(20) In listening to performances and recordings, however, much more information is available than would be found in the score alone. As Nicholas Cook recently reminded us, scores are not only potential objects of analysis, but also function as “scripts” in many of the social contexts in which notation is sounded out—scripts to which a performance serves as a sort of supplement.(21) I am interested in situations in which this supplement removes, or at least reduces, the degree of ambiguity encountered in reading the score, such that the listener is unaware of the ambiguity, or at least less inclined than the reader to describe the structure in question as ambiguous. The performer must choose only one of the possible interpretations, so naturally performances can be compared to one another regarding the choices made by performers.(22) In the case of works or passages for which multiple versions exist in notation (e.g., “ossia” passages in Romantic piano music) or for which there is a pronounced improvisatory element (e.g., Corelli’s slow movements, jazz), this stabilizing effect is perhaps most obvious.(23) In the case of hypermeter, however, it is not the notes that are chosen, but rather the subtle expressive nuances of a performance, including details of timing, dynamics, and timbre, that provide the stabilizing effect.
[1.6] Clearly, the phenomenon I am describing is incommensurate with the (Platonist) notion that for every work there is a singular ideal form. It would seem very difficult to reconcile the notion of alternative stabilization with a theory heavily informed by Western aesthetics and metaphysics. Heinrich Schenker, for example, insisted that for every masterwork there is a single correct interpretation of the voice-leading structure, and a rejection of this claim would amount to a fundamental change to the philosophy of Schenkerian theory.(24) Though I find the question of the interaction of musical ontology and performance fascinating, it is in fact tangential to this study, for I am thematizing perceptions, not speculative metaphysical fictions about the origins of a work or performance.(25) In my view, the issue of ambiguity and stability in GTTM should instead be discussed in relation to the theory’s grounding in Gestalt psychology, a school of thought that sought to explain the coherence of things without recourse to idealism.(26)
[1.7] Contrary to popular belief, the leading exponents of Gestalt psychology did not base their research on the cliché, “the whole is greater than the sum of its parts.” Rather, they claimed that the perception of the whole is categorically different from a summation of perceived parts.(27) Max Wertheimer was the first psychologist to argue that percepts are not put together piecemeal but rather are understood intuitively and immediately according to basic aesthetic principles, such that one should proceed from the whole to the parts rather than the reverse in any attempt to theorize perception.(28) Wertheimer’s most basic principle is the “Law of Prägnanz [precision],” which was most clearly expressed by his colleague Kurt Koffka: “Psychological organization will always be as ‘good’ as the prevailing conditions allow. In this definition the term ‘good’ is undefined. It embraces such properties as regularity, symmetry, simplicity, and others which we shall meet in the course of our discussion.” Some of these “others” include “unity, uniformity, good continuation, simple shape, and closure,” all of which are discussed at some length in Koffka’s encyclopedic Principles of Gestalt Psychology.(29) Lerdahl and Jackendoff explain that the Law of Prägnanz is closely associated with their Preference Rules (PRs), whose main purpose in GTTM is to capture the sense of stability associated with the hierarchical organization of tonal music. (I will have more to say on PRs below.) In fact, they claim that “the preference rules in effect constitute an explicit statement of the Law of Prägnanz as it applies to musical perception.”(30) The intricacies of perceptual stability and instability are perhaps best illustrated in the work of the Edgar Rubin and his circle, who are remembered for their studies on the perception of ambiguous visual stimuli.
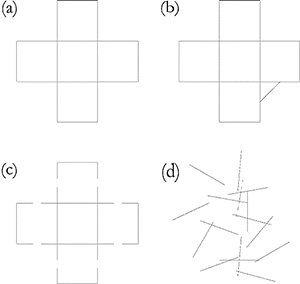
Example 1. Ambiguity and stabilization: (a) the “faces/vase” illusion, (b) faces, (c) vase, (d–e) symmetry effect, (f) tristability, (g) multistability
(click to enlarge)
[1.8] A few variations on Rubin’s famous “faces/vase” drawing will serve as a first attempt at a visual analogy for what I have termed the alternative stabilization phenomenon (Example 1(31)). Let us say we have a score in which two interpretations of the location of a phrase boundary seem equally tenable to the reader. This experience is a bit like looking at Rubin’s drawing (Example 1a) and being unable to decide whether it depicts two faces or a vase. The location of the phrase boundary might be less ambiguous from the listener’s perspective, however, because performing nuances, like a few embellishments to Rubin’s drawing, can increase the perceptual stability of either interpretation (see Example 1b–c). Another visual analogy, which uses a subtler manipulation and also eliminates the representational component of the drawing, thus bringing the analogy closer to GTTM (a formalist theory), comes from the work of Rubin’s student Paul Bahnsen, who examined the perceptual effects of the shape of the border between alternating black and white regions. Perception might be expected to be unstable when all borders are parallel or all borders are irregular, but it is highly stable when borders of either the black or white regions are symmetrical (as in Example 1d–e). This might be seen as an analogy for the projection of phrase boundaries through the use of “phrase rubato,” which (perhaps coincidentally) is itself symmetrical, for the performer typically begins the phrase relatively slowly, accelerates to the climax, and decelerates at the end of the phrase.(32) I should add that some ambiguous figures, like some musical passages, have more than two possible interpretations. For instance, a single curved line (Example 1f) might be seen as the border of a figure to the left, the border of a figure to the right, or simply a line superimposed on a continuous background. This line is referred to as a “tristable” figure, since it can be interpreted in three different ways. Still more extravagant is the ambiguity found in some multistable mosaic patterns (Example 1g). I will leave it to the reader to imagine some manipulations that would stabilize patterns like Example 1(f) and (g).
[1.9] We are now ready to explore some of the ways GTTM might be developed to account more fully for the impact of performance on the listener’s experience of hypermeter. In Part 2, I will examine Lerdahl and Jackendoff’s position on this subject, which appears in the context of an argument against the perception of irregular hypermeter. In Part 3, I will attempt to revise the classification of accent types in GTTM to include a category that I call “Phenomenal Micro-accents” (PMs) and discuss the importance of these accents in the case of otherwise unstable metric and hypermetric structures. In Part 4, I will present analyses of hypermeter in the opening measures of Mozart’s Symphony No. 40 in G Minor in four different recordings and illustrate the stabilizing effects of their different patterns of PMs, and I will also develop formal transformation rules that model the listener’s ability to hear the irregularities in these patterns as modifications of an inferred, perfectly regular metrical pattern. Finally, in Part 5, I will offer a more general critique of Lerdahl and Jackendoff’s position on the relationship between performance and their analytic process, and I will also identify some avenues for further research.
[2] Hypermeter and Performance in GTTM
Example 2. Metrical Structure in the opening measures of the Scherzo from Beethoven’s Symphony No. 2
(click to enlarge)
[2.1] In GTTM, the term “Metrical Structure” (MS) refers to accent patterns within the measure (sometimes called “bar meter”) as well as meter-like organization across spans smaller than measures (i.e., quasi-metric subdivisions of beats) and larger than measures (i.e., hypermeter).(33) In Lerdahl and Jackendoff’s ingenious notational system for MS, a dot under the score represents the point in time corresponding to a beat, and the number of dots in a given column indicates the accentual strength at that point relative to other beats in the hierarchy.(34) Their analysis of the opening of a Beethoven scherzo (Example 2(35)) demonstrates this system well. The local triple meter is shown by the presence of a dot at level (b) under every third dot at level (a). Three levels of hypermeter, all duple, can be inferred by comparing the dots of the remaining pairs of adjacent levels in the example. Levels (b) and (c) show five two-bar hypermeasures, (c) and (d) show two full four-bar hypermeasures, and levels (d) and (e) show a single full eight-bar hypermeasure. For simplicity, I will refer to hypermetric levels by number, with H1 being the first level of hypermeter, H2 the second, and so on.
[2.2] Each of the four main components of GTTM (of which MS is one) is governed by two sets of rules. The practice of developing rule systems stems from the system of transformational linguistics developed by Noam Chomsky, Jackendoff’s mentor.(36) These rules are supposed to model the largely automatic cognitive processing by which musical surfaces are parsed. Many of the principles formalized in the Rule Index of GTTM come from Gestalt psychology and from more recent research in music perception. Preference Rules (PRs) are designed to capture the way experienced listeners interpret a unique combination of structural details.(37) As mentioned above, PRs are concerned mainly with clarifying perceptual stability, and they are applied to each piece ad hoc after the more general constraints captured by Well-Formedness Rules (WFRs) have been applied. Metrical Well-Formedness Rules (MWFRs) determine the number of levels and their patterns of strong and weak beats, while Metrical Preference Rules (MPRs) encourage the most logical alignment of this pattern with events at the musical surface such as dynamic accents, long notes, and cadences.
Example 3. Two interpretations of hypermeter in Mozart, Symphony No. 40 in G Minor, K. 550, I, mm. 1–20.
(click to enlarge)
[2.3] Lerdahl and Jackendoff mention hypermetric ambiguity in their introductory remarks on MS in the opening measures of Mozart’s Symphony No. 40 in G Minor, a passage they consider to be “not untypically complex” in its metrical organization.(38) They use this passage to demonstrate that hypermeter is often restricted to levels close to the foreground, in opposition to the view that hypermeter can operate at even the deepest structural levels.(39) Near the beginning of the passage, odd-numbered measures are more strongly accented than even-numbered measures, but the reverse is true by measure 20. The only way to rationalize this, according to the authors, is to infer a single three-bar hypermeasure in the midst of a series of two-bar hypermeasures. They offer two equally plausible readings of where this eccentric hypermeasure might be found (see Example 3(40)). In reading A, the shift to even-measure accents occurs at what seems to be the latest possible moment, the downbeat of measure 14, while in reading B, the shift occurs at the first sign of change, the downbeat of measure 10.(41)
[2.4] Lerdahl and Jackendoff then claim that, despite the instability created by the irregular hypermeasure, “the performer’s choice . . . can tip the balance one way or the other for the listener.”(42) In other words, a performance might evoke a clear sense of hypermeter in the passage, but no such clarity is available on the basis of the score alone. (This claim calls to mind Example 1, which illustrates how a perceptually unstable figure can be stabilized through subtle manipulations. See especially Example 1b–e.) Although the authors claim that hypermeter can exist in this passage, they abstain from working out in practical terms precisely how features of performance might be understood to stabilize the hypermeter. Instead, they decide only to consider regularly spaced beats in their theory of MS, at least at the tactus (most salient metrical level) and immediately larger levels (MWFR 4). They do propose a special “Metrical Deletion” rule that deals with irregularities arising from situations like phrase elision and overlapping, but neither the rule index nor the formal discussion of MS gives evidence that the analytic implications of the potential “balance-tipping” effect of performance have been accounted for.(43)
[2.5] Although the variability of performance provides Lerdahl and Jackendoff with a pragmatic objection to irregular hypermeter, and consequently to deep levels of hypermeter in most contexts, it is not clear that this difficulty amounts to a theoretical impasse. I would suggest that most experienced listenersapparently including Lerdahl and Jackendoff themselvesperceive some degree of quasi-metrical organization in the Mozart excerpt shown in Example 3 across spans larger than one measure. In order that the theory might better capture the experienced listener’s intuitions, I consider it worthwhile to develop in formal terms the “balance-tipping” effect that Lerdahl and Jackendoff mention. Clearly, irregular hypermeter is more complex than regular hypermeter, and thus more difficult to formalize, but it seems to me that this complexity ought to be confronted rather than avoided. In particular, I would argue that the degree of hypermetric irregularity typically encountered in performances of the Mozart excerpt is not so extreme as to obviate any sense of hypermeter; this excerpt seems to lie in the vast “grey area” between regular and random proportions, between the obvious and the incomprehensible.
Example 4. Coherence or chaos? (a) regular cross, (b–c) modified crosses, (d) random collection of line segments
(click to enlarge)
Example 5. Bernstein’s recomposition of the opening of Mozart’s Symphony No. 40 in G Minor, K. 550; Audio: Performance of Bernstein’s recomposition
(click to enlarge and listen)
[2.6] Gestalt psychology again provides a useful analogy. According to one interpretation of the Law of Prägnanz, the purpose of the act of perception is to simplify or regularize the information given in the stimulus if it is possible to do so (Example 4).(44) Thus, a perfectly regular shape such as the one shown in Example 4a may be altered to some degree, as in Example 4b–c, without causing the lack of integrity found in a random collection of line segments, such as Example 4d. This very principle enables Lerdahl and Jackendoff to explain away the subtle durational irregularities found at the beat-to-beat level in performance; they note that listeners are able to infer a regular pulse underlying a musical surface transformed through tempo rubato.(45) They do not, however, explore the functioning of this type of manipulation at the level of the measure or hypermeasure, and the reason for this again seems to be a practical rather than a theoretical problem, namely, how to determine with precision what should be included in the inferred metrically regular musical surface that preceded the transformation.
[2.7] In the formal language of GTTM, the phenomenon I am describing could best be captured through a series of “transformational rules.” This category of rules, which is separate from the WFRs and PRs, is loosely based on grammatical transformations such as the change from active to passive voice or from present to past tense.(46) The transformational rules in GTTM reverse the changes to the musical surface brought about by processes like phrase overlapping and elision.(47) In order to adhere to this notationally oriented practice, our transformational rules for hypermetric irregularities would need to be able to generate entire measures of inferred music. In an earlier attempt at applying Chomsky’s principle of grammatical transformation to music, Leonard Bernstein did just that: he recomposed the opening of Mozart’s Symphony No. 40 in such a way that regular metrical structures are found at levels H1 and H2, that is, hypermeter at the level of the double- and quadruple-measure (Example 5(48) and accompanying Audio(49)). Bernstein’s newly composed material (measures 1–3, 15–16, 19–20, 23–24, 28–31, and 34–36) amounts to sixteen additional measures, making it two-thirds longer than the passage on which it is based. Lerdahl and Jackendoff claim that this type of approach is untenable, because it is too “hypothetical,” by which I think they mean too far removed from the actual listening experience, and because it is so arbitrary in its details. While I agree with this assessment, I nevertheless find Bernstein’s approach thought-provoking. As I mentioned near the beginning of this paper, meter is now regarded primarily as a construct created by the performer and listener, rather than an inherent and fully determined property of a musical work or score. One property of this construct appears to be that, once formed, it can be separated substantially from the musical surface. For instance, once we know a piece, we can imagine or even physically “feel” its metrical pattern without also imagining other parameters, such as the pitch materials. Indeed, psychologists have found empirical support for the human cognitive ability to form abstract, hierarchical mental representations of musical meter, and this finding seems highly compatible with Lerdahl and Jackendoff’s MS theory and its associated analytic notation.(50) In my view, then, it should be sufficient to show the transformation of irregular hypermeter in an abstract sense rather than proposing transformations at the level of the musical surface. The schematic representation of MS in a given passage can easily be compared to a hypothetical, perfectly regular MS, and processes like metrical expansion and truncation can be reversed.(51) For instance, it is clear that both of the MS interpretations of the Mozart example that Lerdahl and Jackendoff offer (see Example 3) contain a single three-bar hypermeasure amid a stream of two-bar hypermeasures. A transformational rule to regularize this pattern, thus modeling the simplifying function of the Law of Prägnanz in this context, would merely need to reverse this metrical expansion. (I will propose such a rule below; see paragraph 4.6.) The location of the departure from the regular pattern will depend on the performance, but we will nevertheless hear it as a departure from something that is more-or-less regular, stable, and comprehensible. That “something” is the underlying hypermeter.
[2.8] It is tempting to accuse Lerdahl and Jackendoff of succumbing to the influence of an insidious aesthetic bias, the so-called “autonomy ideology,” on the grounds that they are reluctant to formalize the dependency of an analysis on a specific performance. That is, one could speculate that their “balance-tipping” analogy (see the passage from GTTM quoted in paragraph 2.4) is abandoned in their theoretical discussion because it is incommensurable with contemplating the inner workings of an autonomous (i.e., radically independent) musical work. This accusation would be unfair, however, given that Lerdahl and Jackendoff explicitly avoid the discussion of aesthetics; in subsequent publications, they have repeatedly pointed out that GTTM theorizes aspects of the comprehensibility of a work, not its aesthetic qualities, and that these two parameters are not always closely related.(52) GTTM might be regarded as a method for developing the simplest interpretation of a tonal work’s hierarchical dimensions, for bringing the interpretation as close to the Gestalt ideal of “good form” as possible, such that a GTTM-style analysis can be thought of as representing structural intuitions that operate on the most perceptually “stable” events in a piece of tonal music. In other words, although it is a formalist theory, it attempts to escape idealism and instead to account for musical intuitions in terms of psychological principles drawn mainly from the work of the Gestalt school.(53) In this light, it would seem most appropriate to object to the abandonment of the balance-tipping model on the grounds of the Law of Prägnanz (see paragraph 1.7), rather than an aesthetic bias.(54) As we have seen, this law begins, “Psychological organization will always be as 'good' as the prevailing conditions allow.” I would argue that the limiting factorthe “prevailing conditions” alluded to in this definitionshould at least potentially include all of the information contained in the aural stimulus, including features specific to an individual performance. The main obstacle to developing Lerdahl and Jackendoff’s balance-tipping model would therefore seem to be not an ideological conflict but rather the practical difficulty of describing the elements of a performance with adequate precision.
Example 6. (a) Conventional realization of a structurally unambiguous notation, (b) One stable realization of an ambiguous notation, (c) Another stable realization
(click to enlarge)
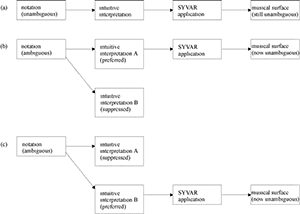
[2.9] It has long been recognized that the projection of a structural interpretation is one function of the expressive nuances that performers add in their realizations of scores. These nuances are sometimes termed “systematic variations” (abbreviated SYVARs), because they can be described in quantitative terms as patterns of departures from mechanical regularity in a given domain, such as speed or loudness.(55) In the case of an unambiguous structure, it would be relatively unproblematic to assume a direct, linear connection between the score and the “musical surface” (i.e., the aural presentation of the music), so long as the hypothetical performer adheres to the same SYVAR conventions that the listener has absorbed through aural experience with the musical idiom (see Example 6a). In such cases, the absence of PRs pertaining to performing nuances in the rule index of GTTM seems unproblematic; in a conventional performance, structural interpretations are projected rather than obfuscated or contradicted.(56) In the case of an ambiguous structure, however, the musical surface that is presented to the listener is often much clearer than the score itself.(57) It should follow that, in the case of ambiguous structures, the role of the performer’s interpretive preference, as expressed through SYVARs, deserves some consideration (see Example 6b–c). The fact that these SYVARs cannot be predicted definitively on the basis of a score makes them no less relevant to a theory of the listener’s intuitions.
[3] Extending the Theory of Phenomenal Accents
[3.1] In this section I will explore some of the implications of Lerdahl and Jackendoff’s fleetingly proposed connection between performing nuance and perceptual stability in the Mozart excerpt. My approach involves extending one category of accents to the extreme foreground, the level at which performing nuances operate, and it is informed by (mostly) post-GTTM investigations of SYVARs in expert performance. I contend that, in the absence of complete metrical stability (i.e., regularity), a class of contextual featuresnamely, features introduced in performancebecomes increasingly relevant to the listener’s sense of metrical structure (MS). Here I am simply transposing an argument from Lerdahl’s “Atonal Prolongational Structure” from the domain of tonality to that of meter; Lerdahl claims that in music where tonal stability is deliberately compromised, a sense of quasi-tonal prolongation might still be inferred on the basis of contextually salient events.(58)
[3.2] The discussion of MS in GTTM begins with an innovative system for classifying the different types of accent cues whose combined effects enable listeners to infer metrical patterns. Lerdahl and Jackendoff’s explanation of the relationships between phenomenal and metrical accents is of crucial importance to the present study, so I shall quote it at some length:
In our judgment it is essential to distinguish three kinds of accents: phenomenal, structural, and metrical. By phenomenal accent we mean any event at the musical surface that gives emphasis or stress to a moment in the musical flow. Included in this category are attack points of pitch events, local stresses such as sforzandi, sudden changes in dynamics or timbre, long notes, leaps to relatively high or low notes, harmonic changes, and so forth. By structural accent we mean an accent caused by the melodic/harmonic points of gravity in a phrase or sectionespecially by the cadence, the goal of tonal motion. By metrical accent we mean any beat that is relatively strong in its metrical context
. . . Phenomenal accent functions as a perceptual input to metrical accentthat is, the moments of musical stress in the raw signal serve as “cues” from which the listener attempts to extrapolate a regular pattern of metrical accents. If there is little regularity to these cues, or if they conflict, the sense of metrical accent becomes attenuated or ambiguous. If on the other hand the cues are regular and mutually supporting, the sense of metrical accent becomes definite and multileveled. Once a clear metrical pattern has been established, the listener renounces it only in the face of strongly contradicting evidence
. . . In sum, the listener’s cognitive task is to match the given pattern of phenomenal accentuation as closely as possible to a permissible pattern of metrical accentuation; where the two patterns diverge, the result is syncopation, ambiguity, or some other kind of rhythmic complexity. Metrical accent, then, is a mental construct, inferred from but not identical to the patterns of accentuation in the musical surface.(59)
Later, they explain what they mean by “local stresses such as sforzandi” and further explain the relationship between stresses and metrical accents:
By local stress we mean extra intensity on the attack of a pitch-event. We include as signs of stress not only those marked by the signs > and ^, but also those indicated by sf, rf, fp, and subito f. In a regular sequence of attacked notes, those with stress will preferably be heard as strong beats.(60)
[3.3] The effects of phenomenal accents on metrical accents are formalized as MPRs 4–5, which address relative stress (i.e., loudness) and length, respectively.(61) All the loudness- and length-related accents shown in their exemplars for these rules occur at the rather blatant level that notation can capture, but I will argue that such accents also occur on a much subtler scale in skilled performance. I will call the latter expressive details dynamic and agogic micro-accents (DMs and AMs), or collectively, phenomenal micro-accents (PMs). In general, their effect on listening should be expected to be rather weak owing to their small scale, but as Lerdahl and Jackendoff demonstrate in the case of the Mozart excerpt, PMs can become extremely important in cases where notational clues offer insufficient support for a single preferred reading. In a sense, AMs seem to be incommensurable with MWFR 4, which states that beats must be evenly spaced. As I mentioned, however, Lerdahl and Jackendoff do acknowledge that even spacing is easily inferred in the case of performances made uneven by expressive timing.(62) I would agree that listeners do seem to “correct” the unevenly spaced beats in expressive performance, but, unlike Lerdahl and Jackendoff, I would draw attention to the fact that important information is communicated in the discrepancy between the actual sounding event and the evenly spaced abstraction.
Example 7. Two metrical arrangements of the melody used in Sloboda, “The Communication of Musical Metre in Piano Performance.”
(click to enlarge)
[3.4] The relationship between metrical accents and what I have called PMs was further clarified in subsequent writings by psychologists John A. Sloboda and Eric Clarke, among others.(63) Whereas Lerdahl and Jackendoff theorized the effects of phenomenal accents on perceived metrical accents, both Sloboda and Clarke studied the effects of perceived meter on PMs. They carried out several experiments to determine the effects of rhythm and meter notation on performance. In one of Sloboda’s studies, several melodies were presented to skilled pianists, who performed the melodies on a grand piano monitored by a computer interface. Among the experimental melodies were several that differed only in the placement of the barline; all other parameters, including pitch materials, rhythmic patterns, and expression marks, were unchanged (see Example 7). A similar experiment included melodies that differed only in the time signature. These experiments showed that skilled pianists usually engage a relatively small repertory of SYVARs to project meter, and that their use of these cues is proportional to their degree of experience.(64)
[3.5] Additional empirical studies conducted by both Sloboda and Clarke confirm that experienced listeners can identify the meter intended by the performer in the case of the ambiguous melodies used in their performance experiments, so PMs would seem to be a key to the understanding of each performer’s conception of meter in any metrically ambiguous passage.(65) Although the purpose of these experiments was to determine principles for the effects of notation on performance, not to theorize the impact of performance cues on the listening experience, these results are nevertheless relevant to our listener-oriented theory of meter and hypermeter. All that is needed is a reversal of orientation. By cross-referencing the SYVARs in a given performance with the conventions for projecting meter, we should be able to infer the performer’s metrical interpretation of a passage. Among the SYVARs that Clarke and Sloboda identify are dynamic stress and lengthening, which I discussed above in the context of Lerdahl and Jackendoff’s MPRs 4–5, as well as the lengthening of the upbeat.(66) I will distinguish downbeat lengthening from upbeat lengthening by referring to the former as “elongation-style” and the latter as “hesitation-style” AMs. Hesitation-style AMs appear to be unrelated to any of the existing MPRs and even seem to contradict MPR 5(a), which states: “Prefer a metrical structure in which a relatively strong beat occurs at the inception of . . . a relatively long pitch-event.”(67) Thus, I consider it the weakest of the three classes of PMs relevant to ambiguous cases of MS. Nevertheless, its systematic use is well documented in Sloboda’s and Clarke’s experiments, and I believe it is widely understood by listeners, so it ought to be reflected in an MPR. Therefore, I will propose the following addition to the Rule Index in GTTM: MPR 5.5 (Hesitation): “Weakly prefer a metrical structure in which a relatively strong beat occurs immediately after a relatively long pitch-event.” (This rule is included in my Appendix 1, “Revised Rule Index for Metrical Structure.”) Assuming that these PM cues (i.e., DMs and the two classes of AMs) might also operate at levels somewhat deeper than surface meter, we now have the theoretical principles needed to assess whether experienced listeners can be expected to infer hypermetric interpretations other than the two predicted by GTTM in the case of the opening of Mozart’s Symphony No. 40 in G Minor.
[4] Performance Analyses and Transformations
[4.1] A summary of the techniques that I use for performance analysis is included as Appendix 2. Essentially, I convert the desired excerpts into sound files and analyze the timing and loudness with audio editing software. I should emphasize that I have made no attempt at an inductive statistical analysis of these performances, that is, to use raw quantitative data as “input” and propose qualitative judgments as “output.” Instead, I prefer to use empirical data selectively (though hopefully not too selectively) in order to articulate qualitative PM judgments and comparisons arrived at through careful listening. I begin the performance-analytic procedure with close listening in order to avoid attributing importance to distinctions that are too fine for the ear to detect under normal listening conditions. Quantitative performance analysis is extremely useful in supporting and refining many observations, and it also facilitates detailed inter-performance comparisons. Like other forms of music analysis, quantitative performance analysis seems helpful in sharpening one’s sensitivity to fine nuancesin this case to gradations of intensity and duration.
[4.2] In GTTM, beats are considered durationless points in time inferred from the musical stimulus. The acoustical correlate to the beat is the onset, or attack point, of a tone that is understood to articulate the beat in question. When we speak loosely of the duration of a beat, we are really talking about the interval between beats, and the corresponding acoustical measure is the inter-onset interval (IOI). Similarly, when we speak of the loudness of a beat, we are describing the loudness of some sound within the IOI whose onset corresponds to the beat in question. The acoustical correlate of beat loudness is the peak amplitude within an IOI, also known as the peak sound level (PSL). When a beat is subdivided, the peak amplitude of the first subdivision is used in estimating DMs.
[4.3] The complete data that I collected from the four recordings that I will discuss are given in Appendix 3. Caution is often needed in interpreting this numerical information, since the values do not always reflect the listening experience accurately. Sometimes distinctions are so subtle that they are imperceptible under normal listening conditions, so it is important to keep the “just-noticeable differences” in mind. Ballpark figures for these are 510% for inter-onset intervals (IOIs) and 0.5–2.0 dB for intensities.(68) Also, both onset perception and intensity perception vary considerably in relation to pitch and timbre.(69) For example, listeners with normal hearing will hear tone x (100 Hz, 50 dBSPL) and tone y (1000 Hz, 20 dBSPL) as being equal in loudness despite their vast differences in amplitude. Researchers have not seemed to come up with a way to adjust for these perceptual considerations, possibly because of complexities that arise in dealing with multi-voice textures, pedaling, and the interactions of overtones. Also, perhaps most importantly, this type of performance analysis does not allow us to examine the intensities of individual voices, so it is sometimes tempting to misread an intensity analysis as a representation of melodic dynamics rather than the net dynamics of all voices combined. My interpretation of DMs will be based largely on the rankings of downbeat intensities relative to one another, not on absolute values, and, in general, I will draw attention only to those performance analysis statistics that seem most clearly to reflect and enhance the actual listening experience.
Example 8. Six interpretations of hypermeter in Mozart, Symphony No. 40, I, mm. 1-20. (a) “Interpretation A,” (b) “Interpretation B,” (c) Mozart/Britten, (d) Mozart/Marriner, (e) Mozart/Walter, (f) Mozart/Bernstein
(click to enlarge)
[4.4] Example 8 includes six hypermetric interpretations of the opening of Mozart’s Symphony No. 40. The first two are those that Lerdahl and Jackendoff identify, and the remaining four are drawn from recordings conducted by Benjamin Britten, Neville Marriner, Bruno Walter, and Leonard Bernstein.(70) It is important to note that, although all six representations use GTTM-style metrical notation, none is derived from the strict application of the rules for MS. (Recall that this is the excerpt that Lerdahl and Jackendoff use to illustrate problems in rationalizing hypermetric irregularity and to justify the restrictive MWFR 4, which insists on even spacing of beats and hyperbeats at the tactus and immediately larger metrical levels.)
[4.5] As I mentioned above (see paragraph 2.7), I will account for the irregularities in these metrical patterns by developing transformational rules that apply to MS abstractions. I will consider the eccentric hypermeasure in each version to be a transformation of an underlying regular hypermeasure. Superficially, it might seem that these transformations fracture the metrical structure at this level, resulting in a series of fragments that I will call metrical structure episodes (abbreviated MSEs). At level H1, I submit that the unity underlying each series of MSEs can be understood with little effort on the part of the listener. At deeper levels, however, an underlying unity cannot always be demonstrated. Nevertheless, in the interest of theorizing a rather subtle aspect of the listening experience, I think it is worthwhile to attempt to show the integrity of each independent MSE, rather than vaguely stating (as Lerdahl and Jackendoff do) that irregularities cause MS to become attenuated at deeper levels. Indeed, this approach allows us to trace in detail the gradual breakdown of MS from level to level.
[4.6] Let us begin with the two readings proposed by Lerdahl and Jackendoff (Example 8a–b). Each of these examples includes one instance of triple meter in the context of a prevailing duple meter at the first level of hypermeter. The eccentric hypermeasure might be understood to result from the process of metrical expansion, the addition of a second weak beat between two strong beats. In order to reveal the regular underlying structure, a rule for the opposite process is required, a process which I will call “metrical contraction.” This rule should simply state that, in order to regularize a pattern such as this, one of the weak beats in the three-beat measure must be deleted. This rule can be stated formally as follows:
Metrical Contraction(71)
Given
(i) a well-formed metrical structure episode M that ends with beats B1
and B2, in which B1 and B2 are adjacent beats at level
Li and B1
is also a beat at level Li+1, and
(ii) a well-formed metrical structure episode N in which B3,
B4, and B5
are adjacent beats at level Li and only B3
is also a beat at level Li+1,
and
(iii) a well-formed metrical structure episode P that begins with beats
B6, B7, and B8, in which
B6, B7, and B8 are
adjacent beats at level Li and both B6 and
B8 are also beats at level Li+1,
and given that M, N, and P are adjacent metrical structure episodes,
then a well-formed metrical structure episode M' can be formed by deleting B5, such that B1, B2, B3, B4, B6, B7, and B8 are adjacent beats at level Li and B1, B3, B6, and B8 are also beats at level Li+1.
[4.7] In a performance that projects Interpretation A (Example 8a), the listener might at first perceive three MSEs in measures 1–23: a series of five duple hypermeasures (measures 1–10), followed by one triple hypermeasure (measures 11–13), followed by five more duple hypermeasures (measures 14–23). If Interpretation B (Example 8b) is projected, the listener would instead perceive three duple hypermeasures (measures 1–6), followed by one triple hypermeasure (measures 7–9), followed by seven duple hypermeasures (measures 10–23). In both cases, the listener might then intuitively reconceive the entire passage as a coherent sequence of eleven duple hypermeasures, as suggested by the Metrical Contraction rule (Example 9a–b).(72) That is not to say that the differences between the two performances will be ignored, but rather that the two performances will be understood as departing from the same underlying metrical structure in different ways.
[4.8] Two of the remaining four interpretations (Example 8c and f) can be understood to show metrical truncations rather than expansions. That is, in the context of a prevailing duple meter at level H1, a new hypermeasure begins before the preceding one has been completed, such that two strong beats are found side-by-side. In order to reverse this process, we require a transformational rule for “metrical completion,” which will stabilize the MS at this level by inserting a weak beat between these strong beats. This rule can be stated formally as follows:
Metrical Completion
Given
(i) a well-formed metrical structure episode M that ends with beats B1, B2,
and
B3, in which B1, B2, and B3 are adjacent beats at level
Li and
both B1 and B3 are also beats at level Li+1, and
(ii) a well-formed metrical structure episode N that begins with beats B4,
B5, and B6, in which B4, B5, and B6 are adjacent beats at
level Li and both B4 and B6 are also beats at level Li+1,
and given that M and N are adjacent metrical structure episodes,
then a well-formed metrical structure episode M' can be formed by inserting beat Bx between beats B3 and B4, such that B1, B2, B3, Bx, B4, B5, and B6 are adjacent beats at level Li and B1, B3, B4, and B6 are also beats at level Li+1.
[4.9] In all four recordings, strong and weak hyperbeats alternate regularly at level H1 in measures 1–10, and measure 20 has a strong accent, so I will focus on what happens in measures 11–20. The shift occurs earliest in Britten’s version through a succession of strong accents on the downbeats of both measure 13 and measure 14 (see Example 8c). The accent at 13.1 relative to 12.1 is achieved through a hesitation-style AM (in this case, an extension of IOI 12.2 by 14.8%) and a DM (an increase in net amplitude by 0.9 dB and three ranking points at the downbeat-to-downbeat level).(73) But 14.1 is stronger still (by nearly 4 dB and two ranking points), and 15.1 sounds softer than 14.1 despite the increase in orchestration. (The decrease in net amplitude is insignificant at 0.1 dB, but, in light of the expanded texture, the absence of an increase in amplitude supports a strong-weak hypermetric pattern in measures 14–15.) A diminuendo added by Britten through measure 15, an abrupt change in orchestration at 16.2, and an absence of clear AMs in these measures create some confusion, but the emphasis on even-numbered downbeats is confirmed in measures 17–20. IOI 18.1 has an elongation-style AM (9.2% longer than 17.1), and 19.1 is markedly softer than 18.1 as well (by a margin of 1.8 dB). To further reinforce the even-measure accents, 20.1 has an elongation-style AM (7.5%) and is the loudest beat in the entire excerpt, which seems especially dramatic in light of the absence of a crescendo in measure 19. The resulting pattern has adjacent strong beats at 13.1 and 14.1, indicative of a metrical truncation, so the passage can be thought of as containing two MSEs (measures 1–13 and 14–20), and a regular underlying pattern can be generated by applying the Metrical Completion rule (Example 10).
Example 10. Regularized version of Example 8(c); Audio: Mozart/Britten, mm. 1–22
(click to enlarge and listen)
Example 11. Regularized version of Example 8(d); Audio: Mozart/Marriner, mm. 1–22
(click to enlarge and listen)
Example 12. Walter’s hypermetric joke. (a) Gullible listener’s preliminary interpretation, as of m. 19, (b) Revised interpretation, after 20.1 is heard, (c) Regularized version; Audio: Mozart/Walter, mm. 1–22
(click to enlarge and listen)
[4.10] In contrast to Britten’s interpretation, Marriner preserves the odd-measure emphasis until the last possible moment, measures 19–20 (see Example 8d). In measures 10–20, this is projected extremely clearly through elongation-style agogic accents at 11.1, 13.1, 15.1, and 17.1 (by 20.0%, 10.9%, 9.4%, and 41.7%, respectively, at the downbeat level) as well as dynamic accents on these same beats (all of which have higher rankings than the even-measure downbeats that surround them). Indeed, 17.1 rather than 20.1 is the loudest downbeat in the excerpt. The arrival of even-measure accentuation at 20.1 seems to be associated mostly with the surface rhythm’s agogic accent, which is further enhanced with an elongation-style AM (6.4%). Note also that 19.1 is the first weak odd-measure downbeat in the excerpt; it is somewhat quieter than 18.1 (-1.7 dB) and about equal in length (IOI 19.1 is only 2 ms or 0.4% longer than 18.1, an imperceptible difference). The adjacent weak beats at 18.1 and 19.1 constitute a metrical expansion, and the pattern can be regularized through the application of the Metrical Contraction rule (Example 11).
[4.11] Walter’s hypermetric interpretation is more complex than the preceding two, and this is largely because of clever ambiguities in his deployment of PMs (see Example 8e). The odd-measure strong beats established in measures 1–10 continue at least through measure 13. 11.1 is both longer (10.2%) and louder than 10.1, and the relation of 13.1 to 12.1 is similar (8.7% longer, 1.2 dB louder overall).(74) It is difficult to offer a hypermetric interpretation of measures 14–16, because the PMs play against the notated surface meter. Performers sometimes refer to this effect as a “negative accent” or “deflection,” and it occurs when a downbeat is considerably quieter than the listener would expect on the basis of the upbeat. (See the final column of Appendix 3c. These are the only downbeats in the entire excerpt that have negative changes in intensity at the beat-to-beat level.) Without a clear projection of surface meter, it is difficult to assess the location and strength of hypermetric accents. In the absence of evidence to the contrary, I would be inclined to hear a continuation of the odd-measure accents through to measure 16. It could be argued that the slight, though noticeable, acceleration into 15.1 supports this reading by giving that beat a special emphasis. (IOI 14.2 is shortened by 11.2%.) Next, two features conspire to encourage us hear a continuation of the odd-measure accents at 17.1: the sudden increase in dynamics and orchestration at 16.2 and the literal repetition of 16.2–17.1 in 17.2–18.1. All else being equal, 17.1–18.1 would most likely be heard as a strong-weak echo effect (Example 12a), a reading consistent with MPR 2.(75) Walter neither underlines nor contradicts this reading, however. The first three downbeats after 16.2 sound equal in loudness (0.4 dB difference), and despite some elongations that enhance the syncopation effect on the second beat of each measure, measures 17–19 sound steady. (All three downbeats are within 5% of the average tempo of the entire excerpt.) Thus, it could be argued that Walter leaves the hypermetric interpretation undefined in measures 17–19. There is, however, a salient accent at 20.1 (loudest downbeat IOI in the excerpt, 1.4 dB louder than 19.1), and in retrospect this might lead us to hear the entire cadential extension (measures 16–20) in the context of an even-measure hypermeter (Example 12b). At that point we would realize that our hunch that 17.1–18.1 was a strong-weak echo was incorrect. In that sense, the metric and hypermetric ambiguities of measures 14–19 (especially measures 17–19) in the Walter recording have a rather humorous effect, and one that adds richness to the listening experience. The reading shown in Example 12b (and in Example 8e) is the final version that emerges once the accent at 20.1 is heard. Walter’s interpretation includes a metrical expansion, this time in measures 15–17, so the pattern can be regularized through the Metrical Contraction rule (Example 12c).
Example 13. Regularized version of Example 8(f); Audio: Mozart/Bernstein, mm. 1–22
(click to enlarge and listen)
[4.12] Bernstein’s hypermetric interpretation (Example 8f) is nearly identical to Marriner’s (Example 8d) at level H1. The most important distinction is that in Bernstein’s recording, there are strongly pronounced PMs at both 19.1 (2.6 dB louder than IOI 18.1) and 20.1 (20.8% elongation, 1.2 dB increase compared to 19.1). Thus, 19.1 is a strong hyperbeat, like all the preceding odd-measure downbeats, rather than a weak hyperbeat, like 19.1 in Marriner’s recording. In the case of Bernstein’s recording, the pattern can be regularized through the Metrical Completion rule (Example 13). At other points in the excerpt, Marriner and Bernstein project the same interpretation by quite different means. For instance, Bernstein’s accent at 11.1 seems to be communicated through timbre rather than loudness and elongation.(76)
[4.13] So far I have been describing only the first level of hypermeter, that is, MS at the level of the double-measure. Lerdahl and Jackendoff suggest that a deeper level of hypermeter should include strong accents at 16.1 and 22.1, because these are points of harmonic arrival and might therefore be understood as structural accents. Stated in the terminology I have developed, this means that measures 16–21 form an MSE containing a three-beat hypermeasure plus a downbeat at level H2 (Example 14). Although Lerdahl and Jackendoff situate this six-bar episode at the “4-bar level,” implying that it is a transformation of two underlying two-bar MSEs, they do not clarify this transformation because they rightly consider it futile to attempt such a thing in music-notational terms and on the basis of the score alone.(77) Overall, Lerdahl and Jackendoff consider level H2, aside from this singular MSE, to be too ambiguous to explore, and they even go so far as to say, “The 4-bar level simply does not have much meaning for this passage.”(78) I would argue that, despite the ambiguity of the score, metrical organization across spans of four or even eight measures can be conveyed, at least episodically, in the performance of this excerpt. Owing to the instability caused by the erosion of regularity at these levels, the MS interpretation becomes increasingly dependent on salient PMs. (Here I am again invoking Lerdahl’s hypothesis that contextual salience becomes crucial to the construction of hierarchical structures when stability conditions are compromised. See paragraph 3.1 above.) Although the structures I am about to describe lie deep within the grey area between stability and instability, or between comprehensibility and incomprehensibility, I think they deserve some consideration.
Example 15. (a) H2 in the first MSE (mm. 1–10) of Mozart/Britten, (b) H3 in this MSE (fragile); Audio: Mozart/Britten, mm. 1–10
(click to enlarge and listen)
[4.14] In Britten’s recording, an MSE consisting of an upbeat plus two duple hypermeasures can be shown at the level H2 in measures 1–10 (Example 15a). This can be confirmed by comparing the beats found at the level H1 within this passage (i.e., beats 1.1, 3.1, 5.1, 7.1, and 9.1). Of these, 1.1 is clearly the weakest. (Indeed, it is ranked last among the first twenty downbeats.) A strong-weak pattern is then established through qualitative differences between 3.1 and 5.1. Whereas the former is prepared with a hesitation-style AM (IOI 2.2 is 7.1% longer than 2.1), the latter is anticipated slightly (IOI 4.2 is 8.8% shorter than 4.1), and this conveys the impression that 3.1 is accented with conviction, while 5.1 occurs almost by accident. Similarly, the DM on 5.1 sounds like a “jolt” in all voices, while 3.1 has a distinct melodic accent.(79) Still clearer is the distinction between 7.1 and 9.1. The former is both louder and longer than the latter (by a margin of 5.2 dB and 9.2%, respectively), and at the measure-to-measure level, 7.1 has a stronger elongation-style AM and a stronger DM than 9.1 (20.8% vs. 5.1%, and 5.3 dB vs. 1.5 dB, respectively). A further distinction can be shown between the two strong beats at the level H2, and this produces a third level of hypermeter in this MSE. Beat 7.1 has a greater DM and AM than 3.1, and this creates an upbeat-downbeat figure (Example 15b). Beats 3.1 and 7.1 are preceded by similar degrees of hesitation (7.1% and 6.3%, respectively), but 7.1 has an additional elongation-style AM (13.6%) as well as a considerably stronger DM than 3.1 (5.3 dB at the downbeat-to-downbeat level, vs. 2.5 dB). Note, however, that this interpretation is rather fragile. It includes only a partial hypermeasure, and the downbeat’s position in the seventh measure of a ten-measure MSE seems unusually late. The latter objection is formalized in GTTM as MPR 2 (Strong Beat Early): “Weakly prefer a metrical structure in which the strongest beat in a group appears relatively early in the group.”(80)
Example 16. (a) H2 in the second MSE (mm. 14–21) of Mozart/Britten, (b) H3 in this MSE (fragile); Audio: Mozart/Britten, mm. 14–21
(click to enlarge and listen)
[4.15] After the conclusion of the first MSE in Britten’s recording, hypermeter seems to be attenuated at level H2 until measure 14. This is because each of the next three strong beats at level H1 (i.e., 11.1, 13.1, and 14.1) has a stronger DM than the last (+0.5 dB, +0.6 dB, and +3.8 dB, respectively). A second MSE (Example 16a) is weakly suggested, however, by PMs in measures 14–20. The distinctions are again largely qualitative. The DM at 20.1 (+2.3 dB compared to IOI 19.1), in combination with the changes in texture, harmony, and dynamics that immediately follow it, seems more prominent than the elongation-style AM at 18.1 (12.4%). Also, as discussed above, the status of 16.1 as a beat at this level is achieved mainly by inference, in light of the complications introduced by the change in texture at 16.2. It would therefore seem reasonable to regard it as a weaker beat than 14.1, which is very strongly stressed (+3.8 dB compared to IOI 13.1) and also considerably stronger than 16.1 (by a margin of 6.1 dB). I will not attempt to continue this MSE beyond measure 21, because the next potential beat, 22.1, also has an accent (a structural accent, in this case), and two strong beats cannot be adjacent in an MSE. Of the four beats in this MSE, the first and last are most strongly accented, so measures 14–19 can be considered to form a three-beat hypermeasure at level H2 (Example 16a). Although it is tempting to consider this an expansion of the duple pattern found in the first MSE, this interpretation lacks a sufficient metrical context according to the criteria I have established, since the second MSE is not directly preceded by a duple MSE.(81) A comparison of the two strong beats at H2 in this MSE (i.e., 14.1 and 20.1) reveals a sufficient distinction to propose a third level of hypermeter here. As in the first MSE, the second of these two hyperbeats is stronger than the first on the basis of both AM and DM cues, and this yields an upbeat-downbeat figure at H3. (IOI 20.1 has 8.7% elongation and is ranked first among the even downbeats in measures 1–20, while 14.1 has 3.1% elongation and is ranked sixth.)
Example 17. (a) H2 in the first MSE (mm. 1–16) of Mozart/Marriner, (b) H3 in the first MSE, (c) H2 at the beginning of the second MSE (mm. 17–23), (d) regularization of H2 in mm. 1–23; Audio: Mozart/Marriner, mm. 1–23
(click to enlarge and listen)
[4.16] The remaining three recordings evince more stable MSEs than Britten’s at the second and third hypermetric levels, and two of them (Marriner’s and Bernstein’s) include some tenable hypermetric transformations at the level H2. In Marriner’s recording, the first MSE continues through measure 16 (Example 17a). Up to measure 10, it projects the same metrical pattern as Britten’s recording (see Example 14), but in Marriner’s version the alternation of strong and weak hyperbeats continues through 15.1. In terms of overall intensity, IOI 11.1 is louder than 9.1 (+7.6 dB) and likewise IOI 15.1 is louder than 13.1 (+8.1 dB). The long crescendo in measures 12–15 adds further emphasis to 15.1, but it also obscures the relationship of 11.1 and 13.1 somewhat; nonetheless, 11.1 has a considerably longer elongation-style AM than 13.1 (35%, vs. 13%), so a strong-weak pattern is projected here. In Marriner’s recording, the first MSE is twice as long as in Britten’s recording, so we might expect that the third hypermetric level is somewhat more stable. Indeed, the hyperbeats at this level (i.e., 3.1, 7.1, 11.1, and 15.1) do evince a weak-strong-weak-strong pattern on the basis of their DMs (ranked sixth, fourth, seventh, and third, respectively, among odd-measure downbeats in measures 1–20). The resulting pattern can be interpreted as an upbeat, a full hypermeasure, and a downbeat (Example 17b). The first MSE ends at measure 16, because 17.1 is a strong beat (indeed, it has the loudest IOI in the excerpt) rather than the weak beat that we had come to expect. This strong beat belongs to another MSE at this level, which begins with a strong-weak-strong pattern among the next three hyperbeats, 17.1, 20.1, and 22.1 (Example 17c). As I mentioned above, the loudest downbeat in the passage is 17.1 in Marriner’s recording, and 22.1 is a strong beat at this level because of the structural accent articulated by the return of tonic harmony.(82) Because these metrical accents are caused by two different categories of accent cues, phenomenal and structural, it would be arbitrary to identify one as being stronger than the other, and furthermore I don’t think either alternative would have much intuitive appeal. For both these reasons, I think it would be artificial to propose a third level of hypermeter for this MSE. It does, however, seem possible to combine the two MSEs at the second level into a single MSE, since they are adjacent and each contains at least one full duple measure. Because there is a sequence of two strong beats at their border (i.e., 15.1 and 17.1), we must use the Metrical Completion rule in order to regularize this pattern (Example 17d).
Example 18. (a) H2 in the first MSE (mm. 1–21) of Mozart/Walter, (b) H3, (c) H4 (extremely fragile); Audio: Mozart/Walter, mm. 1–21
(click to enlarge and listen)
[4.17] Walter’s interpretation is arguably the most stable of the six under consideration. On first hearing, we might consider the first MSE at H2 to end in measure 10, as in Britten’s recording. A pattern of alternating weak and strong hyperbeats seems to be established through DMs in 1.1, 3.1, 5.1, 7.1, and 9.1 (ranked tenth, fifth, ninth, third, and eighth among the odd-measure downbeats in measures 1–20), and this pattern seems to be disrupted by the presence of another weak beat at 11.1 (5.4 dB quieter than IOI 13.1). If we consider 1.1 a strong beat, however, on the basis of its early position (see MPR 2), then a triple-meter pattern is established by measure 7, and this pattern continues uninterrupted through the entire excerpt (Example 18a). According to the latter interpretation, the first MSE of the piece ends at measure 21, because the structural accent at 22.1 would otherwise yield two adjacent strong beats (i.e., 20.1 and 22.1). The four strong beats in this MSE (1.1, 7.1, 13.1, and 20.1) are established as follows: 1.1 is strong because of its relatively early position (MPR 2); 7.1, because it is louder than the surrounding hyperbeats (5.1, 7.1, and 9.1 are ranked ninth, third, and eighth); 13.1, because it is louder than the preceding hyperbeat (+5.4 dB) and has a greater elongation-style AM than the ensuing one (15.9%, vs. 6.0%); and 20.1, because it is the loudest beat in the entire excerpt. On the basis of both DMs and AMs, beats 7.1 and 20.1 are the strongest of these four beats (1.1, 7.1, 13.1, and 20.1 rank twentieth, fifth, eighth, and first in loudness among the twenty downbeats in the excerpt, and IOI 7.1 has the most pronounced AM in the excerpt, an elongation of 30.4% over IOI 6.1.) This creates a weak-strong-weak-strong pattern at H3 (Example 18b). We might tentatively posit a fourth level here as well. It is difficult to choose between 7.1 and 20.1 on the basis of PMs, because 7.1 has the longest IOI in the excerpt and 20.1 the loudest. Nevertheless, the contrasts in texture, dynamics, and harmony that immediately follow 20.1 make it seem the more salient of the two beats, so an upbeat-downbeat figure seems to be the more defensible choice (Example 18c). As we found in both MSEs of Britten’s recording at level H3, the absence of a complete hypermeasure, combined with the extremely late position of the strong beatthis time at the downbeat of the twentieth measure out of twenty-one!makes the H4 interpretation here extremely fragile.
Example 19. (a) H2 in the first MSE (mm. 1–10) of Mozart/Bernstein, (b) H3 in the first MSE, (c) H2 in the second MSE (mm. 11–21), (d) H3 in the second MSE; Audio: Mozart/Bernstein, mm. 1–21
(click to enlarge and listen)
[4.18] As I mentioned previously, Bernstein’s interpretation is nearly identical to Marriner’s at level H1; they differ only in the nature of the transformation immediately preceding 20.1. As we shall see, however, the two interpretations diverge considerably at subsequent levels of MS. In Bernstein’s version, the first MSE continues only to measure 10, because (as in Britten’s recording) weak beats at level H2 are found at both 9.1 and 11.1. The five beats in this MSE (i.e., the odd-measure downbeats in measures 1–10) are differentiated in a way that should by now seem familiar, that is, through an alternation of relatively weak and relatively strong DMs (Example 19a). (Beats 1.1, 3.1, 5.1, 7.1, and 9.1 are ranked tenth, fifth, seventh, fourth, and ninth among the odd-measure downbeats in measures 1–20.) Of the two strong beats in this MSE, 7.1 is the stronger, for it has a more pronounced AM and DM than 3.1. (IOI 7.1 has 11.2% elongation at the beat level, vs. 5.9% in IOI 3.1, and the PSL in IOI 7.1 is 2.8 dB louder than in IOI 3.1). Thus, the first MSE has an upbeat-downbeat figure at H3, much like the one found in Britten’s recording (Example 19b). The weak beat at 11.1 initiates a second MSE (measures 11–21), which also has an alternation of weak and strong hyperbeats (Example 19c). The differentiation of 11.1 and 13.1 is clear on the basis of their DMs (ranked fourteenth and eighth among the downbeats in measures 1–20), as is the differentiation of 15.1, 17.1, 19.1, and 20.1 (ranked fifth, first, third, and second). Also note that, although IOI 13.1 is quieter than 15.1, the latter is less strongly delineated at the beat-to-beat level; whereas IOI 13.1 is louder than 12.2 (+1.0 dB), 15.1 is somewhat quieter than 14.2 (-0.8 dB). Among beats 13.1, 17.1, and 20.1, the three strong beats in the second MSE, the one with the loudest IOI is 17.1, so a weak-strong-weak pattern might be inferred at level H3 (Example 19d).
Example 20. (a) Composite MSE resulting from the regularization of level H2 in Mozart/Bernstein, mm. 1–21, (b) H3 in the composite MSE, (c) H4 in the composite MSE
(click to enlarge and listen)
[4.19] Both MSEs in Bernstein’s recording have duple meter at level H2, and two weak beats are adjacent at the border between the two. This interpretation can therefore be transformed to a regular, well-formed MSE spanning the entire excerpt through the Metrical Contraction rule (Example 20a). This transformation also yields a well-formed MSE at level H3, consisting of an upbeat and two full duple measures (Example 20b). Although these two hypermeasures are conceptually equal in length, the spans of the musical surface to which they correspond (i.e., measures 7–16 and 17–21) are radically different in lengththey cover ten and five measures, respectively. (Incidentally, this progressive shortening is also evident at the level of the hyperbeats in these measures, which span six, four, three, and two measures.) This asymmetry might influence our choice between 7.1 and 17.1 at level H4. Beat 17.1 is clearly the louder of the two (by a margin of 13.2 dB), and it also has a salient hesitation-style AM (10.5% at the beat-to-beat level), while 7.1 has an elongation-style AM (11.2%). Although 17.1 would appear to be the stronger beat on the basis of these PM cues, this does not seem to be an intuitively justifiable reading. It seems that the extremely wide spacing of these hyperbeats diminishes the force of PM comparisons. Instead, 7.1 seems like the stronger beat (see Example 20c), and this reading is supported by the asymmetry between the portions of the musical surface corresponding to the two hyperbeats (see Appendix 3, MPR 5a) and also by the tendency to hear the earlier of two more-or-less equally accented beats as the strong beat (MPR 2).
[4.20] As we have seen, each of the six interpretations under consideration employs a different set of hypermetric transformations and thus conveys a different version of the work. Some might find the diversity among these six interpretations unsettling, and might consider the absence of criteria for determining which is the “correct” or “intended” version to be a shortcoming of the procedure I have developed. To this objection, I would respond that, like the Gestalt theorists and like Lerdahl and Jackendoff, I am interested in understanding structural intuitions without recourse to idealism. In focusing on general principles of perception and on conventions for the projection of meter, I have attempted to sidestep the problematic metaphysical assumption that the work itself is timeless and fully determined prior to any performance of it, an assumption that is often implicit in critical discourse on the relative merits of different interpretations. Instead of imagining an ideal performance, I prefer to use hypothetical, metrically regular abstractions inferred from the interaction of score and performance as the framework for comparing interpretations. In order to use these comparisons to support an argument about the merit of a recording, we would need to postulate specific criteria for critical evaluation. For instance, if we decide that symmetry is important, then we might argue that Britten’s performance is outstanding because of the parallelism between the two MSEs in his version of the Mozart excerpt at levels H2 and H3 (see Examples 15 and 16). If we value musical humor, then we might instead prefer Walter’s interpretation, because of the thwarted expectancy at level H1 in his recording (see Example 12). While this approach to criticism might be interesting, it is important to realize that the comparisons enabled by my adaptations to the Lerdahl-Jackendoff theory are, in themselves, non-judgmental.
[5] Rethinking the Role of Performance in the Lerdahl-Jackendoff Theory
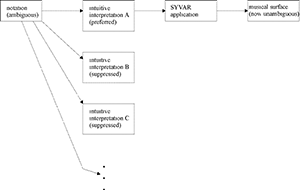
[5.1] If Lerdahl and Jackendoff are correct in characterizing the Mozart example discussed in Part 4 as “a not untypically complex passage” with regard to Metrical Structure, then it would appear that their “balance-tipping” analogy, which I quoted previously (see paragraph 2.4), is in need of some refinement. The expression “tip the balance” implies that performance-specific features are considered relatively late in the analytic process, if at all, after an impasse is reached in the interpretation of a score. That is, in conducting an analysis, we first study the score, and in doing so we discover something that resembles the faces/vase illusion, so we then listen to a recording, and finally decide on a preferred reading. Because the Lerdahl-Jackendoff theory is intended first and foremost to depict the listener’s intuitions, I believe this sequence of events is inappropriate. By beginning with the details of performances in an ambiguous passage, I have shown that more than two different interpretations can be conveyed, and that these interpretations are not necessarily the ones that are the most obvious on the basis of the score. The potential multivalence of a musical structure is sometimes more extravagant than a score-reader can anticipate; some passages are more like mosaics than faces/vase illusions in the range of meanings they can evoke (see Example 1b, j). I therefore suggest that we begin our revision to the schematic representation of the “balance-tipping” model by extending the number of possible interpretations indefinitely (Example 21).
Example 21. Example 6b, extended indefinitely in its range of conceivable intuitive interpretations
(click to enlarge)
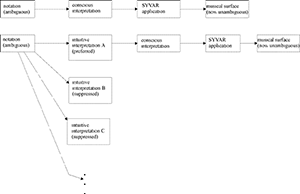
Example 22. (a) The link between ambiguous notation and performance, after Palmer (1989), (b) Synthesis of Example 21 and Example 22(a)
(click to enlarge)
[5.2] To me, the score-reader’s inability to predict a performer’s interpretation in no way indicates a lack of musical intuition, but instead reflects elite performers’ uncanny ability to avoid sounding predictable, an ability that involves a combination of intuition and conscious thought. GTTM goes a long way toward formalizing intuition, but it makes no allowance for the influence a performer’s unpredictable, conscious decisions can have on an experienced listener’s intuitionsindeed, Lerdahl and Jackendoff regard the performer’s construction of an interpretation as a “largely unconscious” process.(83) An influential study by psychologist Caroline Palmer provides a different perspective. In a series of experiments on the performance of works with ambiguous phrase structures, Palmer examines correlations between pianists’ score annotations and SYVAR patterns that are conventionally used to communicate interpretations of phrase structure.(84) Each pianist’s annotations suggest a different structural interpretation, and that interpretation corresponds strongly and uniquely to SYVARs in that individual’s performance. Palmer’s experiment suggests a model of the relationship between ambiguous notation and the sounding musical surface (see Example 22a) that is quite different from, but not incompatible with, the model implied by Lerdahl and Jackendoff through their balance-tipping analogy (see Example 6b–c). Palmer’s model allows maximum room for the performer’s freedom of conscious interpretation, and thus it sheds light on exceptions to Lerdahl and Jackendoff’s assumption that performing nuance arises largely from unconscious interpretation. Thus, we might further revise our schematic representation of the balance-tipping phenomenon by adding conscious interpretation as an intermediate stage between the intuitive understanding of hierarchical structures and the application of SYVARs (Example 22b). A limited form of conscious thought (i.e., preference between two equally legitimate options) was already implicit in Example 4, but Palmer’s model allows us to expand this considerably to include whatever musical (and even extramusical) considerations seem relevant.
[5.3] Throughout this paper, I have attempted to follow Lerdahl and Jackendoff’s lead in theorizing aspects of comprehensibility and remaining silent on aesthetic issues such as, for instance, the thwarting of expectancies or the representation of affect, motion, or aspects of a narrative. Although I would not deny that many of the SYVARs that expert performers use are based on aesthetic considerations such as these, rather than the straightforward projection of an intuitive, stable structural interpretation, I nevertheless see the value in examining aesthetically motivated idiosyncrasies in contradistinction to norms associated with intelligibility. In the realm of linguistics, Noam Chomsky theorized grammatical norms under the rubric of “competence” and referred to the relationship between actual utterances and these norms, including errors and ambiguities, as “performance.”(85) In its inclusion of a place for performers’ diverse conscious interpretative decisions, many of which (hopefully) will be motivated by aesthetic considerations rather than purely matters of musical syntax, the schematic model I have developed might be useful in the development of a theory of musical “performance,” in Chomsky’s sense of the term.(86)
[5.4] If GTTM were designed as a reading theory rather than a listening theory, or if the Mozart example possessed an exceptionally high degree of metrical complexity, then it might be argued that the scheme I am suggesting places too much emphasis on seemingly superficial performing nuances at the expense of more powerful score-based elements. I would answer this objection by reiterating three crucial facts: (1) the theory is clearly intended to capture the experienced listener’s intuitions, so the aural stimulus rather than the score is the more suitable object of inquiry, (2) Lerdahl and Jackendoff suggest that the Mozart example has an unexceptional degree of metrical complexity, and (3) elsewhere Lerdahl suggests that salience conditions become increasingly important to the listener’s construction of hierarchical interpretations in cases where stability is compromised, and in my view this should include violations to MWFR 4, the rule that insists on evenly spaced beats at the tactus and immediately larger metrical levels. I would also point out once again that, in simpler metrical situations that adhere to MWFR 4 at the first few levels of hypermeter, skilled performers and (other) readers should be expected to agree on their interpretations of the score. In the case of an unambiguous structure, therefore, the differences among performances become less relevant, and the score can adequately serve as an substitute for a conventional performance (see Example 6a).
[5.5] I will conclude by mentioning a few ways in which the concepts I have discussed might be developed further. Under close examination, recordings of additional hypermetrically ambiguous passages would no doubt prompt refinements to the metrical transformation rules that I proposed in Part 4. The utility of the metrical transformation rules at the level of local meter might also be assessed, using examples from non-Western and twentieth-century repertories in which temporal organization lies in the grey area between the random and the perfectly regular (e.g., changing meters). It is also important to remember that Metrical Structure is one of four interdependent parameters of hierarchical organization theorized in GTTM, and it remains to be seen whether the metrical transformations I have described would have effects on the other parameters.(87) It might also be interesting to explore the effects of performing nuance within each of the other parameters of the theory. In particular, the projection of phrase-periodic structure and, more recently, the communication of patterns of musical tension in performance have been studied extensively by music psychologists, and this research would inform an examination of the role of performance in the communication of phrase-periodic structure and patterns of tension and relaxation, parameters that Lerdahl and Jackendoff cover under the rubric of Grouping Structure (GS) and Prolongational Reduction (PR), respectively.(88) The techniques for SYVAR analysis that I outline in Part 4 might also help in the development of analytical applications for the copious insights on performance that are found in more recent texts on meter, such as Jonathan Kramer’s The Time of Music, William Rothstein’s Phrase Rhythm in Tonal Music, and Christopher Hasty’s Meter as Rhythm. Indeed, any structuralist theory that purports to illuminate the listening experience should have room for considering the impact of performing nuance, and performance analysis seems especially useful in exploring the inner workings of ambiguous structures.
[6] Appendix 1. Revised Rule Index for Metrical Structure(89)
MWFR 1
Every attack point must be associated with a beat at the smallest metrical level
present at that point in the piece.
MWFR 2
Every beat at a given level must also be a beat at all smaller levels present at
that point in the piece.
MWFR 3(90)
At each metrical level, strong beats are spaced either two or three beats apart.
MWFR 4
The tactus and immediately larger metrical levels must consist of beats equally
spaced throughout the piece. At subtactus metrical levels, weak beats must be equally
spaced between the surrounding strong beats.
MPR 1 (Parallelism)
Where two or more groups or parts of groups can be construed as parallel, they preferably
receive parallel metrical structure.
MPR 2 (Strong Beat Early)
Weakly prefer a metrical structure in which the strongest beat in a group appears
relatively early in the group.
MPR 3 (Event)
Prefer a metrical structure in which beats of level Li that coincide with the
inception of pitch-events are strong beats of Li.
MPR 4 (Stress)
Prefer a metrical structure in which beats of level Li that are stressed are
strong beats of Li.
MPR 5 (Length)
Prefer a metrical structure in which a relatively strong beat occurs at the inception
of either
a. a relatively long pitch-event,
b. a relatively long duration of a dynamic,
c. a relatively long slur,
d. a relatively long pattern of articulation,
e. a relatively long duration of a pitch in the relevant levels of the time-span
reduction, or
f. a relatively long duration of a harmony in the relevant levels of the time-span
reduction(harmonic rhythm).
MPR 5.5 (Hesitation) (paragraph 3.5)
Weakly prefer a metrical structure in which a relatively strong beat occurs immediately
after a relatively long pitch-event.
MPR 6 (Bass)
Prefer a metrically stable bass.
MPR 7 (Cadence)
Strongly prefer a metrical structure in which cadences are metrically stable; that
is, strongly avoid violations of local preference rules within cadences.
MPR 8 (Suspension)
Strongly prefer a metrical structure in which a suspension is on a stronger beat
than its resolution.
MPR 9 (Time-Span Interaction)
Prefer a metrical analysis that minimizes conflict in the time-span reduction.
MPR 10 (Binary Regularity)
Prefer metrical structures in which at each level every other beat is strong.
Metrical Deletion
Given a well-formed metrical structure M in which
i. B1, B2, and B3 are adjacent beats of M at level Li, and B2
is also a beat at level Li+1,
ii. T1 is the time-span from B1 to B2 and T2 is the time-span from
B2 to B3, and
iii. M is associated with an underlying grouping structure G in such a way that
both T1 and T2 are related to a surface time-span T' by the grouping transformation
performed on G of
(a) left elision or (b) overlap,
then a well-formed metrical structure M' can be formed from M and associated
with the surface grouping structure by
(a) deleting B1 and all beats at all levels between B1 and B2 and associating
B2 with the onset of T', or
(b) deleting B2 and all beats at all levels between B2 and B3 and associating
B1 with the onset of T'.
Metrical Contraction (paragraph 4.6)
Given
(i) a well-formed metrical structure episode M that ends with beats B1 and
B2, in which B1 and B2 are adjacent beats at level Li and B1
is also a beat at level Li+1, and
(ii) a well-formed metrical structure episode N in which B3, B4, and B5
are adjacent beats at level Li and only B3 is also a beat at level Li+1,
and
(iii) a well-formed metrical structure episode P that begins with beats B6,
B7, and B8, in which B6, B7, and B8 are adjacent beats at
level Li and both B6 and B8 are also beats at level Li+1,
and given that M, N, and P are adjacent metrical structure episodes,
then a well-formed metrical structure episode M' can be formed by deleting B5,
such that B1, B2, B3, B4, B6, B7, and B8 are adjacent
beats at level Li and B1, B3, B6, and B8 are also beats at level
Li+1.
Metrical Completion (paragraph 4.8)
Given
(i) a well-formed metrical structure episode M that ends with beats B1, B2,
and
B3, in which B1, B2, and B3 are adjacent beats at level Li and
both B1 and B3 are also beats at level Li+1, and
(ii) a well-formed metrical structure episode N that begins with beats B4,
B5, and B6, in which B4, B5, and B6 are adjacent beats at level
Li and both B4 and B6 are also beats at level Li+1,
and given that M and N are adjacent metrical structure episodes,
then a well-formed metrical structure episode M' can be formed by inserting beat
Bx between beats B3 and B4, such that B1, B2, B3, Bx,
B4, B5, and B6 are adjacent beats at level Li and B1, B3,
B4, and B6 are also beats at level Li+1.
[7] Appendix 2. Performance Analysis Techniques
[7.1] Before I begin explaining some basic techniques for the analysis of duration and loudness in recordings, I must once again emphasize that the process should begin with close listening unmediated by a computer. This helps us avoid attributing importance to distinctions that are too fine for the ear to detect under normal listening conditions.
[7.2] When a performer is present as an experimental subject, a computer interface with the instrument can allow the researcher to gather data very efficiently, but data collection is rather more arduous in the case of a recorded performance. At present, there are three basic options for the analysis of recordings: tapping software, spectrographic analysis, and audio editing software (sometimes referred to as waveform analysis). In the first of these approaches, the listener taps along with the perceived beat of the performance, from which the computer calculates rough data on tempo fluctuation.(91) This is the most efficient method for gathering data, and the only realistic method for analyzing complete large-scale works or movements or for making general comparisons of a large number of recordings. However, it is limited to the parameter of tempo, and even in this capacity it is considerably less accurate than the other forms of analysis. Spectrographic analysis, the second approach, is especially useful for gathering information on timbre.(92) This is the preferred method for dealing with orchestral instruments and the human voice (in both live and recorded performances), but it requires cumbersome (and expensive) hardware and a greater knowledge of acoustics and mathematics than many music theorists possess (including the present author). This leaves waveform analysis, in which excerpts from an LP or a CD are converted to digital sound files (e.g., .au or .wav) and analyzed with audio editing software.(93) This method is more accurate than the tapping approach and more user-friendly than the spectrographic, and it can provide reliable information pertaining to loudness and (especially) duration.
[7.3] Once the excerpt has been converted to a sound file, its waveform can be displayed in an audio editing program, and playback can be initiated from any point, with a resolution greater than 1 ms (millisecond).(94) (I prefer Syntrillium CoolEdit, a Shareware program that I have found to be reliable and user-friendly. WaveLab and ProTools are other popular options.) Through a combination of visual and aural observation, one can identify the temporal location of the onset (beginning) of any event, such as a solid chord or an unaccompanied melody note. By using this method, the durations of inter-onset intervals (IOIs) can be calculated at the level of the phrase, measure, beat, or (in some cases) individual note. Some precision is lost in cases where reverb or chord asynchrony makes it difficult to pinpoint the onset, and human error should also be taken into consideration. If pressed, I would estimate the reliability to be no worse than ±20 ms. In general, I like to gather IOI statistics at the level of the tactus, that is, the metrical level that is most salient to the listener (and the performer) and that sometimes provokes toe-tapping. These values can easily be converted to M.M. speeds in beats per minute (bpm).
[7.4] Amplitude is the main physical correlate of intensity, or perceived loudness. The human ear can perceive intensity distinctions across a trillion-fold spectrum, so a logarithmic measure, the decibel (dB), is used to facilitate comparisons. Regardless of their absolute values, any two sounds at the same pitch level that differ in amplitude by 10 dB (e.g., 0 dB and 10 dB, 90 dB and 100 dB) will have intensities in a 10:1 ratio. The same is not true of linear measures, such as duration, which is one reason why we sometimes use percentages rather than absolute durational values when comparing IOIs. Note that the logarithmic function is curved, so the intensity ratio is not always equal to the difference in dB values. In fact, it is only so in the case of 10 dB differences. However, a useful rule of thumb is that a 3 dB difference roughly indicates a doubling in intensity.(95)
[7.5] It is important to realize that two different scales are in common use among those interested in measuring the loudness of music. One is called “Sound Pressure Level” (SPL), and in this case the baseline (0 dB) represents the normal threshold of hearing (i.e., minimum audible intensity) for pitches around 1000 Hz. This scale is used for comparing sounds “in the air.” The other scale, “Electronic Signal Level” (ESL), instead uses the point at which distortion is attenuated as its baseline. The latter scale is used for most forms of electronically mediated sound, including audio editing software. Those who are accustomed to seeing amplitudes in terms of SPL scales, according to which most musical performances fall somewhere between 40 and 90 dB, might be surprised by the readings given by audio editing software, which (if distortion is successfully avoided) fall entirely below 0 dB. Most CD recordings, for example, have ESLs between 90 dB and 0 dB.
[7.6] It should also be noted that, unlike IOIs, absolute intensity values are meaningless in themselves as measures of a performance, because they are dependent upon recording and playback levels.(96) In performance analysis, it is best to concentrate on relative intensities within any given recording. The most useful approach that the current technology enables appears to be the ranking of selected events in terms of loudness. In order to maximize the effectiveness of this, the excerpt should be edited so that the loudest event is amplified to just under 0 dBESL and all other values are amplified proportionally. This process, which can be carried out automatically using the audio editor’s “Normalize” function, widens the range of amplitudes and thus facilitates comparisons. Even if we restrict ourselves to the ranking of relative intensities, caution is required in interpreting amplitude data, since the relationship between amplitude and perceived loudness is extremely complex. Intensity rises in proportion to frequency in the case of isolated pitches, and also in proportion to textural density,(97) so it would be simplistic to regard a quantitative change in intensity as a change in loudness. For this reason, it is safest to compare intensity levels in the case of events that are qualitatively similar in terms of parameters other than perceived loudness. Fortunately, significant changes in orchestration occur only three times in the excerpt used in this study (at beats 14.1, 16.2, and 20.2), and the frequency range is relatively small (e.g., the melody lies within the span of a tenth), but in music with a greater variety of orchestration or pitch, intensity values would be less useful measures of loudness, even for the purpose of ranking the dynamic levels of selected beats.
[7.7] Audio editing software can automatically compute the peak sound level (PSL) within any portion of an audio file.(98) First, as I have just explained, the entire excerpt should be edited using the “Normalize” function. Next, the PSL data can be collected for any span of music. Depending on the objective, it might be appropriate to examine each beat (using the onset points located previously as guides), or even each note within passages whose dynamics or accents seem to be of particular interest. Unfortunately, existing technology does not allow us to analyze each voice in a multi-voice texture independently. It is possible to define frequency limits to the analysis (e.g., to analyze the amplitudes for frequencies between 40 Hz and 1000 Hz), but such an approach would discount the contribution of overtones to the perceived intensity of each pitch.
[8] Appendix 3. Quantitative Performance Analyses
[8.1] Mozart/Britten, I, mm. 1-20
In this and the following tables, TF = tempo fluctuation, a comparison between the local tempo and the average tempo.
m.bt. onset IOI M.M. TF(%) IOI chg. (%), vs. previous
(s) (ms) (bpm) downbeat beat
_________________________________________________________________
1.1 0 585 102 -5.4 N/A N/A
1.2 0.585 623 96.3 -11.2 6.5
2.1 1.208 550 109.1 0.6 -6.0 -11.7
2.2 1.758 589 101.9 -6.0 7.1
3.1 2.347 531 113.0 4.2 -3.5 -9.8
3.2 2.878 550 109.1 0.6 3.6
4.1 3.428 560 107.1 -1.2 5.5 1.8
4.2 3.988 511 117.4 8.3 -8.8
5.1 4.499 589 101.9 -6.0 5.2 15.2
5.2 5.088 566 106.0 -2.2 -3.9
6.1 5.654 524 114.5 5.6 -11.0 -7.4
6.2 6.178 557 107.7 -0.6 6.3
7.1 6.735 633 94.8 -12.6 20.8 13.6
7.2 7.368 499 120.2 10.9 -21.2
8.1 7.867 547 109.7 1.2 -13.6 9.6
8.2 8.414 528 113.6 4.8 -3.5
9.1 8.942 575 104.3 -3.7 5.1 8.9
9.2 9.517 550 109.1 0.6 -4.3
10.1 10.067 490 122.5 13.0 -14.8 -10.9
10.2 10.557 540 111.1 2.5 10.2
11.1 11.097 643 93.3 -13.9 31.2 19.1
11.2 11.740 493 121.7 12.3 -23.3
12.1 12.233 485 123.7 14.1 -24.6 -1.6
12.2 12.718 557 107.7 -0.6 14.8
13.1 13.275 541 110.9 2.3 11.5 -2.9
13.2 13.816 540 111.1 2.5 -0.2
14.1 14.356 557 107.7 -0.6 3.0 3.1
14.2 14.913 569 105.4 -2.7 2.2
15.1 15.482 544 110.3 1.7 -2.3 -4.4
15.2 16.026 572 104.9 -3.2 5.1
16.1 16.598 557 107.7 -0.6 2.4 -2.6
16.2 17.155 627 95.7 -11.7 12.6
17.1 17.782 524 114.5 5.6 -5.9 -16.4
17.2 18.306 589 101.9 -6.0 12.4
18.1 18.895 572 104.9 -3.2 9.2 -2.9
18.2 19.467 531 113.0 4.2 -7.2
19.1 19.998 547 109.7 1.2 -4.4 3.0
19.2 20.545 541 110.9 2.3 -1.1
20.1 21.086 588 102.0 -5.9 7.5 8.7
(20.2) 21.674
m.bt PSL intensity change (dB), vs. previous
(dB_ESL_) odd downbeat even downbeat downbeat beat
________________________________________________________________________
1.1 -26.4 N/A (10) N/A (20)
1.2 -29.4 -3.1
2.1 -20.3 N/A (10) 6.0 (19) 9.1
2.2 -19.8 0.6
3.1 -17.8 8.6 (9) 2.5 (14) 2.0
3.2 -22.7 -4.9
4.1 -19.4 0.9 (9) -1.6 (18) 3.3
4.2 -22.2 -2.8
5.1 -17.0 0.8 (6) 2.4 (9) 5.2
5.2 -25.1 -8.1
6.1 -17.6 1.8 (5) -0.6 (13) 7.5
6.2 -13.5 4.2
7.1 -12.4 4.6 (3) 5.3 (5) 1.1
7.2 -21.1 -8.7
8.1 -19.1 -1.5 (8) -6.8 (17) 2.0
8.2 -20.8 -1.6
9.1 -17.6 -5.2 (8) 1.5 (12) 3.2
9.2 -27.6 -10.0
10.1 -17.9 1.2 (6) -0.3 (15) 9.7
10.2 -18.3 -0.4
11.1 -17.1 0.5 (7) 0.8 (10) 1.2
11.2 -20.3 -3.2
12.1 -17.4 0.5 (4) -0.3 (11) 2.9
12.2 -14.5 2.9
13.1 -16.5 0.6 (5) 0.9 (8) -2.0
13.2 -11.0 5.5
14.1 -12.7 4.7 (3) 3.8 (6) -1.7
14.2 -9.9 2.7
15.1 -12.8 3.7 (4) -0.1 (7) -2.8
15.2 -13.4 -0.7
16.1 -18.8 -6.1 (7) -6.0 (16) -5.3
16.2 -2.1 16.6
17.1 -0.8 12.0 (1) 18.0 (3) 1.3
17.2 -1.0 -0.2
18.1 -0.6 18.1 (2) 0.2 (2) 0.4
18.2 -2.1 -1.5
19.1 -2.4 -1.5 (2) -1.6 (4) -0.3
19.2 -3.4 -1.0
20.1 0 0.6 (1) 2.3 (1) 3.4
[b] Mozart/Marriner, I, mm. 1-20
There is an interesting contrapuntal-temporal effect in this performance. In mm. 1-11, where the melody has a rest on the second beat of each odd-numbered measure, the bass articulates the beat later than expected, but nevertheless the ensuing melody note comes in "on time." Values shown are estimates of the virtual melody onset, an approximation based on the onsets of the second and fourth quarter-note subdivisions of these measures. The bass onsets for these beats are, respectively: 0.564, 2.956, 5.028, 7.283, 9.415, and 11.729 s. PSLs here are based on bass onsets, but IOIs are based on the virtual melody onsets.
m.bt. onset IOI M.M. TF(%) IOI chg. (%), vs. previous
(s) (ms) (bpm) downbeat beat
_________________________________________________________________
1.1 0 573 104.7 -4.2 N/A N/A
1.2 0.573 562 106.8 -2.3 -1.9
2.1 1.135 558 107.5 -1.6 -2.6 -0.7
2.2 1.693 609 98.5 -9.9 9.1
3.1 2.302 482 124.5 13.9 -13.6 -20.9
3.2 2.784 592 101.4 -7.3 22.8
4.1 3.376 558 107.5 -1.6 15.8 -5.7
4.2 3.934 510 117.6 7.6 -8.6
5.1 4.444 626 95.8 -12.3 12.2 22.7
5.2 5.070 542 110.7 1.3 -13.4
6.1 5.612 548 109.5 0.2 -12.5 1.1
6.2 6.160 539 111.3 1.8 -1.6
7.1 6.699 555 108.1 -1.1 1.3 3.0
7.2 7.254 527 113.9 4.2 -5.0
8.1 7.781 539 111.3 1.8 -2.9 2.3
8.2 8.320 575 104.3 -4.5 6.7
9.1 8.895 555 108.1 -1.1 3.0 -3.5
9.2 9.450 552 108.7 -0.6 -0.5
10.1 10.002 549 109.3 0.0 -1.1 -0.5
10.2 10.551 488 123.0 12.5 -11.1
11.1 11.039 659 91.0 -16.7 20.0 35.0
11.2 11.698 519 115.6 5.8 -21.2
12.1 12.217 533 112.6 3.0 -19.1 2.7
12.2 12.750 523 114.7 5.0 -1.9
13.1 13.273 591 101.5 -7.1 10.9 13.0
13.2 13.864 513 117.0 7.0 -13.2
14.1 14.377 584 102.7 -6.0 -1.2 13.8
14.2 14.961 539 111.3 1.8 -7.7
15.1 15.500 639 93.9 -14.1 9.4 18.6
15.2 16.139 725 82.8 -24.2 13.5
16.1 16.864 398 150.8 37.9 -37.3 -45.1
16.2 17.282 580 103.4 -5.4 45.7
17.1 17.842 564 106.4 -2.7 41.7 -2.8
17.2 18.406 597 100.5 -8.0 5.9
18.1 19.003 533 112.6 3.0 -5.5 -10.7
18.2 19.536 553 108.5 -0.7 3.8
19.1 20.089 535 112.1 2.6 0.4 -3.3
19.2 20.624 562 106.8 -2.3 5.0
20.1 21.186 569 105.4 -3.5 6.4 1.2
(20.2) 21.75
m.bt PSL intensity change (dB), vs. previous
(dB_ESL_) odd downbeat even downbeat downbeat beat
________________________________________________________________________
1.1 -24.3 N/A (10) N/A (20) N/A
1.2 -26.6 -2.3
2.1 -20.0 N/A (9) 4.3 (17) 6.6
2.2 -14.9 5.1
3.1 -14.7 9.6 (6) 5.3 (9) 0.2
3.2 -26.5 -11.8
4.1 -18.2 1.8 (6) -3.5 (13) 8.3
4.2 -22.1 -3.9
5.1 -20.0 -5.3 (8) -1.8 (16) 2.1
5.2 -29.0 -9.0
6.1 -16.5 1.8 (5) 3.5 (12) 12.5
6.2 -13.7 2.8
7.1 -9.5 10.5 (4) 7.1 (6) 4.2
7.2 -18.1 -8.6
8.1 -18.9 -2.4 (8) -9.5 (15) -0.9
8.2 -19.7 -0.7
9.1 -22.7 -13.2 (9) -3.8 (19) -3.0
9.2 -28.4 -5.7
10.1 -20.2 -1.2 (10) 2.5 (18) 8.2
10.2 -15.2 5.0
11.1 -15.1 7.6 (7) 5.0 (10) 0.1
11.2 -22.2 -7.0
12.1 -18.2 3.1 (7) -3.1 (14) 3.9
12.2 -15.8 2.4
13.1 -13.6 1.5 (5) 4.6 (7) 2.2
13.2 -12.5 1.1
14.1 -14.3 8.2 (3) -0.7 (8) -1.8
14.2 -8.8 5.5
15.1 -5.5 8.1 (3) 8.8 (5) 3.2
15.2 -8.6 -3.1
16.1 -15.7 -5.7 (4) -10.2 (11) -7.1
16.2 -5.1 10.6
17.1 0 5.5 (1) 15.7 (1) 5.1
17.2 -3.0 -3.0
18.1 -1.5 14.2 (1) -1.5 (2) 1.4
18.2 -4.3 -2.8
19.1 -3.2 -3.2 (2) -1.7 (4) 1.0
19.2 -2.0 1.2
20.1 -1.7 -0.1 (2) 1.6 (3) 0.3
[c] Mozart/Walter, I, mm. 1-20
m.bt. onset IOI M.M. TF(%) IOI chg. (%), vs. previous
(s) (ms) (bpm) downbeat beat
_________________________________________________________________
1.1 0 725 82.8 -10.8 N/A N/A
1.2 0.725 672 89.3 -3.8 -7.3
2.1 1.397 592 101.4 9.2 -18.3 -11.9
2.2 1.989 666 90.1 -2.9 12.5
3.1 2.655 652 92.0 -0.8 10.1 -2.1
3.2 3.307 627 95.7 3.1 -3.8
4.1 3.934 599 100.2 7.9 -8.1 -4.5
4.2 4.533 625 96.0 3.4 4.3
5.1 5.158 609 98.5 6.2 1.7 -2.6
5.2 5.767 631 95.1 2.5 3.6
6.1 6.398 579 103.6 11.7 -4.9 -8.2
6.2 6.977 605 99.2 6.9 4.5
7.1 7.582 755 79.5 -14.4 30.4 24.8
7.2 8.337 540 111.1 19.7 -28.5
8.1 8.877 601 99.8 7.6 -20.4 11.3
8.2 9.478 620 96.8 4.3 3.2
9.1 10.098 591 101.5 9.4 -1.7 -4.7
9.2 10.689 682 88.0 -5.2 15.4
10.1 11.371 645 93.0 0.2 9.1 -5.4
10.2 12.016 609 98.5 6.2 -5.6
11.1 12.625 711 84.4 -9.1 10.2 16.7
11.2 13.336 627 95.7 3.1 -11.8
12.1 13.963 630 95.2 2.6 -11.4 0.5
12.2 14.593 591 101.5 9.4 -6.2
13.1 15.184 685 87.6 -5.6 8.7 15.9
13.2 15.869 649 92.4 -0.4 -5.3
14.1 16.518 678 88.5 -4.6 -1.0 4.5
14.2 17.196 602 99.7 7.4 -11.2
15.1 17.798 638 94.0 1.3 -5.9 6.0
15.2 18.436 682 88.0 -5.2 6.9
16.1 19.118 629 95.4 2.8 -1.4 -7.8
16.2 19.747 625 96.0 3.4 -0.6
17.1 20.372 616 97.4 5.0 -2.1 -1.4
17.2 20.988 664 90.4 -2.6 7.8
18.1 21.652 616 97.4 5.0 0 -7.2
18.2 22.268 634 94.6 2.0 2.9
19.1 22.902 620 96.8 4.3 0.6 -2.2
19.2 23.522 605 99.2 6.9 -2.4
20.1 24.127 580 103.4 11.5 -6.5 -4.1
(20.2) 24.707
m.bt PSL intensity change (dB), vs. previous
(dB_ESL_) odd downbeat even downbeat downbeat beat
________________________________________________________________________
1.1 -20.8 N/A (10) N/A (20) N/A
1.2 -20.8 -0.1
2.1 -12.7 N/A (7) 8.1 (13) 8.2
2.2 -13.8 -1.2
3.1 -9.1 11.7 (5) 3.4 (7) 4.8
3.2 -20.7 -11.6
4.1 -13.7 -1.0 (8) -4.6 (14) 7.0
4.2 -19.6 -5.9
5.1 -15.8 -6.7 (9) -2.1 (18) 3.8
5.2 -21.9 -6.1
6.1 -11.3 2.4 (5) 4.4 (11) 10.6
6.2 -9.3 2.0
7.1 -6.2 9.6 (3) 5.1 (5) 3.1
7.2 -19.4 -13.2
8.1 -16.7 -5.4 (10) -10.5 (19) 2.6
8.2 -18.8 -2.1
9.1 -15.7 -9.5 (8) 1.0 (17) 3.1
9.2 -24.0 -8.2
10.1 -14.7 2.1 (9) 1.1 (15) 9.3
10.2 -15.4 -0.8
11.1 -14.9 0.8 (7) -0.2 (16) 0.5
11.2 -20.2 -5.3
12.1 -10.7 4.0 (3) 4.2 (9) 9.5
12.2 -14.1 -3.4
13.1 -9.5 5.4 (6) 1.2 (8) 4.6
13.2 -8.1 1.4
14.1 -11.9 -1.2 (6) -2.5 (12) -3.8
14.2 -6.4 5.6
15.1 -7.2 2.3 (4) 4.8 (6) -0.8
15.2 -6.2 1.0
16.1 -11.0 1.0 (4) -3.8 (10) -4.8
16.2 -4.0 7.0
17.1 -1.6 5.6 (2) 9.4 (4) 2.4
17.2 -1.5 0.1
18.1 -1.2 9.8 (2) 0.4 (2) 0.3
18.2 -2.5 -1.3
19.1 -1.4 0.2 (1) -0.2 (3) 1.1
19.2 -3.9 -2.5
20.1 0 1.2 (1) 1.4 (1) 3.9
[d] Mozart/Bernstein, I, mm. 1-20
m.bt. onset IOI M.M. TF(%) IOI chg. (%), vs. previous
(s) (ms) (bpm) downbeat beat
_________________________________________________________________
1.1 0 718 83.6 -11.5 N/A N/A
1.2 0.718 727 82.5 -12.6 1.3
2.1 1.445 635 94.5 0.1 -11.6 -12.7
2.2 2.080 606 99.0 4.9 -4.6
3.1 2.686 642 93.5 -1.0 1.1 5.9
3.2 3.328 624 96.2 1.9 -2.8
4.1 3.952 624 96.2 1.9 -2.8 0
4.2 4.576 635 94.5 0.1 1.8
5.1 5.211 690 87.0 -7.9 10.6 8.7
5.2 5.901 631 95.1 0.7 -8.6
6.1 6.532 642 93.5 -1.0 -7.0 1.7
6.2 7.174 617 97.2 3.0 -3.9
7.1 7.791 686 87.5 -7.3 6.9 11.2
7.2 8.477 580 103.4 9.6 -15.5
8.1 9.057 635 94.5 0.1 -7.4 9.5
8.2 9.692 620 96.8 2.5 -2.4
9.1 10.312 642 93.5 -1.0 1.1 3.5
9.2 10.954 590 101.7 7.7 -8.1
10.1 11.544 665 90.2 -4.4 3.6 12.7
10.2 12.209 616 97.4 3.2 -7.4
11.1 12.825 668 89.8 -4.9 0.5 8.4
11.2 13.493 676 88.8 -6.0 1.2
12.1 14.169 536 111.9 18.6 -19.8 -20.7
12.2 14.705 623 96.3 2.0 16.2
13.1 15.328 664 90.4 -4.3 23.9 6.6
13.2 15.992 639 93.9 -0.5 -3.8
14.1 16.631 631 95.1 0.7 -5.0 -1.3
14.2 17.262 635 94.5 0.1 0.6
15.1 17.897 606 99.0 4.9 -4.0 -4.6
15.2 18.503 698 86.0 -8.9 15.2
16.1 19.201 618 97.1 2.8 2.0 -11.5
16.2 19.819 683 87.8 -6.9 10.5
17.1 20.502 576 104.2 10.3 -6.8 -15.7
17.2 21.078 617 97.2 3.0 7.1
18.1 21.695 646 92.9 -1.6 12.2 4.7
18.2 22.341 602 99.7 5.6 -6.8
19.1 22.943 602 99.7 5.6 -6.8 0
19.2 23.545 624 96.2 1.9 3.7
20.1 24.169 727 82.5 -12.6 20.8 16.5
(20.2) 24.896
m.bt PSL intensity change (dB), vs. previous
(dB_ESL_) odd downbeat even downbeat downbeat beat
________________________________________________________________________
1.1 -27.5 N/A (10) N/A (20) N/A
1.2 -29.1 -1.7
2.1 -24.0 N/A (8) 3.5 (17) 5.2
2.2 -19.1 4.8
3.1 -16.6 10.9 (5) 7.4 (7) 2.6
3.2 -24.9 -8.4
4.1 -24.3 -0.4 (9) -7.8 (18) 0.6
4.2 -24.4 -0.1
5.1 -17.5 -0.9 (7) 6.9 (9) 7.0
5.2 -26.8 -9.4
6.1 -19.2 5.1 (6) -1.7 (13) 7.6
6.2 -14.0 5.2
7.1 -13.7 3.7 (4) 5.5 (6) 0.2
7.2 -26.7 -13.0
8.1 -24.4 -5.2 (10) -10.7 (19) 2.3
8.2 -21.2 3.2
9.1 -22.9 -9.2 (9) 1.5 (16) -1.7
9.2 -28.7 -5.8
10.1 -17.8 6.6 (3) 5.1 (10) 10.9
10.2 -20.1 -2.3
11.1 -20.4 2.5 (8) -2.6 (14) -0.3
11.2 -22.1 -1.7
12.1 -18.9 -1.1 (5) 1.5 (12) 3.2
12.2 -18.1 0.8
13.1 -17.2 3.2 (6) 1.7 (8) 1.0
13.2 -16.7 0.5
14.1 -22.8 -3.9 (7) -5.6 (15) -6.1
14.2 -11.7 11.0
15.1 -12.5 4.7 (3) 10.3 (5) -0.8
15.2 -13.5 -1.0
16.1 -18.1 4.6 (4) -5.6 (11) -4.6
16.2 -6.2 11.9
17.1 0 12.5 (1) 18.1 (1) 6.2
17.2 -7.4 -7.4
18.1 -5.3 12.8 (2) -5.3 (4) 2.1
18.2 -5.4 -0.1
19.1 -2.7 -2.7 (2) 2.6 (3) 2.7
19.2 -2.3 0.3
20.1 -1.5 3.8 (1) 1.2 (2) 0.8
[9] Appendix 4. Index of Acronyms
Numbers in parentheses indicate the paragraphs in which terms are introduced.
AM agogic micro-accent (3.3)
DM dynamic micro-accent (3.3)
H1 first, i.e., most superficial, level of hypermeter (2.1)
IOI inter-onset interval (4.2)
MPR metrical preference rule (2.2)
MS metrical structure (2.1)
MSE metrical structure episode (4.5)
MWFR metrical well-formedness rule (2.2)
PM phenomenal micro-accent (3.3)
PR preference rule (2.2)
Alan Dodson
University of Western Ontario
Faculty of Music
Rm. 210, Talbot College
London, Ontario N6A 3K7
Canada
dadodson@uwo.ca
Footnotes
* Catherine Nolan, Caroline Palmer, and the two anonymous
reviewers deserve my special thanks for their helpful suggestions. Dr. Nolan
provided encouragement and expert guidance throughout the project’s development,
and Dr. Palmer offered thorough and unusually quick feedback on my references to
studies in music psychology.
Return to text
1. See especially Jonathan Kramer, The Time of Music: New Meanings, New Temporalities, New Listening Strategies (New York: Schirmer, 1988), Chapter 4: “Meter and Rhythm,” 81–122; Christopher Hasty, Meter as Rhythm (Oxford: Oxford University Press, 1997), “Preface,” vii–xii.
Return to text
2. Stanley Sadie, ed. The New Grove Dictionary of Music and Musicians (London: Macmillan, 1980), s.v. “Metre.”
Return to text
3. Stanley Sadie, ed. The New Grove Dictionary of Music and Musicians, 2nd ed. (London: Macmillan, 2001), s.v. “Metre,” by Justin London.
Return to text
4. See especially Mary Louise Serafine, Music as Cognition: The Development of Thought in Sound (New York: Columbia University Press, 1988), 69–74.
Return to text
5. Joseph Kerman, Contemplating Music: Challenges to Musicology (Cambridge, Mass.: Harvard University Press, 1985), 60–112; Clare Detels, “Autonomist/Formalist Aesthetics, Music Theory, and the Feminist Paradigm of Soft Boundaries,” Journal of Aesthetics and Art Criticism 52/1 (Winter 1994): 113–26; Kevin Korsyn, “Beyond Privileged Contexts: Intertextuality, Influence, and Dialogue,” in Rethinking Music, ed. Nicholas Cook and Mark Everist, 55–72 (Oxford: Oxford University Press, 1999); Susanne Cusick, “Gender, Musicology, and Feminism,” also in Rethinking Music, 471–98.
Return to text
6. Fred Lerdahl and Ray Jackendoff, A Generative Theory of Tonal Music (Cambridge, Mass.: MIT Press, 1983). I will use the abbreviation GTTM in subsequent references to this source.
Return to text
7. Empirical confirmation of claims from GTTM can be found in Irène Deliège, “Grouping Conditions in Listening to Music: An Approach to Lerdahl and Jackendoff’s Grouping Preference Rules,” Music Perception 4/4 (Summer 1987): 325–60; Emmanuel Bigand, “Abstraction of Two Forms of Underlying Structure in a Tonal Melody,” Psychology of Music 18 (1990): 45–59; Nicola Dibben, “The Cognitive Reality of Hierarchic Structure in Tonal and Atonal Music,” Music Perception 12/1 (Fall 1994): 1–25.
Return to text
8. GTTM has been cited widely in the psychological literature on performance since the mid-1980s. See, e.g., Neil P. Todd, “A Model of Expressive Timing in Tonal Music,” Music Perception 3/1 (Fall 1985): 33–58; Eric F. Clarke, “Generative Principles in Music Performance,” in Generative Processes in Music: The Psychology of Performance, Improvisation, and Composition, ed. John A. Sloboda, 1–26 (Oxford: Clarendon, 1988); Caroline Palmer, “Mapping Musical Thought to Musical Performance,” Journal of Experimental Psychology: Human Perception and Performance 15 (1989): 331–46; W. Luke Windsor and Eric F. Clarke, “Expressive Timing and Dynamics in Real and Artificial Musical Performances: Using an Algorithm as an Analytic Tool,” Music Perception 15/2 (Winter 1997): 127–52.
Return to text
9. See especially GTTM, Chapter 1, “Theoretical Perspective,” 1–12; Lerdahl and Jackendoff, “A Reply to Peel and Slawson’s Review of A Generative Theory of Tonal Music,” Journal of Music Theory 29 (1985): 145–60; Lerdahl, “Composing and Listening: A Reply to Nattiez,” in Perception and Cognition of Music, ed. Irène Deliège and John A. Sloboda, 421–28 (Hove, U.K.: Psychology Press, 1997).
Return to text
10. GTTM, 1. Emphasis added.
Return to text
11. They admit, for example, that their theory fails to
consider counterpoint (GTTM, 37).
Return to text
12. The term is derived from “hypermeasure,” coined by Edward T. Cone in
Musical
Form and Musical Performance (New York: Norton, 1968), 40. I will also use the
term “hyperbeat” to designate a beat that belongs to a hypermeasure.
Return to text
13. Among the most influential sources in this genre are
Erwin Stein, Form and
Performance (New York: Knopf, 1962); Cone, Musical
Form and Musical Performance; Janet Schmalfeldt, “On the Relation
of Analysis to Performance: Beethoven’s Bagatelles Op. 126, Nos. 2 and 5,”
Journal
of Music Theory 29 (1985): 1–31; Wallace Berry, Musical Structure and Performance
(New Haven: Yale University Press, 1989). See also the extensive bibliography in
Cynthia Folio, “Analysis and Performance of the Flute Sonatas of J. S. Bach: A Sample
Lesson Plan,” Journal of Music Theory Pedagogy 5 (1991): 133–59. Some more recent
contributions include Joel Lester, “Performance and Analysis: Interaction and Interpretation,”
in The Practice of Performance: Studies in Musical Interpretation, ed. John Rink,
197–216 (Cambridge: Cambridge University Press, 1995); Catherine Nolan, “Reflections
on the Relationship of Analysis and Performance,” College Music Symposium 32–34
(1993–94): 112–39; Richard S. Parks, “Structure and Performance: Metric and Phrase
Ambiguities in the Three Chamber Sonatas,” in Debussy in Performance, ed. James
R. Briscoe, 193–224 (New Haven: Yale University Press, 1999).
Return to text
14. Nicholas Cook, “Analyzing Performance, and Performing
Analysis,” in
Rethinking
Music, ed. Nicholas Cook and Mark Everist, 239–61 (Oxford: Oxford University Press,
1999).
Return to text
15. J. L. Austin, How to Do Things with Words (Cambridge, Mass.: Harvard University
Press, 1962), 3, 6.
Return to text
16. Cook, “Analyzing Performance, and Performing
Analysis,” 239–47; Tim Howell, “Analysis and Performance: The Search for a Middleground,” in Companion to Contemporary Musical Thought, ed. John Paynter,
Tim Howell, Richard Orton, and Peter Seymour, 692–714 (London: Routledge, 1992),
709; Lawrence Rosenwald, “Theory, Text-Setting, and Performance,” Journal of Musicology
11 (1993), 60–63.
Return to text
17. Lester, “Performance and Analysis,” 199–202.
Return to text
18. Foremost in this category are Heinrich Schenker’s views on performance. See,
e.g., the final sentence of Schenker, “The Sarabande of Bach’s Suite No. 3 for Solo
Violoncello [BWV 1009],” trans. Hedi Siegel, in The Masterwork in Music: A Yearbook,
Vol. 2 (1926), ed. William Drabkin, 55–58 (Cambridge: Cambridge University Press,
1996), 58: “Any other interpretation and execution will surely founder, for the
immutable forces that govern this sarabande do not admit an arbitrary interpretation
of any part of the composition.” See also Schenker, The Art of Performance, ed. Heribert Esser, trans. Irene Schreier Scott (Oxford: Oxford University Press, 2000),
3–4, 53–57, 77–78.
Return to text
19. See, e.g., Susanne Cusick, “Gender and the Cultural Work of a Classical Music
Performance,” repercussions 3/1 (Spring 1994), 105–7.
Return to text
20. I prefer the expression “reading from the score” to
both “analyzing the piece,” which is vague, and “score-based analysis,” which
overemphasizes the visual aspect of the activity. Whether we are dealing with
words or music, the word “reading” carries the connotations of aural imagery and
creative participation in an often silent, private performance of sorts. In a
subtle way, the word “reading” emphasizes the analyst’s participation in the
construction of the object of study. As Nicholas Cook once remarked, “when
musicians use the notation for the purposes it is intended for—when, that is,
they read it—they supply a great deal of information which is not actually in
the score.” Nicholas Cook, A Guide to Musical Analysis (London:
Dent, 1987), 227.
Return to text
21. Nicholas Cook, “Between Process and Product: Music and/as Performance,” Music Theory Online 7/2 (April 2001).
Return to text
22. José A. Bowen has also developed a framework for
comparing different realizations of scores, but he concentrates on historical
traditions and trends in performance, such as the convention of slowing down for
the second theme of a work in sonata-allegro form, as well as the ontological
significance of these trends, rather than the perception of structural elements.
See Bowen, “The History of Remembered Innovation: Tradition and Its Role in the
Relationship between Musical Works and Their Performances,”
Journal
of Musicology 11/2 (Spring 1993): 139–73; idem, “Finding the Music in Musicology,”
in Rethinking Music, ed. Nicholas Cook and Mark Everist, 424–51 (Oxford: Oxford
University Press, 1999).
Return to text
23. For insights on these types of ambiguities and
associated ontological problems, see the following: Leo Treitler, “History and the Ontology of the Work,”
Journal
of Aesthetics and Art Criticism 15/3 (Summer 1993): 483–97; Bowen, “History
of Remembered Innovation”; Nicholas
Cook, “At the Borders of Musical Identity: Schenker, Corelli, and the Graces,”
Music
Analysis 18/2 (July 1999): 179–233.
Return to text
24. I will address the latter issue in some detail in a
paper entitled “Rethinking Schenker’s Musical Ontology through Gadamer’s
Critique of Aesthetic Consciousness,” scheduled for presentation at “The
Intellectual Frontiers of Music,” University of Aberdeen, June 25, 2002.
Return to text
25. On the connection of ontology and performance, see Treitler, “History and
the Ontology of the Work”; Bowen, “The History of Remembered Innovation”; and
Cook, “At the Borders of Musical Identity.” See also Peter Johnson, “Play School,”
The Musical Times (June 1995):
275–77, and the ensuing, rather heated scholarly exchange between Jonathan Dunsby
and Peter Johnson, The Musical Times (January 1997): 12–17, (August 1997): 4–11,
(October 1997): 2, (January 1998): 2. Much has also been written on this subject
by Anglo-American philosophers specializing in aesthetics. See especially Peter Kivy,
Authenticities: Philosophical Reflections on Musical Performance (Ithaca:
Cornell University Press, 1995); Lydia Goehr, “Conflicting Ideals of Performance
Perfection in an Imperfect Practice,” in The Quest for Voice: On Music, Politics,
and the Limits of Philosophy, 132–73 (Berkeley: University of California Press,
1998).
Return to text
26. Early research on Gestalt phenomena, including the
work of Christian von Ehrenfels
and Alexius Meinong, was largely speculative. The Berlin school (consisting of Max
Wertheimer, Kurt Koffka, and Wolfgang Köhler, all of whom were students of Carl
Stumpf) is generally regarded to have initiated Gestalt psychology as a scientific
movement, but nevertheless shared the earlier scholars’ interest in aesthetics.
Gestalt psychology is second only to transformational linguistics in its influence
on GTTM.
Return to text
27. Mitchell G. Ash, Gestalt Psychology in German Culture, 1890–1967: Holism and
the Quest for Objectivity (Cambridge: Cambridge University Press, 1995), 1.
Return to text
28. Max Wertheimer, “Untersuchungen zur Lehre von der Gestalt, I,” Psychologische
Forschung 1 (1922): 47–58, condensed and translated as “The General Theoretical
Situation,” in A Source Book of Gestalt Psychology, ed. and trans. Willis D. Ellis,
12–16 (New York: Humanities Press, 1967).
Return to text
29. Kurt Koffka, Principles of Gestalt Psychology (London: Routledge and Kegan
Paul, 1935), 110, 171. See also Wertheimer, “Untersuchungen zur Lehre von der
Gestalt, II,” Psychologische Forschung 4 (1923): 301–50.
Return to text
30. GTTM, 304.
Return to text
31. P. Kruse and M. Stadler, eds., Ambiguity in Mind and Nature: Multistable Cognitive
Phenomena (Berlin: Springer Verlag, 1995): (a) 58, (f) 9, (g) 8. (d–e): Koffka,
Principles of Gestalt Psychology,
195.
Return to text
32. See L. H. Shaffer, “Timing in Solo and Duet Piano
Performances,”
Quarterly Journal
of Experimental Psychology 36A (1984): 577–95; Alf Gabrielsson, “The Performance
of Music,” in The Psychology of Music, 2nd ed., ed. Diana Deutsch,
501–602 (San
Diego: Academic Press, 1999).
Return to text
33. An index of acronyms is included as Appendix 4.
Return to text
34. Lerdahl and Jackendoff were among the first theorists to describe beats not
as sounding events, but instead as points in time inferred from the acoustic signal.
See GTTM, 18; Kramer, The Time of Music, 82, 97.
Return to text
35. GTTM, 28. The annotations indicating metric and hypermetric levels
are mine.
Return to text
36. Noam Chomsky, Syntactic Structures (The Hague: Mouton, 1957).
Return to text
37. See GTTM, 9.
Return to text
38. Ibid., 21–2.
Return to text
39. For a review of this controversy, see Sadie, ed.,
The New Grove, 2nd ed., s.v. “Rhythm: Current
Rhythm Research,” by Justin London.
Return to text
40. GTTM, 24, annotated with beat labels in the form “measure.beat”.
Return to text
41. These two readings are informed by Andrew Imbrie, “‘Extra’ Measures and
Metrical Ambiguity in Beethoven,” in Beethoven Studies, ed. Alan Tyson (New York: Norton,
1973), 45–66. Imbrie uses the terms “conservative” and “radical,” respectively,
for these types of hypermetric shifts.
Return to text
42. GTTM, 25.
Return to text
43. The depth and regularity of hypermeter are
controversial issues. Jonathan Kramer, for example, argues that irregularities
involving the addition or deletion of weak beats need not cause hypermeter to be
attenuated. See Kramer, The Time of Music, 98–102.
Return to text
44. George Hartmann proposed that “eidotropy” is a better translation of the word
“Prägnanz,” as it was used by the Gestalt theorists, than “precision.” Eidotropy
is the tendency of an image or representation to become typical or conventional.
See Hartmann, Gestalt Psychology: A Survey of Facts and Principles (New York:
The Ronald Press, 1935), 48.
Return to text
45. GTTM, 70.
Return to text
46. Transformation plays a much larger role in generative
linguistics than in
GTTM. The distinction is touched upon in GTTM, 62.
Return to text
47. See especially GTTM, 60–61.
Return to text
48. Leonard Bernstein, The Unanswered Question: Six Talks at Harvard (Cambridge,
Mass.: Harvard University Press, 1976), 95–97.
Return to text
49. Leonard Bernstein, adaptation of Mozart, Symphony No.
40 in G Minor, K. 550, first movement, measures 1–24, in Leonard Bernstein at Harvard: The Norton Lectures,
vol. 2: “Musical Syntax,” side 3 (issued New York: CBS Masterworks BL 33019, 1974),
LP vinyl recording.
Return to text
50. See Caroline Palmer and Carol L. Krumhansl, “Mental Representations for Musical
Meter,” Journal of Experimental Psychology: Human Perception and Performance 16/4
(November 1990): 729–41. Further support for the notion that metrical memory is
distinct from pitch memory may be found in the following sources: D. J. Povel and
P. Essens, “Perception of Temporal Patterns,” Music Perception 2 (1985): 411–40;
C. Palmer and C. Q. Pfordresher, “From My Head to Your Ear: The Faces of Meter in
Performance and Perception,” in Proceedings of the Sixth International Conference
on Music Perception and Cognition, ed. C. Woods, et al., 1–9 (Keele, U.K.: Keele University,
2000).
Return to text
51. Jonathan Kramer uses the terms “extension” and
“contraction” for these processes. Kramer, The Time of Music, 102–3.
Return to text
52. See, e.g., Lerdahl and Jackendoff, “Reply to Peel and
Slawson,” 158–9: “The issue in any case is not
one of value but of how listeners organize musical surfaces.” See also Lerdahl,
“Cognitive Constraints on Compositional Systems,” in Generative Processes in
Music,
ed. Sloboda, 231–59.
Return to text
53. More recently, a consensus has emerged that formalism
can be divorced from idealism by considering the latter to be nothing more than
a useful fiction. This postmodern ideology has sometimes been referred to as
“provisional autonomy.” For a passionate defense of it, see Leo Treitler, “The Historiography of Music:
Issues of Past and Present,” in Rethinking Music, ed. Nicholas Cook and Mark Everist,
356–77 (Oxford: Oxford University Press, 1999), 358.
Return to text
54. I do not mean to imply that Gestalt psychology is free
of ideological baggage, but merely that it successfully evades the influence of
neo-Platonic idealism and the aesthetic tradition associated with it. Indeed,
the view that perceptual experience can be explained independently of
socio-historical factors is itself the product of a specifically modernist
socio-historical milieu. See Mitchell G. Ash, “The Academic Environment and the
Establishment of Experimental Psychology,” in Gestalt Psychology in German Culture, 1890–1967: Holism and
the Quest for Objectivity, 17–27 (Cambridge:
Cambridge University Press, 1995).
Return to text
55. In his influential publications in the 1930s, music
psychologist Carl E. Seashore conceived performance expression as departures
from a mechanically regular norm. See Seashore, Psychology of Music (New York: McGraw-Hill, 1938), 29–30. This approach
was later taken up at Uppsala by Ingmar Bengtsson and his colleagues, who coined
the term SYVAR. See Ingmar Bengtsson and Alf Gabrielsson, “Analysis and
Synthesis of Musical Rhythm,” in Studies of Music Performance, ed. Johann Sundberg, 27–59
(Stockholm: Royal Swedish Academy of Music, 1983).
Return to text
56. In this paper, I am adhering to Lerdahl and Jackendoff’s policy of theorizing
aspects of comprehensibility rather than aesthetics. See GTTM, 7–8, as well
as paragraph 5.3, below.
Return to text
57. I do not mean to suggest that performances are
entirely unambiguous in meaning, or that performers never introduce additional
ambiguities by their ironic handling of structures that seem unequivocal on the
basis of the score. Intriguing as such phenomena may be, I will instead focus on
situations in which performing nuances seem to eliminate, or at least mitigate,
some of the ambiguities found in scores.
Return to text
58. Lerdahl, “Atonal Prolongational Structure,” Contemporary Music Review 4 (1989),
73. See also GTTM, 108–9, for a preliminary discussion of the need to distinguish
between structural importance and surface salience.
Return to text
59. GTTM, 17–18.
Return to text
60. GTTM, 78.
Return to text
61. GTTM, 347–8.
Return to text
62. GTTM, 70.
Return to text
63. See John A. Sloboda, “The Communication of Musical Metre in Piano
Performance,” Quarterly Journal of Experimental Psychology 35A (1983):
377–96; idem, “Expressive Skill in Two Pianists: Metrical Communication in Real
and Simulated Performances,” Canadian Journal of Psychology 39/2 (1985):
273–93; Eric Clarke, “Structure and Expression in Rhythmic Performance,” in
Musical Structure and Cognition, ed. P.
Howell, I. Cross, and R. West (London: Academic Press, 1985), 209–37; Clarke,
“Generative Principles.”
Return to text
64. Sloboda found six types of cues that accounted for 82% of the statistically
significant differences in performers’ treatment of alternate metrical renderings
of a melody. These are summarized in Sloboda, “Expressive Skill in Two
Pianists,” 290–91. Sloboda used a metronome
in his experiment, which might account for the relatively insignificant appearance
of AMs in his study. Clarke did not use a metronome, and perhaps consequently, his
study reveals more convincing results pertaining to AMs. See especially Clarke,
“Generative Principles,” 11–14. It would seem that a further implication of Sloboda’s and Clarke’s studies
is that Lerdahl and Jackendoff’s omission of time signatures and barlines from their
analyses of MS is an unnecessary precaution. If the performer uses PM cues that
lie within the listener’s scope of experience, then the performance essentially
makes the time signatures and barlines audible. The only type of performance that
corresponds to their unmeasured notation would be a computer-generated mechanically
regular performance.
Return to text
65. Listeners vary greatly in their ability to decipher
performers’ metrical cues, including DMs and AMs, but these differences appear to be proportionate to the extent
of listeners’ musical experience. See Sloboda, “The Communication of Musical
Metre,” 393.
Return to text
66. Compare nos. 3 and 5 under the “General Discussion” in Sloboda,
“Expressive Skill in Two Pianists,” 290.
Also compare nos. 2 and 3 under the discussion of expressive timing in Clarke,
“Generative Principles,”
19.
Return to text
67. GTTM, 348. See also [6] Appendix 1.
Return to text
68. A. R. Halpern and C. I. Darwin, “Duration Discrimination in a Series of
Rhythmic Events,” Perception and Psychophysics 31/1 (1982): 86–89; E. Zwicker and H. Fastl,
“Just-Noticeable Sound Changes,” in Psychoacoustics: Facts and Models, 2nd ed.,
175–201 (Berlin: Springer-Verlag, 1999), 175–6.
Return to text
69. See J. Vos and R. A. Rasch, “The Perceptual Onset of Musical Tones,”
Perception and Psychophysics 29 (1981): 323–35; Bruno H. Repp, “Patterns of
Note Onset Asynchronies in Expressive Piano Performance,” Journal of the
Acoustical Society of America 100/6 (December 1996): 3917; Scott D. Lipscomb
and Donald Hodges, “Hearing and Music Perception,” in Handbook of Music
Psychology, ed. Donald Hodges, 83–132 (San Antonio,
Tex.: IMR Press, 1996), 113.
Return to text
70. English Chamber Orchestra conducted by Benjamin Britten (recorded Snape, U.K.,
May 1968; issued London: Decca 430 494–2, 1991), compact disc recording; Academy
of St. Martin-in-the-Fields conducted by Neville Marriner (recorded London [ca.
1970]; issued [n.p.]: Philips 6500 162, [1971]; reissued Netherlands: Philips 422
610–2, [1990]), compact disc recording; Columbia Symphony Orchestra conducted by
Bruno Walter (issued New York: Columbia MS 6869, [1966]), LP vinyl recording; Vienna
Philharmonic Orchestra conducted by Leonard Bernstein (recorded 1984; issued Hamburg:
Deutsche Grammophon 413 776–2, 1984), compact disc recording. I will refer to these
recordings as Mozart/Britten, Mozart/Marriner, Mozart/Walter, and Mozart/Bernstein.
Return to text
71. Note that both this rule and the rule for metrical
completion given in paragraph 4.8 apply specifically to duple-meter contexts.
Further transformational rules could readily be constructed to account for
similar phenomena in the context of a prevailing triple meter. According to Lerdahl and Jackendoff’s MWFR3, duple and triple meter
are the only allowable well-formed metrical structures in Western tonal music.
Return to text
72. See also paragraph 2.7, above. Like the authors of GTTM, I will refrain
from speculating on the temporality of the cognitive process of metrical transformation.
For a preliminary exploration of real-time cognitive processing of music, informed
by research on listeners’ parsing of language, see Ray Jackendoff, “Musical Parsing
and Musical Affect,” Music Perception 9/2 (Winter 1991): 199–230.
Return to text
73. See Appendix 2 for an explanation of the terms I use in reference to the quantitative performance analyses.
Return to text
74. According to the amplitude statistics, IOI 10.1 is louder than 11.1, although
the difference (0.24 dB) lies below the threshold of discrimination. This discrepancy
can be attributed to the fact that amplitude stats fail to differentiate between
the contributions of the melody and accompaniment. In this case, the lower strings
seem to be playing measure 10 more intensely than measure 11, probably because of local harmonic
tension and resolution. I would argue that the salient DM in the melody is more
relevant to a discussion of Walter’s MS interpretation. The accent at 13.1 also
seems to be confounded by this effect.
Return to text
75. See also MPR 2 (GTTM, 347), included in my
Appendix 1.
Return to text
76. Actually, 11.1 is a full 2.6 dB quieter than 10.1, but
this reflects only the net intensity, not the melodic accent. Sloboda and Clarke don’t propose timbre-related
PMs, no doubt largely because their subjects were pianists and the piano timbre
cannot normally be controlled independently of dynamic level. Sloboda and
Clarke also describe substitutions such as these. They identify some SYVARs
in different parameters of performance that project the same aspect of a metrical
interpretation. See especially Clarke, “Generative Principles,” 14; Sloboda,
“The Communication of Musical Metre,” 394; and Sloboda, “Expressive Skill in Two
Pianists,” 292.
Return to text
77. GTTM, 25.
Return to text
78. Ibid.
Return to text
79. Again, the intensity data here can be a bit
misleading. In all voices combined, 5.1 is louder than 3.1 by a margin of 0.8
dB, but this measure does not capture melodic accents.
Return to text
80. GTTM, 347. See also Appendix 1.
Return to text
81. Also note that this interpretation conflicts with the
score-based interpretation offered by Lerdahl and Jackendoff (my Example 14 [DjVu] [GIF]), in which 20.1 and presumably 14.1
are considered weak beats. While my interpretation of Britten’s recording is based
mainly on phenomenal accents, Lerdahl and Jackendoff’s interpretation of the score
is based on the effect of the structural accents articulated by the arrival of
dominant and tonic harmonies at measures 16 and 20, respectively. Because of the relative
obscurity of this hypermetrical level after measure 10, I would speculate that the choice
between these two possible MSE interpretations for this recording of the piece will
depend on whether the listener happens to be attending more closely to harmonic
cues or to PMs. As explained in the passage from GTTM quoted above (paragraph
3.2), both phenomenal and structural accents can serve as cues for the construction
of metrical accents. See also GTTM, 30–35.
Return to text
82. Note that this MSE comes very close to the one mentioned by Lerdahl and Jackendoff.
Marriner’s first hyperbeat occurs a measure later than the one shown in Example 14 [DjVu] [GIF], however, and a transformation at level H1 makes the MSE a two-beat rather than a three-beat hypermeasure at level H2.
Return to text
83. GTTM, 63.
Return to text
84. Palmer, “Mapping Musical Thought,” refers to the principles summarized in
Clarke, “Generative Principles,” but neither adopts nor refutes Clarke’s idea of considering GTTM an “input” to the generation
of a performance. Note also that Palmer does not explore the pianists’ hypermetric
interpretation, so the relationship between her findings and my study is rather
tangential. Nevertheless, Palmer clearly demonstrates a situation where the performer’s
conscious intentions have a marked effect on the perception of an ambiguous structure.
Return to text
85. See Noam Chomsky, Aspects of the Theory of Syntax (Cambridge, Mass.: MIT Press,
1965), 4.
Return to text
86. I should also mention that, although Lerdahl and Jackendoff attempt to transpose
the “competence/performance” dichotomy directly to music and to address only competence
in their theory, it should by now be clear that a sharp distinction between the
terms of this dichotomy is somewhat unconvinving in the case of music (or, for that
matter, any performing art). For example, musical competence includes, in addition
to the factors addressed in GTTM, an understanding of performers’ SYVARs,
and conversely musical performance often involves the clarification of ambiguous
musical structures. A full exploration of this problem, which goes much further
than nomenclature, would, no doubt, require a separate article.
Return to text
87. GTTM, 10; Lerdahl and Jackendoff, “Reply to
Peel and Slawson,” 147.
Return to text
88. See especially Palmer, “Mapping Musical Thought”; William E. Frederickson
and Christopher M. Johnson, “The Effect of Performer Use of Rubato on Listener
Perception of Tension in Mozart,” Psychomusicology 15 (1996): 78–86. Lerdahl’s more recent work on pitch
space, which is closely related to Prolongational Reduction, is widely discussed
in Music Perception 13/3 (Spring 1996), a special issue on musical tension that
includes much fodder for further performance-related research.
Return to text
89. This appendix includes all the rules pertaining to MS
in the Rules Index of
GTTM. See GTTM, 347–48. Also included are the new preference rules
and transformational rules that I am proposing, with paragraph references.
Return to text
90. Lerdahl and Jackendoff claim that all their MS rules except MWFR3 and MWFR4
apply to all musical traditions. Note that I have made no such claims with regard
to the performance-related rules, all of which I consider to be specific to the
Western art-music tradition.
Return to text
91. For example, José A. Bowen, “A Computer-Aided Study of
Conducting,” Computing in Musicology
9 (1993–94): 93–103.
Return to text
92. For example, Peter Johnson, “Performance and the Listening
Experience: Bach’s ‘Erbarme Dich,’” in Theory Into Practice: Composition, Performance, and the Listening Experience,
ed. Nicholas Cook, Peter Johnson, and Hans Zender, 68–84
(Leuven, Belgium: Leuven University Press, 1999).
Return to text
93. For example, Christopher M. Johnson, “The Performance of
Mozart: A Study of Rhythmic Timing by Skilled Musicians,” Psychomusicology 15 (1996), 90.
Return to text
94. My methodology for analyzing expressive timing is
based that of Bruno H. Repp.
See his “A Microcosm of Musical Expression: I. Quantitative Analysis of Pianists’
Timing in the Initial Measures of Chopin’s Etude in E Major,” Journal of the Acoustical
Society of America 104/2, part 1 (August 1998), 1087.
Return to text
95. Lipscomb and Hodges, “Hearing and Music Perception,” 114.
Return to text
96. Bruno H. Repp, “A Microcosm of Musical Expression: II. Quantitative Analysis
of Pianists’ Dynamics in the Initial Measures of Chopin’s Etude in E Major,” Journal
of the Acoustical Society of America 105/3 (March 1999), 1974.
Return to text
97. Caroline Palmer and Judith C. Brown, “Investigation in
the Amplitude of Sounded Piano Tones,” Journal of the Acoustical Society of
America 90/1 (1991): 60–66.
Return to text
98. My methodology is similar to Bruno Repp’s, though perhaps less sophisticated.
See Repp, “Microcosm of Musical Expression: II,” 1973–74.
Return to text
Copyright Statement
Copyright © 2002 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason and Tahirih Motazedian, Editorial Assistants