Mapping the Geometries of Pitch-Class Set Similarity Measures via Multidimensional Scaling *
Art Samplaski
KEYWORDS: pitch-class set theory, similarity measures, atonal music, numerical visualization, multidimensional scaling, IcVSIM, ISIM2, ANGLE, RECREL, AMEMB2, ATMEMB
ABSTRACT: A numerical visualization technique called multidimensional scaling (MDS) was applied to the matrices of (dis)similarity ratings from six pitch-class set (pcset) similarity functions to see what types of constructs they actually measure. Three functions that use the interval-class vector (icv) for their computations (Scott and Isaacson’s ANGLE, Isaacson’s IcVSIM and ISIM2) and three that use subset imbedding (Castrén’s RECREL, Rahn’s ATMEMB and AMEMB2) were studied. The ratings of these functions for all trichords, tetrachords, and pentachords (under Tn/I-equivalence) were examined; ratings for each cardinality of set-class separately as well as contiguously grouped together (3+4, 4+5, 3+4+5) were studied. Four-dimensional geometric solutions were found for the icv-based measures while five-dimensional solutions were found for the subset-based measures, based on goodness-of-fit analysis. The configurations show one dimension clearly interpretable as diatonicism vs. chromaticism; other dimensions indicate oppositions such as ”whole-tone” vs. ”anti-wholetone” or ic3- vs. 016-saturation. Still other dimensions are less clear as to good interpretations. The overall results are generally consistent with the idea that these functions all measure constructs relating to familiar scales (diatonic, hexatonic, octatonic, etc.). The results are also compared with several systems of pcset genera. ISIM2 was found to be inconsistent with itself in terms of the geometries it produced. Several set-classes had coordinates near zero along various dimensions in the derived configurations, indicating that in a formal quantitative sense they do not possess the corresponding musical properties being measured; this may raise questions concerning the relative aesthetic worth of some such set-classes.
Copyright © 2005 Society for Music Theory
[1] Over thirty years after the publication of Allen Forte’s The Structure of Atonal Music (Forte 1973), music theorists working with pitch-class sets (henceforth, pcsets) still face a basic problem: how to assess the degree to which two set-classes are similar to each other. A variety of similarity measures have been proposed over the years, and arguments about the merits of these measures now occupy a number of journal pages.(1) Some fundamental questions remain unresolved by this discussion, however. First, what constitutes a “really good” measure of pcset similarity, one that mirrors our “musical intuitions”? Second, for the existing similarity measures, just precisely what musical properties are they measuring?
[2] Attempts to address the former question head-on will get bogged down in arguments of philosophy, epistemology, and aesthetics, because the term “pcset similarity” as used in the vast majority of the literature has ultimately remained vague and nebulous--while we certainly have some intuitive notion of what we mean by the term, we have not expressed clearly what sorts of properties are involved.(2) By contrast, the latter question is both aesthetically neutral--it is, as Sgt. Joe Friday would say, a case of “Just the facts, ma’am”--and readily amenable to analysis. Furthermore, once we have a detailed answer to it, we will be in a much better position to work on the former question. In other words, once we understand what specific musical constructs are actually being measured by various “similarity measures,” we will have a basis for discussing whether those constructs are relevant to our heretofore intuitive concept of “pcset similarity,” and whether other constructs should be included in a list of similarity criteria, or even replace some or all of those being rated by existing measures.
[3] Some similarity measures--those that yield ratings for all possible comparisons, including between set-classes of different cardinality--generate tremendous amounts of data. Humans, however, are (perhaps fortunately) particularly ill-evolved to comprehend massive tables of numbers. This implies that applying numerical visualization techniques to the resulting data would be highly beneficial--to paraphrase the adage, a picture is worth a thousand data points. Such techniques have been developed over the last forty years in a family of computational methods called multidimensional scaling (MDS) and cluster analysis (CA); with computing power now ludicrously cheap, it makes sense to apply them to this problem.(3)
[4] Some, intimately familiar with various similarity measures and the ratings they produce through years of working with them, might wonder, “Why bother? Didn’t Scott and Isaacson (1998) show that most similarity measures are derivable from each other? And as such, don’t they all necessarily measure the same things? After all, the paper gives a table (page 117) showing high correlations between various measures’ ratings.” There are several responses to this. First and foremost, Scott and Isaacson did not show how to derive all then-existing similarity measures from each other. It is in fact possible that some cannot be so derived, e.g., it is difficult to conceive how one might derive Castrén’s (1994) highly recursive RECREL from a non-recursive measure. Such other measures might well rate entirely different similarity factors. Second, for those measures that were co-derivable, the transformations involved are non-linear; and as the burgeoning field of dynamical systems theory can attest, even simple non-linear transformations can generate substantially differing results. As a trivial example, the functions y = x, y = SQRT(x), and y = x2 yield values that are highly correlated, yet their plots look quite different.(4) Without visualizing the graphs but only looking at the correlations, this would not be apparent.
[5] In fact, correlations (as single, all-subsuming numbers for pairs of measures) do nothing to show what constructs might underlie the ratings being produced. For example, the measures “number of steel-reinforced girders in a skyscraper S” and “square footage of office space in a skyscraper S” do not appear prima facie to have anything to do with each other; yet they will always have a high positive correlation because they are both functions of the total volume of a skyscraper. The nature of such underlying constructs and their relationships to the “surface features” being measured might be extremely subtle and non-obvious. Geometric visualization and similar techniques can help us tease out underlying multiple components of similarity, and aid us in deciding whether we could simplify our models by deriving some factors from others.(5) So, we might find that RECREL measures factors A, B, and C while some nonrecursive measure rates factors B and D; this in turn would suggest investigating whether factor D is some function of A or C, or whether all three are expressible in terms of factor E. At the least, we could discuss explicitly the relative worth of all those factors for measuring pcset similarity.
[6] Finally, geometric visualization allows a “reality check” for similarity measures: there might be problems with a measure’s numerical ratings that are not evident from inspection of them, or even from the measure’s verbal description. In fact, I will show that there is at least one similarity measure that fails to be self-consistent in its resulting geometries across various domains, even though its raw numerical ratings are highly correlated with the ratings of other measures that are geometrically self-consistent.
[7] The techniques of MDS/CA are likely unfamiliar to most music theorists. Therefore, in the first part of this article (paragraphs 8-23) I provide a brief and as non-technical as possible overview of several types of MDS/CA and some of the issues involved in their use.(6) The overview is generic, so readers wishing for specific discussion about musical issues may skim or skip it at first, returning only when they have methodological questions about use of the method in a musical situation. In the second part (paragraphs 24-53), I apply MDS to six pcset similarity functions’ ratings for trichords through pentachords, to see what geometric structures they yield (the nouns “function” and “measure” henceforth will be considered interchangeable). Since my purpose here is simply to show what these functions measure and not to investigate why they do so, I shall not attempt any analysis of the underlying mathematics.(7) In the final section (paragraphs 54 ff.) I compare the MDS results with some proposed systems of pcset genera, and discuss some implications as to whether the factors measured by these functions “match up with our musical intuitions.” As part of that discussion, the MDS results raise a potentially controversial question: perhaps the creed that “all set-classes are created equal(lly interesting musically)” is false.
MDS
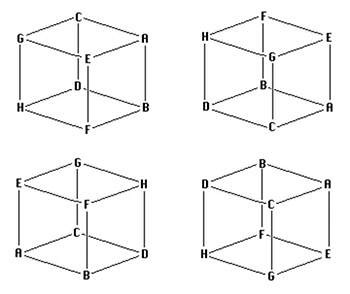
[8] The basic idea behind MDS is very simple. Consider a map of a region with several cities marked on it. If the map is of reasonable quality, it is easy to derive from it the inter-city distance matrix, the set of “as the crow flies” distances between all pairs of cities on the map. (Some readers may already be thinking, what about the curvature of the earth? This is an excellent question, and will be discussed shortly.) The reverse problem--given an inter-city distance matrix, derive the relative locations of the cities--is rather more difficult. MDS is simply a numerical technique to solve this problem: the matrix is fed to a computer program that returns a plot of the relative positions of the cities and/or a set of coordinates for them. In general, we have a set of objects of analytical interest for which we have obtained ratings of relative distance or similarity for all possible pairs;(8) an MDS analysis will yield a geometric configuration of the objects in some abstract (psychological) space, and interpretation of the dimensions of the resulting configuration is up to the researcher. (In the above mileage exercise, such interpretation would be trivial--we would simply need to find the north-south vs. east-west axes--but in general it is more complex.) Note that besides the obvious question of what the dimensions mean (tall-short? bright-dark? etc.), the researcher may have to consider how the configuration is oriented with respect to a pre-existing model they might be testing, since some types of MDS are result-invariant with respect to translation, rotation, and reflection about axes. Figure 1 illustrates this point: all four cubes are the same configuration, but rotated or flipped around one or more axes. If the origins of the coordinate systems are located in the centers of the cubes, the objects in the different setups might appear to have very different coordinates; yet the relationship between them all is clearly invariant.
Table 1. (Very rough) estimated distances in miles between cities in New York State
(click to enlarge)
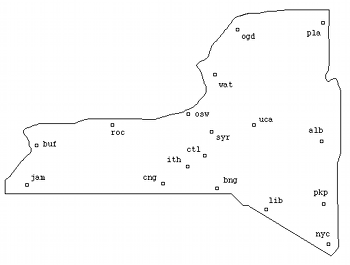
Figure 2a. Map of NY cities listed in Table 1
(click to enlarge)
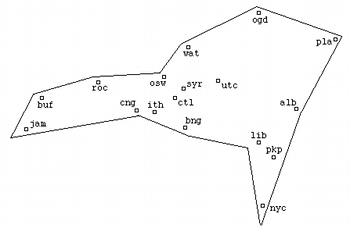
Figure 2b. Derived MDS configuration from data in Table 1
(click to enlarge)
[9] As a simple application of MDS, consider Table 1, which shows estimated distances in miles between a number of cities in New York State, derived from the American Automobile Association’s “Driving Distances” map for the state. (Figure 2a is a hand-drawn plot of their approximate locations.) There is a very large amount of noise (errors) in the table. Only a few of the cities have directly listed driving distances on the AAA map so many of the numbers are extrapolations, or, in some cases, complete guesswork--in particular, nothing remotely resembling a straight-line drive exists from Ogdensburg and Plattsburgh, in the extreme north of the state, to nearly any of the other cities in the table. Even those values listed on the AAA map are for driving distances, and so may not be straight-line. Given the all-important computing maxim of “Garbage In, Garbage Out,” we might well expect that this exercise in geographia speculativa should result in nothing like reality. Nonetheless, the resulting MDS configuration (Figure 2b) shows a recognizable if distorted plot of the various city locations. (The outline of the state was hand-drawn in afterwards.)
[10] A derived geometric configuration may be surprising, given the physical makeup of the objects being investigated. For example, in an MDS analysis of color similarity data originally obtained by Ekman (1954) the stimuli varied along exactly one dimension--the wavelengths of the lights for the colors--yet the program recovered the familiar two-dimensional structure of the color wheel. Researchers should thus be prepared to see more complex structure in the psychological space than they might think present given the stimuli structure. One example in music is the well-known result of Krumhansl and Kessler (1982), which in essence verified Schoenberg’s (1954) chart of key regions: the configuration of the distances between musical keys was seen to lie on a torus (donut-shape), a geometry that had been proposed by several other writers throughout history. The torus was in a space of four dimensions, not three, however;(9) so our cognitive structuring of music is more subtle than we might believe at first.
[11] The concept of MDS
dates to the 1930s, but it was only with a paper by Shepard (1962) and two
papers by Kruskal (1964a, 1964b) that a practical numerical technique was
described. This method, called nonmetric MDS for reasons that do not concern us,
assumes that the distance or proximity values of the matrix are directly related
by some unknown function to distances between the objects in some underlying
abstract N-dimensional Euclidean space, whose distance metric is the generalized
version of the formula familiar from Cartesian geometry, SQRT(x2 + y2 + z2 +
[12] Four broad issues arise. First, how do we determine the best dimensionality for a solution? Second, since in nearly all practical cases we take data from multiple subjects--the rule of thumb is that one needs a minimum of 30 subjects for reliability--and average their matrices together before running an analysis, how might we account for idiosyncrasies in their ratings (different subjects might selectively attend more significantly to certain features in the stimuli, skewing their ratings)? Third, what if there are possible inherent underlying asymmetries between the stimuli? (An obvious instance in music: in a context of functional tonality I->V will be rated rather differently than V->I.) Fourth and ultimately most importantly, how many objects can we study at one time without causing undue stress and fatigue to the subjects from whom we are collecting data? While I do not wish to downplay unduly the seriousness of the latter three questions, they are irrelevant for our purposes since we are concerned with results from abstract functions rather than human subjects. I shall therefore give only the briefest discussion of them.
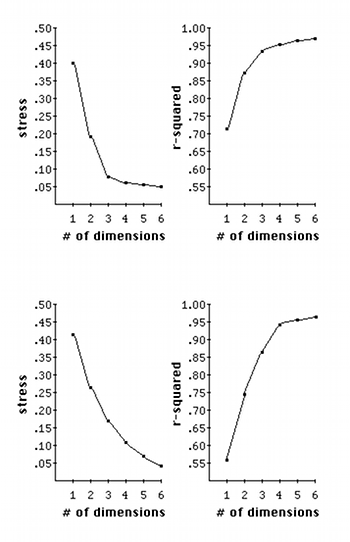
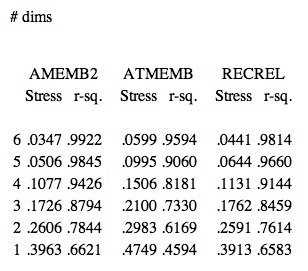
[13] To evaluate individual idiosyncrasies, there is an MDS model called INDSCAL that uses a set of multiple input matrices, one per subject, rather than a single averaged matrix. It permits finding a “group stimulus space” that shows a shared geometric configuration across all subjects, then gives a configuration of the different attentional weights that each subject gives per dimension to the stimuli. Thus, for a two-dimensional configuration a subject who attended equally to the features that correspond to the two dimensions would have their weight coordinates at (1.0, 1.0), while a subject who attended twice as much to the feature corresponding to the first dimension as to the second would have weight coordinates of (1.0, .5).
[14] There are a number of models for dealing with possible asymmetries underlying the data. They have a fair bit of diversity; a brief mention of one, called ASCAL, will illustrate the general idea. ASCAL assumes that the underlying distances between the stimuli are still in some Euclidean space; for each component in the Euclidean distance formula, however, there is a weighting factor assigned to that dimension for every stimulus. So, for a two-dimensional configuration with N stimuli, 4N free parameters are being estimated: two each for the actual coordinates of the stimuli, and two for the dimensional weightings of each stimulus.(12)
[15] The issue of the maximum number of objects that can be studied at one time is sometimes called “the data explosion problem.” Simply put, in order to analyze N objects, ratings must be collected from every subject on N2 pairs of objects. When taking data from humans, one quickly reaches a limit on the number of experimental trials they will be willing to endure (never mind satisfying committees that vett proposed experiments in terms of nationally-mandated guidelines for the ethical treatment of subjects). While there are ways to mitigate the resulting cognitive (and, eventually, physical) fatigue--breaking up data collection into multiple short sessions, and a higher rate of payment for subjects’ time per session--these only work so far. Such limits can be overcome a little more by some indirect methods (having each subject rate only a portion of the total number of pairs is one possibility), but then other types of limits (finding a sufficiently large pool of subjects, and obtaining sufficient funds to pay them all) come into play. Computers, fortunately, do not complain when asked to perform a few billion extra calculations, so the only way data explosion affects us is the limits of available software.
[16] In assessing the proper dimensionality for a solution, it is important to minimize the number of dimensions, both for visualization purposes and for parsimony of explanation: why use three dimensions if two tell us almost everything of interest? If we add too many dimensions, there is eventually too much “wiggle room” within which to fit a solution and the algorithm can no longer derive a unique one.(13) In most cases, long before this situation is reached we already hit a point where we are getting insufficient “bang for the buck” to justify the added complexity.
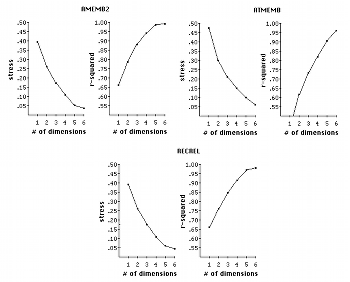
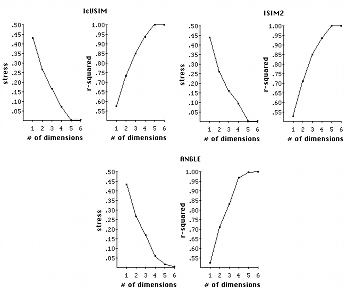
[17] Standard MDS unfortunately contains no test of statistical significance to evaluate whether adding one more dimension will give usefully more explanatory power. Some art in evaluation is thus needed. For a solution of a given dimensionality, we obtain two values: the stress factor mentioned earlier, and the percentage of the variability of the data being explained by the solution, a factor called “r-squared” (notated as r2). One needs to plot the stress and r2 values for solutions of several dimensionalities and look for “elbows” (inflection points) in the plots. If an elbow exists, then by and large the higher-dimensional solutions are not giving significant additional explanation--the plot suddenly flattens out. Figure 3 shows two examples of this. In the upper pair of plots stress drops precipitously from one to three dimensions then basically levels off, indicating that nothing more is being gained at higher dimensions. In the lower pair, the stress plot has no obvious elbow but the r2 plot does have one, indicating that for this data a 4-D solution is probably best. One must hope that one or both plots will have such elbows present. As another rule of thumb, to make reliable judgments about a configuration the number of objects should be at least 3-4 times greater than the highest anticipated dimensionality. If the number of objects is much below this factor, then there will likely be too few constraints on the configuration for it to be reliable.(14)
[18] A poor fit can be caused by several factors, notably by underlying asymmetries in the data. Other problems are the presence of exemplars or prototypes in the set of objects being evaluated--in the set [apple, banana, cherry, fruit, kiwi, orange, watermelon], “fruit” will be almost certainly be considered more similar to all the other objects than any other pair to each other(15)--or if the dimensions involved are “highly separable,” i.e., have little or nothing to do with each other.(16) The problem of separable dimensions in particular led Tversky and others (Tversky 1977; Tversky and Gati 1982; Tversky and Hutchinson 1986) to propose a different way to represent structure in psychological data, called cluster analysis (CA). There is a family of CA models, but they all work similarly: given a proximity or distance matrix, some method is used to pick the pair of objects most like each other, group them into a single cluster, and derive a new reduced matrix. When the process is finished, the objects will be grouped into a binary tree structure (exactly two branches descend from each node, and the objects are “leaves” at the termini of the final branches), where the distance between any pair of objects is related to the length of the path along the branches separating them.
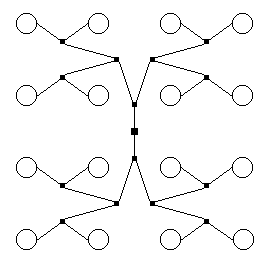
[19] Cluster analysis is certainly more appropriate than MDS for certain situations (e.g., when highly separable dimensions are involved); and even when MDS works for a given situation, CA can aid the researcher in interpreting an otherwise obscure set of dimensions. On the other hand, there are situations where CA gives extremely bad fits. If, for example, the underlying data structure forms a grid, any type of CA will yield a really bad fit since the only way to “move” between objects in the configuration is to traverse the tree connecting them. Figure 4 shows an instance of this--visually, each object (open circle) is equidistant from its vertical or horizontal neighbors, but not at all along the tree (the filled squares are extra nodes generated by the tree-building procedure). The bottom line is, the researcher must be careful and explore many possibilities.(17)
[20] A different type of issue can be termed “robustness”--whether changing the set of objects being compared alters the perceived/computed similarity between the original set of objects. Another example of cities on a map will illustrate. Take two distance matrices, one for just Toronto and its suburbs and the other for those plus various other cities across southern Ontario. If we run these two matrices through an MDS program and normalize the resulting configurations to each fit on an eight-by-ten color glossy photograph, the only change in the second configuration for the suburbs would be the percentage of area they occupied--they would still be at the same relative locations, with simply the scale changed. By contrast, the process of categorization and similarity judgment by humans is highly flexible and context-dependent. For example, consider in your own mind the similarities or differences in the set of animals [cat, cow, dog, moose]. Now consider the set [cat, cow, dog, moose, unicorn]: unicorns are large mammals like cows and moose, but mythical. Now consider instead the set [cat, cow, dog, moose, bonsai unicorn], where the bonsai unicorn looks just like its bigger counterpart but is the size of a chihuahua--does it now group closer to the small mammals? What about the set [cat, cow, dog, moose, turtle]? How about the set [cat, cow, dinosaur, dog, moose, small furry creature from Alpha Centauri, turtle, standard unicorn]? It is likely that your groupings may have altered rather considerably by the end.
[21] Suppose we are presented with two functions Q and R that each purport to measure distances in southern Ontario. We use them to build distance matrices of the two lists of cities above, and examine the resulting MDS configurations. For the first case (only Toronto + suburbs), Q and R yield geometries that agree with each other and with the atlas; R also agrees with the atlas for the larger dataset. In Q’s trans-Ontario configuration, however, some Toronto suburbs do not appear in their expected places: Scarborough (just east of the city) has migrated south and is sitting in downtown Buffalo, while Mississauga (immediately southwest of the city) has shifted eastwards some 200 km, into the middle of Lake Ontario. Geographical features such as cities are stationary (pacite Birnham Wood and James Blish’s Cities in Flight), so we would likely view Q’s usefulness as a distance metric with extreme skepticism, to say the least. It is in this sense of “yields consistent relative MDS geometries, save for scaling, regardless of surrounding context” that R is “robust” and Q is not. Given humans’ flexibility of similarity judgment, most MDS research is usually unconcerned with this issue: the flexibility and context-dependence is normally part of what is being investigated. This article, however, is examining formal, abstract functions, which do not (or, at least, should not) exhibit such subjectivity; it is therefore very much of importance.
[22] In the abstract universe of pcsets, there is no external reality check like an atlas--this is, after all, why we are developing similarity measures--but we can at least demand geometric self-consistency from our functions. If function S yields different geometries than function T and each function is self-consistent, that suggests they are measuring different musical constructs and the situation warrants investigation. If on the other hand S behaves like function Q above, that strongly implies that we should not use it because there is no reason to have any faith in its ratings--all research on pcset similarity has (implicitly) assumed that pcsets are “stationary” objects. Note that it certainly should be possible, and perhaps highly desirable, to build a pcset similarity function that is context-sensitive in its calculations; but I am unaware that anyone has ever attempted to devise such a measure. In particular, none of the functions discussed in this essay incorporate context-dependence in their ratings. If we find a function that yields different relative locations of trichords if we consider trichords and tetrachords as a group vs. trichords in isolation, that is a serious red flag re the function. As mentioned in paragraph 6, it turns out that not all similarity measures pass this test.
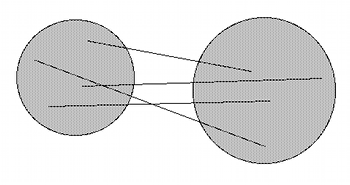
[23] The data obtained from humans in an MDS/CA study are inherently messy; this is why multiple subjects are needed to achieve reliability. Recently a different way to deal with this noisy data has been developed, called Probabilistic MDS (PMDS). Here it is still assumed that there is an underlying Euclidean geometry, but rather than being points in that space the objects are probability distributions like clouds. The centers of such clouds are what occur at the idealized object coordinates; but every similarity judgment is considered to be merely from somewhere within the cloud. (Such judgments of course have a higher probability of being from near the centers of the clouds, but this is not guaranteed.) Thus, each time a subject estimates the distance from object A to object B, their estimate will change (Figure 5); the extent to which the estimates vary is a function of how “spread out” the clouds are along each dimension--the technical term is the degree of variance of the stimuli.(18) A PMDS program can do calculations for several scenarios: when all objects are assumed to have the same degree of variance for all dimensions, when the variance is the same for all objects for any given dimension but can be different for different dimensions, etc. Because PMDS also gives the variance for each dimension in the derived configuration, it is able to do significance testing for different dimensionalities. The price for this increased power is of course much more intractable math;(19) PMDS is a technique still under development at this writing, and a present-day researcher should always run some non-probabilistic MDS model on their data as a reality check.
PCSETS
[24] Let us analyze some pcset similarity functions using MDS. Doing so yields two things. First, the resulting geometries will tell us something about what properties of pcsets the functions are measuring, since each dimension of the configurations involves different properties. Second, if the geometries produced by different functions match up save for rotation, translation, or reflection, then, given that such functions all purport to measure “pcset similarity” (whatever that is), it is reasonable to think that they are in fact either a) measuring the same constructs, whatever those might be, or b) measuring constructs that, while different, are themselves functions of some other underlying construct(s). For narrative simplicity, the above second item will be termed “measuring the same thing(s),” even though that phrase plays rather fast and loose with the situation.
[25] Only such functions as give distinct proximity/distance ratings can be so evaluated; measures like Forte’s (1973) Rn relations are binary so cannot generate a distance matrix for input. Other functions that yield multiple values but only permit comparisons between set-classes of the same cardinality, e.g., Teitelbaum’s (1965) s.i., while evaluable to some degree by MDS, are still not very attractive--there is no way to say that the results of comparing tetrachords have anything to do with the results of comparing heptachords, for example.
[26] For a reasonably-sized selection of functions I chose six, three of which--Scott and Isaacson’s (1998) ANGLE, and Isaacson’s (1990, 1992) IcVSIM and (1996) ISIM2--use interval-class vector (henceforth, icv) content for their calculations, and three--Castrén’s (1994) RECREL, and Rahn’s (1979–80) ATMEMB and AMEMB2--that use subset content.(20) Since RECREL uses Tn-rather than Tn/I-equivalence, only ratings between “-A” forms of asymmetrical set-classes (prime forms in the sense of Forte 1973) were used for this study. Due to possible reflections/rotations between configurations, “reference functions” are needed against which other functions in a category can be compared; ANGLE and RECREL were declared to be the references for their respective categories on the basis of personal aesthetics. The domain to be studied was limited to trichords through pentachords (a total of 3160 distinct set-class pairings), for two reasons. First, it was within the limits of available software. Second, for the icv-based measures the ratings of a set-class and its complement are not independent;(21)the simplest way to avoid any possible resultant systemic problems was to eliminate hexachords et al. from consideration.
Table 2. Correlations of raw data values among functions for all trichords through pentachords
(click to enlarge)
[27] Table 2 gives the correlation matrix for the raw ratings of these functions for this domain. The values are extremely high, suggesting that there is indeed a great deal of correspondence between whatever it is they measure; the notation “p<.001” is a measure of significance, meaning that there is a probability of less than one in a thousand that the observed result might have occurred by chance.(22)The negative signs on the correlations for ATMEMB and AMEMB2 vs. the other measures are not a cause for concern: those two functions rate similarity while the other four functions rate dissimilarity, so naturally the signs will be reversed. The absolute values of the rs and the corresponding p-values are the important things.
[28] By definition, there is no noise in this data: the ratings are exactly what the functions compute for a pair of set-classes. Stress values in the analyses are therefore inherent for the configurations involved, in the sense that there are irreducible ambiguities in the computed ratings. Also by definition, the ratings matrices are all symmetrical; we can thus use the simplest MDS model, which is result-invariant with respect to axial reflection and rotation. This allows us to realign the configurations for the non-reference functions with respect to those for the references in order to compare them. The matrix manipulation technique to do so is called Procrustes rotation; named after the villain of Greek mythology, it is an algorithm that transforms a matrix so as to most closely align it with a given target matrix of equal size. The details of this process are irrelevant.
[29] To examine the issue of robustness mentioned in paragraphs 20-22, the set-classes of each cardinality were analyzed in isolation as well as combinations of contiguous cardinalities. There were thus six datasets for each function. The following shorthand is used:
- cardinality 3 alone: 3x3 dataset (12 set-classes)
- cardinality 4 alone: 4x4 dataset (29 set-classes)
- cardinality 5 alone: 5x5 dataset (38 set-classes)
- cardinalities 3 and 4: 3x4 dataset (41 set-classes)
- cardinalities 4 and 5: 4x5 dataset (67 set-classes)
- cardinalities 3, 4, and 5: 3x5 dataset (79 set-classes)
These were analyzed using SPSS, one of the most widely available statistical packages.(23)It would be extraordinarily tedious (and in fact unnecessary) to examine in detail all six datasets for all six functions; instead, I shall discuss only the results for the 3x5 dataset for the two reference functions ANGLE and RECREL, since it will be easiest to interpret the dimensions due to the wide range of objects involved.(24)Even so, the results may seem somewhat lengthy; as a guide, the order of discussion is as follows. First, the appropriate dimensionalities for the derived configurations are determined (paragraphs 30-34); next, the ANGLE and RECREL configurations for the 3x5 dataset are examined in detail (paragraphs 35-42 and 43-48); third, those configurations are compared with the equivalent configurations for the other four functions via correlational analysis (paragraphs 49-51); finally, the robustness of the different functions for the various cardinalities is examined, also via correlations (paragraphs 52-53).
Dimensionality
[30] Four-dimensional solutions were obtained for the icv-based functions, while five-dimensional ones were found for the subset-based functions. For readers new to MDS, the decision process is given in some detail as illustration; those already familiar with MDS or who want to cut to the chase can skip to paragraph 35, although they should be aware that some peculiarities exist and will be mentioned later on.
Table 3. Stress and r2 values by function, 3x5 dataset
(click to enlarge)
Figure 6a. Stress/r2 plots for 3x5 dataset for subset-based functions
(click to enlarge)
Figure 6b. Stress/r2 plots for 3x5 dataset for icv-based functions
(click to enlarge)
Figure 7. Coordinate values and histogram for ANGLE ic1 vs. ic5 dimension, 3x5 dataset
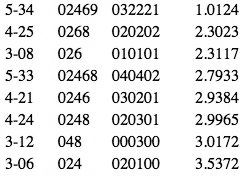
(click to enlarge and see the rest)
[31] Table 3 gives the stress and r2 values for different dimensionalities by function for the 3x5 dataset, since discussion will focus on it; Figures 6a and 6b plot these values for the subset-based and icv-based functions respectively. For RECREL, as we increase from two to six dimensions we see incremental improvements in r2 of .0845 (from 2-D to 3-D), .0685 (from 3-D to 4-D), .0516 (from 4-D to 5-D), and then a sudden drop to .0154 (from 5-D to 6-D). For ANGLE, as we go from two to five dimensions we see incremental improvements in r2 of .1206 (from 2-D to 3-D), .14 (from 3-D to 4-D), and then down to .0285 (from 4-D to 5-D). Those sudden drops in incremental improvement are the elbow points indicating optimal dimensionalities.
[32] There are several oddities in Table 3. For the icv-based functions, the incremental improvement in r2 increases in going from 3-D to 4-D vs. going from 2-D to 3-D. We thus have a set of “reverse elbows” at 3-D; these are apparent (albeit somewhat subtly) on the plots in Figure 6b. Also, the stress values suddenly drop to essentially zero and the r2 values jump up to 1.000 (meaning all variability in the data is explained) at five dimensions for IcVSIM and ISIM2; this phenomenon occurs for them in all except the 3x3 dataset. The latter situation is an absolute indicator of too many dimensions: there is no stress because there are insufficient constraints on the configurations. Meanwhile, reverse elbows usually indicate that a calculation became trapped in a local minimum, and that a configuration should be recomputed--one typically uses the configuration from the next higher dimensionality (minus the extra dimension) as an input seed. For these functions, however, doing so does not change things: something else is involved. The reason will be seen in a few paragraphs.
[33] Although the stress/r2 values for the other datasets have not been shown, those datasets still have an issue of reliability regarding the configurations for the 3x3 and 4x4 datasets due to the small number of data points involved; this must be considered in determining the proper dimensionality for them. It is in fact not possible to compute a 6-D solution for the 3x3 dataset because the number of parameters to be derived (72, 6 coordinates each for 12 set-classes) exceeds the number of data values (66, the number of similarity ratings). For the 3-D, 4-D, and 5-D solutions for that dataset, the numbers of parameters to be derived (36, 48, and 60) are still high compared to the number of data values, so those configurations are also questionable. For the 4x4 dataset, the 6-D solution also has a reliability issue (174 parameters vs. 406 data values). The incremental improvements in stress and r2 for both those datasets do mirror the patterns seen for the larger datasets, however. Since we cannot increase the number of objects in these datasets, we must assume that our decisions for appropriate dimensionality for the larger datasets carry over to these smaller ones.
[34] We are left with the prospect of examining four-and five-dimensional geometries. Visualization of more than three dimensions is typically difficult for humans;(25) furthermore, even if we were to examine only three dimensions’ worth of the configurations at a time, the pictures would be far too crowded at their centers to understand any structure involved. By definition of a Euclidean space, however, each dimension in the configurations is independent of the others. We can thus examine the ordering of set-classes along each dimension separately to interpret what that dimension represents.
ANGLE
[35] The order of dimensions produced by SPSS is arbitrary, so there is no need to adhere to it in the following discussion. Also, rather than repeatedly referring to “dimension one,” etc., I shall use my suggested interpretations for the dimensions as descriptive names. Thus, the phrase “the ic1/ic5 dimension” is a narrative shorthand for “the dimension to which I am assigning an interpretation of ‘an opposition of ic1-saturation vs. ic5-saturation’,” and so forth. For each dimension, the coordinates of the set-classes along the dimension are given plus a histogram for visualization. The units for the coordinates are also arbitrary, although they are on the same scale for all dimensions of a particular configuration.
[36] The most dramatic dimension has the easiest interpretation: ic1-saturation vs. ic5-saturation. The histogram in Figure 7 shows a symmetrical distribution, with [012], its direct supersets, and other ic1-dominant set-classes at one extreme, while [027] and other diatonic subsets are at the opposite end. Most striking, though, is the clustering near zero of 37 set-classes, with large gaps between it and the other groups.
[37] This huge cluster explains the oddities in the stress/r2 tables. In the typical case when a configuration is one or more dimensions beyond optimum, one finds that for some of the dimensions almost all of the coordinate values will be at or near zero. Such an occurrence provides an additional dimensionality check, since it usually indicates that we are learning too little additional information to warrant the extra dimension. At first glance this looks to have happened here.
[38] In reconsidering whether a 4-D solution is appropriate, several factors must be weighed. First, the stress and r2 values show a non-trivial incremental improvement from 3-D to 4-D, arguing that the fourth dimension in the solution is a real one. Second, 42 of the 79 set-classes have non-zero coordinates, and some of those coordinates are decidedly non-zero. If this were a “fake dimension” we would expect fewer non-zero coordinates, and expect those to be closer to zero instead of being clearly grouped towards the extremes. Third, this dimension has a clear and logical interpretation, whereas the situation in the 3-D solution (omitted for space considerations) is muddled--as mentioned in footnote 14, judgment calls are sometimes necessary. Finally, the 5-D solution for RECREL has an almost exact counterpart to this dimension, and its stress/r2 values showed no oddities. This last admittedly risks being an example of circular reasoning: if we are trying to determine whether these functions measure the same things, we should not use the results from one function to decide that the results of another are valid then go back to check what the former measures compared to the latter. I will argue in paragraph 48, however, that ic1-saturation vs. ic5-saturation is equivalent to [012]-saturation vs. [027]-saturation; if two different functions, one examining icv content and the other subset content, find these oppositions in their respective domains, then we should consider the result legitimate.
[39] The presence of certain set-classes in the near-zero clump may seem surprising. For example, 4-10 and 4-11, [0135] and [0235] respectively, are in the clump yet are both diatonic subsets. They do not, however, exhibit relative ic5-saturation. All of the set-classes in the clump have equal ic1 and ic5 content; the first few set-classes with significantly non-zero coordinates have ic1 content one more than ic5 content or vice versa; and the set-classes at the extremes have either zero ic5 or ic1 content while the value of the opposite is at least two, and have zero values for at least one other icv component. This dimension thus provides a graphic (in both senses of the word) example of how to quantitatively clarify one aspect of pcset similarity: what the terms “diatonic” and “chromatic” really signify, as measured by certain abstract functions.
Figure 8. Coordinate values and histogram for ANGLE 016 vs. ic3 dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 9. Coordinate values and histogram for ANGLE whole-tone vs. anti-wholetone dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 10. Coordinate values and histogram for ANGLE hexatonic vs. ic2 dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 13. Coordinate values and histogram for RECREL 024 vs. 016/036 dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 14. Coordinate values and histogram for RECREL 04/014 vs. 012/027 dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 15. Coordinate values and histogram for RECREL 015/04 vs. 036 dimension, 3x5 dataset
(click to enlarge and see the rest)
Figure 16. Coordinate values and histogram for RECREL 016/026 vs. anti-ic6 dimension, 3x5 dataset
(click to enlarge and see the rest)
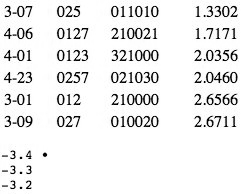
[40] The next dimension can be termed “016-saturation vs. ic3-saturation” or “even distribution around the pitch-chroma wheel vs. pitch-classes clumped at opposite sides of the chroma wheel.” At one extreme in the histogram in Figure 8 are [016] and [0167], followed closely by other sets with imbedded 016s, such as [0156]. Any other similar set-classes will necessarily increase the amount of ic5 and ic1 simultaneously; thus, set-classes like [015] also group at this end of the dimension. At the other end are the diminished triad and the diminished seventh chord. Because the addition of any other pitch-classes would add ics other than ic3/ic6, there is a wide gap between those two set-classes and the others at this end, and the distribution along this dimension is asymmetrical. There is still a fairly large clump of set-classes at near-zero coordinates, although less so than in the ic1/ic5 dimension (only 25 of 79 here). This also contributes to the oddities of the stress/r2 table.
[41] The third dimension is characterizable as “whole-toneness vs. anti-whole toneness.” The distribution histogram in Figure 9 is again asymmetrical. At one extreme are the seven subsets of the whole-tone scale, followed by a large gap; at the other extreme, we again see [016] and [0167], also with a wide gap between them and the next set-classes; but among that group are [036] and [0369]. Evidently for ANGLE, if “whole-tone” means “saturation in ic2 and ic4 together,” then “anti-wholetone” can mean either ic3- or 016-saturation.
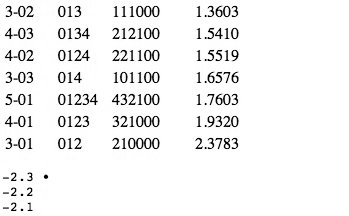
[42] The last dimension in the ANGLE configuration has the most even distribution and is harder to interpret. At the positive end of the histogram in Figure 10 are hexatonic subsets--the augmented triad and its supersets [0148] and [01458]--followed by other pcsets with relatively high ic4-content and zero or minimal ic2- and ic6-content. In contrast, the negative extreme has a seemingly confusing mix of whole-tone ([024], [0246]), diatonic ([0257]) and chromatic or near-chromatic ([013], [0123]) set-classes. The hexatonic scale has the characteristic “ic4-saturation at the expense of ic2 and ic6 content,” so the best interpretation for the negative end of the dimension appears to be the opposite, i.e., “attempts at ic2-saturation at the expense of ic4 and/or ic6.” Since it is impossible to have any ic2 content in set-classes of cardinality three or higher without having some other ics present, we get the “mixed bag” of set-classes here.
RECREL
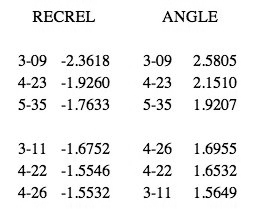
[43] As mentioned, RECREL has an almost exact counterpart to ANGLE’s ic1 vs. ic5 dimension--here better labeled “012-saturation vs. 027-saturation.” The coordinates and histogram in Figure 11 are somewhat different, but the units are arbitrary anyway. The signs are backwards, but they are also arbitrary; by reversing one configuration and comparing the set-class orderings, as shown in Figure 12, it is clear how closely the two match up. The three set-classes at the extremes match in order; there follows a group of three set-classes whose orders almost match; a single set-class that matches; another group of three that almost match up; then a group of eleven; and then the near-zero cluster.
Figure 11. Coordinate values and histogram for RECREL 012 vs. 027 dimension, 3x5 dataset (click to enlarge and see the rest) | Figure 12. Correspondence of set-class orderings between RECREL and ANGLE diatonic/chromatic dimensions, 3x5 dataset (click to enlarge and see the rest) |
[44] The next dimension corresponds to ANGLE’s “whole-tone vs. anti-whole tone” dimension, although not quite so exactly. At the positive extreme of the histogram in Figure 13 are the seven whole-tone subsets, just as for ANGLE; beyond those, however, the orderings diverge somewhat. For the ANGLE configuration, general high ic4 content seemed to come next; here, high 024-content apparently takes precedence. This end of the dimension thus seems to be more strictly “024-saturation.” At the negative end, the three set-classes at the extreme also match, but after that set-classes with higher 016- than 036-content seem to take slight precedence: there are three set-classes before we reach the diminished triad and seventh chord, vs. one for ANGLE. A full interpretation therefore appears to be “024-saturation vs. 016-/036-saturation.”
[45] The next dimension bears some resemblance to ANGLE’s “hexatonic vs. ic2” dimension, but again has differences. At the negative end in the histogram of Figure 14 are the augmented triad and [0148], as for ANGLE. The augmented triad is much more of an outlier here, however; and after those two set-classes the orderings diverge. Here, various pcsets with high 014-content follow, although the diatonic/diminished triads and the diminished seventh chord also appear. The set-classes at the opposite end of this dimension all lack ic4 content, but the pairings that occur are striking: [012] and [027] are farthest out, followed by their immediate supersets [0123] and [0257]; a bit further in are the next level of supersets, [01234] and [02479]. This dimension thus appears to be “04/014-saturation vs. 012/027-saturation.”
[46] The remaining two dimensions correspond much less if at all to dimensions in the ANGLE configuration; this is not surprising since this is a five-dimensional solution instead of a four-dimensional one. As shown in Figure 15, the next dimension has the diminished triad and seventh chord at its positive extreme, leading to an interpretation of “036-content.” The negative end would appear to have “015-content” as its primary characteristic, since [015] and [0156] are the two set-classes at that extreme, and [015] is very much an outlier. The third set-class in is [048], however, and other set-classes with high ic4-content, such as [0148], take precedence over those with 015-content. ([014] has a near-zero coordinate, so this is not about 014-content.) The distribution along the histogram is much more even than in the previous dimensions; this may indicate some sort of conflict between these two characteristics, so that one does not take clear precedence after the extremum. This dimension is thus apparently “015/04-content vs. 036-content.”
[47] The final dimension for RECREL is the most difficult to understand, and a good, solid interpretation in terms of trichord content is elusive. There are no clear outliers at the negative extreme, and the distribution on the histogram in Figure 16 is very even. There is again a potpourri of set-classes; their only common characteristic is a lack of ic6. At the positive end, we have various set-classes with ic6-content and no ic3-content. The two most extreme set-classes are [016] and its direct superset [0167], followed by [026] and its direct superset [0268]; but there is no real separation between the latter pair and the rest of the pack. The diminished triad and seventh chord do occur near this end and they of course have high ic3 content; but they also have relatively high ic6 content. The best interpretation for this dimension thus appears to be “016/026-content at the expense of ic3 vs. depletion of ic6.” Note that this is not an analogue to ANGLE’s 016/ic3 dimension because [036] and [0369] were at the opposite extreme from [016]/[0167] in the latter.
[48] If we consider those dimensions where ANGLE and RECREL appear to give the same results, we see situations where ic-saturation and subset-saturation are in a sense equivalent. In other words, if we try to maximize ic1, we perforce will be led to [012], [0123], etc.; a subset-based measure that views 012-saturation as one aspect of pcset similarity must then yield the same sort of results for that dimension, and a similar line of reasoning applies to ic5/027-content. This says nothing about why R RECREL views 012-content as one aspect of similarity while not viewing, e.g., 013-content (which would lead towards an “octatonic vs. whatever” dimension) as another aspect; it merely explains why it should yield somewhat similar factors as an icv-based function in some situations.
The Other Functions
[49] As noted in paragraph 28, to analyze the other functions for the 3x5 dataset we first apply Procrustes rotation to their configurations so as to most closely align them with those of the reference functions. We then examine correlations of the dimensional coordinates between the two triples of functions. If IcVSIM and ISIM2 measure the same things as ANGLE, corresponding dimensions (e.g., dimension 1 for ANGLE and IcVSIM--we do not care here whether this is the ic1/ic5 dimension or whatever) should be highly correlated while non-corresponding dimensions (dimension 2 for ANGLE vs. dimension 3 for IcVSIM) should have little or no correlation; the same situation should hold true for RECREL, ATMEMB and AMEMB2.(26) It is then only necessary to consider any dimensions in the other functions where this does not hold.
Table 4. Correlations between dimensions of icv-based functions and between dimensions of subset-based functions for 3x5 dataset
(click to enlarge and see the rest)
[50] Table 4 gives the correlations for all dimensions of the 4-D solutions for the icv-based functions, and likewise for the 5-D solutions for the subset-based measures, for the 3x5 dataset. The subset-based functions show the expected situation if these functions all measure the same things: values on the main diagonal (corresponding dimensions) are all extremely high, while the other values are all very low. Recall that the notation “p<.001” means a probability of less than one in a thousand that the observed result might have occurred by chance; conversely, “p>>.05” says there is well over a 5% probability that the results are due to chance.(27)
[51] The same situation holds for ANGLE and IcVSIM, but there are exceptions for ISIM2: ANGLE/IcVSIM dimensions two (the 016 vs. ic3 dimension) have significant negative correlations with ISIM2 dimension three (its hexatonic vs. ic2 dimension), at p<.01 each; and ANGLE dimension three (hexatonic vs. ic2) has a significant negative correlation with ISIM2 dimension two (016 vs. ic3) at p<.05. (IcVSIM’s hexatonic-vs.-ic2 and ISIM2’s 016-vs.-ic3 dimensions “just miss” being correlated at p<.05.) Also, for some pairs of corresponding dimensions in some of the other datasets (omitted for space), ISIM2 has essentially no correlation to ANGLE and IcVSIM (rs are near-zero). This would suggest that ISIM2 measures something different than the latter two functions and should be examined in detail; however, ISIM2 turns out to be non-robust. As a result, it is pointless to compare it with the other icv-based functions.
Robustness
[52] Here, recall, the concern is the self-consistency of a function’s set-class orderings along each dimension across several datasets. For example, trichords occur in the 3x3, 3x4, and 3x5 datasets. The coordinates for trichords in the 3x4 and 3x5 configurations must be extracted from them and compared to the coordinates for the 3x3 dataset. This means subjecting the extracted sub-configurations to Procrustes rotation with the 3x3 configuration as target (because configurations for the other datasets might be reflected and/or rotated about axes), then computing correlations for corresponding dimensions for the various datasets; an equivalent procedure applies for tetrachords and pentachords. If the coordinates for set-classes of a cardinality for a particular dimension are highly correlated across all the datasets involved, then we can conclude that the function is stable and robust for that cardinality with respect to that dimension--the set-classes occur in approximately the same relative ordering regardless of where set-classes of other cardinalities occur along that dimension.(28)
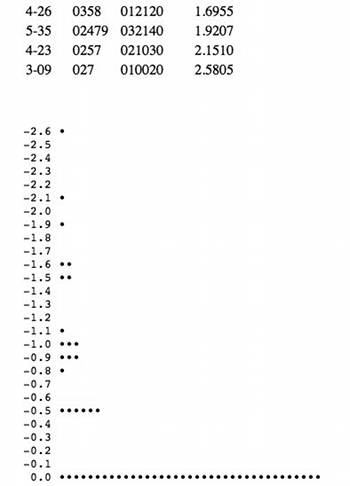
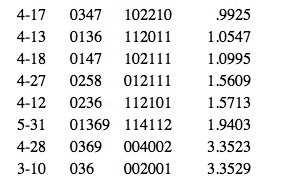
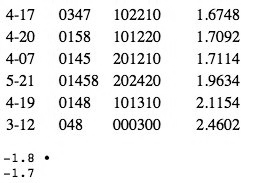
[53] All of the functions except ISIM2 are extremely robust for all dimensions. Except for two correlations for AMEMB2 at .904 and .915, all rs for the other five functions are greater than .96, and nearly all are greater than .99--p<.001 for all cases. By contrast, ISIM2 fails to be robust at p<.05 in several cases. It is not necessary for us to analyze these inconsistencies; that they exist already renders the function unusable for this essay’s purposes. For those wishing to investigate these cases on their own, Table 5 gives the correlation matrices for ISIM2’s non-robust cardinalities and dimensions, and lists the coordinate values for each of the configurations or Procrustes-rotated subconfigurations for those dimensions.(29) The titles “Dimension 2”, etc. reflect the order of dimensions from SPSS for the “base” datasets (3x3, 4x4, or 5x5, as appropriate) involved. The interpretations given are likewise for the base dataset for each particular cardinality/dimension, so do not necessarily match anything in the prior discussions for ANGLE and RECREL; as noted in footnote 24, such interpretations are generally rather tentative due to the smaller number of objects in those datasets.
Pcset genera
[54] The various dimensions of the ANGLE and RECREL configurations show two types of organizations: either different ways of attempted symmetrical distribution of pitch-classes, or symmetrical vs. asymmetrical distributions. Thus, the diatonic set-classes evenly distribute pcs by ic5, while chromatic organization tries not to distribute evenly but rather bunch all pcs up in one section of the chroma circle via ic1 saturation. Several of these organization types correspond to group-theoretic ways of distributing pcs around the chroma circle according to the concept of maximal evenness (Clough and Douthett 1991). As Quinn (2001) also points out, the chromatic, whole-tone, octatonic, hexatonic, and diatonic scales correspond to Hanson’s (1960) idea of interval cycles, with each of those having ics 1 through 5 respectively dominant; and 016/0167 organization corresponds to Hanson’s ic6 interval cycle. The notion of different kinds of pcsets at the extremes of the dimensions invites comparison with various models of pcset families, or genera.
[55] The Oxford Shorter English Dictionary defines genus as “a class of things containing a number of subordinate classes (called species) with certain common attributes.” In certain fields, most notably biology, genus membership is exhaustive and exclusive: every species belongs to exactly one genus. For other fields such as categories of games, the boundaries are not clear-cut--games can have characteristics that arguably render them members of more than one genus. In terms of mathematical, not musical, set theory, the former situation corresponds to classical sets: an object is either a member of a set or it is not, and the truth value of the proposition “X belongs to set Y” is 1 or 0 (true or false in classical logic). The latter situation corresponds to Zadeh’s (1965) fuzzy sets, which let one say “X sort of belongs to Y,” and where the truth value of “X belongs to Y” can be any real number from 0 to 1 inclusive (i.e., a probability value).
[56] Implicit in the definition of genus, whether classical or fuzzy, is the notion that some sort of criteria exist for exclusion as well as inclusion. A genus is defined to provide a distinction between objects that belong to it and those that do not; a genus whose inclusion rule is so broad and liberal as to permit any object of the domain to be a member is not useful. Likewise for a system of genera, significant overlap in members, even if no genus is all-inclusive, limits the system’s utility. This is not to say that there can be no doubtful classifications, since some objects really may be best described as belonging to multiple genera; but it would seem a good rule of thumb that such objects should be a decided minority.
[57] Like similarity functions, multiple genera systems have been proposed; some explicitly come out of pcset theory or investigations influenced by it (e.g., Ericksson 1986; Forte 1988; Parks 1989; Quinn 1997, 2001) while others do not (e.g., Hanson, 1960; Harris, 1989; Hindemith, 1937/42; Wolpert, 1951, 1972). It is beyond the scope of this article to compare all of the various genera systems with the factors found to be measured by the similarity functions studied here. It is possible, though, to look at a sample: the systems of Forte, Parks, and Quinn provide an interesting set of contrasting approaches.
[58] Forte (1988) proposed a system of 12 genera, each generated by one or more trichord progenitors (the trichords are not actually members of the genera); Forte also lists four “supragenera” as a classification level above these. There are tremendous overlaps between the genera: while 17 of the 29 tetrachords belong to only one genus, only one pentachord and no hexachords are singular to a genus. Most set-classes in fact belong to many genera: 29 out of 38 pentachords belong to between 4 and 9 genera, and 6 of 35 hexachords belong to 11(!) genera.(30) This situation strongly implies that Forte’s system is a very poor set of genera in the usual sense (classical or fuzzy) of the term; a much better and more accurate label would appear to be “interlocked network of complexes of set-classes.” Given Forte’s emphasis on families of supersets and the associated K/Kh-relations in his 1973 work, this is not surprising. Because of the membership overlaps and extreme blurring of boundaries among Forte’s groups, it is not practical to try to determine any correspondences between his system and the MDS configurations.
[59] Parks (1989) developed his system for the analysis of Debussy’s music. While he says he was explicitly coming out of the tradition of pcset theory, he is concerned with reflecting one musician’s actual compositional palette rather than developing a scheme ab initio.(31) He posits five genera, four of which correspond to familiar scales (diatonic, whole-tone, chromatic, and octatonic). His fifth genus, termed by him the “8-17/18/19 complex,” is unwieldy: nearly every set-class in the domain of the present article belongs to it, with only 5-1 and 5-35 absent. This suggests that it is not useful as a genus per se--Parks’ own name, “complex,” implies as much--and it is omitted from further consideration here. Of his remaining genera, the diatonic and octatonic are still fairly obese--the former contains 9 trichords/13 tetrachords/10 pentachords, while the latter has 7 trichords/13 tetrachords/7 pentachords--but the situation is nowhere near as bad as for the 8-17/18/19 complex.
[60] There is excellent correspondence between Parks’ whole-tone/chromatic genera and the equivalent groups in the MDS configurations. The seven whole-tone set-classes in the ANGLE-RECREL WT/anti-WT dimension match exactly the trichords through pentachords in Parks’ genus; for the chromatic genus, the seven set-classes at the extremes in the configurations omit 5-2 and 5-3 ([01235] and [01245]) and add 3-3, [014], as compared to Parks’ group of eight.(32) The seven set-classes at the extreme diatonic end of the MDS configurations are in Parks’ diatonic genus, but that genus includes a number of set-classes that occur in the near-zero clump in the configurations. The five set-classes at the ic3 extreme in the MDS configurations ([036], [0236], [0258], [0369], and [01369]) are all members of Parks’ octatonic genus; not much more can be said, because of both the obesity of Parks’ genus and the lack of a good secondary cutoff value for the configurations.
[61] In his 1997 presentation, Quinn used cluster analysis to examine the ratings of a large number of similarity functions for trichords and tetrachords. In comparing the resulting trees he found a good deal of correspondence among the various measures, something not unexpected given the present results. Quinn decided the trees could be parsed into eight large clusters (i.e., genera), but a number of set-classes were borderline: several “fence sitters” (my term) belonged to not just two but multiple groups, and [0135] in particular was listed as belonging to five groups. Because of this, Quinn argued strongly for a fuzzy set theory of pcset similarity. Table 6 reproduces his list of groups from that presentation.
[62] In his 2001 paper, a rather substantial modification of the earlier work, Quinn presented several more cluster analyses on trichords through hexachords as rated by different functions. He also carried out a very interesting Monte Carlo analysis(33) to determine networks of relationships between set-classes of various cardinalities, as measured by several functions. In the paper he gives two examples, one for tetrachords as rated by Morris’ (1979-80) ASIM, and one for hexachords as rated by ATMEMB. He finds six clusters of set-classes in the former and seven in the latter. The set-classes within each cluster have moderate to very strong connections with other cluster members, while the connections between groups are much weaker or nonexistent.
[63] Quinn’s Monte Carlo results show an interlocked network of pcset clusters; in that sense they are more like Forte’s system than Parks’. His clusters are much more successful as a system of genera than Forte’s, though, because his method allows quantitative cutoff values that circumscribe cluster membership and demonstrate the relative strengths of connections between pcsets both intra- and inter-cluster. In his analysis of hexachords as rated by ATMEMB, for example, when only the one percent most similar pcsets are used to develop connections between set-classes he gets strongly connected but essentially isolated clusters. As the cutoff value is liberalized to include the five percent and then ten percent most similar pcsets, the weaker connections between the clusters appear while connections within each cluster are strengthened, and the intra-cluster connections become more differentiated. This subtle distinction is missing in Forte’s complexes, although one could envision Quinn’s network perhaps asymptotically approaching Forte’s in amounts of cross-connection if a sufficiently liberal cutoff value were used. The six ASIM tetrachord clusters correspond to Hanson’s interval cycles and thus to components of the present results. Six of the seven ATMEMB hexachord clusters also correspond to the interval cycles while group B, containing [023457] and ten other set-classes, does not; perhaps significantly, it is the group most interconnected to all the other clusters.
[64] It would be far beyond the scope of this article to attempt a detailed comparison of the present results and the wide-ranging theory put forth in Quinn’s (2004) dissertation, but it is possible to give a brief taste. In his third chapter, “A Generalized Theory of Affinities,” Quinn connects a set of properties first described by Lewin (1959), and termed “Fourier properties” in Lewin (2001), to the general mathematical theory of chord quality he has been developing. For example, a chord has Fourier property six--FOURPROP(6) in Lewin (2001), “the whole-tone property” in Lewin (1959)--if it has “the same number of notes in one whole-tone set as it has in the other.” Of the set-classes studied here, [0167] and [0369] possess this property while the whole-tone subsets do not. (Quinn provides a set of “balance scale” illustrations in his discussion; in that view, [0167] and [0369] are “most balanced” on this scale/property while [0246] et al. are “most unbalanced;” the other set-classes in this article’s domain have varying degrees of unbalance on it.) The ANGLE-RECREL WT/anti-WT dimension thus appears to correspond to Lewin’s FOURPROP(6) or its lack, and to suggest a potential way to quantify it. Possible correspondences between the other configuration dimensions and the other Fourier properties are less exact; more investigation is necessary. Readers, especially those frustrated by the lack of mathematical (vs. statistical) analysis in this article, are again urged to study this important dissertation.
Implications
[65] The above results about genera systems and the MDS configurations offer one possible answer to the broad philosophical question rhetorically posed at the beginning of this essay: just what sorts of “musical intuitions” are involved in our vague but loaded term, “pitch-class set similarity?” Most of the MDS results and some of the systems mentioned (e.g., Parks’ genera) involve familiar scales used by composers; these scales also correspond to group-theoretic models of pitch-chroma distribution. If we are primarily interested in set-classes that derive from such scales/models (as opposed to, say, the various Z-related pcsets or complementary hexachords), then the functions considered here yield ratings that mirror well the similarities and differences between such set-classes.
[66] Suppose we consider one of these proposed genera systems--let us stay with Parks for the sake of argument--to be a general system for pcset categorization. We then face an important issue. Several set-classes in the domain of cardinalities three-to-five simply do not belong to any of Parks’ four usable genera. The MDS results appear to support this in that many set-classes seem to have little of the properties being measured, based on their coordinates along the various dimensions--the huge near-zero clump in the diatonic/chromatic dimension is the most dramatic example. We may be forced to conclude that some set-classes are simply “mongrels” or “garbage” in terms of interesting musical (as opposed to set-theoretical) properties. Note that this is not just a subjective aesthetic judgment but a formal one about set-class structure as computed by multiple abstract functions.(34) This is also distinct from, although not incompatible with, Quinn’s (1997) idea of fuzzy pcset similarity: many pcsets still likely belong to one genus and a few might belong to several genera, but some may not belong to any genera (at least, any musically interesting or useful ones).
Table 7. Set-classes with near-zero coordinate values along two or more dimensions in ANGLE/RECREL configurations, 3x5 dataset
(click to enlarge)
[67] Table 7 lists those trichords through pentachords with coordinates in a “near-zero” category for at least two dimensions in the ANGLE or RECREL configurations. Some judgment calls were involved to decide cutoff values. For example, if a dimension had a number of coordinates between .001 and .15 then a gap to .39, all those small positive coordinates were considered to be near-zero. The Z-related tetrachords [0137]/[0146] and 5-11, [02347], are near-zero in all four dimensions for ANGLE and in three of the five RECREL dimensions; 5-Z12, [01356], also is near-zero in three RECREL dimensions. Several entries are clearly false alarms since they are of obvious musical interest along at least one other dimension: among other cases, the diminished, diatonic, and augmented triads are all on the list. For any set-classes that ultimately remain on the “potential garbage” list, however, it is worth examining the musical literature to see whether any of them have been exploited in any systematic way by atonal composers; and present-day atonal composers should ask themselves whether such set-classes offer worthwhile compositional possibilities.(35) If they do turn out to be musically interesting, the question of what makes them so could very well suggest new approaches to the issue of pcset similarity.
[68] I have deliberately avoided “value-neutral” terms in favor of “provocative” language in the immediately preceding discussion because at this point we must reenter the (emotionally-laden) fray of aesthetic debate, and I feel it appropriate to “get the blood flowing” here. For example, for well over two thousand years, back to the Greater and Lesser Perfect Systems of Greek antiquity, [0235] as a melodic segment with its T-S-T ordered intervallic content has in some sense epitomized “diatonicism.” Yet, its coordinate is zero along the ANGLE-RECREL dimension that appears to measure that construct, indicating it has nothing of whatever property is being measured. Readers may be extremely dismayed by such a result. The entire motivation for this article was to show how numerical visualization techniques like MDS can provide quantitative clarification for concepts like “diatonicism.” As stated in paragraph 2, once we are armed with such information, we now can (and to my mind must) debate how, or whether, to use it. If multiple formal abstract functions indicate that “diatonicism” quantitatively equates to {ic5-content at least two; ic1-content zero; and zero content of at least one other ic}, do we want to accept that definition if it means the exclusion of [0235]? After all, the octatonic scale is saturated with [0235] to a much greater degree than the diatonic scale, so a good case can be made for [0235]’s placement in that genus. If we want to reject this quantification, that is our prerogative; the present results force us to say with greater precision what we are rejecting and why.
[69] So, which similarity functions are “really good?” Such a question is vague to the point of meaninglessness. Better is, “Which functions are most useful?”, since it is at least possible to give operational criteria for “utility.” Castrén (1994) discussed a number of such criteria in detail; while one might quibble with one or another of his desiderata, doing so is besides the point for the present essay. By implication, I consider functions that do not permit some form of quantitative comparison between set-classes of different cardinality to be much less useful than those that do--but people with other priorities might find binary functions like Forte’s (1973) Rn relations useful. For still others needing to compare set-classes of different cardinalities, the present results suggest they mostly have a free hand to choose whichever function most closely matches their own aesthetics. The only caveat appears to be, avoid functions that are not robust, like ISIM2--once robustness has been determined for a function. If such users have deep disagreement with the similarity factors measured by these functions, however, it seems they will have to develop entirely different functions; and it is not at all clear how this might be done, or even if it is possible in principle. There is also the broader issue of the appropriate level of theoretical abstraction within which to examine similarity: most authors use Tn/I-equivalence, but Castrén and some others take exception to this and use Tn-equivalence. This was not addressed here at all.(36)
[70] Finally, there is an entire gastank of worms waiting to be touched off: perception and cognition. The discussion in this article and the other works cited has been about abstract functions that consider formal structural properties of theoretical objects; it is a decidedly non-trivial question whether these results have anything whatsoever to do with how any human perceives actual musical objects. Some of the results here certainly seem to indicate at least a partial alignment between perception and theoretical features, in that set-classes considered highly diatonic, chromatic, or whole-tone by the functions studied here do match up with how we appear to group them based on our intuitive perceptions. This does not, however, account for all possible set-classes; and it says nothing at all about whether, and under what circumstances, other factors affect and/or take precedence for our perceptions of musical similarity.(37) Those questions can only be addressed after numerous empirical studies. At the same time, we must decide whether or not we care if our theories of atonal musical structure take into account how we hear atonal music. Only after we have a consensus re the epistemological stance of the latter and (if we decide yes) the psychological data about the former will we be in a position to develop similarity functions of ultimate utility.
Art Samplaski
P.O. Box 4971
Ithaca, NY 14852
Works Cited
Abbott, Edwin A. 1885/1952. Flatland: A Romance of Many Dimensions (by A Square). Reprint, New York: Dover.
Castrén, Marcus. 1994. RECREL: A Similarity Measure for Set-Classes. Helsinki: Sibelius Academy.
Clough, John, and Douthett, Jack. 1991. “Maximally Even Sets.” Journal of Music Theory 35, 93–173.
Ekman, Gosta. 1954. “Dimensions of Color Vision.” Journal of Psychology 38, 467–474.
Ericksson, Tore. 1986. “The IC Max Point Structure, MM Vectors and Regions.” Journal of Music Theory 30, 95–111.
Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale Univ. Pr.
—————. (1988). “Pitch-Class Set Genera and the Origin of Modern Harmonic Species.” Journal of Music Theory 32, 187–270.
Hanson, Howard. 1960. Harmonic Materials of Modern Music. New York: Appleton-Century-Crofts.
Harris, Simon. 1989. A Proposed Classification of Chords in Early Twentieth-Century Music. New York: Garland.
Hindemith, Paul. 1937/1942. The Craft of Musical Composition, Vol. 1: Theoretical Part (Trans. A. Mendel). New York: Associated Music.
Isaacson, Eric J. 1990. “Similarity of Interval-Class Content between Pitch-Class Sets: The IcVSIM Relation.” Journal of Music Theory 34, 1–28.
—————. 1992. “Similarity of Interval Class Content between Pitch-Class Sets: The IcVSIM Relation and Its Application.” Ph.D. dissertation, Indiana Univ.
—————. 1996. “Issues in the Study of Similarity in Atonal Music.” Music Theory Online 2(7) http://www.mtosmt.org/issues/mto.96.2.7/mto.96.2.7.isaacson.html.
Krumhansl, Carol L. 1995. “Music Psychology: Influences from Music Theory.” Music Theory Spectrum 17, 53–80.
Krumhansl, Carol L., and Kessler, Edward J. 1982. “Tracing the Dynamic Changes in Perceived Tonal Organization in a Spatial Representation of Musical Keys.” Psychological Review 89, 334–368.
Kruskal, J[oseph] B. 1964a. “Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis.” Psychometrika 29, 1–27.
Kruskal, J[oseph] B. 1964b. “Nonmetric Multidimensional Scaling: A Numerical Method.” Psychometrika 29, 115–129.
Kruskal, Joseph B., and Wish, Myron. 1978. Multidimensional Scaling. Newbury Park, CA and London: Sage Publications.
Lewin, David. 1959. “Re: Intervallic Relations between Two Collections of Notes.” Journal of Music Theory 3, 298–301.
—————. 1979–80. “A Response to a Response: On Pcset Relatedness.” Perspectives of New Music 18, 498–502.
—————. 2001. “Special Cases of the Interval Function between Pitch-Class Sets X and Y.” Journal of Music Theory 45, 1–29.
MacKay, David B., and Zinnes, Joseph L. (1999). “PROSCAL: A Program for Multidimensional Scaling.” [Computer program and user's manual; superseded by newest versions, available at www.proscal.com.]
Morris, Robert. 1979–80. “A Similarity Index for Pitch-Class Sets.” Perspectives of New Music 18, 445–460.
—————. 1995. “Equivalence and Similarity in Pitch and Their Interaction with Pcset Theory.” Journal of Music Theory 39, 207–243.
Narmour, Eugene. 1990. The Analysis and Cognition of Basic Melodic Structures: The Implication-Realization Model. Chicago: Univ. Chicago Pr.
—————. 1992. The Analysis and Cognition of Melodic Complexity: The Implication-Realization Model. Chicago: Univ. Chicago Pr.
Parks, Richard S. 1989. The Music of Claude Debussy. New Haven: Yale Univ. Pr.
Quinn, Ian. 1997. “On Similarity, Relations, and Similarity Relations.” Paper presented at the Society for Music Theory national meeting, Phoenix, AZ.
—————. 2001. “Listening to Similarity Relations.” Perspectives of New Music 39(2), 108–158.
—————. 2004. “A Unified Theory of Chord Quality in Equal Temperaments.” Ph.D. dissertation, Eastman School of Music.
Rahn, John. 1979–80. “Relating Sets.” Perspectives of New Music 18, 483–497.
—————. 1989. “Toward a Theory of Chord Progression.” In Theory Only 11(1–2), 1–10.
Ramsay, J. O. 1977. “Maximum Likelihood Estimation in Multidimensional Scaling.” Psychometrika 42, 241–266.
Samplaski, Art. 2004. “Interval Classes and Psychological Space.” Music Theory Online 10(2) http://www.mtosmt.org/issues/mto.04.10.2/mto.04.10.2.samplaski.html.
Schellenberg, E. Glenn. 1996. “Expectancy in Melody: Tests of the Implication-Realization Model.” Cognition 58, 75–125.
—————. 1997. “Simplifying the Implication-Realization Model of Melodic Expectancy.” Music Perception 14, 295–318.
Schoenberg, Arnold. 1954. Structural Functions of Harmony. New York: Norton.
Scott, Damon, and Isaacson, Eric J. 1998. “The Interval Angle: A Similarity Measure for Pitch-Class Sets.” Perspectives of New Music 36(2), 107–142.
Shepard, Roger N. 1962. “The Analysis of Proximities: Multidimensional Scaling with an Unknown Distance Function.” Psychometrika 27, 125–140; 219–246.
Teitelbaum, Richard. 1965. “Intervallic Relations in Atonal Music.” Journal of Music Theory 9, 72–127.
Tversky, Amos. 1977. “Features of Similarity.” Psychological Review 84, 327–352.
Tversky, Amos, and Gati, Itamar. 1982. “Similarity, Separability, and the Triangle Inequality.” Psychological Review 89, 123–154.
Tversky, Amos, and Hutchinson, J. Wesley. 1986. “Nearest Neighbor Analysis of Psychological Spaces.” Psychological Review 93, 3–22.
Wolpert, Franz. 1951. Neue Harmonik: die Lehre von den Akkordtypen, Kurz-Ausgabe. Regensburg: Gustav Bosse.
—————. 1972. Neue Harmonik. Einführung. Erweiterte und ergänzte Neufassung. Wilhelmshaven: Heinrichshofens.
Zadeh, Lofti. 1965. “Fuzzy Sets.” Information and Control 8, 338–353.
Footnotes
* I am grateful to Eric Isaacson for his assistance in providing
the raw data used in the analyses, and to Matt Faranda and Ryan Zawel for
facilitating use of computing facilities at different times. I am also deeply
indebted to Tim Koozin and the anonymous reviewers of this essay for many
valuable suggestions that ultimately made it a readable work.
Return to text
1. Surveys and critiques of most similarity measures can be
found in Castrén (1994), Isaacson (1990, 1992), and Scott and Isaacson
(1998).
Return to text
2. Isaacson (1996) raises some basic conceptual questions.
Quinn (2001) is a well-argued critique of several fundamental issues.
Return to text
3. Rahn (1989) relates an early
attempt to apply computation to the analysis of similarity relations; he was
defeated by the speeds of then-available processors. Computational complexity
has not completely disappeared since then, in that commercially-available
software still has limits that prevent, e.g., a single analysis of all ratings
for trichords through nonachords (a 208 x 208 matrix); but excessive length of
computer runs is no longer an obstacle to such analyses.
Return to text
4. Correlations (denoted by “r”) can vary from a
perfect negative of -1.0 (as quantity A goes up, quantity B goes down by the
same proportion) to a perfect positive of +1.0; for these functions over the
integers 1 to 50, a domain size comparable to the number of pcsets studied here,
y = x/SQRT(x) have r = .983,
y = x/x2 have r = .969, and y = x2/SQRT(x) have r = .911--all close to perfect
positive.
Return to text
5. Narmour’s (1990, 1992)
implication-realization model for melodic expectation is a case in point. He
proposes five interacting factors to account for listeners’ melodic
expectancies; studies by Krumhansl (1995) and Schellenberg (1996, 1997) indicate
that the model can be simplified to just two factors without significant loss of
explanatory power.
Return to text
6. In doing so, I fulfill the promise in my previous
article in this journal (Samplaski 2004, fn. 7) to provide “a detailed but
non-technical tutorial” about MDS and some of the issues in its use.
Nonetheless, this overview must perforce still be very superficial and exclude
the theoretical underpinnings necessary to use the techniques appropriately; I
can but hope that it will stimulate some readers to investigate possible
applications to their own areas of music-theoretic research. The best initial
pointer into the MDS literature remains Kruskal and Wish (1978), even though
there have been a number of developments in the field since then.
Return to text
7. Quinn (2004) has recently completed a dissertation that analyzes in depth the
mathematics behind pcset genera, and by extension, similarity functions. Since
he considers not only twelve-fold division of the octave but other equal
temperaments, his results clarify issues that remain obscured if one examines
only the 12-ET universe. Interested readers should consult this important work.
Return to text
8. The ratings can be obtained in any of several ways: as
direct estimates or impressions of similarity or distance; as same-different
confusion rates (non-identical but similar stimuli are more likely to be
mistaken for each other than dissimilar ones, so high confusion rates correlate
with high similarity); etc.
Return to text
9. Without going deeply into topology, a torus can be
embedded in variously-dimensioned spaces. In a three-dimensional space an
observer on a torus’ surface would notice that the surface was non-Euclidean:
the angle sum of a triangle would not be 180 degrees, etc. If a torus is
embedded in a four-dimensional space, its surface will be “flat” in the sense of
Euclidean geometry. This was the nature of the configuration found by Krumhansl
and Kessler.
Return to text
10. Other distance metrics are possible. One, intuitively
used daily by millions, is the “city-block” or “taxi-cab” metric, where to get
from point A to point B you go J units in the first dimension, then K units in
the next, etc. The general formula for such distance metrics is called the “Minkowski
distance metric.”
Return to text
11. Even this assumption fails in the real world depending
on the precision needed: the builders of the Verrazano Narrows Bridge, between
the NYC boroughs of Staten Island and Brooklyn, had to take the earth’s
curvature into account.
Return to text
12. Note that models such as ASCAL and INDSCAL are not
invariant with respect to rescaling, or to rotation or reflection about axes.
They also have a significantly larger number of free parameters to be estimated
than simpler models. Moreover for INDSCAL, because individual biases are not
canceled out by averaging responses into a single matrix, it can produce a much
poorer fit to the data. A researcher should thus not automatically use one of
these models in hopes of obtaining the most general result.
Return to text
13. In technical terms, as the number of free parameters
being calculated increases relative to the number of data points, there become
too few constraints on the possible configuration.
Return to text
14. If questions remain, the researcher should examine
several different dimensionalities and be prepared to choose on the bases of
clarity and logical interpretation. There are times where a solution one
dimension above or below “optimal” as indicated by the stress/r2
values might be better: 1) if there is a clear interpretation given an added
dimension; or 2) if one configuration is easier to visualize (e.g., a 3-D vs. a
4-D solution), especially in a situation where it is unclear what can be gained
in explanatory power by using the extra dimension.
Return to text
15. In an MDS analysis of N objects, one of which is an
exemplar, the only way to minimize distortion (i.e., stress) is to place the
exemplar at the center of the configuration and arrange the other objects around
it, along the rim of a circle/sphere/equivalent higher surface. One can always
draw a circle through three non-colinear points, a sphere through four
non-coplanar points, etc.; so, adding in the exemplar, an N-dimensional MDS
solution can in general accommodate N+2 objects (where one is an exemplar)
without problems. Of course, for some datasets one will be able to fit more
objects than this along the surface’s rim; and in other cases the limit can be
somewhat liberalized by locating the exemplar off-center in the
circle/sphere/etc., or by using an ellipse/oblate spheroid/etc. as the surface.
This will, though, only go so far: if you try to fit a set of 23 objects
including an exemplar in two or three dimensions, you must expect a fair amount
of stress in the solution.
Return to text
16. An example dating back to the great nineteenth century
psychologist William James is: the moon is like a ball because they are both
round; the moon is also like a gas lantern because they both illuminate; but we
do not think of a ball as being like a gas lantern.
Return to text
17. This study considers only results from MDS, so no
further discussion of CA is necessary; it is mentioned to raise awareness of the
issues that render it appropriate for various situations. Some of Quinn’s (1997,
2001) analyses of pcset similarity measures use CA; as discussed in paragraphs
61–63, he obtains results compatible with those reported here.
Return to text
18. This model underlies MacKay and Zinnes’
(1999) PROSCAL program. A different model underlies an older PMDS program called
MULTISCALE (Ramsay 1977), but we need not worry about the distinctions.
Return to text
19. The present article is a case in point: analyses of
the datasets herein took a few seconds on a PC of moderate speed, using the
statistical package SPSS; the
equivalent analyses on the same machine using PROSCAL took up to forty minutes.
Return to text
20. AMEMB2 is a modification of Rahn’s (1979–80) MEMB2
function by Isaacson for inclusion in the latter’s Winsims calculator, available
at http://theory.music.indiana.edu/isaacso/winsims.html;
Isaacson applies a normalization factor equivalent to that used by Rahn to
derive ATMEMB from his TMEMB function. For narrative simplicity, it seemed
preferable to refer to it as Rahn’s function. Note that while AMEMB2 is
concerned with cardinality-two sets, i.e., interval-classes, it is not an icv-based
function in the sense of ANGLE et al., since it only counts how many
instances of each dyad are mutually imbedded in two pcsets--for example, in
returning a comparison for [0156] and [0167], only one ic6 in the latter is
counted. I thus treat it as a subset-based measure.
Return to text
21. That is, the icv of any nonachord is a
function of the icv of its trichord complement, and similarly for octachords/tetrachords
and heptachords/pentachords; ratings produced by icv-based similarity functions
are therefore also related. The precise functions involved differ for each pair
of cardinalities, but they are systematic for those pairs.
Return to text
22. That value is actually a severe understatement; it is
the limit of accuracy reported by the statistical package used. Obtaining an r
of better than .96 (between ANGLE and RECREL) over 3160 observations is so close
to perfection as to be basically unheard-of for a “real-life” dataset.
Return to text
23. Various additional types of cross-check analyses were
carried out using PROSCAL to the extent possible given the version of the
program available—the 4x5 and 3x5 datasets were too large. These are omitted
for considerations of space, minimization of technical detail, and reader
patience.
Return to text
24. In particular, the 3x3 dataset, with only 12 objects,
is far too sketchy to understand what is going on for most of its configuration.
The same holds true to lesser extents for the other smaller datasets.
Return to text
25. If one is determined to try to visualize a
four-dimensional object, the best starting place is Edwin Abbott’s classic story Flatland
(1885/1952). With modern computer graphics, it is now possible to get a
direct visceral appreciation of such objects via programs that manipulate their
projections onto the screen.
Return to text
26. Since the Procrustes rotation deals with the derived
configurations, which involve the final relative set-class locations in abstract
space, we need not worry that the latter two functions rate similarity while
RECREL rates dissimilarity.
Return to text
27. A p-value of .05 is the typical cutoff value
for empirical studies, in that researchers are usually willing to risk a 1 in 20
chance of reporting a false positive result. (Certain types of studies, e.g.,
clinical drug trials, obviously must set far more stringent standards.)
Return to text
28. There is no possibility of problems due to axial
reflection, since the Procrustes rotation would have handled that.
Return to text
29. The most surprising of these cases is the
disappearance of the ic1/ic5 dimension for cardinality-three set-classes in the
3x4 dataset. Given the coordinates of the rotated subconfiguration, that
dimension appears to involve an “ic3/anti-ic6 vs. ic6/anti-ic3” opposition, as
seen on the second section of
Table 5.
Return to text
30. Forte only lists hexachords up to 6-35 in his table on
pages 264–266 that summarizes the makeup of the genera. From the inclusion rules
on page 192 one can deduce that the remaining 15 hexachords belong to the same
genera as their Z-related counterparts, but it would have been better just to
list them explicitly, since he lists all Z-related tetrachords and pentachords
Return to text
31. Harris (1989) follows this same procedure, except that
he draws from a wide body of musical literature, and he is explicitly not
working from a pcset-influenced background. His system of chord families is much
more complicated than Parks’, but it has a great deal of solid and thoughtful
musicianship behind it. His proposal deserves closer attention by the
music-theoretic community.
Return to text
32. If we adjust cutoff values, we can re-include 5-2 and
5-3, although 5-4 and 5-8 ([01236] and [02346]) will also come along.
Return to text
33. The term refers to a probabilistic process that is
repeatedly carried out (as in, “repeated throws of the dice at Monte Carlo”) to
determine a result. The technique is often used to simulate physical processes;
it has some relation to the stochastic algorithms used to generate a number of
Xenakis’ compositions.
Return to text
34. The speculation two paragraphs ago about Quinn’s
hexachord group B, whose members all had fairly high connections to other
clusters (unlike members of the remaining six groups), applies: might an MDS
analysis of hexachords show all his group B hexachords to be “garbage”
set-classes?
Return to text
35. As an example, if I alternately play 0137/0146 in
closest spacing with the same bass note I feel a definite sense of
tonic/dominant, presumably due to the imbedded minor triad in 0137 and the
semitone neighbor in the soprano in 0146 acting like a leading tone. I could
easily envision exploiting this type of perceived relationship in a composition.
Return to text
36. Using Tn-equivalence raises a number of
questions; in particular, would the dimensionality of the configurations change?
Since a major priority for this essay was to compare RECREL with several other
functions, all of which use Tn/I-equivalence, it was necessary to eliminate the
B-forms of asymmetrical set-classes from consideration, obviating all such
issues. Morris (1995) lists several other possible levels of abstraction. Most
of these have as yet received little or no attention by music theorists, a
situation which sorely needs correction.
Return to text
37. To cite one example, Samplaski (2004) found support
for grouping interval-classes by category of acoustical dissonance, rather than
treating them as separate isolated entities. If other studies confirm this
result, that would strongly imply a need for substantial modification of
existing similarity measures.
Return to text
Copyright Statement
Copyright © 2005 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Rebecca Flore, Editorial Assistant