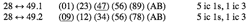Maximally Alpha-Like Operations
Guy Capuzzo
KEYWORDS: Maximally alpha-like operations, alpha, Z-relation, Z-pair, M-relation, TTOs, mappings, pcsets, transformational network
ABSTRACT: Any two Z-related set-classes will map onto one another under 1) TnM or TnMI, or 2) TnM or TnMI in tandem with Morris’s alpha operations, or 3) maximally alpha-like operations, the original contribution of the present paper. This brief “research notes” paper explores the theoretical formulation and analytical application of maximally alpha-like operations.
Copyright © 2008 Society for Music Theory
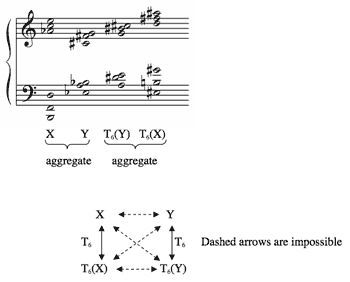
Example 1. Dallapiccola, Quattro Liriche de Antonio Machado, III (1948), mm. 80–85
(click to enlarge)
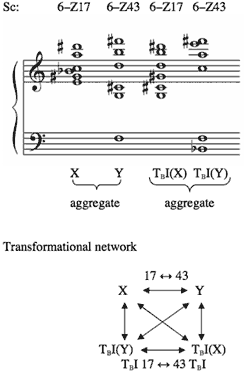
[1] Example 1 shows an excerpt from a Dallapiccola song.(1) The excerpt contains four chords, labeled X, Y, T6(Y), and T6(X). The union of X and Y forms the pc aggregate, as does the union of T6(Y) and T6(X). The passage resists an overarching transformational network such as that at the bottom of Example 1 because there is no Tn, TnI, TnM, or TnMI operation that will map the X and Y forms onto each other. The dashed arrows in the network represent this limitation.
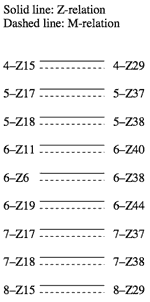
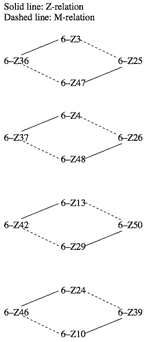
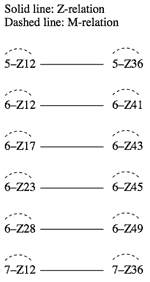
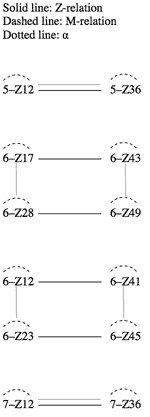
[2] The reason why X and Y cannot map onto one another is that they are Z-related.(2) However, not all Z-pairs (two Z-related scs) work this way. To explain, I shall divide the twenty-three Z-pairs (under the traditional equivalence operations Tn and TnI) into three categories. Example 2 shows the first category, Z-related/M-related. Here each sc maps under TnM or TnMI onto the other sc in the same Z-pair; the two scs are thus Z-related and M-related.(3) Example 3 shows the second category, Z-related/M-variant. Here each sc maps under TnM or TnMI onto a sc in a different Z-pair (thus the term “variant”). Example 4 shows the third category, Z-related/M-invariant. Here each sc in the Z-pair maps onto itself under TnM or TnMI (thus the term “invariant”). This is perhaps the most restrictive of the three categories, in that each sc can only map onto itself. The Z-pair in Example 1, 6–Z28/6–Z49, belongs to this category.(4)
|
Example 2. Z-related/M-related scs (click to enlarge) |
Example 3. Z-related/M-variant scs (click to enlarge) |
Example 4. Z-related/M-invariant scs (click to enlarge) |
[3] Robert Morris has noted that the Z-relation may appear or disappear depending on the canon of operations in use.(5) This is evident in Example 2, where scs in Z-pairs that do not relate by Tn or TnI do relate by TnM or TnMI. To this end, Morris develops a number of operations designed to erase the Z-relation. The most often cited of these operations is alpha (α), whose mappings are
α1 = (01) (23) (45) (67) (89) (AB)
or
α2 = (12) (34) (56) (78) (9A) (B0).(6)
Example 5. Adding α to the Z-related/M-variant scs
(click to enlarge)
Example 6. Adding α to the Z-related/M-variant scs
(click to enlarge)
Example 7. Two maximally α–like operations
(click to enlarge)
Example 8. Redo of the transformational network in Example 1 using 28 ↔ 49
(click to enlarge)
Example 9. Carter, Retrouvailles (2000), mm. 5–10
(click to enlarge)
Example 10. Webern, Op. 7, No. 2 (1910)
(click to enlarge)
Example 11. Stravinsky, “Sacrificial Dance” from The Rite of Spring (1921 edition), R3
(click to enlarge)
For α1, Ian Quinn notes, “each pc in the even whole-tone collection gets transposed up a semitone, and each pc in the odd whole-tone collection down a semitone.”(7) For α2, each pc in the even whole-tone collection is transposed down a semitone, and each pc in the odd whole-tone collection is transposed up a semitone. Applying α1 to a pcset X may yield quite different results than applying α2 to X. For instance, if X = {012478}, a member of 6–Z17[012478], applying α1 to X yields {013569}, a member of sc 6–Z28[013569]. However, applying α2 to X yields {12378B}, another member of 6–Z17. The fact that 6–Z17 and 6–Z28 belong to the same category of Z-pairs (cf. Example 4) suggests that α may be of use in creating mappings for the Z-pairs in Examples 3 and 4.
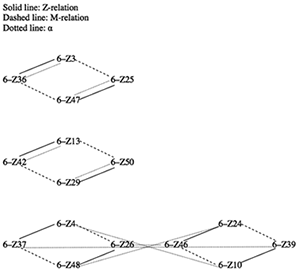
[4] To test this hypothesis, Example 5 applies α to the scs in Example 3. The result is clear: α maps (the pcsets of) four of the eight Z-pairs onto their Z partners, thus erasing the Z-relation for these scs (6–Z3/6–Z36, 6–Z25/6–Z47, 6–Z13/6–Z42, 6–Z50/6–Z29). The four Z-pairs at the bottom of Example 5 do not map onto their Z-partners under α (6–Z4/6–Z37, 6–Z26/6–Z48, 6–Z24/6–Z46, 6–Z39/6–Z10). In like fashion, Example 6 applies α to the scs in Example 4. On the one hand, α resolves the Z-relations between 5–Z12/5–Z36, and between their abstract complements, 7–Z12/7–Z36. On the other hand, α turns the Z-related/M-invariant hexachords into a new set of Z-related/M-variant hexachords (the set is new because the variances differ from those in Examples 3 and 5). The upshot is that the Z-related/M-invariant hexachords are still unable to map onto their Z-partners.
[5] The success of α in resolving every Z-relation save for four Z-pairs in Example 5 and four Z-pairs in Example 6 prompts me to create maximally α-like operations for those Z-pairs.(8) By “maximally α-like,” I am imagining operations whose cycles contain as many interval-class 1s (ic 1s) as possible, since the cycles of α consist of six ic 1s. The ic 1 cycles result in a “small” voice-leading distance between two α-related hexachords—no more than six ics of “work” are required to “move between” them.(9) As a result, maximally α-like operations will come as close as possible to six ics of work in relating hexachords. Ideally, a maximally α-like operation will contain 5 ic 1s, but we shall see that certain cases permit only 4 or even 3 ic 1s. The following sections explore maximally α-like operations in detail.
[6] Let us return to Example 1. There, X = {02458B} and Y = {13679A}. The maximally α-like operation
28 ↔ 49.1 = (01) (23) (47) (56) (89) (AB)
maps X onto Y and vice versa. The label “28 ↔ 49.1” indicates that this operation maps the 6–Z28 member X onto the 6–Z49 member Y and vice versa. “.1” indicates that this is the first of two operations that will map X onto Y and vice versa. 28 ↔ 49.1 is maximally α-like because its cycles contain five ic 1s—(01), (23), (56), (89), (AB)—and one ic 3—(47). Underlines indicate the non-ic 1 cycles.
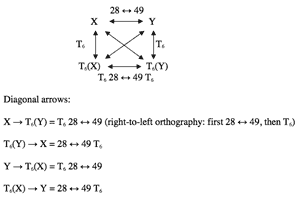
[7] Example 7 lists a second maximally α-like operation
28 ↔ 49.2 = (09) (12) (34) (56) (78) (AB)
that also maps X onto Y and vice versa. 28 ↔ 49.2 also contains five ic 1s—(12), (34), (56), (78), (AB)—and one ic3—(09)—and is thus as α-like as 28 ↔ 49.1. In the abstract, the choice between 28 ↔ 49.1 and 28 ↔ 49.2 is essentially arbitrary, but in a specific musical context, factors such as instrumentation, register, and voicing may suggest one operation over another.
[8] Example 8 renotates the transformational network of Example 1, using 28 ↔ 49. Because the registral spacing of the piano chords does not correspond to either of the 28 ↔ 49 operations, I use the generic label 28 ↔ 49 as opposed to the more specific 28 ↔ 49.1 or 49.2. The 28 ↔ 49 operation allows us to assert the relations that were not possible in Example 1’s network. By reading the network clockwise beginning from X, we follow the chronological procession of the hexachords in Example 1, <X, Y, T6Y, T6X>, and their respective transformations <28 ↔ 49, T6, T6 28 ↔ 49 T6>.
[9] A contextual factor in the definition of maximally α-like operations involves the two pcsets that will map onto one another. Up to this point, the 28 ↔ 49 operations have mapped X = {02458B} onto its literal complement, Y = {13679A}. However, to map X onto T1 of Y = {2478AB}, for example, it will not be possible to define a maximally α-like operation (1-to-1 and onto) since X and T1 of Y share common tones. A simple workaround involves retaining the already-defined 28 ↔ 49 operations, then transposing or inverting the resulting pcset. Because maximally α-like operations do not commute with Tn or TnI, the initial choice of orthography must be adhered to. Throughout this paper, I use right-to-left orthography. For example, the compound operation T1 28 ↔ 49 maps X onto T1 of Y first through the application of 28 ↔ 49 to X (which maps X onto Y), and second through the application of T1 to Y.
[10] Having defined maximally α-like operations for 6–Z28/6–Z49, I now proceed to the Z-pair 6–Z17/6–Z43. Example 9 grounds the discussion with a passage from Carter’s Retrouvailles. Like the Dallapiccola excerpt in Example 1, Retrouvailles features an opening chord X with its literal complement Y, followed by transformations of X and Y that form a second aggregate. Here X = {03489A} and Y = {12567B}, and the lone maximally α-like operation that maps X onto Y (and vice versa) is
17 ↔ 43 = (01) (23) (45) (69) (78) (AB) (5 ic 1s, 1 ic 3)
This operation permits the transformational network at the bottom of Example 9, which strongly recalls the network in Example 8. By reading the Example 9 network clockwise beginning from X, we follow the chronological procession of the hexachords, <X, Y, TBI(X), TBI(Y)>.
[11] I now define the single maximally α-like operation for the Z-pair 6–Z12/6–Z41. Example 10 provides a musical context for the discussion, reproducing a passage that Allen Forte discusses in detail.(10) Forte observes two transformational relations among the chords in Example 10: first, that chord 3 is T9 of chord 1, and second, that chord 3 is T5I of the literal complement of chord 2. The following operation formalizes Forte’s second observation:
12 ↔ 41 = (03) (12) (45) (67) (8B) (9A) (4 ic 1s, 2 ic 3s).
Chord 2 is the 6–Z41 member {04567A} and chord 3 is the 6–Z12 member {234689}. 12 ↔ 41 maps {234689} onto its literal complement {0157AB} and vice versa. The arrows at the bottom of Example 10 indicate the T9 relation from chord 1 to chord 3, and the T5I/12 ↔ 41 relations between chords 2 and 3.(11)
[12] Example 11 grounds the discussion of the final pair of Z-related/M-invariant hexachords, 6–Z23/6–Z45, with a second passage discussed by Forte.(12) The passage contains an opening chord X = {02359B} followed by T2 of X’s literal complement, {03689A}. Because the chords share pcs, a 1-to-1 operation from one to the other is not possible. For this reason, I shall list the two maximally α-like operations that map X = {02359B} onto its literal complement {14678A}:
23 ↔ 45.1 = (07) (12) (34) (56) (89) (AB) (5 ic 1s, 1 ic 5)
and
23 ↔ 45.2 = (01) (27) (34) (56) (89) (AB) (5 ic 1s, 1 ic 5).
Example 12 lists maximally α-like operations for the remaining hexachords in Example 5.
[13] In this brief “research notes” paper, I have explored ways of mapping any Z sc onto its Z partner. For Z-related/M-related scs (Example 2), this is accomplished by TnM or TnMI. For four of the eight Z-related/M-variant Z-pairs (Examples 3 and 5) and two of the six Z-related/M-invariant Z-pairs (Examples 4 and 6), this is accomplished by a combination of α, TnM, and/or TnMI. Finally, for the remaining Z-related/M-variant hexachords (Example 5) and Z-related/M-invariant hexachords (Example 6), this is accomplished by the primary contribution of this paper, maximally α-like operations.
|
Example 12. Maximally α-like operations for the remaining Z-pairs in Example 5 (click to enlarge) |
Example 13. Maximally α-like operations in beat-class space (click to enlarge) |
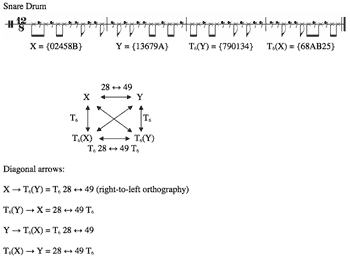
[14] There exist a number of avenues for future work with maximally α-like operations. I begin with spaces other than pc-space. First, maximally α-like operations can be defined for pitches in pitch-space, or beats in beat-class (bc) space. Bc-space is particularly fertile ground for the development of new operations since, to date, theorists have defined bcsets primarily in terms of Tn and TnI.(13) Example 13 illustrates one such application, modeled on the 28 ↔ 49 operation (cf. §6 and Examples 7–8). The snare drum projects two mod-12 bc aggregates. First, X = {02458B} precedes its 28 ↔ 49 transformation, Y = {13679A}. Second, T6 of Y = {790134} precedes T6 of X = {68AB25}. The network in Example 13 is isographic with that in Example 8, and the passage in Example 13 is isographic in bc-space to the passage in Example 1 in pc-space.
[15] Returning to traditional pc-space, maximally α-like operations bear a number of similarities to models of fuzzy Tn and TnI.(14) For the latter models, the benchmarks are the traditional “crisp” Tn and TnI operations, and offset (“degrees of divergence”) is measured from those cycles. In like fashion, maximally α-like operations measure offset from α by specifying the number and “size” of non-ic 1 ics.(15)
Appendix: Definitions
DEF 1: Z-relation: Two pcsets or scs are Z-related if they share an ic vector but do not relate by Tn and/or TnI. The standard gauge of Tn/TnI equivalence is assumed.
DEF 2: Z-pair: Two Z-related pcsets or scs (“Z-partners”).
DEF 3: The two scs in a Z-pair are one of the following:
Z-related/M-related (M maps each sc in the Z-pair onto the other sc in the same Z-pair);
Z-related/M-variant (M maps each sc in the Z-pair onto a sc in a different Z-pair);
Z-related/M-invariant (M maps each sc in the Z-pair onto itself).
DEF 4: An operation is a mapping that is 1-to-1 and onto.
DEF 5: Alpha (α) is an operation whose cycles are α1 = (01) (23) (45) (67) (89) (AB) or α2 = (B0) (12) (34) (56) (78) (9A) (Morris 1982).
DEF 6: A maximally α-like operation is an operation whose cycles mimic those of α as closely as possible by containing the maximal number of ic 1 cycles. An example is (01) (23) (47) (56) (89) (AB). Underlines indicate non-ic 1 cycles.
Guy Capuzzo
UNC at Greensboro School of Music
P.O. Box 26170
Greensboro, NC 27402-6170
g_capuzz@uncg.edu
Works Cited
Alegant, Brian. 2001. “Cross-Partitions as Harmony and Voice Leading in Twelve-Tone Music.” Music Theory Spectrum 23/1: 1–40.
Babbitt, Milton. 1962. “Twelve-Tone Rhythmic Structure and the Electronic Medium.” Perspectives of New Music 1/1: 49–79.
Buchler, Michael. 2000. “Broken and Unbroken Interval Cycles and Their Use In Determining Pitch-Class Set Resemblance.” Perspectives of New Music 38/2: 52–87.
Cohn, Richard. 1992. “Transpositional Combination of Beat-Class Sets in Steve Reich’s Phase- Shifting Music.” Perspectives of New Music 30/2: 146–77.
Forte, Allen. 1973. The Structure of Atonal Music. New Haven: Yale University Press.
—————. 1990. “A Major Webern Revision and Its Implications for Analysis.” Perspectives of New Music 28/1: 224–55.
Lewin, David. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.
—————. 1995. “Generalized Interval Systems for Babbitt’s Lists, and for Schoenberg’s String Trio.” Music Theory Spectrum 17/1: 81–118.
—————. 1998. “Some Ideas about Voice-Leading Between Pcsets.” Journal of Music Theory 42/1: 15–72.
London, Justin. 2002. “Some Non-Isomorphisms Between Pitch and Time.” Journal of Music Theory 46/1-2: 127-51.
Mead, Andrew. 1989. “Some Implications of the Pitch-Class/Order-Number Isomorphism Inherent in the Twelve-Tone System: Part Two.” Perspectives of New Music 27/1: 180–233.
Morris, Robert D. 1982. “Set Groups, Complementation, and Mappings Among Pitch-Class Sets.” Journal of Music Theory 26/1: 101–44.
—————. 1987. Composition with Pitch-Classes. New Haven: Yale University Press.
—————. 1990. “Pitch-Class Complementation and its Generalizations.” Journal of Music Theory 34/2: 175–246.
—————. 1997. “K, Kh, and Beyond.” In Music Theory in Concept and Practice, ed. James Baker, David Beach, and Jonathan Bernard. Rochester: University of Rochester Press: 275–306.
—————. 2001. Class Notes for Advanced Atonal Music Theory. Lebanon, NH: Frog Peak Music.
Quinn, Ian. 2004. “A Unified Theory of Chord Quality in Equal Temperaments.” Ph.D. diss., University of Rochester.
Straus, Joseph N. 2005. “Voice Leading in Set-Class Space.” Journal of Music Theory 49/1: 45–108.
Winham, Godfrey. 1970. “Composition with Arrays.” Perspectives of New Music 9/1: 43–67.
Footnotes
1. Buchler 2000, 52–3 discusses the chords in Example 1 in connection with interval cycles.
Return to text
2. They are also ZC-related (Morris 1982, 103), but the ZC-relation is not required for the present paper’s agenda.
Return to text
3. The status of TnM and TnMI as equivalence operators on par with Tn and TnI is controversial since TnM or TnMI exchanges ic 1 and ic 5 content (Winham 1970, 281–2, Morris 1987, 148, Morris 2001, 52). This can lead to drastically different “equivalent” pcsets, such as {012345} and {024579} (chromatic to diatonic). In the present paper, however, the sets under discussion are Z-pairs, whose ic vectors are identical, thereby rendering this criticism moot. Winham 1970, 282, defends TnM and TnMI, stating, “it would not even be correct to say without qualification that I is a ‘closer’ relation than M5 or M7. For while M5 preserves the intervals 3 and 9 while complementing 2, 4, 8, and 10, and M7 does the opposite, I complements all of these and preserves none; so in that one sense I is the least ‘close’.” Nonetheless, while TnM and TnMI do not change the ic content of a Z-pair, they do change the larger subsets embedded in each sc.
Return to text
4. Morris 1982, 102–9, provides pertinent commentary.
Return to text
5. Again see Morris 1982, 102–9.
Return to text
6. Morris 1982, 115. Morris provides further applications of α in Morris 1990, 223–30 and Morris 1997, 304–6. Applications of α by other scholars include Lewin 1995, 103 ff., Mead 1989, 224 ff., and Quinn 2004, 36–8.
Return to text
7. Quinn 2004, 36.
Return to text
8. Morris 1982 develops operations other than α that change the mappings among Z-partners, but notes that the only way to address 6–Z17/6–Z43 and 6–Z28/6–Z49 is to create a system of equivalence in which the fifty Tn/TnI hexachordal scs collapse into three scs (129–31). This system is not in widespread use.
Return to text
9. The notion of “ics of work” comes from Lewin 1998 and Alegant 2001, 11.
Return to text
10. Forte 1990, 247–9.
Return to text
11. No maximally α-like operation whose cycles contain five ic 1s exists for 12 ↔ 41.
Return to text
12. Forte 1973, 148.
Return to text
13. Babbitt 1962, Lewin 1987, 23, Morris 1987, 299–305, Cohn 1992. Such “isomorphisms” between pitch and rhythm have long been controversial; a recent critique appears in London 2002.
Return to text
14. See, most recently, Straus 2005, 45–50.
Return to text
15. Thanks to Jonathan Salter for writing a computer program to calculate maximally α-like operations, Igor Erovenko (Department of Mathematics and Statistics, UNCG) for help with matters mathematical, and Clifton Callender, J. Daniel Jenkins, Evan Jones, Rachel Mitchell, Robert Morris, Robert Peck, Jonathan Pieslak, Adam Ricci, Caleb Smith, and
the anonymous MTO readers for their suggestions.
Return to text
Copyright Statement
Copyright © 2008 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sean Atkinson, Cara Stroud, and Tahirih Motazedian, Editorial Assistants and Brent Yorgason, Managing Editor
Number of visits: