Constructing Transformational Signification: Gesture and Agency in Bartók’s Scherzo, Op. 14, No. 2, measures 1–32
John Roeder
KEYWORDS: transformational theory, analysis, animation, Lewin, Bartók, gesture, network
ABSTRACT: David Lewin's didactic examples of transformational analysis leave open questions about how to choose the most expressive object families, network types, and visual representations, as well as deeper questions about the nature of “gesture” and the agent “inside the music.” By developing several contrasting analyses of a Bartók passage, this article presents an analytical pragmatics that addresses those questions and explores how animation can bring out a characteristically transformational attitude.
Copyright © 2009 Society for Music Theory
The state of transformational pragmatics
[1.1] The key concepts of David Lewin’s theory of musical transformation, as developed in Generalized Musical Intervals and Transformations (henceforth GMIT) and associated writings, can be sketched readily.(1) A transformational system consists of musical objects (for example, pitches, pc-series, triads, or duration series) united into a family by a semigroup of transformations, each of which changes one object into another in the same family. A network is a directed graph, satisfying certain formal constraints, whose nodes represent objects, and whose arrows, linking the nodes in some way, express the transformational relations among them. Lewin contrasts two basic types of network: in one, which he compares to “blow-by-blow” and other narrative accounts, the nodes represent actual events in the piece, and the arrows assert a hearing of the changes in those events; the other is a transformational space that shows all the family’s objects—even those not appearing in the piece—linked by a minimal set of transformations.
[1.2] Applying this theory in analysis, as exemplified in Lewin’s book Musical Form and Transformation (henceforth MFT), involves constructing networks that identify not only the most important objects, but also the characteristic ways that they are transformed during the piece. These are evident in a network as repeated or similar (technically, isomorphic) transformations or transformation-sequences and can be understood to articulate musical form. More radically, they suggest revising one’s attitude towards the music from that of an external observer to that of “someone inside the music” actively producing it (GMIT, 159). The characteristic transformations are conceived as a repertoire of “available gestures,” from which the insider deliberately selects how best to change (from) one object to another.(2)
[1.3] While these theoretical expositions are illustrated with many network models of actual music, they do not by themselves constitute an analytical methodology. Indeed, at times Lewin seemed to play down the significance of his networks: “they are only metaphorical pictures of certain things that happen over their pieces as wholes, pictures that make manifest certain characteristic (recurrent) transformational motifs” (MFT, xiii). Considering his other writings, one can understand this reticence as an acknowledgement of the complexity of musical experience—involving the interaction of various modes of perception on many dimensions of music—and the cognitive and phenomenological problems of the notion of a musical “object.”(3)
[1.4] Notwithstanding such reservations, however, Lewin published many detailed transformational analyses, whose insights testify persuasively for the value of the theory. Several of them, such as essays on music by Schoenberg and Bach, self-consciously explicate his analytical procedures and values (Lewin 2008 and Lewin 1998). Most notably, the four chapters in MFT “engage issues of large-scale form as they interrelate with transformational analytic structures” (MFT, ix). Lewin intended the second of these, “Making and Using a Pcset Network for Stockhausen’s Klavierstück III,” as a tutorial, and so it explicitly treats such important issues as the relative merits of event-networks and -spaces, the “logic of global proportioning” that governs the selection of objects and the construction of networks, and the tension between the significance of nodes as aural “presences” and as abstract “potentialities” (MFT, 32–36). Taken together, then, these writings do constitute—to a certain extent—a methodology of transformational analysis.
[1.5] I venture to qualify this assertion, however, because I believe that Lewin’s writings do not adequately explain how to apply the theory. For example, while they carefully justify their selection of objects, they do not teach how to select the object family itself. Either they accept the family identified by other analysts, or the music involves an obvious contrapuntal subject.(4) The few discussions that consider various possible object families, such as MFT chapter 4, develop event-network analyses that focus on transformational motives, not on spaces; his spatial-network analyses all involve pcset motives. Does this mean that, for instance, a space involving simply the 12 pitch classes is not suitable for transformational analysis of form? More generally, for passages that admit various possible object families, how does one choose among them and how does the choice affect what the analysis can say?
[1.6] Considered together, the writings also vacillate on the merits of event-networks. In the Stockhausen tutorial, Lewin faulted them because each arrow “has to bear enormous weight in asserting some sort of phenomenological presence” that he cannot in every case hear (MFT, 32), and because they do not show how the gestures’ “contours and boundaries [are] shaped by the abstract proportions of the given universe” (MFT, 41). But it is not clear whether he intended these reservations to be general, methodological ones, or whether they are specific to the difficult piece at hand. In any case, event-networks dominate the other articles and GMIT, which devotes much discussion to the significance of their “precedence ordering” and “input” and “output” nodes (GMIT, 209–218). What sorts of factors determine “presence” and therefore the acceptability of a particular arrow? Are multiple “passes” through spatial networks the only way to clarify form and to show how gestures are constrained by the formal structure of the transformations, or can event networks with acceptable “presence” also achieve these goals?(5)
[1.7] Most frustratingly, given Lewin’s stated rationale for the theory, his analytical writings are unspecific and even contradictory about how to achieve the “inside,” “active” perspective facilitated by networks. What, exactly, is the nature of the “insider” who performs the transformations, and how does it contribute to analytical explication? Must its “gestures” be single arrows, or may they comprise more complex arrow configurations? Is the insider the piece itself (as his narration of spatial network has it, MFT, 37–40), whatever that means? Or must it be human?(6) Is it “I” (GMIT, 159)? Is choice—a quality so pregnant in his description of the insider—evident only retrospectively by external observation, as we attribute purpose to the sequence of transformations, or can we vicariously experience it as real-time agents?
[1.8] Lastly, Lewin’s tutorials employ a very narrow repertoire of transformational systems, essentially transpositional and inversional relations among pcsets. He justified this restriction by his wish to “remain within a certain mainstream of current analytic/theoretical literature in the United States” (MFT, xiii). But it makes his networks seem impractically limited in relevance, especially considering the broadening of theoretical research in the last twenty years. How are the principles of making and using networks affected by the nature of the transformational systems themselves, and by the nature of form in other sorts of music? And how does Lewin’s methodology apply to making more general sorts of networks, such as those proposed by Rahn 2004 and Hook 2007?
[1.9] In sum, it seems that Lewin left open many questions about how to construct meaningful transformational analyses. Other theorists have treated them only sporadically and indirectly. Perhaps inspired by Lewin’s remarks about spatial networks, many focus on discovering new spaces and illustrating them with brief musical excerpts.(7) More strictly analytical applications are naturally concerned with promoting a particular perspective rather than weighing various interpretative possibilities.(8) Only in the relatively constrained context of Klumpenhouwer networks has there been much discussion about the relative merits of various interpretations (Buchler 2007). In the context of this fascinating system-building and analytical investigation, it seems all the more imperative to revisit the pragmatics of “making and using” networks. Much more needs to be said about the goals and principles that should guide the choice of object families and transformations, type of network, and visual layout in order to make analyses persuasive. Explicit consideration of various options for the same passage can show how they both enable and constrain analytical explication. The nascent notions of gesture and agency, so integral to the “transformational attitude,” merit further exploration and development, as do new modes of presentation for making them manifest.
Some preliminary observations and principles
[2.1] To contribute to such a discussion, the following case study develops contrasting approaches to a straightforward but fertile passage: measures 1–32 of the Scherzo to Bartók’s Piano Suite, Op. 14. Example 1 reduces the piano score to a single staff, and adds several colored boxes and verbal annotations to be referenced in the discussion below. The discussion will proceed in the manner of a tutorial, the better to address the questions raised above.
[2.2] To be persuasive, an analysis should reference salient percepts as well as the processes of repetition, development, and change that involve them, considering both regularities and disruptions. I perceive in this passage a series of pitches with equal duration, grouped by changes of contour and interval-size into measures of three. Breaks in the regular rhythm (the notated rests) and changes of register articulate four-measure-long segments. Depending on how the pitch structure is conceived, certain parallelisms among these groups may be evident, as well as some deviations from exact repetition.
[2.3] For example, with reference to the universe of 12-tone equal-tempered pitches, we can make the following observations, which are marked and color-coded on the Example. The colors indicate events that do not simply continue established patterns.
- Measure 2 exactly transposes measure 1 seven semitones lower, and measure 3 exactly transposes
measure 2 by the same interval; measure 4 begins as if it will be an exact transposition of
measure 3 again by the same interval, but instead of continuing that process, the B
 is repeated an octave lower, then a rest interrupts the rhythmic continuity.
is repeated an octave lower, then a rest interrupts the rhythmic continuity.
- Measures 5–6 repeat measures 1–2; measure 7 states the same series of pitches (that is, the same keys on the piano) as
measure 3 but spells them differently; also,
measure 8 differs from measure 4. Measures 9–14 transpose measures 1–6 up 5 semitones, but
measures 15–16 transpose measures 7–8 differently.
- At measure 17, a pitch-inversion of the opening passage seems to begin, but not seven semitones from previous beginnings, and its continuation neither transposes nor inverts any of the preceding four-measure segments.
- Measures 21–24 exactly transpose measures 17–20; measures 25–26 begin a transposition of
measures 21–24 by the same interval, but instead of continuing the transposition,
measures 27–28 reiterate measures 25–26, and add doubling; measures 29–30 octave-transpose
measures 27–28, but add an unexpected note G
 ; then the music seems to derail on the {A,G
; then the music seems to derail on the {A,G } dyad, stuttering it in a crescendo through
measure 32.
} dyad, stuttering it in a crescendo through
measure 32.
These observations are the beginnings of an analysis, in the sense that they characterize the basic perceptual data that an analysis should explain. For example, they affirm that the beginnings of musical groups coincide with notated strong beats, so that we can refer to groups by the measures that contain them.
[2.4] One may justifiably expect more from an analysis than this, however. Its representation of the events and processes should distinguish passages that sound different, or it will not be able to account for form and process that involve that difference. In transformational analysis, ideas of sameness and difference are strictly constrained. Every element must belong to a single family, and elements differ precisely and exclusively by the transformations that define that family.(9) These constraints simplify and focus analytical interpretation. But they make the choice of representation especially critical. The objects and transformations should enable us to express and explain the relations, distinctions, and processes we hear to be important. For example, ordered series of diatonic pitches are not the same as pcsets, so if we wish to make distinctions associated with the former (say, register or spelling) we should not model objects as the latter.
[2.5] The preliminary segmentation of the Bartók passage, above, suggests several possible object-families as pertinent: ordered or unordered sets of pitches or pcs, or individual pitches or pcs. Let us explore some of these alternatives in order to understand how they constrain what we can say about the music in a transformational analysis.
A possible transformational system
[3.1] First, let us follow up on the observation that the smallest groups are arpeggiated augmented triads, by which I mean unordered pitch-class sets (rather than, say, ordered pitch series spelled as diatonic scale members). Only four pc sets (under enharmonic equivalence) belong to that family; let us designate each by the integer 0, 1, 2, or 3, according to whether it contains the pitch class C, C![]() /D
/D![]() , D, or D
, D, or D![]() /E
/E![]() , respectively. Thus the group in
measure 1 is represented by the integer 3, which denotes the presence of pcs from the {G, B, E
, respectively. Thus the group in
measure 1 is represented by the integer 3, which denotes the presence of pcs from the {G, B, E![]() } augmented trichord.
} augmented trichord.
[3.2] Although this representation omits much specific information—indeed, all specific rhythms, pitches, contour, dynamics, and articulation—it has certain properties that are also desirable in transformational analyses more generally. The objects (the four augmented trichords) are perceptually salient, that is, readily apprehended and distinguished (perhaps with training).(10) Also, as a family they exhaustively cover the passage in two senses: every family member makes at least one appearance, and every salient segment in the piece can be represented as a family member. So the representation manifests the commonly valued principle of parsimony, “entia non sunt multiplicanda praeter necessitatem,” which I take to mean that our models should not be more complicated than they need to be to explain everything we want to say about the music.
[3.3] Specifically, as we consider how these objects are related—that is, what repertoire of transformations will define the analytical system—we should similarly weigh the consequences of various possible choices. Each transformation should be telling in the sense that it effectively describes a crucial aspect of our analysis. There should be as many transformations as necessary to account for all the changes that we hear shaping the piece, and to ensure that the system collectively possesses the properties necessary to construct transformational networks. But choosing too large a family of transformations implicitly raises the question of why only a few of them are used, reducing their explanatory value. A large family is even more problematic if the analysis does not expose any transformational repetition in the piece, which is one of the primary motivations for using the theory in the first place (as mentioned above). (In [8.5] below, we will see a situation in which a large family is justified.) For example, since transpositions by 1, 5, and 9 have the same effect on the augmented trichord, there is no point in including them all in the transformational system.
[3.4] There are more parsimonious and telling ways to represent all the ways of changing one augmented triad to another. Consider the following three transformations:
- S, which changes an augmented trichord containing pc a to the augmented trichord a+1, modulo 4;
- S-1, which changes an augmented trichord a to a-1; and
- X, which changes a to a+2.
S and S-1 are inverses of each other; that is, applying the two in succession, such as SS-1, is the same as E, the identity transformation that changes a to itself (a+0), so to speak. Also, X is its own inverse (XX=E). Since SS=X and SSS=S-1, the S, X, and S-1, along with E, constitute a complete, closed group, as necessary. (Their effect is like that of addition on the integer residues modulo 4, but in order to clarify that they act on chords, I will keep referring to them alphabetically.)
[3.5] This choice of transformational group precludes distinctions that are possible with a larger family, for example, hearing the change from measure 1 to measure 2 as transposition by 5, not by 1 or 9. Nevertheless, S, S-1, and X possess an analytically telling property: their actions have clear and distinctive aural "signatures" (MFT, 32). A succession mediated by X involves two augmented trichords that belong to the same whole-tone scale, whereas successions mediated by S and its inverse involve augmented trichords that belong to different whole tone scales. Some audible manifestations of this difference are the interval classes that appear between the connected augmented trichords: in S progressions, they are odd (such as semitones or perfect fifths), whereas in X progressions they are even.
An event-network analysis for the augmented-triad system
[4.1]
Example 2
shows a transformational network that represents the passage as the chronological succession of such objects, taking measure-groups with single pcs, such as
measure 4, to be incomplete instances. Each of its nodes denotes not a generic augmented trichord but the contents of a particular one-measure-long group in the piece (thus implicitly preserving the group-creating distinctions of contour and interval-size that the representation eschews). The transformations from measure-group to measure-group, and between the beginnings of longer groups, are indicated by the letters next to the arrows connecting the integers; for clarity, colors distinguish the four transformations. From top left to lower right, each line except the last represents a distinct longer group, composed of a series of mod 4 integers, each designating one of the four augmented triads. The rationale for grouping the measures this way references the formal properties of the series of transformations, as will be explained below. On the last line, the 0 should be understood to indicate the G![]() (from the {C,E,G
(from the {C,E,G![]() } augmented trichord) that is repeated at the end of this passage together with A, which is represented by the 1 just above it.
} augmented trichord) that is repeated at the end of this passage together with A, which is represented by the 1 just above it.
[4.2] Although this representation ignores contour, register, rests, and note order within the measure, it nevertheless indicates a way of hearing the passage’s form. In other words, the particular transformational sequence of objects exhibits perceptible properties that articulate the beginnings, endings, similarities, contrasts, and continuities of musical groups.
- One of the system transformations, S, is established as characteristic by recurring consecutively seven times at the outset of the passage.
- A formal property of the characteristic transformation is manifested as grouping structure: since SSSS=E,
measures 5–8 exactly repeat measures 1–4, creating a group ending in
measure 4 and a beginning in measure 5. The diagonal E arrow from the first line to the second line on the example indicates this parallelism.
This grouping structure is evident despite the fact that the representation does not include features of
measures 4–5 that signal grouping articulation, but instead involves families of objects
that are more specific than unordered augmented triads, such as the repeated
B the rest, and the return of G5. ,
,
- The first break in the series of Ss is the change into
measure 9, which is X of
measure 8. This contrast helps articulate the beginning of a larger-scale group starting at 9. Yet some continuity can still be heard because
measure 9 is the S-transformation of
measure 5, the beginning of the previous 4-measure group.
- The coherence of measures 1–8 as a large group is solidified by the music after
measure 9, whose first five transformations (all Ss) repeat those of
measures 1–8. And (as was the case at measure 5) since SSSS=E, a repetition of
measures 9–12 begins at measure 13; this repetition is indicated by another diagonal E arrow.
- The contrasting transformation X intrudes again at
measures 14–15, but because the 4-measure group length has been so clearly established, it does not induce a group ending.
Nevertheless, it does suggest subdividing
measures 13–16 into two two-measure groups, a rhythm that is reinforced during the second half of the passage.
- The expected ending of the 4-measure group, measures 13–16, is confirmed at
measure 17 by the only instance of the only other transformation in the group, S-1, extending both from the previous measure and from the beginning of the previous group. And since
measure 17 repeats measure 1, we have a clear sense of beginning again after a break.
- Moreover, we understand the coherent 4-measure group of measures 13–16 to present a new transformational sequence, the alternation of S and X, as an alternative to the reiteration of S in
measures 1–12.
- Taking measures 13–16 as the new model, the second half of the passage (until measure 25) achieves continuity by a regular, predictable alternation of X with S. The four-measure groups subdivide into two-measure groups, each of which features a different whole-tone scale resulting from an X-related chord-pair.
- Since XSXS=X, X also relates successive group beginnings, further distinguishing the two halves of the passage.
- Also, since XX=E,
measure 25 repeats measure 17, motivating the beginning of another large group after the 8-bar coherent group of
measures 17–24.
- The group starting at measure 25 reiterates X the way that the beginning of the piece reiterated S. But because XX=E, this reiteration makes the groups only two measures long.
- The final G
 /A dyad brings closure by recalling the S transformation of 3 to 0 that
concluded the first 16-bar group (indeed the G
/A dyad brings closure by recalling the S transformation of 3 to 0 that
concluded the first 16-bar group (indeed the G is the same pc as the A
is the same pc as the A in
measure 16), and by “explaining” the disruptive X as the composite of 2 Ss.
in
measure 16), and by “explaining” the disruptive X as the composite of 2 Ss.
Across the entire passage, large-scale transformations reproduce, and thus sound motivated by, small-scale transformations. The transformation E from the beginning of the first 16-measure group, measure 1, into the beginning of the second 16-measure group, measure 17, repeats the transformation of the beginning of the first 4-measure group (measure 1) into the beginning of the second 4-measure group (measure 5). The transformation S from the beginning of the first 8-measure group, measure 1, into the beginning of the second 8-measure group, measure 9, replicates the transformation of measure 1 into measure 2. In the second half of the passage, the transformation X from the beginning of the first 4-measure group, measure 17, into the beginning of the second 4-measure group, measure 21, is the same as the transformation of the first measure (17) to the second measure (18).
[4.3] The advantages of choosing this family of transformations are implicit in these observations of their graphical rendering. Every member—even the one, E, that seemed to be a mere mathematical obligation—appears in a formally functional role at some point in the network analysis of the passage. In this sense, every transformation has explanatory value; none is superfluous. Also, identity and difference among the transformations can be heard to have formal functions: consistent series of transformations create continuity, and so inconsistencies create discontinuities that mark grouping boundaries. It is not the mere recurrence of the individual transformations that makes them significant, for repetition is practically inevitable in such a small system. Rather it is the existence of clearly directed series into which the transformations are organized. Repetitions occur here iteratively, in direct succession, and the deviations seem carefully placed to maximize impact. Less-sudden, emergent contrasts of content that distinguish large-scale sections, such as between the X-dominated second half and the S-dominated first half, seem motivated and logically developed.
[4.4] This network analysis also accounts for some of the striking features we first observed in the passage (see [2.3] above). The rest in measure 4 is motivated by arriving at the last of the four possible augmented triads. Measure 17 is represented as the same kind of object as measure 1, suggesting that we hear it in a formal role analogous to a beginning. On the other hand, the network does not show any difference between measures 3–4 and 7–8, and so it does not account for their difference in spelling and cadential pcs.
[4.5] Event-networks like Example 2, presented statically on the page, are common in the analytical literature. Because its nodes represent the contents of timespans, they make a spatial analog of the transformation-produced form, and the temporal sequence can be reconstructed by reading them like a text. However, they also misrepresent temporality to some extent: nodes appear equally and constantly present, obscuring the changes and displacements that are aurally evident. Also, the sheer number of nodes in a longer passage can make structure difficult to see (perhaps for this reason the literature contains few instances of event networks of this size).
Animation of an event network
[5.1] Temporality and clarity can be better served, though, by a technique not readily available to earlier transformational theorists: animating the diagram, such that the nodes appear visually in the order and at the time that the corresponding measure-groups appear in performance.(11) Animation 1 presents such an animation. As each node appears, the arrows that appear pointing to it explain it as the transformation of previous nodes, conforming to the analytical narrative presented in [4.2] above. The appearance of arrows only at the time that the relations they identify become salient helps clarify the grouping structure; note the effect, especially, of the appearance of three arrows at the onsets of measure 9 (0:12), measure 17 (0:24), and measure 25 (0:36; use the playback controls to start the animation at any time). The persistence of the nodes may not conform precisely to how a listener retains the augmented triads in memory, but it does clarify the associations that each transformation makes between current and past augmented triads, and so it too clarifies the developing form. By focusing on one transformation at a time, animation also helps one to hear the aural signatures of the characteristic transformations, for instance, the whole-tone-scale sound of X.
[5.2] A more systematic deficiency of event-networks like Example 2 is that they poorly account for ways of hearing events as occurring, metaphorically at least, in specific positions in a limited, ordered realm of possibilities, and thus of hearing referentiality, departure, distance, and return. Such sensations are common when cognizing melodic pitches as members of a scale or chords as instances of harmonies, and they are conceivable for other families of musical objects as well. It is true that this sort of perception is facilitated by any transformational classification of events as members of an atemporal family, such as Example 2’s reduction of each measure to one of the four augmented triads. Yet since location on Example 2 signifies time of attack, not transformational relationship, the returns to an object-type and repetitions of series of object-types are not immediately evident. (Only the E arrows assist somewhat in pointing out which label identities have formal significance as returns.) Also, the diagram does not represent the difference between X and S transformations very well, because these labels are often given to arrows of the same length pointing in the same direction. Without color there would seem to be no difference at all.
A spatial representation for the augmented-triad system
[6.1] The other type of network Lewin discusses in MFT chapter 2 solves some of these problems. Superficially, it resembles an event-network, connecting nodes containing a single type of music object with arrows labeled by transformations that associate the objects into a family. But rather than each event appearing as a distinct node, each member of the object family (in this case, augmented trichords) appears as a distinct node. Consequently, there are only as many nodes as there are members of the object family. Location in such networks signifies transformational relation, not temporality; a given node may stand for one or many events in the piece, or may even not be realized as an event at all. Also, this type of graph shows all possible transformations from every node to every other, not just those transformations that the analyst wishes to assert between events of the piece. Thus, such a network is not an analysis but a space, a representation of all transformational possibilities within the chosen system.(12)
[6.2] Because spaces and event-networks are both represented by node-arrow systems, the important differences between them are not immediately apparent. Constructing a space for a piece posits a systematic context, that is, an organized set of states to which events belong. The space represents the states, but not the sequence of events that belong to those states. The difference is dramatized by Example 3, a space for analyzing the Bartók passage. It reduces the 31 nodes of Example 2 down to just four, one for each augmented trichord. Four arrows, each labeled with one of the four members of the transformation group, proceed from every node, even if that particular succession (for example, 3 transforming by S-1 to 2) never occurs in the piece.
[6.3] Also, event networks are better suited to show analytically significant network isographies—the repetitions of transformation-complexes that Lewin calls “gestures.” In a spatial network, in which the nodes do not refer to specific events, isographies among subnetworks can be seen, but without further explanation, it is not clear whether or not they are musically relevant to particular pieces. For instance, the repetitions of SSS and XSX stand out in Example 2 but have no representation at all in Example 3. However, the sense in which they can be construed as “gestures” is not evident. On a static network, the act of moving from one node to another is merely a matter, in every case, of shifting one’s attention along an arrow, and even though the arrows are differently labeled and colored, it is not easy to think of an X arrow as a different “gesture” than an S arrow.
[6.4] This space affords a convenient opportunity to see how visual presentation can clarify or obscure transformational structure. Example 4 shows some possible configurations for the case at hand, copying over Example 3 as 4c. (For visual simplicity it omits the E and S-1 arrows, but they should be understood). Although these are formally equivalent, their layouts privilege different features. Network (a) highlights two columns of X-related nodes while orienting S-connections inconsistently on the page; network (b) emphasizes the S-sequence <0,1,2,3>, such that the X arrows appear to leapfrog over adjacent nodes. In contrast, network (c) is clearly superior, because it represents every distinct transformation as a visually distinctive motion: S transformations are depicted as clockwise motion around a rectangle, and X transformations are depicted as motion along a diagonal.
[6.5] A good reason to give distinctive spatial interpretations to different transformations becomes evident when we consider how to use spaces for musical analysis. At first glance, they do not seem very suitable, as they represent a complete repertoire of objects and transformations, not the piece-specific sequence of events. However, to the extent that they clarify the formal properties of the transformations and their differences, they can express the framework and assumptions of an analysis more directly than event-oriented networks such as Example 1. Specifically, Example 4c shows that the piece is being conceived in terms of just four different objects and two transformations (together with the identity and their inverses), and that by repeatedly applying S (or S-1), one can cycle through all four objects and return to the start, signifying the formal function of return.
[6.6] Still, without further annotation or commentary, the symmetrical structure of this network gives no hint of how the piece begins, proceeds, or ends. It conflates distinct events and eliminates order. Moreover, clarity of analytical insight is difficult to achieve on such small, static displays. In large spaces, such as the one Lewin uses to analyze pentachord transformations in Stockhausen’s Klavierstück III (MFT chapter 2), the analyst can show diagrams of paths, each indicating how the notes are sequenced temporally in a particular passage of the music. In smaller spaces, though, tracing all the paths that correspond to the arrows of an event diagram for any reasonable chunk of music—for example, showing all the specific arrow information for the first half of Example 2 as annotations on Example 4c—would produce a confusing visual tangle.
Properties of spatial animations
[7.1] Temporality and clarity can be achieved, however, through animation. Animation 2 shows, in the space of Example 4c, a green circle shifting (abruptly) from one node to another, following the sequence of augmented trichords in the music. Its simplicity is not due to technical limitations (as will soon become evident in later examples) but is intended rather to show certain features that all animations share, even the most minimal ones. With this particular layout of the space, the circle’s changes of location make certain recurring patterns apparent, for example, the shift from a node to the clockwise adjacent node, and the shift from a node to the diagonally opposing node. Of course, these patterns correspond respectively to the transformations S and X that dominate the analysis. The animation helps us perceive their repetition not merely as a labeling identity on a static diagram but more dynamically as a consistent way that augmented trichords change.
[7.2] Because S and X repeat so often, and because the space is arranged so that S- and X- related nodes are contiguous, the shifts associated them with appear as continuous motions from one node to another. That is, the circle appears to perform every S shift (and X shift) as a traversal of the space between the nodes in a set time. Consequently it seems appropriate to call it a “gesture.”(13) Apparent motion also emphasizes the difference in visual orientation of S- and X-changes, further enhancing their gestural qualities.
[7.3] The emergent concreteness of “gesture” in this animation allows us to think more deeply about what that concept entails, addressing the lacunae in Lewin’s writings mentioned in [1.8] above. Note that we attribute the gestures to a visual entity (the shifting circle) that is not properly part of the transformational network at all, since it is neither a node nor an arrow (neither of which moves). What does this entity signify? A benign interpretation is that it is simply a means of focusing the observer on the sequencing of nodes: it entrains then guides the observer’s visual attention into a scanning of the space that corresponds to a hearing of the piece. (This entrainment is facilitated cross-modally in Animation 2 by the perfectly metrical changing of augmented trichords, a feature of this passage that makes it especially apt for such an animation.) A viewer who submits to this guidance acts in two roles. As a participant, the viewer shifts visual attention concurrently with changes in the music. As an observer, the viewer perceives the entire contexts of these shifts—visual and music-structural—and comprehends that they assert an analysis by the designer of the animation. Thus, the circle, in this interpretation, is simply the analyst’s vehicle for directing the viewer’s attention and experience; its motions are expressions of the analyst’s choices. Whatever gestural qualities its motions acquire do not make it a performer or other “inside” agent.
[7.4] There is another interpretation of the circle, however, that attributes agency in a different and expressive way. It involves a basic process of visual perception: our attribution of intentionality to objects that move in certain ways with respect to their environment.(14) To the extent that Animation 2 engages that perception, viewers will regard the circle as an agent that traverses the space through its own intentional acts. This seems consistent with Lewin’s conception of a musical “insider.” And by displacing the attribution of agency from the analyst to the object, viewers focus not only on the visual sequence of nodes but also more closely on those motions in which the object’s agency is manifest. These are moves that contravene established patterns, or moves that seem deliberately prepared.
[7.5] Instances of such agency-endowing moves indeed take place in the visual representation of the augmented-triad changes in the Bartók passage. Animation 3 highlights them by reworking the abstract Animation 2 into a representational environment: four lily pads, one for each of the augmented triads, in a pond inhabited by a fish. This agent’s motions express a willful change from one location in the space to another, and to reinforce that impression, the animation shows the fish moving continuously between pads, rather than shifting abruptly as the circle did. To emphasize the difference between S and X transformations, the fish moves by gliding through the water or by leaping out of the water, respectively. Both of these motions, though distinct, give the transformations a spatial continuity, and thus a more gestural quality, that could only be inferred from the abrupt changes of Animation 2.
[7.6] This resort to representation may strike some readers as strained. As Cook and others have shown, the relation of different media is complex, and the different symbol systems interact in complicated and not always mutually conformant ways (Cook 1998).(15) By representing the agent this way, is the analyst suggesting fishy motivations for its motions? Would these perceived motivations change if the agent was a frog or a water spider? Yet there are distinct differences between this clip and, say, the fanciful animations of Disney’s Fantasia. The physical system and motions are highly constrained to correspond directly to the space and transformations; there is no extraneous information. Nearly all the visual information—static layout, motions, and changes—corresponds directly to some aspect of a purely musical analysis.
[7.7] In particular, due to the choice of transformations and layout of the space, the fish’s motions do not appear to be random or disconnected. Rather, they imply intentional behavior involving the characteristic gestures we observed in the circle animation. For the first 12 seconds (corresponding to measures 1–8; use the playback controls to start or to position the animation at any moment), the fish moves consistently clockwise around the lily pads in the pond, starting with the motion from 3 to 0. This makes the first deviation from this motion, a leap that diagonally crosses the space at measure 9, seem surprising—a sudden revelation of previously hidden capacity—especially when the clockwise motion resumes immediately thereafter. The new gesture clearly articulates the beginning of the larger musical group, on 0, at that moment. The fish leaps again at 0:21 (measures 14–15), this time to node 3. After briefly resuming clockwise motion to 0 (reprising the first motion of the piece), the fish reverses direction back to 3, corresponding to the change into measure 17. After this (testing of the waters?) the leaping motions become much more frequent, alternating strictly with clockwise glides until the fish regains 3, after which the motion is restricted to leaps between 3 and 1. The gradual change from gliding predominately clockwise around all the nodes to leaping exclusively between two of them appears deliberate. It corresponds to the audible change from successions of fifth-related to whole-tone-related augmented trichords. And these apparently purposeful motion-patterns and -changes make the visual grouping structure, corresponding to the musical groups, seem to be the manifestation of a performer’s will—only the performer is not a pianist hitting various keys, but a fish whose gestures metaphorically represent the structure of the pitch changes. Thus the viewer’s attribution of intentionality to objects in transformational animations can be a very powerful expressive tool. The presence of a moving agent, as well as the visual structure of the space, helps represent the characteristic transformations as repeating gestures.
[7.8] Although this space is very minimal, animation conveys many of the observations of the event-network analysis more simply. Still, it does not engage some of the preliminary observations we made about the piece involving specific pitches, apart from the augmented triads to which they belong (see [2.3] above). For instance, it conflates measures with only one pc with measures that contain complete augmented trichords, so
it cannot distinguish
measure 4 from measure 8, or either of them from measure 11. (In this respect, it has the opposite problem from event-networks, identified in paragraph [4.5] above, which can obscure recurring transformational relationships.) It attributes no significance,
for instance, to the enharmonic reinterpretation of
measure 3 in measure 7 that calls attention to the perfect fifth C![]() to F
to F![]() . Nor does it differentiate one ordering or registration of an augmented trichord from another, so it cannot distinguish
measure 1 from measure 17. To the extent that we want to value such distinctions, it seems desirable to consider some other possible transformational systems, engaging the piece at the level of individual events, and involving different transformations, in order to access this level of detail. But we do not want to lose sight of the grouping structure so clearly expressed by the augmented-triad analysis. And we should keep in mind the ideals, floated in [3.2–3.3] above, concerning the size and salience of object- and transformation-sets in whatever system we choose.
. Nor does it differentiate one ordering or registration of an augmented trichord from another, so it cannot distinguish
measure 1 from measure 17. To the extent that we want to value such distinctions, it seems desirable to consider some other possible transformational systems, engaging the piece at the level of individual events, and involving different transformations, in order to access this level of detail. But we do not want to lose sight of the grouping structure so clearly expressed by the augmented-triad analysis. And we should keep in mind the ideals, floated in [3.2–3.3] above, concerning the size and salience of object- and transformation-sets in whatever system we choose.
A different transformational system
Example 5. Characteristic moves of the first pc of each measure from a member of an augmented triad 4-wiggle
(click to enlarge)
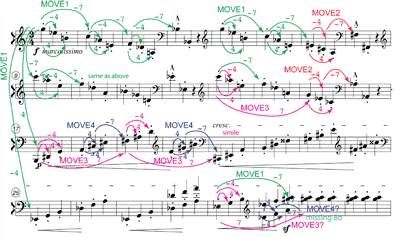
Example 6. Instances of MOVEs in the Scherzo excerpt
(click to enlarge)
[8.1] The elements of this new system are simply the set of twelve pitch classes and the pc transpositions that act upon them. To accommodate the grouping structure exposed above, however, we will need to expand our notion of “characteristic gesture.” Specifically, let us consider each augmented triad to be the result of two transpositions, 4 and its inverse -4, acting upon a referential pitch class. Together they constitute a distinctive two-part change, which we might conceive gesturally as a “wiggle by 4 on both sides” of the referential pc. For instance, transforming the first note of measure 1, G, by these transpositions yields the other two notes in the measure. Also, a 4-wiggle on the incipit of measure 17 yields the other two notes in that measure; that is, this pair of transformations can generate both descending and ascending forms of the augmented trichords that appear in this passage. I will mostly take the group incipits (the first pc of each measure) to be referential, consistent with the contour changes that emphasize them. But in some measures I will consider one of the other pcs to be referential, thus sacrificing a strictly temporal presentation of events within measures in favor of identifying an underlying unity of content.
[8.2] With reference to the pcs preceding it, every incipit can then be understood as the result of one of just four closely related successions of transformations, which I will call MOVEs. Each MOVE is a transposition “down or up by perfect fifth”—more properly, by pc-interval -7 or its inverse, 7—of one of the pcs in 4-wiggle.(16) They are diagrammed as networks in Example 5; to clarify their difference, and to set up some further developments, the 4- and 7-arrows are shown in different dimensions and with different types of arrow shaft. So each is a “gesture” in the sense of a combination of simpler motions, just as a human gesture may combine simpler motions of different limbs; this is a more sophisticated conception of gesture than the single arrows on the previous analyses.
[8.3] Some instances of MOVEs are indicated on the annotated score of Example
6, and the following narrative suggests how well the form and processes of the passage can be heard in terms of them. The greater detail made possible by this choice of objects entails some readings that diverge from those of
- Let us consider the C incipit of measure 2 to be the result of a MOVE1 from the
measure 1 incipit G, from which a 4-wiggle generates the other pcs in measure 1.
- The immediately following events justify this choice: each incipit in
measures 3, 4, 6, and 7 can be heard similarly as the result of a MOVE1 from the preceding measure’s incipit, which generates the other pcs in its measure by a 4-wiggle. This consistent pattern provides a basis for interpreting later developments.
- In measure 5, none of the pcs is 7 from the B
 in
measure 4, so to the extent that we are hearing musical continuity in terms of MOVEs, we will perceive here a caesura and a new beginning. This seems appropriate, given the rest and the change of register. (Contrast this interpretation with that of Example 2, which shows no break in continuity here, because it shows
measure 5 as resulting from yet another reiteration of S.)
in
measure 4, so to the extent that we are hearing musical continuity in terms of MOVEs, we will perceive here a caesura and a new beginning. This seems appropriate, given the rest and the change of register. (Contrast this interpretation with that of Example 2, which shows no break in continuity here, because it shows
measure 5 as resulting from yet another reiteration of S.) - Measure 9 and measure 13 must be analyzed similarly to measure 5, but in all
three cases, as in measures 1-2, MOVE1s generate the incipits of the following
measures, thus propagating that distinctive transformational continuity and
articulating a 4-bar grouping structure.
- Although measure 8 is identical to measure 4 in the analysis of Example 2,
they must be different in this new transformational system, because the measure
8 pc is F
 ,
not B
,
not B .
We could explain F
.
We could explain F as a MOVE1 from the C
as a MOVE1 from the C in measure 7, but that would be inconsistent with the established pattern of
treating the incipit of each measure (in this case, the E
in measure 7, but that would be inconsistent with the established pattern of
treating the incipit of each measure (in this case, the E of measure 7) as both the result of a MOVE1 and the
generator of the other pcs in its measure. Rather, let us regard it as a
different gesture, MOVE2, that is, -7 from the pc
that is -4 from a referential pc. This distinction is justified by later events:
the only other time that MOVE2 appears is at
measure 16, so both instances of this gesture are associated with the caesura to
an 8-measure group. (This representation involves different temporal sensations
than Example 2, which shows only the ubiquitous S
moving into these caesuras. Group endings, in Example 2’s account, arise
retrospectively from transformational changes that follow them,
whereas in
Example 6, some endings are evident prospectively by the distinctive
transformational gestures that produce them.)
of measure 7) as both the result of a MOVE1 and the
generator of the other pcs in its measure. Rather, let us regard it as a
different gesture, MOVE2, that is, -7 from the pc
that is -4 from a referential pc. This distinction is justified by later events:
the only other time that MOVE2 appears is at
measure 16, so both instances of this gesture are associated with the caesura to
an 8-measure group. (This representation involves different temporal sensations
than Example 2, which shows only the ubiquitous S
moving into these caesuras. Group endings, in Example 2’s account, arise
retrospectively from transformational changes that follow them,
whereas in
Example 6, some endings are evident prospectively by the distinctive
transformational gestures that produce them.)
- The next deviation from MOVE1 continuity is
measure 15, none of whose pcs is -7 from a pc in measure 14. Example 6 shows one
possible interpretation: that its incipit G be understood as 7 (not -7) from the
group-beginning we heard in measure 13. In the limited repertoire of
4-wiggles and 7s that have made up the MOVE gestures so far, this so-labeled MOVE3 seems plausible as complementary to, or a reversal of, MOVE1. This hearing suggests the division of measures 13–16 into two two-measure groups (as did the unexpected appearance of X at this point in Example 2), which is reinforced by the fact that measure 15 repeats the pc-series of group-beginnings measure 1 and measure 4, and that it initiates the second MOVE2.
- If MOVE3 appeared only once, this analysis
would not be very convincing. Yet it recurs constantly, generating, as in its
first instance, the incipits of every alternate measure, and so
providing strong continuity across the entire second half of the passage.
- Measure 18 presents a now-familiar deviation: none of the pcs is -7 (or 7)
from a pc in the previous measure. One way to explain it (and the succeeding
even-numbered measures) is to consider the gestures we have invoked so far.
MOVE1 and MOVE2 are related in the sense
that they each involve a -7 move from one of the three pcs of a 4-wiggle. It
seems sensible to imagine completing this repertoire of MOVEs with one that
would involve the remaining pc of the wiggle, namely -7, from the pc that is 4
from the wiggle’s referential pc. If we do, then we can hear the incipit of
measure 19 to be generated by this gesture, which is labeled on the examples as
MOVE4. This explanation deviates from the strictly linear account we have
developed so far: it makes measure 18 (and succeeding even-numbered measures)
seem to appear out of thin air, so to speak, without being generated by a
previous event. This is not necessarily a problem. It ignores the
measure-to-measure continuity (i.e., between 17 and 18) in order to identify the
enhanced continuity towards the incipits of the two-measure groups, each of
which is at once the goal of two distinct MOVEs. And Bartók’s original notation
specifies that the hands alternate every measure during this passage, implying
two independent continuities.
- This analysis has now accounted for all the events of the passage as
participants in MOVEs except for the last dissonant {G
 ,A}
dyad, around measure 31. If the sequential pattern of the second half of the
passage were to continue, we would expect a B
,A}
dyad, around measure 31. If the sequential pattern of the second half of the
passage were to continue, we would expect a B here as the result of both a MOVE3 from the E
here as the result of both a MOVE3 from the E in measure 29 and a MOVE4 from the F in measure 30.
Instead, we can regard the A as a carryover from the 4-wiggle in measure 30, and
the G
in measure 29 and a MOVE4 from the F in measure 30.
Instead, we can regard the A as a carryover from the 4-wiggle in measure 30, and
the G ,
as shown on Example 6, as the result of a MOVE1
from the E
,
as shown on Example 6, as the result of a MOVE1
from the E —perhaps recalling the first gesture of the piece in order to create a sense of
rounding-off and closure.
—perhaps recalling the first gesture of the piece in order to create a sense of
rounding-off and closure.
- Finally, a large-scale aspect of the passage needs to be addressed: why do
the 8-bar groups in measures 9, 17, and 25 begin on the pcs they do? Considering
the incipits of those groups, (respectively C, B, and E
 )
in the contexts of the first pc, G, and the characteristic gestures described
above, a simple explanation suggests itself: they are a large-scale (and
reordered) manifestation of the first transformational gesture of the piece, the
MOVE1 between measure 1 and measure 2. The arrows between
system-beginnings on
Example 6 make this insight explicit: the B and E
)
in the contexts of the first pc, G, and the characteristic gestures described
above, a simple explanation suggests itself: they are a large-scale (and
reordered) manifestation of the first transformational gesture of the piece, the
MOVE1 between measure 1 and measure 2. The arrows between
system-beginnings on
Example 6 make this insight explicit: the B and E initiating the last two 8-bar groups are members of a 4-wiggle centered on the
measure 1 G, from which a MOVE1 generates the C
that begins measure 9.
initiating the last two 8-bar groups are members of a 4-wiggle centered on the
measure 1 G, from which a MOVE1 generates the C
that begins measure 9.
[8.4] Let us compare the results of this analysis with those of Example 2, produced by considering the augmented trichords and transformations S and X. Although they differ in some points, as noted above, they both exemplify some desiderata for constructing meaningful transformational analyses. In both cases, the careful selection of objects and transformations produces a comprehensive account of the passage that asserts a clear grouping structure, processes of continuity within the groups, and particular associations and contrasts that clarify event hierarchy and formal function. Parsimony, so evident in Example 2, is also a feature of Example 6, in the sense that it refers to only two pc transpositions and their inverses.
[8.5] Technically, though, we are overlooking some hidden superfluity in the latter example. If 4 and 7 are considered part of the transformational repertoire, then so must be all composites of them, that is, all the pc transpositions. But we can accept this superfluity in order to gain the distinct advantages of employing selected members of the family. The transpositions 7 and 4 establish themselves as characteristic and form-creating; that is, they articulate not only small-scale grouping structures from measure to measure, but also larger ones, such as measures 9–12, which are a fifth-transposition of measures 1–4. This transformational family has the additional advantage of applying to later passages in this piece that do not involve augmented trichords at all. For instance, Example 7 shows how the 4s and 7s involved in the wiggles and MOVEs of measures 1–32 manifest themselves clearly but in different networks during the next measures of the piece.
[8.6] By diagramming MOVEs on the score, Example 6 presents an event-oriented analysis like
Example 2. Recalling
Animation 1 and
Animation 2, though, we may wonder whether a space, with an animated agent, can present this analysis more compactly and with at least as much “phenomenological presence.” To consider this question fully, and to learn more about how the choice of transformations and objects can enable or constrain various sorts of analytical observations, let us consider several possible proto-spatial networks and agents. Some of them will also enable us to address two issues that were raised in the initial discussion of the piece, but that have so far been studiously ignored: why does the first group end on B![]() and without a complete augmented triad? And why the insistent stuttering on {G
and without a complete augmented triad? And why the insistent stuttering on {G![]() ,A} at the end of this passage? Can we perhaps construct some narrative in which these striking events have a role?
,A} at the end of this passage? Can we perhaps construct some narrative in which these striking events have a role?
Agents and narrative in a quasi-spatial network
[9.1] The layout of Example 5, showing 4s and 7s in different dimensions, suggests one possibility in which an agent can readily be seen to execute a series of purposeful gestures. To set the stage, Example 8 extrapolates Example 5 to show all the pitch-classes arranged one to a square on a parquet floor. From each square the left- and right-neighbors are pc-intervals -4 and 4 away, and the front- and rear-neighbors are -7 and 7 away, respectively; the horizontal strips are colored differently to clarify this arrangement. In this view, the floor’s boundaries are not clear, but some duplication of pitch class is evidently involved (for example, two tiles in the upper-middle left of the example are labeled G and B, just like the two tiles in the immediately right foreground). So the floor is not a minimal space, in the sense of including just one instance of each object. These extra tiles can be used to distinguish different events with the same pitch-class, thus maintaining some of the “phenomenological presence” of a purely event-network, while their layout reinforces the 4 by 7 spatial structure. This redundancy helps explain some relationships in the piece, as we shall see.
[9.2] In Example 8’s representation of the network, a tempting wedge of cheese occupies a B![]() tile. We gaze upon it together with a mouse sitting on a G tile in the foreground. This agent was chosen deliberately to evoke two particular intentionalities highly characteristic of rodents: an instinct for self-protection and a singular determination to eat. The former (heightened by the large area of the floor) is manifested by the mouse’s constant scanning from side to side, and the latter by its motions toward the food. These two gestures enact the two transpositional structures that are characteristic of the piece. Due to the arrangement of the floor, each side-to-side scan brings into view the pcs that belong to the same augmented triad as the pc upon which the mouse stands. That is, the head-wag enacts the “4-wiggle” from a referential pc, which I showed to describe many of the measures in the Bartók excerpt. Forward motion corresponds to a -7 MOVE from one measure to the next. Thus the sequence of events in the piece seems motivated by the mouse’s pursuit of these dual intentions.
tile. We gaze upon it together with a mouse sitting on a G tile in the foreground. This agent was chosen deliberately to evoke two particular intentionalities highly characteristic of rodents: an instinct for self-protection and a singular determination to eat. The former (heightened by the large area of the floor) is manifested by the mouse’s constant scanning from side to side, and the latter by its motions toward the food. These two gestures enact the two transpositional structures that are characteristic of the piece. Due to the arrangement of the floor, each side-to-side scan brings into view the pcs that belong to the same augmented triad as the pc upon which the mouse stands. That is, the head-wag enacts the “4-wiggle” from a referential pc, which I showed to describe many of the measures in the Bartók excerpt. Forward motion corresponds to a -7 MOVE from one measure to the next. Thus the sequence of events in the piece seems motivated by the mouse’s pursuit of these dual intentions.
[9.3] Accordingly,
Animation 4 animates the first four measures of the piece. The mouse glances left then right, taking in E![]() then B, the other pcs of the G augmented triad, in the order that they appear in measure 1. These head-wags, emphasized by flashes of red on the tiles, enact the
then B, the other pcs of the G augmented triad, in the order that they appear in measure 1. These head-wags, emphasized by flashes of red on the tiles, enact the ![]() . It is rewarded for its audacity with a stunning blow from a mousetrap, which is suddenly revealed as the cheese’s cradle. The whack coincides with the dynamic accent on the downbeat of measure 4, and the rodent’s collapse into momentary unconsciousness mimes the subsequent octave descent and rest.
. It is rewarded for its audacity with a stunning blow from a mousetrap, which is suddenly revealed as the cheese’s cradle. The whack coincides with the dynamic accent on the downbeat of measure 4, and the rodent’s collapse into momentary unconsciousness mimes the subsequent octave descent and rest.
[9.4] Although strictly speaking the bait and the trap are not part of the transformational network, the special function they attribute to B![]() with respect to the agent’s gestures is not as whimsical as it may seem. In fact, it suggests how to hear all the events of the passage as contributing to directed motions toward B
with respect to the agent’s gestures is not as whimsical as it may seem. In fact, it suggests how to hear all the events of the passage as contributing to directed motions toward B![]() . In this animation, the motions appear as the mouse’s repeated attempts to gain the bait by various strategies.
Animations 5–7 demonstrate that when the transformational gestures are visualized as physical gestures, they seem to contribute coherently to this narrative.
. In this animation, the motions appear as the mouse’s repeated attempts to gain the bait by various strategies.
Animations 5–7 demonstrate that when the transformational gestures are visualized as physical gestures, they seem to contribute coherently to this narrative.
[9.5]
Animation 5 takes up where Animation 4 left off. Apparently, the mouse is awake and ready for another self-protective scurry to the cheese, which still sits on B![]() in the trap reset by an unseen antagonist. It repeats its previous approach, starting from G and advancing by MOVE1s to C and then F, touching on the pcs of the associated augmented trichords by glancing left then right in 4-wiggles. (The temporal and spatial discontinuity from the end of
Animation 4 and the retracing of the mouse’s steps, nicely conform to the sense of restarting that we observed in the purely transformational account above.) Rather than repeat its trap-springing step onto B
in the trap reset by an unseen antagonist. It repeats its previous approach, starting from G and advancing by MOVE1s to C and then F, touching on the pcs of the associated augmented trichords by glancing left then right in 4-wiggles. (The temporal and spatial discontinuity from the end of
Animation 4 and the retracing of the mouse’s steps, nicely conform to the sense of restarting that we observed in the purely transformational account above.) Rather than repeat its trap-springing step onto B![]() from F, however, it shifts to D
from F, however, it shifts to D![]() as soon as it sees that the coast is clear, then moves forward to G
as soon as it sees that the coast is clear, then moves forward to G![]() . This tile is adjacent to that of B
. This tile is adjacent to that of B![]() , and gives the mouse a position from which it can obtain the cheese while avoiding harm. This motion corresponds to a MOVE2, so the first appearance of this gesture is motivated, in this reading, by the intent of the agent to gain B
, and gives the mouse a position from which it can obtain the cheese while avoiding harm. This motion corresponds to a MOVE2, so the first appearance of this gesture is motivated, in this reading, by the intent of the agent to gain B![]() by a new, non-terminal route. Alas, the heavy load pins the hapless creature to the tile, again terminating its adventure; this motion corresponds to the falling cadence on G
by a new, non-terminal route. Alas, the heavy load pins the hapless creature to the tile, again terminating its adventure; this motion corresponds to the falling cadence on G![]() that ends the
measure 4–8 group. Evidently the cheese must be consumed in place.
that ends the
measure 4–8 group. Evidently the cheese must be consumed in place.
Animation 6. Enactment of measures 9–16
(click to view animation)
Animation 7. Enactment of measures 17–32
(click to view animation)
[9.6]
Animation 6 represents the transformations of measures 9–16 as two further, similarly thwarted ventures. In the first, corresponding to
measures 9–13, the mouse again approaches the cheese, repositioned on B![]() , directly by MOVE1s, as in
Animation 4. This time it begins on C, more exposed but closer to its goal. As it reaches the B
, directly by MOVE1s, as in
Animation 4. This time it begins on C, more exposed but closer to its goal. As it reaches the B![]() , it attempts to avoid the quickly swinging trap by a MOVE1, but falls prostrate on E
, it attempts to avoid the quickly swinging trap by a MOVE1, but falls prostrate on E![]() . On its fourth attempt, again beginning from C, it is assaulted after a single MOVE1 by projectiles (presumably from the malevolent presence that keeps resetting the trap). In an unprecedented gesture (corresponding to a MOVE3 from the C) it falls back to G, then tries by MOVE2 to avoid the onslaught, but a ricocheting arrow immobilizes the wretch on
. On its fourth attempt, again beginning from C, it is assaulted after a single MOVE1 by projectiles (presumably from the malevolent presence that keeps resetting the trap). In an unprecedented gesture (corresponding to a MOVE3 from the C) it falls back to G, then tries by MOVE2 to avoid the onslaught, but a ricocheting arrow immobilizes the wretch on ![]() .
.
[9.7] As portrayed by
Animation 5 and
Animation 6, then, the first four groups involve attempts to achieve and continue on B![]() . Since every attempt is shown to be frustrated, we may intuit the need for a different approach. This sense can help us perceive a purpose for the musical features of the second half of the passage that contrast with the first half—greater continuity, upwards-driving pitch changes, new transformations and gestural combinations, the sense of getting stuck at the end—if we perceive that the visual representations of these features are meaningful in the context of the intentional actions we have attributed so far to the animated agent in this network.
Animation 7, which resumes the animation at
measure 17, presents such a meaningful visualization. It shows the mouse emerging onto a tile labeled B. We have seen such a tile in
Animation 5, but it was not directly in front of a mouse hole, and the tile in front of it was E, not the G
. Since every attempt is shown to be frustrated, we may intuit the need for a different approach. This sense can help us perceive a purpose for the musical features of the second half of the passage that contrast with the first half—greater continuity, upwards-driving pitch changes, new transformations and gestural combinations, the sense of getting stuck at the end—if we perceive that the visual representations of these features are meaningful in the context of the intentional actions we have attributed so far to the animated agent in this network.
Animation 7, which resumes the animation at
measure 17, presents such a meaningful visualization. It shows the mouse emerging onto a tile labeled B. We have seen such a tile in
Animation 5, but it was not directly in front of a mouse hole, and the tile in front of it was E, not the G![]() shown here. So this B is different from the B we heard then, and indeed, as the animation proceeds, we see that it initiates a line of pc interval 7s towards the bait B
shown here. So this B is different from the B we heard then, and indeed, as the animation proceeds, we see that it initiates a line of pc interval 7s towards the bait B![]() , a line we know to include the
measure 1 G; that is, the mouse now faces in the opposite direction. This is another reason (besides evoking vastness) for the network to be redundant: it more clearly shows how B, B
, a line we know to include the
measure 1 G; that is, the mouse now faces in the opposite direction. This is another reason (besides evoking vastness) for the network to be redundant: it more clearly shows how B, B![]() , and G relate by one of the characteristic gestures of the piece.
, and G relate by one of the characteristic gestures of the piece.
[9.8] Given the animations that interpret measures 1–16, which depicted abortive attempts to secure the cheese through -7 moves, we may understand this new state of affairs to suggest that the B![]() is still the intended goal but that the mouse will now try to approach it from the opposite direction, that is, moving by 7s. This visual reversal conforms to the change of register and direction initiated by
measure 17. Appropriately, with the mouse facing in the opposite direction, its characteristic left-right head wags take in the pcs of each augmented triad in exactly the order they appear in this inverted contour. Moreover, its directly forward motion, which portrayed MOVE1 in the first half of the passage, now portrays the inverse MOVE3. A series of these MOVE3s propels the mouse steadily toward the B
is still the intended goal but that the mouse will now try to approach it from the opposite direction, that is, moving by 7s. This visual reversal conforms to the change of register and direction initiated by
measure 17. Appropriately, with the mouse facing in the opposite direction, its characteristic left-right head wags take in the pcs of each augmented triad in exactly the order they appear in this inverted contour. Moreover, its directly forward motion, which portrayed MOVE1 in the first half of the passage, now portrays the inverse MOVE3. A series of these MOVE3s propels the mouse steadily toward the B![]() . A longer-reaching continuity builds as this motion repeats, quite in contrast to the brief spurts of
measures 1–16, and it takes on a clear direction as we see that its goal is the same as before. It is supplemented, however, by rather bizarre events: the appearances of additional mice, who move backwards to merge with the original mouse each time it surges forward by 7. Although these doppelgangers may dispel any illusion of reality we might have harbored about the animation, they do effectively capture the quality of
measures 18, 20, etc. identified in connection with Example 6—that each corresponding augmented triad has no connection to its immediate predecessor, but leads by a MOVE4 to its successor.
. A longer-reaching continuity builds as this motion repeats, quite in contrast to the brief spurts of
measures 1–16, and it takes on a clear direction as we see that its goal is the same as before. It is supplemented, however, by rather bizarre events: the appearances of additional mice, who move backwards to merge with the original mouse each time it surges forward by 7. Although these doppelgangers may dispel any illusion of reality we might have harbored about the animation, they do effectively capture the quality of
measures 18, 20, etc. identified in connection with Example 6—that each corresponding augmented triad has no connection to its immediate predecessor, but leads by a MOVE4 to its successor.
[9.9] The visual implication that B![]() remains a musical goal also helps explain features of the ending of this passage. When the mouse reaches the base of the trap, it is only a step away from dinner, just as the E
remains a musical goal also helps explain features of the ending of this passage. When the mouse reaches the base of the trap, it is only a step away from dinner, just as the E![]() at the base is just one more 7 move from B
at the base is just one more 7 move from B![]() , which we are primed to expect to appear in
measure 27. But exactly here the pitch-change pattern breaks, and the augmented trichords repeat on E
, which we are primed to expect to appear in
measure 27. But exactly here the pitch-change pattern breaks, and the augmented trichords repeat on E![]() then D
then D![]() . In the context of the preceding visualization, we may hear these as the hesitations of the mouse to make its next MOVE3 to B
. In the context of the preceding visualization, we may hear these as the hesitations of the mouse to make its next MOVE3 to B![]() , which would spring the trap. Its dread is dramatized in the animation by showing the mouse and its doppelganger attempt their expected merger upon the B
, which would spring the trap. Its dread is dramatized in the animation by showing the mouse and its doppelganger attempt their expected merger upon the B![]() in
measure 31, but then suspend in limbo above the cheese as A (where the D
in
measure 31, but then suspend in limbo above the cheese as A (where the D![]() doppelganger last glanced) together with A
doppelganger last glanced) together with A![]() (where we expect the next doppelganger to appear) sound a repeated alarm. The withholding of B
(where we expect the next doppelganger to appear) sound a repeated alarm. The withholding of B![]() sets the musical stage for the harmonic contrast of the next section, in which
the B
sets the musical stage for the harmonic contrast of the next section, in which
the B![]() focus is absent.
focus is absent.
[9.10] Animation 8 assembles all these episodes into an animated visualization of the entire passage. Comparing it with the previous analyses helps refine the desiderata for transformational analyses. It is more elaborate than they, but was still designed such that each visual feature—the layout of the network, the form of the agent, its motion—expresses aspects of musical structure and process that we identified in connection with the analysis of Example 6. Owing partly to the choice of agent, and particularly to the details of its moves, the sense of intentionality is much stronger in this clip than in Animation 2 and Animation 3, recalling Lewin’s characterization of a “transformational attitude.” To a greater degree than the other analyses it places the viewer “inside” both the network structure and the mind of the agent.
[9.11] Along with these advantages, however, there are aspects of the animation that may call into question either the representation or the underlying analysis itself. For instance, it may strike us as misleading to have so many instances of the same pc in the network. Specifically, the head-wags do not quite capture the sense of closure inherent in playing all three pcs of an augmented trichord, because there are multiple copies of the pcs in the same horizontal row of the parquet floor. To explore ways of addressing such problems, and to explore further the potential of animation as a medium for transformational analysis, let us consider briefly several alternative visualizations of the same basic transformational structures that are involved in the previous clips.
Gestures, agency, and form on Tonnetze
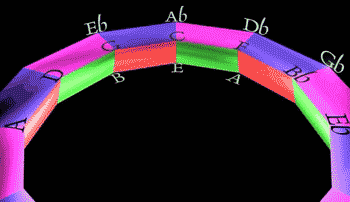
Example 9. A T7–T4 Tonnetz torus
(click to enlarge)
Animation 9. Enactment of measures 1–16 on the network of Example 9 by a moving light
(click to view animation)
Animation 10. Enactment of measures 1–32 by a human agent on a T7–T4 Tonnetz
(click to view animation)
[10.1] Readers familiar with the literature on neo-Riemannian theory may have recognized in the two-dimensional layout of the MOVEs the suggestion of a Tonnetz on transpositions x and y. This is a transformational network on the family of pcs under transposition, such that every pc is connected by transpositions x, -x, y, and -y to four other pcs, and no other transpositions are shown (Cohn 1997 and Hyer 1995). It is a space in the sense that it shows all the pcs without reference to a piece-specific ordering of events. In equal-tempered systems Tonnetze are toruses. Accordingly, Example 9 represents a portion of the T7–T4 Tonnetz: it is constructed of three equilateral dodecagons, the vertices of each labeled by the twelve pitch classes arranged in a chain of transposition by 7 (not all labels are shown, and color is used to clarify the articulations in the figure). The labels on the different dodecagons are rotated with respect to each other such that each cross-section of the torus is a triangle made of the pcs in an augmented trichord. Thus edges lead from every vertex by 4, -4, 7, and -7 to four other vertices.
[10.2] When the series of pcs in the Bartók passage is displayed as an animation in this network, repeated gestures and agency are just as apparent as in the mouse animation, even when the agent is merely abstract.(17) Animation 9 animates measures 1–16 as a light touching each of the pcs in order. One of the dodecagons, with black vertex labels, contains the pcs that are referential in each measure. The “4-wiggle” generating the augmented trichord in each measure is enacted by the light gliding from a black-labeled vertex to each of the other two white-labeled vertices in its augmented-trichord triangle. By thus completely spanning the entire small circumference of the torus, this gesture seems complete and self-sufficient (more so, I think, than the head-wags of the mouse in the previous animation). Glides of the light by -7 or 7 from one vertex to another on the same dodecagon enact each characteristic MOVE. Across this passage, motion is confined to a small portion of the overall torus, and a clockwise tendency is evident—both of which make measure 14 seem like a manifestation of agency, because it violates the established gestural patterns by moving counterclockwise, yet suggests closure by moving in measures 14–15 from the G augmented-trichord triangle (where it began in measure 1) to the C augmented-trichord triangle (where the chord of measure 1 moved, and where the 8-bar segments beginning in measure 9 and the 4-bar segment beginning in measure 13, both of which measure 15 closes, began).
[10.3] The remainder of this passage can be similarly animated, but the shape and labeling of this network makes the repetition of gestures (that is, the network isomorphisms) difficult to apprehend visually. The question also arises whether a more representational agent could enhance the sense of transformational gesture.
Animation 10 addresses these issues. The network it shows has the same toroidal T7–T4 Tonnetz structure as the network of
Animation 9, although the vertex labels and color are now relatively subdued. Here, however, the agent is much farther along on the evolutionary scale: a human figure, formally dressed like a performer, balancing with the aid of a pole at a vertex of the network. It limits its repertoire of gestures, as did the mouse, to a few that correspond to the characteristic transformational gestures I have identified above. For the “4-wiggle,” it touches each end of the pole
to a vertex on its left then on its right, thus completing contact with every member of the augmented triad containing the pc on which it stands. For each MOVE, it leaps in some way clockwise along the long circumference of the torus. In the second half of the passage, two performers face off, with one leaping to merge into the other who advances inexorably counterclockwise along the torus. The thwarting of motion towards B![]() , corresponding to
measures 25–32, is represented by the two performers visibly stuck, then stamping in frustration as their balancing pole sits out of reach on the B
, corresponding to
measures 25–32, is represented by the two performers visibly stuck, then stamping in frustration as their balancing pole sits out of reach on the B![]() .
.
[10.4] The presence of a less primally motivated agent on the Tonnetz gives this animation—and the analysis it performs—a very different affect. The nervous paranoia conveyed by the mouse’s head wags as it tried to avoid the trap is transmuted into the performer’s striving for physical balance, like that of a tightrope walker. So its enactment of the 4-wiggle gives the nonreferential members of each augmented trichord more literally supporting roles and a more visceral sense of completeness. Also, without the bait and trap, the agent’s actions make a more showy and whimsical performance; this feeling is enhanced by its twirling pole-tosses during the transitions between segments and by the apparent changes in the direction of gravitational pull. Consequently the music seems less directed and edgy, more kaleidoscopic and fantastic. However, despite my attempts to constrain such associations, it must be acknowledged that viewers may attribute many diverse and conflicting motivations to such a purportedly complex agent. In general, the more representational the animation, the greater is its potential for connotative misrepresentation.
Animation 11. Enactment of measures 1–32 by a human agent on a T1–T4 Tonnetz
(click to view animation)
[10.5] One weakness of this animation, since it does not privilege B![]() as
Animation 8 did, is that it provides no visual reason for the first segment (measures 1–4) to end.
Animation 11 (in a slower tempo, to facilitate observation; click and hold the fast-forward button for quicker playback) shows that a different but closely related transformational network can provide a suitable context to account for this ending, along with some other visual benefits. In it, we see a toroidal network, like that of
Animation 10, but realizing a different Tonnetz—one in which the dimensional transposition along the dodecagon is T1 instead of T7 (T4 remains in the other dimension). As a flat parquet world, even with an elaborately animated agent, this would be confusing, because the characteristic T7 MOVEs would be hard-to-track diagonal leaps not squaring with the boundaries of the network. In this smaller, more constrained toroidal network, however, MOVEs can be easily tracked as forward motion combined with a 120-degree rotation. In fact, this visual representation provides the perfect motivation for ending the first segment: after three such MOVEs, the agent has spiraled all the way around the torus and returned to the T1 dodecagon on which he started, so it has a level stroll back to the vertex that begins the second segment.
as
Animation 8 did, is that it provides no visual reason for the first segment (measures 1–4) to end.
Animation 11 (in a slower tempo, to facilitate observation; click and hold the fast-forward button for quicker playback) shows that a different but closely related transformational network can provide a suitable context to account for this ending, along with some other visual benefits. In it, we see a toroidal network, like that of
Animation 10, but realizing a different Tonnetz—one in which the dimensional transposition along the dodecagon is T1 instead of T7 (T4 remains in the other dimension). As a flat parquet world, even with an elaborately animated agent, this would be confusing, because the characteristic T7 MOVEs would be hard-to-track diagonal leaps not squaring with the boundaries of the network. In this smaller, more constrained toroidal network, however, MOVEs can be easily tracked as forward motion combined with a 120-degree rotation. In fact, this visual representation provides the perfect motivation for ending the first segment: after three such MOVEs, the agent has spiraled all the way around the torus and returned to the T1 dodecagon on which he started, so it has a level stroll back to the vertex that begins the second segment.
[10.6] Another analytically expressive aspect of the animation on this T1–T4 Tonnetz is its rendering of the second half of the passage. With this transformational configuration, each doppelganger lands directly facing the principal agent, two steps away on the same dodecagon; this gives a greater sense of visual connectedness, matching the obvious musical continuity. More importantly, the larger-scale structure is also clearer. The pairs of agents make one complete spiral around the torus (corresponding to measures 17–18, then 19–20, then 21–22), then two-thirds of another one (corresponding to measures 23–24 and 24–26), motions that create an expectation that they will complete the second spiral. But they do not, and this imparts a sense of frustration to the end of this passage much as did the mouse’s suspended final lunge at the cheese in Animation 8.
Apotheosis
[11.1] This survey of transformational signification has considered and compared the potentials of static networks, gradually appearing static networks, animations with guide objects, and animations with agents for musical analysis. To a certain extent, each assists us to get “inside” the music, in terms of transformational theory, by providing a structure in which we see series of repeating gestures that conform to musical structures and processes. However—beyond the weaknesses mentioned above—some aspects may hinder us from achieving the ideal transformational experience. Unless we empathize sufficiently with the agent, we may feel like uninvolved, passive observers. Also, the toroidal animations are still not quite minimal “spaces” as I have defined them above, because each pc is represented by three different nodes. In light of the ongoing discussions about the desirable features of a transformational analysis, it seems reasonable to seek a truly non-redundant space animated in a way that can more fully engage the viewer, and that can still show the T7/T4 gestures and augmented trichord progressions characteristic of this passage.
Animation 12. A tour of a minimal toroidal space with T7–T4 Tonnetz structure
(click to view animation)
Animation 13. Interactive tour of the space of Animation 12
(click to view animation)
[11.2] Animation 12 provides a passive tour of one possible structure. The network consists primarily of a single closed loop wrapped three times in a spiral around an invisible torus. Arranged regularly along the path are the 12 pcs in a circle of fifths; the clip plays the complete circuit in “descending” order. The wrapping of this loop places in close proximity the pcs that belong to the same augmented trichord. These are connected by straight lines, so the four augmented triads appear as four triangles, one in each cardinal direction of the space. Thus from each point are four paths, corresponding to transpositions by 4, -4, 7, and -7. Evidently, the structure of this space is suitable for displaying many of the trenchantly analytical motions of the spaces above. For example, it can represent the completeness of measures 1–4, as did our very first animation (Animation 1), by motion to all four compass points of the space. And it can also distinguish the different MOVEs of the later animations and the analytical insights they convey, since it carries over the T7/T4 Tonnetz structure of the corresponding networks.
[11.3] Rather than follow yet another animated figure dancing its way around this space, let us consider perhaps the closest possible realization of Lewin’s vision of being “inside” the music: a virtual reality through which the user may freely move by a combination of predefined characteristic gestures. Animation 13, an interactive Flash animation, provides an example using the space displayed in Animation 12. Starting from a given node, the user may freely navigate, using the controls, to any of the four pcs to which the node is connected. As the next pc is reached, it is played, so the user may perform the Scherzo, or may improvise other music using the same repertoire of characteristic gestures. “Analysis” in such a context is not simply narrating a piece; it is inhabiting a world of partially prestructured sounds.
Summary
[12.1] Across these various transformational approaches to the Bartók passage, I have taken care to articulate the goals and principles underlying their construction, proceeding from and elaborating upon those discussed by Lewin in MFT. Achieving an expressive analysis is by no means assured. It is always an art, but certain constant concerns have been evident, which are summarized below as a series of guidelines for choosing objects and transformations:
- Choose the most aurally salient analytical objects that will still belong to a single family and have an economical transformational structure.
- Choose an object family that is complete (including all objects that appear in the piece) but minimal (not entailing many objects that do not appear).
- Choose transformations that occur prominently (preferably manifesting distinctive aural signatures) and repeatedly, so establishing themselves as characteristic, while satisfying the formal constraints necessary for network structure and isography.
- Choose transformations that may be applied to other families of objects in the same composition.
- Organize the transformational network to be homologous with musical form, such that the characteristic gestures correspond to segments, phrases, sections, and the processes that constitute them.
- Event-oriented networks (in which two nodes may have the same content) are good for illustrating isomorphic gestures statically, or for discussing network structures that are not easily visualized as temporal gestures.
- Spaces are most effective for analysis if the pathways taken by the piece are made evident, for example, by the characteristic gestures of an animated agent. Agents and their motions should be designed to focus on the musical processes identified by the analysis (clarifying the musically relevant sameness and difference of gestures), and to elicit viewers’ empathetic participation in the ongoing making of musical structure, while minimizing extraneous connotations.
- Suitably constrained representation can enhance signification.
[12.2] The presentation above of so many different views of the same passage shows that multiple representations are sometimes needed to get at different aspects of a passage, even those that are consistent with each other. This is not to say that there is no best analysis—on the contrary, I have given many bases above for judging which analyses are most effective—but only to acknowledge that, like words, transformational analyses are at best imperfect and incomplete signifiers of musical experience.
John Roeder
University of British Columbia School of Music
6361 Memorial Road
Vancouver, B.C.
V6T 1Z2 Canada
j.roeder@ubc.ca
Works Cited
Buchler, Michael. 2007. “Reconsidering Klumpenhouwer Networks.” Music Theory Online 13.2.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15/1: 9–40.
—————. 1997. “Neo-Riemannian Operations, Parsimonious Trichords, and Their ‘Tonnetz’ Representations.” Journal of Music Theory 41/1: 1–66.
—————. 2003. “A Tetrahedral Graph of Tetrachordal Voice-Leading Space.” Music Theory Online 9.4.
Cook, Nicholas. 1998. Analysing Musical Multimedia. Oxford: Oxford University Press.
Gillespie, Jeffrey. 1992. “Motivic Transformations and Networks in Schoenberg’s Nacht from Pierrot Lunaire.” Intégral 6: 34–65.
Gollin, Edward. 2000. “Representations of Space and Conceptions of Distance in Transformational Music Theories.” Ph.D. dissertation, Harvard.
Hook, Julian. 2007. “Cross-Type Transformations and the Path Consistency Condition.” Music Theory Spectrum 29/1: 1–39.
Hyer, Brian. 1995. “Reimag(in)Ing Riemann.” Journal of Music Theory 39/1: 101–38.
Klumpenhouwer, Henry. 2006. “‘In Order to Stay Asleep as Observers’: The Nature and Origins of Anti-Cartesianism in Lewin’s Generalized Musical Intervals and Transformations.” Music Theory Spectrum 28/2: 277–89.
Lewin, David. 1982/83. “Transformational Techniques in Atonal and Other Music Theories.” Perspectives of New Music 21/1–2: 312–371.
—————. 1986. “Music Theory, Phenomenology, and Modes of Perception.” Music Perception 3/4: 327–92.
—————. 1987. Generalized Musical Intervals and Transformations. New Haven and London: Yale University Press.
—————. 1993. Musical Form and Transformation. New Haven and London: Yale University Press.
—————. 1998. “Notes on the Opening of the F![]() Minor Fugue from WTC I.” Journal of Music Theory 42/2: 235–239.
Minor Fugue from WTC I.” Journal of Music Theory 42/2: 235–239.
—————. 2008. “Transformational Considerations in Schoenberg’s Opus 23, Number 3.” In Music Theory and Mathematics: Chords, Collections, and Transformations, ed. Jack Douthett et al, 197–221. Rochester: University of Rochester Press.
Peck, Robert. 2003. “Klein-bottle Tonnetze.” Music Theory Online 9.3.
Rahn, John. 2004. “The Swerve and the Flow: Music’s Relationship to Mathematics.” Perspectives of New Music 42/1: 142–43.
Reed, Jacob and Matthew Bain. 2007. “A Tetrahelix Animates Bach: Revisualization of David Lewin’s Analysis of the Opening of the ![]()
Rogers, Nancy M. and Michael Buchler. 2003. “Square Dance Moves and Twelve-Tone Operators: Isomorphisms and New Transformational Models.” Music Theory Online.
Satyendra, Ramon. 2004. “An Informal Introduction to Some Formal Concepts from Lewin’s Transformational Theory.” Journal of Music Theory 48/1: 99–141.
Scholl, Brian J. and Patrice D. Tremoulet. 2000. “Perceptual Causality and Animacy.” Trends in Cognitive Science 4/8: 299–309.
Scotto, Ciro G. 2002. “Transformational Networks, Transpositional Combination, and Aggregate Partitions in Processional by George Crumb.” Music Theory Online 8.3.
Zbikowski, Lawrence. 2002. Conceptualizing Music. Oxford: Oxford University Press.
Footnotes
1. My commentary principally references Lewin’s mature formulations of transformational theory in Generalized Musical Intervals and Transformations (Lewin 1987) and Musical Form and Transformation (Lewin 1993). To minimize footnotes, citations of these works in my introductory section will be given by acronym (respectively GMIT and MFT) and page number. The most important antecedent to them is Lewin 1982/83. A detailed summary can be found in Satyendra 2004.
Return to text
2. Lewin describes the insider’s strategy in the first person as follows: “If I want to change Gestalt 1 into Gestalt 2 (as regards content, or location, or anything else), what sorts of admissible transformations in my space...will do the best job?” (GMIT,
159). This passage, rarely quoted in the secondary literature, stands as his
clearest expression of the notion of agency, a central concern of the present
article. Henry Klumpenhouwer (2006) describes the writings of Lewin’s father, citing them as the source of the “anti-Cartesian” strains in Lewin’s writings.
Return to text
3. This recognition is articulated in
Lewin 1986 and carried through even into his last writings (Lewin 2008).
Return to text
4. For instance, the pentachord classes identified by Harvey and Forte, respectively, in the Stockhausen and Webern pieces analyzed in MFT chapters 2 and 3, the BACH motive in Dallapiccola’s “Simbolo” (MFT chapter 1), and the imitative subjects of Bach’s F![]() minor fugue and Schoenberg’s Op. 23, No. 3.
minor fugue and Schoenberg’s Op. 23, No. 3.
Return to text
5. Lewin did urge “attention, at all times in the construction process, to both ‘figural’ (narrative blow-by-blow temporal) and ‘formal’ (abstract spatial) aspects of the task at hand...The methodology of these ongoing processes, rather than the specific shape of this or that specific resultant network model, is what seems essential and characteristic in the art of making a network analysis” (MFT, 53). But this simply leaves open the practical questions I pose.
Return to text
6. “The relations in [a transformational space] exist outside human time in an abstract universe of quasi-spatial potentialities; they cannot be manifested in music except through human gestures that move through chronological time” (MFT, 41).
Return to text
7. Representative examples of space-constructing articles are Cohn 1996 and Peck 2003. A distinctive contribution is Gollin 2000, which thoroughly considers the topic of alternative pathways and their significance in transformational spaces. Naturally, he does not consider event-networks; nor does he concern himself with questions of agency and gesture I raise here.
Return to text
8. Some examples of straightforward analyses that have no cause to discuss analytical pragmatics are the event-network approach by Jeffrey Gillespie in Gillespie 1992, and the more spatial-network treatment in Scotto 2002.
Return to text
9. Hook 2007 discusses some ways that these constraints can be relaxed without violating other important properties of networks.
Return to text
10. Lewin, in MFT chapter 2, provides ear-training exercises to sensitize the reader to the pentachord forms he wants to assert as formally functional.
Return to text
11. Animations have recently started to appear in the
transformational literature. Examples include Rogers and Buchler 2003, Cohn 2003, and Reed and Bain 2007, which I will consider in more detail below. I gratefully acknowledge the assistance of the following collaborators in realizing the animated analyses presented in this article: Andrew Wei (Animations 1, 2, 3, and 13); Ali AbdulHussein (Animations 9 and 12); Kate Lau (Animations 4–8); and Sarah Mah (Animations 10 and 11).
Return to text
12. Gollin elaborates Lewin’s discussion of the significance of spatial networks in his preliminary definition: “A music-transformational space is a particular arrangement of musical elements whose order or structure is determined by a family of normative relations or
transformations among those elements
Return to text
13. To my eye, S becomes continuous almost right away, while X does so only towards the end, when it repeats consecutively. This suggests that the gestural quality of a musical transformation might similarly be heard to develop over the course of a passage.
Return to text
14. For a review of the literature on this phenomenon, see
Scholl and Tremoulet 2000. The authors use the latter term to denote the attribute of intentionality, which I am calling agency. It seems to be perceived universally through an automatic, very low-level modular visual process under certain conditions, for example, when objects change direction or orientation in a way that cannot be accounted for by perceived environmental factors, such as gravity. As yet, no one seems to have studied the animacy of aural objects (or even if such a cross-model analogy is valid); transformational theory, not to mention Schenker’s Tonwille, might benefit from such investigations.
Return to text
15. For more general considerations of cognitive mapping, see also Zbikowski 2002.
Return to text
16. It is through these fifths that one can realize, to a small degree, intuitions about roots and harmonic progression that are relevant to this piece, but not explicitly represented in the transformational networks.
Return to text
17. The elegant animations of Reed and Bain in “A Tetrahelix” make an interesting comparison to this and subsequent clips. Unlike the present discussion, their paper is not concerned with the selections of objects and transformations, or with issues of agency, since they are realizing an existing analysis by Lewin (“Notes on the Opening of the F![]() Minor Fugue”), but they do evaluate various alternative visualizations for conformance and effectiveness.
Minor Fugue”), but they do evaluate various alternative visualizations for conformance and effectiveness.
Return to text
Copyright Statement
Copyright © 2009 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Sean Atkinson, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: