Discrete Fourier Transform and Bach’s Good Temperament
Emmanuel Amiot
KEYWORDS: temperament, tuning, Fourier transform, Lehman, J.S. Bach, Wohltemperierte Klavier
ABSTRACT: The statement by Bradley Lehman that the scribble at the beginning of the first page of the WTC shows how J.S. Bach tuned his harpsichord is much disputed. The use of a mathematical and rather abstract characterization of major scales puts forward a quality of the Lehman temperament that singles it out among all competing temperaments, thereby sustaining his claim.
Copyright © 2009 Society for Music Theory
Introduction
0.1 Lehman’s hypothesis
[0.1.1] In two papers published in 2005 (2005a, 2005b), Bradley Lehman introduced the view that the recipe for the long-lost temperament of Johann Sebastian Bach had in fact been lying for all to see—not unlike Poe’s Purloined Letter—as a scribbling on the front page of the autograph edition of Das Wohltemperirte Clavier, the “Well-Tempered Clavier” (henceforth abbreviated as the WTC). As Lehman’s own learned comparisons with many previously known tunings make clear, this is a vexed question, and his “discovery” aroused a number of refutations, on various grounds.
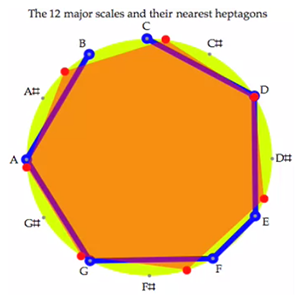
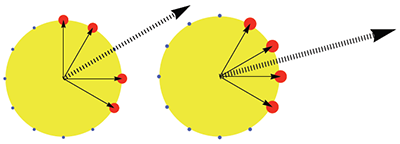
[0.1.2] Lehman’s homepage, with abundant discussions and links, is accessible by clicking here. Here is a short summary of his interpretation of picture 1. Let us recall the gist of the problem of tuning. Twelve just fifths (frequency ratio 3/2) amount to seven octaves plus a Pythagorean comma. Using eleven just fifths leaves a “wolf,” e.g. one ugly fifth, and all tonalities featuring this fifth will sound wrong. The abstract solution is equal temperament, wherein all fifths are reduced by one twelfth of a comma, but then all intervals are out of tune, and all scales sound (equally) disharmonious. The problem of tuning thus consists of adjusting the different fifth sizes, aiming at a temperament wherein all tonalities sound well. This is exactly the meaning of “Wohl Temperirte” as Bach explains it on the first page of the WTC. According to Lehman, the picture before the text (see Figure 1) gives the directions for such a temperament.
[0.1.3] First the picture must be turned over (flipped upside-down); now consider all those loops as directives on how to tune successive fifths, beginning with F-C. The small inner loops represent nudges, slight moves of the tuning-pin.(1) There are either 2, 0 or 1 nudges. The total is 13 nudges (=2+2+2+2+2+0+0+0+1+1+1), suggesting that each nudge should be one thirteenth of the Pythagorean comma(2) in order to get around the circle of fifths smoothly. Eventually, the circle of fifths begins with five short fifths (like numerous generalized meantone temperaments), carries on with three pure fifths and ends with intermediate-size fifths. It is fairly simple to realize in practice, in accordance with the well-known fact (or legend) that Bach tuned a harpsichord in a quarter of an hour. Lehman made a movie showing the tuning of an octave on YouTube, accessible here. The three different sizes of fifths are hard to distinguish when played alone; Lehman’s videos are much more explicative.
0.2. Why it is unprovable . . .
[0.2.1] The unsolvable problem of tuning has been well understood since Ptolemaios at least: twelve just fifths are slightly in excess of seven octaves, (3∕2)12 ≈ 129.75 > 27 = 128, and more generally, there is no way any number of fifths can equal some number of octaves, as the equation (3∕2)n = 2p admits no solutions in integers n, p > 0. Fiddling with the sizes of fifths introduces problems with other “pure” intervals, like the major third, which should ideally be close to 5/4.
[0.2.2] There can be no ideal solution, since a number of different desirable properties compete with one another. Hence the musicological debate on the quality of Lehman’s temperament (henceforth called LT) might go on for ever, as proponents of any other temperament will put forward (usually in good faith) diverse qualities,(3) often sporting personal preferences instead of facts (see for instance the acerbic [Lindley and Ortgies 2006] and its refutation by Lehman).
0.3 . . . or is it ?
[0.3.1] We need some objective quality to assess a temperament, preferably addressing the whole collection of major (and minor) scales—as Bach did, allowing arbitrary modulation in the composition, e.g. tuning the harpsichord once and for all before playing through the 24 tonalities in the WTC.
[0.3.2] The present paper puts forward a geometric quality of temperaments, measured with a single number (the Musical Sameness of Scales, or MSS); as it happens, the comparison of values of MSS for the different tunings in competition so far singles out LT as a clear winner, primus inter pares.
[0.3.3] This MSS makes use of the Discrete Fourier Transform (DFT), a mathematical tool whose relevance to major scales was discovered very recently (Quinn 2004; Amiot 2007). Despite its technicality, the MSS puts forward a musical quality that Bach would have found desirable.
[0.3.4] Its discovery was serendipitous, and has nothing to do with Bach and the WTC. I was investigating the DFT of major scales for purely theoretical reasons, but endeavored to try it on unequal temperaments as an illustration for the Helmholtz “Klang und Ton” workshop in Berlin (May 2007). I came across Lehman’s story while browsing the internet, and included it in my list of various temperaments out of curiosity. Computing values of DFT for all major scales in all these temperaments, I noticed an exceptional quality of LT, only equaled by Werckmeister’s IV, or septenarius.(4) The notion of MSS was formulated in order to sum up this quality in a single number, for the sake of simplicity.
[0.3.5] Of course, I do not claim that the best temperaments (musically speaking) are just the ones with the greatest MSS. For instance, equal temperament gives an infinite value for MSS, but nowadays specialists agree on the fact that the equal temperament was abhorrent to Bach, as it still is to baroque musicians. The computation of MSS should come after all musicological arguments, enabling one to choose among temperaments already acknowledged as musically interesting.
[0.3.6] Readers are invited at this point to listen to the pleasant sound of the recordings in LT, which can be found on this page. Together with the record value of MSS, this makes a convincing case for Lehman’s hypothesis. But arguments, like a razor,(5) cut both ways: some lesser known temperament might achieve a better MSS than LT. Readers are strongly invited to test the temperaments they like best against LT with the formula for MSS given in section 1. The computation is possible even with a pocket calculator (especially if it manages complex numbers) and only takes a few lines of programming with a computer. For instance, some alternative interpretations of Bach’s scribble have been offered, and the values of MSS for these temperaments are of interest.
[0.3.7] On the other hand, should some other temperament with a greater MSS supersede LT one day, the fact will remain that most or all temperaments reportedly in use around Bach’s time have a much smaller MSS, and this will remain a significant hallmark of LT.
1. Sameness of Scales in a Temperament
[1.0.1] I fear it is impossible to appreciate the import of the MSS value without some attempt at understanding the math behind it: most of the strength of the argument derives from Theorem 1. I have made use of footnotes and appendices in order to lighten the reading as much as possible.
[1.0.2] Roughly speaking, the DFT defined below enables one to appraise how close a scale(6) is to the mathematical paradigm of a regular polygon. This makes musical sense, because the largest DFT values characterize the major scales. As it happens, the distribution of these values calculated for the 12 major scales exhibits a very special feature in the case of LT.
[1.0.3] The next subsection (1.1) attempts a non-technical description. Readers averse to mathematics are invited to read it and then skip to section 2, with tables of values of MSS for a number of temperaments. The precise definitions leading to the MSS are given in the sequel of this section (1.2–1.4), but the truly technical parts (the proofs of the Lemma and Theorem) are confined to the last section (3.2).
[1.0.4] I hope that most readers will go through the whole section, thus getting the gist of the argument, even if understanding the actual proofs requires some training in that prolific branch of mathematics called harmonic analysis. The complexity of the diatonic underlies the major scale and is hence responsible for a large part of the beauty of western classic music and the fulfilling emotions that we experience with it.
1.1. Major scales are regular heptagons (almost)
[1.1.1] Consider the C major scale in fifth order: F C G D A E B. A tone-deaf person might not perceive that the interval between the extreme notes, B-F, is smaller than the other fifths. After all, the difference is the smallest possible inside the twelve tone universe, e.g. a semitone (or augmented prime). This means that the sequence of seven notes in the major scale is as close as can be, in the twelve-note ambient universe, to a completely regular sequence (a perfectly regular sequence is the whole tone scale, for instance). This can be seen graphically in Video 1 (the major scale is in blue and the nearest heptagon is in red).
[1.1.2] The mathematical tool that measures such regularities is the Fourier Transform (rigorously defined in the next subsection). It enables one to simplify considerably the data for periodic phenomena: in the domain of sound, for instance, a sound file recording one note played by a musical instrument can be summarized by a few figures giving the Fourier coefficients, which are in this case the weights of the different overtones. In the study of scales, we use a slightly simplified version, called the Discrete Fourier Transform.
[1.1.3] For a perfectly regular scale, like the whole-tone, the value
 (1) of this Fourier Transform would be equal to 1, or 100%. The major scales are the twelve seven-note scales with the greatest value of this
(1) of this Fourier Transform would be equal to 1, or 100%. The major scales are the twelve seven-note scales with the greatest value of this
 (1)—not 100%, but about 98%. This is the most important point about
(1)—not 100%, but about 98%. This is the most important point about
 (1): it characterizes the major scales among all possible seven-note scales.
(1): it characterizes the major scales among all possible seven-note scales.
[1.1.4] Now, in unequal temperaments, all scales are different, if only slightly. Hence, for each tonality A, we compute a different value of
 (1). The MSS is then defined as a measure of the discrepancy of the twelve values of
(1). The MSS is then defined as a measure of the discrepancy of the twelve values of
 (1) for the twelve major scales: the higher the value of MSS, the closer the values of
(1) for the twelve major scales: the higher the value of MSS, the closer the values of
 (1) are to one another.
(1) are to one another.
[1.1.5] For high values of MSS, we expect all (major) scales to be equally close to their abstract model. Indeed, an infinite value of MSS means an equal temperament, wherein all scales sound identically. Hence, MSS can be taken as a measure of how much a temperament achieves Bach’s goal, where all tonalities coexist peacefully inside the same temperament.
1.2. Discrete Fourier Transform of a Scale
[1.2.1] Research on the DFT of scales originated in the preparation of the John Clough Memorial Days in Chicago (July 2005), organized by Richard Cohn and David Clampitt. There, Ian Quinn’s ground-breaking dissertation (2004), wherein he rekindled an original idea of the late David Lewin (1959), aroused interest in DFT among several researchers. Fresh developments may be found in Amiot 2007. But a slightly different track, initiated a few months later by Thomas Noll, led to the present indicator of sameness of scales:
Definition 1. Let all notes inside an octave be given by a real number between 0 and 1; this means
choosing a reference note (say C) and measuring all intervals from there in cents/1200. Then the Discrete Fourier Transform of a scale =
(a1,a2,...an)
![]() [0,1] is the map
[0,1] is the map

(it is the Fourier Transform of the map
![]() ). The values
). The values
 (0),
(0),
 (1) ...
(1) ...
 (n - 1) are the
Fourier coefficients of scale
(n - 1) are the
Fourier coefficients of scale
![]() .
.
[1.2.2] For instance, the (equal) tempered C major scale would be CM = (0, 1∕6, 1∕3, 5∕12, 7∕12, 3∕4, 11∕12) and its DFT is

[1.2.3] It may be useful to recall that the Fourier Transform is in general a tool for checking the periodicities of a given phenomenon. Here, it is easily seen that the map
 is defined from the cyclic group with
n elements
is defined from the cyclic group with
n elements ![]() to the field
to the field
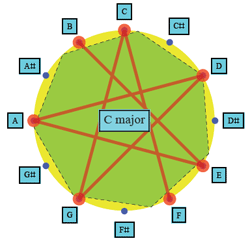
![]() of complex numbers.(7) The notes can be visualized
as the points
of complex numbers.(7) The notes can be visualized
as the points ![]() on the unit circle, which is the quotient structure of frequencies modulo octave: see
Figure 2.
on the unit circle, which is the quotient structure of frequencies modulo octave: see
Figure 2.
1.3. DFT and Maximal Evenness
Lemma 1. | (1)| = 1
(1)| = 1
![]()
![]() is a “regular polygon,” i.e.
is a “regular polygon,” i.e.
![]()
For any other scale, for any t,
| (1)| ≤ 1.
(1)| ≤ 1.
[1.3.1] The first case
| (1)| = 1 occurs for instance when
(1)| = 1 occurs for instance when
![]() is a whole tone scale (in equal temperament), or an augmented triad, or diminished seventh. But of course a seven note scale in a (decent) twelve note temperament cannot be a regular polygon, as 12 cannot be divided into 7 equal integral parts (see
Figure 2). Still, the best approximations of regular polygons are musically interesting scales:
is a whole tone scale (in equal temperament), or an augmented triad, or diminished seventh. But of course a seven note scale in a (decent) twelve note temperament cannot be a regular polygon, as 12 cannot be divided into 7 equal integral parts (see
Figure 2). Still, the best approximations of regular polygons are musically interesting scales:
Theorem 1. Let
![]() be the set of scales of n notes chosen in some equal temperament with m notes (m > n), meaning
be the set of scales of n notes chosen in some equal temperament with m notes (m > n), meaning
![]()
Then the scales in with biggest value of
| (1)| are the Maximally Even Sets.
(1)| are the Maximally Even Sets.
[1.3.2] What are Maximally Even Sets? The ME Sets were defined in Clough and Myerson 1985 and extended in Clough and Douthett 1991. A recent and thorough paper on their features is Douthett and Krantz 2007, and the connection with DFT, discovered in Quinn 2004, is investigated in Amiot 2007. The proofs of the above Lemma and Theorem are relegated to the appendix, together with technical definitions. For the moment let it suffice to mention that
- Informally, a ME set is the “most regular” repartition of n notes in a given temperament.
- ME sets (in equal temperament) are musically prominent scales: for instance the pentatonic, whole tone, major and octatonic scales all are ME sets in twelve tone temperament.
- In several cases, including the major (and pentatonic) scales, this Maximal Evenness implies the “generated” quality, e.g. the major scale is generated by consecutive fifths.
This means that in a given context (here an equal-tempered chromatic ambient universe) the size of | (1)| measures the
regularity of the scale, i.e. its closeness to a regular polygon. The above theorem, as the next proposition, can bear some degree of approximation,(8) and hence both still stand in all common tunings, which are close to equal temperament.
(1)| measures the
regularity of the scale, i.e. its closeness to a regular polygon. The above theorem, as the next proposition, can bear some degree of approximation,(8) and hence both still stand in all common tunings, which are close to equal temperament.
[1.3.3] However, we only need the case of 7-note ME sets in 12-tone temperaments:
Proposition 1. In 12 tone equal temperament, the Maximally Even
Scales with 7 notes (e.g. the seven-note scales
![]() with greatest value of
|
with greatest value of
| (1)| ) are
precisely the 12 major scales.
(1)| ) are
precisely the 12 major scales.
[1.3.4]
Now we can see that | (1)| really measures the closeness of 7-note scale
(1)| really measures the closeness of 7-note scale
![]() to the theoretical regular heptagon, which appears as a common goal, a Platonic model, that major scales strive to approximate as best they can: this is the meaning of the last proposition.(9)
to the theoretical regular heptagon, which appears as a common goal, a Platonic model, that major scales strive to approximate as best they can: this is the meaning of the last proposition.(9)
[1.3.5]
From now on, all we need to remember is this meaning of | (1)|. For instance, if scale
(1)|. For instance, if scale
![]() is a regular heptagon (say a “whole-tone scale” in 14-note equal temperament) then
|
is a regular heptagon (say a “whole-tone scale” in 14-note equal temperament) then
| (1)| = 1; for any major scale A in 12-tone equal temperament,
|
(1)| = 1; for any major scale A in 12-tone equal temperament,
| (1)| ≈ 0.988846. This is a fundamental feature of major scales and not a mere curio: a basic fact about DFT, Parseval’s formula, states that ∑
t=0...n-1 |
(1)| ≈ 0.988846. This is a fundamental feature of major scales and not a mere curio: a basic fact about DFT, Parseval’s formula, states that ∑
t=0...n-1 | (1)|2 = 1 = 100%. Hence, when
|
(1)|2 = 1 = 100%. Hence, when
| (1)| evaluates around 0.98 for a major scale, it means that almost all the energy of the scale is concentrated in this coefficient, as all other Fourier coefficients are negligible. In the case of other, random, seven-note scales, the energy is spread between the seven coefficients: for a chromatic succession of 7 notes,
|
(1)| evaluates around 0.98 for a major scale, it means that almost all the energy of the scale is concentrated in this coefficient, as all other Fourier coefficients are negligible. In the case of other, random, seven-note scales, the energy is spread between the seven coefficients: for a chromatic succession of 7 notes,
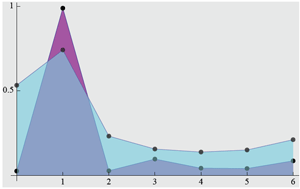
| (1)| is roughly 0.74; see
Figure 3 (the scale with the highest peak is the diatonic; the other one is a random collection of seven notes). It is also worth considering the scales with second best value of |
(1)| is roughly 0.74; see
Figure 3 (the scale with the highest peak is the diatonic; the other one is a random collection of seven notes). It is also worth considering the scales with second best value of | (1)|, which are quite different from major scales ([0234568], e.g. G
(1)|, which are quite different from major scales ([0234568], e.g. G![]() , A
, A![]() , B, C, C
, B, C, C![]() , D, E).
, D, E).
[1.3.6] We are now ready to define the sameness coefficient of scales (MSS) inside a given temperament.
1.4. Sameness Coefficient
[1.4.1] A temperament is simply a collection of 12 tones, i.e. a subset
![]() of [0,1] with 12 elements. Henceforth we will only consider scales with seven notes, that is to say ordered sequences of seven elements of
of [0,1] with 12 elements. Henceforth we will only consider scales with seven notes, that is to say ordered sequences of seven elements of
![]() . Let us assume that the elements of
. Let us assume that the elements of
![]() are given in order:
are given in order:
Definition 2. A temperament, or tuning, is an ordered sequence of twelve different notes:
![]()
Definition 3. A major scale in temperament
![]() is a sequence of the
form
is a sequence of the
form
![]()
where α is a constant and the kis are the indexes of the standard C major scale: 0,2,4,5,7,9,11
Example: say α = 5, we get the notes ai with i = 5, 7, 9, 10, 12 = 0, 14 = 2, 16 = 4, i.e. F major.
[1.4.2] This enables us to compute |![]() (1)| for all
α = 0...11, i.e. for the 12 major scales in
(1)| for all
α = 0...11, i.e. for the 12 major scales in
![]() . For instance, taking for
. For instance, taking for
![]() the so-called
Pythagorean tuning with the “wolf fifth” between A
the so-called
Pythagorean tuning with the “wolf fifth” between A![]() and F, we get the following values for all major scales (in semitone order):
and F, we get the following values for all major scales (in semitone order):
0.9891; 0.9891; 0.9856; 0.9927; 0.9856; 0.9915; 0.9856; 0.9856; 0.9915; 0.9856; 0.9927; 0.9856
[1.4.3] Notice that all scales that do not contain the wolf fifth are isometrical, and hence share the same absolute value of the Fourier coefficient. The most striking fact about these values is their closeness to 1, which reflects the characterization of ME sets in Theorem 1. But the most important feature in a given temperament is the distribution of these values, which are exceptionally close to one another in the case of LT. In order to visualize this phenomenon more easily, we define
Definition 4. The Major Scale Sameness (MSS) of temperament
![]() is the inverse of the biggest discrepancy between values of coefficients
|
is the inverse of the biggest discrepancy between values of coefficients
|![]() (1)| for all twelve major scales in
(1)| for all twelve major scales in
![]() :
:

[1.4.4] This quantity is highest when all values of |![]() (1)| (for all 12 major scales) are the closest, i.e. when all major scales are almost equally similar to the ideal (theoretical) model of the regular heptagon. For instance for Pythagorean tuning, we get a maximum (resp. minimum) value of 0.9927 (resp. 0.9856) and hence
MSS (Pyth) =
(1)| (for all 12 major scales) are the closest, i.e. when all major scales are almost equally similar to the ideal (theoretical) model of the regular heptagon. For instance for Pythagorean tuning, we get a maximum (resp. minimum) value of 0.9927 (resp. 0.9856) and hence
MSS (Pyth) =
![]() ≈
140.
≈
140.
[1.4.5] For LT, no major scale comes higher than |![]() (1)| = 0.991, but none comes lower than 0.987, so the MSS is particularly high:
MSS (LT) =
(1)| = 0.991, but none comes lower than 0.987, so the MSS is particularly high:
MSS (LT) =
![]() ≈
250 (actually a little more; see
Figure 5 below).
≈
250 (actually a little more; see
Figure 5 below).
1.5. Musical relevance: playing in all tonalities
[1.5.1] Most analyses of different temperaments, including Lehman’s, put forward some particular intervals. The MSS coefficient on the other hand is comprehensive: it gives a measure of the sameness of
all major scales in
![]() . Though it tells nothing about the closeness of E-G
. Though it tells nothing about the closeness of E-G![]() to the pure third, it is well in tune with Bach’s own project in
the WTC.(10) A tuning with high MSS means that ALL major scales are similarly close to the theoretical heptagon, i.e. similarly “good.” Or should one say, “wohl”?
Video 1 shows all diatonic scales in LT, together with their closest heptagons. It can be observed that though the 12 scales differ among themselves, they are quite similar in the way they resemble the regular heptagon: this is what MSS is all about.
to the pure third, it is well in tune with Bach’s own project in
the WTC.(10) A tuning with high MSS means that ALL major scales are similarly close to the theoretical heptagon, i.e. similarly “good.” Or should one say, “wohl”?
Video 1 shows all diatonic scales in LT, together with their closest heptagons. It can be observed that though the 12 scales differ among themselves, they are quite similar in the way they resemble the regular heptagon: this is what MSS is all about.
2. Comparison of MSS for different tunings
[2.0.1] This section is devoted to numerical results, i.e. tables of values of MSS.
2.1. Tables
[2.1.1] Let us begin with a computer program for the computation of MSS on a given
![]() . It is convenient to put the values of the 12 elements of
. It is convenient to put the values of the 12 elements of
![]() in some table:
in some table:
![]() = {t0,
t1, ... t11}
= {t0,
t1, ... t11}
To do this, take any table of a temperament in cents and divide by 1200 to get the ais. This will be the input of the function that computes the MSS. Now we loop through the twelve major scales: For α = 0 to 11, compute the scale α and its first Fourier coefficient cα:
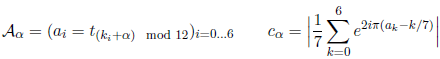
Lastly, find the minimum and the maximum in those 12 values; subtract the former from the latter, and take the inverse(11) of the result:
![]()
[2.1.2] Figure 4 gives this algorithm in Mathematica®, for scales with any number n of notes.
[2.1.3] In Table 1, consecutive fifths are given in cents from the origin; so in the program listed in Figure 4, the variable gamme had to be divided by 1200. All origins (A) have been set to the same value, 0. Of course, different origins can be given for each tuning, but this is equivalent to some rotation on the circle of notes, and the quantity MSS, being geometric in essence, is invariant under such transformations.(12)
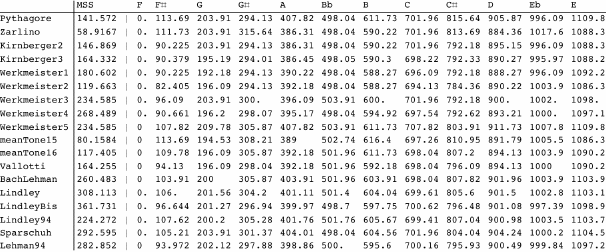
[2.1.4] I selected only a few elements in the extensive family of meantone tunings. Lindley’s tunings are tabulated from Lindley and Ortgies’s acerbic refutation (see Lindley and Ortgies 2006): the first two are built respectively with sevenths of Pythagorean and syntonic comma, and the last is the tuning used in the Michaelstein conference (this one found favor with Lehman). Similarly, I added the Sparschuh tuning and the previous Lehman proposition (dated 1994) as possible competitors, other interpretations of the scribble being, of course, of particular interest.
[2.1.5] I hope that through the process of chain-quotation, the exact values of these tunings have been preserved. As the computations have been carried through the professional software Mathematica®, with 64 bit arithmetic, we can hope to be rid of the rounding errors that blemished several controversies, and that resulted from incompatible unit conventions and inadequate software (Excel®).
[2.1.6] It is quite clear on these values that LT achieves by far the best value of MSS among temperaments prior to WTC, except for Werckmeister 4(13) which reaches almost equal value. It is interesting to see which classical tunings figure well in this table: Kirnberger’s are in good standing, and so is Valloti, but it is notable that the Pythagorean tuning supersedes Zarlino and the meantone temperaments. Remember that MSS measures a closeness between major scales, not the quality of, for instance, the twelve fifths.
[2.1.7] Graphic comparison of a few TeTs is available in this movie, where one can see the value of all Fourier coefficients changing with the different diatonic scales. The value of the leading coefficient a1 is apparent as the radius of a golden disk, whose size varies more or less according to the chosen TeT.
2.2. Minor scales
[2.2.1] As watchful readers will have noticed, the MSS has so far left aside half of the WTC: J.S. Bach also wrote preludes and fugues in all minor tonalities. MSS is originally a measure of “diatonicity”: could it also be used for testing minor scales? If by “minor,” one should understand the harmonic minor scale, then the theoretical relevance is poor.(14) But this natural assumption, taught to every kid in music school, has long been challenged by specialists.(15) Perhaps the most “natural” form of the minor is also diatonic, meaning that MSS is relevant both for minor and major tonalities.
[2.2.2] It might be interesting, though, to try this comparison on other familiar scales, like the ascending melodic minor [023579a].
2.3. First five fifths equal
[2.3.1] Permutations of the values of the different fifths of LT can be
tried. The result is illuminating. As we have already discussed, an optimal value of MSS
[2.3.2] So it should come as no surprise that some possible (nonequal) temperaments improve the value of MSS. This is the case for Werckmeister IV, which, though rational-valued, is a close approximation to equal temperament.(16) I found several such tunings by trying all permutations of the values of fifths that Lehman attributed to the three different kinds of loops in Bach’s scribble. For instance, the one which corresponds to the sequence of adjustments 0, -2, -2, -2, 1, -2, 1, -1, 0, -1, 0, -2,(17) has a much higher value of MSS.
[2.3.3] Such artifacts are generally very close to equal temperament. I did not recognize any known tuning in them, though learned readers might.
[2.3.4] But strikingly again, LT is still a winner when these permutations are confined to the six last fifths, i.e. when we keep the first five fifths equal: here I am discussing adjustments of the form -2, -2, -2, -2, -2 followed by any permutation of 0, 0, 0, -1, -1, -1. This must be relevant, as it was and still is common practice to start the tuning of a keyboard instrument by five equal fifths (often slightly shorter than a pure fifth), thus tuning equally the Guidonian hexachord FCGDAE. I certainly did, long before I ever heard of Bradley Lehman. This is true of all meantone tunings, for instance, and also very obvious for a musician accustomed to tonal music, since it is still desirable to have many equal fifths inside the scale(s) he or she plays in. Many harpsichord, organ, or piano-forte playing readers will acknowledge that they begin their own tunings by equal fifths between F-C-G-D-A-E. See below a discussion of O’Donnell’s objection, though (2006).
2.4. Other values of the wiggles
[2.4.1] One weak point of Lehman’s proposition is his arbitrary calibration of the wiggles as multiples of PC/12 (PC = a Pythagorean comma). On the other hand, changing this value ever so slightly falls within the approximation involved in any practical tuning—this is not exact science! On investigation, I tried variants of LT, replacing the unit PC/12, or 1.955 cents, by values close to it. The value of MSS can thus be increased slightly: if the fundamental wiggle is reduced to 2.16 cents, MSS reaches 278.7 instead of 260. This is the best possible improvement in that direction, with
![]() = {0; 95.685; 196.71;
297.795; 393.42; 498.105; 593.73; 698.355; 797.64; 895.065; 997.95; 1091.78}
= {0; 95.685; 196.71;
297.795; 393.42; 498.105; 593.73; 698.355; 797.64; 895.065; 997.95; 1091.78}
[2.4.2] Of course, a difference of 0.165 cents is hardly perceptible by ear—it is roughly a 150th of a comma! It is only the different order of fifths, the geometry of the scale, and not the change of comma, that explains the record value of MSS; the different value of the comma in Lehman’s first proposition in 1994 (labeled Lehman94 in Table 1) has nothing to do with its poor value of MSS.
2.5. Other interpretations of the wiggles
[2.5.1] Some have questioned the original note of the tuning: is it F—a common practice—or do some further curlicues along the scribble (look again at Figure 1) indicate the position of C, or D, or some other note? As far as the MSS is concerned, this is irrelevant, as a “well tempered” instrument will remain so even if the tuning is transposed, in the sense that all tonalities still sound well. Of course it would be nice to know exactly Bach’s tuning (giving specific different colors, i.e. Affekt, to different tonalities) but MSS cannot discriminate between tunings there, as it is invariant under a change of origin of the tuning.(18) Similarly, MSS cannot help us decide whether turning around the page (as Lehman did) is permitted, or mandatory: the inversion of a tuning shares the same geometric values,(19) and the sequence of wiggles (-1, -1, -1, 0, 0, 0, -2, -2, -2, -2, -2) has the same MSS as LT—a nice feature for contrapuntalists. In other words, using Lehman’s recipe with fourths instead of fifths yields exactly the same value of MSS.
[2.5.2] MSS can help, though, to discuss whether the wiggles mean consecutive fifths or consecutive semitones. This is a strong argument, as O’Donnell points out (O’Donnell 2006) that the order of tonalities in the WTC is given in semitones not in fifths—but Chopin, for instance, did the opposite in his Preludes, which clearly refer to the WTC. Indeed, MSS makes a fair case for O’Donnell’s proposed tunings, as seen from the values of MSS in Table 2, computed from Lehman’s comprehensive answer to O’Donnell:
[2.5.3] Several falsifications, in the sense of Popper, have been tried. In each case, LT emerges a winner. It is clearly a very special temperament, not only in its closeness to Equal Temperament, but in the homogeneity of all 24 scales. This constitutes a strong vindication of Lehman’s claim.
3. Conclusion and perspectives
[3.0.1] The MSS criterion arguably puts emphasis on the sameness of fifths inside the temperament. This goes some way towards explaining why permutations of the wiggles fail to improve MSS, when the first five are kept identical (see subsection 2.3); it also explains the fair value of MSS for Pythagorean (Ptolemaic) tuning, for instance. But this argument has its limits, as the discussion on all permutations of the wiggles proves. Still, it is quite important musically, as keyboard instrument players will readily agree, to find in any major scale a sequence of 3 (and preferably more) identical fifths in a row. This makes it easier to tune together with string instruments, for instance.
[3.0.2] Apart from aesthetic and other indefinitely debatable arguments, the computation of MSS gives a steadfast comparison point for tunings aimed at tonal music. Of course, it should not be considered as the sole criterion for the quality of a tuning—for instance, equal temperament would then be unbeatable, and Pythagorean tuning would be better than Kirnberger’s—but it does make sense to use it, among other criteria, to compare tunings already short-listed for historical and musical reasons.
[3.0.3] A limitation to the discriminating power of MSS is its indifference towards isometric transformations. Starting the tuning with C or F![]() or any note does not change the value of MSS, neither does tuning in fourths instead of fifths, i.e. reversing the cycle of fifths. This last point is one that raised much discussion: is Lehman right in turning around the first page of
the WTC? As we discussed previously, MSS brings no answer there. But consideration of the
phase of the Fourier coefficients (and not only of module), or maybe scrutiny of other Fourier coefficients (e.g.
or any note does not change the value of MSS, neither does tuning in fourths instead of fifths, i.e. reversing the cycle of fifths. This last point is one that raised much discussion: is Lehman right in turning around the first page of
the WTC? As we discussed previously, MSS brings no answer there. But consideration of the
phase of the Fourier coefficients (and not only of module), or maybe scrutiny of other Fourier coefficients (e.g.
![]() (0)), might help refine the analysis (I am indebted to Thomas Noll for these suggestions).
Other measures of the sameness of scales inside a given temperament might, and should, be proposed, as this criterion makes sense when considering
the WTC.(20) For one thing, the MSS is designed primarily for comparison of the major scales, and perhaps some other measurement should give equal standing to the minor scale in some form.
(0)), might help refine the analysis (I am indebted to Thomas Noll for these suggestions).
Other measures of the sameness of scales inside a given temperament might, and should, be proposed, as this criterion makes sense when considering
the WTC.(20) For one thing, the MSS is designed primarily for comparison of the major scales, and perhaps some other measurement should give equal standing to the minor scale in some form.
[3.0.4] The computations made for this paper are by no means exhaustive, and I hope that some other researchers will complete them. I intentionally refrained, though, from computing MSS on many tunings that either fall far from Bach’s universe or appear too arbitrary. Should some major tuning be lacking in this analysis, it is because I was not aware of its existence. Some independent computations—independent from the author’s—have confirmed that LT has a greater value than most of 60 Baroque (or earlier) temperaments.(21)
[3.0.5] A puzzling case is Werckmeister 4, a serious challenger of LT for the value of MSS. It stems from most modern authorities that the relationship of Bach to Werckmeister was more about counterpoint than tuning, but maybe this fresh evidence will rekindle interest in the notion that Bach shared at least some of Werckmeister’s original ideas about tuning.
[3.0.6] My modest intention was to add some nonsubjective evidence to the discussion of Lehman’s hypothesis. In the present state of the calculations in Table 1, the MSS criterion strongly supports Lehman’s theory. Maybe further efforts in the same line will help refine his claim—or crown some other tuning that I cannot foresee.
Appendix: the mathematics of MSS
3.1. Proof of lemma
Proof. From Parseval’s identity (see below), if | (1)| = 1 then for all t
(1)| = 1 then for all t
![]() 1,
1,  (t) = 0. Hence by inverse Fourier transform (Plancherel’s theorem) the elements of
(t) = 0. Hence by inverse Fourier transform (Plancherel’s theorem) the elements of
![]() are given by
are given by
![]()
which puts them on a regular n-gon.
The other assertion | (t)| ≤ 1 is a consequence of Parseval’s identity:
(t)| ≤ 1 is a consequence of Parseval’s identity:
![]()
□
3.2. Proof of theorem
[3.2.1] I give the proof of the theorem in the simpler case(22) when the number of notes n is coprime with the cardinality of the temperament, m. In this paper we have n = 7, m = 12. In such cases, a ME set is generated (Clough and Myerson 1985), i.e. the indexes of its notes are in arithmetic sequence modulo m, with a ratio f of the sequence that is the multiplicative inverse of n mod m. In the case n = 7, m = 12, this expresses the fact that the major scale is a sequence of fifths, i.e. (0, 7, 7 + 7 ≡ 2, 9, 4, 11, 6) or any transposition thereof. The ratio f = 7 is the inverse of n = 7: it checks f × n = 7 × 7 = 1 + 4 × 12 ≡ 1 mod 12.
Proof. I begin with pointing out that the map (k, j)
![]() n × k -
m × j is one-to-one (and onto) from
n × k -
m × j is one-to-one (and onto) from
![]() ×
×
![]() to
to
![]() , where
, where
![]() stands for the cyclic group with
p elements. This morphism (it is well defined, and obviously linear) of
stands for the cyclic group with
p elements. This morphism (it is well defined, and obviously linear) of
![]() -modules is injective:
-modules is injective:
![]()
using Gauss’s lemma (m divides n k but is coprime with n, hence divides k, similarly for n); and hence bijective because the cardinalities of both domain and codomain are finite and equal.
[3.2.2] This enables us to choose n couples (k0, 0), (k1, 1) ... (kn-1,
n - 1) in
![]() ×
×
![]() with
n kj - mj
with
n kj - mj ![]() {0, 1, ... n - 1} (mod m) × n, (choosing j first then
kj) hence
{0, 1, ... n - 1} (mod m) × n, (choosing j first then
kj) hence
![]() stays between 0 and
stays between 0 and
![]()
[3.2.3]
Hence the vectors occurring in the computation of  (1), i.e. the
(1), i.e. the
![]() , are as close together as possible. This maximizes their sum, as the cosines of their projections on the direction of their sum get as close to 1 as possible. This is proved by the following “huddling lemma,” whose general form may be found in
Amiot 2007.
, are as close together as possible. This maximizes their sum, as the cosines of their projections on the direction of their sum get as close to 1 as possible. This is proved by the following “huddling lemma,” whose general form may be found in
Amiot 2007.
Lemma 2. Let
![]() , j = 1 ...
n be n different mth roots of unity. Their sum has length at most
, j = 1 ...
n be n different mth roots of unity. Their sum has length at most
 i.e. the maximum value is obtained when all these points are huddled together.
i.e. the maximum value is obtained when all these points are huddled together.
Proof. Put S = ∑
![]() . Then |
. Then |![]() |≥ Re
|≥ Re
![]() = ∑cos(2kj
π ∕ m). Say for instance that n is odd: then there are exactly
n integers between
= ∑cos(2kj
π ∕ m). Say for instance that n is odd: then there are exactly
n integers between
![]() and
and
![]() .
.
[3.2.4] Unless the kj are precisely these integers, there exists some
j0 with |kj0| >
![]() and a value
k′
and a value
k′ ![]() [
[![]() ,
,
![]() ] that is not one of the
kj. As
] that is not one of the
kj. As
![]()
the sum of cosines is increased when k′ is substituted to kj0. This can be done till all the
kjs are in [![]() ,
,
![]() ], and as there are
n such kjs, they must be the n consecutive integers lying in this range. Then Re
], and as there are
n such kjs, they must be the n consecutive integers lying in this range. Then Re
![]() is at last maximal,
and so is |
is at last maximal,
and so is |![]() | = Re
| = Re
![]() (this last equality is now true by symmetry). The case “n even” is a little trickier but similar and will be left to the reader, as this paper only needs a proof when
n = 7, m = 12.
(this last equality is now true by symmetry). The case “n even” is a little trickier but similar and will be left to the reader, as this paper only needs a proof when
n = 7, m = 12.
□
[3.2.5] We return to the proof of the theorem. The lemma proves that the maximum configuration occurs when
![]()
Multiplying by f = n-1 mod m yields
![]()
i.e. an arithmetic progression with ratio f. The most general case is obtained by translation (i.e. a transposition, musically speaking) of this one.
□
Acknowledgements
I am indebted to the members of the American new wave of musicologists who renewed the interest in the study of scales, through the novel notions of ME sets, and later Well Formed Scales: the late J. Clough, G. Myerson, J. Douthett, N. Carey and particularly David Clampitt who, together with Richard Cohn, kindled my interest in the topic by inviting me to the John Clough Memorial Days; to Ian Quinn whose fascinating work on “chord quality” revived David Lewin’s idea on Discrete Fourier Transform and gave me a starting point for fruitful research; and to Thomas Noll who shrewdly perceived that DFT could be extended to non equal temperaments with a slightly different formula, and also gave me the incentive to explore this alley when he invited me to the Helmholtz “Klang und Ton” workshop in Berlin. I also thank Bill Sethares, a great specialist of Fourier Transform for consonance issues, for his useful advice and encouragements. Last but not least, my wife helped me tremendously with the wording of this paper, despite its technicality.
This paper is dedicated to the memory of Marcel Mesnage, who unfortunately did not live to see it. A delicate composer, computer wizard, and pioneer researcher, he was first and foremost a delicious man.
Emmanuel Amiot
Prof. in CPGE, Perpignan
1, rue du Centre
F 66570 St Nazaire
manu.amiot@free.fr
Works Cited
Amiot, Emmanuel. 2007. David Lewin and Maximally Even Sets. Journal of Mathematics and Music 1 (3): 157–72.
Carey, Norman, and David Clampitt. 1989. Aspects of Well Formed Scales. Music Theory Spectrum 11 (2): 187–206.
Clough, John, and Jack Douthett. 1991. Maximally Even Sets. Journal of Music Theory 35: 93–173.
Clough, John, and Gerald Myerson. 1985. Variety and Multiplicity in Diatonic Systems. Journal of Music Theory 29: 249–70.
Douthett, Jack, and Richard Krantz. 2007. Maximally Even Sets and Configurations: Common Threads in Mathematics, Physics, and Music. Journal of Combinatorial Optimization 14 (4): 385–410. http://www.springerlink.com/content/g1228n7t44570442
Lehman, Bradley. 2005a. Bach’s Extraordinary Temperament: Our Rosetta Stone–1. Early Music 33: 3–24.
—————. 2005b. Bach’s Extraordinary Temperament: Our Rosetta Stone–2. Early Music 33: 211–32.
Lewin, David. 1959. Re: Intervallic Relations Between Two Collections of Notes. Journal of Music Theory 3: 298–301.
Lindley, Mark, and Ibo Ortgies. November 2006. Bach-style Keyboard Tuning. Early Music 34: 613–24.
O’Donnell, John. November 2006. Bach’s Temperament, Occam’s Razor, and the Neidhardt Factor. Early Music 34: 625–34.
Quinn, Ian. 2004. A Unified Theory of Chord Quality in Equal Temperaments. Ph.D. dissertation, Eastman School of Music.
Footnotes
1. Counterclockwise, i.e. decreasing the size of the fifth.
Return to text
2. Lehman uses one twelfth of a comma, which is indistinguishable in practice.
Return to text
3. For instance, many pages have been written about the quality of the single third E-G![]() in LT versus other ways of tuning; but the overall number of nice “tertiam minorem,” as Bach calls them, might also be considered of equal or greater importance than that of major thirds, or the size of whole tones, or any other plausible feature of a given temperament.
in LT versus other ways of tuning; but the overall number of nice “tertiam minorem,” as Bach calls them, might also be considered of equal or greater importance than that of major thirds, or the size of whole tones, or any other plausible feature of a given temperament.
Return to text
4. In the rectified version, assuming the value 176/196 in the division of the monochord should be read as 175/196, as many have corrected.
Return to text
5. Occam’s razor? See
O’Donnell 2006.
Return to text
6. Meaning a sequence of notes in a given temperament.
Return to text
7. Adding n to t does not change the value of
 (t).
(t).
Return to text
8. The DFT is a continuous map: if | (1)|
> |
(1)|
> |![]() (1)|
in equal temperament, the small modifications of arguments
(1)|
in equal temperament, the small modifications of arguments
![]() and
and
![]() resulting from nudging some notes away from their equal tempered position, will only slightly disturb the values
|
resulting from nudging some notes away from their equal tempered position, will only slightly disturb the values
| (1)|, |
(1)|, |![]() (1)| and the inequality will still stand.
(1)| and the inequality will still stand.
Return to text
9. Obviously this appears as a mathematical feature, not a musical one. The fact that the major scale is Maximally Even is highly relevant to tonal functions. This is discussed in the literature on ME sets and the reader is invited to consult the references given in the bibliography.
Return to text
10. Admittedly Bach does mention major and minor thirds on the front page,
plus tones and semi tones (see Figure 1), but he insists on the possibility of playing
all these intervals in all 24 tonalities.
Return to text
11. In order to facilitate comparison.
Return to text
12. Incidentally, it is also invariant under inversion (which amounts to reversing the lists), as the inverse of any major scale is also a major scale.
Return to text
13. I wonder whether this temperament ever had practical importance—who ever managed to tune a 196/139 interval by ear?
Return to text
14. Still I felt compelled to compute the mSS, the equivalent of MSS for harmonic minor scales, and rather strangely, it concurs with Table 1.
Return to text
15. “It may be of some interest that Johann Sebastian Bach in his manual on thorough bass (reprinted in Phillip Spitta’s biography of Bach as Appendix XII to Vol. VII) expressly states the identity of the minor mode with the Aeolian system” (p. 46, Heinrich Schenker [Harmony], Oswald Jonas, ed., Elisabeth Mann Borghese, trans. 1954, reprinted MIT Press 1973).
Return to text
16. Hearing the WTC in this tuning should be an interesting experience, considering it is so far the only competitor to LT
for MSS.
Return to text
17. Whereas LT gives -2, -2, -2, -2, -2, 0, 0, 0, -1, -1, -1[, 0]. The unit chosen by Lehman is a twelfth of a
Pythagorean comma.
Return to text
18. Transposition, in the musical sense, does not change the absolute value of the DFT.
Return to text
19. The DFT is turned into its conjugate. See
Amiot 2007.
Return to text
20. For instance, some Haussdorf distance between polygons up to isometric transformations.
Return to text
21. I want to thank Thomas Dent, a careful reader of an earlier version of my published paper in MTO 15.2, for pointing out a numerical blunder that affected several values in Tables 1 and 2. They have been corrected as of October 11, 2009. Fortunately, the conclusion that the Major Scale Similarity of the temperament proposed by B. Lehman is greater than almost all previous temperaments is still valid. I certainly hope that musicologists will compute their own values for MSS, and that this approach becomes a standard tool for appreciating the quality of a temperament.
Return to text
22. It still stands in the most general case, following the framework of
Amiot 2007.
Return to text
Copyright Statement
Copyright © 2009 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor and Cara Stroud and Tahirih Motazedian, Editorial Assistants
Number of visits: