Coaching Mozart’s String Quintet in E-Flat Major: Finding the Rhythmic Shape

[1] Years ago I had the distinct privilege of coaching five members of a major symphony orchestra in a rehearsal of the first movement of Mozart’s String Quintet in E-Flat Major, K. 614. Although I had spent many hours contemplating this movement when analyzing it for my doctoral dissertation, I wondered about which aspects (if any) of my very detailed analysis might be of value in preparing suggestions for the performers. I thought back to the words of Edward T. Cone, who suggested that the key to meaningful interpretation lies in understanding “the rhythmic life of a composition” (Cone 1968, 31). In the past few decades we have witnessed a dramatic rise in the number of analytical studies devoted to musical rhythm (particularly as it relates to pitch structure) and more authors are paying attention to how such analytical insights can inform and enliven musical performance.⁽¹⁾ It is the purpose of the present study to explore this area, using the first movement of K. 614 as a test case. My coaching of this movement with the string quintet was recorded, and several excerpts from that recording session are included as MP3 files to accompany the musical examples.

[2] My methodology will follow Heinrich Schenker’s ideas about rhythm and meter, as explained by Carl Schachter and William Rothstein.⁽²⁾ In my discussion I hope to strike a balance between a consideration of higher-level rhythmic structures (phrase structure and hypermeter) and the treatment of rhythms that occur on the musical surface; indeed, I intend to illustrate the interaction of these. The principal goals of the analysis are: (1) the identification of a “basic rhythmic shape” for a given passage, which may be enhanced in performance by slight adjustments in tempo, intensity, or duration (Wallace Berry’s terms tempo and articulation [Berry 1989, 2–3]); (2) the exploration of how this basic shape interacts with other materials, and how this interaction may affect performance; and (3) a consideration of rhythmic structure in relation to pitch structure, including the explanation of passages in which the phrase rhythm contains an irregularity due to the compression or expansion of measure groups, and possible responses to these irregularities in performance.

[3] Before going any further, I offer several caveats pertaining to my approach. First, by my concept of a basic rhythmic shape, I do not mean to make complex music inappropriately simple; rather, the basic rhythmic shape acts as a point of reference for the discussion of a particular passage. Second, I do not claim that my performance suggestions to the quintet constitute the ultimate way to perform a given passage; I merely suggest one valid way among many. Third, I agree with William Rothstein and Joel Lester when they caution us that not all analytical findings could or should be projected in a musical performance (Rothstein 1995, 238; Lester 1995, 210); I hope to avoid matters that, while of interest to the analyst, are simply too arcane to be underscored by the performers. Finally, some readers might identify my interpretive suggestions as the very things that an intuitive performer might do solely by intuition. I have no problem with this view, for I believe that analytical findings can often serve to justify largely intuitive performance decisions.⁽³⁾

[4] The beginning of the first movement of the Quintet in E-Flat, K. 614, is given in Example 1. An MP3 of the quintet’s performance from my coaching session is provided. The opening (measures 1–4) juxtaposes two contrasting ideas in two different registers: x, a hunt topic featuring an upper neighbor-note pattern in the one-line octave (measures 1–2); and y, a more refined melody descending from the two-line to the one-line octave (measures 3–4). How should my performers approach idea x, given the high redundancy of its accented upper neighbor-note figure? A possible answer may be found if we consider idea x in its larger context, as it relates to idea y (whose interpretation is clearer). In idea y unaccented sixteenth notes “push” into the following beat; I suggested that the violinists compress these sixteenths slightly so as to move forward to the following eighth, with a slight separation between note groupings to compensate for the minute amount of time gained by this process. Horizontal arrows on the score indicate these note compressions, while vertical strokes show slight separations between note groupings that compensate for these compressions.⁽⁴⁾ The push in idea y is strongest into the downbeat of measure 4 (since this downbeat is preceded by four sixteenths rather than two, and the remainder of bar 4 is melodically and harmonically static), suggesting a crescendo into the third dotted-quarter-note beat of the four-beat group: 1 - 2 | 3 - 4 (marked below the first violin part). If we consider measures 3–4 from a compositional point of view, the same shape obtains. Example 2a provides a recomposition of idea y that regularizes the rate of descent in the melodic line; note that the falling third is mechanically repeated in sequence three times to cover the ground from b² to a¹. In Mozart’s more subtle conception (Example 2b), however, there is a clear accelerando in the descent at the end of measure 3 so as to introduce the goal (a¹) on beat 1 of measure 4, rather than beat 2. This quickening in the tonal motion propels the unit forward to the downbeat of measure 4, again projecting the shape 1 - 2 | 3 - 4 . I suggested to the performers that the same pattern of stress can be applied to motive x (Example 1) since it clearly establishes the meter, yet respects the forward drive produced by the repetition of the neighbor-note pattern. This interpretation is reinforced in measures 11–12, when the first measure of idea x is integrated into a new statement containing an agogic accent on beat 3 of the four-beat group: again, the configuration 1 - 2 | 3 - 4 , that dominates the remainder of the theme and can be regarded as the basic rhythmic shape for the passage (hereafter called the brs).⁽⁵⁾

[5] The brs can be described as a Vierer—Joseph Riepel’s term for a four-unit grouping in his Anfangsgründe (Riepel 1754, 3); in our case, there is special emphasis on the third unit through a local phenomenal accent.⁽⁶⁾ Although our first examples of the brs pertain to the beat level, I will argue that the brs can also operate recursively over higher levels of rhythmic structure, with phenomenal and/or structural accents on the third of four durational units.⁽⁷⁾ A consideration of phrase rhythm in its broader outlines in the first theme of K. 614 will provide an illustration of how this can occur and will further inform a sensitive performance of the passage.

[6] The theme (Example 1) consists of a single sentence: the first subphrase in measures 1–4 is a fine example of William Caplin’s “compound basic idea” (with its contrasting x and y segments); the second subphrase in measures 5–8 presents the varied repetition of this idea, while measures 9–19 constitute the expanded continuation, with its customary fragmentation, liquidation, and cadence.⁽⁸⁾ Each subphrase coincides with one four-bar hypermeasure; this quadruple hypermeter is shown just above the cello line throughout Example 1. In subphrases 1 and 2 the fourth bar of the group receives emphasis because of the change of harmony and the completion of the brs at the dotted-quarter-note level. The same holds true for the third hypermeasure, with the greatest stress occurring in measure 12; this unit is then extended in bar 13 by a prolongation of the V⁷ chord and a sequential repetition of the Vln. I figure from the previous measure. I directed the performers to play the extension at a slightly lower dynamic level, with a very slight reduction in tempo.⁽⁹⁾

[7] The brs even embraces the entire theme, as illustrated in Example 3. In the voice leading sketch ideas x and y are placed on the upper and middle staves, respectively. Idea x articulates an ascent from to , while idea y outlines a series of unfolding sixths, b¹ /g² – a¹ /f² – g¹/e². The latter implies two melodic lines, one descending from to in the two-line octave, the other from to in the one-line octave. These two trajectories converge at bar 9 when x (the hunt topic previously associated with the lower register) is now transferred to the higher, more “refined” register of y, signaling the arrival of the primary melodic tone, g² (). The reconciliation of ideas x and y with respect both to topic and pitch structure, therefore, occurs at the beginning of subphrase 3, at the same time that x and y are being integrated rhythmically on the musical surface. The structural accent thus placed on the third subphrase produces the brs at the phrase level, this shape now encompassing the entire theme (as shown above Example 3). I directed the quintet to make measures 9–13 the focal point of attention in the pacing of the performance of the entire theme; the music should progress to and recess from these bars, and the greatest amount of energy should be expended within them.⁽¹⁰⁾ At first, this suggestion startled the players, since they had grouped measures 1–8 separately from measures 9–19 in their conceptualization of the theme. However, my approach eventually won them over, particularly since it shaped the theme as a single, cohesive unit, and allowed them to see the “forest” instead of the individual “trees.”

[8] Carl Schachter addresses a similar issue involving phenomenal and structural accents in a Vierer in his insightful analysis of the Minuet from Beethoven’s First Symphony (Schachter 2000, 59–68). Schachter observes these accents on the even-numbered downbeats of the quadruple hypermeasures of the opening theme (e.g., measures 2 and 4); these accents, of course, are in conflict with the natural metrical accents on the odd-numbered bars of each four-bar unit. This conflict is resolved by the conclusion of the Minuet portion of the movement when the structural and phenomenal accents are brought into proper alignment with the hypermeter. His approach to the Vierer in the Minuet thus differs somewhat from my approach in the Mozart Quintet, since my brs does not strongly contradict the given meter or hypermeter, and the brs operates on many different rhythmic levels, from dotted-quarter-note beat to quadruple hypermeasure—and beyond, as we will see below.

[9] The transition and second theme of K. 614, I are shown in Example 4. An MP3 of the coached performance is again provided. As indicated by the numbers above the music, the transition (measures 20–38) can be viewed as a single phrase of eight measures, with several expansions. The seventh and eighth measures of the unit (measures 26–27) are repeated in measures 28–29 and 30–31; the final repetition of the eighth basic bar at measure 31 is extended by an eight-measure unit prolonging V of B in measures 31–38, which establishes its own surface duple hypermeter. The local reinterpretation of measure 31 as strong bears upon performance: I asked the first violinist to treat measure 31 as a “new beginning.” The absence of any specific dynamic markings except for the initial forte in each instrument raises questions about the shaping of the various segments of the transition, questions that might again be answered by an examination of the rhythmic issues in this section.

[10] In addition to providing the customary modulation to connect from first to second group, the transition also contains a rhythmic link between the principal thematic areas, involving Mozart’s treatment of idea x. The motive in its original form (now called x¹) begins in measure 20 in the second viola, then is imitated in the first viola in the following bar. The latter statement (labeled x²) commences, in effect, a beat early, shifting the first trilled neighbor note to the strong beat in measure 22. This shift has several important consequences. First, it prepares the rhythmic pattern for x³ found in Theme II in measures 39–40, where the neighbor (without trill) again appears on a strong rather than weak beat. Second, it sets up a substantial surface emphasis on measure 22, the strong measure, and a complementary release for measure 23, the following weak measure. (This pattern of stress and release correlates well with the harmonic pattern of dissonant dominant seventh in measure 22 resolving to consonant triad in measure 23.) As a result, the brs may be heard at the bar level in measures 20–23, and the pairs of bars which follow in sequence (measures 24–25 and 26–27) can be understood as a response to 22–23, with similar shaping by the performers (stress for the strong bar, release for the weak bar). The expansion of the F major chord in measures 31–38 contains clear references to the basic rhythmic shape at the beat level. As shown by the circled pitches in Example 4, the basic pitch contour at the dotted-quarter-note level in first violin and first viola, measures 31–32 and 33–34, suggests the pattern 1 - 2 | 3 - 4 , with an appropriate crescendo into the downbeats of measures 32 and 34. For the dynamic curve of measures 31–38 as a whole, the brs is again appropriate, now at the two-bar level: I directed the performers to begin at mf for measures 31–32, increase to f for measures 33–34, then peak at ff in measure 35 (the beginning of the third pair of bars). A decrescendo back to mf in measures 35–38 is appropriate for the descending register transfer in Vln. I, and also leads smoothly to the piano dynamic level for Theme II.

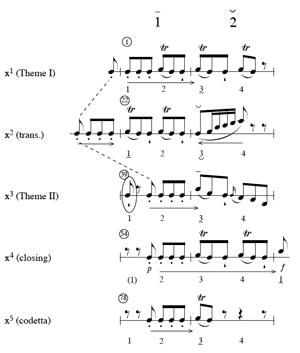
[11] In contrast to the irregularities of the transition, the second theme is quite stable and regular, consisting of a parallel period with eight-measure antecedent and consequent phrases. The melodic structure comprising a descending fifth-progression, with interruption, is typical for a period of this kind. As mentioned previously, the variant x³ appears in measures 39–40, its upper neighbor note now sounding on a strong beat (measure 40, beat 1)—a pattern first established with x² in the transition. However, the motive is now stabilized metrically with the addition of a downbeat eighth note at measure 39. This addition enables x³ to begin on a strong bar, unlike the situation at measure 21 of the transition. As a consequence, the variant of idea x at the beginning of Theme II is the most stable version encountered. The added downbeat also creates the brs at the beat level, the accented incomplete neighbor sounding on the third beat of the four-beat group, as shown.⁽¹¹⁾ The same dynamic curve may be used for virtually every two-bar group of the theme, thus reflecting its high degree of rhythmic stability. Example 5 summarizes the metamorphosis of idea x throughout the exposition, showing how its motivic material is shifted first to the left (transition), then to the right (Theme II) in relation to the prevailing duple hypermeter. Note that in the closing material, x⁴ retains the same metrical position as x³, but without the strength of the added downbeat heard at measure 39; hence, the statement of x⁴ beginning in the second half of measure 54 pushes to the downbeat of measure 56, producing the shape (1) - 2 | 3 - 4 , 1 at the dotted quarter-note level. This subphrase is clearly out of phase with the hypermeter, and offers the greatest contrast to the basic shape heard in x¹ and x³.⁽¹²⁾ In the codetta (measures 78ff.) the brs is reinstated for x⁵ at the close of the exposition. I asked the quintet to shape each of these variants of x carefully, as stipulated in Example 5.⁽¹³⁾ Given the high degree of surface redundancy for this motivic idea, the performers appreciated the variety of approaches to its execution.

[12] A play between regularity and irregularity characterizes the development section (Example 6; MP3 provided). In measures 78ff. the duple hypermeter is shown at the bottom of each system, while the counting of half-bars is listed under Vln. I. As mentioned previously, the statements of x⁵ in the codetta, measures 78–79 and 80–81, suggest the brs in performance. As the motive is fragmented in measures 82–86 the trilled neighbor note begins to appear on both strong and weak beats, with a final “spinning out” in first violin (measures 84–86) that expands the phrase and creates a sense of hypermetrical disorientation. The repetition of the expanded unit in measures 87–89 to facilitate a sudden tonal shift increases the effect of this instability.⁽¹⁴⁾ To enhance this ambiguity, I suggested a slight crescendo that pushes to the end of each expanded hypermeasure, followed by a slight exaggeration of the rests in measures 86 and 89. In measures 97–99 and 107–109, where similar expansions occur using x² and its fragments,⁽¹⁵⁾ a different approach is warranted: since the shape of x² pushes into a strong downbeat and then recedes, a decrescendo is appropriate. It was also important for the performers to recognize that measures 97 and 107 are strong bars, as a consequence of the one-measure expansions that precede them. The material in measures 119–124 might have presented a situation similar to the one at the beginning of the development, where a series of x⁵ fragments obscured the hypermeter. Instead, Mozart restates the material from measures 84–86 as measures 122–124; ironically enough, this material—originally disruptive at measures 84–86—is no longer in conflict with the duple hypermeter, since it begins on a weak bar rather than a strong one. This change at the close of the development section provides a stronger point of reference for idea x¹ at the beginning of the recapitulation: if the performers strongly present duple measure groups in measures 119–124, the duple shaping for x¹ in measures 125–126 (using the brs) now seems quite appropriate, and supports the same interpretation for x at the beginning of the exposition.

[13] In order to illustrate the broader rhythms of the development, thereby informing the performers’ sense of pacing and large-scale goals for this section, I prepared a durational reduction, provided in Example 7a. Reducing each bar of the original music to a single quarter-note beat produces this representation; thus, the two-measure groups of the original (i.e., its duple hypermeasures) are now shown as single measures in 2/4 time.⁽¹⁶⁾ This version of the music enables us to recognize irregularities such as the single-bar expansions at measures 86 and 89 much more easily, since these suffixes create apparent bars of 3/4 time instead of the regular 2/4. The accompanying voice leading graphs in Examples 7b and 7c furnish further information about the pitch structure of the development (in relation to the end of the exposition). The basic tonal content for the section, shown in graph c, consists of the prolongation of the dominant following the pattern V^5-7. The melodic motion from f² (, measure 78) to a² (measure 119) is filled in with a large-scale passing tone, g², at measure 110, harmonized by the submediant. The addition of III⁶ (V⁶/VI) at measure 107 produces an ascending 5-6 pattern in measures 78–110 (with bass G at measure 100 as an added root). The a² at measure 113 generates another 5-6 progression; at the same time, the resolution of bass C (measure 110) to bass B (measure 119) is embellished by a passing C, an interesting enharmonic foil to the passing B heard previously in the bass at measure 107. Sketch b provides further details of harmony and voice leading.⁽¹⁷⁾

[14] A comparison of sketch a with sketches b and c allows us to ascertain relationships between durational events and tonal events, as a method of perceiving the overall pacing of the section. For example, reduction a shows that the 2/4 hypermeasures combine in groups of four to form larger hypermeasures, indicated by the bold bar lines at measures 90, 100, 110, and 119. The first large hypermeasure contains the passing subdominant area, the second the mediant harmony; the third large unit (measure 110) comprises the motion from VI toward V, the fourth the prolongation of the dominant. The most interesting irregularities occur in the third hypermeasure of higher order, measures 110–118. First, a contraction reduces the second small hypermeasure to a single bar, measure 112; I asked the first violinist to be aware of the a² in measure 113 as a new hypermetrical downbeat. This interpretation follows the pitch structure (graph b), since a² initiates a descending fifth motion to d² at measure 119. The descending fifth constitutes an unfolding into the inner voice of the V⁷, as shown. Comparing sketches a and b at this point, it may be observed that the initial pace of the descending fifth is one pitch per quarter-note value of the reduction (a bar of the actual score) in measures 113 and 114; the pace then slows to one pitch per two bars for f² (measures 115–116) and e² (measures 117–118). The expansions of f² and e² represent a “written-out decelerando,” to use Rothstein’s term (Rothstein 1989, 80–87). Once this expansion is recognized, we may ascertain that the B major chord in measure 116 is not the structural dominant, which only arrives at measure 119. Hence, the performers should not give undue emphasis to measure 116 (or measure 118), as the interaction of tonal and durational events clearly demonstrates.

[15] With regard to the pacing of tonal events for the development section as a whole, note that the substantive tonal motion—the move through VI back to V—is concentrated in the second half of the section, in the third and fourth large hypermeasures. Could the brs even be applied at the higher hypermetrical level, to encompass the entire development section (as proposed by the stress mark under the large numeral 3 at measure 110)? Such a viewpoint, is, to be sure, controversial; as Justin London and others have pointed out, it becomes increasingly difficult to perceive patterns of stress and release as musical units become longer and longer.⁽¹⁸⁾ Yet, one cannot ignore the sudden acceleration in the rate of tonal motion in measures 110–118, after the relatively static harmonic content of measures 90–99 and 100–109. In working with the quintet, I suggested a push forward to the third large unit as climax, followed by a receding motion in the fourth unit as the dividing dominant is prolonged.

[16] In summary, I have attempted to illustrate an approach to musical rhythm in performance that addresses intricate musical details as well as large-scale rhythmic issues (i.e., phrase structure in relation to hypermeter), using my own coaching of the first movement of the Mozart E-Flat Major String Quintet, K. 614, as a test case. I leave it to the reader who listens to the recorded examples from the coaching session to judge whether or not my attempt has produced a musically successful result.

[17] Is the presence of a basic rhythmic shape in the E-Flat Major Quintet a special case, or might we discover the same construct at work in other pieces by Mozart, as well as other composers? I would not presume to make too broad a claim for the brs; after all, a pattern of accentuation that embraces so many different time spans is not likely to be duplicated in a great number of pieces. However, I can cite a few examples that merit further study along these lines. The first movement of Mozart’s Quartet in D, K. 499 (“Hoffmeister”) features a main theme with a brs similar to the one encountered in K. 614: 1 - 2 | 3 - 4, with a strong agogic accent on the third half-note beat in cut time (Example 8a). The second movement of Beethoven’s Quartet in F, Op. 59, No. 1 has been the subject of several rhythmic studies. In his analysis of its principal rhythm, Carl Schachter has pointed out the lack of “forward momentum” in its first two bars, followed by a sixteenth-note push into the fourth bar;⁽¹⁹⁾ using the approach in the present study, we could assign the brs 1 - 2 - 3 - 4, as indicated in Example 8b. Interestingly enough, Dave Headlam has shown how “the higher-level rhythmic organization of the first key area is a large-scale reflection of the structure of the principal rhythm”: after the initial antecedent phrase (measures 1–8), a series of three consequent phrases (that he labels consequent 1, consequent 2, and consequent 3) are needed before the music “breaks through” to its harmonic goal, V/V, in the following transition (Headlam 1985, 121–22). Hence, cons. 1–cons. 2–cons. 3–trans. could also articulate the pattern 1 - 2 - 3 - 4, in the manner of the brs. Although the correspondence between the principal rhythm and the first key area is somewhat more selective than in the present study, the approach is certainly similar from a qualitative (if not strictly quantitative) standpoint.

[18] The validity of both levels of meaning—the broader hypermeter as well as the specific rhythmic pattern—is addressed in the book The Art of Quartet Playing: The Guarneri Quartet in Conversation with David Blum. With regard to hypermeter, Arnold Steinhardt (the first violinist) says: “I believe there’s truth in the traditional concept of strong and weak bars within a phrase.” While cautioning against a rigid approach to this principle, he maintains that “even if the traditionally weak bar has been specially emphasized by the composer . . . I still acknowledge somewhere inside me the presence of the strong bar” (Blum 1986, 150). If anyone doubts the propriety of delving so deeply into the intricacies of musical detail—as we have done here—Steinhardt offers this thought, with which I will close:

Some musicians fear that a detailed examination of a phrase may smother spontaneity and lead to self-consciousness . . . Maybe it really works the other way around. Perhaps spontaneity depends upon a real perception of the musical line and its possibilities . . . When a composer wrote a work, he felt the function of every note. The interpreter has to enter as much as possible into the composer’s creative workshop (Blum 1986, 149).

Joseph C. Kraus
Florida State University
College of Music
132 N. Copeland St.
Tallahassee, FL 32306-1180
jkraus@fsu.edu

Works Cited

Berry, Wallace. 1987. Structural Functions in Music. 2nd ed. Mineola, NY: Dover.

—————. 1989. Musical Structure and Performance. New Haven and London: Yale University Press.

Blum, David. 1977. Casals and the Art of the Interpretation. Berkeley: University of California Press.

—————. 1986. The Art of Quartet Playing: The Guarneri Quartet in Conversation with David Blum. Ithaca: Cornell University Press.

Caplin, William. 1998. Classical Form: A Theory of Formal Functions for the Instrumental Music of Haydn, Mozart, and Beethoven. New York and Oxford: Oxford University Press.

Cone, Edward T. 1968. Musical Form and Musical Performance. New York: Norton.

Headlam, Dave. 1985. “A Rhythmic Study of the Exposition in the Second Movement of Beethoven’s Quartet Op. 59, No. 1.” Music Theory Spectrum 7: 114–138.

Larson, Steve. 1983. “On Analysis and Performance: The Contribution of Durational Reduction to the Performance of J. S. Bach’s Two-Part Invention in C Major.” In Theory Only 7.1: 31–45.

Larson, Steve and Cynthia Folio. 1991. Review of Musical Structure and Performance, by Wallace Berry. Journal of Music Theory 35.2: 298–309.

Lerdahl, Fred and Ray Jackendoff. 1983. A Generative Theory of Tonal Music. Cambridge, MA: MIT Press.

Lester, Joel. 1995. “Performance and Analysis: Interaction and Interpretation.” In The Practice of Performance: Studies in Musical Interpretation, ed. John Rink, 197–216. Cambridge: Cambridge University Press.

London, Justin. 2004. Hearing in Time: Psychological Aspects of Meter. New York and Oxford: Oxford University Press.

Mozart, Leopold. 1756/1951. Versuch einer gründlichen Violinschule. Rev. ed., trans. Editha Knocker as A Treatise on the Fundamental Principles of Violin Playing. Rev. ed. London: Oxford University Press. (Reprint edition in Early Music Studies, no. 6, 1985.)

Quantz, Johann Joachim. 1752. Versuch einer Anweisung die Flöte traversiere zu spielen. Berlin: Voss. (3rd ed., Breslau: J. F. Korn, the elder, 1789.)

Riepel, Joseph. 1754. Anfangsgründe zur musikalischen Setzkunst. Vol. 1, De rhythmopoeïa, oder von der Tactordnung. 2nd ed. Regensburg: J. L. Montag.

Rolf, Marie and Elizabeth West Marvin. 1990. “Analytical Issues and Interpretive Decisions in Two Songs by Richard Strauss.” Intégral 4: 67–103.

Rothstein, William. 1989. Phrase Rhythm in Tonal Music. New York and London: Schirmer Books.

—————. 1995. “Analysis and the Act of Performance.” In The Practice of Performance: Studies in Musical Interpretation, ed. John Rink, 217–240. Cambridge: Cambridge University Press.

—————. 2005. “Like Falling off a Log: Rubato in Chopin’s Prelude in A-flat Major (op. 28, no. 17).” Music Theory Online 11.1.

Schachter, Carl. 1976. “Rhythm and Linear Analysis: A Preliminary Study.” The Music Forum 4: 281–334.

—————. 1980. “Rhythm and Linear Analysis: Durational Reduction.” The Music Forum 5: 197–232.

—————. 1987. “Rhythm and Linear Analysis: Aspects of Meter.” The Music Forum 6.1: 1–59.

—————. 2000. “Playing What the Composer Didn’t Write: Analysis and Rhythmic Aspects of Performance,” in Pianist, Scholar, Connoisseur: Essays in Honor of Jacob Lateiner, ed. Bruce Brubaker and Jane Gottlieb, 47–68. Stuyvesant, NY: Pendragon Press.

Schmidt, Christoph and Naphtali Wagner. 1999. “KV 614: Schock und Struktur in der Wiener Klassik [K. 614: Shock and structure in Viennesse Classicism],” trans. Katharina Berger and Ludwig Holtmeier. Musik und Aesthetik 3.10 (April 1999): 28–46.

Temperley, David. 2003. “End-Accented Phrases: An Analytical Exploration.” Journal of Music Theory 47.1: 125–154.

Türk, Daniel Gottlieb. 1789/1982. Klavierschule or School of Klavier Playing: Instructions in Playing the Clavier for Teachers and Students, trans. Raymond H. Haggh. Lincoln, NE: University of Nebraska Press.

Footnotes

1.  For example, Steve Larson (1983) has applied durational reduction in making performance recommendations for J. S. Bach’s C-major Invention; Marie Rolf and Elizabeth West Marvin (1990) have included hypermetrical analysis in their interpretive comments for two songs from Richard Strauss’s Opus 27. William Rothstein (1995) has discussed hypermetrical conflict in Chopin’s A Major Waltz, Op. 42. Two more recent studies are important antecedents for the present article: Carl Schachter’s brilliant treatment of “rhythmic imbroglio” in the Menuetto from Beethoven’s Symphony No. 1 (2000, 59–68) and William Rothstein’s insightful discussion of rubato in Chopin’s Prelude in A Major (2005).
Return to text

2.  Carl Schachter 1976, 1980, and 1987. William Rothstein (1989) offers a particularly comprehensive approach.
Return to text

3.  In this I would disagree with Wallace Berry’s strictures against relying on intuition (1989, 217); rather, I see pure intuition and pure analytic reasoning as extremes of a continuum, where the broad midsection of this continuum contains a field of “play” where intuition and analysis can interact with one another in an interdependent fashion. For a similar view, see the review of Berry’s Musical Structure and Performance by Steve Larson and Cynthia Folio (1991, 301).
Return to text

4.  These arrows and strokes, as well as the tenuto markings and hairpins at the top of each system in Example 1 (and in subsequent score excerpts), are my own suggestions; they are not part of the autograph score. The compression of short values in performance is discussed at some length by David Blum in Casals and the Art of the Interpretation (1977, 70–79). Though one might assume that Casals’ recommendations reflect a Romanticized approach to the execution of Classic music, treatises from the later eighteenth century do address this issue. For example, in chapter 6, ¶48 of his Klavierschule, Türk recommends lingering on dotted notes, then shortening the notes that follow (1789, 350–351). Similar instructions can be found in Leopold Mozart’s Versuch (1756), ch. 12, ¶21, p. 224.
Return to text

5.  Strictly speaking, the concept under discussion here is really a basic accentual shape, where an accent is perceived on the third of four rhythmic pulses. I prefer the term basic rhythmic shape since it communicates the idea that a particular pattern of accent can apply over various time spans, imparting a dynamic contour to specific rhythmic patterns on the musical surface, as well as shaping units on higher levels of rhythmic structure. The brs is “rhythmic” in the sense that it affects the flow of musical time in a distinct manner.
Return to text

6.  According to Lerdahl and Jackendoff (1983, 17), a phenomenal accent is “any event at the musical surface that gives emphasis or stress to a moment in the musical flow.” Phenomenal accents are to be distinguished from metrical accents (strong beats within the meter) and structural accents (“caused by melodic/harmonic points of gravity,” particularly cadences).
Return to text

7.  This distinguishes my concept of the basic rhythmic shape—a persistent grouping pattern with an accent on one of its pulses—from the concept of basic (pitch) shape in the work of Schoenberg, Ratz, and Caplin: my brs can operate recursively over differing structural levels, while the previous approaches do not.
Return to text

8.  See Caplin (1998, 69) for a discussion of the model sixteen-measure sentence (with compound basic idea).
Return to text

9.  The melodic sequence in measure 13 is interesting, since it echoes the rhythmic pattern from measure 12 (with its agogic accent on the downbeat), which helped to clarify the best choice of shape for motive x in the opening measures. The repetition of measure 13 further emphasizes this source of clarification.
Return to text

10.  For a full treatment of progression and recession see Berry 1987. He also applies these concepts to excerpts from Chopin’s A Major Prelude, Op. 28, No. 7 and Bach’s Sarabande from Suite No. 3 for Unaccompanied Cello (1989, 36–39).
Return to text

11.  Though some readers might consider dynamic emphasis on dissonant tones to be a “Romantic” concept, performance treatises from the eighteenth century recommend this practice rather consistently. See, for example, Mozart 1756, 171 (ch. 9, ¶8) and Türk 1789, 340 (¶32). In a celebrated example from his Versuch, Johann Joachim Quantz divides dissonances into three classes (mezzoforte, forte, and fortissimo), all to be performed more loudly than their consonant resolutions: Quantz 1752, 227–230 and Tab. 24, Fig. 1 (the famous Affetuoso di molto). For a discussion of Mozart’s treatment of “eccentric” dissonances in K. 614 in relation to the theories of Schenker and Adorno, see Schmidt and Wagner 1999.
Return to text

12.  David Temperley (2003, 132–36) observes a preference for end-accented groups near to the end of sonata-form expositions. He discusses several examples of closing themes that feature end-accented phrases.
Return to text

13.  This entire discussion of motive x calls to mind William Rothstein’s 2005 treatment of the principal six-note Ur-rhythm in Chopin’s A Major Prelude (¶¶ 6–21). As in the present study, he adds right-pointing and left-pointing arrows on the music to indicate accelerando and ritardando. He assigns three different forms to the six-note motive in the Chopin Prelude, following Hugo Riemann’s terminology (¶¶9–10 and Example 2); motive x in the present study could also have a “complete” form (x¹), an “incomplete” form (x⁵) and “over-complete” forms with extra pitches (x² and x³). In fact, the brs in the present article could apply to Rothstein’s “over-complete” Ur-rhythm in his Example 2c, at the dotted-quarter-note level.
Return to text

14.  The lack of stability leads William Caplin (1998, 146–47) to interpret measures 87–89 as a “pre-core transitional introduction,” with the core of the development beginning at measure 90 (see his Example 10.6). I also consider measures 87–89 to be transitional in nature, with the development section proper beginning in measure 90. The fact that Caplin begins the development at measure 87 is more a difference in labeling than any real difference of opinion about how measures 87–89 function. Caplin goes on to analyze measures 90–99 as a sentential model (with presentation and continuation) that is repeated in sequence in measures 100–109 (with motivic liquidation in the continuation).
Return to text

15.  Actually x⁵, in the manner of x², since the motive pushes to a strong beat 1 (rather than 3). Refer to Example 5.
Return to text

16.  I hear duple (rather than quadruple) hypermeasures as primary in the development for two reasons. First, Mozart begins the development by repeating a two-bar unit—not a four-bar one—in measures 90–93. Although these bars could certainly combine to form a four-bar group, he immediately obscures this perception of four-bar groupings in the following music by introducing the expansions in measures 96 and 99. The same sequence of events occurs in measures 100–109; moreover, the contraction at measure 112 and the six-bar large hypermeasure at the very end of the development also interfere with the perception of four-bar units.
Return to text

17.  First, the motion from the dominant (measure 78) to the mediant (measure 100) is embellished by a passing area in A major at measure 90. At the same time, the soprano moves from the outer-voice f² (measure 78) to the inner-voice d² (measure 100); the soprano voice is regained with the g² at measure 107. The addition of the passing subdominant area at measure 90 requires further voice leading correctives to avoid parallel fifths: the G⁷ chord at measure 87 and the D at measure 97. Note that the bass B at measure 119 and the soprano a² at measure 124 are non-coincident, and connected by a diagonal line.
Return to text

18.  Basing his claim on empirical studies of “rhythmic perception and performance,” Justin London (2004, 27) claims that if the listener is to perceive regularly recurring attack points as part of a regular meter, the upper limit for the time interval between those attack points (the “interonset interval”) is 5 to 6 seconds. Given the very fast tempo of the first movement of K. 614, one can certainly make a case for hearing duple hypermeasures, but the entrainment of the large hypermeasures is questionable: although the interonset interval between large hypermetric beats is about 3 seconds, the numerous phrase expansions would create a non-isochronous cycle in measures 90–99 and 100–109, immediately contradicted by the contrasting contraction and expansions in measures 110–118.
Return to text

19.  Schachter 1976, 315–16, particularly his Example 13b.
Return to text

Copyright Statement

Copyright © 2009 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.

Prepared by William Guerin, Cara Stroud, and Tahirih Motazedian, Editorial Assistants
Number of visits: