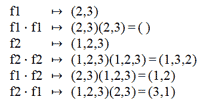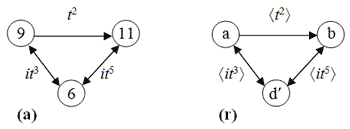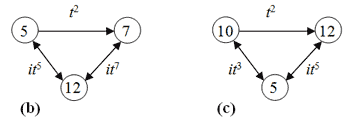A GAP Tutorial for Transformational Music Theory
Robert W. Peck
KEYWORDS: computer-assisted research, transformational music theory, group theory, Klumpenhouwer networks, neo-Riemannian theory
ABSTRACT: GAP (an acronym for Groups, Algorithms, and Programming) is a system of computational discrete algebra that may function as an application for experimentation in transformational music theory. In particular, it offers tools to music theorists that are not readily available elsewhere. This tutorial will show how GAP may be used to generate algebraic group structures well known to music theorists. Furthermore, it will investigate how these structures may be applied to the study of transformation theory, using familiar concepts from Klumpenhouwer-network and neo-Riemannian theories.
Copyright © 2011 Society for Music Theory
[1.1] GAP (an acronym for Groups, Algorithms, and Programming) is a mathematical software package that has great potential as a tool for researchers and students of transformational music theory. Whereas many computer resources are available to music theorists in the investigation of pitch-class set theory and serial theory—pitch-class set calculators, matrix generators, and the like—few, if any, permit users to construct, analyze, and manipulate algebraic systems themselves. Such techniques, however, are an increasingly large part of the transformation theorist’s methodologies. It is often necessary to consider concepts such as the subgroup structure of a group, or to determine a group’s automorphisms. Whereas one can do such calculations by hand, the speed at which GAP performs them can dramatically increase efficiency of time for research. From a pedagogical point of view, GAP provides students of transformation theory a resourceful and effective environment for experimentation, and a means of providing preliminary empirical proofs for their results.
[1.2] GAP was developed by and for mathematicians and other computational scientists. It began in 1986 as a project by four students at RWTH Aachen University, in Aachen, North Rhine-Westphalia, Germany: Johannes Meier, Alice Niemeyer, Werner Nickel, and Martin Schönert. Its first public release was in 1988, with version 2.4. Since that time, it has undergone a number of revisions, and has assumed worldwide recognition,(1) although it has not received much attention in music-theoretical research.(2) GAP 4.4.12 is the latest version. It is free and is available for Windows, Macintosh, and UNIX operating systems, along with all its documentation, at www.gap-system.org. An interactive online version is also available via Sage (see [2.18] below).
[1.3] This tutorial endeavors to introduce some of the utilities in GAP to the music-theoretic community in the context of familiar transformation-theoretical concepts: transformation groups and their actions, Klumpenhouwer networks, and neo-Riemannian theory. Therefore, it presupposes a basic—but not advanced—understanding of these concepts, and no prior knowledge of GAP. After an initial section that describes the basics of the GAP environment (how to input commands, interpret output, get help, etc.), we generate the transposition group T, the transposition and inversion group T/I, and the affine group TTO. We examine how these groups act on the set of pitch classes and on sets of pitch-class sets, and perform various tests that relate them to well-known abstract-algebraic structures. Next, we use GAP to study Klumpenhouwer networks, generating the automorphism groups from which K-net isographies derive. Finally, we consider the Schritt and Wechsel group of neo-Riemannian theory, how it relates to the transposition and inversion group, how these are subgroups of Hook’s (2002) Uniform (and Quasi-uniform) Triadic Transformations, and how to generate other related groups of contextual operations.
[2] Orthographic conventions and GAP commands
[2.1] Throughout this tutorial we use certain orthographic (i.e., notational) conventions, which sometimes differ from those commonly used in music theory. In some instances, these conventions are required by GAP; at other times, they are not necessary, but are more consistent with standard mathematical conventions. For instance, although it is not required by GAP, we represent all operations with lowercase letters:
g := (1,2,3)
h := (1,2)
This notation differs from the common practice in music theory of using uppercase letters for certain operators, such as Tn and I. For these particular operators, we instead use tn and i, respectively (see section [3] below). Operations also appear in cyclic notation. In the case of g above, the parenthetical expression (1,2,3) tells us that, under g, the integer 1 moves to 2, 2 moves to 3, and 3 moves back to 1. The result is a permutation of order 3 (i.e., a 3-cycle). In contrast, under h, 1 moves to 2, and 2 moves directly back to 1 (i.e., a 2-cycle, or involution). Then, the composition of g and h, gh = (1,2,3)(1,2), sends 1 to 2 under g, but then 2 back to 1 under h. Hence, it fixes (or stabilizes) 1. Further, it sends 2 to 3 under g, where it remains under h; and it sends 3 to 1 under g, and 1 to 2 under h. Overall, it stabilizes 1, sends 2 to 3, and 3 to 2, so gh = (2,3).(3)
[2.2] We use multiplicative notation rather than additive notation, even for abelian (i.e., commutative) groups:
g × h, or gh
(rather than g + h)
Furthermore, GAP uses right-functional orthography (i.e., read from right to left). That is, in the composition gh, perform g first, then h. This practice differs from the left-functional notation commonly used in music theory, where, for instance, the operation TnI means invert first (I), then transpose by n (Tn).
[2.3] We represent sets, groups, and other algebraic structures with uppercase letters:
G := ![]() g, h
g, h![]()
Here, the angle brackets signify that G is the group generated by g and h. Additionally, we give functions that map such structures to one another (morphisms) with Greek letters; but as GAP reads only ASCII characters, we spell out these Greek letters:
pi : Gpi → H, where gpi × hpi = (g × h) pi,
for all g,h ∈ G
In GAP, we use exponential notation for functions, as in the example above, rather than prefix notation, which is more common in music-theoretical writing. In other words, we write Gpi, rather than pi(G). In this case, Gpi indicates a function pi that maps G to H, where gpi is the image of g in the mapping, hpi is the image of h, and so on. Such functions may be homomorphisms, as in this example; isomorphisms, which are one-to-one; surjective homomophisms; or automorphisms, which are isomorphisms of a group to itself.
[2.4] Right-functional orthography is also consistent with GAP’s use of exponential notation for functions. The product of functions alpha and beta (in that order) applied to a structure G receives the exponential notation:
(Galpha)beta = Galpha⋅ beta
whereas in prefix notation we would have:
beta(alpha(G)) = beta ⋅ alpha(G)
reading from the right to the left.
[2.5] In cases where gh indicates a composition of group elements that act on a set S, or on a member x of that set, we once again use exponential notation, such as Sgh, or xgh, rather than prefix notation, such as h(g(S)) or h(g(x)). Finally, because we use multiplicative notation, we also use exponential notation for exponents in the usual sense (powers):
g × g = g2, g × g × g = g3, etc.
[2.6] Throughout this tutorial, GAP commands are given in
red, and GAP’s corresponding output appear in
blue.(4) N.B.: GAP is case sensitive. All commands are entered at the GAP prompt “gap>” (see the bottom of
Example 1), and end in a semicolon (followed by
![]() [enter]). GAP commands may be typed with or without spaces. In GAP, we may define various objects using the standard notation “:=” for definition. These objects include operations:
[enter]). GAP commands may be typed with or without spaces. In GAP, we may define various objects using the standard notation “:=” for definition. These objects include operations:
gap> g := (1,2,3);
(1,2,3)
gap> h := (1,2);
(1,2)
GAP places the output on the line(s) below the defining commands. In this case, the output confirms the definition by redisplaying the cyclic permutations that g and h represent.
[2.7] We may similarly define algebraic structures:
gap> G := Group(g,h);
Group([ (1,2,3), (1,2) ])
gap> N := Subgroup(G,[g]);
Group([ (1,2,3) ])
Again, the output confirms the structure that is being defined: the group generated by g and h in the first case, and the subgroup of G generated by g in the second. Notice, however, that the output alone of the second command does not indicate that N is the subgroup of G generated by g.
[2.8] We may also call objects from one of GAP’s libraries:
gap> D_6 := DihedralGroup(6);
<pc group of size 6 with 2 generators>
Here, the dihedral group of order 6 is a purely abstract algebraic structure, not a permutation group such as G above. The output confirms the size of the group, tells how many generators GAP uses to build the group, and references a particular type of abstract structure: a “pc group.” The term “pc” in the output does not abbreviate “pitch-class,” as appears commonly in music theory. Rather, it stands for “polycyclic,” a type of group structure that includes the dihedral groups. Then, the elements of the D6 are not permutations, such as (1,2,3) and (1,2), but rather compositions of abstract generators f1 (of order 2) and f2 (of order 3), as seen in the output of the following command.
[2.9] We may define morphisms and other mappings:
gap> pi := IsomorphismGroups(D_6,G);
[ f1, f2 ] -> [ (2,3), (1,2,3) ]
The output for this command tells us that GAP has located an isomorphism from D6 to G; otherwise, the output would indicate “fail.” (N.B.: In cases such as this one, where more than one possible isomorphism exists, GAP selects only one to display.) The isomorphism pi is a mapping of every element of D6 to one of G, but the output presents this isomorphism merely in terms of (abstract) generators of D6, f1 and f2, and their images in G, from which the mappings of the additional group elements may be derived (e.g., h = (1,2) = (2,3)(1,2,3) in G is the image of f1 ⋅ f2 in D6). Table 1 provides a mapping for all six elements in each of the respective groups.
[2.10] We may display objects, including those defined previously:
gap> g;
(1,2,3)
gap> List(G);
[ (), (1,3,2), (1,2,3), (2,3), (1,3), (1,2) ]
Whereas the output to the “g;” command above displays a single cyclic permutation, the output for “List(G);” presents all six group elements in G. The empty parentheses, (), in the output that follows the latter command denotes the identity element of the group—for example, the trivial permutation, which sends each member of the set on which G acts (i.e., the integers 1, 2, and 3) to itself.
[2.11] Additionally, we may determine products, factors, quotients, etc.:
gap> g*h;
(2,3)
gap> g^2;
(1,3,2)
gap> DirectProduct(G,D_6);
<group of size 36 with 4 generators>
gap> G/N;
Group([ f1 ])
The outputs of the first two commands above are straightforward enough from the preceding discussion, but those of the third and fourth commands need further comment. The output of the third command tells us that the direct product is a group of order 36 (or 62, accordingly, as the two groups in the direct product are of size 6), and that it has four generators (i.e., the respective generators of G and D6: g and h, and f1 and f2). The fourth command calls a quotient group, which consists of the various cosets of N in G. The f1 in the output to this line signifies one of those cosets, and does not refer to the other f1 above (a generator of D6).
[2.12] In GAP, we may perform various functions, arithmetic and otherwise:
gap> 1*2*3;
6
gap> Size(G);
6
and run various tests:
gap> Size(G) = Factorial(3);
true
gap> g*h = h*g;
false
gap> IsAbelian(G);
false
[2.13] We may enter two or more commands on a single line (each followed by a semicolon), and GAP displays their respective output on adjacent successive lines:
gap> H := Subgroup(G,[h]); Size(H);
Group([ (1,2) ])
2
Long commands may be broken by
![]() (enter) before reaching the semicolon. In these instances, GAP continues the command line on a subsequent line with a simple “>” prompt:
(enter) before reaching the semicolon. In these instances, GAP continues the command line on a subsequent line with a simple “>” prompt:
gap> Size(InnerAutomorphismsAutomorphismGroup(

> AutomorphismGroup(G)));
1
The syntax of the above command is complex, but follows a certain logic. In a series of parentheticals, we are asking GAP first to establish the automorphism group for G (AutomorphismGroup(G)); second, to determine which of the automorphisms in this group are inner, hence derive from conjugation by a group element (InnerAutomorphismsAutomorphismGroup); and finally, to display how many of these inner automorphisms exist (Size). The output tells us that the inner automorphism group for G contains only one member.
[2.14] We may suppress output for a command that would normally produce it by following the command with two semicolons:
gap> List(H);;
GAP stores a history of command lines for any one session. Users may recall a previous command by using the ↑ (up-arrow) key repeatedly as needed, and/or with the ↓ (down-arrow) key, to scroll through the history. Finally, to end a session, we use:
gap> quit;
[2.15] Rather than retyping GAP commands into every session, we may create programs, which are stored as normal text files. The programs may then be loaded into a GAP session. In this way, we can easily set up an environment for continued experimentation. For instance, all the commands used in sections [3]-[5] of this tutorial appear in the text file “SampleGAPprogram.txt” that accompanies this article. To load this program into a GAP session, we use the command:(5)
gap> Read("SampleGAPprogram.txt");
Notice that there is no output following this command, even though the commands the program contains would normally produce it. Consequently, there is no particular need for a program to include commands other than definitions. Once such a program is read, the user can simply call display commands, describe further definitions, run tests, and so on. Programs may also contain remarks, which GAP does not treat as commands. Remarks are prefaced with the pound sign, and do not end with a semicolon:
gap> # This is a remark. It is not a command.
Again, there is no output.
[2.16] Help for GAP users is available in several ways. First, the GAP website offers a number of online manuals, including tutorials, FAQ, examples, and instructions for joining the GAP Forum e-mail distribution list. Help is also available within a GAP session; one may find help on a particular topic by typing a search term preceded by a question mark (again, the semicolon is not used):
gap> ?orbit
Help: several entries match this topic - type ?2 to get match [2]
[1] Tutorial: Orbit
[2] Reference: Orbit
[3] Reference: Orbit Stabilizer Methods for Polycyclic Groups
[4] Reference: Orbits
[5] Reference: Orbits!operation/attribute
[6] Reference: OrbitsDomain
[7] Reference: OrbitLength
[8] Reference: OrbitLengths
[9] Reference: OrbitLengthsDomain
[10] Reference: OrbitStabilizer
[11] Reference: OrbitStabilizerAlgorithm
[12] Reference: OrbitPerms
[13] Reference: OrbitsPerms
[14] Reference: OrbitStabChain
[15] Reference: OrbitPowerMaps
[16] Reference: OrbitFusions
[17] Extending: Orbits
[18] Extending: OrbitsishOperation
[19] Extending: OrbitishFO
[20] New Features: OrbitGenerators
[21] New Features: OrbitGeneratorsInv
[22] New Features: OrbitGeneratorsOfGroup
At a subsequent GAP prompt (which need not be immediate), we may enter the number of the entry we wish to read, following a question mark:
gap> ?2
> Orbit( <G>[, <Omega>], <pnt>, [<gens>, <acts>, ] <act>)
The orbit of the point <pnt>is the list of all images of <pnt>under the action.
(Note that the arrangement of points in this list is not defined by the operation.)
The orbit of <pnt>will always contain one element that is *equal* to <pnt>, however for performance reasons this element is not necessarily *identical* to <pnt>, in particular if <pnt>is mutable.
gap> g:=Group((1,3,2),(2,4,3));;
gap> Orbit(g,1);
[ 1, 3, 2, 4 ]
gap> Orbit(g,[1,2],OnSets);
[ [ 1, 2 ], [ 1, 3 ], [ 1, 4 ], [ 2, 3 ], [ 3, 4 ], [ 2, 4 ] ]
(See Section "Basic Actions" for information about specific actions.)
> Orbits( <G>, <seeds>[, <gens>, <acts>][, <act>] )!
{operation/attribute}
> Orbits( <xset>)!{operation/attribute}
-- <space> page, <n>next line, <b> back, <p> back line, <q> quit --
GAP then prompts for some form of continuation or exit from the manual; for example, n or q
The [space],
n, etc., are not followed by a semicolon (nor by ![]() ).
).
[2.17] On encountering an error, the output provides a description of the problem, whether it is syntactical:
gap> Size(Group(g);
Syntax error: ) expected
Size(Group(g);
^
or logical:
gap> G/H;
Error, <N> must be a normal subgroup of <G> called from
<function>( <arguments>) called from read-eval-loop
Entering break read-eval-print loop ...
you can 'quit;' to quit to outer loop, or
you can 'return;' to continue
brk>
In the latter instance, we are given the opportunity to exit the description by typing
brk> quit;
at the break prompt, or by continuing the description:
brk> return;
Error, <H> must be contained in <G> called from
oper( super, sub ) called from
Index( G, N ) called from
oper( super, sub ) called from
NaturalHomomorphismByNormalSubgroupNCOrig( G, N ) called from
NaturalHomomorphismByNormalSubgroupNC( G, N ) called from
...
Entering break read-eval-print loop ...
you can 'quit;' to quit to outer loop, or
you can 'return;' to continue
brk>
Entering either brk> return; or brk> quit; at this point continues or quits the description accordingly.
[2.18] Users may also access GAP on the World Wide Web via the mathematics software system Sage: http://www.sagemath.org/. Including GAP, Sage has interfaces for Mathematica, Magma, and several other mathematics applications useful to music theorists. Therefore, in addition to computational discrete algebra, Sage may be used to study other algebras, calculus, number theory, cryptography, numerical computation, combinatorics, graph theory, and the like.
[2.19] To work in an online GAP session in Sage, create a notebook (or edit a pre-existing notebook). First, go to www.sagenb.org. Then, either sign in to an existing account, or register for a new one and sign in. For a new notebook, click on “new worksheet,” and title it. This takes you to a worksheet (see Example 2). From the drop-down menu near the top, select “gap” (“sage” is the default). Type a GAP command into the first cell, and click on the corresponding “evaluate” link to display its output. A new cell appears, in which you may type the next command, and so on. You may save your worksheet (by clicking the “save” button), and publish your worksheet (by clicking the “publish” button). The latter gives you a URL, through which others may view your notebook. For example, a notebook “GAP – MTO,” which contains all of the commands in this tutorial, may be found at http://sagenb.org/pub/1117/.
[3] Generating the T, T/I, and TTO groups
[3.1] Now let us build some familiar music-theoretical groups using GAP. In this section, we generate the transposition group T, the transposition and inversion group T/I, and the affine group TTO that includes the transpositions, inversions, and various multiplicative operations. We also examine how GAP can model these groups’ actions on pitch classes and pitch-class sets, and how they relate to various abstract algebraic structures.
[3.2] Call T the musical transposition group (mathematically, a translation group).(6) T has an action on the set PCS of twelve pitch classes (residue classes of the infinite set of chromatic pitches under enharmonic and octave equivalence). We may use GAP to model groups such as T, using a permutation representation on some subset of the positive integers. Such representations in GAP do not incorporate the integer 0, to which the pitch class C is usually mapped.(7) Instead, we map pitch class C to the integer 12.
[3.3] Put
C♯ = 1
D = 2E♭ = 3
∶
B = 11
C = 12
Hence, we may define a unit transposition t (translation), a pitch-class transposition “up” one semitone:
gap> t := (1,2,3,4,5,6,7,8,9,10,11,12);
(1,2,3,4,5,6,7,8,9,10,11,12)
In other words, t is merely another notation for the operation that is more commonly written T1, using instead a lowercase letter for the variable name. The output shows t in cyclic notation: under t, pitch class 1 maps to 2, 2 to 3, and so on through 11 to 12, and 12 back to 1.
[3.4] We may compose operators using multiplication, such as t with t (T1 with T1):
gap> t*t;
(1,3,5,7,9,11)(2,4,6,8,10,12)
Notice that the output for this command contains two cycles: one that passes through the even pitch classes, and one that passes through the odd pitch classes. Such cycles are by definition distinct.
[3.5] We may also use exponents for an operator composed with itself, as before: (8)
gap> t^2;
(1,3,5,7,9,11)(2,4,6,8,10,12)
Here, t2 agrees with the operation commonly notated as T2.
[3.6] We may show inverses:(9)
gap> t^-1;
(1,12,11,10,9,8,7,6,5,4,3,2)
gap> (t^2)^-1;
(1,11,9,7,5,3)(2,12,10,8,6,4)
In other words, t-1 conforms to T11 (= T-1), and (t2)-1 = t-2 to T10 (= T-2). We may also test for such equivalences:
gap> (t^2)^-1 = t^10;
true
[3.7] We can use t as a generator of a group, T:
gap> T := Group(t);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12) ])
The output for this command confirms that T is the group generated by t, where t is the permutation (1,2,3,4,5,6,7,8,9,10,11,12). T is isomorphic to the cyclic group of order 12, C12:
gap> IsomorphismGroups(T,CyclicGroup(12));
[ (1,5,9)(2,6,10)(3,7,11)(4,8,12), (1,4,7,10)(2,5,8,11)(3,6,9,12) ] ->
[ f3, f1*f2 ]
The output for this command needs some explanation. First, GAP is telling us that it has located an isomorphism from T to C12; otherwise, it would return the message “fail.” However, rather than describing the isomorphism in terms of the generator t of T that we defined previously, GAP uses t3 and t4 (T3 and T4), which together also generate T. (The specific reason for this choice of generators has to do with GAP’s internal programming logic, and is somewhat outside the scope of this tutorial.) Then, GAP maps these generators to f3 and f1 ⋅ f2, abstract generators of the cyclic group of order 12 that are stored in GAP’s internal library. Again, the important point here is that an isomorphism exists.
[3.8] We may verify the order of T:
and display its elements:gap> Size(T);
12
gap> List(T);
[ (), (1,9,5)(2,10,6)(3,11,7)(4,12,8),(1,5,9)(2,6,10)(3,7,11)(4,8,12),
(1,11,9,7,5,3)(2,12,10,8,6,4), (1,7)(2,8)(3,9)(4,10)(5,11)(6,12),
(1,3,5,7,9,11)(2,4,6,8,10,12), (1,12,11,10,9,8,7,6,5,4,3,2),
(1,8,3,10,5,12,7,2,9,4,11,6), (1,4,7,10)(2,5,8,11)(3,6,9,12),
(1,10,7,4)(2,11,8,5)(3,12,9,6), (1,6,11,4,9,2,7,12,5,10,3,8),
(1,2,3,4,5,6,7,8,9,10,11,12) ]
In this output, GAP returns the elements in cyclic notation, in the order t0, t8, t4, t10, t6, t11, t7, t3, t9, t5, t (T0, T8, T4, T10, etc.). (As before, GAP’s logic for listing the elements according to this scheme is outside the scope of this tutorial, but this ordering is also featured in the next few sections.)
[3.9] GAP can determine the orbit of a pitch class under the members of the T group, shown here using pitch class 1:
gap> Orbit(T,1);
[ 1, 9, 5, 11, 7, 3, 12, 8, 4, 10, 6, 2 ]
The orbit consists of the members of the set of pitch classes to which pitch class 1 maps under the elements of the T group. That is, 1 maps to 1 under t0 (T0), to 9 under t8 (T8), to 5 under t4 (T4), and so on, through all twelve pitch-class transpositions. Notice here that GAP’s ordering of pitch classes in the output follows the same ordering of group elements in the output to the “List(T);” command above. Furthermore, because the action of T on PCS is transitive,
gap> IsTransitive(T);
true
pitch class 1 maps to all twelve members of the set of pitch classes.
[3.10] GAP can also display the orbit of an unordered set of pitch classes (a pcset), such as a C major triad {0,4,7} (recalling that we use the integer 12 in place of pitch class 0):
gap> Orbit(T,[4,7,12],OnSets);
[ [ 4, 7, 12 ], [ 4, 8, 11 ], [ 3, 8, 12 ], [ 2, 6, 9 ], [ 1, 6, 10 ],
[ 2, 5, 10 ], [ 1, 5, 8 ], [ 5, 9, 12 ], [ 1, 4, 9 ], [ 3, 7, 10 ],
[ 2, 7, 11 ], [ 3, 6, 11 ] ]
Here, the output shows (in successive square-bracketed sets) the pitch-class sets to which the C major triad maps under members of the transposition group: C major, E major,
[3.11] GAP can also model orbits of pcsets on which the action of T is not faithful, such as the augmented triad {0,4,8}:
gap> Orbit(T,[4,8,12],OnSets);
[ [ 4, 8, 12 ], [ 2, 6, 10 ], [ 1, 5, 9 ], [ 3, 7, 11 ] ]
Here, the output shows the four augmented triads to which {0,4,8} can map under the members of the transposition group. We say the action of T is not faithful on this set of sets, because certain non-identity elements of the group (specifically t4 [T4] and t8 [T8]) are indistinguishable from t0 [T0]; that is, they hold all four augmented triads invariant.
[3.12] Next, define the inversion operation i (the label we use in GAP for the operation I, or I0):
gap> i := (1,11)(2,10)(3,9)(4,8)(5,7);
(1,11)(2,10)(3,9)(4,8)(5,7)
The output for this command merely echoes the cycles of pitch classes we use to define the operation. (N.B.: Both the input and the output omit the singleton cycles of pitch-classes 0 [= 12, in GAP] and 6, both of which are held invariant under inversion). Moreover, because GAP uses right-functional instead of left-functional orthography, our notation for the composition of inversion with transposition always appears in the opposite order than that which is typically found in music theory. For instance, the operation T1I (or I1) appears as it; T2I (or I2) as it2; and so on.
[3.13] Together, t and i generate the transposition and inversion group T/I:
gap> TI := Group(t,i);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ])
Again, the output shows the cycles of the operations we use to generate the group. T/I is isomorphic to the dihedral group of order 24, D24:
gap> IsomorphismGroups(TI,DihedralGroup(24));
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ] ->
[ f2, f1*f3*f4^2 ]
As with the output for the command above that demonstrated an isomorphism of T to C12, this output tells us that GAP has found an isomorphism from T/I to D24; and, as before, it gives the isomorphism in terms of various generators of the respective groups. Unlike the earlier example—wherein GAP substituted generators t3 [T3] and t4 [T4] of T for the generator t [T1] that we had used to define the group—GAP does not make such a substitution in this instance. Rather, it uses the generators t [T1] and i [I0] of T/I that we supplied. Then, the isomorphism maps these generators to generators of the abstract group D24, f2 and f1 ⋅ f3 ⋅ f42 that are stored in GAP’s library.
[3.14] We incorporate Morris’s (1982) multiplicative operation m (usually given as M or M5 in music-theoretical writings) on pitch classes. That is, m : x ↦ 5x mod 12, for all x ∈ PCS:(11)
gap> m := (1,5)(2,10)(4,8)(7,11);
(1,5)(2,10)(4,8)(7,11)
Again, the output confirms the cycles we entered, and both the input and the output omit the singleton cycles.
[3.15] Adjoining m to T/I yields a group TTO of order 48, the set of affine transformations on ℤ12:
gap> TTO := Group(t,i,m);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7),
(1,5)(2,10)(4,8)(7,11) ])
The output for this command confirms that TTO is the group generated by these cycles. TTO is isomorphic to the direct product of the dihedral groups of orders 6 and 8, D6 × D8:
gap> IsomorphismGroups(TTO,DirectProduct(

> DihedralGroup(6),DihedralGroup(8)));
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7),
(1,5)(2,10)(4,8)(7,11) ] -> [ f2*f4, f1*f3*f4*f5, f1*f5 ]
In the output to this command, the generators t [T1], i [I0], and m [M5] of TTO are mapped to products of f1, f2, f3, f4, and f5, generators that GAP’s internal library uses to construct the relevant abstract group of order 48. Again, the important point here is that GAP has indeed located an isomorphism.
[4] Klumpenhouwer-network isographies
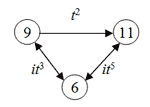
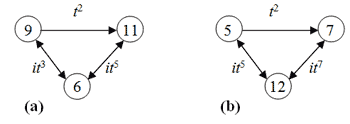
[4.1] One way that we might use GAP as a tool for music theory is in the study of Klumpenhouwer networks (Lewin 1990, Klumpenhouwer 1991). Klumpenhouwer networks, or K-nets, are directed graphs with nodes (vertices) labeled in the set of pitch classes and arrows (edges) in the T/I group (see Figure 1).
gap> t^2; i*t^3; i*t^5;
(1,3,5,7,9,11)(2,4,6,8,10,12)
(1,2)(3,12)(4,11)(5,10)(6,9)(7,8)
(1,4)(2,3)(5,12)(6,11)(7,10)(8,9)
Entering the labels that correspond to the arrows in GAP, as above, produces an output that displays the cycle(s) in which the node contents lie. For instance, the (single-headed) arrow that connects the node populated by pc 9 to that populated by 11 is labeled t2 (T2); its cycles are as follows:
(1, 3, 5, 7, 9, 11)(2, 4, 6, 8, 10, 12)
The pitch class 9 maps to the pitch class 11 (underlined), which, in turn, maps to 1, 3, 5, 7, and ultimately back to 9. Hence, it is a cycle of length 6 (a 6-cycle). Because pitch class 11 continues on to 1 and does not return directly to 9, we use a single-headed arrow in the network.
[4.2] On the other hand, the cycles of operations in Figure 1 that connect pitch classes 9 and 6, and 11 and 6—it3 and it5 (I3 and I5) respectively—are involutions. That is, they are their own inverses. Entering their corresponding arrow labels yields the following cycles of length 2 (2-cycles):
(1, 2)(3, 12)(4, 11)(5, 10)(6, 9)(7, 8)
(1, 4)(2, 3)(5, 12)(6, 11)(7, 10)(8, 9)
In the first 2-cycle, pitch class 6 maps to 9, and 9 to 6; in the second, 6 maps to 11, and vice versa. Hence, the network incorporates double-headed arrows to connect their associated nodes.
[4.3] Entire networks may relate to one another via isographies, which correspond to members of the automorphism group for T/I, Aut(T/I):
gap> AutTI := AutomorphismGroup(TI);
<group of size 48 with 4 generators>
The output indicates that Aut(TT/I) is a group of order 48, and it gives the number of generators that GAP uses to build it. As Lewin 1990 points out, this group—which acts on the twenty-four members of T/I—is isomorphic to TTO. We call this isomorphism alpha:(12)
gap> alpha := IsomorphismGroups(TTO,AutTI);
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7), (1,5)(2,10)(4,8)(7,11) ] ->
[ [ (1,6,11,4,9,2,7,12,5,10,3,8), (1,3)(4,12)(5,11)(6,10)(7,9) ] ->
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,2)(3,12)(4,11)(5,10)(6,9)(7,8) ],
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,3)(4,12)(5,11)(6,10)(7,9) ] ->
[ (1,8,3,10,5,12,7,2,9,4,11,6), (1,2)(3,12)(4,11)(5,10)(6,9)(7,8) ],
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,3)(4,12)(5,11)(6,10)(7,9) ] ->
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ] ]
Under alpha, GAP sends the previously defined generators of TTO: t, i, and
m (T1, I0, and M5), to three automorphisms of the T/I group that together generate the Aut(T/I) group. These automorphisms appear in the output (following the first arrow “->”) in terms of their respective actions on (arbitrary) generators of the T/I group: t5 and it4 (T5 and I4).(13) We may use Lewin’s (Lewin 1990) notation to label these automorphisms: F![]() u,j
u,j![]()
![]() 1,11
1,11![]()
![]() 11,7
11,7![]()
![]() 5,4
5,4![]()
![]() 1,11
1,11![]()
![]() 11,7
11,7![]()
![]() 5,4
5,4![]()
[4.4] As Aut(T/I) is isomorphic to TTO, and TTO contains T/I as a subgroup, it follows that Aut(T/I) contains a subgroup that is isomorphic to T/I; we call this subgroup
Hyp(T/I) (or hyper-T/I). It consists of the T/I automorphisms with
u ∈ {1,11}. Call isographies that derive from automorphisms with u = 1 positive, and those with u = 11 negative. We may take the T/I automorphism that is the image of t (T1) under alpha, F![]() 1,11
1,11![]()
![]() 11,7
11,7![]()
gap> HypTI := Group(t^alpha,i^alpha);
<group with 2 generators>
We recall from [2.4] that the exponential notation used in this command (e.g., “t^alpha”) signifies a function, in this case an isomorphism. Then, the output provides merely a terse description of the structure being generated: a group with two generators; but it does not indicate size, or any other outward information.
[4.5] Using an adaptation of Lewin’s later (Lewin 1994) notation for hyper-T/I operators to our present orthography—![]() tj
tj![]()
![]() 1, j
1, j![]()
![]() itj
itj![]()
![]() 11, j
11, j ![]()
![]() t11
t11![]()
![]() t
t![]()
![]() 1,j
1,j![]()
gap> hyp_t := (t^11)^alpha;
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,2)(3,12)(4,11)(5,10)(6,9)(7,8) ] ->
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,3)(4,12)(5,11)(6,10)(7,9) ]
Notice that in the output to this command, the generator t5 (T5) of T/I maps to itself, and the generator it3 (I3) maps to it3+1 = it4 (I4).
[4.6] Similarly, GAP maps i (I0) under alpha to the automorphism we call ![]() it7
it7![]()
![]() i
i![]()
gap> hyp_i := (i^alpha)*((t^7)^alpha);
[ (1,8,3,10,5,12,7,2,9,4,11,6), (1,2)(3,12)(4,11)(5,10)(6,9)(7,8) ] ->
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,8)(2,7)(3,6)(4,5)(9,12)(10,11) ]
Again, the output for this command shows an action on generators of the T/I group that results in a mapping of the group to itself; specifically, it demonstrates a mapping of t7 to t5 (T7 to T5), and it3 maps to it(-3+0) = it9 (I3 to I9 ).
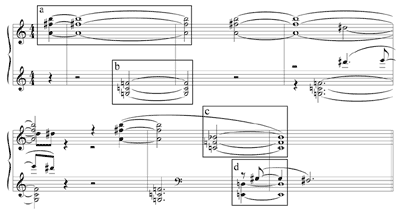
Example 3. Schoenberg, Sechs kleine Klavierstücke, op. 19, no. 6, measures 1–6 (following Lambert 2002)
(click to enlarge)
Figure 2. Two positively isographic K-nets from Lambert 2002
(click to enlarge)
Figure 3. Two negatively isographic K-nets from Lambert 2002
(click to enlarge)
[4.7] Following Philip Lambert’s (Lambert 2002) analysis, Example 3 presents the first six measures of Arnold Schoenberg’s Sechs kleine Klavierstücke, op. 19, no. 6.(14)
[4.8] We note that the network labeled (a) in Figure 2—corresponding to the trichord labeled “a” in the example—relates to that labeled (b) by ![]() t2
t2![]()
![]() t2
t2![]()
gap> (t^2)^(hyp_t^2);
(i*t^3)^(hyp_t^2); (i*t^5)^(hyp_t^2);
(1,3,5,7,9,11)(2,4,6,8,10,12)
(1,4)(2,3)(5,12)(6,11)(7,10)(8,9)
(1,6)(2,5)(3,4)(7,12)(8,11)(9,10)
We recall that, as a hyper-operator, ![]() t2
t2![]()
![]() t2
t2![]()
[4.9] Similarly, the network labeled (a) in Figure 3 relates by ![]() it3
it3![]()
![]() it3
it3![]()
gap> (t^2)^(hyp_i*hyp_t^3);
(1,11,9,7,5,3)(2,12,10,8,6,4)
gap> (i*t^3)^(hyp_i*hyp_t^3);
(1,11)(2,10)(3,9)(4,8)(5,7)
gap> (i*t^5)^(hyp_i*hyp_t^3);
(1,9)(2,8)(3,7)(4,6)(10,12)
Again, the output shows the image (in cyclic notation) of network (a)’s arrows under the relevant hyper-operator, ![]() it3
it3![]()
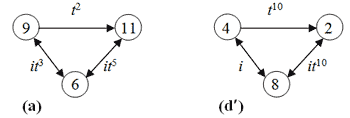
[4.10] It is now possible to determine the hyper-operator that relates network (b) to (d'), using the hyper-operators that relate (a) to (b) and (a) to (d'). We know already that ![]() t2
t2![]()
![]() t2
t2![]()
![]() it3
it3![]()
![]() t2
t2![]()
![]() it3
it3![]()
gap> (t^2)^(((hyp_t^2)^-1)*hyp_i*hyp_t^3);
(1,11,9,7,5,3)(2,12,10,8,6,4)
gap> (i*t^5)^(((hyp_t^2)^-1)*hyp_i*hyp_t^3);
(1,11)(2,10)(3,9)(4,8)(5,7)
gap> (i*t^7)^(((hyp_t^2)^-1)*hyp_i*hyp_t^3);
(1,9)(2,8)(3,7)(4,6)(10,12)
The cycles in the output agree with those of the operators that label the arrows in (d'), t10, i, and it10 (T10, I0, and I10).
[4.11] The composition of hyper-operators ![]() t2
t2![]()
![]() it3
it3![]()
![]() it5
it5![]()
gap> ((hyp_t^2)^-1)*hyp_i*hyp_t^3 = hyp_i*hyp_t^5;
true
We may use it together with ![]() t2
t2![]()
![]() it3
it3![]()
[4.12] We can further define a hyper-m (hyper-M5) operation ![]() m
m![]()
gap> hyp_m := m^alpha*((t^4)^alpha);
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ] ->
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,11)(2,10)(3,9)(4,8)(5,7) ]
As previously, the output here shows the action of the hyper-operator on (arbitrary) generators of the T/I group: t (T1) and i (I0), which get sent to t5 (T5) and i (I0), respectively.
[4.13] Then, define a hyper-mi operation ![]() mi
mi![]()
gap> hyp_mi := hyp_m*hyp_i;
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ] ->
[ (1,8,3,10,5,12,7,2,9,4,11,6), (1,11)(2,10)(3,9)(4,8)(5,7) ]
This latter hyper-operator sends tn to t7n, and itn to it7n+0, as demonstrated by the T/I generators in the output.
[4.14] Klumpenhouwer (Klumpenhouwer 1998) observes, however, that the action of Lewin’s Hyp(T/I) operators on networks does not necessarily agree with the action of T/I on the nodes of congruent networks. For instance, the network labeled (b) in Figure 5 relates by ![]() t10
t10![]()
gap> InnTI := InnerAutomorphismsAutomorphismGroup(AutTI);
<group with 2 generators>
which has a natural action of T/I on itself. Here, the command “InnerAutomorphismsAutomorphismGroup(AutTI);” is telling GAP to locate the subset of inner automorphisms in the automorphism group Aut(T/I).
[4.15] The inner automorphisms in fact form a normal subgroup of the full automorphism group, Aut(T/I), consisting of those automorphisms that derive from conjugations by group elements, where conjugation of element a by b equals the composition b-1ab. (GAP also uses exponential notation for conjugation; hence, ab signifies a conjugated by b.) Hence, Klumpenhouwer describes hyper-t operations [tx], in square brackets, that conjugate the members of T/I by tx (conjugation by Tx).(18) Such conjugations send tn to t-x(tn)tx = tn (Tn to Tn), and itn to t-x(itn)tx = itn+2x (In to In+2x); and hyper-itx operations [itx] that send tn to (itx)-1(tn)itx = t-n (Tn to T-n), and itn to (itx)-1(itn)itx = it-n+2x (In to I-n+2x). Thus, the network (b) in Figure 5 relates by [t5] (conjugation by T5) to that in (c), matching the t5 operation on PCS that relates congruent nodes:
gap> (t^2)^(t^5); (i*t^5)^(t^5);
(i*t^7)^(t^5); (1,3,5,7,9,11)(2,4,6,8,10,12)
(1,2)(3,12)(4,11)(5,10)(6,9)(7,8)
(1,4)(2,3)(5,12)(6,11)(7,10)(8,9)
The output shows the appropriate cycles of operators that label the arrows in (c). Note as well the use of exponential notation in the command (e.g., “(t^2)^(t^5);”), signifying conjugation by t5 (T5).
[4.16] We cannot describe an isomorphism between Hyp(T/I) and Inn(T/I), as Hyp(T/I) is of size 24, and Inn(T/I) is only of size 12. We may, however, describe a group homomorphism beta that maps Hyp(T/I) to Inn(T/I):
gap> beta := ActionHomomorphism(HypTI,InnTI);
<action homomorphism>
The output for this command merely denotes the presence of a homomorphism. The kernel of beta—those elements of Hyp(T/I) that map to the identity element of Inn(T/I)—is nontrivial:
gap> ker_beta := Kernel(beta);
<group with 1 generators>
gap> Size(ker_beta);
2
As the output indicates, the kernel consists of two elements of Hyp(T/I). Using the “List” command, we discover that these two elements consist of the hyper-operators ![]() t0
t0![]()
![]() t6
t6![]()
gap> List(ker_beta);
[ IdentityMapping( Group([ (1,2,3,4,5,6,7,8,9,10,11,12),
(1,11)(2,10)(3,9)(4,8)(5,7) ]) ),
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,10)(2,9)(3,8)(4,7)(5,6)(11,12) ] ->
[ (1,6,11,4,9,2,7,12,5,10,3,8), (1,4)(2,3)(5,12)(6,11)(7,10)(8,9) ] ]
First, ![]() t0
t0![]()
![]() t6
t6![]()
![]() t0
t0![]()
![]() t6
t6![]()
gap> ker_beta = Center(HypTI);
true
[4.17] Consequently, we cannot distinguish between permutations on T/I induced by conjugation by t0 or t6 (T0 or T6), shown here on the generators t and i:
gap> t^(t^0) = t^(t^6); i^(t^0) = i^(t^6);
true
true
or by different members of any coset (left or right) of the kernel:(19)
gap> t^(t^1) = t^(t^7); i^(t^1) = i^(t^7);
true
true
gap> t^(i*t^4) = t^(i*t^10); i^(i*t^4) = i^(i*t^10);
true
true
and so on for all the other cosets.
[5] Neo-Riemannian theory
[5.1] Another area of music-theoretic research for which GAP is useful is neo-Riemannian theory. This theory deals largely with contextual operations on the set of consonant triads, or Klänge.(20) To that end, define an arbitrary consonant (major or minor) triad as an unordered pitch-class set (pcset):(21)
gap> CM := [4,7,12];
[ 4, 7, 12 ]
Call the orbit of a pitch-class set under T/I a set-class (in this case, the set of pcsets to which a C major triad maps under the elements of the T/I group), and label the set-class of consonant triads K:
gap> K := Orbit(TI,CM,OnSets);
[ [ 4, 7, 12 ], [ 1, 5, 8 ], [ 5, 8, 12 ], [ 2, 6, 9 ], [ 4, 7, 11 ],
[ 1, 6, 9 ], [ 3, 7, 10 ], [ 3, 6, 10 ], [ 2, 7, 10 ], [ 3, 6, 11 ],
[ 4, 8, 11 ], [ 2, 5, 9 ], [ 3, 8, 11 ], [ 2, 5, 10 ], [ 5, 9, 12 ],
[ 1, 4, 8 ], [ 4, 9, 12 ], [ 1, 4, 9 ], [ 1, 6, 10 ], [ 3, 7, 12 ],
[ 1, 5, 10 ], [ 3, 8, 12 ], [ 2, 7, 11 ], [ 2, 6, 11 ] ]
K, as a set, has twenty-four members (twelve major triads and twelve minor triads, all represented above) on which T/I acts:(22)
gap> TI_K := Action(TI,K,OnSets);
Group([ (1,2,4,7,11,15,19,23,22,18,14,10) (3,6,9,13,17,21,24,20,16,12,8,5),
(1,3)(2,5)(4,8)(6,10)(7,12)(9,14)(11,16) (13,18)(15,20)(17,22)(19,24)(21,23) ])
In the output, we see that GAP maps the twenty-four members of K to the integers [1 .. 24]. In fact, its particular mapping of K to these integers has a basis in its memory of our definition in [3.13] of T/I as being the group generated by t and i (T1 and I0). If we assign order numbers to the twenty-four triads in the output of the previous command, then C major [4, 7, 12] is 1, C-sharp major [1, 5, 8] is 2, F minor [5, 8, 12] is 3, D major [2, 6, 9] is 4, E minor [4, 7, 11] is 5, and so on. Then, the generator t (T1) carries 1 to 2, 2 to 4, 4, to 7, etc.; and i (I0) takes 1 to 3, 2 to 5, and the like. Table 2 provides a list of these triads and their corresponding labels. The action of the T/I group on the set of twelve pitch classes is isomorphic to its action on the twenty-four members of K. Call this isomorphism gamma:
gap> gamma := IsomorphismGroups(TI,TI_K);
[ (1,2,3,4,5,6,7,8,9,10,11,12), (1,11)(2,10)(3,9)(4,8)(5,7) ] ->
[ (1,2,4,7,11,15,19,23,22,18,14,10)(3,6,9,13,17,21,24,20,16,12,8,5),
(1,8)(2,12)(3,14)(4,16)(5,10)(6,18)(7,20)(9,22)(11,24)(13,23)(15,21)(17,19) ]
Define the image of t under gamma:
gap> t_K := Image(gamma,t);
(1,2,4,7,11,15,19,23,22,18,14,10)(3,6,9,13,17,21,24,20,16,12,8,5)
and the image of i under gamma:
gap> i_K := Image(gamma,i);
(1,8)(2,12)(3,14)(4,16)(5,10)(6,18)(7,20)(9,22)(11,24)(13,23)(15,21)(17,19)
[5.2] T/I’s action on K has a permutation representation on [1 .. 24] that is a subgroup of the symmetric group on that set:(23)
gap> S_24 := SymmetricGroup(24);
Sym( [ 1 .. 24 ] )
gap> IsSubgroup(S_24,TI_K);
true
A classical result in transformational music theory (Lewin 1987) states that the centralizer in S24 of T/I’s action on K is the Schritt/Wechsel group, S/W, of neo-Riemannian theory:(24)
gap> SW := Centralizer(S_24,TI_K);
Group([ (1,2,4,7,11,15,19,23,22,18,14,10) (3,5,8,12,16,20,24,21,17,13,9,6),
(1,3)(2,6)(4,9)(5,10)(7,13)(8,14)(11,17) (12,18)(15,21)(16,22)(19,24)(20,23) ])
(The output here shows a particular Schritt and Wechsel pair as the generators of S/W.) This result is related to one in permutation group theory, which states that because the action of T/I on K is regular (simply transitive),
gap> IsRegular(TI_K);
true
it is isomorphic to its centralizer (Dixon and Mortimer 1996). Call this isomorphism delta:
gap> delta := IsomorphismGroups(TI_K,SW);
[ (1,2,4,7,11,15,19,23,22,18,14,10)(3,6,9,13,17,21,24,20,16,12,8,5),
(1,3)(2,5)(4,8)(6,10)(7,12)(9,14)(11,16)(13,18)(15,20)(17,22)(19,24)(21,23) ] ->
[ (1,2,4,7,11,15,19,23,22,18,14,10)(3,5,8,12,16,20,24,21,17,13,9,6),
(1,3)(2,6)(4,9)(5,10)(7,13)(8,14)(11,17)(12,18)(15,21)(16,22)(19,24)(20,23) ]
We note that delta sends T/I to S/W, which GAP shows in the output terms of generators for the respective groups, as they act on K.
[5.3] Call s (unit Schritt) the image of t under delta:
gap> s := Image(delta,t_K);
(1,2,4,7,11,15,19,23,22,18,14,10)(3,5,8,12,16,20,24,21,17,13,9,6)
It sends the major triads “up” by a semitone (C major,
gap> w := Image(delta,i_K);
(1,9)(2,13)(3,14)(4,17)(5,18)(6,10)(7,21)(8,22)(11,24)(12,23)(15,20)(16,19)
Recall the mapping in Table 2. We note that w is a Wechsel. It sends each major triad to a minor triad, and vice versa, where the respective triadic roots form a consistent interval: 1 goes to 9 (C major to G minor), 2 to 13 (
[5.4] The canonical neo-Riemannian exchanges with parsimonious voice leading (parallel, relative, and leading-tone) may then be defined as follows:
gap> p := w*s^7;
(1,20)(2,16)(3,15)(4,12)(5,11)(6,19)(7,8)(9,23)(10,24)(13,22)(14,21)(17,18)
gap> r := w*s^10;
(1,17)(2,21)(3,22)(4,24)(5,23)(6,18)(7,20)(8,19)(9,14)(10,13)(11,16)(12,15)
gap> l := w*s^3;
(1,5)(2,3)(4,6)(7,9)(8,10)(11,13)(12,14)(15,17)(16,18)(19,21)(20,22)(23,24)
Moreover, other useful operations, such as Cohn’s (Cohn 2004) hexatonic pole, may be defined as compositions of these exchanges:
gap> hp := l*p*l;
(1,13)(2,17)(3,18)(4,21)(5,22)(6,14)(7,24)(8,23)(9,10)(11,20)(12,19)(15,16)
[5.5] Next, generate the cyclic T group acting on consonant triads:
gap> T_K := Group(t_K);
Group([ (1,2,4,7,11,15,19,23,22,18,14,10) (3,6,9,13,17,21,24,20,16,12,8,5) ])
Again, the output shows the cycles of the generator t (T1) as it acts on K. The centralizer in S24 of T’s action on K is another well-known group in neo-Riemannian theory, Hook’s (Hook 2002) set of 288 uniform triadic transformations (UTTs),
gap> CinS_24ofT_K := Centralizer(S_24,T_K);
Group([ (1,2,4,7,11,15,19,23,22,18,14,10) (3,6,9,13,17,21,24,20,16,12,8,5),
(3,5,8,12,16,20,24,21,17,13,9,6), (1,3)(2,6)(4,9)(5,10)(7,13)(8,14)(11, 17)
(12,18)(15,21)(16,22)(19,24)(20,23) ])
gap> Size(CinS_24ofT_K);
288
of which S/W is a subgroup:
gap> IsSubgroup(CinS_24ofT_K,SW);
true
[5.6] We can arrive at an isomorphic structure on [1 .. 24] that is perhaps more intuitive. Let [1 .. 12] represent the pitch classes that function as the roots of the major triads, and let [13 .. 24] represent the roots of the minor triads, where x and x+12 belong to the same pitch class. (That is, 1 and 13 both map to the pitch class C#; 2 and 14 to D; ..., 12 and 24 to C.) See Table 3.
[5.7] Hook’s UTTs are given in the form ![]() σ, t+, t-
σ, t+, t-![]()
gap> minus := (1,13)(2,14)(3,15)(4,16)(5,17)(6,18)

>(7,19)(8,20)(9,21)(10,22)(11,23)(12,24);
(1,13)(2,14)(3,15)(4,16)(5,17)(6,18)(7,19)(8,20)(9,21)(10,22)(11,23)(12,24)
gap> plus := minus^2;
()
Then, t+ represents the transposition (translation) factor on the T-orbit of major triads,
gap> t^plus;
(1,2,3,4,5,6,7,8,9,10,11,12)
where we now conjugate t (T1, as it acts on [1 .. 12]) by the “plus” operation; and t- on minor triads,
gap> t^minus;
(13,14,15,16,17,18,19,20,21,22,23,24)
given by conjugating t by the “minus” operation, which carries [1 .. 12] to [13 .. 24] as a set.
[5.8] We may model UTTs such as Hyer’s (Hyer 1995) dominant relation d = ![]() +, 5, 5
+, 5, 5![]()
![]() - ,3, 9
- ,3, 9![]()
gap> d := (t^plus)^5*(t^minus)^5*plus;
(1,6,11,4,9,2,7,12,5,10,3,8)(13,18,23,16,21,14,19,24,17,22,15,20)
gap> nhp := (t^plus)^3*(t^minus)^9*minus;
(1,16)(2,17)(3,18)(4,19)(5,20)(6,21)(7,22)(8,23)(9,24)(10,13)(11,14)(12,15)
The output of the first command sends 1 to 6 to 11, etc., in one orbit; and 13 to 18 to 23, etc., in another. Under our new labeling system, these integers refer to
[5.9] Hook 2002 further describes a larger group, QTT, which adjoins the usual inversion operation to the UTTs. We can form this group as a wreath product of T/I acting on [1 .. 12] by S2 (the symmetric group of degree 2, consisting of two permutations, ( ) and (1,2)).
gap> QTT := WreathProduct(TI,SymmetricGroup(2));
<permutation group of size 1152 with 5 generators>
QTT contains several musically relevant subgroups of order 24, including Clough’s (Clough 1998) abelian (so-called) S/I group:(26)
gap> schritt := t^plus*(t^minus)^-1*plus;
(1,2,3,4,5,6,7,8,9,10,11,12)(13,24,23,22,21,20,19,18,17,16,15,14)
gap> inversion := i^plus*i^minus*minus;
(1,23)(2,22)(3,21)(4,20)(5,19)(6,18)(7,17)(8,16)(9,15)(10,14)(11,13)(12,24)
gap> SI := Group(schritt,inversion);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,24,23,22,21,20,19,18,17,16,15,14),
(1,23)(2,22)(3,21)(4,20)(5,19)(6,18)(7,17)(8,16)(9,15)(10,14)(11,13)(12,24) ])
gap> IsAbelian(SI);
true
[5.10] In addition to the usual inversion operation, Kochavi 2002 describes five contextual inversion operators (cios) that may act on the set of consonant triads:(27)
gap> i215 := m^plus*m^minus*minus;
(1,17)(2,22)(3,15)(4,20)(5,13)(6,18)(7,23)(8,16)(9,21)(10,14)(11,19)(12,24)
gap> i216 := (m*i)^plus*(m*i)^minus*minus;
(1,19)(2,14)(3,21)(4,16)(5,23)(6,18)(7,13)(8,20)(9,15)(10,22)(11,17)(12,24)
gap> i217 := i^plus*i^minus*(t^minus)^6*minus;
(1,23,7,17)(2,22,8,16)(3,21,9,15)(4,20,10,14)(5,19,11,13)(6,18,12,24)
gap> i218 := (m*i)^plus*(m*i)^minus*(t^minus)^6*minus;
(1,19,7,13)(2,14,8,20)(3,21,9,15)(4,16,10,22)(5,23,11,17)(6,18,12,24)
gap> i219 := m^plus*m^minus*(t^minus)^3*minus;
(1,17,4,20,7,23,10,14)(2,22,5,13,8,16,11,19)(3,15,6,18,9,21,12,24)
These cios may be used with t (acting on [1 .. 24]) to generate nonabelian order-24 groups with an element of order 12:
gap> TI215 := Group(t^plus*t^minus,i215);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,14,15,16,17,18,19,20,21,22,23,24),
(1,17)(2,22)(3,15)(4,20)(5,13)(6,18)(7,23)(8,16)(9,21)(10,14)(11,19)(12,24) ])
gap> TI216 := Group(t^plus*t^minus,i216);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,14,15,16,17,18,19,20,21,22,23,24),
(1,19)(2,14)(3,21)(4,16)(5,23)(6,18)(7,13)(8,20)(9,15)(10,22)(11,17)(12,24) ])
gap> TI217 := Group(t^plus*t^minus,i217);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,14,15,16,17,18,19,20,21,22,23,24),
(1,23,7,17)(2,22,8,16)(3,21,9,15)(4,20,10,14)(5,19,11,13)(6,18,12,24) ])
gap> TI218 := Group(t^plus*t^minus,i218);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,14,15,16,17,18,19,20,21,22,23,24),
(1,19,7,13)(2,14,8,20)(3,21,9,15)(4,16,10,22)(5,23,11,17)(6,18,12,24) ])
gap> TI219 := Group(t^plus*t^minus,i219);
Group([ (1,2,3,4,5,6,7,8,9,10,11,12)(13,14,15,16,17,18,19,20,21,22,23,24),
(1,17,4,20,7,23,10,14)(2,22,5,13,8,16,11,19)(3,15,6,18,9,21,12,24) ])
Now we can identify (up to isomorphism) each of these groups, using GAP’s Small Group Library (see Table 4(28)):(29)
Table 4. Isomorphism classes of the nonabelian subgroups
of order 24 in M with an element of order 12
(click to enlarge)
gap> IdGroup(TI);
[ 24, 6 ]
gap> IdGroup(TI215);
[ 24, 5 ]
gap> IdGroup(TI216);
[ 24, 10 ]
gap> IdGroup(TI217);
[ 24, 4 ]
gap> IdGroup(TI218);
[ 24, 11 ]
gap> IdGroup(TI219);
[ 24, 1 ]
[5.11] Whereas QTT contains subgroups that are isomorphic to all the groups of order 24 with an element of order 12,(30) it does not contain these particular subgroups. Rather, Douthett and Peck 2007 give a group of order 4608, M, which does contain Kochavi’s cios.(31) M is a wreath product of TTO acting on [1 .. 12] by S2:
gap> M := WreathProduct(t(TTO,SymmetricGroup(2));
<permutation group of size 4608 with 7 generators>
[5.12] The two abelian groups of order 24 with an element of order 12 appear also as subgroups in M. Clough’s S/I group (from [5.9] above) is an example:
gap> IdGroup(SI);
[ 24, 9 ]
Its isomorphism class is as follows:
S/I ≅ [24, 9] ≅ C12 × C2
The remaining case is left as an exercise for the reader.(32)
[6] Conclusions
[6.1] The preceding discussion is intended to demonstrate GAP’s usefulness in studying transformational music theory. Whereas most of the examples recreate well known models, it has not been our purpose here to discover novel results. Nevertheless, GAP may function quite effectively in the pursuit of new theoretical systems. Moreover, it can be a valuable tool in transformation theory pedagogy, affording teachers and students an environment for experimentation with either existing or original concepts.
[6.2] In addition to the standard group-theoretical topics we have addressed thus far, GAP has many additional applications. It can be used to study other discrete algebraic structures, such as monoids, semigroups, fields, rings, vector spaces, matrices, and the like. What GAP is not capable of doing (at least not efficiently) is working with continuous and other infinite spaces, such as those found in Callendar, Quinn, and Tymoczko 2008. These topics may be explored computationally as well, but using applications other than GAP.
Robert W. Peck
Louisiana State University
Baton Rouge, LA 70803
rpeck@lsu.edu
Works Cited
Aschbacher, Michael. 1986. Finite Group Theory. Cambridge: Cambridge University Press.
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice Leading Spaces.” Science 320: 346–348.
Clough, John. 1998. “A Rudimentary Geometric Model for Contextual Transposition and Inversion.” Journal of Music Theory 42, no. 2: 297–306.
Cohn, Richard. 1998. “An Introduction to Neo-Riemannian Theory: A Survey and Historical Perspective.” Journal of Music Theory 42, no. 2: 167–180.
—————. 2004. “Uncanny Resemblances: Tonal Signification in the Freudian Age.” Journal of the American Musicological Society 57, no. 2: 285–323.
Dixon, John D., and Brian Mortimer. 1996. Permutation Groups. New York: Springer-Verlag.
Douthett, Jack, and Robert Peck. 2007. “An Order 1152 Group of Triadic Transformations and Its Relevance to Existing Musical Theoretical Structures.” Paper presented at the “Special Session on Mathematical Techniques in Musical Analysis,” American Mathematical Society/Mathematical Association of America Joint National Meeting, New Orleans, Louisiana.
GAP Group, The. 2008. GAP—Groups, Algorithms, and Programming, Version 4.4.12. <http://www.gap-system.org>
Hook, Julian. 2002. “Uniform Triadic Transformations.” Journal of Music Theory 46, nos. 1–2: 57–126.
Hyer, Brian. 1995. “Reimag(in)ing Riemann.” Journal of Music Theory 39, no.1: 101–138.
Klumpenhouwer, Henry. 1991. A Generalized Model of Voice-Leading for Atonal Music. Ph.D. diss., Harvard University.
—————. 1998. “The Inner and Outer Automorphisms of Pitch-Class Inversion and Transposition: Some Implications for Analysis with Klumpenhouwer Networks.” Intègral 12: 81–93.
Kochavi, Jonathan H. 2002. Contextually Defined Musical Transformations. Ph.D. diss., State University of New York, Buffalo.
Lambert, Philip. 2002. “Isographies and Some Klumpenhouwer Networks They Involve.” Music Theory Spectrum 24, no. 2: 165-195.
Lewin, David. 1984. “Amfortas’s Prayer to Titurel and the Role of D in Parsifal: The Tonal Spaces of the Drama and the Enharmonic C-flat/B.” Nineteenth-Century Music 8, no. 3: 336–349.
—————. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.
—————. 1990. “Klumpenhouwer Networks and Some Isographies that Involve Them.” Music Theory Spectrum 12, no. 1: 83–120.
—————. 1994. “A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg’s Opus 11, No. 2.” Journal of Music Theory 38, no. 1: 79–101.
Morris, Robert D. 1982. “Set Groups, Complementation, and Mappings among Pitch-Class Sets.” Journal of Music Theory 26, no. 1: 101–44.
—————. 1987. Composition with Pitch-Classes. New Haven: Yale University Press.
Peck, Robert. 2005. “GAP (Groups, Algorithms, and Programming): A Tool for Computer-Assisted Research in Music Theory.” Poster presented at Society for Music Theory National Meeting, Cambridge, Massachusetts.
—————. 2009. “Wreath Products in Transformational Music Theory.” Perspectives of New Music 47, no.1: 193–210.
Satyendra, Ramon, ed. 1998. Journal of Music Theory 42, no. 2.
Smyth, David. 2008. “More About Wagner’s Chromatic Magic.” Paper presented at the 31st Annual Meeting of Society for Music Theory, Nashville, Tennessee.
Starr, Daniel V. 1978. “Sets, Invariance, and Partitions.” Journal of Music Theory 22, no. 1: 136–83.
Starr, Daniel, and Robert Morris. 1974. “The Structure of All-Interval Series.” Journal of Music Theory 18, no. 2: 364–89.
—————. 1977–78. “A General Theory of Combinatoriality and the Aggregate.” Perspectives of New Music 16, no. 1: 3–35; and 16, no. 2: 50–84.
<http://www.sagemath.org/>
Stein, William, et al. 2009. Sage Mathematics Software, Version 3.4. The Sage Development Team.
<http://www.sagemath.org/>
Footnotes
1. A partial bibliography, including hundreds of published works that cite GAP, can be found at <www.gap-system.org/Doc/Bib/gap-published.html>.
Return to text
2. One example of GAP’s use in a music-theoretical context is Peck 2005.
Return to text
3. The interested reader may also consult Dixon and Mortimer 1996 for more information.
Return to text
4. GAP does not use this color coding; it is used here for clarity of presentation.
Return to text
5. For GAP to read the command as it is given here, the program needs to be stored in the same directory from which GAP is launched. For example, using the default installation for Windows, that directory is C:\ gap4r4\bin.
Return to text
6. Mathematicians refer to operations that music theorists normally call “transpositions” as “translations.” Mathematically speaking, a translation moves every point the same distance in the same direction, whereas a transposition exchanges only two elements in a set, and holds all other elements invariant.
Return to text
7. GAP does, in fact, allow for modular arithmetic, but its inclusion here would add a level of complexity that is not necessary for our purposes. See the Help manual under gap> ?modulo.
Return to text
8. The caret symbol “^” has several possible meanings in GAP, all relating to exponential notations. Here, it is meant literally as an exponent (i.e., t squared). It may also signify a function (see [4.3]), or a conjugation (see [4.15]).
Return to text
9. Note the use of parentheses in the second subsequent GAP command (“gap> (t^2)^-1;”). They are necessary, as exponentiation is generally non-associative.
Return to text
10. Music theorists frequently incorporate the notation “T/I” for the usual transposition and inversion group. This notation could be confusing to mathematicians, who might interpret it as a quotient (or factor) group, T mod I. As the subgroup generated by i is not normalized by T, however, such a quotient is not possible. For that reason, GAP renders an error if we attempt to label this group “T/I,” hence we use merely “TI” in GAP.
Return to text
11. For earlier accounts of the m operation, particularly in the context of serial theory, see Starr and Morris 1974 and 1977–78, and Starr 1978. For a later, fuller treatment, see Morris 1987.
Return to text
12. N.B.: When reading the accompanying program, “SampleGAPprogram.txt,” GAP may assign to alpha a different isomorphism of TTO to Aut(T/I) than the one shown in the output here: for instance, it may send TTO generators t, i, and m to hyper-operators F![]() 1,7
1,7![]() , F
, F![]() 11,5
11,5![]() , and F
, and F![]() 5,8
5,8![]() . As a result, we provide alternate definitions in the sample program for hyper-t and hyper-i than those that appear below in [4.5] and [4.6]; namely, put gap> hyp_t := (t^7)^alpha; and gap> hyp_i := i^alpha*t^alpha. (Under this particular mapping, the hyper-m operation in [4.12] does not require re-defining.) The definitions that appear in the online Sage Notebook “GAP—MTO” are yet again slightly different.
. As a result, we provide alternate definitions in the sample program for hyper-t and hyper-i than those that appear below in [4.5] and [4.6]; namely, put gap> hyp_t := (t^7)^alpha; and gap> hyp_i := i^alpha*t^alpha. (Under this particular mapping, the hyper-m operation in [4.12] does not require re-defining.) The definitions that appear in the online Sage Notebook “GAP—MTO” are yet again slightly different.
Return to text
13. Our GAP representation of the T/I group may be generated by any t operator of order 12 (t, t 5, t 7, or t 11) and any it n. Why GAP chooses here to model these automorphisms on generators t 5 and it 4 may seem arbitrary, but in fact has a basis in its programming beyond the scope of this tutorial. Incidentally, GAP may choose generators other than t 5 and it 4 on different computers running precisely the same software, or when reading a program vs. a series of typed commands. In these cases, we would need to redefine the hyper-t, -i, and -m operations in [4.5], [4.6], and [4.9] accordingly.
Return to text
14. In turn, Lambert’s (2002) analysis of op. 19, no. 6, takes Lewin’s (1990) analysis of three of the piece’s sonorities as its point of departure.
Return to text
15. Lambert (2002) offers initially a different interpretation of the trichord labeled “d” in our Example 3, which he calls “(d).” Subsequently, he offers a reinterpretation, which he labels “(d').” As we incorporate the latter interpretation here, we retain its labeling.
Return to text
16. We can take for granted the existence of an inverse here, as the automorphisms of a group themselves form a group, and a group provides an inverse for each of its elements axiomatically.
Return to text
17. This extension to K-net theory appears in Appendix B of Lewin 1990. There, he uses his earlier notation for these automorphisms: hence, F![]() 5,0
5,0![]() for the hyper-m operation
for the hyper-m operation ![]() m
m![]() we describe here; and F
we describe here; and F![]() 7,0
7,0![]() for hyper-mi,
for hyper-mi, ![]() mi
mi![]() .
.
Return to text
18. Note that Klumpenhouwer 1998 incorporates square brackets [ ] for hyper-operators that obtain from the inner automorphism group (i.e., those which obtain under conjugation), in contrast to the angle brackets ![]()
![]() Lewin 1994 uses for hyper-operators that derive from the Hyp(T/I) group.
Lewin 1994 uses for hyper-operators that derive from the Hyp(T/I) group.
Return to text
19. Because the kernel is a normal subgroup (gap> IsNormal(HypTI,ker_beta); true), it does not matter whether we multiply on the left or the right in forming the cosets.
Return to text
20. Lewin 1987 contains the first major work in neo-Riemannian theory, although in this regard it draws on certain aspects of his earlier work (such as Lewin 1984). Cohn 1998 also offers an excellent introduction to the theory; indeed, the entire issue of Journal of Music Theory 42, no. 2 (Satyendra 1998) is devoted to neo-Riemannian topics.
Return to text
21. In reading the subsequent command, recall our earlier use of the integer 12 for pitch class C. In addition, neo-Riemannian theory commonly incorporates the notation “+” for major triads and “-” for minor triads. In GAP, we cannot use these symbols in variable names, as GAP considers them to be arithmetic operators. Therefore, we use “M” for major (e.g., “CM” in the subsequent command is read “C major”).
Return to text
22. Similar to the situation in [4.3], fn. 12, GAP assigns a different mapping of K to [1 .. 24] when reading “SampleGAPprogram.txt.” As a result, in the program we obtain a different ordering for the neo-Riemannian operations Schritt s and Wechsel w that appear below in [5.3]. Therefore, in the program, we must redefine the operations p, r, and l from [5.4] accordingly with gap> p := w*s^9;, gap> r := w;, and gap> l := w*s^5;. Another, similar situation obtains in the Sage Notebook “GAP—MTO.”
Return to text
23. S24 is a sizeable group, of order 24! (gap> Size(S_24); 620448401733239439360000). Nevertheless, GAP is able to process the subsequent commands that incorporate it nearly instantaneously.
Return to text
24. The centralizer in S24 of T/I’s action on K consists of all permutations on [1 .. 24] that commute with every member of T/I.
Return to text
25. The minus operation (minus), defined in the subsequent command, is in essence the Parallel exchange; it is an involution that sends
Return to text
26. Clough 1998 presents a group acting on consonant triads generated by a unit Schritt and an inversion, which he labels the “S/I group.” Whereas the group does contain the twelve familiar Schritts, it does not contain all twelve inversions. (Clearly, two inversions compose to form a transposition, not a Schritt.) In the same vein, he describes an isomorphic “T/W group.” Hook 2002 discusses these groups in the context of the QTT group.
Return to text
27. Our labeling of Kochavi’s (2002) contextual inversions (i215, i216, ..., i219) follows the numbering of Figures in his dissertation (Figures 2.15, 2.16, ..., 2.19, respectively) in which they are presented (and otherwise unlabeled).
Return to text
28. In Table 4, the notation “Dic6” refers to the dicyclic group of order 24 (= 4 ⋅ 6); “Q8” to the quaternion group of order 8; and “C3 ![]() C8” to the semidirect product of C3 by C8.
C8” to the semidirect product of C3 by C8.
Return to text
29. The output for the subsequent gap> IdGroup(TI); command shows [ 24, 6 ], which tells us that T/I is isomorphic to the sixth group listed in GAP’s classification of the fifteen groups of order 24. The Small Group Library is not installed for Sage; hence, the last seven commands presented here are not included in the Sage Notebook “GAP—MTO.”
Return to text
30. Fifteen groups of order 24 (up to isomorphism) exist, but seven of them do not possess an element of order 12, which is necessary if we want to model an operation such as transposition in these groups.
Return to text
31. M, in the context of Douthett and Peck 2007, stands for “Mother Group.” It is not to be confused with Morris’s (1982) M operation.
Return to text
32. One may alternatively consult the theorem in §3.8 of Hook 2002.
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Brent Yorgason, Managing Editor
Number of visits: