What Do I Hear Now, Groupwise?
Ciro Scotto
KEYWORDS: Milton Babbitt, superarray, motive, contrapuntal, all-partition array
Copyright © 2011 Society for Music Theory
[1] Groupwise (1983) is a chamber work from Babbitt’s third stylistic period consisting of flute (doubling alto flute and piccolo), violin, viola, violoncello, and piano. The structural foundation of compositions from this period is known in the literature as a superarray, a composite of multiple simultaneously unfolding all-partition arrays (Mead 1994). In a paper presented at the 1989 SMT national conference, I argued superarray compositions appear to be fundamentally different from the compositions of the preceding periods (Scotto 1989). They appear to embody a change in the aggregate compositional process where the perception of aggregate boundaries is essential to aurally differentiating one aggregate, the basic linear and columnar unit of aggregate composition, from another. The pitch duplications generated by a superarray obscure the perception of chromatic completion, which is one method of aurally differentiating aggregates. Perceiving aggregate boundaries in a superarray composition is analogous to perceiving state lines on a cross-country drive of the United States. The map directing the trip indicates crisp divisions between all states. The experience of those divisions while driving can be crisp, imperceptible, or anything in between. Sometimes, especially in the Plains States, the map may be the only indication that a state line has been crossed. Other times, the change is crisp and immediately detectable, such as crossing the Columbia River from Portland, Oregon, to Vancouver, Washington.
[2] In a later article, I argued superarray compositions might also signal a change from a generative model of motivic structure to a holistic model where the development of motivic material is a non-hierarchical and non-teleological process (Scotto 2002). In this model, motives are analogous to plateaus that form from areas of coagulation and rise above a plane, and then they collapse and are absorbed back into the plane. Their common planar origin makes all plateaus motivic. Although the plateaus emanate from the same source, they can be structurally non-equivalent as well as similar or even equivalent. Associations among plateaus create a constantly developing non-hierarchical and non-teleological motivic surface. The contrapuntal arrangement of component arrays in the superarray of Groupwise facilitates making associations among plateaus. Moreover, while the pitch duplications of the superarray may obscure crisply perceiving aggregate boundaries, they may actually facilitate making structural associations among plateaus, which will also facilitate hearing the effect of aggregate changes (rather than their boundaries) as the piece progresses.
[3] The all-partition array functioning as the building block of the superarray for Groupwise consists of six simultaneously unfolding twelve-tone rows and fifty-eight partitions. To fill out all fifty-eight partitions, the array uses all forty-eight members of the row class, and the beginning and end of a group of six rows divides the fifty-eight partitions into eight subgroups or blocks. The D-hexachord 6-32[0,1,2,6,7,8], which generates three hexachordal areas, serves as the foundation of the twelve-tone row for Groupwise. Row pairs within each array block are hexachordally combinatorial, and since each row pair represents one of the D-hexachord’s three hexachordal areas, each block contains rows from all three hexachordal areas (Mead 1994).
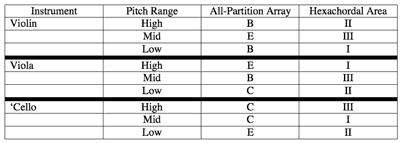
Example 1. Hexachordal area assigned to the pitch ranges of the string instruments.
(click to enlarge)
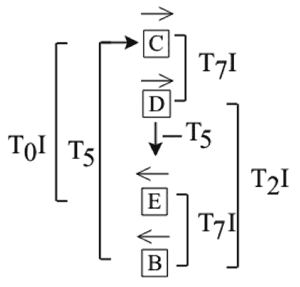
Example 2. Transformational relationships among all-partition arrays B, C, D, and E.
(click to enlarge)
[4] The instrumental assignment of all-partition arrays in Groupwise suggests the work is a chamber concerto for flute with accompaniment. The superarray consists of five complete all-partition arrays. The pitch range of each instrument is divided into three pitch-spans (low-range, mid-range, and high-range), and a pitch range is assigned to a hexachordally combinatorial row pair from one of the three hexachordal areas. The hexachordally combinatorial row pairs for the flute and piano all belong to a single all-partition array while the hexachordally combinatorial row pairs for the violin, viola, and ’cello belong to three different arrays. Labeling the five all-partition arrays A through E the assignments are: (A) flute; (B) violin, high and low range/viola, mid-range; (C) viola, low-range/’cello, high and mid-range; (D) piano; and (E) violin, mid-range/viola, high-range/’cello, low-range. As Mead points out and as Example 1 illustrates, even though each string instrument is assigned hexachordally combinatorial row pairs from different all-partition arrays, the three pitch ranges contain row pairs from each of the hexachordal areas for the D-hexachord (Mead 1994). The more limited range of the flute compared to the other instruments has the effect of packing more pitch material into a smaller space, giving the flute very dense lyrical lines compared to the more sparsely packed lines of the other instruments (the piano, for instance).(1) The transformational relationships among the five all-partition arrays also suggest a unique role for the flute. While either Tn or TnI relate arrays B, C, D, and E to each other, the operation TnM relates the flute array to the other arrays (Mead 1994). Of course, the immediate effect of this operation is that any interval-class 5 in the accompanying all-partition arrays becomes interval-class 1 in the flute array.(2)
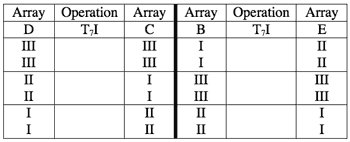
[5] Although the flute and its array may be the soloist, the focus of this study is the fertile soil for motivic association created by the contrapuntal arrangement of the accompanying arrays. The transformational relationships among all-partition arrays B, C, D, and E play an important role in that arrangement (see Example 2). The left and right arrows indicate arrays E and B are retrograde related to C and D. The same operation, T7I, relates non-retrograde related array pairs, so the hexachordal areas within an array pair follow the same transformational pattern (see Example 3). That is, hexachordal area III maps onto itself under T7I, and hexachordal areas II and I map onto each other.(3) Similarly, the operation T5 relates non-retrograde related array pairs C/B and D/E by mapping the hexachordal areas within an array pair onto each other with the same pattern.(4)
|
Example 3. Mapping of hexachordal area in array pairs B/E and D/C. (click to enlarge) |
Example 4. The fifteen non-null subsets of four objects using all-partition arrays B, C, D, and E as objects. (click to enlarge) |
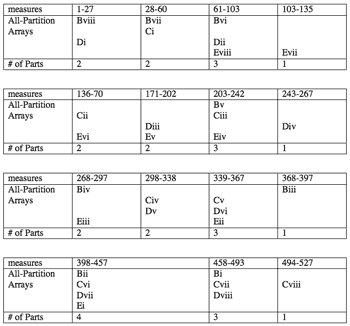
Example 5. Ordering of the fifteen subsets produced by the four all-partition arrays and the form that results from the ordering.
(click to enlarge)
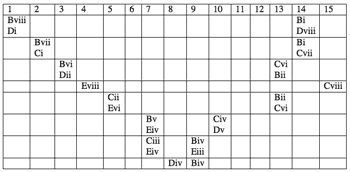
[6] Mead informs us that the “four constituent arrays are laid out to yield the ubiquitous fifteen subsets of the four projecting ensembles” (Mead 1994, 234). While the 24-1=15 subsets produced by four objects accounts for the sections and for the various solos, duets, and trios of Groupwise, the arrangement of those subsets and their resulting counterpoint must still be addressed. Moreover, the counterpoint of arrays is neither as mechanical nor arbitrary as the generating mechanism makes it sound. Example 4 illustrates the fifteen non-null subsets produced by the four all-partition arrays. Besides the one set with four members and the four sets with one member, six subsets have two members and four subsets have three members. The fifteen subsets are an unordered collection, so they have 15! possible orderings. Babbitt’s ordering of the subsets essentially creates a form with four nearly identical sections (see Example 5).(5)
[7] The last section of each division contains a single block from one of the four all-partition arrays, and a trio of blocks always precedes the “solo” block. Subgroups one, two, and three each have two duets preceding the trio. The placement of the single subset containing four parts is especially suggestive. The example illustrates that the quartet of array blocks substitutes for the two duets of the first three subgroups. Essentially, the quartet is two stacked duets. The beginning of the fourth subgroup is a culminating point from a pitch density perspective since all the arrays are contributing pitch-class material. Although the first three subgroups contain constantly changing instrumental combinations and registral shifts within instruments, the overall pattern of pitch-class density is constant. The climactic point in the piece breaks two patterns. First, pitch-class density reaches a level exceeding all previous levels. Second, the constantly changing instrumental combinations and registral shifts stop since all the accompanying instruments in all their pitch ranges are playing.
Example 6. Invertible contrapuntal array blocks.
(click to enlarge)
Example 7. Quasi-symmetrical structure of the pairs of invertible countrapuntal array- blocks.
(click to enlarge)
Example 8. Paired invertible countrapuntal array-blocks containing large row-segments.
(click to enlarge)
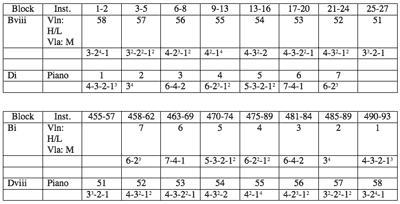
[8] Even more interesting than the ordering of the fifteen array subsets is the contrapuntal arrangement of the array blocks and array partitions it produces. Within each subset of array blocks, the partitions align in a partition contra partition fashion. For example, partition 58 from block Bviii, 3-24-1, aligns with partition 1 from block Di, 4-3-2-13, in measures 1–2. The alignment of partitions generated from blocks Bviii/Di in the first section of the work occurs again as a subset of the trio in measures 458–493. However, this time Bi aligns with Dviii. The partitions and their alignment remains the same, but the partitions switch from one array block to another (see Example 6). Moreover, the partitions in the paired array blocks are retrograde related. For example, the partitions (and the row segments contained in the partitions) in block Di are the retrograde of the partitions in block Bi. If the paired blocks are members of the same array, the row segments within partitions will all be related to each other by the transformation relating the arrays. Furthermore, the instrumental combinations and ranges of the pitch-class material will remain the same. Essentially, Babbitt has created a type of invertible array counterpoint. Even more remarkable is the quasi-symmetrical relationship the pairs of invertible countrapuntal array-blocks create in the overall form of the work (see Example 7).
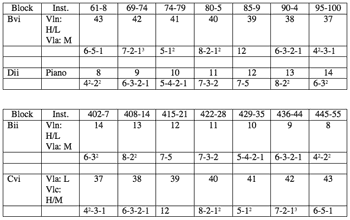
[9] Partitions in the paired invertible array-blocks containing large row segments create environments especially rich with plateaus for motivic association. For example, the landscape created by invertible countrapuntal array-blocks Bvi/Dii and Cvi/Bii contains particularly fertile soil (see Example 8). Since the arrays are transformations of each other, the row segments in all the partitions will always be order number identical. For example, the eight note segment in partition 40 of block Bvi is the segment of T7I(P) contained in order numbers four through eleven, and the eight note segment in partition 40 of block Cvi is the segment of RT0I(P) also contained in order numbers four through eleven. Moreover, the transformation relating one array to another will also relate every order-number-identical row segment. For example, since T5 relates arrays B and C, it also relates the eight pitch-class order-number-identical row segments in partition 40 and the order-number-identical six-note segments in partition 38 of array blocks Bvi and Cvi. The same transformations relate the contrapuntal counterparts to partition 40 in each array pair (partition 11). Of course, the pitch realization of the partitions can either enhance or obscure connecting motivic material (compare Examples 9 and 10).
|
Example 9. Pitch-realization of partitions 40 and 11 from array blocks Bvi and Dii, respectively (for clarity, the example excludes pitch-class material from other array blocks in the violin part). (click to enlarge) |
Example 10. Pitch-realization of partitions 40 and 11 from array blocks Cvi and Bii, respectively (for clarity, the example excludes pitch-class material from other array blocks in the violin part). (click to enlarge) |
[10] While the phrase “multiple simultaneously unfolding arrays” is a verbose but accurate and neutral way of describing the serial structure of compositions from Babbitt’s third stylistic period, “superarray” has become the accepted and abbreviated alternative descriptor. However, the term can be problematic. The superarray view of multiple simultaneously unfolding arrays does not adequately capture their potential for altering the compositional process because, in some ways, the term implies more of the same only bigger. At least for Groupwise, the term “contrapuntal array composition” more adequately captures the process associated with the simultaneously unfolding arrays. In this small tribute to the monumental contribution Babbitt’s music has made to the craft of composition, I have tried to demonstrate that Groupwise may use a familiar structure but not in a familiar way. For example, contrapuntal arrays introduce an element of repetition that is not characteristic of Babbitt’s earlier works. Moreover, while the repeated pitch classes produced by contrapuntal arrays make hearing aggregate boundaries more difficult, the repeated and paired partition segments facilitate making motivic associations that create a coherent but constantly developing non-hierarchic and non-teleological motivic surface.
Ciro Scotto
University of South Florida
School of Music
Music Theory
4202 East Fowler Ave., MUS 101
Tampa, FL 33620
cscotto1@usf.edu
Works Cited
Mead, Andrew. 1994. An Introduction to the Music of Milton Babbitt. Princeton: Princeton University Press.
Scotto, Ciro. 1989. “What Do You Hear, Groupwise?” Presented at The Society for Music Theory National Conference, Austin, Texas.
—————. 2002. “The Conflict Between Particularism and Generalism in Andrew Mead’s Introduction to the Music of Milton Babbitt.” Journal of Music Theory 46: 285–345.
Footnotes
1. Besides its more lyrical and densely packed lines, the flute is the only instrument in the ensemble that doubles another instrument. Moreover, when the flute switches to the alto flute or piccolo, trichordal arrays rather than all-partition arrays generate its pitch material. Both of these structural features of Groupwise suggest that the flute essentially functions as a solo instrument.
Return to text
2. A more complete study of the effect of the TnM operation on the pitch material in the flute is, of course, beyond the scope of this small study.
Return to text
3. The operation T7I is one of four inversion operations (T1I, T4I, T7I, and TtI) that maps hexachordal area III of the row for Groupwise onto itself with C=0. Although each operation will not change the pitch-class content of hexachordal area III, they will change the order of the pitch classes within the hexachordal area. However, the ordering induced by T7I does not appear to be a significant factor in its choice. Therefore, any operation from this set will produce equivalent results.
Return to text
4. The operation T5 maps the hexachordal areas in the following pattern: I→II, II→III, and III→I.
Return to text
5. Mead presents a different chart of the superarray structure in An Introduction to the Music of Milton Babbitt: 234.
Return to text
Copyright Statement
Copyright © 2011 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: