Interval Permutations
Drew F. Nobile
KEYWORDS: Interval permutations, intervals, post-tonal analysis, mathematical modeling, set-class, space, Schoenberg, The Book of the Hanging Gardens
ABSTRACT: This paper presents a framework for analyzing the interval structure of pitch-class segments (ordered pitch-class sets). An “interval permutation” is a reordering of the intervals that arise between adjacent members of these pitch-class segments. Because pitch-class segments related by interval permutation are not necessarily members of the same set-class, this theory has the capability to demonstrate aurally significant relationships between sets that are not related by transposition or inversion.
I begin with a theoretical investigation of interval permutations followed by a discussion of the relationship of interval permutations to traditional pitch-class set theory, specifically focusing on how various set-classes may be related by interval permutation. A final section applies these theories to analyses of several songs from Schoenberg’s op. 15 song cycle The Book of the Hanging Gardens.
Copyright © 2013 Society for Music Theory
Example 1. Schoenberg, Op. 15, No. 14, opening: rhythm and contour establish a relationship between the first two gestures in the piano and voice
(click to enlarge and hear the audio)
Example 2. All ordered pitch-class intervals are 6, 7, 10, or 11 in the opening two gestures of Song No. 14. The bracketed interval sequences, which represent instances of rhythmic motive x, are related by interval permutation
(click to enlarge)
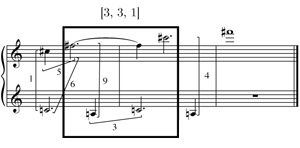
[1] Example 1 shows the score to the opening measures of “Sprich nicht immer von dem Laub,” the fourteenth song from Schoenberg’s Book of the Hanging Gardens, op. 15. Upon first listen, one is drawn to the relationship between the piano’s gesture in the first measure and the vocal line in the second. The two most immediately perceptible domains—contour and rhythm—solidify this relationship: the two gestures have opposite contour and the voice presents the same two rhythmic motives as the piano in reverse order, as shown in the example. These surface relationships would lead any analyst to search for a deeper relationship between these two gestures, especially in the realm of pitch. While the first three notes of the voice’s gesture give hope that this might be a retrograde inversion of the piano’s, this turns out not to be the case. Set-class analysis also proves unsatisfying: one might point out that set-class (016) makes several appearances, but this does not seem to be a unifying principle, as it is difficult to account for every note without invoking questionable segmentations. A salient relationship emerges, however, when we consider the ordered pitch-class intervals between successive notes, as shown in Example 2. Specifically, we see that all of these intervals are either 6, 7, 10, or 11 semitones. If we focus on the intervals within each gesture’s rhythmic motive x, bracketed in Example 2, we see that both of these motives contain one instance of each of these intervals but in a different order: the piano’s interval sequence is 11, 10, 6, 7, while the voice’s is 11, 7, 10, 6. Despite the fact that the two pentachords involved in these interval sequences are not members of the same set-class, their shared interval content associates them in an aurally salient way. This type of association is the focus of this paper; I will call such a relationship an interval permutation.
[2] I will return to this analysis in the final section of the paper, after providing a theoretical model of interval permutations and investigating their interactions with pitch-class set theory. The theory of interval permutations is based on two basic structures: the pitch-class segment and the interval series. A pitch-class segment is simply an ordered set of pitch-classes; these pitch-classes need not necessarily be distinct, though for practical reasons we will want to restrict ourselves to segments that contain at least two distinct pitch-classes. For example, the piano gesture in measure 1 of Example 1 can be represented as the segment (C, B, A,
Example 3. All possible permutations of the interval series [6, 1, 3]
(click to enlarge)
[3] An interval permutation is a reordering of an interval series. For example, [11, 6, 7, 10, 11], [10, 7, 6, 11, 11], and [6, 11, 10, 7, 11] are all interval permutations of the interval series [11, 10, 6, 7, 11] from the first measure of the Schoenberg example. An interval series of length n can be permuted in n! (“n factorial”) different ways if it does not have any duplicate intervals (the presence of duplicate intervals will reduce the number of distinct permutations). For example, a three-member series can be permuted in six different ways, as shown in Example 3 for the interval series [6, 1, 3]. In this example, the pitch-class segments are shown as vertical structures ordered from lowest to highest. The interval series can be alternatively written as a vertical stack, as shown between the staves in Example 3, which should be read from bottom to top.
[4] Not all of the sonorities in Example 3 are members of the same set-class; in fact, three different set-classes are represented in this example, namely (0146), (0236), and (0136).(2) In order to represent the relationship between pitch-class segments whose interval series are related by permutation I will introduce the terms series class and permutation class. A series class is a set of all interval series that are related to each other by permutation. A permutation class is a set of all pitch-class segments whose interval series are in the same series class. While these two equivalence classes are clearly closely related, they differ greatly in magnitude: there are six interval series in the same series class as [6, 1, 3] (these are precisely the six interval series shown below the staves in Example 3), while the permutation class related to this series class consists of 72 distinct pitch-class segments: the six shown in Example 3, plus those six transposed to begin on all twelve pitch-classes. A permutation class will always have twelve times as many members as its associated series class.
[5] Permutation classes partition the set of all possible pitch-class segments such that all members of each permutation class can be said to be in some way similar to each other and dissimilar from every segment not in that permutation class. There are many definitions of the word “similar” and many music-theoretical concepts that purport to model similarity measures, and I make no claims that the current one is the similarity measure between pitch-class segments. I do, however, maintain that pitch-class segments that are related by interval permutation are similar in a directly audible way. This claim depends first on the assumption that the pitch-class segments reflect an ordering that is aurally apparent: we need to be able to perceive the pitch-classes in that specific order. This is not problematic when the segments reflect temporal ordering of melodic fragments (as in Examples 1 and 2) or vertical ordering of chords (as in Example 3), but other orderings might raise questions as to their aural salience.(3) When we perceive a pitch-class segment in order, the intervals between adjacent elements are one of the most immediately perceived relationships. An aural comparison of two pitch-class segments in the same permutation class will reveal a strong similarity between them based on the fact that the intervals are the same—a similarity that will not arise between two segments of different permutation classes.
Permutation groups and interval swaps
[6] This section demonstrates the relationship between interval permutations and the “symmetric group of order n,” written Sn, which is the group of all permutations of the natural numbers from 1 to n. Specifically, the set of interval permutations on an interval series X of length n can be thought of as an action of Sn on the members of X’s series class.(4) In order to show this, some formalism is required: we can formally define an interval series as a function INTVALUE from the natural numbers 1, . . . , n to the integers mod 12 (ℤ12) such that the expression INTVALUE(s) = i means that the sth interval in the series has value i. For example, the interval series [6, 1, 3] is defined by the INTVALUE function such that INTVALUE(1) = 6, INTVALUE(2) = 1, and INTVALUE(3) = 3. If π is a permutation in Sn, then π sends every number from 1 to n to some (not necessarily distinct) number from 1 to n. The permutation π can therefore act on the INTVALUE function as such:
π ◦ INTVALUE(s) = INTVALUE(π(s))
In other words, π sends the interval that originally occupied the sth position to the π(s)th position. Note that π does not act on the intervals themselves, but rather on the positions of the intervals. For example, the permutation that turns the interval series [6, 1, 3] into [1, 3, 6] can be defined such that π(1) = 3 (meaning that the first interval becomes the third interval), π(2) = 1 (the second interval becomes the first), and π(3) = 2 (the third interval becomes the second). With this action, any permutation in Sn will send an interval series to some other series within the same series class. Furthermore, for any two interval series X and Y that are in the same series class, there exists at least one permutation in Sn that will map X to Y.(5) This group action is therefore equivalent to interval permutations on a given series class.
Example 4. Any interval permutation can be written as the product of swaps or adjacent swaps
(click to enlarge)
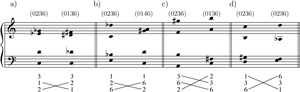
[7] Demonstrating that interval permutations are equivalent to an action of Sn allows us to import results from group theory. Some of these results are obvious, such as transitivity (if A is a permutation of B and B is a permutation of C then A is a permutation of C) or the existence of an identity permutation (A is always a permutation of A), but some are more revealing: for example, any permutation can be written as a product of interval swaps, which are permutations that swap the positions of two intervals (Dummit and Foote 2003, 107).(6) Example 4 illustrates this: the permutation in Example 4a sends the series [7, 4, 5, 9] to [9, 4, 7, 5], which Example 4b shows is equivalent to swapping the first and fourth intervals and then swapping the third and fourth intervals. Example 4c shows a different way of dividing this permutation into two swaps. Example 4d shows that this permutation can also be written as a product of adjacent interval swaps, i.e., swaps of intervals that occur next to each other in the interval series. Any interval permutation can be written as a product of adjacent swaps.
Example 5. Bartók, String Quartet No. 3, measures 1–4 (reduction): the first violin’s melody moves against a held tetrachord, effecting several adjacent interval swaps
(click to enlarge and hear the audio)
[8] Adjacent interval swaps are interesting in a musical sense because they can result from motion of a single pitch-class from one segment to the next. In Example 4d, each successive chord retains four pitch-classes from the previous chord while a single pitch-class moves. Example 5 shows this process in the opening passage from Bartók’s String Quartet no. 3: in this passage, the cello, viola, and second violin hold a chromatic tetrachord throughout the first violin’s melody. The held tetrachord has interval series [1, 2, 11] (from lowest to highest notes), but the first violin’s melody lies in between the top two notes of this tetrachord, dividing the interval of 11 into two intervals.(7) The first violin’s first two notes,
Reversals, rotations, and circular interval series
Example 6. A reversal and two rotations of a pitch-class segment. Reversals always preserve set-class membership, but rotations in general do not
(click to enlarge)
[9] In addition to swaps and adjacent swaps, there are two other types of permutation that are of interest: reversals and rotations. A reversal is a permutation that simply reverses the order of the intervals of a series. In the formal terms defined above, a permutation π is a reversal if π(s) = −s mod n for all s from 1 to n, where n is the length of the interval string. Example 6a shows the pitch-class segment (C, E,
Example 7. Rotations of a circular interval series preserve set-class membership
(click to enlarge)
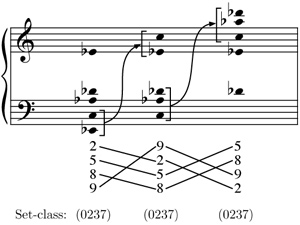
[10] A rotation preserves the ordering of an interval series but shifts the intervals cyclically. In other words, π is a rotation if π(s) = s + k mod n, where k is any integer. For example, there are four rotations of the interval series [4, 2, 3, 1]: itself, [2, 3, 1, 4], [3, 1, 4, 2], and [1, 4, 2, 3], the last two of which are shown in Examples 6c and 6d. Unlike reversals, rotations generally do not preserve set-class membership; the pitch-class segments in Examples 6a, 6c, and 6d are members of (02368), (01468), and (01368) respectively. There is a special type of interval series, however, for which rotations will always produce a member of the same set- class: those whose intervals sum to zero mod 12, which I will call circular interval series. Circular interval series always describe pitch-class segments whose first and last notes are the same, and so rotating the series can produce the same pitch-class set in a different order, as shown in Example 7. In this example, the first interval series [9, 8, 5, 2] is circular because 9 + 8 + 5 + 2 = 0 mod 12. This interval series is rotated by one position to obtain the second series [8, 5, 2, 9], and as the pitch realization shows, the lowest two pitch-classes are thrown up to the top of the chord. The two pitch-class segments are different because the ordering has changed, but they both represent the same unordered pitch-class set.(9) The same relationship exists between the second and third interval series in Example 7, and all three pitch-class sets are the same member of set-class (0237). Of course, the specific transposition level of the pitch-class segments is not given by the interval series, and so it is not always the case that rotations of a series will produce the same exact pitch-class set. However, rotations of a circular series will always produce a transposition of the original pitch-class set; in the specific case of the interval series [9, 8, 5, 2] shown in Example 7, all rotations will produce an I-form of set-class (0237) (i.e., a form related by inversion to the prime form of this set-class).
Transposition and inversion
Example 8. The inversion (b) of the interval series in (a) produces an inversion of the pitch-class segment
(click to enlarge)
[11] Transposition does not affect interval structure, as an interval series remains the same if its pitch-class segment is transposed. If the segment is inverted, however, the intervals will also become inverted. This applies no matter what the axis of (pitch-class) inversion is, just as long as the same axis is applied to all pitch-classes. Example 8a shows pitch-class segment (B,
Relation to previous literature
[12] The idea of describing an ordered set of pitch-classes by listing the intervals between adjacent members goes back at least to Richard Chrisman’s “successive interval-arrays” (1971), which were intended as a classification system for what we now call set-classes (Chrisman’s article pre-dates Forte’s The Structure of Atonal Music [1973b]; he later relates his theory to Forte’s in Chrisman 1977). Successive interval arrays are essentially the same as interval series, but the pitch-class segments they describe are always in ascending order within the span of an octave (like a scale), and always begin and end on the same pitch-class. The successive interval-arrays therefore always represent circular interval series. The Romanian composer and theorist Anatol Vieru, who developed a theory of “modes” (pitch-class sets) independently of Forte and his North American colleagues, organizes them based on the interval successions that arise when the pitch-classes are arranged as a scale, resulting in a classification scheme very similar to Chrisman’s (Vieru 1993 and 1985; see also Nolan 2002, 294). While Chrisman does discuss “cyclical permutations” (= rotations) of the successive interval-arrays (which will always produce a transposition of the original pitch-class set), neither he nor Vieru discusses more general permutations that might produce members of different set-classes.
[13] Roeder 1987 contains a more extensive study of the properties of interval series, with a focus on representing them geometrically. Roeder, who actually uses the term “interval series,” constructs “ordered interval spaces,” which are n-dimensional toroidal graphs whose points represent interval series. (For example, the interval series [6, 1, 3], representing a four-element pitch-class segment, is represented by the point (6, 1, 3) in a three-dimensional torus.) These graphs reveal certain relationships among interval series, such as a shared interval in the same position or the presence of two adjacent intervals that sum to the same value. Roeder also constructs a metric for measuring “distances” between pitch-class segments based on their interval series, which provides an easy way to measure intervallic similarity (383–84).(11) Certain permutations, such as reversals or rotations, are visible on Roeder’s graphs (through reflection about a linear axis), but more general permutations are not easily represented in Roeder’s geometrical spaces. Other authors, especially Morris (1995a) and Väisälä (1999), have discussed interval series as they relate to pitch (as opposed to pitch-class) structure. Morris’s PCINT is essentially an interval series, and he discusses the effects of certain pitch operations (such as Bernard’s “infoldings” and “unfoldings” [1987]) on PCINT and its pitch-interval counterpart INT.(12)
[14] With one exception, discussions of structures similar or identical to the notion of interval series do not consider the effects of permuting their component intervals. The lone study to deal in depth with the concept of interval permutations is Alan Chapman’s dissertation (1978), which introduces the concept of “VP [for Voice Pair] interval set”—his term for interval series. The VP interval set can be “prolonged” through expression in various permutations, such as “exchanges” (= adjacent swaps), “circular permutation” (= rotations) and “reversals.” Chapman deals exclusively with tetrachords presented as four-voiced chords, and the VP interval sets always represent the three intervals in ascending order (bass/tenor, tenor/alto, alto/soprano). As a result, all of his permutations are rotations or reversals, or a combination of the two.
Example 9. Based on Example 3.12 from Chapman 1978, 86. Permutations of a three-member interval series can express as many as three different set-classes. Interval series related by reversal are bracketed, and will always express the same set-class
(click to enlarge)
[15] One of the most interesting lines of inquiry taken in Chapman’s dissertation is an investigation of how different set-classes are related by interval permutation. Chapman notes that a three-member interval series can, when permuted, express as many as three different set-classes, the group of which he calls a “VP triple.” Example 9 adapts one of Chapman’s examples, which shows that the interval series [5, 4, 1] can be permuted to express set-classes (0237), (0137), and (0157). Three is the maximum number of different set-classes that a three-member series can express in permutation: of the six possible permutations of the series, three pairs will be related by reversal and therefore will express the same set-class, as previously demonstrated (these reversal pairs are bracketed in Example 9). Of course, many interval series cannot be permuted to express three different set-classes; in fact, as Chapman shows, only 34 of the 286 three-member interval series can be permuted to express three different tetrachordal set-classes (90). Chapman’s Chapter 3 categorizes these 286 series in terms of their various possibilities of set-class expression, demonstrating how the study of interval series relates to the study of pitch-class sets. Chapman’s categorization is somewhat unwieldy given the large number of possible interval series, and this is probably why this section was omitted from his Journal of Music Theory article based on his dissertation (Chapman 1981). It is also perhaps why the study of set-class relationships based on interval permutation did not take hold in the music theory community. Yet I believe that this aspect is one of the most promising in the study of interval permutations, and the following section represents an attempt to revitalize this idea by simplifying Chapman’s categorization and expanding on his preliminary investigation of the various ways in which different set-classes can be related by interval permutation.
Interval Permutations and Set-Class Relations
[16] One source that was noticeably absent from my discussion above is Forte’s “basic interval patterns” (BIPs), defined and discussed in Forte 1973a. The reason for its omission is that the BIPs are fundamentally different from interval series: BIPs are unordered collections of interval classes. Nevertheless, one of Forte’s goals is to relate different set-classes based on their intervallic properties, which is also the goal of the current section. My approach will proceed in the opposite direction from Forte’s: Forte essentially asks, “given a set-class, what are the different configurations of intervals that can express this set-class,” while I will ask, “given an interval series, what are the different set-classes that are expressed by permutations of this interval series?” In the interest of space, the following discussion will be restricted to tetrachordal set-classes, with the understanding that the methodology employed may easily be extended to apply to set-classes of any cardinality.
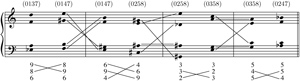
Example 10. All 48 possible three-member interval series for set-class (0236)
(click to enlarge)
[17] To answer Forte’s question: For any tetrachordal set-class, there can be as many as 48 interval series of length three that express a member of that set-class.(13) Example 10 shows the 48 different three-member interval series that express set-class (0236). The top line gives the 24 different orderings of the prime form {C, D,
Example 11. a) Derivation of the four interval series [2, 1, 3], [1, 3, 6], [3, 6, 2], and [6, 2, 1] from the single circular interval series [2, 1, 3, 6]; b) The circular interval series [2, 1, 3, 6] plotted on a circle
(click to enlarge)
Example 12. The six circular interval series associated with set-class (0236) express six different orderings of the pitch-class set {C, D,
(click to enlarge)
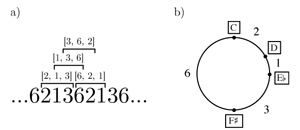
[18] We can achieve a further reduction by dividing the 24 prime-form interval series into six groups of four. Consider the four interval series [2, 1, 3], [1, 3, 6], [3, 6, 2], and [6, 2, 1], which correspond to the first chords of each “measure” in Example 10. These four series are almost rotations of one another, but not quite; in fact, they are all derived from the same interval series of length four. That series is the circular interval series [2, 1, 3, 6], and all four of the interval series mentioned above can be obtained by taking the first three intervals of some rotation of this circular interval series. Example 11 shows how this derivation works: Example 11a shows that if the intervals 2,1,3, and 6 are listed and repeated, then any three consecutive intervals will produce one of the four three-interval series in question, while Example 11b plots this circular interval series on a circle such that any three consecutive clockwise intervals will produce one of these four three-interval series.
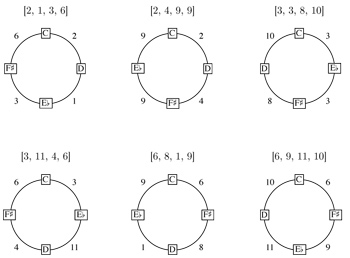
[19] All 24 of the prime-form interval series of set-class (0236) shown in Example 10 can be derived in this way from one of the following six circular interval series:
[2, 1, 3, 6], [2, 4, 9, 9], [3, 3, 8, 10], [3, 11, 4, 6], [6, 8, 1, 9], and [6, 9, 11, 10]
Each of these circular interval series is associated with a specific ordering of the pitch-class set {C, D,
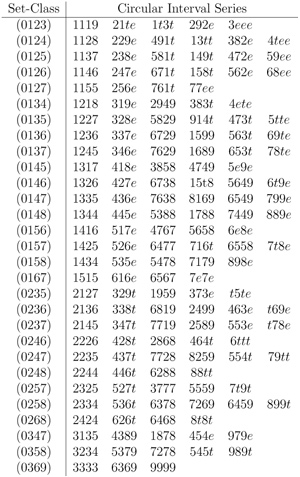
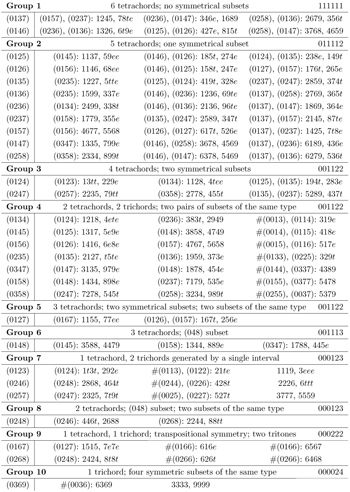
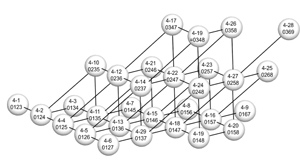
Table 1. The 29 tetrachordal set-classes and their associated circular interval series
(click to enlarge)
[20] In each of the four “measures” of Example 10 (separated by double bars), there is exactly one series derived from each of these circular series. The total number of interval series for set-class (0236) has now been reduced from 48 to six such that each of the other 42 series is permutationally related to one of these six. Using this same method, we can find the circular interval series for every tetrachordal set-class. Table 1 shows the circular interval series associated with each of the 29 tetrachordal set-classes. To save space, the circular interval series in this table are written without brackets or commas and with the letters t and e standing for intervals 10 and 11. Each of these circular interval series can be rotated or reversed without changing its set-class association. Notice that the 15 symmetrical set-classes all have fewer than six circular interval series associated with them, while the 14 non-symmetrical set-classes all have six. The relationship of interval series to symmetry will be explored in detail in a later section.
Relationships Among Set-Classes
[21] Each four-interval circular series can be permuted to express more than one set-class. While there are up to 24 distinct permutations of each four-interval series, we know that reversals and rotations will not alter the set-class, so we will only want to look at permutations that are not equivalent to reversal and/or rotation. In fact, rotational and reversal equivalence partition the 24 permutations into only three equivalence classes—in other words, there exist three permutations that are not rotations or reversals of each other such that every other permutation is a rotation and/or reversal of one of these three.(14) This means that every one of these circular interval series can be permuted to express only three (or fewer) set-classes.
[22] Consider the circular interval series [2, 1, 3, 6]. We saw in the previous section that this series is associated with set-class (0236). Two permutations of this series are [1, 2, 3, 6] and [1, 3, 2, 6]—no two of these three series are related by rotation or reversal, and every other permutation of [2, 1, 3, 6] can be obtained by reversals and/or rotations of one of these three. Reading from Table 1, we see that the series [1, 2, 3, 6] expresses set-class (0136) and the series [1, 3, 2, 6] expresses (0146). In other words, set-classes (0236), (0136), and (0146) are related via permutations of the circular interval series [2, 1, 3, 6].
Example 13. Interval permutations on set-class (0236) produce members of set-classes (0136), (0146), and (0236)
(click to enlarge)
[23] This means that a pitch-class segment in set-class (0236) that instances the interval series [2, 1, 3, 6] can progress to a member of (0136) or (0146) via interval permutation. (By “instances the interval series [2, 1, 3, 6]” I mean that this segment’s interval series, which will have length three, is derived from the four-interval circular series [2, 1, 3, 6] in the manner of Example 11.) Furthermore, this means that any interval permutation on this pitch-class segment will result in a member of (0136), (0236), or (0146). Example 13 gives some examples of these permutations: Example 13a shows an adjacent interval swap that takes a member of (0236) to a member of (0136); Example 13b shows an adjacent interval swap that takes a member of (0236) to a member of (0146); Example 13c shows a rotation that takes a member of (0236) to a member of (0136); and Example 13d shows a reversal that takes a member of (0236) to a different member of (0236).
Table 2. The number of set-classes an interval series can express via permutation depends on how many distinct intervals it contains
(click to enlarge)
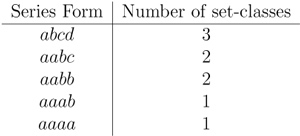
[24] Many four-interval series express even fewer than three set-classes. The number of set-classes an interval series expresses depends on how many of its intervals are the same. If all four intervals are different (i.e., the series is of the form abcd), then it will have 24 distinct permutations, and so will express three different set-classes (as was the case with [2, 1, 3, 6] above). If two of the intervals are the same (aabc), there are only 12 distinct permutations, so this type of interval series will only express two different set-classes. For example, the series [3, 3, 8, 10] expresses (0236) in that order and expresses (0134) in the permutation [3, 8, 3, 10]. Every other permutation of this series is related to one of these two via rotation and/or reversal, so no other set-classes are obtainable by permutation. The same holds for series of the form aabb; for example, [1, 1, 5, 5] expresses (0127) and [1, 5, 1, 5] expresses (0167). Series of the form aaab or aaaa can only express one set-class because every permutation is equivalent to a rotation or a reversal of this series; an example of the former is [5, 5, 5, 9], which expresses set-class (0257), and an example of the latter is [3, 3, 3, 3], which expresses set-class (0369). These relationships are summarized in Table 2.
[25] Since a set-class can have up to six four-interval series associated with it, and each of those series can be permuted to express as many as two other set-classes, then it would seem that each set-class could be related via interval permutation to as many as 12 other set-classes. Actually, the maximum number of related set-classes is only six. As seen in the previous section, when all intervals in a series are inverted, the resultant pitch-class segment is in the same set-class as the original. Two interval series that are inversionally related will therefore express the same three (or fewer) set-classes in their various permutations. For example, we saw above that the interval series [2, 1, 3, 6] expresses set-classes (0236), (0136), and (0146) via permutation; the interval series [10, 6, 9, 11], which is a retrograde inversion (plus rotation) of this series, also express these same three set-classes (this can be verified in Table 1). The six four-interval series associated with a particular set-class will group into three inversionally-related pairs, and each of these three pairs will be able to express up to two other set-classes. A set-class can therefore be related to up to six other set-classes by permutation of its interval series.
Example 14. Set-class (0137) is related by permutation to six other set-classes
(click to enlarge)
Example 15. Set-class (0148) is related by permutation to three other set-classes
(click to enlarge)
Table 3. The 29 set-classes and their permutational relations
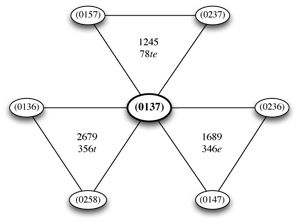
(click to enlarge)
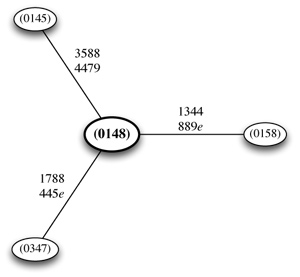
[26] It is rarely the case that a set-class is in fact related to six other set-classes, however. For this to occur, all six of its associated four-interval series would have to have four distinct intervals (see Table 2). In other words, this set-class must not have two instances of any single interval—this means that its interval vector must consist of all 1s and/or 0s. The only tetrachordal set-classes that have this property are (0137) and (0146), the two “all-interval tetrachords.” Example 14 graphically shows the all-interval tetrachord (0137) and its six related set-classes. The interval series that relate each group of three set-classes are shown within the triangles—these interval series are listed with their intervals in increasing order rather than in any specific order, since any ordering will result in a member of one of the three indicated set-classes. These interval series are grouped into inversionally-related pairs, as discussed above. Because (0137) is an all-interval set-class, all six of these interval series are of the form abcd. The set-class (0148), on the other hand, is associated with only three other set-classes, because all of its interval sets are of the form aabc, as shown graphically in Example 15.
[27] Table 3 lists all of the permutation relationships among tetrachordal set-classes. The left column lists the 29 tetrachordal set-classes, and each of the three columns on the right lists set-classes that share a circular interval series with the set-class on the left, as well as the two inversionally-related interval series that relate that particular group of set-classes.(15) For example, set-class (0146) appears in the left column of the second row; the second column shows that set-classes (0236) and (0136) are related to (0146) by permutation of the interval series [1, 3, 2, 6] and [6, 10, 9, 11] (which are abbreviated as 1326 and
[28] Table 3 is organized based on how many other set-classes a given set-class is related to from most (six) to fewest (one). This organization divides the 29 tetrachordal set-classes into ten groups, as shown in the table. The first group contains those set-classes that are related to the maximum six other set-classes, which are precisely the two all-interval tetrachord classes (0137) and (0146), as discussed above. The second group contains set-classes that are related to five other set-classes; these are all non-symmetrical set-classes that contain exactly one symmetrical trichord subset. For example, both (0125) and (0126) contain the symmetrical subset (012), (0135) contains (135), etc. Because of this symmetrical subset, these set-classes will contain two instances of one interval (and its complement); for example, (0125) and (0126) contain two instances of interval 1 (and 11), and (0135) contains two instances of interval 2 (and 10). Because this is the only symmetrical subset, no other interval will appear twice. Therefore, two of the six interval sets associated with each of these set-classes will be of the form aabc, and these two will be inversions of each other. This pair of interval sets will therefore relate to only one other set-class (see Table 2), while the other two pairs will relate to two.
[29] There is an interesting relationship between the number of related set-classes and interval vectors. Of course, the all-interval tetrachords, which compose Group 1 in Table 3, both have interval vector <111111>. The set-classes in Group 2 do not all have the same interval vector, but their interval vectors are all very similar: they all have one 0, four 1s, and one 2. For example, (0125) has interval vector <211110> and (0136) has interval vector <112011>. All of the groups in Table 3 comprise set-classes whose interval vectors are related in this way. These interval vector entries are listed on the right side of the heading for each group in Table 3 in ascending order. The interval vector types are not necessarily unique to one specific group: for example, Groups 3, 4, and 5 all have the interval vectors with two 0s, two 1s, and two 2s. This is because this type of interval vector is achieved by three different types of set-classes: set-classes that have two different symmetrical trichord subsets, set-classes that have two pairs of trichord subsets of the same type, and set-classes that have two symmetrical subsets and two subsets of the same type.
Example 16. Some interval permutations on tetrachords produce trichords with one note doubled
(click to enlarge)
[30] The set-classes in Groups 3 and 4 are all related to four other set-classes, but in Group 4, two of those four are trichords rather than tetrachords. A four-interval circular series can produce a trichord when it is composed of two pairs of complementary intervals; i.e., if it is of the form [a, b, −a, −b]. Consider Example 16: the interval series [3, 11, 9] (derived from the circular series [1, 3, 11, 9]) expresses set-class (0134), on the left of the example, while its permutation [11, 3, 9] expresses the trichord set-class (013), in the middle of the example. This is because intervals 3 and 9 are complements (mod 12), so when they are adjacent they produce a doubled note. In this case, the A is doubled, and so we get an instance of the multiset-class (0013). The same logic applies to the permutation [3, 9, 11], on the right of the example, which expresses multiset-class (0114). Trichord multiset-classes are preceded by the symbol “#” in Table 3.(16)
[31] Groups 6, 7, and 8 contain set-classes in which one interval appears three times. The set-classes in Group 7 are generated by a single interval—for example, (0123) is generated by interval 1—and so they all contain two interval series of the form aaab, which will not express any other set-class (as demonstrated in Table 2). Groups 6 and 8, both of which consist of only one set-class, contain set-classes that have a (048) subset. These set-classes will contain three instances of interval class 4, but these three will never appear in the same interval series (since they sum to 0 mod 12, the fourth interval would have to be 0 to make it circular, which would express a trichord rather than a tetrachord). However, every one of their circular interval series will contain two instances of interval 4 (or 8), and hence will be of the form aabc, which limits the total number of related set-classes to three. Table 3 shows that Group 8’s set-class—(0248)—is related to only two other set-classes because it contains two (026) subsets.
[32] Group 9 contains the two tetrachord classes that are transpositionally symmetrical, i.e., those that are made up of two disjoint tritones. Because of the two tritones, there will be two different interval series that express the same set-classes: for example, the interval series [1, 6, 6, 11] and [5, 6, 6, 7] both express (0167) and the multiset-class (0166), despite the fact that these two interval series are not related by inversion. Group 10, of course, contains only set-class (0369), which is the most symmetrical, and therefore least intervallically diverse, of the tetrachord classes. There is a loose relationship between these ten groups of set-classes and symmetry; for the most part, the higher the group number, the greater the level of symmetry. This is certainly true at the extremes: Groups 1 through 3 contain all non-symmetrical set-classes, with the number of symmetrical subsets increasing with each subsequent group, and Groups 9 and 10 contain the most symmetrical set-classes. However, this is less true in the middle groups: Group 6 contains (0148) which is neither inversionally nor transpositionally symmetrical, while Groups 4 and 5 contain all inversionally symmetrical set-classes. It is always true, however, that members of the same group have the same level of symmetry.
Paths Among Set-Classes
Example 17. A progression through different set-classes that alternates retaining interval content and pitch-class content
(click to enlarge)
[33] The relationships shown in Table 3 permit progressions like that shown in Example 17. This example shows a chord progression that alternately permutes the intervals and revoices the pitch-classes. The first chord is a (0137) tetrachord that instances the interval series [6, 8, 9], which progresses to an (0147) tetrachord via an adjacent interval swap. This (0147) tetrachord is shown as the pitch-class segment (F, B,
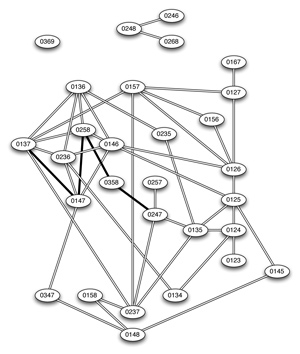
[34] What if we were to continue the progression in Example 17 until we could not proceed to a set-class that we had not yet encountered? Would we be able to cycle through all 29 tetrachordal set-classes? The answer to that question is almost. In fact, we can construct a progression that hits all but four of the tetrachord classes. These four outliers are (0369), (0246), (0248), and (0268). Table 3 shows that (0369) is not related by permutation to any other tetrachord class, and that (0246), (0248), and (0268) are related only to each other.(17) Therefore, it is impossible to progress to a member of (0369) via an interval permutation from any other set-class, and it is impossible to progress to (0246), (0248), or (0268) from any set-class that is not one of those three. The 25 other tetrachord classes can all proceed to each other via interval permutations and/or revoicings in the manner of Example 17.
Example 18. Diagram showing tetrachordal set-classes that can be related by interval permutation
(click to enlarge)
[35] There can be many different paths between any two set-classes. For example, Example 17 shows that (0137) can progress to (0358) via (0147) and (0258). However, looking back at Table 3, we see that (0137) can bypass (0147) and progress directly to (0258) and then (0358). In fact there are many other paths between (0137) and (0358); for example, (0137) – (0136) – (0235) – (0135) – (0247) – (0358). Example 18 is a graphic version of Table 3 that visually represents these types of paths. This figure contains one node for each tetrachordal set-class, and set-classes that can be related by interval permutation are connected with double lines. Notice that (0369) is not connected to any other node, and (0246), (0248), and (0268) are separated from the rest of the nodes, as discussed above. The progression from Example 17 is traced in dark lines on this diagram: we begin with (0137) on the west (left) side, then proceed southeast to (0147), then north to (0258), then southeast to (0358) and southeast again to (0247).
Interval Permutation Spaces
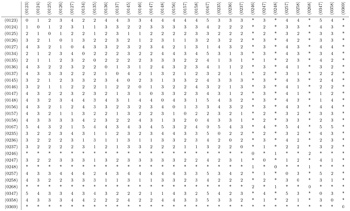
Table 4. Distances between tetrachordal set-classes based on the space of Example 18. Undefined distances are marked with an asterisk
(click to enlarge)
Example 19. Straus’s “parsimonious voice-leading space for tetrachord classes.” (Reproduced from Straus 2005a, 56.)
(click to enlarge)
[36] Example 18 defines a compositional space on the tetrachordal set-classes.(18) Set-classes that are connected in this space are related by interval permutation—meaning that there exists a pitch-class segment in one that is related by interval permutation to some pitch-class segment in the other. Based on this space, we can define a distance measure between two set-classes S and T as the smallest number of “moves” in the space that can take us from S to T. For example, the distance from (0137) to (0358) is 2, because (0137) is connected to (0258) which is connected to (0358), and there is no shorter path between these two set-classes. This distance function satisfies the criteria of a metric space: the distance between S and T is always nonnegative and is zero if and only if S = T, it is reflexive (DIST(S, T) = DIST(T, S)), and the triangle inequality is satisfied: DIST(S, T) + DIST(T, R) ≥ DIST(S, R).(19) Table 4 gives the distances between any pair of tetrachordal set-classes based on the space in Example 18.(20) These distances reflect how intervallically similar two set-classes are, with smaller distances corresponding to a greater level of intervallic similarity.
[37] This space offers an alternative to the more typical voice leading-based spaces, such as those presented in Straus 2005a and Callender, Quinn, and Tymoczko 2008 (hereafter CQT).(21) Straus’s tetrachord space, reproduced as Example 19, relates tetrachordal classes that are almost transpositionally related—in Straus’s terms, that are related by “near-transposition.” Set-classes that have this relationship are related by parsimonious voice leading, i.e., there exists a parsimonious move (one voice moving a semitone while the others stay) that relates the two set-classes. CQT’s space is a continuous version of Straus’s space; while CQT derive their space by folding ℝn in various ways, the result is very similar to Straus’s.(22) Although both of these spaces are based on voice-leading proximity, and hence are fundamentally different from the space in Example 18, it is useful to compare the different spaces to see what, if any, similarities do exist. One similarity that is immediately apparent is that the set-classes (0123), (0124), (0125). (0126), and (0127) form a line in both spaces. In addition, the two set-classes that only connect to one other set-class in Example 18—(0123) and (0167)—have this same property in Straus’s space. In general, however, the voice-leading spaces are quite different from the interval permutation space, and model different compositional practices.
Analytical Examples: Schoenberg’s Op. 15 Song Cycle
Song No. 1, measures 1–8
Example 20. Schoenberg, The Book of the Hanging Gardens, Op. 15, No. 1, measures 1–8, piano
(click to enlarge and hear the audio)
[38] This final section applies the theory of interval permutations in brief analyses of selections from Schoenberg’s Book of the Hanging Gardens song cycle, op. 15. These analyses are not intended to serve as validation of this theory, but rather they aim to demonstrate various ways in which interval permutations might be applied in conjunction with traditional set-based analysis to the post-tonal repertoire. Example 20 shows the opening piano part of the first song of the cycle. This passage opens with the melodic pitch-class segment (
[39] Let us set aside the second phrase for now and focus on the other three. The first five notes form an important motive that recurs throughout the song in both the voice and piano parts. Allen Forte (1992, 288–90) points out that this motive’s set-class, (0124), dominates the entire phrase, as any four consecutive notes in the first two measures will constitute a form of this tetrachord class. (The second and third of these are formed by the interval series [11, 2, 2] and its reversal [2, 2, 11], shown under the staff in Example 20.) The third phrase, in contrast, expresses set-class (0135). Looking back at Example 18 or Table 3 will tell us that (0124) and (0135) are related by permutation of the circular interval series [2, 8, 3, 11], and Schoenberg exploits this relationship in the melodic intervals of these two phrases. Even though Forte considers these two phrases to be separate motives, we can see that they are connected in their interval structure, which unifies their sound despite the difference in set-class. After this third phrase, the held E is followed by a repeat of the opening motive,
Example 21. Three examples of pitch-class set {
(click to enlarge)
[40] The second phrase begins as a repeat of the first but gets interrupted after three notes by a high
[41] Examining the interval structure of the opening measures to the op. 15 song cycle reveals connections beyond those of set-class analysis alone. We saw in Example 20 that the (0124) sets in the first and fourth phrases and the (0135) set in the third phrase are all related by interval permutation. The second phrase, on the other hand, is the anomaly with its unrelated interval series. This phrase dismantles the first phrase by abruptly interrupting what at first seems to be a repeat: the high
Song No. 11, measures 1–4
Example 22. Song No. 11, measures 1–4
(click to enlarge and hear the audio)
Example 23. Song No. 11, measures 22–24, voice (lower staff) and piano RH
(click to enlarge)
[42] Example 22 shows the first four measures of Song no. 11. The opening motive in the piano’s right hand is a linear statement of the pitch-class segment (
Example 24. Different interval series of Lewin’s X and N chords in measures 3–4 of Song No. 11
(click to enlarge)
[43] David Lewin (1973) highlights two chords in measures 3–4, which are reproduced in Example 24a. Lewin calls these two tetrachords “X” and “N” respectively; these specific chords reoccur throughout the song, often with the same voicings. The X tetrachord, a member of (0125), has interval series [10, 5, 8] (reading upwards). This interval series can also express, via permutation, set-classes (0126) and (0146). The N tetrachord is a member of (0126), but its interval series [10, 6, 7] is not a permutation of the first chord’s. Lewin points out that both chords consist of a (012) trichord paired with pitch-class F; this (012) subset is transposed down a semitone from X to N, from {C,
Song No. 14
Example 25. Song No. 14, measure 1, piano
(click to enlarge)
[44] I will conclude this study as I began it, with some analytical observations on Song no. 14 from The Book of the Hanging Gardens. Example 25 shows the first piano gesture of this song, previously seen in Examples 1 and 2. This gesture has interval series [11, 10, 6, 7, 11], but as the example shows, the first four intervals of this series, namely [11, 10, 6, 7], form an important subseries. This shorter interval series is associated with what I called “rhythmic motive x” in Example 1, while the remaining interval 11 is associated with “rhythmic motive y.” Both of these rhythmic motives recur often throughout this short song, and rhythmic motive y—quarter note–eighth note—always pairs with the pitch motive of a descending semitone. In the case of this opening piano gesture, motive y’s descending semitone produces pitch-class A, which was already heard within rhythmic motive x earlier that measure. So the total pitch content of these six notes is a pentachord, specifically a member of set-class (01236). The normal form of this pentachord is shown on the lower staff of Example 25. The four-interval series that expresses this pentachord in measure 1, namely [11, 10, 6, 7], has 24 distinct permutations, which can express twelve different set-classes (accounting for the fact that reversals express the same set-class). In fact, because the subset {11, 6, 7} sums to zero mod 12, any permutation in which these three intervals are concurrent (i.e., whenever interval 10 is first or last) will contain a duplicate pitch-class, and therefore will express a tetrachord rather than a pentachord. This applies to twelve of the 24 permutations of this interval series, and so six of the twelve permutationally related set-classes will be tetrachords. Specifically, this interval series can be permuted to express tetrachordal set-classes (0126), (0127), (0136), (0137), (0146), and (0157), and pentachordal set-classes (01236), (01237), (01257), (01268), (01368), and (02368).
Example 26. Song No. 14, measures 2–3, voice
(click to enlarge)
Example 27. Song No. 14, measure 4, voice
(click to enlarge)
Example 28. Song No. 14, measure 11, piano
(click to enlarge)
[45] As we saw earlier, a permutation of this interval series is immediately presented in the vocal phrase in measure 2, shown in Example 26. This phrase contains rhythmic motives x and y in reverse order, beginning with y’s descending semitone and ending with x, the latter of which instances the interval series [11, 7, 10, 6], as shown bracketed in the example. This interval series is a permutation of the interval series in measure 1 and expresses set-class (01268). The “extra” two intervals that precede this series are 11 and 7—the same two that begin the series proper—and the interval 11 accompanies motive y. In contrast to measure 1, these extra intervals add one new pitch-class (D) to x’s pentachord, making the entire phrase a member of the hexachordal set-class (012678), as shown in the lower staff of Example 26.
[46] Example 27 shows a different permutation of our interval series that occurs in the vocal line of measure 4. In this measure, the interval series expresses the tetrachordal set-class (0127) with the
[47] The final measure of this song contains another permutation of this interval series, namely [11, 10, 7, 6], as shown in Example 28. This example, like Examples 25 and 26, expands this interval series by affixing repetitions of some of the component intervals after the interval series is complete. In this case, intervals 6 and 11 reappear at the end. This last interval 11 is created by a final iteration of motive y. The first half of this measure is related to the piano’s opening gesture (Example 25), which instanced rhythmic motive x with interval series [11, 10, 6, 7]. This series is related to the current series by adjacent interval swap, and the pitch-class segment (B,
[48] The first five pitch-classes in measure 11 create a member of set-class (01237), which is a new set-class that is arrived at via interval permutation from our previous examples. The statement of motive y at the end adds the pitch-class D, which makes the total pitch-class content of this measure a member of set-class (012367). In these four examples from Song no. 14, we have seen members of set-classes (01236), (01268), (012678), (0127), (01237), and (012367) all created from various combinations of intervals 6, 7, 10, and 11. These intervals interact with rhythmic and pitch motives from the first notes of the song through the final measure. The analysis of this song through the lens of interval permutations demonstrates Schoenberg’s ability to present highly varied musical material under a single unifying principle.
Conclusion
[49] The concept of interval permutations is at its core a remarkably simple idea: rearrange the intervals of an ordered set of pitch-classes to get a different ordered set of pitch-classes. Perhaps this simplicity is to blame for why music theorists did not pick up on Alan Chapman’s exposition of the idea in 1978, despite the fact that the concept of interval series remained in common use through the work of Chrisman, Regener, Morris, Roeder, and others, as discussed earlier. Yet, as evidenced through the brief discussions above of a few Schoenberg songs, expanding our analytical vocabulary to include interval permutations reveals relationships that are often missed by set-class-based analysis alone. The framework’s simplicity is perhaps its most attractive feature, as it guarantees a direct connection with our perception: the basic elements are intervals and the basic operation is reordering, and so it is quite easy to perceive an aural similarity between two permutationally related segments. Furthermore, since interval permutations do not model traditional transposition and inversion operations, this similarity is fundamentally different from that between, say, two inversionally related members of (0146). This difference does not mean that the two analytical techniques are incompatible, though, and in fact interval permutations interact with set-class theory in interesting ways.
[50] These implications were explored in the middle section of this article, specifically relating to tetrachordal set-classes. This led to a taxonomy of the 29 tetrachord classes based on their intervallic properties, as shown in Table 3, as well as a spatial representation of these set-classes in Example 18 and a metric for measuring distances between two set-classes in Table 4. While the discussion focused on tetrachords, the methodology is easily generalizable to larger set-classes. The complexity increases quickly as the sets get larger, however; each circular interval series for a pentachordal set-class can be permuted to express as many as twelve different set-classes (for tetrachords, this number was three), and for hexachords each series can theoretically express as many as 60 different set-classes, though in practice several of these will be duplicates. Nevertheless, the interval permutation framework has the capability of revealing salient relationships among sets of all sizes, and I am confident that further applications of this tool will be rewarding in both the analytical and theoretical realms.
Drew F. Nobile
The University of Chicago
Department of Music
1010 East 59th Street
Chicago, IL 60637
nobile@uchicago.edu
Works Cited
Benjamin, William E. 1979. “Ideas of Order in Motivic Music.” Music Theory Spectrum 1: 23–34.
Bernard, Jonathan W. 1987. The Music of Edgard Varèse. New Haven: Yale University Press.
Boss, Jack. 2009. “The Musical Idea and the Basic Image in an Atonal Song and Recitation of Arnold Schoenberg.” Gamut 2, no. 1: 223–66.
Callender, Clifton, Ian Quinn, and Dmitri Tymoczko. 2008. “Generalized Voice-Leading Spaces.” Science 320: 346–48.
Chapman, Alan. 1978. “A Theory of Harmonic Structures for Non-Tonal Music.” PhD Diss., Yale University.
—————. 1981. “Some Intervallic Aspects of Pitch-Class Set Relations.” Journal of Music Theory 25, no. 2: 275–90.
Chrisman, Richard. 1971. “Identification and Correlation of Pitch-Sets.” Journal of Music Theory 15, nos. 1–2: 58–83.
—————. 1977. “Describing Structural Aspects of Pitch-Sets Using Successive-Interval Arrays.” Journal of Music Theory 21, no. 1: 1–28.
Clough, John. 1998. “A Rudimentary Geometric Model for Contextual Transposition and Inversion.” Journal of Music Theory 42, no. 2: 297–306.
Cohn, Richard. 1996. “Maximally Smooth Cycles, Hexatonic Systems, and the Analysis of Late-Romantic Triadic Progressions.” Music Analysis 15: 9–40.
—————. 1998. “Neo-Riemannian Operations, Parsimonious Trichords, and Their Tonnetz Representations.” Journal of Music Theory 41: 1–66.
—————. 2003. “A Tetrahedral Graph of Tetrachordal Voice-Leading Space.” Music Theory Online 9, no. 4.
Douthett, Jack, and Peter Steinbach. 1998. “Parsimonious Graphs: A Study in Parsimony, Contextual Transformations, and Modes of Limited Transposition.” Journal of Music Theory 42, no. 2: 241–63.
Dummit, David S., and Richard M. Foote. 2003. Abstract Algebra, 3rd edition. Hoboken, NJ.: Wiley.
Fiore, Thomas, and Ramon Satyendra. 2005. “Generalized Contextual Groups.” Music Theory Online 11, no. 3.
Forte, Allen. 1973a. “The Basic Interval Patterns.” Journal of Music Theory 17, no. 2: 234– 72.
—————. 1973b. The Structure of Atonal Music. New Haven: Yale University Press.
—————. 1992. “Concepts of Linearity in Schoenberg’s Atonal Music: A Study of the Opus 15 Song Cycle.” Journal of Music Theory 36, no. 2: 285–382.
Kochavi, Jonathan. 1998. “Some Structural Features of Contextually-Defined Inversion Operators.” Journal of Music Theory 42, no. 2: 307–20.
Lambert, Philip. 2000. “On Contextual Transformations.” Perspectives of New Music 38, no. 1: 45–76.
Lewin, David. 1973. “Toward the Analysis of a Schoenberg Song (Op. 15, No. XI).” Perspectives of New Music 12, nos. 1–2: 43–86.
—————. 1977. “Forte’s ‘Interval Vector,’ My ‘Interval Function,’ and Regener’s ‘Common-Note Function.’” Journal of Music Theory 21, no. 2: 194–237.
—————. 1987. Generalized Musical Intervals and Transformations. New Haven: Yale University Press.
Morris, Robert. 1987. Composition with Pitch-Classes: A Theory of Compositional Design. New Haven: Yale University Press.
—————. 1991. Class Notes for Atonal Music Theory. Lebanon, N.H.: Frog Peak Music.
—————. 1995a. “Equivalence and Similarity in Pitch and Their Interaction with PCSet Theory.” Journal of Music Theory 39, no. 2: 207–43.
—————. 1995b. “Compositional Spaces and Other Territories.” Perspectives of New Music 33: 328–58.
—————. 1998. “Voice-Leading Spaces.” Music Theory Spectrum 20: 175–208.
Nolan, Catherine. 2002. “Music Theory and Mathematics.” In The Cambridge History of Western Music Theory, ed. Thomas Christensen, 272–304. Cambridge: Cambridge University Press.
Regener, Eric. 1974. “On Allen Forte’s Theory of Chords.” Perspectives of New Music 13, no. 1: 191–212.
Robinson, Thomas. 2009. “Pitch-Class Multisets.” PhD Diss., City University of New York.
Roeder, John. 1987. “A Geometric Representation of Pitch-Class Series.” Perspectives of New Music 25, nos. 1–2: 362–409.
Straus, Joseph N. 2003. “Uniformity, Balance and Smoothness in Atonal Voice Leading.” Music Theory Spectrum 25: 305–52.
—————. 2005a. “Voice Leading in Set-Class Space.” Journal of Music Theory 49, no. 1: 45–108.
—————. 2005b. Introduction to Post-Tonal Theory, 3rd edition. Englewood Cliffs, NJ: Prentice Hall.
—————. 2011. “Contextual Inversion Spaces.” Journal of Music Theory 55, no. 1: 43–88.
Tymoczko, Dmitri. 2011. A Geometry of Music: Harmony and Counterpoint in the Extended Common Practice. New York: Oxford University Press.
Väisälä, Olli. 1999. “Concepts of Harmony and Prolongation in Schoenberg’s Op. 19/2.” Music Theory Spectrum 21, no. 2: 230–59.
Vieru, Anatol. 1985. “Modalism—a ‘Third World.’” Perspectives of New Music 24, no. 1: 62–71.
—————. 1993. The Book of Modes, 2nd edition. Bucharest: Editura Musicala.
Footnotes
1. While pitch-class segments can theoretically be ordered in any way that the analyst deems salient, for the purposes of this paper I will stick to temporal ordering for melodic lines and registral ordering (lowest to highest) for simultaneities.
Return to text
2. Set-classes will be identified by their prime forms following the conventions set out in Straus 2005b, with parentheses and no commas between successive elements.
Return to text
3. The standard “normal” and “prime” orderings are convenient for identifying features of a pitch-class set but generally do not represent an immediately perceptible ordering. See Lewin 1977 and Benjamin 1979 for discussions of ordering of pitch-class sets.
Return to text
4. Dummit and Foote’s Abstract Algebra textbook (2003) contains a basic discussion of symmetric groups in relation to group theory (29–33) as well as a detailed introduction to group actions (Chapter 4).
Return to text
5. If all of the intervals in X and Y are distinct, then there will be exactly one permutation that maps X to Y, but if there are duplicate intervals there will be more than one. Furthermore, if there are duplicate intervals there exists at least one permutation besides the identity that maps an interval series to itself. The set of all permutations that map an interval series X to itself is called the “stabilizer of X,” and this set will be a subgroup of Sn (see Dummit and Foote 2003, 52–52). For example, the interval series [1, 6, 3, 3] maps to itself under the identity permutation as well as the permutation that swaps the third and fourth intervals. These two permutations together form a subgroup of S4.
Return to text
6. The standard mathematical term for these is “transpositions,” but to avoid confusion with pitch-class transposition, I will use “swaps” instead.
Return to text
7. Chrisman (1971, 74–75) discusses such “partitionings” of intervals.
Return to text
8. Straus (2005b, Chapter 5) discusses this relationship in reference to twelve-tone series.
Return to text
9. Since the doubled note is different, these represent different pitch-class multisets even when ordering is ignored. Multisets and multiset-classes will be discussed in the following section; see also Robinson 2009.
Return to text
10. Contextual inversions are loosely defined as inversions whose axis is defined in terms of members of the set rather than a fixed point. The Neo-Riemannian LPR group, for example, is a group of contextual transformations (see especially Cohn 1996 and 1998 and Douthett and Steinbach 1998). For investigations of the mathematical properties of contextual transformations, see Clough 1998, Kochavi 1998, and Fiore and Satyendra 2005, and for more general discussions of contextual transformations, see Lambert 2000 and Straus 2011.
Return to text
11. Roeder’s metric is defined as “the absolute sum of the differences, considered as interval classes, of the intervals in each order position of X and Y respectively,” where X and Y are two interval series (1987, 383). So, for example, the difference between [6, 3, 1] and [5, 2, 4] would be 1 + 1 + 3 = 5. This idea foreshadows Straus’s “voice-leading offset” (2003), which measures how close two (unordered) pitch-class sets are to being transpositions of one another.
Return to text
12. In earlier writings, Morris uses INT to denote an ordered set of intervals of either type. See Morris 1987 and 1991.
Return to text
13. This is because there are 4! = 24 possible orderings of the four pitch-classes in both prime and inverted forms.
Return to text
14. Since reversals have order two in Sn, in S4 there are 24/2 = 12 equivalence classes based on reversal equivalence; and since rotations have order four, these 12 will be divided into 12/4 = 3 equivalence classes based on both rotation and reversal equivalence. This means that any set of four or more permutations will necessarily include a pair of permutations that are related to each other by rotation and/or reversal.
Return to text
15. The interval series are ordered based on the set-class in the left column, as they were in Table 1; for example, [1, 2, 4, 5] appears in the row of (0137) and its permutation [1, 4, 2, 5] appears in the row of (0157).
Return to text
16. In general, an interval series of length n will express a set-class of size n + 1. However, if any subseries of that series sums to 0 (mod 12), that will produce a doubled note, reducing the size of the set-class by 1. Circular series have at least one such subseries (namely the entire series), so they will express set-classes of length n at the most. This is why the four-interval series in Table 3 express tetrachords rather than pentachords. In general, a series of length n with k distinct (but not necessarily disjoint) subseries that sum to 0 (mod 12) will express a set-class of size (n − k) + 1. The multiset expressed by an interval series of length n will always contain n + 1 (not necessarily distinct) members (in other words, the pitch-class segment that this interval series expresses will have length n + 1, but some of its notes might be the same).
Return to text
17. This is because all of these set-classes contain intervals that fall entirely within a subgroup of ℤ12: (0369) contains only intervals that are multiples of 3, which are all members of the subgroup {0, 3, 6, 9}, or ℤ12/ℤ3, and (0246), (0248), and (0268) contain only even intervals, which are all members of the subgroup {0, 2, 4, 6, 8, 10}, or ℤ12/ℤ2. No combination of these intervals will sum to any interval outside the subgroup, and so permutations must remain in the subgroup. Every circular interval series of every other tetrachord class contains at least two odd intervals and at least two intervals that are not multiples of 3.
Return to text
18. For more on the general concept of compositional spaces, see Morris 1987, 1995b, and 1998.
Return to text
19. Because the space is not connected, however, this is not a well-defined metric space, since there exist S and T such that DIST(S, T) is undefined. The subspace of the 25 connected set-classes is a well-defined metric space.
Return to text
20. Due to the constraints of two dimensions, the physical distances on Example 18 do not correspond at all to the distances shown in Table 4.
Return to text
21. Other examples of voice-leading spaces can be found in Morris 1998, Cohn 2003, and Tymoczko 2011.
Return to text
22. CQT’s space is difficult to visualize; an attempt is made in Figure S5, E through H, in the supporting online material to their paper. The relationship of Straus’s spaces to CQT’s is more easily seen in their respective trichord spaces; see Straus 2005a, 54, 54, and CQT 2008, 347. Tymoczko 2011, Chapter 3, expands on the spaces from CQT, but does not spend much time discussing set-class space.
Return to text
23. See also the analysis in Straus 2005b, 47–52, which also focuses on statements of (0347) throughout the song. Straus admits that his analysis is “heavily indebted” to Lewin’s (78).
Return to text
Copyright Statement
Copyright © 2013 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits: