Dissonant Harmony and “Seed-Tones”: Organicism in the Piano Music of Dane Rudhyar
Michael K. Trinastic
KEYWORDS: Dane Rudhyar, dissonant harmony, organicism, piano, ultra-modernism, interval cycles, tone, Schenkerian analysis, seed-tones, twelve-tone music, dodecaphony, dissonance, harmony, quintal harmony, sounding board, gongs, bells, space, dissonant tonic, harmonic series, overtones, undertones, “Stars,” Granites, Second Pentagram, Third Pentagram.
ABSTRACT: French-American composer Dane Rudhyar’s (1895–1985) vision of dissonance as a spiritual discipline was profoundly influential upon American ultra-modernist composers in the 1920s and ’30s. Rudhyar’s own compositions manifest his theoretical ideas, which revolve around a mystical conception of Tone as the totality of all possible musical sounds. His prose reveals several interrelated methods of creating Tone: using the piano’s sounding board as a gong, employing dissonant harmony (relating pitches by geometric relationships, which manifest as interval cycles), applying “the new sense of space” (beginning from wholeness, which requires equal divisions of the octave), and creating organic forms by basing each composition on a “seed-tone” (a dissonant tonic sonority). Rudhyar’s theoretical writings suggest two compatible methods of constructing seed-tones: building quintal sonorities (which exemplify dissonant harmony in Rudhyar’s theory) and employing “interpenetrating harmonic series.” These two methods facilitate the identification of seed-tones and their elaborations in Rudhyar’s piano music. Schenkerian-style graphs accompany detailed analyses of two of Rudhyar’s piano pieces: “Stars” and the first movement of Granites. Rudhyar’s seed-tones may suggest new analytic perspectives for other post-tonal repertoire. In addition, Rudhyar’s connection of dissonance with spirituality serves as a reminder that many early-twentieth-century pioneers in atonality and dodecaphony perceived a numinousness in this new music.
Copyright © 2014 Society for Music Theory
[1.1] The music of French-American composer Dane Rudhyar (1895–1985) has remained virtually untouched by analysis for almost a century. Even though Rudhyar’s importance in the development of American music has been increasingly acknowledged by historians in the past two decades, his compositions have still received only the most superficial attention. Some of this neglect may result from Rudhyar's musical language itself, which—because of its highly idiosyncratic, personal nature—does not readily invite analysis.(1) Indeed, Garland 1982 describes Rudhyar’s piano music as “aurally difficult” because of the “absence of tonal, harmonic relationships in the classical sense . . . combined with the strongly through-composed qualities of the pieces (37–38). Rudhyar's music lacks not only common-practice-period tonality but also formal systems such as the twelve-tone method (which Schoenberg developed during Rudhyar's most active compositional period: the 1920s). Thus Rudhyar's music presents many of the same analytical challenges posed by the free-atonal music of the Second Viennese School. However, as this essay will demonstrate, a close analysis of Rudhyar's music reveals a structural integrity all the more striking because it is belied by a highly improvisatory surface.
[1.2] Rudhyar’s own anti-formalist rhetoric further discourages analysis of his music and also had a lasting effect on the views of his fellow American “ultra-modernists,” for whom he served as a spiritual leader in the 1920s and ‘30s after his immigration from France to America in 1916. Rudhyar’s “passionate espousal of utopian modernism” deeply affected the young Ruth Crawford, according to Judith Tick, who describes him as a “messianic figure” (1997, 49). The charismatic Frenchman's “rejection of reason” had a liberating effect on Crawford’s compositional development, causing her to disdain counterpoint and to experiment with the symbolic, mystical power of the single tone (Tick 1997, 50, 72, and 83). Similarly, Carol Oja paints Rudhyar as “a high priest . . . exploring the connection of dissonance to the spirit” (1999, 129) and a foil to the other acknowledged leader of the ultra-moderns, Charles Seeger. While the latter developed a “systematic theory of ‘dissonant counterpoint,’” Rudhyar “expressed little interest in systems of any kind, preferring poetic odysseys” (Oja 1999, 130). Moreover, Oja claims, “In explaining his concept of sound, Rudhyar never resorted to technical descriptions. Doing so would have violated his campaign against formalism” (1999, 135). After observing that “the most fundamental of Rudhyar’s theories had to do with ‘tone,’ an elusive concept grounded in his utopian hopes,” Oja concludes that “‘tone,’ as manifested in Rudhyar’s own music, was achieved mainly through a buildup of sound” (1999, 141).
[1.3] Indeed, Rudhyar was fond of quoting Varese’s maxim that “Music must sound!” (1984). However, a close reading of Rudhyar’s own writings on music reveals that he is much more careful in his harmonic constructions than his anti-formalist rhetoric might suggest. In his 1928 treatise, The Rebirth of Hindu Music, Rudhyar declares:
Resonance is not born of the Harmonic Series, as usually said by Western musicians. The basis for harmony (or the science of chord formation) is not the Harmonic Series, as usually believed, but the cycles of fifths and fourths. True melodies are founded on modes . . . which are segments of the Harmonic Series; but true chords or true polyphony (two methods of creating resonance) ought to be constructed on principles resulting from various cyclic aspects of the zodiacs of sound. (1928c, 88–89, emphasis original)
Thus, Rudhyar clearly does offer some technical descriptions of his musical vision. To be sure, they are buried among poetic effusions, numerological justifications, and occult metaphors. Yet the substance of his music theory remained remarkably consistent throughout his long life. Several decades later, he was still emphasizing harmonic constructions based on fifths:
Most of my music is more or less based on series of fifths. If you listen attentively, those of you who are musicians—in ‘Stars’ for instance, and also at the end of ‘Sunburst’—you will hear constantly repeated such series of fifths. You will find it also at the end of the last movement of Syntony, ‘Apotheosis.’ The fifths of course are not always perfect fifths. . . . The chords in order to become harmonized—a dissonant kind of harmony—do not depend on tonality but on the proper spacing of dissonant centers. (Rudhyar 1972)
The above passages may raise more questions than they answer; however, they do make one thing clear: Rudhyar had an enduring interest in harmony based on series of fifths—an interest that paradoxically binds him to the Western musical tradition he claimed to be so eager to overthrow.
[1.4] Douglas Kahn makes a similar point, arguing that although Rudhyar’s thought relies upon an “Eastern” critique of the West, his philosophy actually “becomes a means through which ‘the West’ is fortified” (Kahn 2004, 118). Interpreting Rudhyar as a prophet of the liberation of sound prefiguring John Cage, Kahn concludes that Rudhyar’s loyalty to “the harmonic tradition of Western art music” is contradictory (2004, 111). Rudhyar himself recognized this paradox, explaining, “Even today when this musical substance is breaking up, when fundamental ideas begin to be questioned and various racial attitudes to music, Eastern and Western, are coming in contact, it is an almost hopeless task for any composer to try to escape from tempered scales, pianos and standardized orchestrations, to bring forward a new ‘sense of tone’” (1928b, emphasis original). Thus, although Rudhyar’s ends were genuinely revolutionary, his means were strikingly practical. Ultimately, this seeming contradiction is consistent with his mystical philosophy; Rudhyar holds the mystic’s belief that true revolution can only occur through a change in human consciousness, rather than through developments in external conditions.
[1.5] Changing the spiritual condition of the listener is the very purpose of music in Rudhyar’s vision of the new composer. Expressing a sentiment that would be anathema to Cage, Rudhyar laments the fact that “Human beings may live much of the time in a world filled with sounds, yet lose the sense of music” (1984). Whereas Cage seeks to remove the composer’s will from the act of composition, Rudhyar boldly declares that “harmonic sound as a magical force directed by the will of the evoker (no longer a composer) . . . is the central fact of the new musical philosophy” (1973b, 56). He champions music as sound not for sound's sake but in order to revitalize music as a means of human communication. “Music,” according to Rudhyar, “is to be heard, and what the tones produce in the hearer is the important thing” (1962, 184). In light of the above considerations, it is clear that while Rudhyar's anti-formalist invective about the liberation of sound may have been conspicuously influential upon his contemporaries in the 1920s, it is but merely one chapter in a lifelong philosophy of music that is as yet little understood.
[1.6] One author who has grappled with the full scope of Rudhyar's vision is Deniz Ertan; Ertan’s Dane Rudhyar: His Music, Thought, and Art (2009) is the first book-length musicological study dedicated to Rudhyar’s work. Emphasizing that “over the years his whole vision did not change direction but continued to grow and deepen, providing a body of work that is essentially consistent throughout,” Ertan argues that “because of the reciprocal relationship between his creative and speculative activities, his work in all . . . fields needs to be viewed as a whole” (2009, 2). Indeed, Rudhyar was a true Renaissance man who produced not only music, but also paintings, philosophy, astrology, poetry, and fiction. Ertan’s interdisciplinary approach helps elucidate the entirety of Rudhyar’s vision, and her book is easily the most comprehensive secondary source on his thought. However, to the music theorist seeking insight into the structure of his music, the fact that Ertan’s book dedicates more space to color plates of his paintings than to excerpts from his music is somewhat disappointing. Ertan does analyze several of Rudhyar’s compositions, a pioneering effort that is commendable in itself, given the almost total lack of scrutiny his music has received. Even in these analyses, however, Ertan’s emphasis remains on Rudhyar’s philosophy; she mostly explores the poetic and symbolic application of his philosophical ideas to his music.(2)
[1.7] In this essay, I complement Ertan’s groundbreaking exegesis of Rudhyar’s philosophy with a technical exploration of his music. The intersection of philosophy and music in Rudhyar’s output recalls Scriabin, and it is no coincidence that Rudhyar singled out the Russian composer as prophet of the music of the future. Methodologically, my analyses of Rudhyar follow in the footsteps of some of the more illuminating studies of Scriabin. In “Structure as Prism for Mystical Philosophy,” for instance, James M. Baker explains that his purpose is “not simply to trace through [Scriabin’s] music programmatic descriptions of particular concepts” but rather to show that “the work of art and the artist’s ideology are independent reflections of the artist’s intuition” (1997, 74–75). Similarly, Taruskin 1997 argues that Scriabin’s “mystic chord” is not merely symbolic or programmatic but a musical device that precipitates an experience in the listener because of its “uncanny stasis,” which results from its position “on a sort of cusp between two nonfunctional pitch collections”: the octatonic, and the whole-tone. “Because ego identification with musical process conventionally depends on functionally directed harmony, [when hearing the mystic chord] we are on the verge of not merely the intimation, or the representation, but the actual experience of ego transcendence” (344, emphasis added). Thus, Scriabin’s philosophical end of ego transcendence finds a technical means in his harmonic innovations. Likewise, if Rudhyar’s music expresses his mystical philosophy, it does so not merely by symbolizing certain concepts (in the manner of a Wagnerian Leitmotiv) but by actually causing (or at least attempting to cause) a palpable change in the spiritual condition of listeners; recall his conviction that “Music is to be heard, and what the tones produce in the hearer is the important thing, program or no program” (1962, 184).
[1.8] What Rudhyar seeks to create in the listener is an experience of Tone, a word he often capitalizes to distinguish his particular sonic ideal from the everyday meaning of the term. He defines Tone as “the quality inherent in the musical space which the human ear perceives as sound and to which the human mind, developed according to a particular culture, can respond as music” (1982, 136, emphasis original). Since Tone is a quality of musical space itself (which in Rudhyar’s somewhat nebulous conception is the entire range of possible sounds), no particular sound can create Tone in isolation; rather, Tone can only be evoked by the way in which various sounds are combined. This essay will show how Rudhyar creates Tone through four interrelated techniques:
- by employing the piano as a gong to create “living tones”;
- by using dissonant harmony to create “tone pleromas”;
- by applying “the new sense of space,” which begins from wholeness rather than emptiness; and
- by employing “seed-tones,” which organically integrate a composition’s diverse sounds in a single sonority.
Rudhyar describes each of these four methods in detail in his musical and philosophical prose, although it often takes considerable effort to understand how his mystical ideas relate to standard music theoretical concepts. Rudhyar’s piano music exploits the sounding board to integrate myriad disparate tones into complex multipartite sonorities resembling the sounds of gongs and bells, which often feature many non-harmonic partials. His dissonant harmony constructs “tone pleromas” by combining individual tones connected by geometric relationships (as opposed to arithmetic ones), which manifest musically as cycles of equal intervals (i.e., the circle of fifths). The “new sense of space” similarly implies interval cycles because of its emphasis on beginning with musical space as a whole and then partitioning it. Finally, Rudhyar’s “seed-tones” act as dissonant tonic sonorities that guarantee the organic integrity of his compositions. We will now investigate each of these four methods in detail before observing how they function in several short Rudhyar piano pieces, including “Stars” (1931) from the Third Pentagram and the first movement of Granites (1929).
The Creation of “Living Tones” through the Piano
[2.1] Rudhyar conceives of Tone as “a living entity” unlike notes, which are merely black marks on paper (1972). He identifies living tones in the gongs of Asia (and, to a lesser extent, in the bells of Europe) with their “wondrous throbbing resonances” (1930b, 27). To Rudhyar these devices are “the greatest instrumental perfection of tone yet reached by man” (1930a, 34), so understanding what he hears in these sacred instruments will begin to elucidate his theory of Tone.
[2.2] The fundamental quality attracting Rudhyar to these “‘magical’ instruments” (1973a, 60) is the way they integrate a multitude of tones into one:
In a gong—in those huge gongs from Java, China and even to some extent in India—you have a brotherhood of tones. . . . In the gong we hear a companionship of tones potentially brought together in a definite form and a definite structure, and as it were hammered together so as to create a compound tone which is infinitely resonant and contains in itself a multitude of tones. (1972)
Furthermore, by integrating a wide range of sounds, these masses of vibrating metal make “sonorous space” itself “tangible” (Rudhyar 1928c, 80). Since Tone is a quality of musical space itself rather than a property of individual sounds, it can be made audible only through the integration of particular sounds into what Rudhyar calls “holistic resonances” and “tone pleromas” (1982, 136). The term “pleroma” originates with the Christian Gnostics, who used it to describe “infinite fulness [sic] of Being” (Rudhyar 1930b, 8). Musically, “A pleroma of sounds refers to the process of harmonization through which differentiated vibratory entities are made to interact and interpenetrate in order to release a particular aspect of the resonance inherent in the whole of the musical space, its holistic resonance, its Tone (Rudhyar 1982, 139–40). Because gongs and bells produce true tone pleromas (Rudhyar 1928c, 80) and “the most stirring holistic resonances” (Rudhyar 1982, 141), they are the supreme instrumental means of conjuring Tone. As illustrated by Rudhyar’s vivid descriptions of the sounds of gongs, his vision of Tone was not just a glorification of “the single tone” (that phrase which was so influential on the young Ruth Crawford) but—on the contrary—a preference for those complex multipartite sonorities which impart to sound a living quality.
[2.3] Rudhyar's desire for sonic integration makes the piano his instrument of choice. Whereas the modern orchestra certainly puts a diverse palette of sounds at the composer’s disposal, Rudhyar finds it sorely lacking in its capacity to integrate them. According to Rudhyar, “The tone of the modern orchestra lacks homogeneity because of the fact that all instruments are like individuals telling their tale, each from its own point of view, with no feeling of relationship to the whole—a fit symbol for our modern civilized world!” (1923). Though admitting that “orchestras perform extraordinarily difficult scores, technically speaking,” he argues that the difficulty with his own music “seems to be its ‘inwardness’ or feeling-depth. It must be deeply felt by the performer, or else it seems unintegrated” (1923, 61). Thus Rudhyar values the piano as “a microcosm which one person can directly control and, at least to some extent, mold with his or her will and imagination—with his or her feeling-intuition of Tone” (1982, 195).
[2.4] Furthermore, for practical purposes, the piano’s seven-octave range encompasses the totality of our musical space—a crucial concept for Rudhyar’s “new sense of space.” The piano’s range represents the entirety of our musical space in another way, too, because seven octaves span twelve perfect fifths (Rudhyar 1982, 133), which encapsulate all twelve pitch-classes of equal temperament. Stacked fifths are fundamental to Rudhyar’s conception of dissonant harmony.
[2.5] Rudhyar’s preference for the piano may at first seem contradictory in light of his glorification of non-Western music and his call “to realize melodic continuity between successive notes and do away with cut-and-dried keyboard scales” (1962, 185). Indeed, part of his reliance on the piano is practical, as he considers it “an almost hopeless task for any composer to try to escape from tempered scales, pianos and standardized orchestrations” (1928b). Sobering as this concession to practicality may be, it reveals that Rudhyar is most concerned not with exploring a kaleidoscope of new sounds but with revolutionizing the way in which available sounds are integrated. In addition to placing the totality of musical space within control of a single performer, the piano offers an unparalleled means of integration: its sounding board.
[2.6] Rudhyar envisions the piano’s steel sounding board as the modern Western equivalent of the gongs and bells he so admires. Taking advantage of this feature, however, requires a
new type of piano playing based on the realization that the piano is a sort of big gong, that the important factor in the instrument is not the keyboard, not even the separate strings, but the homogeneous sounding-board or table of resonance which, especially with the help of the pedal, gives birth to tone-masses, to complex, synthetic entities of sound. Build these tone-masses according to the principle of dissonant harmony, and the piano becomes transformed into a gong. (1930b, 29)
Rudhyar acknowledges that this new pianism is presaged by the tone-clusters of Henry Cowell (1930b, 29). Despite the audible pianistic affinities between these two composers, however, the theoretical justifications behind their harmonic innovations diverge significantly. Whereas for Cowell the overtone series is an inexhaustible fount of new harmonic relationships, for Rudhyar it generates merely the music of the past. While Cowell seeks to extend harmonic practice via the relationships between higher, previously unused overtones (Cowell 1996, x–xi, 13–16), Rudhyar’s dissonant harmony aims to transcend the harmonic series altogether.
Dissonant Harmony and Tone Pleromas
[3.1] Rudhyar’s musical concept of dissonant harmony grows from his social philosophy, which contrasts “culture” with “civilization.” In his usage, a culture is a group of people united by their common ancestry. Their social organization, the tribal order, exhibits “unanimous consensus in all vital matters, and complete dependence upon nature” (Rudhyar 1977, 14). They are “rooted in [the land] almost as profoundly as trees in the soil,” and thus all cultures are “locality-centered” and everything cultural has a “fundamentally biological character” (Rudhyar 1977, 8, emphasis original).
[3.2] Conversely, a civilization is a diverse group of people united by a common purpose. Lacking shared cultural heritage, they intentionally create unity—or, in Rudhyar’s words, “multi-unity,” a term indicative of the members’ original independence. This social organization, the companionate order, is “a process of planetary scope” (Rudhyar 1977, 4) born of “the intuitions, the visions, the discoveries of great human minds reaching after universal principles, cosmic laws, and an understanding of rhythmic processes transcending the birth-growth-decay cycle of culture-wholes” (Rudhyar 1977, 13, emphasis original). Thus, civilization is based not on the biological and local conditions which unite cultures, but on “a ‘higher’—because more inclusive—level which we may call, for lack of better terms, spiritual-mental” (Rudhyar 1977, 15).
[3.3] The tribal order and the companionate order correspond with two types of musical harmony: the consonant order and the dissonant order, respectively. Describing the relationships between the frequencies of pitches, Rudhyar explains, “The Consonant Order is based on ‘arithmetical series,’—in music, on the series of overtones issued from one fundamental. The Dissonant Order is founded upon ‘geometrical series’—for instance the cyclical series of twelve fifths or twelve fourths (which I called Zodiacs of Sounds)” (1973a, 59).(3) Summarizing this distinction, Rudhyar writes that “music is built on one of two types of series or progressions: series of frequencies where the initial tone adds itself to itself, and series of intervals where the initial interval adds itself to itself” (1928c, 82).
[3.4] While a shared fundamental guarantees the consonant order’s unity a priori, the dissonant order only achieves unity as the composer synthetically combines pitches to conjure Tone. For Rudhyar, the harmonic series of the consonant order is
the perfect archetype and symbol of the tribe, each octave of overtones corresponding in a way to a generation. The entire series is in a strict sense the progeny of the fundamental, the Divine Ancestor (Abraham, Manu, etc.) and a definite flow of sympathetic resonance is manifest in all its members. (1928a, 6, emphasis original)
The dissonant order, on the other hand, replaces the gravitational pull of the fundamental with a striving toward Tone. Individual tones “seek the interpenetrative condition of dissonant chords—pleromas of sounds. These are limited in content; each has its own principle of organization, which determines the tone of the pleroma” (Rudhyar 1982, 145). These particular pleromas can then be recombined into more complex pleromas. “Dissonances are synthetized [sic] into harmonic resonances which are relatively consonant on the spiritual plane, i.e., in the subjective consciousness of the hearer. These higher consonances break again into higher dissonances. There is no definite finality to the process” (Rudhyar 1928a, 12). Ultimately, “all these tones ideally commune in the vast Tone of the all-encompassing pleroma of the musical space experienceable by human ears” (Rudhyar 1982, 145). This ultimate pleroma, the totality of musical space, is the cornerstone of another pivotal Rudhyarian concept: “the new sense of space.”
The New Sense of Space
[4.1] According to Rudhyar, there are two ways of conceptualizing musical space: “as an empty container of single, essentially separate musical notes, or as a fullness of tone, a pleroma of sounds. The concept prevalent in Western culture is the first alternative. I am attempting to give a concrete formulation to the latter” (1982, 133). To achieve this “fullness of tone” it is not enough to simply combine lots of big chords or freely amalgamate a diversity of sounds; on the contrary, the lumping together of different sounds is precisely what Rudhyar has in mind when describing the old sense of space: “Today most, and perhaps practically all artists face their canvas or sheet of paper as if it were empty space, i.e., a blank negation, the receptacle into which they have to project more or less at haphazard things invented by them, lines, shadows, colors” (1930b, 4). This adding together of sundry objects recalls the arithmetic relationships of the consonant order (1 + 1 = 2, 2 + 1 = 3, etc.). The new sense of space, on the other hand, achieves fullness by beginning with a whole, which is then partitioned. “Space being the infinite potentiality of forms, has first to be differentiated as a geometrical Form, or proportion. This geometrical Form, or ground-plan, represents the differentiation of space” (Rudhyar 1930b, 11). Thus, the new sense of space calls for a way to geometrically divide the totality of musical space into equal subdivisions. In practice, this manifests as divisions of equal-tempered pitch space into cycles of equal intervals (Rudhyar's dissonant order) such as the interval-class-5 cycle (the circle of fifths), the ic2 cycle (the whole tone scale), the ic3 cycle (the diminished seventh chord), the ic4 cycle (the augmented triad), the ic6 cycle (the tritone), or the ic1 cycle (the chromatic scale).(4)
[4.2] The interval cycle most important to Rudhyar is the cycle of fifths, which by spanning the aggregate implies the totality of musical space. By building chords out of fifths, he saturates the listener’s ear with all twelve tones until “That of which the groups of tones are but differentiated aspects reveals itself. That is to the chromatic tones as white light is to the seven colors. What is it? The psychic reality of Tone” (Rudhyar 1927, emphasis original). Of course, Schoenberg’s twelve-tone technique similarly cycles through the aggregate, but the precompositionally determined tone-row is anathema to Rudhyar with his disdain for extrinsic musical laws. Moreover, Rudhyar’s dissonant harmony, unlike Schoenberg’s, implies voicing in fifths: “the proper spacing of dissonant centers” (Rudhyar 1972). These dissonant centers are not literal pitch-classes but points in musical space that may shift slightly (usually by no more than a half-step) without destroying the overall effect of ic5-based spacing. Explicitly acknowledging that “the fifths of course are not always perfect fifths” (1972), Rudhyar freely mixes perfect, augmented, and diminished fifths. While Rudhyar’s free combination of three different interval classes—ic4 (augmented fifths), ic5 (perfect fifths), and ic6 (diminished fifths)—may seem to contradict his goal of dividing musical space into equal intervals, it is important to remember that his primary concern is not with pitch classes, interval classes, or set classes, but rather with creating a sense of musical space. The overall effect of dividing pitch space into fifths can survive the alteration of individual tones by a half step.(5) The significance of spacing also helps explain Rudhyar's preference for the ic5 cycle over the similarly dodecaphonic ic1 cycle; the expansive sound of stacked fifths naturally evokes the vast totality of musical space.(6)
Organicism through Seed-tones
[5.1] Let us not forget that despite the grandeur of Rudhyar’s holistic vision of musical space, he hears it originating in single tones. For Rudhyar space is within tones: “Musical space deals not so much with the Form of a symphony or sonata, but with the inner structure of single tones perceived as aural entities, not as abstract visual points on paper” (1930b, 15–26). What gives a single tone significance for Rudhyar is the fact that it is a whole unto itself, with its own intrinsic structure. “Every tone is a complex sound made up of many sonal elements. We may say . . . that every tone is a chord, be it only the chord constituted by its constitutive overtones or in general subtones. But what is a chord if not a sort of spatial arrangement, or ordering, of sonal elements?” (1930b, 23, emphasis original). Furthermore, he argues that the “form in space of the tones (basic chords or even timbre of instruments)” (1930a, 35) can project itself onto the outer space: that is, “the musical score as a pattern made of abstract musical notes” (1930b, 24). This relationship between the inner structure of chords and the outer structure of a composition implies organic form: “forms growing out of Space by an inherent necessity as a plant grows out of seed and soil. . . . It is the constant relating of the many forms to the one Space-substance, seeing forms as parts of an organic whole, with parts fulfilling definite functions within this whole” (Rudhyar 1930b, 6). This organicism manifests as an intrinsic relationship between the harmonic and timbral structure of a composition’s basic chords (its inner space) and the pattern of its notes on the page (its outer structure).
[5.2] Rudhyar's notorious anti-formalism, then, is actually an impassioned defense of organic form, although it has often been misinterpreted as a call for formlessness. Anticipating just such a misunderstanding, Rudhyar explains:
Personally, I have used almost exclusively in my music so far what is so badly called atonality. Tonality, in the sense of ‘a principle of tone unity,’ is to me a requirement. But there are many possible ‘principles of unity’; when new ones are used, people, not understanding the new principle, consider that there is nothing but chaos. (1962, 184)
Thus, Rudhyar decries not form itself but rather arbitrary formal laws imposed from the outside: the recycled forms of neo-classicism, the precompositionally determined tone row, or Seeger’s rule of dissonant counterpoint reversing convention to make dissonance normative. Emphasizing that “law and anarchy are inseparable polar opposites” (1975, 179, emphasis original), Rudhyar laments the fact that “we make no difference between a rule imposed from the outside and an inherent or instinctive compulsion to act according to a structural order” (1975, 170, emphasis original). “The important point,” he argues, “is whether or not the ‘system of rules and regulations’ is external to that which is being ruled, or inherent in whatever follows the rules” (1975, 170). Thus Rudhyar’s primary formal concern is organicism: the intrinsic relationship between the whole and the parts of a work of art.
[5.3] Rudhyar's organicism suggests an affinity with the ideas of Heinrich Schenker, for whom “the concept of organic coherence” is “inherent in the works of the great masters” and “the very secret and source of their being” (1979, xxi), and the Ursatz (fundamental structure) is “the mark of unity” and “the resolution of all diversity into ultimate wholeness” (1979, 5). Schenker’s claim that “the great composers—in contrast to performers and listeners—experienced even their most extended works not as a sum total of measures or pages, but as entities which could be heard and perceived as a whole” (1979, xxiii, emphasis added) strikingly recalls Rudhyar’s contrast between the old sense and new sense of space. Just as in Schenker’s thought “The overtone series, this vertical sound of nature, this chord in which all the tones sound at once, is transformed into a succession, a horizontal arpeggiation” (1979, 10), in Rudhyar's dissonant harmony, each composition “emerges from a ‘seed-tone’” which is “often, but not necessarily, a chord unfolding its internal potential of resonance into melodic-harmonic roots, stems, and branches” (1982, 197). Relating the notes of Rudhyar composition to its seed-tone may help us understand its structure in the same way that Schenkerian analysis elucidates tonal forms as expansions of their tonic triads.(7)
[5.4] A composition’s seed-tone may be a chord that acts as a dissonant tonic sonority prolonged throughout the piece. However, the notion of prolongation in atonal music has been controversial to say the least, so before delving into Rudhyar's music, a brief digression is in order. This debate has been summarized elsewhere (Baker 1983), so I will limit my discussion to those issues most applicable to Rudhyar’s theoretical writings and musical works. Some theorists have claimed that the lack of a distinction between consonance and dissonance precludes the possibility of applying Schenkerian analysis to atonal music. Joseph Straus argues that “unless we know which harmonies are consonant and which are dissonant, we will not be able to determine reliably which notes are structural and which are embellishing. Atonal music . . . does not systematically distinguish between consonance and dissonance” (1997, 239; see also Pearsall 1991). To surmount this problem, other analysts have tried to find Ursätze in atonal works, in essence retaining tonal conventions of consonance and dissonance (Baker 1990). Both sides of this debate, however, assume incorrectly that a Schenkerian approach to atonal music requires the preservation of the trappings of tonal music: prolongations, triadic structures, the Ursatz, and a clear distinction between consonance and dissonance. In so doing they cling to the means of Schenkerian analysis while forgetting its end—the demonstration of organic unity. If we are to understand post-tonal music organically, we must discover its own intrinsic laws, not subject it to the laws of tonality.
[5.5] The beauty of Rudhyar's music is that it transcends the thorny issue of distinguishing consonance and dissonance by instead establishing dissonance as a method of harmony. The structure of his music is determined not by the dialectical, hierarchy-generating functions of consonance and dissonance but by the “inner space” (that is, the intrinsic structure) of a seed-tone sonority serving as dissonant tonic. Investigations into prolongations of dissonant chords (Morgan 1976) often meet the objection that no reliable method exists to identify such a sonority (Baker 1983, 157). While a universal method is indeed unlikely, Rudhyar's theories provide ample clues to reveal seed-tones in his own works.
Identifying Rudhyar's Seed-tones
[6.1] Rudhyar's principles of dissonant harmony suggest two distinct but compatible ways of constructing a seed-tone: (1) building a chord of stacked fifths, which through their geometric relationships exemplify the dissonant order; and (2) combining commensurate overtones from two independent harmonic series (since overtones of a single series are united a priori by the consonant order). The former method is straightforward enough, but the latter requires a more detailed understanding of what I call interpenetrating harmonic series.
[6.2] If dissonant harmony is to combine tones from distinct harmonic series, it must somehow make audible the tones’ allegiances to different fundamentals. In our equal-tempered universe, there is no audible difference between, say, one G3 derived from a harmonic series on C2 and another G3 from a series on
several of [their] harmonics . . . would coincide. They would therefore be reinforced. In other words the ‘sea of sound’ produced by the blending of these harmonics would not be homogeneous but it would present a certain INNER RHYTHM. The reinforced harmonics would appear as centers of tonal pression [sic]. A form would outline itself. (1923, emphasis original)
It is this “inner rhythm” which gives interpenetrating harmonic series the intrinsic structure required of a seed-tone.
[6.3] Although interpenetrating harmonic series will generate slight discrepancies in frequency between their commensurate overtones (i.e., the G3 in a C2 harmonic series is only approximately equivalent to the G3 in an
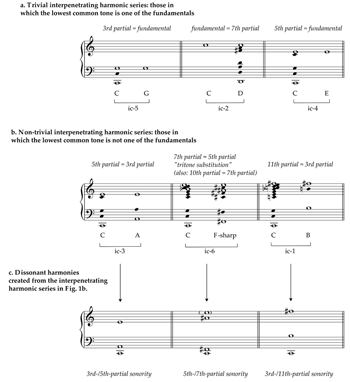
Figure 1. Interpenetrating harmonic series and the dissonant sonorities derived from them
(click to enlarge)
[6.4] Applying these reflections on interpenetrating harmonic series, I chart the intersections of overtones for each of the six possible interval-class relationships between two fundamentals (Figure 1). In each case, I seek the lowest pitch class appearing in both harmonic series. Several of these cases—those with fundamentals related by ic5, ic2, and ic4—are trivial because one of the fundamentals appears in the harmonic series of the other below any commensurate overtones (Figure 1a). For example, the lowest pitch class shared by the C2-series and the G3-series is D5 (ninth and third partial, respectively); however, G3 itself appears as only the third partial above C2, overshadowing any opportunity for blending the series via the D5, given its weakness as a higher overtone in relation to the G3. In effect, the consonant order already unites the two fundamentals, precluding any opportunity for dissonant harmony.
[6.5] More fruitful possibilities arise with fundamentals related by ic3, ic6, and ic1 (Figure 1b). The first of these, in which the shared overtone is the third partial of one series and the fifth partial of the other, produces a compound sonority (Figure 1c) which is a first-inversion minor triad (E4 above A2 and C2): a tonal consonance which the harmonically progressive Rudhyar does not conspicuously exploit.
[6.6] The second relationship, in which the fundamentals are related by ic6 and the shared harmonic is the fifth partial of one series and the seventh partial of the other, resembles jazz harmony’s tritone substitution. Scriabin often employs this 5th-/7th-partial sonority in his transitional middle period works (Baker 1980), which may help explain Rudhyar's admiration for the Russian composer. Moreover, Rudhyar himself exploits the 5th-/7th-partial sonority—for example, in the middle section of “Stars.”
[6.7] The final possible relationship between fundamentals, that of ic1, is perhaps the most characteristically Rudhyarian. The resulting sonority (Figure 1c), consisting of
Figure 2. Dane Rudhyar, “The Earth Pull,” measures 1–2
(click to enlarge)
Figure 3. Dane Rudhyar, “The Earth Pull,” measures 29–41
(click to enlarge)
Figure 4. Dane Rudhyar, “Sunburst,” measures 20–28
(click to enlarge)
[6.8] In “The Earth Pull,” from Rudhyar's 1974 set of piano pieces, Second Pentagram,(9) the 3rd-/11th-partial sonority appears in both the opening (Figure 2) and closing (Figure 3) measures at the same transposition level shown in Figure 1c. In actual compositional practice the individual tones of this sonority sometimes appear in different registers than they do in its idealized form from Figure 1c; however, the inner rhythm created by the blending of commensurate overtones still occurs because of the reccurence of pcs in higher octaves of the harmonic series (i.e., the sixth partial is an octave above the third partial). Moreover, Rudhyar maintains the integrity of the 3rd-/11th-partial sonority by consistently placing
[6.9] The same sonority resonates throughout the final nine bars of “Sunburst” from the Third Pentagram, amidst foreground fluctuations in the upper voices (Figure 4). As in “The Earth Pull,” the final measures (measures 24–28) feature the 3rd-/11th-partial sonority as part of a stacked-fifth sonority, this time including E as well as G and D. The consistency of Rudhyar's voicing (
[6.10] The presence of this same sonority at the beginnings and endings of several Rudhyar compositions suggests that it is a referential harmony, like the tonic triad of a tonal composition. Combining this observation with the fact that it exemplifies both the 3rd-/11th-partial sonority and quintal harmony, it becomes clear that this sonority must be one of Rudhyar’s seed-tones.
Analysis of “Stars”
[7.1] For a more comprehensive analysis of a movement also based on this 3rd-/11th-partial sonority, we now turn to “Stars,” another short piano piece from the Third Pentagram (see the full score in Appendix 1). Although this movement's pan-diatonic and altered dominant harmonies may superficially sound more like Debussy than “dissonant harmony,”(10) “Stars” nonetheless exemplifies Rudhyar's dissonant order because it grows out of a seed-tone of stacked fifths.
[7.2] “Stars” evokes a persistent sense of stasis; a given harmony often seems not to progress but rather to transform into the following harmony. This is because harmonic shifts occur not via the introduction of new chords but through limited transformations of the seed-tone, which are of three characteristic types: (1) the expansion or contraction of the stack of fifths by adding or removing tones from its top or bottom (including simultaneous expansion at one end and contraction at the other, which is essentially transposition); (2) the isolation of subsets of the stack; and (3) the chromatic alteration of a pitch to change two adjoining perfect fifths into an augmented fifth and a diminished fifth.
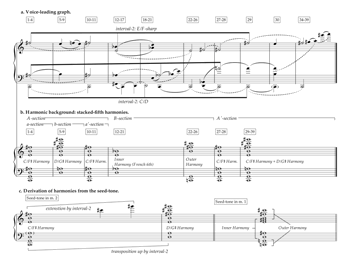
Figure 5. Analysis of Rudhyar’s “Stars”
(click to enlarge)
[7.3] “Stars” begins with a quintal chord in “root position”: a stack of perfect fifths ascending from C2 to
[7.4] Immediately following the initial downbeat Rudhyar fills the seed-tone’s gap not with the expected A3 but with
[7.5] From a broader perspective, we see that “Stars” is in ternary form, the B-section starting at the rolled chord in measure 12 and the A'-section beginning with the reappearance of the seed-tone in measure 27 (Figure 5b). The initial A-section is itself a miniature ternary form, featuring a four-bar a-section anchored by the seed-tone on the downbeats of measures 1, 3, and 4.(12) The local b-section (measures 5–9) presents an E-centric melody over a five-eighth-note ostinato which outlines three perfect fifths: B3/
[7.6] As the seed-tone returns to its original pitch level for the a'-section (measures 10–11), ascending lines recall the harmonies of the b-section, suggesting a synthesis of the C/
[7.7] The movement’s B-section is divided into two subsections straddling the climax in measure 22, the first of which is a developmental passage focused on the French-sixth sonority created by the intrusion of the
[7.8] As the movement reaches its fff climax (measure 21), the Inner Harmony is swept away by a 32nd-note flourish (measure 22) constructed from the complementary subset of the seed-tone—that is, precisely those tones not in the Inner Harmony: C2, G2, B4,
[7.9] The climax also continues the drama begun with the chromatically altered tone
[7.10] The
[7.11] In the movement’s closing bars (measures 33–35), Rudhyar transposes the ostinato’s D/A dyad up an octave, bringing out the half-step voice-leading from
Analysis of Granites, First Movement
[8.1] The first movement of Rudhyar's 1929 piano suite Granites (see Appendix 2) grows out of the interaction of two harmonic series that function quite differently from the interpenetrating overtone series in “Stars,” “The Earth Pull,” and “Sunburst.” More specifically, two harmonic series unfold simultaneously, recalling the counterpoint between the fundamental line and the bass arpeggiation of a Schenkerian Ursatz. Unlike the preceding examples, here one harmonic series ascends from its fundamental through its overtones while the other descends through its “undertones.”
[8.2] The questionable validity of undertones necessitates a brief digression justifying their place in this analysis. Rudhyar himself calls the physical existence of undertones “a great mystery” which “can probably never be solved except on a philosophical or occult basis” (1928c, 61). One solution to this mystery is offered by Cowell, who explains that although undertones are not directly produced by a sounding body, “it is difficult to avoid them in resonation.” Through resonance, a sounding tone will cause sympathetic vibrations not only in bodies that vibrate at the sounding frequency, but also in those bodies which vibrate at frequencies producing the sounding tone as an overtone; in other words, the undertone series is simply the collection of those frequencies which could serve as a fundamental for the given tone (Cowell 1996, 22). This explanation of undertones parallels Rudhyar’s more poetic conceptualization of undertones “as the very roots of the seed-tones. . . . [A]s the roots are hidden in the soil, likewise we cannot normally detect undertones by means of our mere physical sense of hearing” (1928c, 61, emphasis original). As products of resonance, undertones are a natural tool for Rudhyar since, as we have seen, he understands a composition's seed-tone as “a chord unfolding its internal potential of resonance” (1982, 197).
Figure 6. Analysis of Rudhyar’s Granites, first movement
(click to enlarge)
Figure 7. Derivation of the triads in measure 2 of the first movement of Granites from the overtone series on A
(click to enlarge)
[8.3] In the first movement of Granites, an F1/A3 dyad serving as the seed-tone expands symmetrically through an overtone series on A and an undertone series on F. Rudhyar’s voicing of this dyad takes advantage of the two tones’ mutual resonance, with A3 positioned as the fifth partial of F1. The movement’s opening announces the seed-tone by four repetitions of a head motive, which descends from C5 through B3 to the F1/A3 dyad (Appendix 2, measures 1–4, and Figure 6a). Answering the head motive is an ascent through four root-position triads (measures 2–3): A minor,
[8.4] The head motive also establishes B as upper neighbor to A; however, the music that follows creates considerable ambiguity as to which tone is structural and which is embellishing. The three tones F, A, and B form an 026 trichord, which acts as a referential set-class appearing at various transposition levels both within individual chords and over longer spans of music. It almost always appears, though, in the same “inversion,” with a major third and a tritone above the bass.
[8.5] The odd partials of the two harmonic series growing out of the F and A in contrary motion (Figure 6c) create a series of four dyads (F/A,
[8.6] From the outset, repetition of the F/A dyad prolongs Harmony I as the texture thickens until measure 6, where a quick, cadential succession of chords heralds the arrival of Harmony II on the last chord in measure 6a with its
[8.7] The accented chord on the downbeat of measure 8 marks the beginning of Harmony III with the
[8.8] These repeated chords build up to a new arrival point on the downbeat of measure 9, marking the arrival of Harmony IV. This chord immediately creates some ambiguity as to whether A or G is the structural soprano note over the bass
[8.9] Beyond Harmony IV, the two harmonic series coincide on B (
[8.10] The movement's final two sub-measures dramatize the competition between the A and the B via a descending minor seventh which emphasizes the A registrally but the B agogically (measures 12b–12c). Ultimately, however, neither tone emerges as the victor, for the goal of the movement is the fusion of the B with the seed-tone's F and A, in both of whose harmonic series it claims membership—a perfect example of Rudhyar's creation of Tone through integration.
Conclusion
[9.1] As illustrated by the foregoing analyses, Rudhyar’s music does not employ the dissonant order to the exclusion of the consonant order but rather thrives on the creative interplay between these two harmonic idioms. This is consistent with Rudhyar’s notorious disdain for formal systems; ultimately the dissonant order is supposed to foster a new kind of listening rather than serve as a systematic method of composition. With this in mind, it should be clear that my analyses do not attempt to demonstrate an all-encompassing system behind Rudhyar’s musical language; yet it is my hope that they do reveal a genuine integrity in Rudhyar’s music underlying its more obvious mutability. It should be readily apparent that the two works discussed in detail, “Stars” and the first movement of Granites, employ quite different strategies of musical structure. Yet some similarities are also apparent: the use of quintal or quartal chords as referential harmonies and the exploitation of resonance through overtone and undertone relationships. I suspect these harmonic techniques appear throughout Rudhyar’s oeuvre, but analyses of other works would be required to demonstrate this.
[9.2] An even more important similarity, however, is the presence in both works of a seed-tone—a unifying structure which I would argue is essential to Rudhyar’s goal of creating in the listener the experience of Tone. It is only by learning to hear seemingly dissonant tones as part of such an integrated harmonic kernel that listeners begin to pursue dissonance as a spiritual discipline; and it is by unfolding the inner form of such a seed-tone into the notes of composition that Rudhyar’s music “teaches” listeners this new way of hearing. While theoretical problems remain with the notion of dissonant prolongation, Rudhyar’s music overcomes these hurdles not only through his sensitive engagement with the intervallic structure and resonance of his seed-tones but also through brute force repetition of the seed-tone and the formal brevity of his compositions. The aphoristic quality of the pieces analyzed here is by no means exceptional. Whether or not a seed-tone could serve as dissonant tonic for a larger movement with greater harmonic departures remains an open question.
[9.3] Rudhyar’s association of dissonance with spirituality may seem surprising given the prevailing assumptions linking dissonance with academic dodecaphony (i.e., Milton Babbitt, Pierre Boulez) and spirituality with consonant, diatonic harmony (i.e., Arvo Pärt, John Tavener). Thus it is worth recalling that among early twentieth-century pioneers in atonality, such a spiritual perspective was widespread. Scriabin’s mysticism is well known, but let us not forget that Schoenberg compares twelve-tone space with “Swedenborg’s heaven,” and, in works strikingly reminiscent of Rudhyar’s, declares that “the unity of musical space demands an absolute and unitary perception” (1984, 223, emphasis original). Similarly, Olivier Messiaen’s music not only expresses his Roman Catholic faith, but through its “modes of limited transposition” evokes, in the composer’s own words, “a certain effect of tonal ubiquity,” recalling Rudhyar’s Tone; moreover, Messiaen’s desire to lead his listener to a “theological rainbow” (1956, 21, emphasis original) parallels Rudhyar’s claim that “the psychic reality of Tone” is “to the chromatic tones as white light is to the seven colors” (1927). Regardless of Rudhyar’s marginalization, his spiritual vision of dissonance is not only a unique expression of his personal philosophy but—on the contrary—also a bond between him and other modernist harmonic innovators.
Appendix 1. Score to “Stars” (click to enlarge and see the rest) | Appendix 2. Score to Granites (First Movement) (click to enlarge and see the rest) |
Michael K. Trinastic
1008A Clarendon St.
Durham, NC 27705
trinastm@gmail.com
Works Cited
Baker, James M. 1980. “Scriabin's Implicit Tonality.” Music Theory Spectrum 2 (Spring): 1–18.
—————. 1983. “Schenkerian Analysis and Post-Tonal Music.” In Aspects of Schenkerian Theory, ed. David Beach, 153–86. New Haven, CT: Yale University Press.
—————. 1990. “Voice-Leading in Post-Tonal Music: Suggestions for Extending Schenker's Theory.” Music Analysis 9, no. 2: 177–200.
—————. 1997. “Structure as Prism for Musical Philosophy.” In Music Theory in Concept and Practice, ed. James M. Baker, David W. Beach, and Jonathan W. Bernard, 53–96. Rochester, NY: University of Rochester Press.
Chennevière, Daniel. 1913. Claude Debussy et son oeuvre. Paris: A. Durand.
Cowell, Henry. 1996. New Musical Resources. New York: Cambridge University Press.
Ertan, Deniz. 2009. Dane Rudhyar: His Music, Thought, and Art. Rochester: University of Rochester Press.
Garland, Peter. 1982. Americas. Santa Fe: Soundings Press.
Kahn, Douglas. 2004. “Ether Ore: Mining Vibrations in American Modernist Music.” In Hearing Cultures: Essays on Sound, Listening, and Modernity, ed. Veit Erlmann, 108–30. New York: Berg.
Masselos, William. 1994. Masselos Plays Mayer and Rudhyar. Composers Recordings/CRI.
Messiaen, Olivier. 1956. The Technique of my Musical Language, trans. John Satterfield. Paris: Alphonse Leduc.
Morgan, Robert P. 1976. “Dissonant Prolongation: Theoretical and Compositional Precedents.” Journal of Music Theory 20, no. 1: 49–91.
Nevins, Maureen. 1993. “Dane Rudhyar (1895–1985) and Music: His Life, Writings, and Compositions.” M.A. Thesis, University of Montreal.
Oja, Carol J. 1999. “Dane Rudhyar’s Vision of American Dissonance.” American Music 17, no. 2: 129–45.
Pearsall, Edward R. 1991. “Harmonic Progressions and Prolongations in Post-Tonal Music.” Music Analysis 10, no. 3: 345–55.
Rudhyar, Dane. 1923. “The Harp as Cosmic Symbol.” The Eolian Review 2, no. 2 (March). Available online via The Dane Rudhyar Archival Project. Accessed March 27, 2014.
—————. 1927. “Carl Ruggles, Pioneer—As Seen by a Fellow Modernist,” Musical America 46, no. 19 (August): 3, 20. Available online via The Dane Rudhyar Archival Project. Accessed March 27, 2014.
—————. 1928a. Dissonant Harmony: A New Principle of Musical and Social Organization. Carmel, CA: HAMSA Publications.
—————. 1928b. “The Dualism of Musical Substance.” Pro Musica Quarterly 6, no. 3 (March): 4–11. Available online via The Dane Rudhyar Archival Project. Accessed March 27, 2014.
—————. 1928c. The Rebirth of Hindu Music. Adyar, Madras, India: Theosophical Publishing House.
—————. 1930a. “The Mystic’s Living Tone.” Modern Music 7, no. 3 (April–May): 32–36.
—————. 1930b. The New Sense of Space. Carmel, CA: HAMSA Publications.
—————. 1962. “Oriental Influence in American Music.” In American Composers on American Music: A Symposium, ed. Henry Cowell, 184–85. New York: Frederick Ungar Pub. Co.
—————. 1972. “The Transforming Power of Tone.” Lecture given at Live Oak Park Theatre, Berkeley, CA, April. Available online via The Dane Rudhyar Archival Project. Accessed March 27, 2014.
—————. 1973a. “Concerning My Music.” Soundings 6 (Spring): 57–61.
—————. 1973b. “A New Philosophy of Music.” Soundings 6 (Spring): 54–56.
—————. 1975. Occult Preparations for a New Age. Wheaton, IL: The Theosophical Publishing House.
—————. 1977. Culture, Crisis, and Creativity. Wheaton, IL: The Theosophical Publishing House.
—————. 1982. The Magic of Tone and the Art of Music. Boulder, CO: Shambhala Publications, Inc.
—————. 1984. “When Does Sound Become Music?” Available online via The Dane Rudhyar Archival Project. Accessed March 27, 2014.
Schenker, Heinrich. 1979. Free Composition, trans. Ernst Oster. New York: Longman, Inc.
Schoenberg, Arnold. 1984. “Composition with Twelve Tones (1).” In Style and Idea, ed. Leonard Stein, 214–45. Los Angeles, CA: University of California Press.
Straus, Joseph. 1997. “Voice-Leading in Atonal Music.” In Music Theory in Concept and Practice, ed. James M. Baker, David W. Beach, and Jonathan W. Bernard, 237–74. Rochester, NY: University of Rochester Press.
Taruskin, Richard. 1997. Defining Russia Musically. Princeton, NJ: Princeton University Press.
Tick, Judith. 1997. Ruth Crawford Seeger : A Composer's Search for American Music. New York: Oxford University Press.
Discography
Discography
Rudhyar, Dane. 2009. Four Pentagrams, Paeans, Granites, Prophetic Rite. Ron Squibbs. Aucourant Records, AUREC 0909, 1 compact disc.
Footnotes
1. One also thinks of Rudhyar’s countryman Satie in this vein, although his sonic palette could hardly be more different from Rudhyar's.
Return to text
2. Ertan 2009 analyzes Rudhyar’s “Solitude” (the second movement of Tetragram No. 5) (34-40), Theurgy (95–100), Three Melodies (112–17), and Transmutation (124–28).
Return to text
3. An arithmetical series is one in which each term is generated by adding a constant to the preceding term; in the case of the overtone series, that constant is the frequency of the fundamental. A geometrical series, on the other hand, is one in which each term is generated by multiplying the preceding term by a constant; in the case of the cycle of fifths, that constant is 3:2, the ratio between the two tones of a perfect fifth. I have used here the term “cycle of fifths” instead of the more familiar “circle of fifths” because the latter implies the functional progressions of tonality, which are not what Rudhyar has in mind when he describes these “Zodiacs of Sound.”
Return to text
4. This is perhaps why Rudhyar claimed that there was an “indisputable line of musical inheritance” between himself and Liszt (1973a, 58), given the prevalence of interval cycles (notably diminished seventh chords and augmented triads) in the Hungarian composer's late music (i.e., “Nuages Gris,” “Die Trauer-Gondel I,” “Unstern!”). In addition, Rudhyar’s desire to divide up musical space into equal intervals is precisely what happens in equal temperament itself—a fact that ameliorates the contradiction between Rudhyar’s desire to overthrow “standardized Western tunings” and his continued reliance on equal temperament.
Return to text
5. Consider also the analogous case in third-based harmony; chords freely mix ic3 (minor thirds) and ic4 (major thirds) without eroding the sense of tertian harmony.
Return to text
6. Although Taruskin has written off as “chimerical” attempts to explain Scriabin's “mystic chord” as a “construction of fourths” since two of the fourths are augmented and one is diminished (1997, 342), this explanation of the Russian composer's harmony may merit reconsideration in light of Rudhyar’s admiration for Scriabin and his quintal harmony mixing augmented, diminished, and perfect fifths.
Return to text
7. Despite the commonalities in their visions of organic unity, Rudhyar and Schenker are at odds regarding its proper source. Rudhyar’s quest for dissonant harmony opposes Schenker’s glorification of the consonant order: a Rudhyarian concept which neatly describes Schenker's derivation of the Ursatz from the harmonic series as well as his belief that “The origin of every life, whether of nation, clan, or individual, becomes its destiny” (1979, 3).
Return to text
8. Similarly, Rudhyar’s frequent use of major sevenths and minor ninths also serves “to induce strong beat tones and sharpen the impact of a tone within a melodic line,” according to his widow Leyla Rudhyar Hill (Ertan 2009, 151).
Return to text
9. Rudhyar’s Second Pentagram is part of a series of four Pentagrams that reorganize the movements of his 1931 score Moments (Nevins 1993, 164–66).
Return to text
10. It is worth recalling here that Rudhyar, at the tender age of 17, when his name was still Daniel Chennevière, authored a book on Debussy, Claude Debussy et son oeuvre (Chennevière 1913).
Return to text
11. Taruskin explains Scriabin’s “mystic chord” as a variant of the French sixth, “the most basic Scriabin harmony of all” (1997, 342).
Return to text
12. I use lowercase here to distinguish the sections of this local ternary form (a-section, b-section) from the sections of the entire movement (A-section, B-section).
Return to text
13. Cowell, too, interprets triads dualistically: “If undertones as well as overtones are hypothetically taken as a working basis, the richness of polyharmonic material that can be formed by the combination of relationships with inexorable logic is surprising, for the reason that every tone may be made the base of both major and minor triads. Thus, on the overtones of C we can base the major triad of C, and on the undertones we can base a minor chord, called by its lowest tone, F minor” (1996, 27).
Return to text
14. Roman numerals here simply indicate order of appearance rather than tonal functions.
Return to text
15. Rudhyar is fond of subdividing measures via dashed barlines. I append lowercase letters to measure numbers (i.e., “measure 8a” for the first sub-measure of measure 8, “measure 9c” for the third sub-measure of measure 9, etc.) to indicate these sub-measures.
Return to text
Copyright Statement
Copyright © 2014 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Michael McClimon, Editorial Assistant
Number of visits:
20988