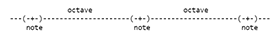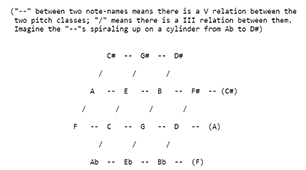An Algebraic Approach to Mathematical Models of Scales
Mark Lindley and Ronald Turner-Smith
KEYWORDS: group, halfgroup, harmony, dodecaphony, semitones, temperament, Landini, Matteo da Perugia, Dufay, Schutz, Louis Couperin
ABSTRACT: Although mathematical models of the scale have always been characteristic of Western music theory, in the last 200 years they have not been very much improved (although some interesting properties of scales have been defined in recent years). This article describes our effort in a new book to contribute to this part of music theory by using some appropriate concepts of modern algebra.
Copyright © 1993 Society for Music Theory
Figure 1. A sequence of constructions abstracted from the pitch continuum
(click to enlarge)
Figure 2. Three pitches in one pitch class
(click to enlarge)
[1] Our sequence of mathematical constructions is listed in Figure 1. Our point of departure is the pitch continuum, which is not a mathematical construction but an intuition, since pitch is subjective. (Pitches as we hear them cannot be measured, but only judged.) Our first construction is a positive-number line for the sound-wave frequencies, which can be measured and which almost wholly determine the pitches.
[2] It is the differences between pitches that interest us musically. Experience teaches us that there is a logarithmic relation between these subjectively judged differences and the differences among the corresponding pitch frequencies. So our second construction is a number line for the logarithms of the frequencies. We use logarithms to the base 2; this choice is due to another aspect of musical experience: the musical interval between two notes whose frequencies are in the ratio 2:1 is an octave, and notes one or more octaves apart from each other are intuitively heard as manifestations of the same note on different levels. Normally a scale repeats itself in each octave (there are exceptions, but they can be treated as special cases), so musicians today speak of pitch classes (see Figure 2)—that is, of equivalence classes of notes that are one or more octaves apart from each other—and of “pitch-class intervals” or “pitch-class relations”, which are the analogous equivalence classes of musical intervals. With logarithms to the base 2 it is very easy to define the addition of logarithms-mod-1 (which we call “flogs”) in such a way that the sum will be musically valid when the flogs for two pitch-class relations are added.
[3] For a simple example, let us see how the flog for a 5th with a frequency ratio of 3:2, when added to itself, yields a flog for a whole- tone. It is readily reckoned that, to three decimal places, log 3 to the base 2 = 1.585, and hence log (3/2) to the base 2 = 0.585. Now instead of adding 0.585 + 0.585 and getting 1.170 for a major 9th (which differs by 1 from the log for a whole-tone), we reckon in terms of flogs and write .585 + .585 = .170. This is illustrated in GIF 1.
[4] According to Max Weber,(1) there are two rational ways to construct a system of tones: by means of harmonic relations or else by dividing the octave into equal parts. From this hypothesis can be derived two types of generators for our pitch-class relations (see Figure 1e): either equal- division (whereby 1/n-octave is taken as a flog), or else harmonic (which will be described below). We are content to consider these two types in our book, but would admit any other valid type that could be adequately defined.
[5] Our next construction is the algebraic pair: (set, Abelian group), to which such generators give rise. The groups operate on the sets; the operation is addition. A positive number in a group means “add so much,” but in a set means an amount that is per se so much. (There is of course no such thing as a “negative” or an “absolute-zero” pitch.)
Figure 3. Three notes in one pitch class
(click to enlarge)
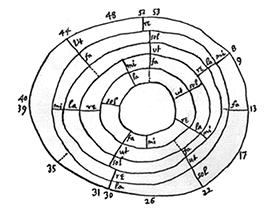
GIF 2. Some types of algebraic structure
(click to enlarge)
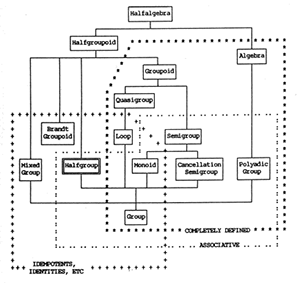
[6] Although music theorists have always represented notes as points, we provide, for the sake of greater validity, that each note in the scale will occupy a small neighborhood on the number line, in order to give every note some leeway for things like vibrato, inexact intonation etc. (We define the musical intervals as between the centres of these neighborhoods.) Thus the elements of our pitch-class sets are equivalence classes of neighborhoods around points-mod-1 (see Figure 3). To reach the highest degree of validity, one ought to allow that the neighborhoods for different notes in the same system may differ in size, and that in certain cases (for example, when a violinist has a wide vibrato) the neighborhoods for notes adjacent in the scale may overlap, obliging one to treat the neighborhoods as fuzzy sets. For the sake of simplicity, however, our book uses a kind of a modelling in which the neighborhoods have definite borders, do not overlap, and are uniform in any one system. We also postulate that in every system the leeway is at least a couple of ten-thousandths of an octave. Thus we reach (at Figure 1h) our next construction: “ideal systems”. Each ideal system has a set of non-overlapping neighborhoods (and is thus finite) and a subset of one of our groups. This subset, which we call an “embedded halfgroup”, is an unusual, indeed novel, algebraic structure: it is associative (when the sums are defined) and has an identity element and inverses, but is not closed with regard to group multiplication (compounds of the operation). The place of halfgroups vis a vis semigroups, quasigroups etc. in halfalgebra is indicated in GIF 2.(2)
[7] We wonder if in some cases the size of the neighborhood might guarantee a set of pitch classes small enough to be musically useful. Music is not only an art of sonorities but also (among other things) a cognitive game, and most composers wish to “juggle” with a set of pitch classes that is big enough to enable them to sustain an interesting 5-, 10- or 20-minute-long game of this kind—for which only three or four pitch classes would be insufficient—but not so big that the listener cannot grasp the cognitive game intuitively—for which, say, 40 pitch classes would be too many. One needs an intermediate number, something like 7, 8, 10, 12, 15 or 20. Gregorian chant normally has 7 or 8; Giovanni Gabrieli and Schutz had 14; some other well-known Renaissance composers (Costeley, Bull) composed music for 19 pitch classes; Bach, Debussy and the Beatles had 12. In non-Western music, the sizes of the sets are comparable. Now we have noticed that in outdoor genres—for instance, marching-band music—the intonation is not very exact (that is, the neighborhoods for the notes are quite wide) and the number of pitch classes in a phrase is normally closer to 7 than to 12. Is there a cause-and-effect relation here, in that such bands are usually unable to project chromatic harmony because their intonation is so inexact? The question has not been investigated (as the concept of pitch-class-leeways is new); we raise it in order to show that just where we come to our unusual algebraic structure (the halfgroup) we find a music-theory question which calls for empirical treatment—namely, the possible relation between (a) the limiting of the set which is due to the pitch- class leeways and (b) the limiting which one would want in any case for the sake of a cognitively viable juggling of the pitch classes.
[8] It was by means of a natural mapping that we went over from notes and musical intervals to pitch classes and pitch-class relations; so now we return by reversing the natural mapping and thereby pulling back the system to an “unbounded” scale (repeating itself indefinitely, octave after octave) from which limited scales, each with a highest and a lowest note, can readily be derived (Figure 1i–j). One could then go farther, to scales in which certain pitch classes are omitted in certain octaves, or to scales in which every interval has a little something extra added to it (and thus the frequency-ratio for the octave, for instance, is a little bigger than 2:1, as on the piano) and so on. We prefer, however, to concentrate our attention on systems.
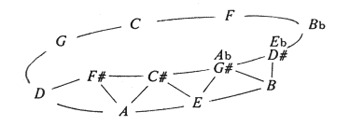
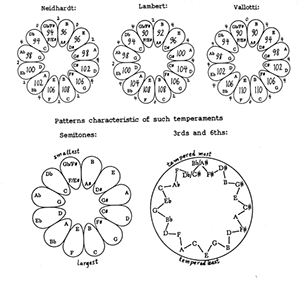
[9] Most systems of Western music have had harmonic generators. There is a series of such generators, which—so experience teaches us—can be derived mathematically from the following series of primes: 2, 3, 5, 7. Our adaptation of the traditional Roman numerals of music theory for these generators is shown in Figure 4. With the first generator alone (which we write with the Roman numeral “I”), one can make a kind of minimal music in which all the notes belong to the same pitch class; with the first two generators (I and V), one obtains the most familiar kind of Medieval harmony, in which the 5ths (and their compounds and inversions), but not any 3rds, are used as consonant intervals; with the first three generators (I, V and III) one obtains the triadic harmony of the Renaissance; and with all four (I, V, III and VII), one has certain aspects of later harmony.
[10] The extra “smaller flogs” (positive or negative) referred to in Figure 4 are used to obtain one or more equations between the generators, and thereby more pitch-class relations with a pitch-class set of a given size. These small amounts, which we designate with the letter “t”, are necessary for this, because no multiple of the flog of one prime number can be equal to another such flog. (It is well known that no power of one prime number can have another prime as a factor.) The use of such small extra amounts is traditionally called “tempering”, and in practice, temperaments—systems with tempered consonances—have been normal since the Renaissance.
Figure 5. A rough classification of orders of intervallic magnitude
(click to enlarge)
GIF 3. Reckoning the size of a chromatic semitone
(click to enlarge)
[11] How small should these small amounts be? To answer this question we have to classify empirically certain intervallic magnitudes, or rather, certain ranges of magnitude. Some amounts that are too small to be used for melodic intervals between notes (or for pitch-class relations) are nonetheless big enough—in the form of deviations from, say, log 3 or log 5—to disturb a generating harmonic pitch-class relation by making the resulting intervals sound out of tune. A rough classification is shown in Figure 5. This is only a first approximation; empirically there is no particular validity in a tenfold relation between the different ranges. For example, while the semitones in equal temperament are each 1/12 octave, a semitone between an untempered major 3rd (i.e. where t^III^ = 0) and an untempered minor 3rd would be only some 6% of an octave (this is reckoned in GIF 3), so it would be better to say that the range of magnitudes for melodic steps is “20ths” rather than “10ths” of an octave. Also, an amount which would very likely render a 5th sour can in certain cases serve for the tempering of a major 3rd. (Such is the case in equal temperament, where the major 3rds are tempered by a little more than 1% of an octave; whereas a 5th tempered by such an amount would be melodically and harmonically too ugly to use in many kinds of music.) Thus the concept of ranges or orders of intervallic magnitude needs to be refined empirically by means of psycho- acoustical probings and a reading of the old music treatises (which often discuss temperaments). In general, however, tempering is taken to mean the dividing up of such inconvenient magnitudes as are labeled “out-of- tune-ness” in Figure 5 into smaller, less noxious amounts to be distributed amongst a suitable chain of generating pitch-class relations.
Figure 6. A table showing how to find the most feasible equations nV = III
(click to enlarge)
Figure 7. Branches in our system-tree
(click to enlarge)
[12] In order to find the most feasible possibilities for tempering “two- dimensional” systems (systems with V and III as generators, but not VII), we ask the following question: If one multiplies flog 3 by 1, -1, 2, -2, 3, -3 and so on, then which are the multiples that approach successively closer to flog 5 or its inversion? In the last (full) column of Figure 6 we see the smallest flogs by which it is possible to temper V and III at once by distributing the various such differences evenly amongst the group of generators.(3) The first two such flogs—T^1^ and T^2^—are too big (they would mar the pitch-class relations); T^3^ is good; T^4^ is nearly insignificant, hence very good; to make use of T^5^ would involve more than 45 pitch classes—too many for traditional composition. Thus the equations at the far right in Figure 6 represent the most likely possibilities. They are the most feasible equations between harmonic generators for a two-dimensional system.
[13] Now we are ready to discuss our system tree (see Figure 7). We include those possibilities that have been significant in the history of Western composition and theory. There are harmonic and equal-division systems, according to the type of generator. Among harmonic systems we have those of one, two or three dimensions, according to the number of generators (apart from the identity element). Also among harmonic systems, we distinguish between coherent sytems (in which all the pitch classes make one chain of 5ths) and non-coherent systems—which have proven musically so awkward that no well-known composer has ever written music for such a system, even though many theorists since the 16th century have described non-coherent, two-dimensional systems without any tempered intervals. (Mostly they were theorists who did not understand the problem to which tempering is the solution.)
[14] Among coherent systems, we have temperaments and (one-dimensional) untempered systems. Then we have regular temperaments (in which each kind of consonant interval is of uniform size), semi-regular temperaments (discussed below), and irregular temperaments, in which some 5ths are tempered a little more than others and hence the 3rds etc. also vary. Certain irregular temperaments have been quite important historically.
[15] Among regular, two-dimensional temperaments, there are two main types (as we have seen in connection with Figure 6); and when both of their defining equations (4V = III; -8V = III) are true for the same system, then we have an intersection of the two types, which is so important historically that it has its own name, “equal temperament”; and this name can refer as well to an equivalent one-dimensional type (i.e. with a “circle” of twelve 5ths but no consonant 3rds) which may conceivably have played a role in the history of lute music in the 15th century, and also to a three-dimensional type which practically everyone would agree is to be found in the music of, say, Villa-Lobos (and which we believe is to be found in some earlier music as well: think of how Wagner will resolve an appoggiatura to a 7th-chord from which the harmony is then just as free to move as it would be, in 17th-century harmony, from a triad).
Figure 8. Diagram of a meantone system with 14 pitch classes
(click to enlarge)
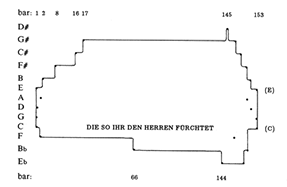
GIF 4. Schütz, “Die so ihr den Herren fürchtet” (SWV 164)
(click to enlarge and see the rest)
[16] Apart from equal temperament, there is a spectrum of musically good
possibilities for each of the two types MT and QP (see Figure 7h). Meantone
temperaments were very important for Renaissance and early Baroque music.
They usually put at the composer’s disposition two or three flats and
three or four sharps: if three flats and four sharps, then in all the 14
pitch classes (7 chromatic and 7 diatonic) mentioned above in connection
with Gabrieli and Schutz. (See Figure 8. It is well known that some keyboard
instruments had 14 keys per octave, i.e. with “split keys” for
GIF 5. A 15th-century quasi-Pythagorean system and some evidence of its use: music in which triads with an explicit sharp are especially salient
(click to enlarge and see the rest)
[17] A quasi-Pythagorean temperament with twelve pitch classes was of
some importance in the first half of the 15th century. The 5ths were
either untempered or else so little tempered that no one at all was
aware of it. The five chromatic pitch classes were linked to
[18] For some of the regular temperaments in our system tree, there is an equivalent equal-division system—that is, physically the same though differently conceived (see Figure 7i–j). In a harmonic system there exists consonance (since the harmonic generators are the most consonant pitch-class relations) and hence nearly always also its counterpart, dissonance; and there is an important distinction between diatonic semitones (between two notes with different letter-names) and chromatic semitones (between two notes with the same letter-name). In an equal- division system there is no consonance, and therefore no dissonance. If the generator is 1/12-octave and if all twelve of the ensuing pitch classes are in the system, then one composes “mit zwoelf nur auf einander bezogenen Toenen” (in Arnold Schoenberg’s words) and there is no distinction between diatonic and chromatic semitones: they are all qualitatively as well as quantitatively alike. This aspect of Schoenberg’s dodecaphonic music is just as important as his atonality (the fact that each movement or piece is not somehow centered on one privileged pitch class), which is often said to be its most basic technical characteristic.
GIF 6. Lewin’s analysis of a passage from Parsifal
(click to enlarge)
Figure 9. Some formulas distinguishing F1 and F2
(click to enlarge)
GIF 7. A diagram made by Isaac Newton
(click to enlarge)
Figure 10. The V and III relations in Newton’s system
(click to enlarge)
GIF 8. Some 18th-century irregular temperaments
(click to enlarge)
GIF 9. Louis Couperin, Pavane in F#-minor, first section
(click to enlarge)
[19] With such a perspective on how various systems have affected the art
of composition, one can appreciate better the technical significance of
enharmonic modulations in Romantic music. In most enharmonic modulations
a given semitone is used first as a chromatic semitone and then as a
diatonic one, or vice versa. More and more in the course of the 19th
century, the significance of enharmonic modulations lay not so much in
their momentary effect as in the way they enabled composers to exploit
the same physical scale in terms of two systems at once: harmonic and
equal-division. Thus David Lewin’s analytical sketch (reproduced in
GIF 6) of a well-known phrase in the prelude to Wagner’s Parsifal(8)
includes not only Roman numerals for a traditional harmonic analysis, but
also Arabic numerals to show how 3 + 3 + 1 = 7 semitones (adumbrating the
salient “Zauber-motif” in Parsifal) lead from
[20] It is possible to distinguish certain “families” of equal-division
systems (see Figure 7j) equivalent to the various kinds of temperaments.
Figure 9 includes formulas (derived in one of the appendices of our book)
for their generators. GIF 7 reproduces a diagram by Isaac Newton(9)
showing how an equal-division system with 1/53-octave as generator and
with 15 pitch classes is equivalent to the harmonic system represented
in Figure 10. The diatonic semitones, labeled “mi-fa” in GIF 7, amount to
5/53-octave; the chromatic semitones amount to 4/53. Newton’s harmonic
system is not coherent, but if he had provided for an additional pitch
class at “4” in the diagram, it would have made at once a good
[21] Among the irregular temperaments, the most important historically
were those used in the late 17th and 18th centuries. For most composers
of that time, the various keys had much more individual character than
they do today, and many contemporary music theorists said that it was
due to the irregular temperaments of the day. An irregular temperament
based on a circle of twelve Vs can be described as a variant of equal
temperament, so in GIF 8 the sizes of each semitone in three such 18th-
century schemes (by J. G. Neidhardt, J. H. Lambert and Vallotti) are
described as some percent of 1/12-octave. The numbers at the outer
edges of those diagrams show the differences between semitones that
are adjacent in the circle of 5ths (in the sense that E-F and
[22] On the silent screen we cannot demonstrate the acoustical
differences amongst the different keys in such a system. But we can
describe how, in the first section of Louis Couperin’s famous
[23] In early 15th-century music such as represented in GIF 6, the
distinctly euphonious quality of a 3rd or 6th with a sharp in the quasi-
Pythagorean temperament is sometimes especially salient because it occurs
right after (or right before) a prominent harmonic 3rd or 6th that is
tempered by an entire comma (that is, by nearly as much as
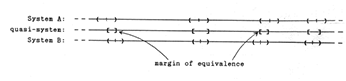
GIF 10. The “margin of equivalence” between two physically different systems with the same number of pitch classes (in this case, four)
(click to enlarge)
[24] To measure the difference between any two systems that are physically almost but not quite the same, we have devised a “margin of equivalence”, and with it the concept of “quasi-systems” which have no generators (and thus no subset of a group of pitch-class relations) but only a set of pitch classes, whose neighborhoods are, however, unequal. To put it very briefly: if two systems have the same number of pitch classes, then the margin of equivalence is the smallest overlap—i.e. where the notes differ most when the two systems are aligned as well as possible (as illustrated in GIF 10).
[25] We hope that our book in which these and some related ideas are
elaborated upon(12) will prove of value to music theory and to the study
of music history. Renaissance and Baroque theorists took only some
limited steps away from Medieval models of scales (by accepting ratios
involving 5 and 7 as prime factors, and then by accepting irrational
ratios), and even today many music theorists more or less vaguely favor
the ancient Pythagorean idea that “Music is sonorous number.” Here our
algebraic approach could be of value, not only with regard to irregular
temperaments (where the pitch-class relations have to be represented as
functions of the pitch classes and not as numbers in their own right),
but also for the designing of experiments to investigate the various
musical and psycho-acoustical phenomena that give rise to pitch-frequency
leeways for the notes. (Instead of a general leeway u, one could
distinguish u^1^, u^2^, u^3^
Mark Lindley
P.O. Box 1125
Cambridge MA 02238–1125
USA
Ronald Turner-Smith
19 Risingholme Road
Harrow, Middx HA3 7EP
England
Footnotes
1. Max Weber, Die rationalen und soziologischen Grundlagen der Musik,
ed. Theodor Kroyer (Munich 1921). (The English translation published in
1958 is, alas, so inadequate that it quite misrepresents Weber’s
thinking.)
Return to text
2. All the terms in GIF 2 except “halfgroup” are defined in Richard
Herbert Bruck, A Survey of Binary Systems (Springer, Hamburg 1958).
On the basis of our cordial correspondence with Eytan Agmon we think
that a 12-oriented theory of diatonicism (as described in his “A
mathematical model of the diatonic system” in Journal of Music Theory,
33:1) can be improved upon, insofar as validity in regard to certain music
is concerned (e.g. Gregorian chant), by an acceptance of the concept of
halfgroups as applicable to music.
Return to text
3. When we go from one n to the next we get a rather lower T^n^ because
s^n^ is smaller while at the same time m^n^ is bigger. (However, since
each T is an average of some t^V^s and a t^III^; one of those t’s may be
less than T if the other is more.) Some intermediate multiple might
yield a slightly lower average t (if the quasi-s is not as much bigger
as the multiple is smaller), but it is reasonable, once the multiple
becomes bigger than, say, 15 or 20, to demand a distinctly lower average
t in return for involving more pitch classes.
Return to text
4. GIF 4a shows a diagram from page 144 of our book and GIFs 4b, 4c,
and 4d show some relevant excerpts from the piece to which the diagram
refers, “Die so ihr den Herren fuerchtet” (SWV 364). Twenty diagrams of
this kind (with relevant musical examples) are included in Lindley,
“Heinrich Schutz: intonazione della scala e struttura tonale” (with a
long abstract in English), in Recercare, vol. i (1990).
Return to text
5. Lindley, “Pythagorean Intonation and the Rise of the Triad”, Royal
Musical Association Research Chronicle 16 (1980).
Return to text
6. The diagram is on page 55 of our book.
Return to text
7. These examples (GIFs 5b–5g) show the conclusions of sections from
the following pieces: Landini, “O fanciula giulia;” Matteo da Perugia,
“A qui fortune” and “Le grant desir;” a Kyrie for organ from the Faenza
Codex; Dufay, “Mon chier amy;” and a prelude from the Buxheim Organ
Book (no. 242).
Return to text
8. David Lewin, Generalized Musical Intervals and Transformations
(Yale, 1987), p. 161. The 3 + 3 + 1 diagram ends with a high
Return to text
9. GB-Cu add. 4000, fol. 105v. (Reproduced on page 57 of our book.)
Return to text
10. Helmholtz for his “Harmonium mit natuerlicher Stimmung” used a system
of this latter kind with 24 pitch classes. See Hermann von Helmholtz,
On the Sensations of Tone, tr. Alexander J. Ellis, 2nd ed. (London,
1885), 316–19, or for a more succinct account, the entry on “Just
intonation” in The New Grove Dictionary of Musical Instruments.
Return to text
11. It may be worth repeating that this is a French style. According to
Bach’s concept of the chromatic scale, which is reflected in what we know
about his tuning (Lindley, “Bach’s Harpsichord Tuning”, The Musical
Times, vol. 126, December) as well as his music, harmony in “extreme”
keys is less constrained.
Return to text
12. Mathematical Models of Musical Scales (Verlag fur Systematische
Musikwissenschaft, Postfach 9026, DW-5300 Bonn, Germany).
Return to text
Copyright Statement
Copyright © 1993 by the Society for Music Theory. All rights reserved.
[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.
[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:
This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.
[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.
This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.
Prepared by Natalie Boisvert, Cynthia Gonzales, Rebecca Flore and Cara Stroud, Editorial Assistants