Conventional Harmonic Wisdom and the Scope of Schenkerian Theory: A Reply to John Rothgeb

I

[1] In “Functional Harmony Revisited: A Prototype- Theoretic Approach” (henceforth, FHR), I have proposed a modified version of Hugo Riemann’s functional harmonic theory.⁽¹⁾ John Rothgeb, in a recent MTO contribution, objects to the (modified) theory on two main counts. First, given an approach to tonal pitch-structure (such as Heinrich Schenker’s) that emphasizes context in general and voice leading in particular, (modified) functionalism is superfluous or trivial at best, if not downright pernicious; second, the theory leads to a deplorable intellectual regression, since it negates such remarkable theoretical achievements as Schenker’s notions of “scale-step” (Stufe) and “composing-out” (Auskomponierung).⁽²⁾

[2] I shall begin the present essay by responding to Rothgeb’s objections; neither, I hope to demonstrate, stands up under scrutiny. However, I believe that Rothgeb is nonetheless correct in sensing that a serious conflict indeed exists between “conventional [harmonic] wisdom,” of which functionalism is apparently an important ingredient, and certain tenets of Schenker’s theory.⁽³⁾ In the second part of this essay, therefore, I shall attempt to isolate the source of this conflict; I shall conclude the essay by considering the conflict’s implications as far as the scope of Schenkerian theory is concerned.⁽⁴⁾

[3] Rothgeb purports to establish the superfluousness of functional theory, vis a vis an approach that emphasizes context and voice leading, by analyzing the concluding bars of Schumann’s “Am Kamin” from Kinderszenen (see Example 1); he concentrates in particular on the “vertical event” marked “X.” For present purposes, Rothgeb’s argument may be reduced to three essential claims: “strong horizontalism,” “weak horizontalism,” and “contextualism.”

[4] Strong horizontalism. According to strong horizontalism, X is a more-or-less accidental result of linear motion; in particular, the note a “ . . . serves as . . . an escape tone or an incomplete upper neighbor, . . . [or better yet] an anticipation of the third of the coming tonic harmony” (paragraph 6). It follows that “the note a in no sense functions as a harmonic root here. The chord under discussion is not an inversion of an a-minor triad” (paragraph 8).

[5] For all that Schenker would have us believe that linear motion in tonal music—apparently by some divine miracle—tends to yield precisely triads and seventh chords as vertical sonorities, strong horizontalism is a patently absurd position. In Example 2 Schumann’s X is replaced by an impostor vertical event *X (Schumann’s concluding tonic is also slightly altered in the example: it now features ³ in the soprano rather than ¹). In voice-leading terms, X and *X are exactly analogous (the f in *X is also an escape tone or anticipation of the coming tonic harmony); yet *X is plainly unacceptable.

[6] In view of Example 2 one might concede that X is not totally unconstrained as a vertical event (although it nonetheless falls short of being a triad); X, one might propose, is consonant. However, Example 3a, where Schumann’s cadence is transposed to minor, exposes the uselessness of such a move. The relationship between X’ and *X’ in Examples 3a and 3b is exactly analogous to the relationship between X and *X in Examples 1 and 2, even though X’ is dissonant. Moreover, when it comes to seventh chords, the consonance criterion must in any event be abandoned. In paragraph 8 Rothgeb explains “the origin of Schumann’s II as a result of extending the bass of IV and letting the treble anticipate the fifth of the coming V.” Would Rothgeb be willing to accept on equal terms a IV chord that similarly anticipates the third of the coming V?

[7] Once one concedes that X is a triad (rather than some accidental collection of pitches), one must also concede that X is an a-minor triad in first inversion, that is, a III6 chord. To be sure, the function of X is not specified by the III6 label; the purpose of (modified) functionalism is precisely to fill-in this theoretical void. According to (modified) functionalism, X “has dominant function”; X, in other words, is a member of a set of triads—a category—whose prototype is V. The relationship between X and V, moreover, is one of maximal similarity, that is, the two triads have two tones in common.

[8] As it happens, Rothgeb also sees a relationship between X and a hypothetical V: “people who hear musically will have a strong predilection to hear this final [falling] fifth [in the bass] as representing V–I even though its penultimate member does not bear the 5/3 sonority which alone would provide full congruence between scale-degree meaning and vertical chord” (paragraph 8). Indeed, given this statement (together with Rothgeb’s earlier concession that I, IV, and V “are indeed primary in some meaningful sense”), one begins to wonder what the dispute is all about. Nonetheless, from his discussion of the IV/II relationship (see especially paragraph 8, as well as paragraph 16 and n. 14), one suspects that Rothgeb would object to seeing the V/III relationship in terms of common tones; rather, for Rothgeb the V/III relationship is once again a matter of voice leading.

[9] Weak horizontalism. Weak horizontalism concedes that X is a triad (thus X is a III⁶ chord—no “shudder-quotes” required); moreover, weak horizontalism sees an essential relationship between X and a hypothetical V chord. However, unlike functionalism, that sees the V/III relationship in terms of common tones, weak horizontalism prefers to see a 5–6 linear exchange (Example 4).

[10] Unlike strong horizontalism, weak horizontalism is by no means an absurd position. Indeed, it appears that no convincing counter-argument to weak horizontalism existed prior to my 1991 paper entitled “Linear Transformations Between Cyclically Generated Chords,” where it was pointed out that our ability to describe chordal relationships in tonal music both “harmonically” and “linearly”—as in Example 4—cannot be taken for granted.⁽⁵⁾ For example, within a 7-note cyclic set the triad and seventh chord are the only generated chords that form linear connections in any pairwise combination (that is, any triad or seventh chord can connect linearly to any other triad or seventh chord), assuming that the linear connections satisfy a certain “efficiency” constraint. The essential idea involved is illustrated (for triads only) in Example 5. The article mentioned proceeds to propose definitions for “triad” and “seventh chord” based on this linear criterion.

[11] Once “triad” and “seventh chord” are defined on the basis of voice-leading considerations, the pernicious harmony/voice-leading dichotomy loses much of its force. In particular, to say that III is related to V by virtue of two common tones, and to say that III⁶ is related to V by virtue of a 5–6 linear exchange, is to make two logically equivalent statements.⁽⁶⁾ All the same, to base a functional harmonic theory on voice leading would be a poor choice indeed. In a “deceptive cadence” V–VI, for example, it makes little sense to say that the VI is related to a hypothetical I by virtue of a 5–6 linear exchange; yet in terms of common tones, the case is exactly analogous to the V/III relationship initially discussed. In other words, the common-tone relationship between a “secondary” triad and a “primary” one is theoretically more general than the (logically equivalent) voice-leading relationship, which seems to play a more restricted, context-related role.

[12] Contextualism. One may agree that X is a III⁶ chord with a strong “aura” of V, yet nonetheless disagree with functionalism concerning a necessary, a-priori relationship between the two chords. The V/III relationship, one may argue, is purely contextual, and can be replaced by any “X/Y” relationship whatsoever.

[13] The doctrine of contextualism is with us at least since 1934, when Oswald Jonas has stated that functionalism “had to fail, because it neglected the fact that two occurrences of the same chord could be worlds apart in meaning, and that everything depended on context.”⁽⁷⁾ Rothgeb echoes the idea in paragraph 9 of his commentary:

When I say that in this case [i.e., Schumann’s “Am Kamin”] “III” means V, the word means may be explicated as “constitutes, or is included within, a harmonic expression of.” “III” may equally mean I; “II” may mean IV; indeed, instances of “X” meaning Y are legion in the repertoire of tonal music, and virtually no a-priori limits can be set on the ranges of “X” and “Y”.⁽⁸⁾

[14] Although Rothgeb concedes in a footnote that “certain limits would probably stand up under scrutiny,” his statement is surely a gross misrepresentation of musical reality. Can “III” mean IV? Can “II” mean I? Can “IV” mean V? In fact, the examples of “X meaning Y” that Rothgeb cites are exactly those which functional theory allows.

[15] Since Rothgeb proceeds in the next paragraph to consider Schenker’s notion of “scale-step,” I suspect that when he speaks of no a-priori constraints on “X meaning Y” he has in mind hierarchical subordination rather than functional significance. In Schenker’s theory, III (for example) may participate in prolonging IV, as IV may participate in prolonging V. And indeed, when it comes to hierarchy, functionalism seems to suffer badly in comparison to Schenker’s theory, which introduced the profound idea of structural levels (recursive embedding) to tonal theory. However, in FHR I have claimed that (modified) functionalism “is compatible with a hierarchical approach” (page 203); I should now like to make good this claim.

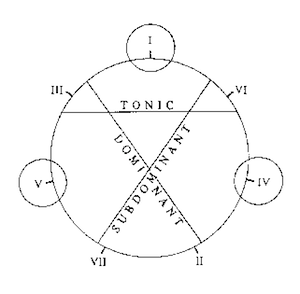
[16] Functional Auskomponierung.⁽⁹⁾ Figure 1a reproduces Figure 2c from FHR. Note that the figure is drawn from the vantage point of the tonic triad, whose referential status is assumed a priori. This means that Figure 1a would generate—in conjunction with a theory of chord progression—functionally interpreted progressions that prolong I (e.g., I–IV–V–I), and only I; thus Figure 1a may be termed a I-Stufe functional diagram.

[17] Figure 1a may be analyzed in terms of two independent components: a circle of third-related triads, and a “functional grid” by which the seven triads are divided into three categories, and where, for each category, a specific triad is selected as prototype. Suppose now that one rotates the circle of triads in Figure 1a—but not the underlying functional grid!—in such a way that V occupies the former position of I (Figure 1b); we now have a V-Stufe functional diagram. In conjunction with the same theory of chord progression, Figure 1b generates functionally interpreted progressions that prolong V, e.g. V–I–V (T–S–T), V–IV–V (T–D–T), V–II–V (T–D–T), etc. In a similar fashion, any of the seven harmonic degrees may assume a Stufe role. To create a functional hierarchy one begins by generating a I-Stufe progression (say, I–II–V–I) at the highest level. One then selects any harmonic degree from this progression—say, II—as a lower-level Stufe, and (using the appropriate functional diagram) generates a hierarchically subordinate, functionally interpreted progression (say, II–I–II); in a recursive fashion, one may create functionally interpreted progressions embedded to any arbitrary hierarchical depth.

[18] Example 6 illustrates a typical progression generated by the theory of functional Auskomponierung. Carl Schachter, who invented the progression, views the II and V chords in measures 2–3 as prolonged or composed-out (Auskomponiert) entities.⁽¹⁰⁾ It is important to realize that even though voice leading plays a crucial role in the Auskomponierung process (note the voice exchanges), other factors (such as rhythm and meter) are equally involved. In FHR I have drawn a clear distinction between the functional potential of a given triad, which is given a priori, and the realization of that potential, which is context-dependent (page 206). For example, the potential of I to assume dominant function in a II-Stufe progression (such as II–I–II) is given a-priori in (modified) functional theory; to bring this potential into musical fruition, however, may require a coordination among several compositional variables, as Example 6 illustrates. Schenker has made a lasting contribution to tonal theory in emphasizing the crucial contextual role of voice leading. However, Schenker also believed that voice leading can be promoted above and beyond any other principle as the basis for a theory of tonal structure; this latter belief is the source of some serious conflicts with the type of “conventional harmonic wisdom” that (modified) functionalism represents.

II

[19] In the preceding section I have presented arguments which I believe set to rest Rothgeb’s objections to (modified) functionalism. In particular, strong horizontalism, weak horizontalism, and contextualism have been shown to be either plainly unacceptable or irrelevant doctrines, which leaves Rothgeb’s claims concerning the superfluousness of (modified) functionalism without support. Moreover, the idea of functional Auskomponierung renders Rothgeb’s complaint concerning the intellectual poverty of functionalism (relative to Schenker’s theory) no longer valid. Indeed, (modified) functionalism agrees with the Schenkerian approach on two important points: (1) tonal pitch structure is hierarchical in nature; (2) voice leading plays a crucial role in rendering the assumed hierarchy cognitively accessible. Nonetheless, it would be wrong to pretend that a serious conflict between the two theories does not exist. In the present section I should like to isolate the source of this conflict.

[20] For Schenker, all tonal structure is ultimately referable to the Ursatz a theoretic construct whose rationale is essentially linear-contrapuntal: a dissonant passing-tone in the top voice is rendered consonant by means of a bass-arpeggiation. How does the Ursatz conflict with conventional harmonic wisdom? One conflict is immediately apparent. As far as the Ursatz is concerned, there are only two basic harmonic states, “tonic” and “dominant”; a third harmonic state (say, “subdominant”) does not exist, or if it does, its status within the tonal hierarchy is, by definition, inferior.

[21] Even in terms of Schenker’s own theory, the idea that IV or II6 represent some sort of “leaping passing-tone” configuration in the bass surely leaves much to be desired. Moreover, Schenker’s account forces an uncomfortable analogy between the functions of IV and II⁶, on the one hand, and III (and even I⁶), on the other. However, I believe that Schenker’s cavalier attitude towards the subdominant is problematic at a more basic, intuitive level. For while the subdominant may be the only component of a T–S–D–T progression whose removal does not violate a certain sense of progressional syntax, by conventional harmonic wisdom the difference between T–D–T and T–S–D–T is nonetheless crucial. Perhaps a linguistic analogy could help clarify this point. Consider the phrase “He ate his heart out.” Although the deletion of “his heart out” yields a syntactically acceptable expression, something essential is surely lost in “reducing” “He ate his heart out” to “He ate.” I have often heard the complaint that a musical phrase is robbed of its essence once the “structural subdominant” is removed; I believe such a complaint—even when it comes from an undergraduate student—deserves to be treated with respect.

[22] Schenker’s Ursatz is at odds with conventional harmonic wisdom not only concerning the status of the subdominant; an even more severe conflict, I believe, concerns the dominant. By conventional harmonic wisdom, I–V⁷–I is one of the least contextually constrained progressions; the progression retains its functional sense as T–D–T in countless possible realizations, which may vary considerably in terms of voice leading, bass progression, or registration. In Schenker’s Ursatz, on the other hand, I–V–I is conceived in terms of severe a-priori contextual constraints. Note, for example, that even such a simple deviation from the Ursatz-model where the bass, rather than leaping up a fifth from I to V, leaps down a fourth, is something to be accounted for. This hopeless “contextualization of the dominant” (together with the “a-priorization of voice leading”) ultimately leads to the utterly absurd position where I–V⁶–I (say) is seen as more closely related to (say) I–V–I than to I–V–I.

III

[23] Lest I should be once again accused of inciting intellectual regress, let me hasten to point out that my critique of Schenker’s Ursatz applies only in so far as the construct is claimed to constitute a theory of tonality, a theory by which conventional harmonic wisdom is condescendingly dismissed. I have no objection whatsoever to a more limited interpretation of what the Ursatz stands for, for example, that the Ursatz (or some Ursatz-like configuration) is an analytic construct, hypothesized to describe the structure of some specific piece of music (or possibly a group of pieces); as such, the Ursatz may be seen as a contextualized harmonic progression, situated at some (possibly deep) level of compositional structure. Indeed, as a contextualized I–V–I progression Schenker’s Ursatz makes much compositional sense, for it lends the progression, from the linear point of view, a clear sense of purpose and direction.

[24] I am well aware that for some readers, giving up Schenker’s grand vision of tonality as an unfolding in time of the Chord of Nature may seem an exceedingly dear price to pay. But I also believe that for many others, who—like myself—deeply cherish the analytic insights that Schenker’s approach has to offer, and yet are unable to turn their backs on conventional harmonic wisdom, there is simply no other choice. As someone whose involvement with the Schenkerian approach over the years has been more than casual, I know how difficult it can be to admit that Schenker delivers less than he promises. Nonetheless, I believe it is essential that the scope of Schenkerian theory be seriously reassessed. For if, as Rothgeb would have us believe, there is simply no way in which the ideas of Heinrich Schenker and Hugo Riemann may be reconciled, tonal theory is a very small town indeed.

Eytan Agmon
Bar-Ilan University
Department of Musicology
52900 Ramat-Gan
Israel
agmone@ashur.cc.biu.ac.il

Footnotes

1. Music Theory Spectrum 17:2 (1995), 196–214.
Return to text

2. John Rothgeb, “Re: Eytan Agmon on Functional Theory,” Music Theory Online 2.1 (1996).
Return to text

3. The expression “conventional [harmonic] wisdom” appears in n. 12 of Rothgeb’s commentary. The condescending tone in which this expression is used recurs in Rothgeb’s reference to “the language of the completely conventional harmony textbook” in paragraph 11, and his reference to “most undergraduate students” in paragraph 14.
Return to text

4. At least two of Rothgeb’s grievances seem to reflect plain miscomprehension of my text. His discussion in paragraphs 14–15 of “II as IV” is totally beside the point in view of the category/chord distinction on which modified functionalism so crucially depends (see especially FHR, page 204). Similarly, one of Rothgeb’s central lines of attack on FHR, concerning the role of context in harmonic theory (of which more shall be said subsequently), seems oblivious of the important distinction on page 206 between the functional potential of a given chord, which the theory proposed in FHR sets out to describe, and the realization of that potential in context (which, strictly speaking, lies outside the scope of the proposed theory). To be sure, for someone who does not believe in harmonic functions in the first place, my claim that a certain functional potential (specifically, the subdominant function of VII) can hardly ever be realized, is an easy target for critique, especially since that claim is supported in part by an appeal to a hypothetical theory of chord progression. However, in terms of discrediting the theory as a whole the effect of such critique is negligible.
Return to text

5. Eytan Agmon, “Linear Transformations Between Cyclically Generated Chords,” Musikometrika 3 (1991), 15–40.
Return to text

6. See “Linear Transformations,” pages 22–3. In n. 14 Rothgeb refers to the “equivocality of the chord, in which the 6 may in principle represent either a linear element or the root of an inverted chord.”
Return to text

7. Oswald Jonas, Introduction to the Theory of Heinrich Schenker, trans. and ed. John Rothgeb (New York: Longman, 1982), 127 (emphasis added).
Return to text

8. I have added emphasis to Rothgeb’s “virtually no a-priori limits.”
Return to text

9. Only the bare outlines of the theory are sketched here; I hope to flesh-out the details in a separate study.
Return to text

10. Carl Schachter, “Analysis by Key: Another Look at Modulation,” Music Analysis 6:3 (1987), 292. In light of the present discussion, Auskomponierung may seem to apply only to functionally interpreted progressions that begin and end on the same chord (e.g., II–I–II). However, any functionally interpreted progression referable to a given scale degree may be said to prolong or compose- out that degree. For example, I–V–VI, as a I-Stufe progression, may be said to prolong I.
Return to text

Copyright Statement

Copyright © 1996 by the Society for Music Theory. All rights reserved.

[1] Copyrights for individual items published in Music Theory Online (MTO) are held by their authors. Items appearing in MTO may be saved and stored in electronic or paper form, and may be shared among individuals for purposes of scholarly research or discussion, but may not be republished in any form, electronic or print, without prior, written permission from the author(s), and advance notification of the editors of MTO.

[2] Any redistributed form of items published in MTO must include the following information in a form appropriate to the medium in which the items are to appear:

This item appeared in Music Theory Online in [VOLUME #, ISSUE #] on [DAY/MONTH/YEAR]. It was authored by [FULL NAME, EMAIL ADDRESS], with whose written permission it is reprinted here.

[3] Libraries may archive issues of MTO in electronic or paper form for public access so long as each issue is stored in its entirety, and no access fee is charged. Exceptions to these requirements must be approved in writing by the editors of MTO, who will act in accordance with the decisions of the Society for Music Theory.

This document and all portions thereof are protected by U.S. and international copyright laws. Material contained herein may be copied and/or distributed for research purposes only.